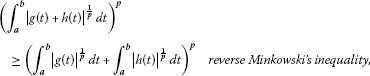Abstract
In this paper we expand Jensen’s inequality to two-variable convex functions and find the lower bound of the Hermite-Hadamard inequality for a convex function on the bounded area from the plane.
Similar content being viewed by others
1 Introduction
Let μ be a positive measure on X such that . If f is a real-valued function in , for all and φ is convex on , then
The inequality (1) is known as Jensen’s inequality [1].
In recent years, there have been many extensions, refinements and similar results of the inequality (1). Recall that the function is convex on Δ if
holds for all and . A function is called co-ordinated convex on Δ if the partial functions , and , are convex for all and . Note that every convex function is co-ordinated convex, but the converse is not generally true; see [2]. Also note that if F is a convex function on and g, h are real-valued functions such that , then may be not convex on ℝ.
In this paper under suitable conditions, we expand Jensen’s inequality to two-variable convex functions and deduce some further important inequalities. Finally, we find a lower bound for the integral
where F is convex on the convex bounded area by , and , .
2 Main results
Theorem 1 Let p be a non-negative continuous function on such that . If g and h are real-valued continuous functions on and
for all , and F is convex on
then
and
The inequalities hold in reversed order if f is concave on Δ.
Proof Denote
and
Then by L’Hospital’s rule, we have and . So, α and β are continuous on . Denote
We will show that . We have
By the convexity of F, we obtain
So, we get
Hence,
By easy calculation, we see that
Therefore,
Thus,
So,
The proof is complete. For the proof of (3), set .
Note the inequalities (2) and (3) are sharp because . □
Corollary 1 Let g and h be real-valued continuous functions. Then we have
-
(i)
for , ,
-
(ii)
for ,
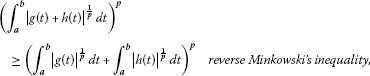
-
(iii)
for ,
(iv)
Proof (i) The function
is concave, so by the inequality (3), we have
Hence,
Now, set and . We obtain
-
(ii)
The function is convex for and is concave for . So, by the inequality (3), we have
so
Now, set and . We get
So,
The proof of (iii) is similar to that of (ii) and can be omitted. For the proof of (iv), note is convex on . Now, apply the inequality (3). □
Remark 1 By similar assumptions, we can prove Theorem 1 for an n-variable convex function F on and obtain the inequality
In particular, we can obtain a similar inequality for Holder and Minkowski inequalities. For example, by the concavity of
we can get the inequality
3 Hermite-Hadamard inequality
Let be a convex function, then the following inequality is known as the Hermite-Hadamard inequality [3] and [4]:
In [5], Dragomir established the following similar inequality (4) for convex functions on the co-ordinates on a rectangle from the plane .
Theorem 2 Suppose is a convex function on the co-ordinates on △. Then one has the inequalities
Also Dragomir investigated the Hermite-Hadamard inequality on the disk [6] and [7].
In [8], Matejíčka proved the left-hand side of the Hermite-Hadamard inequality of several variables for a convex function on certain convex compact sets. In the following theorem, we prove the left-hand side of the Hermite-Hadamard inequality in another way and as a result of Theorem 2.
Theorem 3 Let △ be a bounded area by a convex function h and a concave function g on such that for any , . Also, let F be a two-variable convex function on △. Then one has the inequality
Proof Since F is convex on △, hence f is co-ordinated convex on △. So, , is convex on for all . By the left-hand side of the Hermite-Hadamard inequality (4), we have
Integrating this inequality on , we obtain
So,
Now, let . By the inequality (2), we get
The proof is complete. □
References
Rudin W: Real and Complex Analysis. McGraw-Hill, New York; 1974.
Dragomir SS: On Hadamard’s inequality for the convex mappings defined on a ball in the space and application. Math. Inequal. Appl. 2000, 3: 177–187.
Mitrinovic DS, Lackoric JB: Hermite and convexity. Aequ. Math. 1985, 28: 229–232. 10.1007/BF02189414
Zabandan G: A new refinement of the Hermite-Hadamard inequality for convex functions. JIPAM. J. Inequal. Pure Appl. Math. 2009., 10(2): Article ID 45
Dragomir SS: On the Hadamard’s inequality for convex functions on the co-ordinates in a rectangle from the plane. Taiwan. J. Math. 2001, 5: 775–788.
Dragomir SS: On Hadamard’s inequality on a disk. J. Inequal. Pure Appl. Math. 2000., 1: Article ID 2
Dragomir, SS, Pearce, CEM: Selected Topics on Hermite-Hadamard Inequalities. RGMIA Monographs, Victoria University (2000)
Matejíčka L: Elementary proof of the left multidimensional Hermite-Hadamard inequality on certain convex sets. J. Math. Inequal. 2010, 4(2):259–270.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zabandan, G., Kılıçman, A. A new version of Jensen’s inequality and related results. J Inequal Appl 2012, 238 (2012). https://doi.org/10.1186/1029-242X-2012-238
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2012-238