Duality in nondifferentiable minimax fractional programming with B-(p, r)- invexity

Abstract

In this article, we are concerned with a nondifferentiable minimax fractional programming problem. We derive the sufficient condition for an optimal solution to the problem and then establish weak, strong, and strict converse duality theorems for the problem and its dual problem under B-(p, r)-invexity assumptions. Examples are given to show that B-(p, r)-invex functions are generalization of (p, r)-invex and convex functions

AMS Subject Classification: 90C32; 90C46; 49J35.

1 Introduction

The mathematical programming problem in which the objective function is a ratio of two numerical functions is called a fractional programming problem. Fractional programming is used in various fields of study. Most extensively, it is used in business and economic situations, mainly in the situations of deficit of financial resources. Fractional programming problems have arisen in multiobjective programming [1, 2], game theory [3], and goal programming [4]. Problems of these type have been the subject of immense interest in the past few years.

The necessary and sufficient conditions for generalized minimax programming were first developed by Schmitendorf [5]. Tanimoto [6] applied these optimality conditions to define a dual problem and derived duality theorems. Bector and Bhatia [7] relaxed the convexity assumptions in the sufficient optimality condition in [5] and also employed the optimality conditions to construct several dual models which involve pseudo-convex and quasi-convex functions, and derived weak and strong duality theorems. Yadav and Mukhrjee [8] established the optimality conditions to construct the two dual problems and derived duality theorems for differentiable fractional minimax programming. Chandra and Kumar [9] pointed out that the formulation of Yadav and Mukhrjee [8] has some omissions and inconsistencies and they constructed two modified dual problems and proved duality theorems for differentiable fractional minimax programming.

Lai et al. [10] established necessary and sufficient optimality conditions for non-differentiable minimax fractional problem with generalized convexity and applied these optimality conditions to construct a parametric dual model and also discussed duality theorems. Lai and Lee [11] obtained duality theorems for two parameter-free dual models of nondifferentiable minimax fractional problem involving generalized convexity assumptions.

Convexity plays an important role in deriving sufficient conditions and duality for nonlinear programming problems. Hanson [12] introduced the concept of invexity and established Karush-Kuhn-Tucker type sufficient optimality conditions for nonlinear programming problems. These functions were named invex by Craven [13]. Generalized invexity and duality for multiobjective programming problems are discussed in [14], and inseparable Hilbert spaces are studied by Soleimani-damaneh [15]. Soleimani-damaneh [16] provides a family of linear infinite problems or linear semi-infinite problems to characterize the optimality of nonlinear optimization problems. Recently, Antczak [17] proved optimality conditions for a class of generalized fractional minimax programming problems involving B-(p, r)-invexity functions and established duality theorems for various duality models.

In this article, we are motivated by Lai et al. [10], Lai and Lee [11], and Antczak [17] to discuss sufficient optimality conditions and duality theorems for a nondifferentiable minimax fractional programming problem with B-(p, r)-invexity. This article is organized as follows: In Section 2, we give some preliminaries. An example which is B-(1, 1)-invex but not (p, r)-invex is exemplified. We also illustrate another example which (-1, 1)-invex but convex. In Section 3, we establish the sufficient optimality conditions. Duality results are presented in Section 4.

2 Notations and prelominaries

Definition 1. Let f : X → R (where X ⊆ Rⁿ ) be differentiable function, and let p, r be arbitrary real numbers. Then f is said to be (p, r)-invex (strictly (p, r)-invex) with respect to η at u ∈ X on X if there exists a function η : X × X → Rⁿ such that, for all x ∈ X, the inequalities

$$\begin{array}{l}\frac{1}{r}{e}^{r(f(x)}\ge \frac{1}{r}{e}^{r(f(u)}\left[1+\frac{r}{p}\nabla f(u)(e^{p\eta (x\mathrm{,}u)}-1)\right](>\text{if }x\ne u)\text{for}p\ne \mathrm{0,}r\ne \mathrm{0,}\\ \frac{1}{r}{e}^{r(f(x)}\ge \frac{1}{r}{e}^{r(f(u)}\left[1+r\nabla f(u)(e^{p\eta (x\mathrm{,}u)}-1)\right](>\text{if}x\ne u)\text{for}p=\mathrm{0,}r\ne \mathrm{0,}\\ f(x)-f(u)\ge \frac{1}{p}\nabla f(u)(e^{p\eta (x\mathrm{,}u)}-1)(>\text{if }x\ne u)\text{for }p\ne \mathrm{0,}r=\mathrm{0,}\\ f(x)-f(u)\ge \nabla f(u)\eta (x\mathrm{,}u)(>\text{if }x\ne u)\text{for }p=\mathrm{0,}r=\mathrm{0,}\end{array}$$

hold.

Definition 2[17]. The differentiable function f : X → R (where X ⊆ Rⁿ ) is said to be (strictly) B-(p, r)-invex with respect to η and b at u ∈ X on X if there exists a function η : X × X → Rⁿ and a function b : X × X → R₊ such that, for all x ∈ X, the following inequalities

$$\begin{array}{c}\frac{1}{r}b\left(x,u\right)\left(e^{r\left(f\left(x\right)-f\left(u\right)\right)}-1\right)\ge \frac{1}{p}\nabla f\left(u\right)\left(e^{p\eta \left(x,u\right)}-1\right)\left(>\mathsf{\text{if }}x\ne u\right)\mathsf{\text{for }}p\ne 0,r\ne 0,\\ \frac{1}{r}b\left(x,u\right)\left(e^{r\left(f\left(x\right)-f\left(u\right)\right)}-1\right)\ge \nabla f\left(u\right)\eta \left(x,u\right)\left(>\mathsf{\text{if}}x\ne u\right)\mathsf{\text{for}}p=0,r\ne 0,\\ b\left(x,u\right)\left(f\left(x\right)-f\left(u\right)\right)\ge \frac{1}{p}\nabla f\left(u\right)\left(e^{p\eta \left(x,u\right)}-1\right)\left(>\mathsf{\text{if}}x\ne u\right)\mathsf{\text{for }}p\ne 0,r=0,\\ b\left(x,u\right)\left(f\left(x\right)-f\left(u\right)\right)\ge \nabla f\left(u\right)\eta \left(x,u\right)\left(>\mathsf{\text{if}}x\ne u\right)\mathsf{\text{for }}p=0,r=0,\end{array}$$

hold. f is said to be (strictly) B-(p, r)-invex with respect to η and b on X if it is B-(p, r)-invex with respect to same η and b at each u ∈ X on X.

Remark 1[17]. It should be pointed out that the exponentials appearing on the right-hand sides of the inequalities above are understood to be taken componentwise and 1 = (1, 1, ..., 1) ∈ Rⁿ .

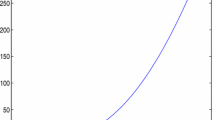
Example 1. Let X = [8.75, 9.15] ⊂ R. Consider the function f : X → R defined by

$$f\left(x\right)=log\left({sin}^{2}x\right).$$

Let η : X × X → R be given by

$$\eta \left(x,u\right)=12\left(1+u\right).$$

To prove that f is (-1, 1)-invex, we have to show that

$$\frac{1}{r}{e}^{rf\left(x\right)}-\frac{1}{r}{e}^{rf\left(u\right)}\left[1+\frac{r}{p}\nabla f\left(u\right)\left(e^{p\eta \left(x,u\right)}-1\right)\right]\ge 0,\mathsf{\text{for}}p=-1\mathsf{\text{and}}r=1.$$

Now, consider

$$\begin{array}{c}\phi =e^{f\left(x\right)}-e^{f\left(u\right)}\left[1-\nabla f\left(u\right)\left(e^{-\eta \left(x,u\right)}-1\right)\right]\\ ={sin}^{2}x+sin2u\left(e^{-12\left(1+u\right)}-1\right)-{sin}^{2}u\\ \ge 0\forall x,u\in X,\end{array}$$

as can be seen form Figure 1.

Figure 1

φ = sin²x + sin 2 u ( e^-12(1+u)- 1) - sin²u.

Hence, f is (-1, 1)-invex.

Further, for x = 8.8 and u = 9.1, we have

$$\begin{array}{c}\vartheta =f\left(x\right)-f\left(u\right)-{\left(x-u\right)}^T\nabla f\left(u\right)\\ =2log\left(\frac{sinx}{sinu}\right)-\frac{\left(x-u\right)sin2u}{{sin}^{2}u}\\ =-0.570057225<0\end{array}$$

Thus f is not convex function on X.

Example 2. Let X = [0.25, 0.45] ⊂ R. Consider the function f : X → R defined by

$$f\left(x\right)=-x^2+log\left(8\sqrt{x}\right).$$

Let η : X × X → R and b : X × X → R₊ be given by

$$\eta \left(x,u\right)=log\left(1+2u^2\right)$$

and

$$b\left(x,u\right)=4{sin}^{2}x+{sin}^{2}u,$$

respectively.

The function f defined above is B-(1, 1)-invex as

$$\begin{array}{c}\varphi =b\left(x,u\right)\left(e^{\left(f\left(x\right)-f\left(u\right)\right)}-1\right)-\nabla f\left(u\right)\left(e^{\eta \left(x,u\right)}-1\right)\\ =\left[4{sin}^{2}x+{sin}^{2}u\right]\left[e^{\left(u^2-x^2\right)}\sqrt{\frac{x}{u}}-1\right]-\left[u-4u^3\right]\\ \ge 0\forall x,u\in X,\end{array}$$

as can be seen from Figure 2.

Figure 2

$\varphi =\left[4{sin}^{2}x+{sin}^{2}u\right]\left[e^{\left(u^2-x^2\right)}\sqrt{\frac{x}{u}}-1\right]-\left[u-4u^3\right]$.

However, it is not (p, r) invex for all p, r ∈ (-10¹⁷, 10¹⁷) as

$$\begin{array}{c}\psi =\frac{1}{r}{e}^{rf\left(x\right)}-\frac{1}{r}{e}^{rf\left(u\right)}\left[1+\frac{r}{p}\nabla f\left(u\right)\left(e^{p\eta \left(x,u\right)}-1\right)\right]\\ =\frac{1}{r}{e}^{1.461296176\times r}-\frac{1}{r}{e}^{1.469291258\times r}\left[1+0.45\times \frac{r}{p}\left(e^{0.3021765186\times p}-1\right)\right]\end{array}$$

(for x = 0.4 and u = 0.42)

< 0 as can be seen from Figure 3.

Figure 3

$\psi =\frac{1}{r}{e}^{1.461296176\times r}-\frac{1}{r}{e}^{1.469291258\times r}\left[1+0.45\times \frac{r}{p}\left(e^{0.3021765186\times p}-1\right)\right]$.

Hence f is B-(1, 1)-invex but not (p, r)-invex.

In this article, we consider the following nondifferentiable minimax fractional programming problem:

(FP)

$$\begin{array}{c}\underset{x\in R^n}{min}\underset{y\in Y}{sup}\frac{l\left(x,y\right)+{\left(x^{T}Dx\right)}^{1∕2}}{m\left(x,y\right)-{\left(x^{T}Ex\right)}^{1∕2}}\\ \mathsf{\text{subject to }}g\left(x\right)\le 0,x\in X\end{array}$$

where Y is a compact subset of R^m , l(., .): Rⁿ × R^m → R, m(., .): Rⁿ × R^m → R, are C¹ functions on Rⁿ × R^m and g(.): Rⁿ → R^p is C¹ function on Rⁿ . D and E are n × n positive semidefinite matrices.

Let S = {x ∈ X : g(x) ≤ 0} denote the set of all feasible solutions of (FP).

Any point x ∈ S is called the feasible point of (FP). For each (x, y) ∈ Rⁿ × R^m , we define

$$\varphi \left(x,y\right)=\frac{l\left(x,y\right)+{\left(x^{T}Dx\right)}^{1∕2}}{m\left(x,y\right)-{\left(x^{T}Ex\right)}^{1∕2}},$$

such that for each (x, y) ∈ S × Y,

$$l\left(x,y\right)+{\left(x^{T}Dx\right)}^{1∕2}\ge 0\mathsf{\text{and }}m\left(x,y\right)-{\left(x^{T}Ex\right)}^{1∕2}>0.$$

For each x ∈ S, we define

$$H\left(x\right)=\left\{h\in H:g_h\left(x\right)=0\right\},$$

where

$$\begin{array}{c}H=\left\{1,2,\dots ,p\right\},\\ Y\left(x\right)=\left\{y\in Y:\frac{l\left(x,y\right)+{\left(x^{T}Dx\right)}^{1∕2}}{m\left(x,y\right)-{\left(x^{T}Ex\right)}^{1∕2}}=\underset{z\in Y}{sup}\frac{l\left(x,z\right)+{\left(x^{T}Dx\right)}^{1∕2}}{m\left(x,z\right)-{\left(x^{T}Ex\right)}^{1∕2}}\right\}.\\ K\left(x\right)=\left\{\left(s,t,ỹ\right)\in N\times R_{+}^s\times R^{\mathsf{\text{ms}}}:1\le s\le n+1,t=\left(t_1,t_2,\dots ,t_s\right)\in R_{+}^s\right.\end{array}$$

with $\left.\sum _{i=1}^s{t}_i=1,ỹ=\left({ȳ}_1,{ȳ}_2,\dots ,{ȳ}_s\right)\mathsf{\text{with}}{ȳ}_i\in Y\left(x\right)\left(i=1,2,\dots ,s\right)\right\}.$

Since l and m are continuously differentiable and Y is compact in R^m , it follows that for each x* ∈ S, Y (x*) ≠ ∅, and for any ${ȳ}_i\in Y\left(x^{*}\right)$, we have a positive constant

$$k_{\circ }=\varphi \left(x^{*},{ȳ}_i\right)=\frac{l\left(x^{*},{ȳ}_i\right)+{\left({x^{*}}^{T}D{x}^{*}\right)}^{1∕2}}{m\left(x^{*},{ȳ}_i\right)-{\left({x^{*}}^{T}E{x}^{*}\right)}^{1∕2}}.$$

2.1 Generalized Schwartz inequality

Let A be a positive-semidefinite matrix of order n. Then, for all, x, w ∈ Rⁿ ,

$$x^{T}Aw\le {\left(x^{T}Ax\right)}^{\frac{1}{2}}{\left(w^{T}Aw\right)}^{\frac{1}{2}}.$$

(1)

Equality holds if for some λ ≥ 0,

$$Ax=\lambda Aw.$$

Evidently, if ${\left(w^{T}Aw\right)}^{\frac{1}{2}}\le 1$, we have

$$x^{T}Aw\le {\left(x^{T}Ax\right)}^{\frac{1}{2}}.$$

If the functions l, g, and m in problem (FP) are continuously differentiable with respect to x ∈ Rⁿ , then Lai et al. [10] derived the following necessary conditions for optimality of (FP).

Theorem 1 (Necessary conditions). If x* is a solution of (FP) satisfying x*^TDx* > 0, x*^TEx* > 0, and ∇g _h (x*), h ∈ H(x*) are linearly independent, then there exist $\left(s,t^{*},ȳ\right)\in K\left(x^{*}\right)$, k_o ∈ R₊, w, v ∈ Rⁿ and ${\mu }^{*}\in R_{+}^p$ such that

$$\sum _{i=1}^s{t}_i^{*}\left\{\nabla l\left(x^{*},{ȳ}_i\right)+Dw-k_{\circ }\left(\nabla m\left(x^{*},{ȳ}_i\right)-Ev\right)\right\}+\nabla \sum _{h=1}^p{\mu }_h^{*}{g}_h\left(x^{*}\right)=0,$$

(2)

$$l\left(x^{*},{ȳ}_i\right)+{\left({x^{*}}^{T}D{x}^{*}\right)}^{\frac{1}{2}}-k_{\circ }\left(m\left(x^{*},{ȳ}_i\right)-{\left({x^{*}}^{T}E{x}^{*}\right)}^{\frac{1}{2}}\right)=0,i=1,2,\dots ,s,$$

(3)

$$\sum _{h=1}^p{\mu }_h^{*}{g}_h\left(x^{*}\right)=0,$$

(4)

$$t_i^{*}\ge 0\left(i=1,2,\dots ,s\right),\sum _{i=1}^s{t}_i^{*}=1,$$

(5)

$$\left\{\begin{array}{c}\hfill w^{T}Dw\le 1,v^{T}Ev\le 1,\hfill \\ \hfill {\left({x^{*}}^{T}D{x}^{*}\right)}^{1∕2}={x^{*}}^{T}Dw,\hfill \\ \hfill {\left({x^{*}}^{T}E{x}^{*}\right)}^{1∕2}={x^{*}}^{T}Ev.\hfill \end{array}\right.$$

(6)

Remark 2. All the theorems in this article will be proved only in the case when p ≠ 0, r ≠ 0. The proofs in the other cases are easier than in this one. It follows from the form of inequalities which are given in Definition 2. Moreover, without limiting the generality considerations, we shall assume that r > 0.

3 Sufficient conditions

Under smooth conditions, say, convexity and generalized convexity as well as differentiability, optimality conditions for these problems have been studied in the past few years. The intrinsic presence of nonsmoothness (the necessity to deal with nondifferentiable functions, sets with nonsmooth boundaries, and set-valued mappings) is one of the most characteristic features of modern variational analysis (see [18, 19]). Recently, nonsmooth optimizations have been studied by some authors [20–23]. The optimality conditions for approximate solutions in multiobjective optimization problems have been studied by Gao et al. [24] and for nondifferentiable multiobjective case by Kim et al. [25]. Now, we prove the sufficient condition for optimality of (FP) under the assumptions of B-(p, r)-invexity.

Theorem 2 (Sufficient condition). Let x* be a feasible solution of (FP) and there exist a positive integer s, 1 ≤ s ≤ n + 1, $t^{*}\in R_{+}^s$, ${ȳ}_i\in Y\left(x^{*}\right)\left(i=1,2,\dots s\right)$, k_o ∈ R₊, w, v ∈ Rⁿ and ${\mu }^{*}\in R_{+}^p$ satisfying the relations (2)-(6). Assume that

(i) $\sum _{i=1}^s{t}_i^{*}\left(l\left(.,{ȳ}_i\right)+{\left(.\right)}^{T}Dw-k_{\circ }\left(m\left(.,{ȳ}_i\right)-{\left(.\right)}^{T}Ev\right)\right)$ is B-(p, r)-invex at x* on S with respect to η and b satisfying b(x, x*) > 0 for all x ∈ S,

(ii) $\sum _{h=1}^p{\mu }_h^{*}{g}_h\left(.\right)$ is B _g -(p, r)-invex at x* on S with respect to the same function η, and with respect to the function b _g , not necessarily, equal to b.

Then x* is an optimal solution of (FP).

Proof. Suppose to the contrary that x* is not an optimal solution of (FP). Then there exists an $\bar{x}\in S$ such that

$$\underset{y\in Y}{sup}\frac{l\left(\bar{x},y\right)+{\left({\bar{x}}^{T}D\bar{x}\right)}^{1∕2}}{m\left(\bar{x},y\right)-{\left({\bar{x}}^{T}E\bar{x}\right)}^{1∕2}}<\underset{y\in Y}{sup}\frac{l\left(x^{*},y\right)+{\left({x^{*}}^{T}D{x}^{*}\right)}^{1∕2}}{m\left(x^{*},y\right)-{\left({x^{*}}^{T}E{x}^{*}\right)}^{1∕2}}.$$

We note that

$$\underset{y\in Y}{sup}\frac{l\left(x^{*},y\right)+{\left({x^{*}}^{T}D{x}^{*}\right)}^{1∕2}}{m\left(x^{*},y\right)-{\left({x^{*}}^{T}E{x}^{*}\right)}^{1∕2}}=\frac{l\left(x^{*},{ȳ}_i\right)+{\left({x^{*}}^{T}D{x}^{*}\right)}^{1∕2}}{m\left(x^{*},{ȳ}_i\right)-{\left({x^{*}}^{T}E{x}^{*}\right)}^{1∕2}}=k_{\circ },$$

for ${ȳ}_i\in Y\left(x^{*}\right)$, i = 1, 2, ..., s and

$$\frac{l\left(\bar{x},{ȳ}_i\right)+{\left({\bar{x}}^{T}D\bar{x}\right)}^{1∕2}}{m\left(\bar{x},{ȳ}_i\right)-{\left({\bar{x}}^{T}E\bar{x}\right)}^{1∕2}}\le \underset{y\in Y}{sup}\frac{l\left(\bar{x},y\right)+{\left({\bar{x}}^{T}D\bar{x}\right)}^{1∕2}}{m\left(\bar{x},y\right)-{\left({\bar{x}}^{T}E\bar{x}\right)}^{1∕2}}.$$

Thus, we have

$$\frac{l\left(\bar{x},{ȳ}_i\right)+{\left({\bar{x}}^{T}D\bar{x}\right)}^{1∕2}}{m\left(\bar{x},{ȳ}_i\right)-{\left({\bar{x}}^{T}E\bar{x}\right)}^{1∕2}}<k_{\circ },\mathsf{\text{ for}}i=1,2,...,s.$$

It follows that

$$l\left(\bar{x},{ȳ}_i\right)+{\left({\bar{x}}^{T}D\bar{x}\right)}^{1∕2}-k_{\circ }\left(m\left(\bar{x},{ȳ}_i\right)-{\left({\bar{x}}^{T}E\bar{x}\right)}^{1∕2}\right)<0,\mathsf{\text{ for}}i=1,2,...,s.$$

(7)

From (1), (3), (5), (6) and (7), we obtain

$$\begin{array}{c}\sum _{i=1}^s{t}_i^{*}\left\{l\left(\bar{x},{ȳ}_i\right)+{\bar{x}}^{T}Dw-k_{\circ }\left(m\left(\bar{x},{ȳ}_i\right)-{\bar{x}}^{T}Ev\right)\right\}\\ \le \sum _{i=1}^s{t}_i^{*}\left\{l\left(\bar{x},{ȳ}_i\right)+{\left({\bar{x}}^{T}D\bar{x}\right)}^{\frac{1}{2}}-k_{\circ }\left(m\left(\bar{x},{ȳ}_i\right)-{\left({\bar{x}}^{T}E\bar{x}\right)}^{\frac{1}{2}}\right)\right\}\\ <0=\sum _{i=1}^s{t}_i^{*}\left\{l\left(x^{*},{ȳ}_i\right)+{\left({x^{*}}^{T}D{x}^{*}\right)}^{\frac{1}{2}}-k_{\circ }\left(m\left(x^{*},{ȳ}_i\right)-{\left({x^{*}}^{T}E{x}^{*}\right)}^{\frac{1}{2}}\right)\right\}\\ =\sum _{i=1}^s{t}_i^{*}\left\{l\left(x^{*},{ȳ}_i\right)+{x^{*}}^{T}Dw-k_{\circ }\left(m\left(x^{*},{ȳ}_i\right)-{x^{*}}^{T}Ev\right)\right\}.\end{array}$$

It follows that

$$\begin{array}{c}\sum _{i=1}^s{t}_i^{*}\left\{l\left(\bar{x},{ȳ}_i\right)+{\bar{x}}^{T}Dw-k_{\circ }\left(m\left(\bar{x},{ȳ}_i\right)-{\bar{x}}^{T}Ev\right)\right\}\\ <\sum _{i=1}^s{t}_i^{*}\left\{l\left(x^{*},{ȳ}_i\right)+{x^{*}}^{T}Dw-k_{\circ }\left(m\left(x^{*},{ȳ}_i\right)-{x^{*}}^{T}Ev\right)\right\}.\end{array}$$

(8)

As $\sum _{i=1}^s{t}_i^{*}\left(l\left(.,{ȳ}_i\right)+{\left(.\right)}^{T}Dw-k_{\circ }\left(m\left(.,{ȳ}_i\right)-{\left(.\right)}^{T}Ev\right)\right)$ is B-(p, r)-invex at x* on S with respect to η and b, we have

$$\begin{array}{c}\frac{1}{r}b\left(x,x^{*}\right)\left\{e^{r\left[\sum _{i=1}^s{t}_i^{*}\left(l\left(x,{ȳ}_i\right)+x^{T}Dw-k_{\circ }\left(m\left(x,{ȳ}_i\right)-x^{T}Ev\right)\right)-\sum _{i=1}^s{t}_i^{*}\left(l\left(x^{*},{ȳ}_i\right)+x^{*T}Dw-k_{\circ }\left(m\left(x^{*},{ȳ}_i\right)-x^{*T}Ev\right)\right)\right]}-1\right\}\\ \ge \frac{1}{p}\left\{\sum _{i=1}^s{t}_i^{*}\left(\nabla l\left(x^{*},{ȳ}_i\right)+Dw-k_{\circ }\left(\nabla m\left(x^{*},{ȳ}_i\right)-Ev\right)\right)\right\}\left\{e^{p\eta \left(x,x^{*}\right)}-1\right\}\end{array}$$

holds for all x ∈ S, and so for $x=\bar{x}$. Using (8) and $b\left(\bar{x},x^{*}\right)>0$ together with the inequality above, we get

$$\frac{1}{p}\left\{\sum _{i=1}^s{t}_i^{*}\left(\nabla l\left(x^{*},{ȳ}_i\right)+Dw-k_{\circ }\left(\nabla m\left(x^{*},{ȳ}_i\right)-Ev\right)\right)\right\}\left\{e^{p\eta \left(\bar{x},x^{*}\right)}-1\right\}<0.$$

(9)

From the feasibility of $\bar{x}$ together with ${\mu }_h^{*}\ge 0$, h ∈ H, we have

$$\sum _{h=1}^p{\mu }_h^{*}{g}_h\left(\bar{x}\right)\le 0.$$

(10)

By B _g -(p, r)-invexity of $\sum _{h=1}^p{\mu }_h^{*}{g}_h\left(.\right)$ at x* on S with respect to the same function η, and with respect to the function b _g , we have

$$\frac{1}{r}{b}_g\left(\bar{x},x^{*}\right)\left\{e^{r\left[\sum _{h=1}^p{\mu }_h^{*}{g}_h\left(\bar{x}\right)-\sum _{h=1}^p{\mu }_h^{*}{g}_h\left(x^{*}\right)\right]}-1\right\}\ge \frac{1}{p}\sum _{h=1}^p\nabla {\mu }_h^{*}{g}_h\left(x^{*}\right)\left\{e^{p\eta \left(\bar{x},x^{*}\right)}-1\right\}.$$

Since b _g (x, x*) ≥ 0 for all x ∈ S then by (4) and (10), we obtain

$$\frac{1}{p}\sum _{h=1}^p\nabla {\mu }_h^{*}{g}_h\left(x^{*}\right)\left\{e^{p\eta \left(\bar{x},x^{*}\right)}-1\right\}\le 0.$$

(11)

By adding the inequalities (9) and (11), we have

$$\begin{array}{c}\frac{1}{p}\left\{\sum _{i=1}^s{t}_i^{*}\left(\nabla l\left(x^{*},{ȳ}_i\right)+Dw-k_{\circ }\left(\nabla m\left(x^{*},{ȳ}_i\right)-Ev\right)\right)+\sum _{h=1}^p\nabla {\mu }_h^{*}{g}_h\left(x^{*}\right)\right\}\\ \left\{e^{p\eta \left(\bar{x},x^{*}\right)}-1\right\}<0,\end{array}$$

which contradicts (2). Hence the result.   □

4 Duality results

In this section, we consider the following dual to (FP):

$$\begin{array}{cccc}\hfill \left(FD\right)\hfill & \hfill \underset{\left(s,t,ȳ\right)\in K\left(a\right)}{max}\hfill & \hfill \underset{\left(a,\mu ,k,v,w\right)\in H_1\left(s,t,ȳ\right)}{sup}\hfill & \hfill k\hfill \end{array},$$

where $H_1\left(s,t,ȳ\right)$ denotes the set of all $\left(a,\mu ,k,v,w\right)\in R^n\times R_{+}^p\times R_{+}\times R^n\times R^n$ satisfying

$$\sum _{i=1}^s{t}_i\left\{\nabla l\left(a,{ȳ}_i\right)+Dw-k\left(\nabla m\left(a,{ȳ}_i\right)-Ev\right)\right\}+\nabla \sum _{h=1}^p{\mu }_h{g}_h\left(a\right)=0,$$

(12)

$$\sum _{i=1}^s{t}_i\left\{l\left(a,{ȳ}_i\right)+a^{T}Dw-k\left(m\left(a,{ȳ}_i\right)-a^{T}Ev\right)\right\}\ge 0,$$

(13)

$$\sum _{h=1}^p{\mu }_h{g}_h\left(a\right)\ge 0,$$

(14)

$$\left(s,t,ȳ\right)\in K\left(a\right),$$

(15)

$$w^{T}Dw\le 1,v^{T}Ev\le 1.$$

(16)

If, for a triplet $\left(s,t,ȳ\right)\in K\left(a\right)$, the set $H_1\left(s,t,ȳ\right)=\varnothing$, then we define the supremum over it to be -∞. For convenience, we let

$${\psi }_1\left(.\right)=\sum _{i=1}^s{t}_i\left\{l\left(.,{ȳ}_i\right)+{\left(.\right)}^{T}Dw-k\left(m\left(.,{ȳ}_i\right)-{\left(.\right)}^{T}Ev\right)\right\}.$$

Let S_FD denote a set of all feasible solutions for problem (FD). Moreover, let S₁ denote

$$S_1=\left\{a\in R^n:\left(a,\mu ,k,v,w,s,t,ȳ\right)\in S_{\mathsf{\text{FD}}}\right\}.$$

Now we derive the following weak, strong, and strict converse duality theorems.

Theorem 3 (Weak duality). Let x be a feasible solution of (P) and $\left(a,\mu ,k,v,w,s,t,ȳ\right)$ be a feasible of (FD). Let

(i) $\sum _{i=1}^s{t}_i\left(l\left(.,{ȳ}_i\right)+{\left(.\right)}^{T}Dw-k\left(m\left(.,{ȳ}_i\right)-{\left(.\right)}^{T}Ev\right)\right)$ is B-(p, r)-invex at a on S ∪ S₁ with respect to η and b satisfying b(x, a) > 0,

(ii) $\sum _{h=1}^p{\mu }_h{g}_h\left(.\right)$ is B _g -(p, r)-invex at a on S ∪ S₁ with respect to the same function η and with respect to the function b _g , not necessarily, equal to b.

Then,

$$\underset{y\in Y}{sup}\frac{l\left(x,y\right)+{\left(x^{T}Dx\right)}^{1∕2}}{m\left(x,y\right)-{\left(x^{T}Ex\right)}^{1∕2}}\ge k.$$

(17)

Proof. Suppose to the contrary that

$$\underset{y\in Y}{sup}\frac{l\left(x,y\right)+{\left(x^{T}Dx\right)}^{1∕2}}{m\left(x,y\right)-{\left(x^{T}Ex\right)}^{1∕2}}<k.$$

Then, we have

$$l\left(x,{ȳ}_i\right)+{\left(x^{T}Dx\right)}^{1∕2}-k\left(m\left(x,{ȳ}_i\right)-{\left(x^{T}Ex\right)}^{1∕2}\right)<0,\mathsf{\text{for}}\mathsf{\text{all}}{ȳ}_i\in Y.$$

It follows from (5) that

$$t_i\{l(x\mathrm{,}{\overline{y}}_i)+{(x^{T}Dx)}^{1/2}-k(m(x\mathrm{,}{\overline{y}}_i)-{(x^{T}Ex)}^{1/2}\}\le \mathrm{0,}$$

(18)

with at least one strict inequality, since t = (t₁, t₂, ..., t _s ) ≠ 0.

From (1), (13), (16) and (18), we have

$$\begin{array}{c}{\psi }_1\left(x\right)=\sum _{i=1}^s{t}_i\left\{l\left(x,{ȳ}_i\right)+x^{T}Dw-k\left(m\left(x,{ȳ}_i\right)-x^{T}Ev\right)\right\}\\ \le \sum _{i=1}^s{t}_i\left\{l\left(x,{ȳ}_i\right)+{\left(x^{T}Dx\right)}^{\frac{1}{2}}-k\left(m\left(x,{ȳ}_i\right)-{\left(x^{T}Ex\right)}^{\frac{1}{2}}\right)\right\}\\ <0\le \sum _{i=1}^s{t}_i\left\{l\left(a,{ȳ}_i\right)+a^{T}Dw-k\left(m\left(a,{ȳ}_i\right)-a^{T}Ev\right)\right\}\\ ={\psi }_1\left(a\right).\end{array}$$

Hence

$${\psi }_1\left(x\right)<{\psi }_1\left(a\right).$$

(19)

Since $\sum _{i=1}^s{t}_i\left(l\left(.,{ȳ}_i\right)+{\left(.\right)}^{T}Dw-k\left(m\left(.,{ȳ}_i\right)-{\left(.\right)}^{T}Ev\right)\right)$ is B-(p, r)-invex at a on S ∪ S₁ with respect to η and b, we have

$$\begin{array}{c}\frac{1}{r}b\left(x,a\right)\left\{e^{r\left[\sum _{i=1}^s{t}_i\left(l\left(x,{ȳ}_i\right)+x^{T}Dw-k\left(m\left(x,{ȳ}_i\right)-x^{T}Ev\right)\right)-\sum _{i=1}^s{t}_i\left(l\left(a,{ȳ}_i\right)+a^{T}Dw-k\left(m\left(a,{ȳ}_i\right)-a^{T}Ev\right)\right)\right]}-1\right\}\\ \ge \frac{1}{p}\left\{\sum _{i=1}^s{t}_i\left(\nabla l\left(a,{ȳ}_i\right)+Dw-k\left(\nabla m\left(a,{ȳ}_i\right)-Ev\right)\right)\right\}\left\{e^{p\eta \left(x,a\right)}-1\right\}.\end{array}$$

From (19) and b(x, a) > 0 together with the inequality above, we get

$$\frac{1}{p}\left\{\sum _{i=1}^s{t}_i\left(\nabla l\left(a,{ȳ}_i\right)+Dw-k\left(\nabla m\left(a,{ȳ}_i\right)-Ev\right)\right)\right\}\left\{e^{p\eta \left(x,a\right)}-1\right\}<0.$$

(20)

Using the feasibility of x together with μ _h ≥ 0, h ∈ H, we obtain

$$\sum _{h=1}^p{\mu }_h{g}_h\left(x\right)\le 0.$$

(21)

From hypothesis (ii), we have

$$\frac{1}{r}{b}_g\left(x,a\right)\left\{e^{r\left[\sum _{h=1}^p{\mu }_h{g}_h\left(x\right)-\sum _{h=1}^p{\mu }_h{g}_h\left(a\right)\right]}-1\right\}\ge \frac{1}{p}\sum _{h=1}^p\nabla {\mu }_h{g}_h\left(a\right)\left\{e^{p\eta \left(x,a\right)}-1\right\}.$$

As b _g (x, a) ≥ 0 then by (14) and (21), we obtain

$$\frac{1}{p}\sum _{h=1}^p\nabla {\mu }_h{g}_h\left(a\right)\left\{e^{p\eta \left(x,a\right)}-1\right\}\le 0.$$

(22)

Thus, by (20) and (22), we obtain the inequality

$$\frac{1}{p}\left\{\sum _{i=1}^s{t}_i\left(\nabla l\left(a,{ȳ}_i\right)+Dw-k\left(\nabla m\left(a,{ȳ}_i\right)-Ev\right)\right)+\sum _{h=1}^p\nabla {\mu }_h{g}_h\left(a\right)\right\}\left\{e^{p\eta \left(x,a\right)}-1\right\}<0,$$

which contradicts (12). Hence (17) holds.   □

Theorem 4 (Strong duality). Let x* be an optimal solution of (FP) and ∇g _h (x*), h ∈ H(x*) is linearly independent. Then there exist $\left(\bar{s},\bar{t},{ȳ}^{*}\right)\in K\left(x^{*}\right)$ and $\left(x^{*},\bar{\mu },\bar{k},\bar{v},\bar{w}\right)\in H_1\left(\bar{s},\bar{t},{ȳ}^{*}\right)$ such that $\left(x^{*},\bar{\mu },\bar{k},\bar{v},\bar{w},\bar{s},\bar{t},{ȳ}^{*}\right)$ is a feasible solution of (FD). Further, if the hypotheses of weak duality theorem are satisfied for all feasible solutions $\left(a,\mu ,k,v,w,s,t,ȳ\right)$ of (FD), then $\left(x^{*},\bar{\mu },\bar{k},\bar{v},\bar{w},\bar{s},\bar{t},{ȳ}^{*}\right)$ is an optimal solution of (FD), and the two objectives have the same optimal values.

Proof. If x* be an optimal solution of (FP) and ∇g _h (x*), h ∈ H(x*) is linearly independent, then by Theorem 1, there exist $\left(\bar{s},\bar{t},{ȳ}^{*}\right)\in K\left(x^{*}\right)$ and $\left(x^{*},\bar{\mu },\bar{k},\bar{v},\bar{w}\right)\in H_1\left(\bar{s},\bar{t},{ȳ}^{*}\right)$ such that $\left(x^{*},\bar{\mu },\bar{k},\bar{v},\bar{w},\bar{s},\bar{t},{ȳ}^{*}\right)$ is feasible for (FD) and problems (FP) and (FD) have the same objective values and

$$\bar{k}=\frac{l\left(x^{*},{ȳ}_i^{*}\right)+{\left({x^{*}}^{T}D{x}^{*}\right)}^{1∕2}}{m\left(x^{*},{ȳ}_i^{*}\right)-{\left({x^{*}}^{T}E{x}^{*}\right)}^{1∕2}}.$$

The optimality of this feasible solution for (FD) thus follows from Theorem 3.   □

Theorem 5 (Strict converse duality). Let x* and $\left(ā,\bar{\mu },\bar{k},\bar{v},\bar{w},\bar{s},\bar{t},{ȳ}^{*}\right)$ be the optimal solutions of (FP) and (FD), respectively, and ∇g _h (x*), h ∈ H(x*) is linearly independent. Suppose that $\sum _{i=1}^s{t}_i\left(l\left(.,{ȳ}_i\right)+{\left(.\right)}^{T}Dw-\bar{k}\left(m\left(.,{ȳ}_i\right)-{\left(.\right)}^{T}Ev\right)\right)$ is strictly B-(p, r)-invex at a on S ∪ S₁ with respect to η and b satisfying b(x, a) > 0 for all x ∈ S. Furthermore, assume that $\sum _{h=1}^p{\mu }_h{g}_h\left(.\right)$ is B _g -(p, r)-invex at a on S ∪ S₁ with respect to the same function η and with respect to the function b _g , but not necessarily, equal to the function b. Then $x^{*}=ā$, that is, $ā$ is an optimal point in (FP) and

$$\underset{y\in Y}{sup}\frac{l\left(ā,{ȳ}^{*}\right)+{\left({ā}^{T}Dā\right)}^{1∕2}}{m\left(ā,{ȳ}^{*}\right)-{\left({ā}^{T}Eā\right)}^{1∕2}}=\bar{k}.$$

Proof. We shall assume that $x^{*}\ne ā$ and reach a contradiction. From the strong duality theorem (Theorem 4), it follows that

$$\underset{y\in Y}{sup}\frac{l\left(x^{*},{ȳ}^{*}\right)+{\left({x^{*}}^{T}D{x}^{*}\right)}^{1∕2}}{m\left(x^{*},{ȳ}^{*}\right)-{\left({x^{*}}^{T}E{x}^{*}\right)}^{1∕2}}=\bar{k}.$$

(23)

By feasibility of x* together with μ _h ≥ 0, h ∈ H, we obtain

$$\sum _{h=1}^p{\mu }_h{g}_h\left(x^{*}\right)\le 0.$$

(24)

By assumption, $\sum _{h=1}^p{\mu }_h{g}_h\left(.\right)$ is B _g -(p, r)-invex at a on S ∪ S₁ with respect to η and with respect to the b _g . Then, by Definition 2, there exists a function b _g such that b _g (x, a) ≥ 0 for all x ∈ S and a ∈ S₁. Hence by (14) and (24),

$$\frac{1}{r}{b}_g\left(x^{*},ā\right)\left\{e^{r\left[\sum _{h=1}^p{\mu }_h{g}_h\left(x^{*}\right)-\sum _{h=1}^p{\mu }_h{g}_h\left(ā\right)\right]}-1\right\}\le 0.$$

Then, from Definition 2, we get

$$\frac{1}{p}\sum _{h=1}^p\nabla {\mu }_h{g}_h\left(ā\right)\left\{e^{p\eta \left(x^{*},ā\right)}-1\right\}\le 0.$$

(25)

Therefore, by (25), we obtain the inequality

$$\frac{1}{p}\left\{\sum _{i=1}^s{t}_i\left(\nabla l\left(ā,{ȳ}_i\right)+Dw-\bar{k}\left(\nabla m\left(ā,{ȳ}_i\right)-Ev\right)\right)\right\}\left\{e^{p\eta \left(x^{*},ā\right)}-1\right\}\ge 0.$$

As $\sum _{i=1}^s{t}_i\left(l\left(.,{ȳ}_i\right)+{\left(.\right)}^{T}Dw-\bar{k}\left(m\left(.,{ȳ}_i\right)-{\left(.\right)}^{T}Ev\right)\right)$ is strictly B-(p, r)-invex with respect to η and b at $ā$ on S ∪ S₁. Then, by the Definition of strictly B-(p, r)-invexity and from above inequality, it follows that

$$\begin{array}{c}\frac{1}{r}b\left(x^{*},ā\right)\times \\ \left\{e^{r\left[\sum _{i=1}^s{t}_i\left(l\left(x^{*},{ȳ}_i\right)+x^{*T}Dw-\bar{k}\left(m\left(x^{*},{ȳ}_i\right)-x^{*T}Ev\right)\right)-\sum _{i=1}^s{t}_i\left(l\left(ā,{ȳ}_i\right)+{ā}^{T}Dw-\bar{k}\left(m\left(ā,{ȳ}_i\right)-{ā}^{T}Ev\right)\right)\right]}-1\right\}>0.\end{array}$$

From the hypothesis $b\left(x^{*},ā\right)>0$, and the above inequality, we get

$$\begin{array}{c}\sum _{i=1}^s{t}_i\left(l\left(x^{*},{ȳ}_i\right)+{x^{*}}^{T}Dw-\bar{k}\left(m\left(x^{*},{ȳ}_i\right)-{x^{*}}^{T}Ev\right)\right)\\ -\sum _{i=1}^s{t}_i\left(l\left(ā,{ȳ}_i\right)+{ā}^{T}Dw-\bar{k}\left(m\left(ā,{ȳ}_i\right)-{ā}^{T}Ev\right)\right)>0.\end{array}$$

Therefore, by (13),

$$\sum _{i=1}^s{t}_i\left(l\left(x^{*},{ȳ}_i\right)+{x^{*}}^{T}Dw-\bar{k}\left(m\left(x^{*},{ȳ}_i\right)-{x^{*}}^{T}Ev\right)\right)>0.$$

Since t _i ≥ 0, i = 1, 2, ..., s, therefore there exists i* such that

$$l\left(x^{*},{ȳ}_i^{*}\right)+{x^{*}}^{T}Dw-\bar{k}\left(m\left(x^{*},{ȳ}_i^{*}\right)-{x^{*}}^{T}Ev\right)>0.$$

Hence, we obtain the following inequality

$$\frac{l\left(x^{*},{ȳ}_i^{*}\right)+{\left({x^{*}}^{T}D{x}^{*}\right)}^{1∕2}}{m\left(x^{*},{ȳ}_i^{*}\right)-{\left({x^{*}}^{T}E{x}^{*}\right)}^{1∕2}}>\bar{k},$$

which contradicts (23). Hence the results.   □

5 Concluding remarks

It is not clear that whether duality in nondifferentiable minimax fractional programming with B-(p, r)-invexity can be further extended to second-order case.