Abstract
The objective of this paper is to obtain a mixed symmetric dual model for a class of non-differentiable multiobjective nonlinear programming problems where each of the objective functions contains a pair of support functions. Weak, strong and converse duality theorems are established for the model under some suitable assumptions of generalized convexity. Several special cases are also obtained.
MS Classification: 90C32; 90C46.
Similar content being viewed by others
1 Introduction
Dorn [1] introduced symmetric duality in nonlinear programming by defining a program and its dual to be symmetric if the dual of the dual is the original problem. The symmetric duality for scalar programming has been studied extensively in the literature, one can refer to Dantzig et al. [2], Bazaraa and Goode [3], Devi [4], Mond and Weir [5, 6]. Mond and Schechter [7] studied non-differentiable symmetric duality for a class of optimization problems in which the objective functions consist of support functions. Following Mond and Schechter [7], Hou and Yang [8], Yang et al. [9], Mishra et al. [10] and Bector et al. [11] studied symmetric duality for such problems. Weir and Mond [6] presented two models for multiobjective symmetric duality. Several authors, such as the ones of [12–14], studied multiobjective second and higher order symmetric duality, motivated by Weir and Mond [6].
Very recently, Mishra et al. [10] presented a mixed symmetric dual formulation for a non-differentiable nonlinear programming problem. Bector et al. [11] introduced a mixed symmetric dual model for a class of nonlinear multiobjective programming problems. However, the models given by Bector et al. [11] as well as by Mishra et al. [10] do not allow the further weakening of generalized convexity assumptions on a part of the objective functions. Mishra et al [10] gave the weak and strong duality theorems for mixed dual model under the sublinearity. However, we note that they did not discuss the converse duality theorem for the mixed dual model.
In this paper, we introduce a model of mixed symmetric duality for a class of non-differentiable multiobjective programming problems with multiple arguments. We also establish weak, strong and converse duality theorems for the model and discuss several special cases of the model. The results of Mishra et al. [10] as well as that of Bector et al. [11] are particular cases of the results obtained in the present paper.
2 Preliminaries
Let Rn be the n-dimensional Euclidean space and let  be its non-negative orthant. The following convention will be used: if x, y ∈ Rn , then
be its non-negative orthant. The following convention will be used: if x, y ∈ Rn , then  ;
;  ;
;  ; x ≰ y is the negation of x ≰ y.
; x ≰ y is the negation of x ≰ y.
Let f(x, y) be a real valued twice differentiable function defined on Rn × Rm . Let  and
and  denote the gradient vector of f with respect to x and y at
denote the gradient vector of f with respect to x and y at  . Also let
. Also let  denote the Hessian matrix of f (x, y) with respect to the first variable x at
denote the Hessian matrix of f (x, y) with respect to the first variable x at  . The symbols
. The symbols  ,
,  and
and  are defined similarly. Consider the following multiobjective programming problem (VP):
are defined similarly. Consider the following multiobjective programming problem (VP):

where X is an open set of Rn , f i : X → R, i = 1, 2,..., p and h : X → Rm .
Definition 2.1 A feasible solution  is said to be an efficient solution for (VP) if there exists no other x ∈ X such that
is said to be an efficient solution for (VP) if there exists no other x ∈ X such that  .
.
Let C be a compact convex set in Rn . The support function of C is defined by

A support function, being convex and everywhere finite, has a subdifferential [7], that is, there exists z ∈ Rn such that

The subdifferential of s(x|C) is given by

For any set D ⊂ Rn , the normal cone to D at a point x ∈ D is defined by

It is obvious that for a compact convex set C, y ∈ N C (x) if and only if s(y|C) = xTy, or equivalently, x ∈ ∂s(y|C).
Let us consider a function F : X × X × Rn → R (where X ⊂ Rn ) with the properties that for all (x, y) ∈ X × X, we have
(i)F(x, y; ·) is a convex function, (ii)F(x, y; 0) ≧ 0.
If F satisfies (i) and (ii), we obviously have F(x, y; -a) ≧ - F(x, y; a) for any a ∈ Rn .
For example, F(x, y; a) = M1||a|| + M2||a||2, where a depends on x and y, M1, M2 are positive constants. This function satisfies (i) and (ii), but it is neither subadditive, nor positive homogeneous, that is, the relations
(i')F(x, y; a + b) ≦ F(x, y; a) + F(x, y; b), (ii')F(x, y; ra) = rF(x, y; a) are not fulfilled for any a, b ∈ Rn and r ∈ R+. We may conclude that the class of functions that verify (i) and (ii) is more general than the class of sublinear functions with respect the third argument, i.e. those which satisfy (I') and (ii'). We notice that till now, most results in optimization theory were stated under generalized convexity assumptions involving the functions F which are sublinear. The results of this paper are obtained by using weaker assumptions with respect to the above function F.
Throughout the paper, we always assume that F, G : X × X × Rn → R satisfy (i) and (ii).
Definition 2.2 Let X ⊂ Rn , Y ⊂ Rm . f(·, y) is said to be F-convex at  , for fixed y ∈ Y, if
, for fixed y ∈ Y, if

Definition 2.3 Let X ⊂ Rn , Y ⊂ Rm . f(x,·) is said to be F-concave at  , for fixed x ∈ X, if
, for fixed x ∈ X, if

Definition 2.4 Let X ⊂ Rn , Y ⊂ Rm . f(·, y) is said to be F-pseudoconvex at  , for fixed y ∈ Y, if
, for fixed y ∈ Y, if

Definition 2.5 Let X ⊂ Rn , Y ⊂ Rm . f(x,·) is said to be F-pseudoconcave at  , for fixed x ∈ X, if
, for fixed x ∈ X, if

3 Mixed type multiobjective symmetric duality
For N = {1, 2,..., n} and M = {1, 2,..., m}, let J1 ⊂ N, K1 ⊂ M and J2 = N\J1 and K2 = M\K1. Let |J1| denote the number of elements in the set J1. The other numbers |J2|, |K1| and |K2| are defined similarly. Notice that if J1 = ∅, then J2 = N, that is, |J1| = 0 and |J2| = n. Hence,  is zero-dimensional Euclidean space and
is zero-dimensional Euclidean space and  is n-dimensional Euclidean space. It is clear that any x ∈ Rn can be written as x = (x1, x2),
is n-dimensional Euclidean space. It is clear that any x ∈ Rn can be written as x = (x1, x2),  ,
,  . Similarly, any y ∈ Rm can be written as y = (y1, y2),
. Similarly, any y ∈ Rm can be written as y = (y1, y2),  ,
,  . Let
. Let  and
and  be twice continuously differentiable functions and e = (1, 1,..., 1) ∈ Rl.
be twice continuously differentiable functions and e = (1, 1,..., 1) ∈ Rl.
Now we can introduce the following pair of non-differentiable multiobjective programs and discuss their duality theorems under some mild assumptions of generalized convexity.
Primal problem (MP):








Dual problem (MD):








where

 and
and  is a compact and convex subset of
is a compact and convex subset of  for i = i = 1, 2,..., l and
for i = i = 1, 2,..., l and  is a compact and convex subset of
is a compact and convex subset of  for i = 1, 2,..., l. Similarly,
for i = 1, 2,..., l. Similarly,  is a compact and convex subset of
is a compact and convex subset of  for i = 1, 2,..., l and
for i = 1, 2,..., l and  is a compact and convex subset of
is a compact and convex subset of  for i = 1, 2,..., l.
for i = 1, 2,..., l.
Theorem 3.1(Weak duality). Let (x1, x2, y1, y2, z1, z2, λ) be feasible for (MP) and (u1, u2, v1, v2, w1, w2, λ) be feasible for (MD). Suppose that for i = 1, 2,..., l,  is F1-convex for fixed v1,
is F1-convex for fixed v1,  is F2-concave for fixed x1,
is F2-concave for fixed x1,  is G1-convex for fixed v2 and
is G1-convex for fixed v2 and  is G2-concave for fixed x2, and the following conditions are satisfied:
is G2-concave for fixed x2, and the following conditions are satisfied:
-
(I)
F 1(x 1, u 1; a) + (u 1) Ta ≧ 0 if a ≧ 0;
-
(II)
G 1(x 2, u 2; b) + (u 2) Tb ≧ 0 if b ≧ 0;
-
(III)
F 2(v 1, y 1; c) + (y 1) Tc ≧ 0 if c ≧ 0; and
-
(IV)
G 2(v 2, y 2; d) + (y 2) Td ≧ 0 if d ≧ 0.
Then H(x1, x2, y1, y2, z1, z2, λ) ≰ G(u1, u2, v1, v2, w1, w2, λ).
Proof. Assume that the result is not true, that is H(x1, x2, y1, y2, z1, z2, λ) ≤ G(u1, u2, v1, v2, w1, w2, λ). Then, since λ > 0, we have

By the F 1-convexity of  , we have
, we have

, for i = 1,2,..., l.
From (7), (14) and F1 satisfying (i) and (ii), the above inequality yields

By the duality constraint (8) and conditions (I), we get

From (10), (16) and the above inequality, we obtain

By the F2-concavity of  , we have, for i = 1, 2,..., l,
, we have, for i = 1, 2,..., l,

From (7), (14) and F2 satisfying (i) and (ii), the above inequality yields

By the primal constraint (1) and conditions (III), we get

From (3), (18) and the above inequality, we obtain

Using  and
and  for i = 1, 2,..., l, it follows from (17) and (19), that
for i = 1, 2,..., l, it follows from (17) and (19), that

Similarly, by the G1-convexity of  and G2-concavity of
and G2-concavity of  , for i = 1, 2,..., l, and condition (II) and (IV), we get
, for i = 1, 2,..., l, and condition (II) and (IV), we get

From (20) and (21), we have

which is a contradiction to (15). Hence H(x1, x2, y1, y2, z1, z2, λ) ≰ G(u1, u2, v1, v2, w1, w2, λ).
Remark 3.1. Theorem 3.1 can be established for more general classes of functions such as F1-pseudoconvexity and F2-pseudoconcavity, and G1-pseudoconvexity and G2-pseudoconcavity on the functions involved in the above theorem. The proofs will follow the same lines as that of Theorem 3.1.
Strong duality theorem for the given model can be established on the lines of the proof of Theorem 2 of Yang et al. [9].
Theorem 3.2(Strong duality). Let  be an efficient solution for (MP), fix
be an efficient solution for (MP), fix  in (MD), and suppose that
in (MD), and suppose that
(A1) either the matrices  and
and  are positive definite; or
are positive definite; or  and
and  are negative definite; and
are negative definite; and
(A2) the sets  and
and  are linearly independent.
are linearly independent.
Then  is feasible for (MD) and the corresponding objective function values are equal. If in addition the hypotheses of Theorem 3.1 hold, then there exist
is feasible for (MD) and the corresponding objective function values are equal. If in addition the hypotheses of Theorem 3.1 hold, then there exist  ,
,  such that
such that  is an efficient solution for (MD).
is an efficient solution for (MD).
Mishra et al. [10] gave weak and strong duality theorems for the mixed model. However, we note that they did not discuss the converse duality theorem for the mixed dual model. Here, we will give a converse duality theorem for the model under some weaker assumptions.
Theorem 3.3(Converse duality). Let  be an efficient solution for (MD),
be an efficient solution for (MD),  in (MP), and suppose that
in (MP), and suppose that
(B1) either the matrices  and
and  are positive definite; or
are positive definite; or  and
and  are negative definite; and
are negative definite; and
(B2) the sets  and
and  are linearly independent.
are linearly independent.
Then  is feasible for (MP) and the corresponding objective function values are equal. If in addition the hypotheses of Theorem 3.1 hold, then there exist
is feasible for (MP) and the corresponding objective function values are equal. If in addition the hypotheses of Theorem 3.1 hold, then there exist  ,
,  such that
such that  is an efficient solution for (MP).
is an efficient solution for (MP).
Proof. Since  be an efficient solution for (MD), by the modifying Fritz-John conditions [7], there exist α ∈ Rl ,
be an efficient solution for (MD), by the modifying Fritz-John conditions [7], there exist α ∈ Rl ,  ,
,  , β1 ∈ R, β2 ∈ R,
, β1 ∈ R, β2 ∈ R,  ,
,  , δ ∈ Rl such that
, δ ∈ Rl such that

















From (22) and (23), we get

From (31)-(34), we have

Substituting (40) into (39), we obtain

Since λ > 0, it follows from (37), that δ = 0. From δ = 0 and (30), the above equation yields

From (A1) and (41), we obtain

From (22), (23), (42) and (A2), we get

If β1 = 0, then from (43) and (42), β2 = 0, α = 0, α1 = 0, α2 = 0, and from (24) and (26), μ1 = 0, μ2 = 0. This contradicts (38). Hence β1 = β2 > 0 and α > 0.
From (38) and (42), we have

By (24), (38) and (43), we have

By (26), (38) and (43), we have

From (24), (35), (42) and (43), we have

From (26), (36), (42) and (43), we have

Hence from (12)-(14) and (44)-(48),  is feasible for (MP). Now from (28), (42) and α > 0, we have
is feasible for (MP). Now from (28), (42) and α > 0, we have  , i = 1, 2,..., l, that is
, i = 1, 2,..., l, that is

From (29), (42) and α > 0, we have

Finally, from (25), (27), (49) and (50), for all i = 1, 2,..., l, we give,

Thus  . By the weak duality and (51),
. By the weak duality and (51),  is an efficient solution for (MD).
is an efficient solution for (MD).
4 Special cases
In this section, we consider some special cases of problems (MP) and (MD) by choosing particular forms of compact convex sets, and the number of objective and constraint functions:
-
(i)
If F(x, y; ·) is sublinear, then (MP) and (MD) reduce to the pair of problems (MP2) and (MD2) studied in Mishra et al. [10].
-
(ii)
If F(x, y; ·) is sublinear, |J 2| = 0, |K 2| = 0 and l = 1, then (MP) and (MD) reduce to the pair of problems (P1) and (D1) of Mond and Schechter [7]. Thus (MP) and (MD) become multiobjective extension of the pair of problems (P1) and (D1) in [7].
-
(iii)
If F(x, y; ·) is sublinear and l = 1, then (MP) and (MD) are an extension of the pair of problems studied in Yang et al. [9].
-
(iv)
From the symmetry of primal and dual problems (MP) and (MD), we can construct other new symmetric dual pairs. For example, if we take
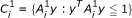 and
and 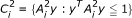 , where
, where 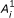 ,
, 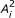 , i = 1,2,,..., l, are positive semi definite matrices, then it can be easily verified that
, i = 1,2,,..., l, are positive semi definite matrices, then it can be easily verified that  , and
, and  , i = 1, 2,..., l. Thus, a number of new symmetric dual pairs and duality results can be established.
, i = 1, 2,..., l. Thus, a number of new symmetric dual pairs and duality results can be established.
References
Dorn WS: A symmetric dual theorem for quadratic programming. J Oper Res Soc Jpn 1960, 2: 93–97.
Dantzig GB, Eisenberg E, Cottle RW: Symmetric dual nonlinear programs. Pacific J Math 1965, 15: 809–812.
Bazaraa MS, Goode JJ: On symmetric duality in nonlinear programming. Oper Res 1973, 21: 1–9. 10.1287/opre.21.1.1
Devi G: Symmetric duality for nonlinear programming problem involving g-convex functions. Eur J Oper Res 1998, 104: 615–621. 10.1016/S0377-2217(97)00020-9
Mond B, Weir T: Symmetric duality for nonlinear multiobjective programming. In Recent Developments in Mathematical Programming. Edited by: Kumar S. Gordon and Breach, London; 1991.
Weir T, Mond B: Symmetric and self duality in multiobjective programming. Asia Pacific J Oper Res 1991, 5: 75–87.
Mond B, Schechter M: Nondifferentiable symmetric duality. Bull Aust Math Soc 1996, 5: 177–188.
Hou SH, Yang XM: On second order symmetric duality in nondifferentiable programming. J Math Anal Appl 2001, 255: 491–498. 10.1006/jmaa.2000.7242
Yang XM, Teo KL, Yang XQ: Mixed symmetric duality in nondifferentiable mathematical programming. Indian J Pure Appl Math 2003, 34: 805–815.
Mishra SK, Wang SY, Lai KK, Yang FM: Mixed symmetric duality in nondifferentiable multiobjective mathematical programming. Eur J Oper Res 2007, 181: 1–9. 10.1016/j.ejor.2006.04.041
Bector CR, Chandra S: Abha: On mixed symmetric duality in multiobjective programming. Opsearch 1999, 36: 399–407.
Yang XM, Yang XQ, Teo KL, Hou SH: Second order symmetric duality in non-differentiable multiobjective programming with F-convexity. Eur J Oper Res 2005, 164: 406–416. 10.1016/j.ejor.2003.04.007
Yang XM, Yang XQ, Teo KL, Hou SH: Multiobjective second order symmetric duality with F-convexity. Eur J Oper Res 2005, 165: 585–591. 10.1016/j.ejor.2004.01.028
Chen X: Higher-order symmetric duality in nondifferentiable multiobjective programming problems. J Math Anal Appl 2004, 290: 423–435. 10.1016/j.jmaa.2003.10.004
Acknowledgements
This study was supported by the Education Committee Project Research Foundation of Chongqing (No.KJ110624), the Doctoral Foundation of Chongqing Normal University (No.10XLB015) and Chongqing Key Lab of Operations Research and System Engineering.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
All authors carried out the proof. All authors conceived of the study, and participated in its design and coordination. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, J., Gao, Y. Non-differentiable multiobjective mixed symmetric duality under generalized convexity. J Inequal Appl 2011, 23 (2011). https://doi.org/10.1186/1029-242X-2011-23
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2011-23



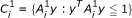 and
and 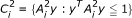 , where
, where 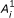 ,
, 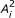 , i = 1,2,,..., l, are positive semi definite matrices, then it can be easily verified that
, i = 1,2,,..., l, are positive semi definite matrices, then it can be easily verified that  , and
, and  , i = 1, 2,..., l. Thus, a number of new symmetric dual pairs and duality results can be established.
, i = 1, 2,..., l. Thus, a number of new symmetric dual pairs and duality results can be established.