1. Introduction

It is well known that the theory of differential inequalities plays an important role in the qualitative and quantitative studies of differential equations [1–3]. In recent years, various inequalities have been established such as the Halanay inequalities in [4–6], the delay inequalities in [7–10], and the impulsive differential inequalities in [11–13]. Using the linear inequality techniques, many results have been done on the stability and dynamical behavior for differential systems, see [4–13] and the references cited therein. For example, [11] presents an extended impulsive delay Halanay inequality and deals with the global exponential stability of impulsive Hopfield neural networks with time delays. In [13], the authors establish a delay differential inequality with impulsive initial conditions and derive some sufficient conditions ensuring the exponential stability of solutions for the impulsive differential equations. However, linear differential inequalities do not work in the studies for nonlinear differential equations. With the development of the theory on nonlinear differential equations (e.g., see [14, 15]), it is necessary to study the corresponding nonlinear differential inequalities. In [16], the authors develop a new nonlinear delay differential inequality that works well in studying a class of nonlinear delay differential systems. Indeed, nonlinear delay differential inequalities with impulses are seldom discussed in the literature. Therefore, in further researches of nonlinear systems, it is beneficial to obtain some new nonlinear impulsive delay differential inequalities. Our goal in this article is to do some investigations on such problems.

Indeed, impulsive effects and delay effects widely exist in the real world. Impulsive delay differential equations provide mathematical models for many phenomena and processes in the field of natural science and technology. In the last few decades, the stability theory of impulsive functional differential equations has obtained a rapid development, and many interesting results have been reported, see [1–8, 16–23]. Recently, exponential stability has attracted increasing interest in both theoretical research and applications [20–22, 24]. However, the existing works mainly focus on linear impulsive functional differential equations [17–19, 25]. There exist very little works devoted to the investigations of exponential stabilities for nonlinear impulsive functional differential systems.

Motivated by the above discussions, in this article, we shall establish a new nonlinear impulsive delay differential inequality, which improves some recent works in the literature [9–12, 16, 18] and can be applied to the dynamical analysis of nonlinear systems. Based on the inequality, some sufficient conditions guaranteeing the local exponential stability of nonlinear impulsive functional differential equations are derived. Finally, two examples are given to show the effectiveness and advantages of our proposed results.

2. Preliminaries

Let ℝ denote the set of real numbers, ℝ+ the set of nonnegative real numbers, ℤ+ the set of positive integers, and ℝ n the n-dimensional real space equipped with the Euclidean norm | · |. Consider the following impulsive functional differential systems

(2.1)

where x ∈ ℝ n , the impulse times {t k } satisfy 0 ≤ t0 < t1 < ⋯ < t k < ⋯ and limk→+∞t k = +∞, and x' denotes the right-hand derivative of x. Also, assume f ∈ C([tk-1, t k ) × Ψ, ℝ n ), meanwhile φ ∈ Ψ, Ψ is an open set in PC([-τ, 0], ℝ n ), where PC([-τ, 0], ℝ n ) = {ψ: [-τ, 0] → ℝ n |ψ is continuous except at a finite number of points t k , at which and exist and }. For ψ ∈ Ψ , the norm of ψ is defined by ||ψ|| = sup-τ≤θ≤0|ψ(θ)|. For each t ≥ t0, x t ∈ Ψ is defined by x t (s) = x(t + s), s ∈ [-τ, 0]. For each k ∈ ℤ+, I k (t,x) ∈ C(t0, ∞) × ℝ n , ℝ n ).

In this article, we suppose that there exists a unique solution of system (2.1) through each (t0, φ), see [23] for the details. Furthermore, we assume that f(t, 0) = 0, and I k (t, 0) = 0, k ∈ ℤ+, so that x(t) = 0 is a solution of system (2.1), which is called the trivial solution.

We now introduce some definitions that will be used in the sequel.

Definition 2.1. ([5]) A function V: [-τ, ∞) × Ψ → ℝ+ belongs to class v0 if

  1. (i)

    V is continuous on each set [t k - 1, t k ) × Ψ and 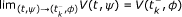exists,

  2. (ii)

    V (t, x) is locally Lipschitzian in x and V (t, 0) ≡ 0.

Definition 2.2. ([5]) Let V ∈ v0, for any (t, ψ) ∈ [tk - 1, t k ) × Ψ, the upper right-hand Dini derivative of V (t, x) along a solution of system (2.1) is defined by

Definition 2.3. ([6]) The trivial solution of system (2.1) is said to be exponentially stable, if for any initial data , there exists a λ > 0, and for every ε > 0, there exists δ = δ(ε) > 0 such that

whenever || φ || < δ and t0 ∈ ℝ+.

Definition 2.4. ([5]) Let x(t) = x(t, t0, φ) be a solution of system (2.1) through (t0, φ). Then the trivial solution of (2.1) is said to be globally exponentially stable if for any t0 > 0, there exist constants λ > 0 and M ≥ 1 such that

3. Main results

First, we present a nonlinear impulsive delay differential inequality.

Lemma 3.1. Assume that there exist constants p > 0, q > 0, θ > 1, and function m(t) ∈ PC([t0 - τ, ∞), ℝ+) satisfying the scalar impulsive differential inequality

where a k , b k ∈ ℝ+, . Moreover, there exists a constant M ≥ 1 such that. Thenimplies

(3.1)

where λ satisfies

(3.2)

Proof. We first note that implies that there exists a scalar λ > 0 such that the inequality (3.2) holds.

Now, we shall show

where a0 = 1, b0 = 0.

In order to do this, let

Now we only need to show that

It is clear that for t ∈ [t0 - τ, t0] by the definition of .

Take k = 1, we can prove that for t ∈ [t0, t1). Suppose on the contrary, then there exists some t ∈ [t0, t1) such that .

Let , then , , t ∈ [t0 - τ , t*], and D+L(t*) ≥ 0. Calculating the upper right-hand Dini derivative of L(t) along the solution of (2.1), it can be deduced that

which is a contradiction. So we have proven for all t ∈ [t0, t1).

Furthermore, we have

Next we shall show . Suppose on the contrary, then there exists some t ∈ [t1, t2) such that . Let , then , and , t ∈ [t0 - τ , t** ], D+L(t**) ≥ 0. Calculating the upper right-hand Dini derivative of L(t) along the solution of (2.1), it can be deduced that

which is a contradiction. So we have proven for all t ∈ [t1, t2).

By the method of induction, we prove that for t ∈ [t k -1, t k ], k ∈ ℤ+,

i.e.,

So (3.1) holds. The proof of Lemma 3.1 is complete.

Remark 3.1. In [9–18], the authors got some results for linear differential inequalities under the assumption that p > q. Note in our result, the restriction p > q is completely removed if the initial value satisfies some certain conditions.

Remark 3.2. It should be noted that if p > q, then , which implies that (3.1) holds for any initial value . In this sense, Lemma 3.1 becomes the well known case, see [16]. Hence, our development result has wider adaptive range than those in [9–12, 16, 18].

Next, based on Lemma 3.1, we shall construct a suitable Lyapunov function to derive some conditions guaranteeing the exponential stability of the trivial solution of system (2.1).

Theorem 3.1. Assume that there exist function V (t, x) ∈ v0, and constants 0 < c1 ≤ c2, m > 0, p > 0, q > 0, θ > 1 such that the following conditions hold:

  1. (i)

    c 1||x|| m ≤ V (t, x) ≤ c 2||x|| m , (t, x) ∈ (ℝ+,ℝ n );

  2. (ii)

    For t ≥ t 0, t ≠ t k ,

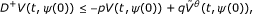
where;

  1. (iii)

    For any ψ ∈ PC([ - τ , 0], Rn ),

where.

Then the trivial solution of system (2.1) is exponentially stable.

Proof. Let x(t) = x(t, t0, φ) be any solution of system (2.1) with initial value (t0, φ). By condition (iii), we know that there exists M ≥ 1 such that .

For any given , choose some δ > 0 such that . When ||φ|| < δ < ε, we have . Using Lemma 3.1 and the condition (i), we derive

i.e.,

By the definition 2.3, the trivial solution of system (2:1) is exponentially stable. This completes the proof.

Remark 3.3. From the proof of the Theorem 3.1, it follows that if p > q, θ → 1+, the trivial solution of system (2.1) is globally exponentially stable.

4. Examples

In this section, we shall give two examples to illustrate the effectiveness of our results.

Example 1. Consider the impulsive functional differential equation as follows:

(4.1)

where θ > 1, a(t) ≥ a > 0, 0 < |b(t)| ≤ b, 0 ≤ τ (t) ≤ τ, for all t ≥ t0.

Property 4.1. The trivial solution of system (4.1) is exponentially stable.

Proof. Choose V (t) = |x(t)|. When t ≠ t k , calculating the derivative of D+V (t) along the solution of (4.1), we get

where . Furthermore,

Hence, by Theorem 3.1, the trivial solution of system (4.1) is exponentially stable.

Example 2. Consider the following impulsive functional differential equation with distributed delays:

(4.2)

where θ > 1, a > 0, b ∈ ℝ.

Property 4.2. The trivial solution of system (4.2) is exponentially stable.

Proof. Choose V (t) = |x(t)|. When t ≠ t k , calculating the derivative of D+V (t) along the solution of (4:2), we get

where . Furthermore, we have

Hence, by Theorm 3.1, the trivial solution of system (4.2) is exponentially stable.

Remark 3.4 It should be noted that the sufficient conditions ensuring the exponential stabilities of (4.1) and (4.2) are easily to check, which show the advantages of our results.