1 Introduction

Noncentrosymmetric superconductors are superconductors without inversion centers. The broken inversion symmetry results in antisymmetric spin-orbit coupling (ASOC) which can lead to interesting superconducting properties, such as mixed pairing order parameters [5–7], helical phases [8–10], novel magnetoelectric responses [11–14], large enhancement of the upper critical field \(H_{c2}\) [14, 15] or topological superconductivity [16–20]. In the past two decades, many noncentrosymmetric superconductors have been discovered [21]. To understand the superconducting properties of noncentrosymmetric superconductors, a common procedure was to construct normal state Hamiltonians which respect the crystal symmetry, and then to further include ASOC and study its effect on superconductivity. However, the normal state topological properties of these noncentrosymmetric superconductors have usually been ignored in previous studies.

In recent years, tremendous progress had been made in the understanding of the topological properties of band structures. Particularly, many topologically nontrivial band crossings which describe unconventional fermions, such as Weyl, Kramers Weyl and unconventional multifold fermions have been discovered [1–4, 22–25]. These multifold band crossings give rise to finite Chern numbers on Fermi surfaces enclosing the band crossing points. The case of multifold fermions is particularly interesting, as the nonsymmorphic and time-reversal (TR) symmetry can enforce multiple degeneracies and result in large Chern numbers on Fermi surfaces enclosing the band crossing points, even in the absence of ASOC. Unlike Weyl points, which usually result in short Fermi arc states, multifold fermion crossing points result in incredibly long Fermi arc states which span a large portion of the surface Brillouin zone. So far, two multifold fermion semimetals, namely, AlPt [1] and XSi (X = Rh,Co) [2–4], have been identified, and their long Fermi arc states have been observed through ARPES experiments recently. However, they are not superconducting, and it is not known how the normal state topology resulting from multifold fermions can affect the superconducting properties in realistic materials.

In this work, we point out that \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) and \(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\), which are well-studied noncentrosymmetric superconductors [26–29], are superconducting multifold fermion metals and the normal state topological properties of these materials have been ignored in previous studies. Through NMR [28–30], specific heat [31, 32] and penetration length [27] measurements, it has been suggested that \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) and \(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\) are fully gapped and gapless superconductors, respectively. We first identify topological band crossing points in \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) and \(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\) which are relevant to the Fermi surface topology through symmetry analysis and ab initio calculations. Several 2-fold, 4-fold and 6-fold band crossings which correspond to Weyl, Kramers Weyl, spin-1 and multifold fermions were found and are listed in Table 1. Fermi arcs which span long distances in the surface Brillouin zone on the (001) surfaces are found in \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\). Second, by introducing superconducting pairing to the bands near the Fermi energy, we show that the gapless superconducting states of the \(\mathrm{A}_{1}\) and \(\mathrm{A}_{2}\) representations, which are relevant to \(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\), are topological and possess dispersionless Majorana surface modes. A fully gapped DIII topological superconducting phase in \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) is also discussed. Finally, we point out that several other well studied noncentrosymmetric superconductors, such as \(\mathrm{Mo} _{3}\mathrm{Al} _{2}\mathrm{C}\), PdBiSe, \(\mathrm{Y}_{2}\mathrm{C}_{3}\) and \(\mathrm{La} _{2}\mathrm{C}_{3}\) are also multifold fermion metals with rich topological band structures. This work motives a revisit for the study of noncentrosymmetric superconductors which are platforms for investigating the interplay between superconductivity and topologically nontrivial Fermi surfaces.

Table 1 Unconventional fermions found in \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) and \(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\) by first-principles calculation. Indices correspond to those in Fig. 1
Full size table

2 Multifold fermions in \(\text{Li}_{2}\text{Pd}_{3}\text{B}\) and \(\text{Li}_{2}\text{Pt}_{3}\text{B}\)

Both \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) and \(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\) have a cubic structure, and they belong to the chiral space group \(P4_{3}32\) (No. 212) with point group O [33]. Its generators contain the following (screw) rotation operations (in Seitz symbol):

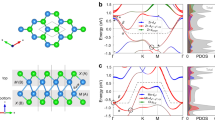
$$\begin{aligned} &\biggl\{ 2_{001}\Big\| \frac {1}{2},0,\frac {1}{2}\biggr\} , \qquad \biggl\{ 2_{010}\Big\| 0,\frac {1}{2},\frac {1}{2}\biggr\} , \\ &\bigl\{ 3^{+}_{111}\|0\bigr\} , \qquad \biggl\{ 2_{110}\Big\| \frac {1}{4},\frac {3}{4},\frac {1}{4}\biggr\} . \end{aligned}$$
(1)

The chiral multifold fermions originate from these screw rotations [22]. Ab initio calculations (see Additional file 1) are used to obtain the band structures of \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) and \(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\), as depicted in Fig. 1. In reciprocal space, the cubic Brillouin zone has nonequivalent high symmetry points \(\Gamma (0, 0, 0 )\), \(\mathrm{X} (\pi /a, 0, 0 )\), \(\mathrm{M} (\pi /a, \pi /a, 0 )\) and \(\mathrm{R} (\pi /a, \pi /a, \pi /a )\) (with primitive lattice constant a), as shown in Fig. 2a. The band structures of \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) and \(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\) were calculated more than a decade ago [33], but the unconventional crossing points that correspond to the multifold fermions have not been identified. Recently, it was pointed out in [22] that \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) possesses a six-fold degenerate point at the R point. In this work, we point that there are indeed a large number of unconventional crossing points near the Fermi energy of \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) and \(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\) and these topological crossing points have important impacts on the topological properties of the Fermi surfaces and the superconducting states.

Figure 1
figure 1

Band structure of \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) (a-d) and \(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\) (a-d) from first-principles calculations with SOC self-consistently included. Bands that cross the Fermi energy are marked in red, and the topological band crossing points which can be described by unconventional fermions are depicted in enlarged plots. The degeneracies corresponding to unconventional fermions are enumerated and listed in Table 1

Full size image
Figure 2
figure 2

(a) The bulk, the \((001)\) surface and the \((111)\) surface Brillouin zones of a cubic lattice. (b) The Fermi surface of \(\mathrm{Li}_{2}\mathrm{Pd}_{3}\mathrm{B}\). It can be seen that there are Fermi pockets enclosing all of the TRIMs. (c) Surface Fermi arcs of \(\mathrm{Li}_{2}\mathrm{Pd}_{3}\mathrm{B}\). The colormap represents the logarithm of spectral weight on the (001) surface. Near the Fermi energy, there are 12 Fermi arcs near the M̄ pocket. (d) The energy dependence of the k-points of a closed loop is indicated by dashed lines in (c). The energy spectral flow is calculated, revealing that the total topological charge of \(C = 12\)

Full size image

In \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) and \(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\), time-reversal symmetry forces two copies of spin-1 fermions to be degenerate at R [34], giving a 6-fold degeneracy as depicted in Fig. 1d. This is referred to as double spin-1 in Table 1. On the other hand, we found a 4-fold degeneracy at Γ (e.g., labeled as No. 14 in Fig. 1g) corresponds to the spin-3/2 or the so-called Rarita-Schwinger-Weyl (RSW) fermions with a monopole charge of ±4. The corresponding irreducible representations and an effective \(k\cdot p\) Hamiltonian linear in k for the two aforementioned unconventional fermions are included in the Additional file 1. For the bands which cross the Fermi energy (denoted in red in Fig. 1), 15 unconventional degenerate points are identified which are associated with unconventional chiral fermions. The locations of these points are labeled in Fig. 1, and the degeneracy and the topological charges of the Fermi surfaces enclosing these points are summarized in Table 1.

Focusing on the \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) case, the Kramers Weyl fermions at M, which is a TRIM, are doubled by nonsymmorphic symmetries, giving double Kramers Weyl fermions [34]. We further identified two Weyl fermions (No. 2, 3 in Table 1) along the M-Γ line with a total Berry curvature charge of +2. It is interesting that these Weyl points have to be taken into account for the observed surface spectrum.

When a nondegenerate Fermi surface in the Brillouin zone encloses the band crossing points, it can acquire a finite Chern number, and there can be surface Fermi arc states connecting surfaces with different Chern numbers. The Fermi surface of \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) is depicted in Fig. 2b. Figure 2c visualizes the calculated surface spectral function \(\mathcal{A}_{s}(E,\boldsymbol{k})=-\frac{1}{\pi}\operatorname{Im} \operatorname{Tr} G_{s}(E,\boldsymbol{k})\) of the (001) surface of \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\), where \(G_{s}(E,\boldsymbol{k})\) is the surface Green’s function. As many as 12 Fermi arcs emerge from the M̄ pocket. The M̄ surface pocket is a projection of the R and M pockets of the 3D Brillouin zone, and the rest of the states enclosing the M̄ pocket are projections of pockets around the Γ point in the 3D Brillouin zone. The energy dispersion of the Fermi arc states are depicted in Fig. 2d. Note that all the Fermi arc states around the M̄ pocket have positive Fermi velocity along the a-b-c-d lines defined in Fig. 2c. This suggests that the gapped surface enclosing the M and R points in the 3D Brillouin zone has a total Chern number of 12. This is consistent with the fact that the two Fermi surfaces at the R point carry a total monopole charge of 4 and the eight Weyl points (No. 2, 3 in Table 1 together with Weyl points related by 4-fold rotation symmetry) near M carry a total monopole charge of 8.

For the case of \(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\), the effect of ASOC is stronger than that in \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) which can be seen from the larger band splitting. Larger ASOC might affect superconductivity as will be discussed later, but topology are essentially the same. Band dispersions are more complicated for \(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\), making it impossible to separate Fermi arcs from bulk states in surface projection.

3 Gapless pairing in \(\text{Li}_{2}\text{Pt}_{3}\text{B}\)

As shown in the previous sections, the band structure of \(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\) is highly topologically nontrivial, and the Fermi surface topological properties cannot be captured by simple effective models. All the nontrivial crossing points enclosed by the Fermi surface has to be taken into account, which determines the Chern number of the Fermi surface. Therefore, in our calculations, we first construct the Wannier orbitals from first-principles calculations with the Wannier90 package [35] and the Hamiltonian is diagonalized to obtain the eigenstates \(|\phi _{\nu , \boldsymbol{k}}\rangle\). The realistic band structures obtained allows us to fully incorporate the topological properties of the normal state Fermi surface when studying the superconducting phase. For simplicity, we assign the same pairing order parameter \(\Delta _{\nu , \boldsymbol{k}}\) to all the bands. The pairing \(\Delta _{\nu , \boldsymbol{k}}\) transforms as one of the irreducible representations (IR) of the point group O, which is the factor group of \(P4_{3}32\). With this method, we can classify all the symmetry-allowed pairing functions up to their leading order in k corresponding to the irreducible representations of point group O, as listed in the Table S1 of Additional file 1.

Using Ginzburg-Landau analysis, higher dimensional representations either break crystal symmetries or time-reversal symmetry [36–39] (see also Additional file 1), which has not been observed experimentally. Therefore, in this work, we focus on pairings associated with the one-dimensional representations. The space group \(P4_{3}32\) allows two one-dimensional representations, \(A_{1}\) and \(A_{2}\), as listed in Table 2. The pairing in the \(A_{1}\) representation includes the conventional s-wave and the extended s-wave pairing and the pairing in the \(A_{2}\) representation is gapless, as it requires a sign change of order parameter under \(\mathrm{C}_{4}\) rotation.

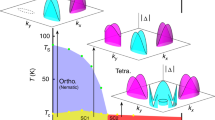
Table 2 Possible pairing phases of \(\mathrm{Li}_{2}\mathrm{Pt}_{3}\mathrm{B}\) labeled by the 1D IR of O point group. In each IR, the pairing function \(\Delta _{\nu , \boldsymbol{k}}\) can be expanded in terms of the basis functions. The \(\eta _{\zeta}\) with \(\zeta =1, 2, 3, \ldots \) there are the coefficients for the basis functions in \(\mathrm{A}_{1}\) and \(\mathrm{A}_{2}\) IR respectively
Full size table

\(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\) has been experimentally found to be a gapless superconductor through penetration length [27], NMR [29, 30] and specific heat measurement [31, 32]. This was suggested to be a consequence of ASOC in the previous literature [27]. From the symmetry analysis, we find that the \(A_{2}\) pairing phase with \(\Delta _{\nu , \boldsymbol{k}} = \eta _{3} (\cos k_{x}a-\cos k_{y}a)(\cos k_{y}a- \cos k_{z}a)(\cos k_{z}a-\cos k_{x}a)\) satisfies the gapless condition. It is evident from the pairing function that there are many nodal planes such as the \(k_{x}=k_{z}\) plane. When the nodal planes intersect with the Fermi surface, nodal lines are formed, e.g., bright lines in Fig. 3a. The projection of the nodal lines on the surface Brillouin zone can create pockets which are filled by dispersionless Majorana modes on the (111) surfaces, as shown in Fig. 3b. To understand the topological origin of the dispersionless Majorana modes on the (111) surface, we can parameterize the Hamiltonian as \(\mathcal{H}_{\mathrm{BdG}}(\bar{k}_{x}, \bar{k}_{y}, \bar{k}_{z})\), where \(\bar{k}_{z} \) is along the (111) direction and \(\bar{k}_{x}\) and \(\bar{k}_{y}\) are momenta parallel to the (111) surface. By taking \(\bar{k}_{x}\) and \(\bar{k}_{y}\) as numbers, \(\mathcal{H}_{\mathrm{BdG}}(\bar{k}_{x}, \bar{k}_{y}, \bar{k}_{z})\) can be regarded as a 1D AIII class Hamiltonian \(\mathcal{H}_{\mathrm{BdG},\bar{k}_{x}, \bar{k}_{y}}(\bar{k}_{z})\) which depends on \(\bar{k}_{z}\) only. The topological invariant can be written as:

$$ N_{\bar{k}_{x}, \bar{k}_{y}} = \frac{1}{2\pi}\operatorname{Im} \int \mathrm{d}\bar{k}_{z}\operatorname{Tr} \bigl[\partial _{\bar{k}_{z}}\ln Q(\bar{k}_{x}, \bar{k}_{y}, \bar{k}_{z})\bigr], $$
(2)

which determines the number of zero energy Majorana modes at the point \((\bar{k}_{x}, \bar{k}_{y})\) of the surface Brillouin zone [40–42]. Here, \(Q(\bar{k}_{x}, \bar{k}_{y}, \bar{k}_{z})=H_{0}(\bar{k}_{x}, \bar{k}_{y}, \bar{k}_{z})-i\Delta (\bar{k}_{x}, \bar{k}_{y}, \bar{k}_{z})\) and \(H_{0}(\bar{k}_{x}, \bar{k}_{y}, \bar{k}_{z})\) is the normal state Hamiltonian.

Figure 3
figure 3

Gapless topological phases of \(\mathrm{Li}_{2}\mathrm{Pt}_{3}\mathrm{B}\). (a) The projected bulk spectral function in the \((111)\) direction at \(E=0\) in the \(\mathrm{A}_{2}\) phase, with \(\eta _{3}=0.16\text{ eV}\). High value in spectral functions corresponds to projected nodal lines. (b) The surface spectral function of the \((111)\) surface at \(E=0\) in the \(\mathrm{A}_{2}\) phase. Nodal lines shown in (a) separate the surface Majorana pockets in (b). (c) Bulk spectral functions in the \(\mathrm{A}_{1}\) phase. (d) The surface spectral function of the \((111)\) surface in the \(\mathrm{A}_{1}\) phase. (e) The phase diagram for the \(\mathrm{A}_{1}\) phase with different \(\eta _{1}/\eta _{2}\)

Full size image

It is important to note that the \(\mathrm{A}_{1}\) pairing phase can also result in a gapless spectrum. As shown in Fig. 3e, there is a wide range of parameter regime of \(\eta _{1}/\eta _{2}\) for \(\mathrm{A}_{1}\) pairing \(\Delta _{\nu , \boldsymbol{k}} = \eta _{1}+\eta _{2} ( 3 - \cos k_{x}a - \cos k_{y}a - \cos k_{z}a )\) where the system is gapless. This happens when the k dependence of \(\Delta _{\nu , \boldsymbol{k}}\) induces a sign change on a connected Fermi surface, and the zeros of \(\Delta _{\nu , \boldsymbol{k}}\) correspond to the nodal lines. Importantly, there are also dispersionless surface Majorana modes on the surfaces, as shown in Fig. 3d. The topological origin of the Majorana modes can be determined by Eq. (2) as well. Therefore, we conclude that the multifold fermion material \(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\) is likely to be a gapless topological superconductor with Majorana surface modes.

4 Fully gapped pairing phase in \(\text{Li}_{2}\text{Pd}_{3}\text{B}\)

For the case of \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\), with the \(\mathrm{A}_{1}\) representation, the superconducting properties of the system depend on \(\eta _{1}\) and \(\eta _{2}\) of the order parameter \(\Delta _{\nu , \boldsymbol{k}} = \eta _{1}+\eta _{2} ( 3 - \cos k_{x}a - \cos k_{y}a - \cos k_{z}a )\). The topological invariant of the DIII class topological superconductor is given by

$$ N_{\mathrm{DIII}}=\frac{1}{2}\sum _{\nu}\operatorname{sgn} (\Delta _{ \nu , \boldsymbol{k}_{\mathrm{F}}} )C_{\nu}, $$
(3)

where \(\Delta _{\nu , \boldsymbol{k}_{\mathrm{F}}}\) is the pairing on the Fermi surface of the ν-th band with Chern number \(\mathrm{C}_{\nu}\) [43]. Interestingly, there is a large parameter regime of \(\Delta _{\nu , \boldsymbol{k}_{\mathrm{F}}}\), as shown in Fig. 4e, where the pairing of the large Fermi pockets near Γ and the two Fermi pockets enclosing the R point have different signs. In this case, a DIII class topological superconductor is obtained [44]. In the topological regime, the two nearly degenerate Fermi pockets enclosing the R point have a total Chern number of 4 and the same pairing sign, while the rest of the Fermi surfaces have a total Chern number of −4 which is opposite to the R pocket. As indicated by Eq. (3), the opposite Chern numbers and pairing sign of the two groups of Fermi surfaces will lead to a finite total topological invariant of the DIII class topological phase \(N_{\mathrm{DIII}} =4\). As a result, we expect that four Majorana cones appear on the (001) surface of the material. This is verified numerically by setting \(\eta _{1} / \eta _{2} = -5\), and four Majorana cones are found on the (001) surface state. It is interesting to note that on the (111) surface, the \(\mathrm{C}_{3}\) rotational symmetry forces the Majorana cones to be pinned at the surface Brillouin zone center Γ̅ and results in two Majorana cones with linear and cubic dispersion, respectively, as shown in Fig. 4c and 4d. This cubic dispersion Majorana cone is a manifestation of the existence of multifold fermions, particularly the spin-3/2 fermions, as pointed out in [45, 46].

Figure 4
figure 4

(a) Four Majorana cones on the (001) surface of \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) in the DIII topological phases with fully gapped \(A_{1}\) pairing. The colormap represents the logarithm of quasi-particle spectral function weight on the (001) surface at \(E=0\). The inset indicates that the sign of projected pairing potential is positive (red) on the R pocket and negative (blue) on the rest. This pairing corresponds to \(\eta _{1}/\eta _{2}=-5\), \(\eta _{2}=10\text{ meV}\), leading to an \(N_{\text{gap}} = 4\) phase. (b) A zig-zag cut passing through all the Majorana cones is made and the corresponding energy spectrum is calculated. (c) and (d) show the energy spectrum of Majorana states on the (111) surface of \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) in its DIII topological superconducting phase. The red solid lines and blue dashed lines in (d) represent the respective surface Majorana bands on the two sides. The different dispersion on the two sides is due to the breaking of inversion. Clearly on both (111) surface sides, there are two Majorana cones with linear and cubic dispersions. (e) Different \(\eta _{1}/\eta _{2}\) ratios in the \(\mathrm{A}_{1}\) pairing shown in Table 2 give different topological superconducting phases

Full size image

We would like to emphasis that the topological superconducting phase in \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) can be achieved without an odd parity pairing, which is sometimes referred to as Fu-Berg criteria [21, 38, 45–48]. Since in previous systems, the opposite Chern numbers originate from different spin channel, which naturally requires a spin-triplet pairing to achieve non-trivial topology given by Eq. (3). In contrast, the different Chern numbers in \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) are from multifold fermions, which does not necessarily require ASOC.

5 Other superconducting materials with multifold fermions

In this work, we show that the normal state topology plays an important role in determining the superconducting properties of \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) and \(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\). We expect that the normal state topological properties are important in many other noncentrosymmetric superconductors as well. By revisiting the space group of noncentrosymmetric superconductors [21, 49–52], we can further identify several superconductors with multifold fermions, such as \(\mathrm{Mo} _{3}\mathrm{Al} _{2}\mathrm{C}\), PdBiSe, \(\mathrm{Y}_{2}\mathrm{C}_{3}\) and \(\mathrm{La} _{2}\mathrm{C}_{2}\) whose normal state topological properties have been ignored in previous studies.

Their first-principles band structures are shown in Fig.S2 in Additional file 1. Due to their nonsymmorphic symmetries, plentiful unconventional fermions with 3-, 4-, 6- and 8-fold degeneracy appear at high-symmetry k points, and some of them are near the Fermi level and thus influence the superconducting phases. Their possible topological superconducting phases can be further studied with the same numerical and theoretical methods presented in this work.

6 Conclusion

In this work, we showed that \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) and \(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\) are multifold fermion metals with unconventional degenerate points at time-reversal invariant momenta due to nonsymmorphic symmetry. This results in Fermi surfaces with higher Chern numbers, even in the absence of ASOC. We showed that there are long Fermi arc states in \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\) at the Fermi energy. Interestingly, \(\mathrm{Li} _{2}\mathrm{Pd} _{3}\mathrm{B}\), being a fully gapped superconductor, is a candidate material of a DIII class topological superconductor. On the other hand, superconducting \(\mathrm{Li} _{2}\mathrm{Pt} _{3}\mathrm{B}\), being gapless, is likely to be a nodal topological superconductor with dispersionless Majorana surface modes. We also identified several other superconducting multifold fermion superconductors, which can also provide new platforms to study the interplay between normal state topology and superconductivity.