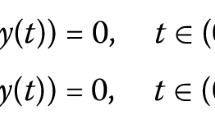1 Introduction

The partial differential equations of fractional order, which are considered as an extension of the partial differential equations of integer order, play a crucial role in the mathematical modeling of real objects see [1, 2, 5, 15, 23, 31, 33, 37,38,39, 43,44,45, 47, 48].

Since the derivative of fractional order, is a generalization of the derivative with integer order, it makes mathematical modeling more accurate. For example in [29] the authors show that the fractional derivative plays a crucial role in a numerical method used to simulate an earthquake response in buildings and in [42] the authors study why fractional dynamics is needed in machine learning and optimal randomness.

So far, different types of fractional derivatives have been defined, such as the Riemann-Liouville [39], Hadamard [34], Grunwald-Letnikov [46], Weyl [53], Caputo [28] and Caputo-Fabrizio [27] derivative. Although the Caputo-Fabrizio derivative, with its exponential Kernel, aimed to give a better description of the dynamics of systems with memory effect than other classic fractional derivatives, its associated integral was not fractional. To fix this defect, Atangana and Baleanu launched a new fractional operator in the Caputo and Riemann-Liouville sense [18]. Atangana-Baleanu derivative by the nonlocal and nonsingular kernel, Mittag-Leffler function, attracts more interest in applying in different fields. In the field of optimal control, the fractional derivative, in particular the Atangana-Baleanu yields improved results compared to the classical derivative (see [13, 19, 20, 32, 36]). In [26], the authors applied successfully the Caputo and Atangana-Baleanu fractional derivatives in data fitting.

Several studies have been devoted to the existence of the solutions of the fractional differential equations via various approaches, see [6, 7, 12, 17, 24, 40, 41, 51, 52]. Many latest studies in the existence theory focus on the fractional equations with the integral boundary conditions, which improve the classical conditions in the development of mathematical modeling, [11, 17, 35].

This paper which draws inspiration from the aforementioned works, investigates the existence of a solution to the following high-order fractional boundary value problem

$$\begin{aligned} \left\{ \begin{array}{lc} {}^{ABC}_{a}{D}^{\zeta } x(t)=f(t,x(t),y(t),x^{\prime }(t),y^{\prime }(t),\ldots ,x^{(n-1)}(t),y^{(n-1)}(t)), \\ {}^{ABC}_{a}{D}^{\gamma } y(t)=g(t,x(t),y(t),x^{\prime }(t),y^{\prime }(t),\ldots ,x^{(n-1)}(t),y^{(n-1)}(t)), \\ \end{array}\right. \end{aligned}$$
(1)

in which \(t\in \left[ a,b\right]\) and completed by two integral boundary conditions of the form

$$\begin{aligned} \left\{ \begin{array}{lc} x(a)=x^{'}(a)=\ldots = x^{(n-2)}(a)=0, &{} \lambda x^{(n-1)}(b)=\int _{a}^{b}y(s)ds,\\ y(a)=y^{'}(a)=\ldots = y^{(n-2)}(a)=0, &{}\mu y^{(n-1)}(b)=\int _{a}^{b}x(s)ds,\\ \end{array}\right. \end{aligned}$$
(2)

where \(\zeta ,\gamma \in (n-1,n]\) for some \(n\in {\mathbb {N}}\), \(\lambda ,\mu \in {\mathbb {R}}\), \(f,g:[a,b]\times {\mathbb {R}}^{2n}\times {\mathbb {R}}^{2n}\rightarrow {\mathbb {R}}\) are continuous functions, and \({}^{ABC}_{a}{D}^{\zeta }\) denotes the \(\zeta\) order of Atangana-Baleanu fractional derivative in the (left) Caputo sense.

To investigate the existence of the solutions in the space \(C^{n-1}([a,b])\), which is equipped with the measure of noncompactness introduced in [16], we use the Schauder fixed point theorem [50] and the generalized Darbo fixed point theorem [30].

This paper is organized as follows. In section two, the needed preliminaries from the Atangana-Baleanu fractional calculus are stated. In the third section which is the main section, firstly by setting the appropriate solution space, we provide a modified version of the measure of noncompactness on the solution space. So by introducing the main conditions of the problem (1, 2), through some preliminary lemmas and propositions we prove the main result. Also two examples have been studied in order to show the application of the main theorem.

2 Preliminaries of Fractional Calculus

Firstly, we recall the Sobolev space \(H^1(a,b)\) where \(a<b\) and

$$\begin{aligned} H^1(a,b)=\{u\in L^2(a,b); \,u'\in L^2(a,b)\}. \end{aligned}$$

Here \(u'\) is taken in the weak (distributional) sense; see [25] for more details.

Let us refer to [3, 18], from which most of the contents in this section has been adapted.

Definition 2.1

Let \(f \in H^{1} (a,b)\), \(\alpha \in [0,1]\), \(E_\alpha (t)=\sum _{k=0}^\infty \frac{t^k}{\Gamma (\alpha k+1)}\) is Mittag-Leffler function and \(B(\alpha )>0\) is a normalization function satisfying \(B(0)=B(1)=1\).

The Atangana-Baleanu fractional derivative with Mittag-Leffler nonlocal and nonsingular kernel in the (left) Caputo sense is defined by

$$\begin{aligned} ({}^{ABC}_{a}{D}^{\alpha } f)(t)=\frac{B(\alpha )}{1-\alpha }\int _{a}^{t}f'(x)E_{\alpha }\left[-\alpha \frac{(t-x)^{\alpha }}{1-\alpha }\right]dx,\ \ \text {for}\ \ \alpha \in [0,1); \end{aligned}$$
(3)

and \(({}^{ABC}_{a}{D}^{1} f)(t)=f'(t)\). The associated fractional integral is

$$\begin{aligned} ({}^{AB}_{a}{I}^{\alpha } f)(t)&=\frac{1-\alpha }{B(\alpha )}f(t)+\frac{\alpha }{B(\alpha )}({}_{a}{I}^{\alpha } f)(t). \end{aligned}$$
(4)

where \(({}_{a}I^{\alpha }f)(t)=\frac{1}{\Gamma (\alpha )}\int _{a}^{t}(t-s)^{\alpha -1}f(s)ds\) for \(\alpha >0\) and \(({}_{a}I^{0}f)(t)=f\).

Lemma 2.2

[3, 4, 18] If \(\alpha \in (0,1)\) and \(f \in H^{1}(a,b)\), then

$$\begin{aligned} ({}^{AB}_{a}{I}^{\alpha }{}^{ABC}_{a}{D}^{\alpha } f )(t)&=f(t)-f(a). \end{aligned}$$
(5)
$$\begin{aligned} ({}^{ABC}_{a}{D}^{\alpha }{}^{AB}_{a}{I}^{\alpha }f)(t)=f(t) -f(a)E_{\alpha }\left(-\frac{\alpha }{1-\alpha }(t-a)^{\alpha }\right). \end{aligned}$$
(6)

The high-order ABC-derivative and integral are defined in [4] as follows.

Definition 2.3

Let \(\alpha \in (n-1,n]\) for some \(n\in {\mathbb {N}}\) and f be such that \(f^{(n-1)}\in H^{1}(a,b)\). Then the AB-derivative of \(\alpha\)-order in the (left) Caputo sense is defined by

$$\begin{aligned} ({}_{a}^{ABC}D^{\alpha }f)(t) = ({}_{a}^{ABC}D^{\alpha -n+1}f^{(n-1)})(t), \end{aligned}$$
(7)

Moreover, the associated fractional integral of \(\alpha\)-order is defined by

$$\begin{aligned} ({}_{a}^{AB}I^{\alpha }f)(t)={}_{a}I^{n-1}({}_{a}^{AB}I^{\alpha -n+1}f)(t). \end{aligned}$$
(8)

Remark 2.4

Obviously, for \(\alpha \in (0,1]\), since \(n=1\), (8) becomes (4). Also, since \(f^{0}(t)=f(t)\), thus the formula (7) generalizes the formula (3).

The following proposition explains the action of the AB- fractional Integral on the ABC-derivative and vice versa.

Proposition 2.5

Let \(\alpha \in (n-1,n]\) for some \(n\in {\mathbb {N}}\) and f be such that \(f ^{n-1}\in H^{1}(a,b)\). Then we have

$$\begin{aligned} ({}^{AB}_{a}{I}^{\alpha }{}^{ABC}_{a}{D}^{\alpha } f )(t)&=f(t)- \sum _{k=0}^{n-1}\frac{{f^{(k)}(a)}}{k!} (t-a)^{k}. \end{aligned}$$
(9)
$$\begin{aligned} ({}^{ABC}_{a}{D}^{\alpha }{}^{AB}_{a}{I}^{\alpha } f )(t)=f(t)- f(a)E_{\alpha -n+1}\left(-\frac{\alpha -n+1}{n-\alpha }(t-a)^{\alpha -n+1}\right). \end{aligned}$$
(10)

Proof

The proof of (9) can be found in [4]. The proof of (10) is based on the definition, and one can check that easily. So we omit it for the sake of brevity. \(\square\)

3 Main Results

In this paper we discuss the existence of solution for system (1)-(2). Due to its boundary conditions we set \(C^{n-1}([a,b]) \times C^{n-1}([a,b])\) as the Banach framework for our investigation; where \(C^{n-1}([a,b])\) denotes the space of \(n-1\) times continuously differentiable functions on [a, b] with the standard norm, i.e.;

$$\begin{aligned} \Vert g\Vert _{n-1}=\max \{\Vert g\Vert _\infty ,\Vert g'\Vert _\infty ,...,\Vert g^{(n-1)}\Vert _\infty \}, \ \ \text {for all} \ g\in C^{n-1}([a,b]); \end{aligned}$$

where \(\Vert g\Vert _\infty =\max \{\vert g(t)\vert , t\in [a,b]\}\)

Let \(\zeta ,\gamma \in (n-1,n]\) for some \(n\in {\mathbb {N}}\), \(\lambda ,\mu \in {\mathbb {R}}\) and \(\phi , \psi\) as two real functions on [a, b]. Suppose the system

$$\begin{aligned} {}^{ABC}_{a}{D}^{\zeta } x(t)&=\phi (t), \ \ t\in \left[ a,b\right] , \end{aligned}$$
(11)
$$\begin{aligned} {}^{ABC}_{a}{D}^{\gamma } y(t)&=\psi (t), \ \ t\in \left[ a,b\right] , \end{aligned}$$
(12)

with the following boundary conditions:

$$\begin{aligned} x(a)&=x^{'}(a)=\ldots = x^{(n-2)}(a)=0, \end{aligned}$$
(13)
$$\begin{aligned} y(a)&=y^{'}(a)=\ldots = y^{(n-2)}(a)=0, \end{aligned}$$
(14)

and

$$\begin{aligned} \lambda x^{(n-1)}(b)&=\int _{a}^{b}y(s)ds, \end{aligned}$$
(15)
$$\begin{aligned} \mu y^{(n-1)}(b)&=\int _{a}^{b}x(s)ds. \end{aligned}$$
(16)

Lemma 3.1

Let \(\phi , \psi \in C([a,b])\) and \(\Delta := \lambda \mu -(\frac{(b-a)^{n}}{n!})^{2}\ne 0\). The solution \((x,y)\in C^{n-1}[a,b]\times C^{n-1}[a,b]\) of the boundary value system (11)-(16) is given by

$$\begin{aligned} x(t)&= \dfrac{s_{1}(\phi ,\psi )}{(n-1)!}(t-a)^{n-1}+c_{1}({}_{a} I^{n-1}\phi )(t)+c_{2}({}_{a}I^{\zeta }\phi )(t), \end{aligned}$$
(17)
$$\begin{aligned} y(t)&= \dfrac{s_{2}(\phi ,\psi )}{(n-1)!}(t-a)^{n-1}+d_{1}({}_{a} I^{n-1}\psi )(t)+d_{2}({}_{a}I^{\gamma }\psi )(t); \end{aligned}$$
(18)

where

$$\begin{aligned} s_{1}(\phi ,\psi )&=\frac{1}{\Delta } \Bigg ( -\lambda \mu c_{1}\phi (b)-\lambda \mu c_{2}({}_{a}I^{\zeta -n+1}\phi )(b)\nonumber \\&+\mu d_{1}\int _{a}^{b}({}_{a}I^{n-1}\psi )(s)ds\nonumber \\&+\mu d_{2}\int _{a}^{b}({}_{a}I^{\gamma }\psi )(s)ds -\frac{(b-a)^{n}}{n!} ( \mu d_{1}\psi (b)+ \mu d_{2}({}_{a}I^{\gamma -n+1}\psi )(b)\nonumber \\&-c_{1}\int _{a}^{b}({}_{a}I^{n-1}\phi )(s)ds - c_{2}\int _{a}^{b}({}_{a}I^{\zeta }\phi )(s)ds \big ) \Bigg ), \end{aligned}$$
(19)

and

$$\begin{aligned} s_{2}(\phi ,\psi )&=\frac{1}{\Delta } \Bigg ( -\frac{(b-a)^{n}}{n!} (c_{1}\lambda \phi (b) + c_{2}\lambda ({}_{a}I^{\zeta -n+1}\phi )(b)\nonumber \\&- d_{1}\int _{a}^{b}({}_{a}I^{n-1}\psi )(s)ds- d_{2}\int _{a}^{b}({}_{a}I^{\gamma }\psi )(s)ds) \nonumber \\&-\lambda \mu d_{1}\psi (b)-\lambda \mu d_{2}({}_{a}I^{\gamma -n+1}\psi )(b)\nonumber \\&+\lambda c_{1}\int _{a}^{b}({}_{a}I^{n-1}\phi )(s)ds +\lambda c_{2}\int _{a}^{b}({}_{a}I^{\zeta }\phi )(s)ds \big ) \Bigg ); \end{aligned}$$
(20)

in which \(c_{1}=\dfrac{n-\zeta }{B(\zeta -n+1)}\), \(c_{2}=\dfrac{\zeta -n+1}{B(\zeta -n+1)}\), \(d_{1}=\dfrac{n-\gamma }{B(\gamma -n+1)}\) and \(d_{2}=\dfrac{\gamma -n+1}{B(\gamma -n+1)}\).

Proof

In view of Proposition 2.5, by exerting the fractional integral \({}_{a}^{AB}I^{\zeta }\) on (11) under the condition (13), we obtain

$$\begin{aligned} x(t) -\frac{x^{n-1}(a)}{(n-1)!}(t-a)^{n-1}=c_{1}({}_{a}I^{n-1}\phi )(t) + c_{2}({}_{a}I^{\zeta }\phi )(t). \end{aligned}$$
(21)

Similarly, by exerting the fractional integral \({}_{a}^{AB}I^{\zeta }\) on equation (12) with (14), we obtain

$$\begin{aligned} y(t) -\frac{y^{n-1}(a)}{(n-1)!}(t-a)^{n-1}= d_{1}({}_{a}I^{n-1}\psi )(t) + d_{2}({}_{a}I^{\gamma }\psi )(t). \end{aligned}$$
(22)

By differentiating \(n-1\) times of (21) at \(t=b\) and regarding the condition (15), we derive

$$\begin{aligned} \frac{1}{\lambda }\int _{a}^{b} y(s)ds -x^{(n-1)}(a)= c_{1}\phi (b)+ c_{2}({}_{a}I^{\zeta -n+1}\phi )(b). \end{aligned}$$
(23)

Similarly, from (22), regarding the condition (16), we derive

$$\begin{aligned} \frac{1}{\mu }\int _{a}^{b} x(s)ds -y^{(n-1)}(a)= d_{1}\psi (b)+ d_{2}({}_{a}I^{\gamma -n+1}\psi )(b). \end{aligned}$$
(24)

Now, by inserting the formulation of y(s) from (22) into (23), we deduce

$$\begin{aligned}&\dfrac{d_{1}}{\lambda }\int _{a}^{b}({}_{a}I^{n-1}\psi )(s)ds +\frac{d_{2}}{\lambda }\int _{a}^{b}({}_{a}I^{\gamma }\psi )(s)ds + \frac{y^{(n-1)(a)}}{\lambda n!}(b-a)^{n}-x^{(n-1)}(a)\nonumber \\&=c_{1}\phi (b)+ c_{2}({}_{a}I^{\zeta -n+1}\phi )(b). \end{aligned}$$
(25)

Similarly, by inserting the formulation of x(s) from (21) into (24), we deduce

$$\begin{aligned}&\frac{c_{1}}{\mu }\int _{a}^{b}({}_{a}I^{n-1}\phi )(s)ds +\frac{c_{2}}{\mu }\int _{a}^{b}({}_{a}I^{\zeta }\phi )(s)ds + \frac{x^{(n-1)(a)}}{\mu n!}(b-a)^{n}-y^{(n-1)}(a)\nonumber \\&=d_{1}\psi (b)+ d_{2}({}_{a}I^{\gamma -n+1}\psi )(b). \end{aligned}$$
(26)

Obviously, from the system (25) and (26), one can obtain the quantities \(x^{(n-1)}(a)\) and \(y^{(n-1)}(a)\). Since \(x^{(n-1)}(a), y^{(n-1)}(a)\) are dependent to \(\phi ,\psi\), we denote \(x^{(n-1)}(a)\) and \(y^{(n-1)}(a)\) by \(s_{1}(\phi ,\psi )\) and \(s_{2}(\phi ,\psi )\), respectively. Thus, x(t) and y(t) have a form according to (17) and (18), respectively. \(\square\)

We consider two operators \(\Theta _{1}:C^{n-1}([a,b])\times C^{n-1}([a,b]) \rightarrow C^{n-1}([a,b])\) and \(\Theta _{2}:C^{n-1}([a,b])\times C^{n-1}([a,b]) \rightarrow C^{n-1}([a,b])\), where for each \((x,y) \in C^{n-1}([a,b])\times C^{n-1}([a,b])\), \(\Theta _{1}(x,y)\) and \(\Theta _{2}(x,y)\) are given by

$$\begin{aligned} \Theta _{1}(x,y)(t)&= s_{1}(\phi _{x,y},\psi _{x,y})\frac{(t-a)^{n-1}}{(n-1)!}+c_{1}({}_{a}I^{n-1} \phi _{x,y})(t)+c_{2}({}_{a}I^{\zeta }\phi _{x,y})(t) \end{aligned}$$
(27)
$$\begin{aligned} \Theta _{2}(x,y)(t)&= s_{2}(\phi _{x,y},\psi _{x,y})\frac{(t-a)^{n-1}}{(n-1)!}+d_{1}({}_{a}I^{n-1} \psi _{x,y})(t)+d_{2}({}_{a}I^{\gamma }\psi _{x,y})(t), \end{aligned}$$
(28)

where

$$\begin{aligned} \phi _{x,y}(t)&=f(t,x(t),y(t),x^{\prime }(t), y^{\prime }(t),\ldots ,x^{(n-1)}(t),y^{(n-1)}(t)),\\ \psi _{x,y}(t)&=g(t,x(t),y(t),x^{\prime }(t), y^{\prime }(t),\ldots ,x^{(n-1)}(t),y^{(n-1)}(t)), \end{aligned}$$

and \(s_{1},s_{2},c_{1},c_{2},d_{1},d_{2}\) are introduced in Lemma 3.1. Hence regarding to the Lemma 3.1 evidently we deduce the following Corollary.

Corollary 3.2

Suppose that \(\Delta := \lambda \mu -(\frac{(b-a)^{n}}{n!})^{2}\ne 0\). Then \((x,y)\in C^{n-1}([a,b])\times C^{n-1}([a,b])\) is a solution of system (1)-(2) if and only if \(\Theta _1(x,y)=x\) and \(\Theta _2(x,y)=y\).

Let us define the operator \(\Theta : C^{n-1}([a,b]) \times C^{n-1}([a,b]) \rightarrow C^{n-1}([a,b]) \times C^{n-1}([a,b])\) by \(\Theta (x,y) = (\Theta _{1}(x,y), \Theta _{2}(x,y))\). Hence, due to Corollary 3.2, we derive the following Corollary.

Corollary 3.3

\((x,y)\in C^{n-1}([a,b])\times C^{n-1}([a,b])\) is a solution of system (1)-(2) if and only if (x, y) be a fixed point of \(\Theta\).

The various measures of noncompactness are defined on the known spaces such as bounded continuous functions \(BC(R^{+})\), [22]; K-times continuously differentiable functions \(C^{k}(\Omega )\), [16]; Lebesgue spaces \(L^{p}(R^{n})\), [10]; Holder spaces \(C^{k,\gamma }(\Omega )\), [49]; Sobolev spaces \(W^{n,p}([0,T])\), [14].

Let us recall, in details a measure of noncompactness on k-times continuously differentiable functions \(C^{k}([a,b])\), according to [16].

Theorem 3.4

[16] Suppose Y is a bounded subset of \(C^{k}([a,b])\). For \(g\in Y, \varepsilon > 0, i\in \lbrace 0,\ldots k \rbrace\), let \(\omega (g,\varepsilon , i)= max \lbrace \vert g^{(i)}(t_{2}) - g^{(i)}(t_{1})\vert ; \ t_{1},t_{2}\in ([a,b]), \ \vert t_{1}-t_{2}\vert < \varepsilon \rbrace\), \(\omega _{k}(g,\varepsilon )= max \lbrace \omega (g,\varepsilon , i); \ 0\le i \le k\rbrace\), \(\omega _{k}(Y,\varepsilon )= sup \lbrace \omega _{k}(g,\varepsilon ); \ g\in Y\rbrace\) Then, \({\overline{\omega }}_{k}: {\mathfrak {M}}_{C^{k}([a,b])}\rightarrow [0,\infty )\) which is given by \({\overline{\omega }}_{k}(Y)= \lim \limits _{\varepsilon \rightarrow 0} \omega _{k} (Y,\varepsilon )\) is a measure of noncompactness on \(C^{k}([a,b])\).

By the following Lemma, we may compute the measure of noncompactness \({\overline{\omega }}_{k}\) on \(C^{k}([a,b])\) with a more simple formulation.

Lemma 3.5

Every bounded subset of \((C^{k}([a,b]),\Vert . \Vert _{k})\) is relatively compact in \((C^{k-1}([a,b]),\Vert . \Vert _{k-1})\).

Proof

Firstly, we prove that every bounded subset of \((C^{k}([a,b]),\Vert . \Vert _{k})\) is uniformly equicontinuous in \((C^{k-1}([a,b]),\Vert . \Vert _{k-1})\). Let Y be as a bounded subset of \(C^{k}([a,b])\) and \(r > 0\) such that for each \(g\in Y, \ \Vert g \Vert _{k}\le r\). For each \(\varepsilon > 0\), if \(\vert t_{2}-t_{1}\vert < \varepsilon\), then by mean value theorem, we have

$$\begin{aligned} \vert g(t_{2})-g(t_{1})\vert&\le \Vert g^{\prime } \Vert _{\infty }\vert t_{2}-t_{1}\vert \le r \vert t_{2}-t_{1}\vert , \nonumber \\ \vert g^{\prime }(t_{2})-g^{\prime }(t_{1})\vert&\le \Vert g^{\prime \prime } \Vert _{\infty }\vert t_{2}-t_{1}\vert \le r \vert t_{2}-t_{1}\vert \nonumber \\ \vdots \nonumber \\ \vert g^{(k-1)}(t_{2})-g^{(k-1)}(t_{1})\vert&\le \Vert g^{(k)} \Vert _{\infty }\vert t_{2}-t_{1}\vert \le r \vert t_{2}-t_{1}\vert . \end{aligned}$$

Hence, for each \(\varepsilon > 0\), by letting \(\delta =\dfrac{\varepsilon }{r}\), if \(\vert t_{2}-t_{1}\vert < \delta\) then \(\Vert g(t_{2})- g(t_{1})\Vert _{k-1}< \varepsilon\), for every \(g\in Y\). This means that Y is equicontinuous on \(C^{k-1}([a,b])\). Thus, if \(\lbrace g_{n}\rbrace \subset Y\) be an arbitrary sequence, and \(\varepsilon > 0\), by the uniform equicontinuity of \(\lbrace g_{n}\rbrace\) on \(C^{k-1}([a,b])\), there is a \(\delta > 0\) such that for all n, \(\Vert g_{n}(u) - g_{n}(v)\Vert _{k-1} < \dfrac{\varepsilon }{3}\), for all \(u,v\in [a,b]\) with \(\vert u-v\vert < \delta\).

Since [a, b] is compact, there is a finite number of points \(t_{1},\ldots ,t_{m}\) in [a, b] for which [a, b] is converted by the family of balls, centered in \(\lbrace t_{i}\rbrace _{i=1}^{m}\) with radius \(\delta\).

For each \(i\in \lbrace 1,\ldots ,m\rbrace\), \(\lbrace g_{n}(t_{i})\rbrace _{n=1}^{\infty }\) which is a bounded sequence in \({\mathbb {R}}\) has a convergent subsequence \(\lbrace g_{n_{j}}(t_i)\rbrace _{j=1}^{\infty }\) of \(\lbrace g_{n}(t_i)\rbrace _{n=1}^{\infty }\), that is convergent and as a result, Cauchy, which means \(\vert g_{n_{s}}(t_{i}) - g_{n_{l}}(t_{i})\vert < \dfrac{\varepsilon }{3}\) for \(i\in \lbrace 1,\ldots ,m\rbrace\), and \(n_{s},n_{l}\ge N\). Therefore, for any \(t\in [a,b]\), there is \(i\in \lbrace 1,\ldots ,m\rbrace\), such that \(\vert t-t_{i}\vert < \delta\) and so for \(n_{s},n_{l}\ge N\),

$$\begin{aligned} \Vert g_{n_{s}}(t)- g_{n_{l}}(t)\Vert _{k-1}&\le \Vert g_{n_{s}}(t)- g_{n_{s}}(t_{i})\Vert _{k-1} + \Vert g_{n_{s}}(t_{i})- g_{n_{l}}(t_{i})\Vert _{k-1} \\&+ \Vert g_{n_{l}}(t_{i})- g_{n_{l}}(t)\Vert _{k-1}\le \dfrac{\varepsilon }{3}+\dfrac{\varepsilon }{3}+\dfrac{\varepsilon }{3}=\varepsilon . \end{aligned}$$

Thus \(\lbrace g_{n_{j}}\rbrace _{j=1}^{\infty }\) is Cauchy in \(C^{k-1}[a,b]\) and since \(C^{k-1}[a,b]\) is a complete normed space, \(\lbrace g_{n_{j}}\rbrace _{j=1}^{\infty }\) converges to a function in \(C^{k-1}([a,b])\).

Consequently, it has been proved that any bounded subset of \(C^{k}([a,b])\) is sequentially relatively compact and, thus, relatively compact in \(C^{k-1}([a,b])\). \(\square\)

Corollary 3.6

For every bounded subset Y of \(C^{k}([a,b])\), we have \({\overline{\omega }}_{k-1}(Y)=0\).

Corollary 3.7

For every bounded subset Y of \(C^{k}([a,b])\), we have \({\overline{\omega }}_{k}(Y)= \lim \limits _{\varepsilon \rightarrow 0} \sup \limits _{g\in Y} \ \omega (g,\varepsilon ,k)\).

Proof

For any \(g\in Y\), we have \(\omega _{k}(g,\varepsilon )= max\lbrace \omega _{k-1}(g,\varepsilon ), \omega (g,\varepsilon ,k)\rbrace\). Thus, \(\omega _{k}(Y,\varepsilon )= max\lbrace \omega _{k-1}(Y,\varepsilon ), \sup \limits _{g\in Y} \omega (g,\varepsilon ,k)\rbrace\).

Then,\({\overline{\omega }}(Y)= max \lbrace {\overline{\omega }}_{k-1}(Y), \lim \limits _{\varepsilon \rightarrow 0} \sup \limits _{g\in Y} \ \omega (g,\varepsilon ,k)\rbrace =\lim \limits _{\varepsilon \rightarrow 0} \sup \limits _{g\in Y} \ \omega (g,\varepsilon ,k).\) \(\square\)

In the sequel, we set the following conditions on the system (1)–(2).

(C0) \(\Delta := \lambda \mu -(\frac{(b-a)^{n}}{n!})^{2}\ne 0\).

(C1) \(f,g: [a,b] \times {\mathbb {R}}^{2n}\rightarrow {\mathbb {R}}\) are continuous functions satisfying:

$$\begin{aligned}&\vert f(t,x_{0},y_{0},\ldots ,x_{n-1},y_{n-1}) - f (t,u_{0},v_{0},\ldots ,u_{n-1},v_{n-1})\vert \le \\&\varphi \big (\max \lbrace \vert x_{0}-u_{0}\vert , \vert y_{0}-v_{0}\vert ,\ldots ,\vert x_{n-2}-u_{n-2}\vert , \vert y_{n-2}-v_{n-2}\vert \rbrace \\&, \max \lbrace \vert x_{n-1}-u_{n-1}\vert ,\vert y_{n-1}-v_{n-1}\vert \rbrace \big ) \end{aligned}$$

and

$$\begin{aligned}&\vert g(t,x_{0},y_{0},\ldots ,x_{n-1},y_{n-1})- g (t,u_{0},v_{0},\ldots ,u_{n-1},v_{n-1})\vert \le \\&\varphi \big (\max \lbrace \vert x_{0}-u_{0}\vert , \vert y_{0}-v_{0}\vert ,\ldots ,\vert x_{n-2}-u_{n-2}\vert , \vert y_{n-2}-v_{n-2}\vert \rbrace \\&, \max \lbrace \vert x_{n-1}-u_{n-1}\vert ,\vert y_{n-1}-v_{n-1}\vert \rbrace \big ); \end{aligned}$$

where \(\varphi : [0,\infty )^{2}\rightarrow [0,\infty )\) is a non-decreasing and upper semicontinuous function with respect to it’s components and for every \(t > 0, \ \varphi (t,t) < t\).

(C2) \({\mathcal {K}}_{0}:= \max \lbrace \vert f(t,0,\ldots ,0)\vert ,\vert g(t,0,\ldots ,0)\vert ; \ t\in [a,b] \rbrace < \infty\).

For \(r>0\), denote \(B_r:=\{x\in C^{n-1}([a,b]); \Vert x\Vert _{n-1}\le r\}\).

Lemma 3.8

For every \((x,y)\in B_{r}\times B_{r}\), we have

$$\begin{aligned} \max \{\Vert \phi _{x,y} \Vert _{\infty }, \Vert \psi _{x,y} \Vert _{\infty } \}\le \varphi (r,r)+{\mathcal {K}}_{0}. \end{aligned}$$

Proof

$$\begin{aligned} \vert \phi _{x,y}(t)\vert&\le \vert f(t,x(t),y(t),x^{\prime }(t),y^{\prime }(t),\ldots ,x^{n-1}(t),y^{n-1}(t))-f(t,0,\ldots ,0)\vert \\&+ \vert f(t,0,\ldots ,0)\vert \\&\le \varphi (\max \lbrace \vert x(t)\vert ,\vert y(t)\vert ,\ldots , \vert x^{n-2}(t)\vert ,\vert y^{n-2}(t)\vert , \vert x^{n-1}(t)\vert ,\vert y^{n-1}(t)\vert \rbrace \\&+\vert f(t,0,\ldots ,0)\vert \\&\le \varphi (r,r) + {\mathcal {K}}_{0}. \end{aligned}$$

Similarly, the estimate for \(\psi _{x,y}\) will derived. \(\square\)

Lemma 3.9

For any \(m \ge 0\) and \((x,y)\in B_{r} \times B_{r}\), we have

$$\begin{aligned} \Vert {}_{a} I^{m} \phi _{x,y} \Vert _{\infty }&\le \Vert \phi _{x,y} \Vert _{\infty }\frac{(b-a)^{m}}{\Gamma (m+1)}, \end{aligned}$$

and

$$\begin{aligned} \Vert {}_{a} I^{m}\psi _{x,y} \Vert _{\infty }&\le \Vert \psi _{x,y} \Vert _{\infty }\frac{(b-a)^{m}}{\Gamma (m+1)} \end{aligned}$$

Proof

$$\begin{aligned} \vert ({}_{a} I^{m}\phi _{x,y})(t) \vert&\le \dfrac{1}{\Gamma (m)}\vert \int _{a}^{t}(t-s)^{m-1}\phi _{x,y}(s) ds \vert \\&\le \dfrac{\Vert \phi _{x,y} \Vert _{\infty }}{\Gamma (m)}\vert \int _{a}^{t} (t-s)^{m-1}ds\vert \le \dfrac{\Vert \phi _{x,y} \Vert _{\infty }(b-a)^{m}}{\Gamma (m+1)}. \end{aligned}$$

Similarly, the estimate for \({}_{a}I^{m}\psi _{x,y}\) will derived. \(\square\)

Proposition 3.10

For each \(m > 0\), \(\lbrace {}_{a}I^{m}\phi _{x,y}\rbrace _{(x,y)\in ( B_{r} \times B_{r})}\) and \(\lbrace {}_{a}I^{m}\psi _{x,y}\rbrace _{(x,y)\in ( B_{r} \times B_{r})}\) are equicontinuous subsets of \(C([a,b],\Vert . \Vert _{\infty })\).

Proof

For each \(\varepsilon > 0\) and \(t_{1},t_{2}\in [a,b]\), with \(\vert t_{1}-t_{2}\vert < \varepsilon\), we have

$$\begin{aligned} \vert ({}_{a}I^{m}\phi _{x,y})(t_{2}) - {}_{a}I^{m}\phi _{x,y})(t_{1})\vert&\le \dfrac{1}{\Gamma (m)}\vert \int _{t_{1}}^{t_{2}}(t_{2}-s)^{m-1}\phi _{x,y}(s)ds \vert \\&+\vert \int _{a}^{t_{1}}((t_{2}-s)^{m-1}- (t_{1}-s)^{m-1})\phi _{x,y}(s)ds \vert \\&\le \dfrac{\Vert \phi _{x,y} \Vert _{\infty }}{\Gamma (m+1)}\Bigg [\vert t_{2}- t_{1}\vert ^{m} + \vert (t_{2}- a)^{m} \\&- (t_{2}- t_{1})^{m}- (t_{1}- a)^{m}\vert \Bigg ]\\&\le \dfrac{\varphi (r,r) +{\mathcal {K}}_{0}}{\Gamma (m+1)}\Bigg [\vert t_{2}- t_{1}\vert ^{m} + \vert (t_{2}- a)^{m} \\&- (t_{2}- t_{1})^{m}- (t_{1}- a)^{m}\vert \Bigg ] \end{aligned}$$

Since the right hand side of the last inequality tends to zero, uniformly, with respect to \((x,y)\in B_{r} \times B_{r}\) when \(\varepsilon \rightarrow 0\), we can find that \(\delta = \delta (\varepsilon ) > 0\), where if \(\vert t_{1}-t_{2} \vert < \delta\), then \(\Vert ({}_{a}I^{m}\phi _{x,y})(t_{2}) - {}_{a}I^{m}\phi _{x,y})(t_{1})\Vert < \varepsilon\), for all \((x,y)\in B_{r} \times B_{r}\). \(\square\)

Lemma 3.11

For every \((x,y) \in B_{r}\times B_{r}\), we have \(\vert s_{1} (\phi _{x,y},\psi _{x,y})\vert \le \varsigma _{1}(\varphi (r,r)+{\mathcal {K}}_{0})\) and \(\vert s_{2} (\phi _{x,y},\psi _{x,y})\vert \le \varsigma _{2}(\varphi (r,r)+{\mathcal {K}}_{0});\) where

$$\begin{aligned} \varsigma _{1}&:= \frac{1}{\vert \Delta \vert } \big (c_{1}\vert \lambda \mu \vert + c_{2}\vert \lambda \mu \vert \dfrac{(b-a)^{\zeta -n+1}}{\Gamma (\zeta -n+2)}+d_{1}\vert \mu \vert \dfrac{(b-a)^{n}}{\Gamma (n)} +d_{2}\vert \mu \vert \dfrac{(b-a)^{\gamma +1}}{\Gamma (\gamma +1)}\\&+ d_{1}\vert \mu \vert \dfrac{(b-a)^{n}}{ n!} + d_{2}\vert \mu \vert \dfrac{(b-a)^{\gamma +1}}{n! \Gamma (\gamma -n+2)} + c_{1}\dfrac{(b-a)^{2n}}{n!\Gamma (n)} + c_{2}\dfrac{(b-a)^{\zeta +n +1}}{n!\Gamma (\zeta +1)}\big ) \end{aligned}$$

and

$$\begin{aligned} \varsigma _{2}&:= \frac{1}{\vert \Delta \vert } \big (d_{1}\vert \lambda \mu \vert + d_{2}\vert \lambda \mu \vert \dfrac{(b-a)^{\gamma -n+1}}{\Gamma (\gamma -n+2)}+c_{1}\vert \lambda \vert \dfrac{(b-a)^{n}}{\Gamma (n)} +c_{2}\vert \lambda \vert \dfrac{(b-a)^{\zeta +1}}{\Gamma (\zeta +1)}\\&+ c_{1}\vert \lambda \vert \dfrac{(b-a)^{n}}{ n!} + c_{2}\vert \lambda \vert \dfrac{(b-a)^{\zeta +1}}{n! \Gamma (\zeta -n+2)} + d_{1}\dfrac{(b-a)^{2n}}{n!\Gamma (n)} + d_{2}\dfrac{(b-a)^{\gamma +n +1}}{n!\Gamma (\gamma +1)}\big ), \end{aligned}$$

in which \(c_1, c_2, d_1, d_2\) are introduced in the Lemma 3.1.

Proof

By the definition of the Riemann-Liouville fractional integral of order \(\alpha\), which is

$$\begin{aligned} ({}_{a}I^{\alpha }f)(t)=\frac{1}{\Gamma (\alpha )}\int _{a}^{t}(t-s)^{\alpha -1}f(s)ds, \end{aligned}$$

and since \(\Vert \phi _{x,y}\Vert _\infty , \Vert \psi _{x,y}\Vert _\infty\) are

$$\begin{aligned} \Vert \phi _{x,y}\Vert _\infty =\max \{\vert \phi _{x,y}(t)\vert , t\in [a,b]\}, \\ \Vert \psi _{x,y}\Vert _\infty =\max \{\vert \psi _{x,y}(t)\vert , t\in [a,b]\}, \end{aligned}$$

and by using Lemma 3.8, we have

$$\begin{aligned} \vert s_{1} (\phi _{x,y},\psi _{x,y})\vert&\le \dfrac{1}{\vert \Delta \vert }\Bigg [ c_{1}\vert \lambda \mu \vert \vert \phi _{x,y}(b) \vert + c_{2}\vert \lambda \mu \vert \vert ({}_{a}I^{\zeta - n+1}\phi _{x,y})(b)\vert \\&+d_{1}\vert \mu \vert \vert \int _{a}^{b}({}_{a}I^{n-1}\psi _{x,y})(s)ds\vert + d_{2}\vert \mu \vert \vert \int _{a}^{b}({}_{a}I^{\gamma }\psi _{x,y})(s)ds\vert \\&+\dfrac{(b-a)^{n}}{n!}d_{1}\vert \mu \vert \vert \psi _{x,y}(b)\vert + \dfrac{(b-a)^{n}}{n!}d_{2}\vert \mu \vert \vert ({}_{a}I^{\gamma - n+1}\psi _{x,y})(b)\vert \\&+ \dfrac{(b-a)^{n}}{n!}c_{1} \vert \int _{a}^{b}({}_{a}I^{n-1}\phi _{x,y})(s)ds\vert +\dfrac{(b-a)^{n}}{n!}c_{2} \vert \int _{a}^{b}({}_{a}I^{\zeta }\phi _{x,y})(s)ds\vert \Bigg ]\\&\le \dfrac{1}{\vert \Delta \vert }\Bigg [ c_{1}\vert \lambda \mu \vert + c_{2}\vert \lambda \mu \vert \dfrac{(b-a)^{\zeta -n+1}}{\Gamma (\zeta -n+2)}+d_{1}\vert \mu \vert \dfrac{(b-a)^{n}}{\Gamma (n)} +d_{2}\vert \mu \vert \dfrac{(b-a)^{\gamma +1}}{\Gamma (\gamma +1)}\\&+ d_{1}\vert \mu \vert \dfrac{(b-a)^{n}}{ n!} + d_{2}\vert \mu \vert \dfrac{(b-a)^{\gamma +1}}{n! \Gamma (\gamma -n+2)} + c_{1}\dfrac{(b-a)^{2n}}{n!\Gamma (n)} + c_{2}\dfrac{(b-a)^{\zeta +n +1}}{n!\Gamma (\zeta +1)}\Bigg ] \\&\times max ( \Vert \phi _{x,y}\Vert _{\infty },\Vert \psi _{x,y} \Vert _{\infty } ) \\&= \varsigma _{1}max ( \Vert \phi _{x,y}\Vert _{\infty },\Vert \psi _{x,y} \Vert _{\infty } )\\&\le \varsigma _{1}(\varphi (r,r)+{\mathcal {K}}_{0}) \end{aligned}$$

Similarly, it can be shown that \(\vert s_{2} (\phi _{x,y},\psi _{x,y})\vert \le \varsigma _{2}(\varphi (r,r)+{\mathcal {K}}_{0})\). \(\square\)

Proposition 3.12

There exists \(r > 0\) such that \(T_{1},T_{2}\) maps \(B_{r}\times B_{r}\) onto \(B_{r}\), provided \(\max \{\eta _{1},\eta _{2}\} < 1\), where

$$\begin{aligned} \eta _{1}:= \max \limits _{0\le m \le n-2}\left\lbrace \dfrac{(b-a)^{n-1-m}}{\Gamma (n-m)},1\right\rbrace (\varsigma _{1}+c_{1}) +c_{2} \max \limits _{0\le m \le n-1}\left\lbrace \dfrac{(b-a)^{\zeta -m}}{\Gamma (\zeta -m+1)}\right\rbrace \\ \end{aligned}$$

and

$$\begin{aligned} \eta _{2}:= \max \limits _{0\le m \le n-2}\left\lbrace \dfrac{(b-a)^{n-1-m}}{\Gamma (n-m)},1\right\rbrace (\varsigma _{2}+d_{1}) +d_{2} \max \limits _{0\le m \le n-1}\left\lbrace \dfrac{(b-a)^{\gamma -m}}{\Gamma (\gamma -n+1)}\right\rbrace ; \end{aligned}$$

in which \(\varsigma _{1},\varsigma _{2}\) are introduced in the Lemma 3.11.

Proof

For every \(m\in \lbrace 0,\ldots , n-2\rbrace\), we have

$$\begin{aligned} \dfrac{d^{m}T_{1}(x,y)}{dt^{m}} = s_{1}(\phi _{x,y},\psi _{x,y})\frac{(t-a)^{n-1-m}}{(n-1-m)!} + c_{1}({}_{a}I^{n-1-m}\phi _{x,y})(t) + c_{2}({}_{a}I^{\zeta -m}\phi _{x,y})(t) \end{aligned}$$

and

$$\begin{aligned} \dfrac{d^{n-1}T_{1}(x,y)}{dt^{n-1}} = s_{1}(\phi _{x,y},\psi _{x,y}) + c_{1}\phi _{x,y}(t) + c_{2}({}_{a}I^{\zeta -n+1}\phi _{x,y})(t) \end{aligned}$$

Thus, by Lemma 3.9

$$\begin{aligned} \Vert T_{1}(x,y) \Vert _{n-1}\le \vert s_{1}(\phi _{x,y},\psi _{x,y}) \vert \max \limits _{0\le m\le n-2}\left\lbrace \dfrac{(b-a)^{n-1-m}}{(n-1-m)!},1 \right\rbrace \\+c_{1}\max \limits _{0\le m\le n-2}\left\lbrace \dfrac{(b-a)^{n-1-m}}{\Gamma (n-m)},1 \right\rbrace \Vert \phi _{x,y} \Vert _{\infty } \\+c_{2}\max \limits _{0\le m\le n-2}\left\lbrace \dfrac{(b-a)^{\zeta -m}}{\Gamma (\zeta -m +1)} \right\rbrace \Vert \phi _{x,y} \Vert _{\infty } \end{aligned}$$

Hence, by Lemma 3.11

$$\begin{aligned} \Vert T_{1}(x,y)\Vert _{n-1}\le \Bigg (\max \limits _{0\le m \le n-2}\left\lbrace \dfrac{(b-a)^{n-1-m}}{\Gamma (n-m)},1\right\rbrace (\varsigma _{1}+c_{1}) \\\ \ \ \ \ \ \ \ +c_{2} \max \limits _{0\le m \le n-1}\left\lbrace \dfrac{(b-a)^{\zeta -m}}{\Gamma (\zeta -m+1)}\right\rbrace \Bigg ) \Bigg (\varphi (r,r)+{\mathcal {K}}_{0} \Bigg ):=\eta _{1}\varphi (r,r)+\xi _{1} \end{aligned}$$

Thus, \(\Theta _{1}\) is a self map on \(B_{r}\times B_{r}\) provided \(\eta _{1}\varphi (r,r)+ \xi _{1} \le r\). Since \(\varphi (r,r) < r\) and due to the assumption, \(\eta _{1} < 1\), the desired result will be obtained for \(r > \dfrac{\xi _{1}}{1- \eta _{1}}\). Similarly, we obtain

$$\begin{aligned} \Vert \Theta _{2}(x,y)\Vert _{n-1}\le \Bigg (\max \limits _{0\le m \le n-2}\left\lbrace \dfrac{(b-a)^{n-1-m}}{\Gamma (n-m)},1\right\rbrace (\varsigma _{2}+d_{1})\\\ \ \ \ \ \ \ \ +d_{2}\max \limits _{0\le m \le n-1}\left\lbrace \dfrac{(b-a)^{\gamma -m}}{\Gamma (\gamma -n+m)}\right\rbrace \Bigg ) \Bigg (\varphi (r,r)+{\mathcal {K}}_{0} \Bigg )\\:=\eta _{2}\varphi (r,r)+\xi _{2} \end{aligned}$$

Thus, for \(r >\dfrac{\xi _{2}}{1- \eta _{2}}\), \(\Theta _{2}\) maps \(B_{r}\times B_{r}\) onto \(B_{r}\). Hence, by choosing \(r > \max \lbrace \dfrac{\xi _{1}}{1-\eta _{1}}, \dfrac{\xi _{2}}{1-\eta _{2}} \rbrace\), both \(\Theta _{1}\) and \(\Theta _{2}\) are self maps on \(B_{r}\times B_{r}\). \(\square\)

Proposition 3.13

\(\lbrace \Theta _{1}(x,y)\rbrace _{(x,y)\in B_{r} \times B_{r}}\) and \(\lbrace \Theta _{2}(x,y)\rbrace _{(x,y)\in B_{r} \times B_{r}}\) are equicontinuous subsets of \(C^{n-1}([a,b])\), provided \(\varphi (t,s)\le {\overline{\varphi }}(t)\) for some functions \({\overline{\varphi }}: [0,\infty )\rightarrow [0,\infty )\) which is non-decreasing and upper semicontinuous and for \(t > 0\), \({\overline{\varphi }}(t) < t\).

Proof

Regarding Lemma 3.5, we shall only check that \(\lbrace \dfrac{d^{n-1}\Theta _{1}(x,y)}{dt^{n-1}}\rbrace _{(x,y) \in B_{r}\times B_{r}}\) be equicontinuous on [a, b]. Since

$$\begin{aligned} \dfrac{d^{n-1}\Theta _{1}(x,y)}{dt^{n-1}} = s_{1}(\phi _{x,y},\psi _{x,y}) + c_{1}\phi _{x,y}(t) + c_{2}({}_{a}I^{\zeta -n+1}\phi _{x,y})(t), \end{aligned}$$

and according to Proposition 3.10, \(\lbrace ({}_{a}I^{\zeta -n+1})\rbrace \phi _{(x,y)\in B_{r}\times B_{r} }\) is equicontinuous. Thus it remains that we show \(\lbrace \phi _{x,y} \rbrace\) is equicontinuous on \(B_{r}\times B_{r}\). Indeed,

$$\begin{aligned} \vert \phi _{x,y}(t_{2}) - \phi _{x,y}(t_{1}) \vert&\le \vert f(t_{2},x(t_{2}),y(t_{2}),\ldots , x^{n-1}(t_{2}), y^{n-1}(t_{2})\\&- f (t_{2},x(t_{1}),y(t_{1}),\ldots , x^{n-1}(t_{1}), y^{n-1}(t_{1})\vert \\&+ \vert f(t_{2},x(t_{1}),y(t_{1}),\ldots , x^{n-1}(t_{1}), y^{n-1}(t_{1}) \\&- f(t_{1},x(t_{1}),y(t_{1}),\ldots , x^{n-1}(t_{1}), y^{n-1}(t_{1}) \vert \\&\le {\overline{\varphi }}(\max \lbrace \vert x(t_{2})-x(t_{1})\vert , \vert y(t_{2})-y(t_{1})\vert ,\ldots \\&, \vert x^{n-2}(t_{2})-x^{n-2}(t_{1})\vert , \vert y^{n-2}(t_{2})-y^{n-2}(t_{1})\vert \rbrace ) +\Lambda (\delta ) \\&\le {\overline{\varphi }}(r \vert t_{2}-t_{1}\vert ) +\Lambda (\delta )\\&\le r \vert t_{2}-t_{1}\vert + \Lambda (\delta ), \end{aligned}$$

in which

$$\begin{aligned} \Lambda (\delta ) = \sup _{\vert t_{1}-t_{2}\vert < \delta } \lbrace&\vert f(t_{2},x(t_{1}),y(t_{1}),\ldots , x^{n-1}(t_{1}), y^{n-1}(t_{1})\\&- f(t_{1},x(t_{1}),y(t_{1}),\ldots , x^{n-1}(t_{1}), y^{n-1}(t_{1}) \vert \rbrace . \end{aligned}$$

Since \(\lim \limits _{\delta \rightarrow 0}\Lambda (\delta ) = 0\), thus for an arbitrary \(\varepsilon > 0\) we can choose \(\delta _1 > 0\) where for \(\delta <\delta _{1}\), we have \(\Lambda (\delta ) < \dfrac{\varepsilon }{2}\) and by taking \(\delta \le min\lbrace \delta _{1},\dfrac{\varepsilon }{2r} \rbrace\), we have

$$\begin{aligned} \vert \phi _{x,y}(t_{2}) - \phi _{x,y}(t_{1})\vert \le \dfrac{\varepsilon }{2} + \dfrac{\varepsilon }{2} = \varepsilon . \end{aligned}$$

\(\square\)

Theorem 3.14

Assume the conditions (C0)–(C2). Then the boundary value system (1)–(2) has at least one solution in \(C^{n-1}([a,b])\), provided \(\max \{\eta _{1},\eta _{2} \}< 1\), where \(\eta _{1},\eta _{2}\) are introduced in the proposition 3.12.

Proof

Let the well defined operator \(\Theta : C^{n-1}([a,b]) \times C^{n-1}([a,b]) \rightarrow C^{n-1}([a,b]) \times C^{n-1}([a,b])\) by \(\Theta (x,y) = (\Delta _{1}(x,y), \Theta _{2}(x,y))\), where \(\Theta _1, \Theta _2\) are introduced in (27) and (28); respectively. For \(r > 0\) introduced in the Proposition 3.12, we have \(\Theta (B_{r} \times B_{r})\subset B_{r} \times B_{r}\). Let us prove the assertion in two cases. If \(\varphi\) satisfies the condition of Proposition 3.13, \(\Theta _{1}\) and \(\Theta _{2}\) are equicontinuous on \(B_{r} \times B_{r}\), where regarding the Arzela-Ascoli Theorem, \(\Theta _1\), \(\Theta _2\) are compact operators on \(B_r\times B_r\). Therefore, by Schauder fixed point theorem [8], \(\Theta\) has at least one fixed point in \(B_{r} \times B_{r}\), and due to the Corollary 3.3, the boundary value system (1)–(2) has at least one solution in \(B_{r} \times B_{r}\).

In the case that \(\varphi\) does not satisfy the condition of Proposition 3.13, since \(\varphi\) can not be replaced by \({\overline{\varphi }}\), which is independent of s we can not necessarily deduce that \(\Theta _{1},\Theta _{2}\) are compact operators, whereas by using the concept of measure of noncompactness on \(C^{n-1}([a,b])\) and applying a generalization of Schauder fixed point theorem, named generalized Darbo theorem (see [9], Corollary 2.2) we deduce the existence of a fixed point for the operator T. Firstly, we claim that

$$\begin{aligned} {\overline{\omega }}_{n-1}(\Theta _{1}(B_{r}\times B_{r})) \le c_{1}\varphi ({\overline{\omega }} _{n-1}(B_{r})) \end{aligned}$$

To this end, let \(\varepsilon > 0, t_{1},t_{2}\in [a,b]\) and \(\vert t_{1}-t_{2}\vert \le \varepsilon\). Then we have

$$\begin{aligned} \omega (\Theta _{1}(x,y),\varepsilon , n-1)&=\max \limits _{t_{1},t_{2}\in [a,b],\vert t_{1}-t_{2}\vert< \varepsilon } \lbrace \vert \dfrac{d^{n-1}\Theta _{1}(x,y)(t_{2})}{dt^{n-1}} - \dfrac{d^{n-1}\Theta _{1}(x,y)(t_{1})}{dt^{n-1}} \vert \rbrace \nonumber \\&\le \max \limits _{t_{1},t_{2}\in [a,b],\vert t_{1}-t_{2}\vert < \varepsilon } \lbrace c_{1}\vert \phi _{x,y}(t_{2}) - \phi _{x,y}(t_{1})\vert \nonumber \\&+ c_{2}\vert ({}_{a}I^{\zeta -n+1}\phi _{x,y})(t_{2}) - ({}_{a}I^{\zeta -n+1}\phi _{x,y})(t_{1}) \vert \rbrace \nonumber \\&= c_{1}\omega (\phi _{x,y},\varepsilon ,0) + c_{2}\omega ({}_{a}I^{\zeta -n+1} \phi _{x,y},\varepsilon ,0). \end{aligned}$$
(29)

Moreover,

$$\begin{aligned} \vert \phi _{x,y}(t_{2}) - \phi _{x,y}(t_{1}) \vert&\le \vert f(t_{2},x(t_{2}),y(t_{2}),\ldots , x^{n-1}(t_{2}), y^{n-1}(t_{2}))\nonumber \\&- f (t_{2},x(t_{1}),y(t_{1}),\ldots , x^{n-1}(t_{1}), y^{n-1}(t_{1}))\vert \nonumber \\&+ \vert f(t_{2},x(t_{1}),y(t_{1}),\ldots , x^{n-1}(t_{1}), y^{n-1}(t_{1}) )\nonumber \\&- f(t_{1},x(t_{1}),y(t_{1}),\ldots , x^{n-1}(t_{1}), y^{n-1}(t_{1})) \vert \nonumber \\&\le \varphi \Big (\max \lbrace \vert x(t_{2})-x(t_{1})\vert , \vert y(t_{2})-y(t_{1})\vert ,\ldots \nonumber \\&, \vert x^{n-2}(t_{2})-x^{n-2}(t_{1})\vert , \vert y^{n-2}(t_{2})-y^{n-2}(t_{1})\vert \rbrace \nonumber \\&,\max \lbrace \vert x^{n-1}(t_{2})-x^{n-1}(t_{1})\vert ,\vert y^{n-1}(t_{2})-y^{n-1}(t_{1})\vert \rbrace \Big ) +\Lambda (\varepsilon )\nonumber \\&\le \varphi \Big (r \vert t_{2}-t_{1}\vert , \max \lbrace \vert x^{n-1}(t_{2})-x^{n-1}(t_{1})\vert ,\vert y^{n-1}(t_{2})-y^{n-1}(t_{1})\rbrace \Big ) \nonumber \\&+\Lambda (\varepsilon )\nonumber \\&\le \varphi (r \varepsilon , \max \lbrace \omega (x,\varepsilon , n-1), \omega (y,\varepsilon , n-1)\rbrace )+ \Lambda (\varepsilon ) ; \end{aligned}$$
(30)

where

$$\begin{aligned} \Lambda (\varepsilon ) = \sup _{\vert t_{1}-t_{2}\vert < \varepsilon } \lbrace \vert&f(t_{2},x(t_{1}),y(t_{1}),\ldots , x^{n-1}(t_{1}), y^{n-1}(t_{1})\\&- f(t_{1},x(t_{1}),y(t_{1}),\ldots , x^{n-1}(t_{1}), y^{n-1}(t_{1}) \vert \rbrace . \end{aligned}$$

Hence

$$\begin{aligned} \omega (\Theta _{1}(x,y),\varepsilon , n-1)&\le c_{1}\varphi (r \varepsilon , \max \lbrace \omega (x,\varepsilon , n-1), \omega (y,\varepsilon , n-1)\rbrace )\\&\ \ \ +c_2\omega ( {}_{a}I^{\zeta -n+1} \phi _{x,y},\varepsilon ,0)+\Lambda (\varepsilon ). \end{aligned}$$

Thus,

$$\begin{aligned} \sup _{(x,y)\in B_r\times B_r}\omega _{n-1}(\Theta _{1}(B_{r}\times B_{r}),\varepsilon )&= c_{1}\sup _{(x,y)\in B_r\times B_r}\varphi (r \varepsilon , \omega _{n-1} (B_{r},\varepsilon )) \\&+ c_2\sup _{(x,y)\in B_{r}\times B_{r}}\omega ( {}_{a}I^{\zeta -n+1} \phi _{x,y},\varepsilon ,0)+\Lambda (\varepsilon ). \end{aligned}$$

By uniform continuity of f on \([a,b] \times [-r,r]^{2n-2}\), \(\Lambda (\varepsilon ) \rightarrow 0\), as \(\varepsilon \rightarrow 0\). Further, from Proposition 3.10 we deduce that \(\omega ( {}_{a}I^{\zeta -n+1} \phi _{x,y},\varepsilon ,0)\rightarrow 0\) as \(\varepsilon \rightarrow 0\) uniformly with respect to \((x,y)\in B_{r}\times B_{r}\). Therefore,

$$\begin{aligned} {\overline{\omega }}_{n-1}(\Theta _{1}(B_{r}\times B_{r})) \le c_{1}\varphi ({\overline{\omega }} _{n-1}(B_{r})). \end{aligned}$$

Similarly, we have

$$\begin{aligned} {\overline{\omega }}_{n-1}(\Theta _{2}(B_{r}\times B_{r})) \le d_{1}\varphi ({\overline{\omega }} _{n-1}(B_{r})). \end{aligned}$$

If \(\rho : {\mathfrak {M}}_{C^{n-1}([a,b]) \times C^{n-1}([a,b])}\rightarrow [0,\infty )\) is defined by \(\rho (Y_{1} \times Y_{2})= max\lbrace {\overline{\omega }}_{n-1}(Y_{1}),{\overline{\omega }}_{n-1}(Y_{2}) \rbrace\), it is known that \(\rho\) is a measure of noncompactness on \(C^{n-1}([a,b]) \times C^{n-1}([a,b])\), based on [21]. Further, since, \(\Theta (B_{r}\times B_{r})\subseteq \Theta _{1}(B_{r}\times B_{r})\times \Theta _{2}(B_{r}\times B_{r})\), we have

$$\begin{aligned} \rho (\Theta (B_{r}\times B_{r}))&\le \rho (\Theta _{1}(B_{r}\times B_{r})\times \Theta _{2}(B_{r}\times B_{r}))\\&=\max \lbrace {\overline{\omega }}_{n-1}(\Theta _{1}(B_{r}\times B_{r})) , {\overline{\omega }}_{n-1}(\Theta _{2}(B_{r}\times B_{r}))\rbrace \\&=\max \lbrace c_{1},d_{1}\rbrace \varphi ( {\overline{\omega }}_{n-1}(B_{r} )) \\&= \max \lbrace c_{1},d_{1}\rbrace \varphi (\rho (B_{r}\times B_{r})). \end{aligned}$$

Indeed \(\max \lbrace c_{1},d_{1}\rbrace<\max \lbrace \eta _{1},\eta _{2}\rbrace < 1\) Thus, by applying Corollary 2.2 of [9], for \(\Upsilon (t)= \max \lbrace c_1,d_1\rbrace \varphi (t)\) which is admissible, \(\Theta\) has at least one fixed point in \(C^{n-1}([a,b]) \times C^{n-1}([a,b])\); which, due to the Corollary 3.3, means that the boundary value system (1),(2) has at least one solution in \(B_{r} \times B_{r}\). \(\square\)

Example 3.15

Consider

$$\begin{aligned} \left\{ \begin{array}{lc} {}^{ABC}_{0}{D}^{\frac{10}{6}} x(t)=\frac{1}{4}\sin (x(t)+y(t))-\dfrac{1}{5\sqrt{1+t^2}} \arctan (y'(t))+\frac{1}{4}\sqrt{1+(x'(t))^2} \\ {}^{ABC}_{0}{D}^{\frac{7}{4}} y(t)=\frac{1}{10(1+t^2)}\cos (x(t))+\dfrac{y'(t)e^{-t}}{1+y'(t)}\\ \end{array}\right. \end{aligned}$$
(31)

for \(t\in [0,1]\), completed by two integral boundary conditions of the form

$$\begin{aligned} \left\{ \begin{array}{lc} x(0)=0,&{} x^{'}(1)= \int _{0}^{1}y(s)ds,\\ y(0)=0,&{} y^{'}(1)=\frac{1}{2}\int _{0}^{1}x(s)ds.\\ \end{array}\right. \end{aligned}$$
(32)

This system is an example of the system (1)-(2) with \([a,b]=[0,1]\), \(\zeta =\frac{10}{6},\gamma =\frac{7}{4},\) and thus \(n=2\). Moreover, \(\lambda =1, \mu =2\),

$$\begin{aligned} f(t,x_0,y_0,x_1,y_1)=\frac{1}{4}\sin (x_0+y_0)-\dfrac{1}{5\sqrt{1+t^2}} \arctan (y_1)+\frac{1}{4}\sqrt{1+x_1^2} \end{aligned}$$

and

$$\begin{aligned} g(t,x_0,y_0,x_1,y_1)=\frac{1}{10(1+t^2)}\cos (x_0)+\dfrac{y_1e^{-t}}{1+y_1}. \end{aligned}$$

evidently, according to the condition (C0) we have \(\Delta = \dfrac{7}{4} \ne 0\). Further, we have

$$\begin{aligned} \vert f(t,x_0,y_0,x_1,y_1)-f(t, u_0,v_0,u_1,v_1)\vert&\le \frac{1}{4}\vert \sin (x_0+y_0)-\sin (u_0+v_0)\vert \\&\quad +\frac{1}{5\sqrt{1+t^2}}\vert \arctan (y_1)-\arctan (v_1)\vert \\&\quad +\frac{1}{4}\vert \sqrt{1+x_1^2}-\sqrt{1+u_1^2}\vert \\&\le \frac{1}{4}(\vert x_0-u_0\vert +\vert y_0-v_0\vert )\\&\quad +\frac{1}{5}\vert y_1-v_1\vert +\frac{1}{4}\vert x_1-u_1\vert . \end{aligned}$$

Moreover,

$$\begin{aligned} \vert g(t,x_0,y_0,x_1,y_1)-g(t, u_0,v_0,u_1,v_1)\vert&\le \frac{1}{10}\vert \cos (x_0)-\cos (y_0)\vert \\&\ \ \ +e^{-t}\vert \frac{y_1}{1+y_1}-\frac{v_1}{1+v_1}\vert \\ {}&\le \frac{1}{10}\vert x_0-u_0\vert +\frac{1}{e}\vert y_1-v_1\vert . \end{aligned}$$

Therefor, with \(\varphi (t,s):=\frac{1}{2}t+\frac{9}{20}s\) condition (C1) is fulfilled. Also according to condition (C2), \(\kappa _0=\frac{1}{10}\) and using maple, we obtain \(\varsigma _1=0.5749179761\), \(\varsigma _2=0.5881253745\) and so \(\eta _1=0.7892822650\) and \(\eta _2=0.8013351624\). Hence due to the Theorem 3.14, the system (31)-(32) has a solution in \(C^1([0,1])\).

Here, we applied the following normalization function, that is involved in the Definition of Atangana-Baleanu fractional derivative,

$$\begin{aligned} B(t):={\left\{ \begin{array}{ll} 6t+1; \ \ \ \ \ \ \ \ \ 0\le t\le \frac{2}{3};\\ 5;\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{2}{3}<t<\frac{3}{4};\\ -16t+17;\ \ \ \frac{3}{4}\le t\le 1. \end{array}\right. } \end{aligned}$$

Example 3.16

Consider

$$\begin{aligned} \left\{ \begin{array}{lc} {}^{ABC}_{1}{D}^{\frac{19}{7}} x(t)=\frac{1}{5}\ln (1+\vert x(t)\vert )+\frac{1}{2}y''(t)-\frac{1}{20}e^{\cos (y(t)+x''(t))} \\ {}^{ABC}_{1}{D}^{\frac{7}{3}} y(t)=\dfrac{x^2(t)}{1+x^2(t)}-\frac{1}{10}(1+\vert y(t)+y'(t)\vert )^\frac{1}{2}+\frac{1}{12}\sin (x''(t))\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +\frac{1}{10}e^{-x'(t)}+\frac{1}{15}y''(t) \end{array}\right. \end{aligned}$$
(33)

for \(t\in [1,2]\), completed by two integral boundary conditions of the form

$$\begin{aligned} \left\{ \begin{array}{lc} x(1)=x'(1)=0,&{} x^{''}(2)= 4\int _{1}^{2}y(s)ds,\\ y(1)=y'(1)=0,&{} y^{''}(2)=\frac{1}{3}\int _{1}^{2}x(s)ds.\\ \end{array}\right. \end{aligned}$$
(34)

This system is an example of the system (1)-(2) with \([a,b]=[1,2]\), \(\zeta =\frac{19}{7},\gamma =\frac{7}{3},\) and thus \(n=3\). Moreover, \(\lambda =\frac{1}{4}, \mu =3\),

$$\begin{aligned} f(t,x_0,y_0,x_1,y_1,x_2,y_2)=\frac{1}{5}\ln (1+\vert x_0\vert )+\frac{1}{2}y_2-\frac{1}{20}e^{\cos (y_0+x_2)} \end{aligned}$$

and

$$\begin{aligned} g(t,x_0,y_0,x_1,y_1,x_2,y_2)=\dfrac{x_0^2}{1+x_0^2}-\frac{1}{10}(1+\vert y_0+y_1\vert )^\frac{1}{2}+\frac{1}{12}\sin (x_2)+\frac{1}{10}e^{-x_1}+\frac{1}{15}y_2. \end{aligned}$$

evidently, according to the condition (C0) we have \(\Delta = \dfrac{13}{18} \ne 0\). Further, we have

$$\begin{aligned} \vert f(t,x_0,y_0,x_1,y_1,x_2,y_2)&-f(t, u_0,v_0,u_1,v_1,u_2,v_2)\vert \\&\le \frac{1}{5}\vert \ln (1+\vert x_1\vert )-\ln (1+\vert u_1\vert )\vert \\&\ \ \ +\frac{1}{2}\vert y_2-v_2\vert +\frac{1}{20}\vert e^{\cos (y_0+x_2)-e^{\cos (v_0+u_2)}}\vert \\&\le \frac{1}{5}\ln (1+\vert x_1-u_1\vert )+\frac{1}{2}\vert y_2-v_2\vert \\&\ \ \ +\frac{e}{20}(\vert y_0-v_0\vert +\vert x_2-u_2\vert ). \end{aligned}$$

The last inequality is due to the the monotonicity of \(\ln (1+t)\) and the boundedness of the derivative of \(e^{\cos (t)}\). Moreover, we have

$$\begin{aligned}&\vert g(t,x_0,y_0,x_1,y_1,x_2,y_2) -g(t, u_0,v_0,u_1,v_1,u_2,v_2)\vert \\&\le \vert \frac{x_0^2}{1+x_0^2}-\frac{u_0^2}{1+u_0^2}\vert +\frac{1}{10}\big \vert (1+ \vert y_0-y_1\vert )^\frac{1}{2} -(1+\vert v_0-v_1\vert )^\frac{1}{2}\big \vert \\&\ \ \ \ +\frac{1}{12}\vert \sin (x_2)-\sin (u_2)\vert +\frac{1}{15}\vert y_2-v_2\vert +\frac{1}{10}\vert e^{-x_1}-e^{-u_1}\vert \\&\le \frac{3\sqrt{3}}{8}\vert x_0-u_0\vert +\frac{1}{20} \big (\vert y_0-v_0\vert +\vert y_1-v_1\vert \big )+\frac{1}{12}\vert x_2-u_2\vert \\&\ \ \ \ +\frac{1}{15}\vert y_2-v_2\vert +\frac{1}{10e}\vert x_1-u_1\vert , \end{aligned}$$

where the last inequality comes from the boundedness of the derivative of the functions \(\frac{t^2}{1+t^2}\), \(\sqrt{1+t}\), \(\sin t\) and \(e^{-t}\).

Since

$$\begin{aligned} \frac{1}{5}\ln (1+t)+\left(\frac{e}{10}+\frac{1}{2}\right) t\le \big (\frac{3\sqrt{3}}{8}+\frac{1}{10}t+\frac{1}{12}+\frac{1}{15}+\frac{1}{10e}\big)t. \end{aligned}$$

Therefor, by considering

$$\begin{aligned} \varphi (t,s):=\big (\frac{3\sqrt{3}}{8}+\frac{1}{10}t+\frac{1}{10e}\big )t+(\frac{1}{12}+\frac{1}{15})s \end{aligned}$$

condition (C1) is fulfilled. Also according to condition (C2), \(\kappa _0=\frac{1}{10}\) and using maple, we obtain \(\varsigma _1=0.7570714840\), \(\varsigma _2=0.2708016058\) and so \(\eta _1=0.9709550528\) and \(\eta _2=0.4787913740\). Hence due to the Theorem 3.14, the system (33, 34) has a solution in \(C^1([0,1])\).