Modulational Instability and Location Controllable Lump Solutions with Mixed Interaction Phenomena for the (2+1)-Dimensional Myrzakulov-Lakshmanan-IV Equation

Abstract

Under consideration is a $(2+1)$-dimensional spin nonisospectral Myrzakulov-Lakshmanan-IV (ML-IV) equation, which has close relation with the celebrated nonlinear Schrödinger equation. In the first place we study the modulational instability (MI) for this equation and deduce its formation mechanism for diverse localized waves from the plane wave background. Secondly, in view of the known nonisospectral Lax pair of this equation, we first successfully extend the generalized $(n, N-n)$-fold Darboux Transformation (DT) from $(1+1)$-dimensional equation to this $(2+1)$-dimensional equation. As an application of the resulting DT, we derive some location controllable dark and bright lump, periodic wave and mixed breather-lump solutions, it is shown that the position of these localized waves can be controlled by some special parameters, so that we can move them to the positions we want. Especially, the dynamical behaviors of these localized waves are illustrated graphically. These results may have potential value for the study of applied ferromagnetism and nano magnetism.

1 Introduction

Recently, Myrzakulov et al. have proposed a new integrable $(2+1)$-dimensional spin model called the Myrzakulov-Lakshmanan IV equation, which has the following form [1]:

$$\begin{aligned}{} & {} \textrm{i}\digamma _t+2\varepsilon _1Z_x+\textrm{i}\varepsilon _2(\digamma _{xy} +[\digamma _x,Z])_x+(\omega \digamma )_x+\tfrac{1}{\omega }[\digamma ,W]=0, \nonumber \\{} & {} u_x-\tfrac{\textrm{i}}{4}tr(\digamma \times [\digamma _x,\digamma _y])=0,\nonumber \\{} & {} \omega _x-\tfrac{\textrm{i}}{4}\varepsilon _2[tr(\digamma ^2_x)]_y=0,\nonumber \\{} & {} \textrm{i}W_x+\omega [\digamma ,W]=0, \end{aligned}$$

(1)

where $Z=\tfrac{1}{4}([\digamma ,\digamma _y]+2\textrm{i}u\digamma )$, $\left[ A,B\right] =AB-BA$, x and y are spatial variables, while t is a time variable, $\textrm{i}$ is an imaginary unit, the subscript indicates that the partial derivative is related to the variables $x,y,\,t$, other variables and their related significance can refer to Ref. [1]. Equation (1) is considered as one of the nonlinear $(2+1)$-dimensional integrable evolutions of the illustrious integrable spin $(1+1)$-dimensional continuum Heisenberg ferromagnetic system [2,3,4], which describes various magnetic interactions under the continuum limits of classical and semiclassical. Integrable nonlinear spin systems are known to own distinctive geometric and gauge invariance features and may have considerable potential values in applied magnetism and nanophysics. The gauge equivalent counterpart of Eq. (1) has the form [1]:

$$\begin{aligned}{} & {} \textrm{i}q_t+\varepsilon _1q_{xy}+\textrm{i}\varepsilon _2q_{xxy}-\nu q+\textrm{i}(wq)_x -2\textrm{i}p=0,\nonumber \\{} & {} \nu _x+2\varepsilon _1\delta (|q|^2)_y-2\textrm{i}\varepsilon _2\delta (q^*_{xy}q-q^*q_{xy})=0,\nonumber \\{} & {} w_x-2\varepsilon _2\delta (|q|^2)_y=0,\nonumber \\{} & {} p_x-2\textrm{i}\omega p-2\eta q=0,\nonumber \\{} & {} \eta _x+\delta (q^*p+p^*q)=0, \end{aligned}$$

(2)

where the symbol $*$ stands for the complex conjugate of the corresponding variable, p and q are complex valued potential functions of the variables x, y, t, whereas $\nu , w$ and $\eta$ are real valued potential functions, $\omega , \ \varepsilon _1, \ \varepsilon _2$ are arbitrary constants, and $\delta =\pm 1$. In this paper, we only consider the case of $\delta =1$. The corresponding Lax representation of Eq. (2) reads [1]:

$$\begin{aligned} \phi _{x}=U \phi , \ \ \phi _{t}=(2\varepsilon _1\lambda +4\varepsilon _2\lambda ^2)\phi _y+V\phi , \end{aligned}$$

(3)

in which

$$\begin{aligned} U=-\textrm{i}\lambda \sigma _3+U_0,\quad V=\lambda V_2+V_1+\dfrac{\textrm{i}}{\lambda +\omega }V_0, \end{aligned}$$

with

$$\begin{aligned} \sigma _3& = \left( \begin{array}{cc} 1 &{} 0\\ 0 &{} -1\\ \end{array}\right) , \quad U_0=\left( \begin{array}{cc} 0 &{} q \\ delta q^* &{} 0\\ \end{array}\right) , \quad V_0=\left( \begin{array}{cc} \eta &{} -p \\ delta p^* &{} -\eta \\ \end{array}\right) ,\\ V_2& = \textrm{i}w\sigma _3+2\textrm{i}\varepsilon _2\sigma _3U_{0y}, V_1=-\dfrac{\textrm{i}}{2}\nu \sigma _3\\{} & {} +\left( \begin{array}{cc} 0 &{} \textrm{i}\varepsilon _1q_y-\varepsilon _2q_{xy}-wq \\ \textrm{i}\varepsilon _1\delta q^*_y+\varepsilon _2\delta q^*_{xy}+w\delta q^*&{} 0\\ \end{array}\right) , \end{aligned}$$

where $\phi =\phi (x,y,t)=(\varphi (x,y,t), \psi (x,y,t))^\textrm{T}$ is the complex eigenfunction, which satisfies the compatibility condition $\phi _{xt}=\phi _{tx}$ and $\phi _{xy}=\phi _{yx}$, $\lambda \in {\mathbb {C}}$ is the spectral parameter related to y and t that satisfies the following evolution equation $\lambda _t=(2\varepsilon _1\lambda +4\varepsilon _2\lambda ^2)\lambda _y$. Equation (2) is just a zero-curvature equation $U_t-V_x+[U,\,V]-(2\varepsilon _1\lambda +4\varepsilon _2\lambda ^2)U_y=0$ with $[U,\, V]\equiv UV-VU$ in which $2\times 2$ matrices U and V must satisfy the linear nonisospectral problem. In Ref. [5], for Eq. (2), the soliton, breather, rogue wave, asymptotic analysis and DT have been researched. We know that Eq. (2) has a variety of parameter selections, these parameters will produce abundant reduction results. For instance, when the parameters $\varepsilon _1=1$ and $\varepsilon _2=0$, we can obtain the $(2+1)$-dimensional Schrödinger-Maxwell-Bloch system via Eq. (2). In Refs. [6,7,8,9], soliton, breather and various rogue wave structures have been studied by DT for $(2+1)$-dimensional Schrödinger-Maxwell-Bloch system, the nonlocal DT and exact solutions have also been established in Ref. [10]. If we choose the parameters $\varepsilon _1=0$ and $\varepsilon _2=1$, we can certainly get the $(2+1)$-dimensional complex mKdV-Maxwell-Bloch system through Eq. (2). In Refs. [11,12,13], the multi-soliton, breather and abundant rogue wave structures of $(2+1)$-dimensional complex mKdV-Maxwell-Bloch system have also been investigated pass through the DT, the corresponding nonlocal DT and exact solutions have also been established in Ref. [14]. We choose $\varepsilon _1=p=\eta =0$ and $\varepsilon _2=1$, Eq. (2) can reduce to $(2+1)$-dimensional complex mKdV equation, its multi-soliton and periodic solutions have been studied via DT in Refs. [15, 16]. We choose $\varepsilon _2=p=\eta =0$ and $\varepsilon _1=1$, Eq. (2) can reduce to $(2+1)$-dimensional nonlinear Schrödinger equation, its DT, soliton, breather, abundant rogue wave shapes, rational and semi-rational solutions and their dynamics have been investigated in Refs. [17,18,19,20]. In Ref. [21], the author especially studies the lump and rogue wave solutions based on periodic background in a Heisenberg ferromagnetic spin chain. These abundant reduced equations have laid a good foundation for us to investigate some physical phenomena. However, in terms of the plane wave background, for Eq. (2), the modulational instability (MI), location controllable multi-lump, periodic wave (PW) and mixed lump-breather interaction phenomenons have not been researched by using the generalized $(n,N-n)$-fold DT yet. Thus, this will become the main content of our next research.

This article will be organized as below: In Sect. 2, we will not only study the MI of Eq. (2), but also explain its generation principle from the plane wave background. In Sect. 3, generalized $(n,N-n)$-fold DT will be established for the $(2+1)$-dimensional Eq. (2). In Sect. 4, in terms of the generalized $(1, N-1)$-fold DT, we will establish location controllable multi-lump and PW solutions for Eq. (2). In Sect. 5, we will exhibit the mixed breather-lump and PW-lump interaction structures by using the generalized $(2,N-2)$-fold DT. Our summary will be discussed in the last section.

2 MI Analysis of ML-IV Equation

MI is a basic physical phenomenon in nonlinear science. It is a nonlinear process in which continuous wave or quasi continuous wave generates self-modulation of amplitude and frequency through nonlinear dispersive media, making the perturbation superimposed on continuous wave or quasi continuous wave grow exponentially. In the development and research of nonlinear equations, MI can determine the generation mechanism of breather and lump by numerical analysis. By analyzing and labeling the modulation stability (MS) and MI areas, we can easily explore the conditions for exciting soliton, plane wave, breather and lump. Subsequently, we will analyze the MI of Eq. (2) on plane wave background. First, we consider the plane wave seed solutions:

$$\begin{aligned}{} & {} q_0= ae^{\textrm{i}(kx+my+\mu t)}, \quad w_0=w_1, \quad \nu _0=m(k^2\varepsilon _2-k\varepsilon _1)-w_1k-\mu +\dfrac{2b}{a},\nonumber \\{} & {} \eta _0=\dfrac{(2\omega -k)b}{2a}, \quad p_0=\textrm{i}be^{\textrm{i}(kx+my+\mu t)}, \end{aligned}$$

(4)

where $a, b, k, m, \mu$ and $w_1$ are arbitrary real constants. For convenience of calculation, we take these parameters $w_1=2, \omega =\varepsilon _1=\varepsilon _2=1$ in advance, then we rewrite the seed solutions (4) after adding perturbations:

$$\begin{aligned}{} & {} q_{(0)}= q_0(1+f_{1+}e^{\textrm{i}\Omega (-\alpha x-\beta t+y)}+f_{1-}^* e^{-\textrm{i}\Omega (-\alpha ^*x-\beta ^*t+y)}), \nonumber \\{} & {} w_{(0)}=w_0(1+f_{2+}e^{\textrm{i}\Omega (-\alpha x-\beta t+y)} +f_{2-}^*e^{-\textrm{i}\Omega (-\alpha ^*x-\beta ^*t+y)}), \nonumber \\{} & {} \nu _{(0)}=\nu _0(1+f_{3+}e^{\textrm{i}\Omega (-\alpha x-\beta t+y)} +f_{3-}^*e^{-\textrm{i}\Omega (-\alpha ^*x-\beta ^*t+y)}), \nonumber \\{} & {} \eta _{(0)}=\eta _0(1+f_{4+}e^{\textrm{i}\Omega (-\alpha x-\beta t+y)} +f_{4-}^*e^{-\textrm{i}\Omega (-\alpha ^*x-\beta ^*t+y)}), \nonumber \\{} & {} p_{(0)}=p_0(1+f_{5+}e^{\textrm{i}\Omega (-\alpha x-\beta t+y)}+f_{5-}^* e^{-\textrm{i}\Omega (-\alpha ^*x-\beta ^*t+y)}), \end{aligned}$$

(5)

where $f_{1\pm }, f_{2\pm }, f_{3\pm }, f_{4\pm }$ and $f_{5\pm }$ are small perturbations of the Fourier modes, $\Omega$ is the modulational frequency, $\alpha$ and $\beta$ are called propagation parameters, and they are complex numbers. we can substitute Eq. (5) into Eq. (2) to obtain the following ten linear algebraic equations

$$\begin{aligned} \left\{ \begin{array}{ll} a^2f_{1+}+a^2f_{1-}+\alpha f_{2+}=0,\\ a^2f_{1+}+a^2f_{1-}+\alpha f_{2-}=0,\\ (k-2)f_{1+}+(k-2)f_{4+}+(\Omega \alpha -k+2)f_{5+}=0,\\ (k-2)f_{1-}+(k-2)f_{4-}-(\Omega \alpha +k-2)f_{5-}=0,\\ a^2f_{1+}-a^2f_{1-}-\tfrac{1}{2}\Omega \alpha (k-2)f_{4+}-a^2f_{5+}+a^2f_{5-}=0,\\ a^2f_{1+}-a^2f_{1-}-\tfrac{1}{2}\Omega \alpha (k-2)f_{4-}-a^2f_{5+}+a^2f_{5-}=0,\\ \left[ (m+\Omega )\alpha -k+1\right] a^3f_{1+}+[(m-\Omega )\alpha -k+1]a^3f_{1-} +\left[ -\left[ \tfrac{1}{2}(mk^2-(m+2)k-\mu )\right] \alpha a-\alpha b\right] f_{3+}=0,\\ \left[ (m+\Omega )\alpha -k+1\right] a^3f_{1+}+[(m-\Omega )\alpha -k+1]a^3f_{1-} +\left[ -\left[ \tfrac{1}{2}(mk^2-(m+2)k-\mu )\right] \alpha a-\alpha b\right] f_{3-}=0,\\ \{\left[ \Omega ^3\alpha ^2+\alpha (\alpha m-2k+1)\Omega ^2+[(-2km+m+2) \alpha +k^2+\beta -k]\Omega \right] a-2b\}f_{1+}+(2\Omega \alpha -2k)af_{2+} \\ +\left[ (-mk^2+(m+2)k+\mu )a-2b\right] f_{3+}+2bf_{5+}=0,\\ \{\left[ -\Omega ^3\alpha ^2+\alpha (\alpha m-2k+1)\Omega ^2 +[(2km-m-2)\alpha -k^2-\beta +k]\Omega \right] a-2b\}f_{1-} +(-2\Omega \alpha -2k)af_{2-} \\ +\left[ (-mk^2+(m+2)k+\mu )a-2b\right] f_{3-}+2bf_{5-}=0. \end{array}\right. \end{aligned}$$

(6)

Linear algebraic equations (6) have nontrivial solutions only when $\alpha , \beta , \Omega , a, \ b, k, m$ satisfies the following dispersion relations, namely

$$\begin{aligned} \beta _{\mp }=\dfrac{J_1 \mp J_2}{4a^3+(-\Omega ^2\alpha ^2+k^2-4k+4)a}, \end{aligned}$$

(7)

where

$$\begin{aligned} J_1& = 16a^5+[-8\Omega ^2\alpha ^2+(8km-4m-8)\alpha -12k+16]a^3\\{} & {} -(-\Omega \alpha +k-2)[\Omega ^2\alpha ^2 +(-2km+m+2) \alpha +k^2-k] \\{} & {} (\Omega \alpha +k-2)a-2b(k-2)\alpha , \\ J_2& = 16\sqrt{\left( \tfrac{1}{4}\Omega ^2\alpha ^2-a^2\right) \left[ \left( -\tfrac{1}{2}m\alpha +k-\tfrac{1}{2}\right) a^3 +\tfrac{1}{4} (-\Omega \alpha +k-2)\left( -\tfrac{1}{2}m\alpha +k-\tfrac{1}{2}\right) (\Omega \alpha +k-2)a-\tfrac{1}{4}\alpha b\right] ^2}. \end{aligned}$$

To facilitate analysis, when $\alpha =\tfrac{\textrm{i}}{4}$, we take $\beta _1=\beta _{-}$, where $b=k=m=1$, take $\beta _2=\beta _{+}$, where $a=b=m=1$. Then we define the MI gains $G_\tau =|\Im (\Omega \beta _\tau )| \ (\tau =1,2)$, and the symbol $\Im$ is called this expression’s imaginary part. Thus, we can sum up the generation factors of MI gains as follows:

• (i) MI generation factor of $G_1$ is $a\ne 0$;

• (ii) MI generation factor of $G_2$ is $k\ne \tfrac{1}{2}$;

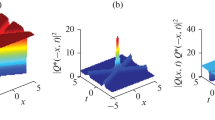
In Fig. 1a1 and b1, for MI gain $G_1$, we clearly show the detailed distribution states on the coordinate axis $\Omega$ and a; In Fig. 1a2 and b2, for MI gain $G_2$, we also clearly show the detailed distribution states on the coordinate axis $\Omega$ and k. In these figures, we mark the MI and MS areas in detail. Notably, on the line $\Omega =0$, the perturbations are unstable and can excite lump in Fig. 1b1 and b2 except two points $\Omega =0, a=0$ and $\Omega =0, k=0$. In Fig. 1b1 and b2, we can observe that the two red lines $a=0$ and $k=\tfrac{1}{2}$ are MS areas where solitons can be excited. The relevant proof of instability on the line $\Omega =0$ can refer to Ref. [22]. In the MI areas, we can obtain lump and breather, while in the MS areas, we can obtain soliton and plane wave.

Fig. 1

Shape (above) and density (below) of MI gains $G_1$ and $G_2$: (a1) (b1) shows $\Omega$ and a when $b=k=m=1, \alpha =\tfrac{\textrm{i}}{4}$; (a2) (b2) shows $\Omega$ and k when $a=b=m=1, \alpha =\tfrac{\textrm{i}}{4}$, (b1) and (b2) are MI gain spectrums of (a1) and (a2), respectively

It should be noted that we have given the values of the corresponding parameters in advance for the convenience of analysis, in fact, we can certainly determine other parameter values and analyze other MI gains, however, in order to save space, we will not analyze other parameters here.

3 Generalized $(n, N-n)$-Fold DT

The DT method is an effective way to seek for exact solutions of lax integrable nonlinear equations [23, 24]. Near term, generalized $(n, N-n)$-fold DT has not only been came up, but also applied to solve some $(1+1)$-dimensional continuous and discrete nonlinear equations [25,26,27,28], there is no doubt that we can not only get the soliton solutions by this method, but also get the rational solutions and their mixed interaction structures by it. However, we have not studied how to extend this method to the nonisospectral $(2+1)$-dimensional nonlinear systems. Therefore in this section, we will try extending this generalized DT to the nonisospectral $(2+1)$-dimensional equation (2). Next, for Eq. (2), we will use the known Lax pair (3) to construct the generalized $(n, N-n)$-fold DT. Firstly, we know that there is a form about gauge transformation as below

$$\begin{aligned} \widetilde{\phi }=T{(\lambda )}\phi \ , \end{aligned}$$

(8)

where $\phi =\phi (x,y,t)=(\varphi (x,y,t), \psi (x,y,t))^\textrm{T}$ (T represents the transpose) satisfies Lax pair (3). We will determine the Darboux matrix $T(\lambda )$ later, which is a $2\times 2$ order matrix, and $\widetilde{\phi }=\widetilde{\phi }(x,y,t)=(\widetilde{\varphi }(x,y,t), \widetilde{\psi }(x,y,t))^\textrm{T}$ is required to satisfy the Lax pair in the same form as (3). Concurrently, $\widetilde{\phi }$ must also subject to $\widetilde{\phi }_{x}=\widetilde{U} \widetilde{\phi }, \widetilde{\phi }_{t}=(2\varepsilon _1\lambda +4\varepsilon _2 \lambda ^2)\widetilde{\phi }_y+\widetilde{V}\widetilde{\phi }$, where $\widetilde{U}, \widetilde{V}$ have the same forms as U, V, respectively, except that $q, w, \nu , \eta , p$ are replaced by $\widetilde{q}, \widetilde{w}, \widetilde{\nu }, \widetilde{\eta }, \widetilde{p}$. With the relevant knowledge of DT, we have the following expression

$$\begin{aligned} T_{x}+TU-\widetilde{U}T=0,\quad T_{t}+TV-\widetilde{V}T -(2\varepsilon _1\lambda +4\varepsilon _2\lambda ^2)T_y=0. \end{aligned}$$

(9)

With the help of symbolic computation, a classical DT matrix T will be established as below

$$\begin{aligned} T(\lambda ) = \left( \begin{array}{cc} \lambda ^{N}+\sum \limits _{j=0}^{N-1}A^{(j)}\lambda ^{j} &{}\sum \limits _{j=0}^{N-1}B^{(j)} \lambda ^{j} \\ -\sum \limits _{j=0}^{N-1}{B^{(j)}}^{*} \lambda ^{j} &{}\lambda ^{N}+\sum \limits _{j=0}^{N-1}{A^{(j)}}^{*}\lambda ^{j} \end{array}\right) , \end{aligned}$$

(10)

where N is a positive integer, $A^{(j)}$ and $B^{(j)}\ (j=0,1,...,N-1)$ are a class of unknown functions related to $x, y\$and t that will be obtained later. According to (9), we can get the transformations between potential functions

$$\begin{aligned}{} & {} \widetilde{q}_N=q_0+2\textrm{i}B^{(N-1)}, \nonumber \\{} & {} \widetilde{w}_N=w_0+4\textrm{i}A^{(N-1)}_y\varepsilon _2, \nonumber \\{} & {} \widetilde{\eta }_N=\eta _0+\Gamma _1\varepsilon _1+\Gamma _2\varepsilon _2 -\textrm{i}A^{(N-1)}_t+(\textrm{i}q_0w_0-2B^{(N-1)}w_0)|B^{(N-1)}|^2 \textrm{i}q_0^*w_0, \nonumber \\{} & {} \widetilde{\nu }_N=\nu _0-4\textrm{i}A^{(N-1)}_y\varepsilon _1 +(8\textrm{i}A^{(N-1)}A^{(N-1)}_y-8\textrm{i}B^{(N-1)^*} B^{(N-1)}_y-4B^{(N-1)^*}q_{0y}\nonumber \\{} & {} \quad -4B^{(N-1)}q_{0y}^* -8\textrm{i}A^{N-2}_y)\varepsilon _2, \nonumber \\{} & {} \widetilde{p}_N=p_0+\Xi _1\varepsilon _1+\Xi _2\varepsilon _2 +\textrm{i}B^{(N-1)}_t+(\textrm{i}q_0w_0-2B^{(N-1)}w_0)A^{(N-1)^*}\nonumber \\{} & {} \quad -B^{(N-1)} \nu _0-\textrm{i}q_0w_0A^{(N-1)}+2B^{(N-2)}w_0, \end{aligned}$$

(11)

where

$$\begin{aligned}{} {} \Gamma _1&=2\textrm{i}B^{(N-1)^*}B^{(N-1)}_y-2\textrm{i}A^{(N-1)} A^{(N-1)}_y+B^{(N-1)}q_{0y}^*+B^{(N-1)^*}q_{0y}+2\textrm{i}A^{(N-2)}_y,\\{} \Xi _1& =2\textrm{i}B^{(N-1)}A^{(N-1)}_y+(A^{(N-1)^*}-A^{(N-1)})q_{0y} +2\textrm{i}A^{(N-1)^*}B^{(N-1)}_y-2\textrm{i}B^{(N-2)}_y,\\{} {} \Gamma _2& =-2B^{(N-1)^*}B^{(N-1)}_{xy}-\textrm{i}B^{(N-1)}q_{0xy}^* +\textrm{i}B^{(N-1)^*}q_{0xy}\\{} & {} \quad +[-(8\textrm{i}B^{(N-1)}+4q_0)B^{(N-1)^*} +4\textrm{i}A^{(N-1)^2}-4\textrm{i}A^{(N-2)}]A^{(N-1)}_y \\{} & {} \quad +(4\textrm{i}B^{(N-2)^*}-4\textrm{i}B^{(N-1)^*}A^{(N-1)}) B^{(N-1)}_y\\{} & {} \qquad + (2B^{(N-2)}-2B^{(N-1)}A^{(N-1)})q_{0y}^*+(2B^{(N-2)^*} -2B^{(N-1)^*}A^{(N-1)})q_{0y} \\{} & {} \quad -4\textrm{i}A^{(N-1)}A^{(N-2)}_y+4\textrm{i}A^{(N-3)}_y,\\{} {} \Xi _2& =-2(A^{(N-1)}+\omega )B^{(N-1)}_{xy}-\textrm{i}(A^{(N-1)}-A^{(N-1)^*}) q_{0xy}\\{} & {} \qquad +[-(8\textrm{i}B^{(N-1)}+4q_0)A^{(N-1)^*} -(4\textrm{i}\omega +4\textrm{i}A^{(N-1)})B^{(N-1)}\\{} & {} \quad + 4\textrm{i}B^{(N-2)}-4q_0\omega ]A^{(N-1)}_y +(-2\omega A^{(N-1)}+2B^{(N-1)}B^{(N-1)^*}\\{} & {} \quad +2\omega A^{(N-1)^*} -2A^{(N-2)}+2A^{(N-2)^*})q_{0y}+[4\textrm{i}\omega A^{(N-1)^*} \\{} & {} \quad +4\textrm{i}(B^{(N-1)}B^{(N-1)^*}+A^{(N-2)^*})]B^{(N-1)}_y\\{} & {} \quad -4\textrm{i}(\omega B^{(N-2)}_y-B^{(N-1)}A^{(N-2)}_y+B^{(N-3)}_y) +2B^{(N-1)^2}q_{0y}^*. \end{aligned}$$

For the sake of acquiring the novel solutions of Eq. (2), we must determine $A^{(N-1)}, A^{(N-2)}, A^{(N-3)}, B^{(N-1)}, B^{(N-2)}$ and $B^{(N-3)}$ in (11), and these unknown functions are also our next major goal.

According to Darboux matrix (10), we can clearly observe that det$T(\lambda )$ is a 2Nth order polynomial related to $\lambda$. Suppose that the spectral parameters $\lambda _i\ (\lambda _i\ne 0, i=1,2,...,n)$ are the $n \ (1\le n\le N)$ different solutions of detT. Let $\phi (\lambda _i)=\left( \varphi (\lambda _i),\psi (\lambda _i)\right) ^{\textrm{T}}$ be n linearly independent solutions in the form of column vector for Lax pair (3) based on the $\lambda =\lambda _i\ (i=1,2,...,n)$. In addition, we need to ensure that $T(\lambda _i)\phi (\lambda _i)=0$, however, it only gives 2n algebraic equations so that 2N unknown functions $A^{(N-1)}$ and $B^{(N-1)}$ cannot be obtained when $n<N$. In order to get linear algebraic equations that can solve 2N unknown functions, for every $\lambda _i$, we need to expand

$$\begin{aligned} T(\lambda _i+\varepsilon )\phi (\lambda _i+\varepsilon ) =\sum \limits _{\kappa =0}^{+\infty }\sum \limits _{j=0}^{\kappa }T^{(j)} (\lambda _i)\phi ^{(\kappa -j)}(\lambda _i)\varepsilon ^\kappa , \end{aligned}$$

(12)

where

$$\begin{aligned}{} & {} T^{(\kappa )}(\lambda _i)=\dfrac{1}{\kappa !} \dfrac{\partial ^\kappa }{\partial \lambda _i^\kappa }T(\lambda _i),\nonumber \\{} & {} \phi ^{(\kappa )}(\lambda _i)=\dfrac{1}{\kappa !}\dfrac{\partial ^\kappa }{\partial \lambda _i^\kappa }\phi (\lambda _i)=\left( \dfrac{1}{\kappa !} \dfrac{\partial ^\kappa }{\partial \lambda _i^\kappa }\varphi (\lambda _i), \dfrac{1}{\kappa !}\dfrac{\partial ^\kappa }{\partial \lambda _i^\kappa } \psi (\lambda _i)\right) ^{\textrm{T}}, \ (\kappa =0,1,...). \end{aligned}$$

(13)

Substituting the condition

$$\begin{aligned} \lim \limits _{\varepsilon \rightarrow 0}\dfrac{T(\lambda _i+\varepsilon ) \phi (\lambda _i+\varepsilon )}{\varepsilon ^{\kappa _i}} =0, i=1,2,...,n, \kappa _i=0,1,...,r_i, \end{aligned}$$

(14)

into Eq. (12), where the parameters $\kappa _i$ and $r_i$ are non-negative integers and $r_i$ must satisfy the relation $N=\sum \nolimits _{i=1}^n(n+r_i)$. Subsequently, we will smoothly derive a linear algebraic system containing 2N equations as follows

$$\begin{aligned} \left\{ \begin{array}{ll} T^{(0)}(\lambda _i)\phi ^{(0)}(\lambda _i)=0,\\ T^{(0)}(\lambda _i)\phi ^{(1)}(\lambda _i)+T^{(1)}(\lambda _i)\phi ^{(0)}(\lambda _i)=0,\\ T^{(0)}(\lambda _i)\phi ^{(2)}(\lambda _i)+T^{(1)}(\lambda _i)\phi ^{(1)}(\lambda _i)+T^{(2)} (\lambda _i)\phi ^{(0)}(\lambda _i)=0,\\ ......,\\ \sum \limits _{j=0}^{r_i}T^{(j)}(\lambda _i)\phi ^{(r_i-j)}(\lambda _i)=0, \end{array}\right. \end{aligned}$$

(15)

from which can adopt n suitable spectral parameters $\lambda _i$ and uniquely determine 2N unknown functions $A^{(j)}$, $B^{(j)}$$(0\le j\le N-1)$ by Eq. (15). Through the description of the above process, once the original seed solution $q_0, w_0, \nu _0, \eta _0$ and $p_0$ of Eq. (2) are given, then $A^{(N-1)}, A^{(N-2)}, A^{(N-3)}, B^{(N-1)}, B^{(N-2)}, B^{(N-3)}$ from Eq. (11) are as follows:

$$\begin{aligned} A^{(N-1)}& = \dfrac{\Delta A^{(N-1)}}{\Delta _N}, \qquad A^{(N-2)} =\dfrac{\Delta A^{(N-2)}}{\Delta _N},\nonumber \\ A^{(N-3)}& = \dfrac{\Delta A^{(N-3)}}{\Delta _N}, \qquad B^{(N-1)} =\dfrac{\Delta B^{(N-1)}}{\Delta _N}, \nonumber \\& = \dfrac{\Delta B^{(N-2)}}{\Delta _N},\qquad B^{(N-3)} =\dfrac{\Delta B^{(N-3)}}{\Delta _N}, \end{aligned}$$

(16)

where $\Delta _N=$det$([\Delta ^{(1)}_{m_1+1}, \Delta ^{(2)}_{m_2+1},...,\Delta ^{(n)}_{m_n+1}]^{\textrm{T}})$, and $\Delta ^{(i)}_{m_i+1}=(\Delta ^{(i)}_{j,s})_{2(m_i+1)\times 2N}$, in which $\Delta ^{(i)}_{j,s}\ (1\le j\le 2m_i+2, 1\le s \le 2N)$ will be clearly shown as follows:

$$\begin{aligned} \Delta ^{(i)}_{j,s}=\left\{ \begin{array}{ll} \sum \limits _{\kappa =0}^{j-1}C_{N-s}^\kappa \lambda _i^{N-s-\kappa }\varphi _i^{j-1-\kappa }, \ for\ \ 1\le j\le m_i+1, 1\le s\le N, \\ \sum \limits _{\kappa =0}^{j-1}C_{2N-s}^\kappa \lambda _i^{2N-s-\kappa }\psi _i^{j-1-\kappa }, \ for\ \ 1\le j\le m_i+1, N+1\le s\le 2N, \\ \sum \limits _{\kappa =0}^{j-(N+1)}C_{N-s}^\kappa \lambda _i^{(N-s-\kappa )*}\psi _i^{(j-1-N-\kappa )*}, \ for\ \ m_i+2\le j\le 2(m_i+1), 1\le s\le N, \\ -\sum \limits _{\kappa =0}^{j-(N+1)}C_{2N-s}^\kappa \lambda _i^{(2N-s-\kappa )*}\varphi _i^{(j-N-1-\kappa )*}, \ for\ \ m_i+2\le j\le 2(m_i+1), N+1\le s\le 2N, \end{array}\right. \end{aligned}$$

while $\Delta A^{(N-1)}, \Delta A^{(N-2)}, \Delta A^{(N-3)}, \Delta B^{(N-1)}, \Delta B^{(N-2)},$ and $\Delta B^{(N-3)}$ will be uniquely determined by the determinant $\Delta N$ substituting its first, second, third, $(N+1)$th, $(N+2)$th and $(N+3)$th columns via the vector $(g^{(1)},...,g^{(n)})^{\textrm{T}}$ with $g^{(i)}=(g_j^i)_{2(m_i+1)\times 1}$, its form is as follows

$$\begin{aligned} g_j^i=\left\{ \begin{array}{ll} -\sum \limits _{\kappa =0}^{j-1}C_{N}^\kappa \lambda _i^{N-\kappa }\varphi _i^{(j-1-\kappa )}, \ for\ \ 1\le j\le m_i+1, \\ -\sum \limits _{\kappa =0}^{j-N-1}C_{N}^\kappa \lambda _i^{(N-\kappa )*}\psi _i^{(j-N-1-\kappa )*}, \ for\ \ m_i+2\le j\le 2(m_i+1). \end{array}\right. \end{aligned}$$

In general, we call the transformations (8) and (11) as generalized $(n,N-n)$-fold DT, which adopts n spectral parameters, while conventional N-fold DT adopts N spectral parameters, which is the difference between them. We usually use n to represent the number of spectral parameters adopted in the generalized $(n,N-n)$-fold DT, while $N-n$ denotes the sum of the derivative orders in the Taylor expansion for eigenfunction $\phi _n$. In this paper, we will use this method to obtain multi-lump, PW and abundant mixed interaction structures for Eq. (2).

Remark 1

(N, 0)-fold DT can be obtained by reducing generalized $(n,N-n)$-fold DT, it includes conventional N-fold DT when $n = N, r_i=0\ (1 \le i \le N)$, if we apply Taylor expansion at each $\lambda _i$, we will get the lump and PW solutions for Eq. (2), conversely, we can get the soliton and breather solutions for Eq. (2). Generalized $(1,N-1)$-fold DT can be obtained by reducing generalized $(n,N-n)$-fold DT, when $n=1$ and $r_1=N-1$, we can get lump solutions of Eq. (2) based on the plane wave background. In the same background, generalized$(2,N-2)$-fold DT can also be get by reducing generalized $(n,N-n)$-fold DT, when $n=2$ and $r_1+r_2=N-2$, we can certainly get mixed interaction solutions of Eq. (2) for different localized waves. When $2<n<N$, abundant localized wave interaction solutions can also be obtained by using generalized $(n,N-n)$-fold DT, while it is not involved in this paper. Next, we can generate some multi-lump and mixed interaction solutions based on the plane wave background for Eq. (2) with the help of this method.

4 Location Controllable Multi-lump and PW Solutions via the Generalized $(1,N-1)$-Fold DT

In order to obtain the PW and lump solutions for Eq. (2), in this section, in terms of the generalized $(1,N-1)$-fold DT, we will only use a spectral parameter. Subsequently, we can substitute the plane wave seed solutions (4) into Lax pair (3), and obtain the fundamental solution of Eq. (2) as below:

$$\begin{aligned} \phi =\left( \begin{array}{ll} \varphi \\ \psi \end{array}\right) =\left( \begin{array}{cc} \left( C_1m_{-}e^{\xi [x+\textrm{i}y+\sigma t+\delta (\varepsilon )]}+C_2m_{+}e^{-\xi [x+\textrm{i}y+\sigma t+\delta (\varepsilon )]}\right) e^{\tfrac{\textrm{i}(kx+my+\mu t)}{2}} \\ \left( C_1e^{\xi [x+\textrm{i}y+\sigma t+\delta (\varepsilon )]}+C_2e^{-\xi [x+\textrm{i}y+\sigma t+\delta (\varepsilon )]}\right) e^{\tfrac{-\textrm{i}(kx+my+\mu t)}{2}}\\ \end{array}\right) , \end{aligned}$$

(17)

with

$$\begin{aligned}{} & {} m_{\mp }=\dfrac{\textrm{i}k+2\textrm{i}\lambda \mp \sqrt{-4a^2-k^2-4k\lambda -4\lambda ^2}}{2a}, \ \xi =\dfrac{\sqrt{-4a^2-k^2-4k\lambda -4\lambda ^2}}{2},\\{} & {} \delta (\varepsilon )=\sum \limits _{i=0}^{N} (g_i+\textrm{i}h_i)\varepsilon ^{2i}, \\{} & {} \sigma =\dfrac{(\lambda +\omega )\left[ 4\textrm{i}\varepsilon _2\lambda ^2 +(2\textrm{i}\varepsilon _1-2m\varepsilon _2) \lambda +km\varepsilon _2-m\varepsilon _1-1\right] a+b}{(\lambda +\omega )a}, \end{aligned}$$

where $\varepsilon$ is an extremely small parameter, while $g_i$ and $h_i \ (i = 0, 1, 2,..., N)$ are real value parameters, $C_1$ and $C_2$ are two arbitrary constants. The main objective of this article is to obtain some PW and lump solutions of Eq. (2), therefore, for different spectral parameters, we can adopt the two optional Taylor series expansions mentioned later. Subsequently, let the spectral parameter $\lambda =\lambda _1+\varepsilon ^2$ in (17), at the same time, the vector function $\phi$ is expanded by Taylor series around $\varepsilon =0$, in terms of the explicit calculation, we can get

$$\begin{aligned} \phi (\varepsilon ^2)=\sum \limits _{\kappa =0}^{\infty }\phi ^{(\kappa )} \varepsilon ^{2\kappa }=\phi ^{(0)}+\phi ^{(1)}\varepsilon ^{2} +\phi ^{(2)}\varepsilon ^{4}+\phi ^{(3)}\varepsilon ^{6}+\cdots , \end{aligned}$$

(18)

where $\phi ^{(\kappa )}=(\varphi ^{(\kappa )}, \psi ^{(\kappa )})^{\textrm{T}}, (\kappa =0, 1, 2 \cdots )$ can be uniquely obtained through (13) and (17).

To obtain the multi-lump solutions of Eq. (2), with the help of symbolic computation, we set $M=-\tfrac{k}{2}\pm a\textrm{i}$ and think over two types Taylor series expansion conditions as follows:

Type-I: Choosing $C_1=-C_2=\tfrac{1}{\varepsilon }, a=k=1, \lambda = \lambda _1+ \varepsilon ^2$ with $\lambda _1=M$ and adopting Taylor series expansion at $\varepsilon =0$ for (17). Then, these vectors $\phi ^{(\kappa )}=(\varphi ^{(\kappa )},\psi ^{(\kappa )})^{\textrm{T}}$ are the polynomial functions related to x, y, t, so that the rational bright-dark lump solutions can be easily established for Eq. (2). The relevant expansion expressions of the first type of (17) are as follows:

$$\begin{aligned} \varphi ^{(0)}& = \left( \tfrac{2}{5}+\tfrac{2\textrm{i}}{5}\right) [5\textrm{i}h_0-6\textrm{i}t +5\textrm{i}y+5g_0-8t+5x-5] e^{\frac{\textrm{i}}{2}(x+y+t)},\nonumber \\ \psi ^{(0)}& = \left( \tfrac{2}{5}+\tfrac{2\textrm{i}}{5}\right) [5\textrm{i}h_0 -6\textrm{i}t+5\textrm{i}y+5g_0-8t+5x] e^{-\frac{\textrm{i}}{2}(x+y+t)},\nonumber \\ \varphi ^{(1)}& = \left\{ \left( \tfrac{1168}{375}+\tfrac{2576}{375}\textrm{i}\right) t^3 -\tfrac{136}{25}\left[ \left( \tfrac{31}{17}+\textrm{i}\right) x\right. \right. \nonumber \\{} & {} \left. +\left( \tfrac{31}{17}\textrm{i}-1\right) y +\left( \tfrac{31}{17}+\textrm{i}\right) g_0-\tfrac{31}{17} -\textrm{i}+\left( \tfrac{31}{17}\textrm{i}-1\right) h_0\right] t^2-\tfrac{4}{5} \left\{ (\textrm{i}-7)g_0^2 \right. \nonumber \\{} & {} +[(-2-14\textrm{i})h_0+(2\textrm{i}-14)x+14-2\textrm{i} -(2+14\textrm{i})y]g_0\nonumber \\{} & {} +(7-\textrm{i})h_0^2+[(-2-14\textrm{i})x +2+14\textrm{i}+(14-2\textrm{i})y]h_0\nonumber \\{} & {} +(\textrm{i}-7)x^2+[14-2\textrm{i}-(2+14\textrm{i})y]x -\tfrac{631}{20}-\tfrac{167}{20}\textrm{i}+(7-\textrm{i})y^2\nonumber \\{} & {} \left. +(2+14\textrm{i})y\right\} t+\left( \tfrac{2}{3}\textrm{i} -\tfrac{2}{3}\right) g_0^3+(2+ 2\textrm{i})(\textrm{i}x-\textrm{i}-y-h_0)g_0^2\nonumber \\{} & {} -2\left\{ (\textrm{i}-1)h_0^2+[(2\textrm{i}-2)y-2-2\textrm{i} +(2+2\textrm{i})x]h_0\right. \nonumber \\{} & {} \left. +(\textrm{i}-1)y^2+(-2-2\textrm{i} +(2+2\textrm{i})x)y+\tfrac{5}{4} -\tfrac{5}{4}\textrm{i}+(1-\textrm{i})x^2 +(2\textrm{i}-1)x\right\} g_0\nonumber \\{} & {} +\left( \tfrac{2}{3}+\tfrac{2}{3}\textrm{i}\right) h_0^3 -(2+2\textrm{i})(\textrm{i}x -\textrm{i}-y)h_0^2-\tfrac{1}{2} (1+\textrm{i})(8\textrm{i}xy-8\textrm{i}y \nonumber \\{} & {} +4x^2-4y^2-8x+5)h_0+\left( \tfrac{2}{3}\textrm{i}-\tfrac{2}{3}\right) x^3 -(2+2\textrm{i})(\textrm{i}+y)x^2-(2+2\textrm{i}) \left( \textrm{i}y^2 -\tfrac{5}{4}\textrm{i}-2y\right) x\nonumber \\{} & {} \left. +\tfrac{1}{6}(1+\textrm{i}) (12\textrm{i}y^2+4y^3 +12\textrm{i}h_1-3\textrm{i}-15y+12g_1)\right\} e^{\frac{\textrm{i}}{2}(x+y+t)},\nonumber \\ \psi ^{(1)}& = \left\{ \left( \tfrac{1168}{375}+\tfrac{2576}{375}\textrm{i}\right) t^3 -\tfrac{136}{25}\left[ \left( \tfrac{31}{17}+\textrm{i}\right) x\right. \right. \nonumber \\{} & {} \left. +\left( \tfrac{31}{17} \textrm{i}-1\right) y +\left( \tfrac{31}{17}+\textrm{i}\right) g_0 +\left( \tfrac{31}{17} \textrm{i}-1\right) h_0\right] t^2 \nonumber \\{} & {} -\tfrac{4}{5}\left\{ (\textrm{i}-7) g_0^2+[(-2-14\textrm{i})h_0-(2+14\textrm{i})y +(2\textrm{i}-14)x]g_0+(7-\textrm{i}) h_0^2\right. \nonumber \\{} & {} \left. +[(14-2\textrm{i})y-(2+14\textrm{i})x]h_0 +(7-\textrm{i})y^2-(2+14\textrm{i})xy -\tfrac{491}{20}-\tfrac{187}{20}\textrm{i}+(\textrm{i}-7)x^2\right\} t\nonumber \\{} & {} +\tfrac{2}{3}(\textrm{i}-1)g_0^3+(2+2\textrm{i})(\textrm{i}x-y-h_0) g_0^2-(2+2\textrm{i})\nonumber \\{} & {} \left[ -\textrm{i}x^2+(2h_0+2y)x+\textrm{i}(h_0 +y+\tfrac{1}{2}) \left( h_0+y-\tfrac{1}{2}\right) \right] g_0\nonumber \\{} & {} +\tfrac{2}{3}(1+\textrm{i})h_0^3 -(2+2\textrm{i})(\textrm{i}x-y)h_0^2 -\tfrac{1}{2}(1+\textrm{i}) (8\textrm{i}xy+4x^2-4y^2+1)h_0\nonumber \\{} & {} \left. +\tfrac{1}{6}(1+\textrm{i}) (4\textrm{i}x^3-12\textrm{i}xy^2-12x^2y+4y^3 +12\textrm{i}h_1+3 \textrm{i}x+12g_1-3y)\right\} e^{-\frac{\textrm{i}}{2}(x+y+t)}. \end{aligned}$$

(19)

Type-II: Choosing $C_1=-C_2=a=k=1, \lambda = \lambda _1+ \varepsilon ^2$ with $\lambda _1\ne M\ (e.g., \lambda _1=M+1)$ and adopting Taylor series expansion at $\varepsilon =0$ for (17). Then, these vectors $\phi ^{(\kappa )}=(\varphi ^{(\kappa )},\psi ^{(\kappa )})^{\textrm{T}}$ are the combinations of polynomial functions and exponential related to x, y, t, so that the PW solutions can be easily established for Eq. (2). Here, we only list an expansion expression of solution (17) as follows:

$$\begin{aligned} \varphi ^{(0)}&=-e^{\left( \tfrac{\textrm{i}}{2}-\sqrt{2\textrm{i}-1}\right) x +\tfrac{\textrm{i}}{2}y+\left( \tfrac{\textrm{i}}{2}-\tfrac{58}{13}\sqrt{2\textrm{i}-1}\right) t -\sqrt{2\textrm{i}-1}g_0}\nonumber \\&\left[ (\sqrt{2\textrm{i}-1}-1 -\textrm{i}) e^{\tfrac{1}{13}\sqrt{2\textrm{i}-1}[26x+13\textrm{i}y +(116+4\textrm{i})t+13(\textrm{i}h_0+2g_0)]} \right. \nonumber \\&\quad \left. +(\sqrt{2\textrm{i}-1}+1+\textrm{i})e^{-\tfrac{\textrm{i}}{13} \sqrt{2\textrm{i}-1}(4t+13y+13h_0)}\right] , \nonumber \\ \psi ^{(0)}&=e^{\left( -\tfrac{\textrm{i}}{2}-\sqrt{2\textrm{i}-1}\right) x -\tfrac{\textrm{i}}{2}y-\left( \tfrac{\textrm{i}}{2}+\tfrac{58\sqrt{2\textrm{i}-1}}{13}\right) t-\sqrt{2\textrm{i}-1}g_0}\nonumber \\&\quad \left[ e^{\tfrac{\sqrt{2\textrm{i}-1}}{13}[26x+13\textrm{i}y +(116+4\textrm{i})t+13(\textrm{i}h_0+2g_0)]} -e^{-\tfrac{\textrm{i} \sqrt{2\textrm{i}-1}}{13}(4t+13y+13h_0)}\right] . \end{aligned}$$

(20)

Next, we only choose $M=-\tfrac{k}{2}-a\textrm{i}$ and primarily discuss three cases: $N=1, 2, 3$. For the convenience of calculation, we only discuss parameters $a=b=\omega =m=\mu =k=\varepsilon _1=\varepsilon _2=w_1=1$.

4.1 Location Controllable Bright-Dark First-order Lump and PW Solutions

When $N=1$, based on the transformations (11), in terms of the seed solutions (4) and generalized (1, 0)-fold DT, it will produce the following expressions

$$\begin{aligned}&\widetilde{q}_1=e^{\textrm{i}(x+y+t)}+2\textrm{i}B^{(0)}, \ \ \widetilde{w}_1=1+4\textrm{i}A^{(0)}_y, \nonumber \\&\widetilde{\eta }_1=\tfrac{1}{2}+\Gamma _1+\Gamma _2 -\textrm{i}A^{(0)}_t+(\textrm{i}e^{\textrm{i}(x+y+t)} -2B^{(0)})|B^{(0)}|^2\textrm{i}e^{-\textrm{i}(x+y+t)}, \nonumber \\&\widetilde{\nu }_1=(8\textrm{i}A^{(0)}A^{(0)}_y-8\textrm{i}B^{(0)^*} B^{(0)}_y-4B^{(0)^*}\textrm{i}e^{\textrm{i}(x+y+t)} +4B^{(0)}\textrm{i}e^{-\textrm{i}(x+y+t)})-4\textrm{i}A^{(0)}_y,\nonumber \\&\widetilde{p}_1=\textrm{i}e^{\textrm{i}(t+x+y)}+\Xi _1+\Xi _2+\textrm{i} B^{(0)}_t+(\textrm{i}e^{\textrm{i}(x+y+t)}-2B^{(0)})A^{(0)^*}-\textrm{i} e^{\textrm{i}(x+y+t)}A^{(0)}, \end{aligned}$$

(21)

in which $A^{(0)}=\dfrac{\Delta A^{(0)}}{\Delta _1}, B^{(0)} =\dfrac{\Delta B^{(0)}}{\Delta _1}$, where

$$\begin{aligned} \Delta _{1}=\left| \begin{array}{cc} \varphi ^{(0)} &{} \psi ^{(0)} \\ \psi ^{(0)^*} &{} -\varphi ^{(0)^*} \end{array}\right| , \Delta A^{(0)}=\left| \begin{array}{cc} -\lambda _1\varphi ^{(0)} &{} \psi ^{(0)} \\ -\lambda _1^*\psi ^{(0)^*} &{} -\varphi ^{(0)^*} \end{array}\right| , \Delta B^{(0)}=\left| \begin{array}{cc} \varphi ^{(0)} &{} -\lambda _1\varphi ^{(0)} \\ \psi ^{(0)^*} &{} -\lambda _1^*\psi ^{(0)^*} \end{array}\right| . \end{aligned}$$

Adopting Type-I, on the basis of (19) and (21), we can acquire the bright-dark first-order lump solutions of Eq. (2), which can be rewritten as

$$\begin{aligned} \widetilde{q}_1=\dfrac{\gimel _1}{\gimel _2}e^{\textrm{i}(x+y+t)}, \ \ \widetilde{w}_1=\dfrac{\gimel _3}{\gimel _2^2}, \ \ \widetilde{\eta }_1=\dfrac{1}{3200}\dfrac{\gimel _3+\gimel _4}{\gimel _5^2}, \ \ \widetilde{\nu }_1=\dfrac{\gimel _6}{\gimel _2^2}, \ \widetilde{p}_1=\dfrac{\gimel _7}{\gimel _2^2}e^{\textrm{i}(x+y+t)}, \end{aligned}$$

(22)

where

$$\begin{aligned} \gimel _1& = -10(x^2+y^2+4t^2)+(10-20g_0)x-(20h_0+20\textrm{i})y +(24\textrm{i}-16+32x+24y+32g_0+24h_0)t-20\textrm{i}h_0 \\{} & {} -10(g_0^2+h_0^2-g_0)+5,\\ \gimel _2& = 10(x^2+y^2+4t^2)+(20g_0-10)x+20h_0y +(16-32x-24y-32g_0-24h_0)t+10(g_0^2+h_0^2-g_0)+5,\\ \gimel _3& = 1600t^4+(1280-2560x-1920y-2560g_0-1920h_0)t^3 +[1824x^2+(3648g_0+1536y+1536h_0-1824)x \\{} & {} +1376y^2+(1536g_0+2752h_0-768)y+1824g_0^2+(1536h_0-1824) g_0+1376h_0^2-768h_0-880]t^2\\{} & {} +\left\{ -640x^3 +(960-1920g_0-480y-480h_0)x^2 +[-640y^2+(480-960g_0-1280h_0) y-1920g_0^2\right. \\{} & {} +(1920-960h_0)g_0 -640h_0^2+480h_0+320]x -480y^3+(320-640g_0-1440h_0)y^2 \\{} & {} +\left[ -480g_0^2 +(480-1280h_0)g_0-480h_0^2+960 h_0-240 -480(2h_0-2) \left( h_0+\tfrac{4}{3}\right) \right] y\\{} & {} -640g_0^3 +(960-480h_0)g_0^2+(320-640h_0^2+480h_0)g_0 -480\left( h_0^2-2h_0 +\tfrac{1}{2}\right) \\{} & {} \left. \left( j_0+\tfrac{4}{3}\right) \right\} t+100x^4 +(400g_0-200)x^3 +(600g_0^2+200h_0^2+400h_0y\\{} & {} +200y^2-600g_0+200)x^2+[(400g_0-200)y^2+(800g_0h_0-400h_0-800)y +400g_0^3-600g_0^2 \\{} & {} +(400h_0^2+400)g_0-200h_0^2-800h_0-100]x +100y^4 +400h_0y^3 +(200g_0^2+600h_0^2-200g_0+100)y^2\\{} & {} +(400h_0g_0^2 +(-400h_0-800)g_0+400h_0^3 +200h_0+400)y +100g_0^4 -200g_0^3 +(200h_0^2+200)g_0^2\\{} & {} +(-200h_0^2-800h_0-100) g_0+100h_0^4+100h_0^2+400h_0+25,\\ \gimel _4& = 80(x^2-y^2+28t^2)+(160g_0+1120h_0+1120y-80)x\\{} & {} +(1120g_0-160h_0-560)y+(800-1600g_0-1600h_0 \\{} & {} -1600x-1600y) t+80(g_0^2-h_0^2-7h_0)+(1120h_0-80)g_0, \\ \gimel _5& = \dfrac{1}{4}(x^2+y^2+4t^2)-\dfrac{1}{5}(4x+3y+4g_0+3h_0-2)t +\left( \dfrac{1}{2}g_0-\dfrac{1}{4}\right) x+\dfrac{1}{2}h_0y+\dfrac{1}{4} \left( g_0^2-g_0+h_0^2+\dfrac{1}{2}\right) , \\ \gimel _6& = 400(x^2-y^2)+448t^2+(800g_0-400)x-800h_0y+(640-1280x+960y -1280g_0+960h_0)t+400 \\{} & {} (g_0^2-h_0^2-g_0),\\ \gimel _7& = -100\textrm{i}h_0^4+(2560\textrm{i}x+1920\textrm{i}y +2560\textrm{i}g_0+1920\textrm{i}h_0-960-1280\textrm{i})t^3\\{} & {} +[-1824\textrm{i}x^2+(-3648\textrm{i}g_0-1536\textrm{i}h_0 -1536\textrm{i}y+768+1824\textrm{i})x-1376\textrm{i}y^2\\{} & {} +(-1536\textrm{i}g_0-2752\textrm{i}h_0+1376+768\textrm{i})y -1824\textrm{i}g_0^2+(-1536\textrm{i}h_0+768 \\{} & {} +1824\textrm{i})g_0-1376\textrm{i}h_0^2+(1376+768 \textrm{i})h_0-384-192\textrm{i}]t^2+\{640\textrm{i}x^3\\{} & {} +(1920\textrm{i}g_0+480\textrm{i}h_0+480\textrm{i}y-240-960\textrm{i}) x^2+[640\textrm{i}y^2+(960\textrm{i}g_0+1280\textrm{i}h_0\\{} & {} -640-480 \textrm{i})y+1920\textrm{i}g_0^2+(960\textrm{i}h_0 -480 -1920\textrm{i})g_0+640\textrm{i}h_0^2\\{} & {} +(-640-480\textrm{i})h_0+240+480\textrm{i}]x +480\textrm{i}y^3+(640\textrm{i}g_0+1440h_0-720\\{} & {} -320\textrm{i})y^2+[480\textrm{i}g_0^2+(1280\textrm{i} h_0-640 -480\textrm{i})g_0 +1440\textrm{i}h_0^2+(-1440-640\textrm{i})h_0\\{} & {} +320-320\textrm{i}]y +640\textrm{i}g_0^3+(480\textrm{i}h_0-240 -960\textrm{i})g_0^2 +[640\textrm{i}h_0^2+(-640-480\textrm{i})h_0\\{} & {} +240+480\textrm{i}]g_0+480\textrm{i}h_0^3+(-720-320\textrm{i}) h_0^2+(320-320\textrm{i})h_0+40-80\textrm{i}\}t+(20-40\textrm{i})h_0\\{} & {} +(-400\textrm{i}g_0+200\textrm{i}) x^3+[-200\textrm{i}y^2+(-400\textrm{i}h_0+200)y -600\textrm{i}g_0^2-200\textrm{i}h_0^2+600\textrm{i}g_0\\{} & {} -180\textrm{i}+200h_0]x^2+\{(-400\textrm{i}g_0+200\textrm{i})y^2 +[(-800\textrm{i}h_0+400)g_0+400\textrm{i}h_0-200+80\textrm{i}]y\\{} & {} -400\textrm{i}g_0^3+600\textrm{i}g_0^2+(-400\textrm{i}h_0^2 -360\textrm{i}+400h_0)g_0+200\textrm{i}h_0^2+(80\textrm{i}-200)h_0\\{} & {} -40+80\textrm{i}\}x+80\textrm{i}h_0^2+(200-400 \textrm{i}h_0)y^3 +(80\textrm{i}-200\textrm{i}g_0^2-600 \textrm{i}h_0^2+200\textrm{i}g_0\\{} & {} +600h_0)y^2+[(200-400\textrm{i} h_0)g_0^2+(400\textrm{i}h_0-200 +80\textrm{i})g_0+20-40\textrm{i} -400\textrm{i}h_0^3+600h_0^2\\{} & {} +160\textrm{i}h_0]y-1600\textrm{i}t^4 -100\textrm{i}g_0^4 +(-200\textrm{i}h_0^2-180\textrm{i} +200h_0)g_0^2+[200\textrm{i}h_0^2\\{} & {} +(80\textrm{i}-200)h_0 -40+80\textrm{i}]g_0+200h_0^3-100\textrm{i}x^4 -100\textrm{i}y^4+20-15\textrm{i}+200\textrm{i}g_0^3. \end{aligned}$$

The above expressions contain two arbitrary parameters $g_0$ and $h_0$, which can control the position of the first-order lumps. The relevant shapes of first-order lump are shown in Fig. 2. In terms of Fig. 2a1–e1, we can distinctly observe that the solution q owns bright lump shapes with single wave peak and double wave troughs, w owns the bright lump shapes with double wave peaks and double wave troughs, solution $\eta$ has the dark lump shapes with double wave peaks and double wave troughs, solution $\nu$ owns the dark lump shapes with double wave peaks and single wave trough, and p has dark lump shapes with single wave peak and four wave troughs. The positions, maximum and minimum of the wave peaks and troughs of these lump solutions are listed in Table 1. In Fig. 2, we also show the lump structures with different parameters at different time. When the parameters $g_0=h_0=0$, we can clearly see that the lumps $q, w, \eta , \nu$ and p propagate along the positive directions of x and y with the increase of time. In Fig. 2a2–e2, with the increase of $h_0$, when $t=g_0=0$, we can find that the lumps propagate along the negative direction of y, with the increase of $g_0$, when $t=h_0=0$, the lumps propagate along the negative direction of x. More importantly, we find that the characteristics of $g_0$ and $h_0$ for the control position are also applicable to the higher-order lumps.

Fig. 2

Shape (above) and density (below) plots of the bright-dark first-order lump solutions $q, w, \eta , \nu$ and p through the expansions (22) with different positional parameters at different time: (a1)–(e1) $t=g_0=h_0=0$; (a2)–(e2) $t=3, g_0=5, h_0=10$

Table 1 Position of the maximum and minimum of the lump solutions (22)

According to the above Type-II, we take $\lambda _1=M+1$, on the basis of (20) and (21), the bright-dark first-order PW solutions can be easily obtained for Eq. (2), the related structures of the first-order PW are displayed in Fig. 3. Because of the complexity of the PW solutions, we here only give the structures of first-order PWs $\widetilde{q}_1, \widetilde{\eta }_1$ as shown in Fig. 3. When $g_0=h_0=0$, the PW solutions q and $\eta$ propagate along the positive direction of y with the increase of time in Fig. 3(a1)(a2)–(b1)(b2). With the increase of $h_0$, when $t=g_0=0$, the PW solutions q and $\eta$ propagate along the negative direction of y in Fig. 3(a3)–(b3). With the increase of $g_0$, when $t=h_0=0$, the PW solutions q and $\eta$ propagate along the negative direction of x in Fig. 3 (a4)–(b4).

Fig. 3

Shape (above) and density (below) plots of the bright-dark first-order PW solutions q and $\eta$ via the expansions (20) and (21) with different positional parameters at different time: (a1)(b1) $t=g_0=h_0=0$; (a2)(b2) $t=2, g_0=h_0=0$; (a3)(b3) $t=g_0=0, h_0=6$; (a4)(b4) $t=h_0=0, g_0=6$

4.2 Location Controllable Bright-Dark Second-Order Lump and PW Solutions

When $N=2$, based on the transformations (11), in terms of the seed solutions (4) and generalized (1, 1)-fold DT, it will produce the following expressions

$$\begin{aligned}&\widetilde{q}_2=e^{\textrm{i}(x+y+t)}+2\textrm{i}B^{(1)}, \ \ \widetilde{w}_2=1+4\textrm{i}A^{(1)}_y, \nonumber \\&\widetilde{\eta }_2=\tfrac{1}{2}+\Gamma _1+\Gamma _2 -\textrm{i}A^{(1)}_t+(\textrm{i}e^{\textrm{i}(x+y+t)} -2B^{(1)})|B^{(1)}|^2\textrm{i}e^{-\textrm{i}(x+y+t)}, \nonumber \\&\widetilde{\nu }_2=(8\textrm{i}A^{(1)}A^{(1)}_y-8\textrm{i} B^{(1)^*}B^{(1)}_y-4B^{(1)^*}\textrm{i}e^{\textrm{i}(x+y+t)} +4B^{(1)}\textrm{i}e^{-\textrm{i}(x+y+t)}-8\textrm{i}A^{(0)}_y) -4\textrm{i}A^{(1)}_y,\nonumber \\&\widetilde{p}_2=\textrm{i}e^{\textrm{i}(t+x+y)}+\Xi _1+\Xi _2 +\textrm{i}B^{(1)}_t+(\textrm{i}e^{\textrm{i}(x+y+t)}-2B^{(1)}) A^{(1)^*}-\textrm{i}e^{\textrm{i}(x+y+t)}A^{(1)}+2B^{(0)}, \end{aligned}$$

(23)

in which $A^{(1)}=\dfrac{\Delta A^{(1)}}{\Delta _2}, A^{(0)} =\dfrac{\Delta A^{(0)}}{\Delta _2}, B^{(1)}=\dfrac{\Delta B^{(1)}}{\Delta _2}, B^{(0)}=\dfrac{\Delta B^{(0)}}{\Delta _2}$, where

$$\begin{aligned} \Delta _{2}=\left| \begin{array}{cccc} \lambda _1\varphi ^{(0)} &{} \varphi ^{(0)} &{} \lambda _1\psi ^{(0)} &{}\psi ^{(0)}\\ \lambda _1^*\psi ^{(0)^*} &{} \psi ^{(0)^*} &{} -\lambda _1^*\varphi ^{(0)^*} &{} -\varphi ^{(0)^*} \\ \lambda _{1}\varphi ^{(1)}+\varphi ^{(0)} &{} \varphi ^{(1)} &{} \lambda _1\psi ^{(1)}+\psi ^{(0)} &{} \psi ^{(1)} \\ \lambda _1^*\psi ^{(1)^*}+\psi ^{(0)^*} &{} \psi ^{(1)^*} &{} -\lambda _1^*\varphi ^{(1)^*}-\varphi ^{(0)^*} &{} -\varphi ^{(1)^*} \end{array}\right| , \end{aligned}$$

$\Delta A^{(1)}, \Delta A^{(0)}, \Delta B^{(1)}$ and $\Delta B^{(0)}$ can be uniquely determined by determinant $\Delta _2$ substituting its first, second, third and fourth columns by the vector $(-\lambda _1^2\varphi ^{(0)}, -\lambda _1^{2*}\psi ^{(0)^*}, -\lambda _1^2\varphi ^{(1)}-2\lambda _1\varphi ^{(0)}, -\lambda _1^{2*}\psi ^{(1)^*}-2\lambda _1^*\psi ^{(0)^*})^{\textrm{T}}$.

Owing to the complexity of the second-order lump and PW solutions, we will leave out the expressions of explicit analytical solutions here. From (23), adopting the expansion of Type-I, we can obtain the second-order bright-dark lump solutions of Eq. (2), adopting the expansion of Type-II, we can also obtain the second-order bright-dark PW solutions of Eq. (2), which include four arbitrary parameters $g_i, h_i, (i=0,1)$, these parameters can not only control the position but also change the arrangement shape for second-order lump and PW.

However, because the propagation characteristics of second-order lumps $q, w, \eta , \nu$ and p are similar to the first-order lumps, we merely give the relevant images of w and $\eta$ in Figs. 4 and  5 by selecting various parameter combinations. In Fig. 4, with the increase of time, when $g_i=h_i=0$, the second-order bright-dark lumps w and $\eta$ not only propagate along the positive direction of x and y, but also separate into three first-order bright-dark lumps and arrange into triangles. In particular, if $t=g_i=h_i=0$, the strong interaction of second-order lump can be clearly displayed (see Fig. 4(a2)(b2)). When $g_1=10^3$ or $h_1=10^3$ and $g_0=h_0=0$, the second-order lumps can split into three first-order lumps and arrange into a triangle in Fig. 5(a1)(a2)–(b1)(b2). When the parameters $g_0=8, g_1=0, h_0=10, h_1=10^3$, the second-order lumps are not only divide into three first-order lumps, but also arrange into triangles and propagate along the negative directions of x and y in Fig. 5(a3)(b3).

Fig. 4

Shape (above) and density (below) plots of the bright-dark second-order lump solutions w and $\eta$ via the expansions (23) with smae positional parameters at different time: (a1)–(b3) $g_i=h_i=0, (i=0,1)$

Fig. 5

Shape (above) and density (below) plots of the bright-dark second-order lump solutions w and $\eta$ via the expansions (23) with different positional parameters at same time: (a1) (b1) $t=g_i=h_i=0, (i=0,1)$ except $g_1=10^3$; (a2) (b2) $t=g_i=h_i=0$ except $h_1=10^3$; (a3) (b3) $t=g_1=0, g_0=8, h_0=10, h_1=10^3$

In Fig. 6, we show the relevant structures of second-order PW solutions q and w, respectively. The strong interaction of second-order PW can be clearly displayed in Fig. 6(a1)(b1) when $t=g_i=h_i=0$. We can also find that the second-order PW will split into two first-order PWs with the increase of time and propagate along the positive y direction when $g_i=h_i=0$ in Fig. 6(a2)(b2). In Fig. 6(a3)(b3)–(a4)(b4), changing $g_1$ and $h_1$ will split the second-order PW into two first-order PWs, while changing $g_0$ and $h_0$ will control the position of the PW. Under the control of $g_0$ and $h_0$, the position change of the second-order PW is consistent with the first-order PW.

Fig. 6

Shape (above) and density (below) plots of the second-order PW solutions q and w via the expansions (23) with different positional parameters at different time: (a1) (b1) $t=g_i=h_i=0, (i=0,1)$; (a2) (b2) $t=8, g_i=h_i=0$; (a3) (b3) $t=g_i=h_i=0$ except $g_1=10^3$; (a4) (b4) $t=g_1=0, g_0=2, h_0=8$ except $\ h_1=10^4$

4.3 Location Controllable Bright-Dark Third-Order Lump Solutions

If we use the expansion of Type-II, we can certainly obtain the third-order PW solutions of Eq. (2). However, the expressions of the third-order PW solutions are extremely complex, therefore, we merely discuss the third-order lump solutions in this section.

When $N=3$, based on the transformations (11), in terms of the seed solutions (4) and generalized (1, 2)-fold DT, it will produce the following expressions

$$\begin{aligned}&\widetilde{q}_3=e^{\textrm{i}(x+y+t)}+2\textrm{i}B^{(2)}, \ \widetilde{w}_3=1+4\textrm{i}A^{(2)}_y, \nonumber \\&\widetilde{\eta }_3=\tfrac{1}{2}+\Gamma _1+\Gamma _2 -\textrm{i}A^{(2)}_t+(\textrm{i}e^{\textrm{i}(x+y+t)} -2B^{(2)})|B^{(2)}|^2\textrm{i}e^{-\textrm{i}(x+y+t)}, \nonumber \\&\widetilde{\nu }_3=(8\textrm{i}A^{(2)}A^{(2)}_y -8\textrm{i}B^{(2)^*}B^{(2)}_y-4B^{(2)^*}\textrm{i}e^{\textrm{i}(x+y+t)} +4B^{(2)}\textrm{i}e^{-\textrm{i}(x+y+t)}-8\textrm{i}A^{(1)}_y) -4\textrm{i}A^{(2)}_y,\nonumber \\&\widetilde{p}_3=\textrm{i}e^{\textrm{i}(t+x+y)}+\Xi _1+\Xi _2 +\textrm{i}B^{(2)}_t+(\textrm{i}e^{\textrm{i}(x+y+t)}-2B^{(2)}) A^{(2)^*}-\textrm{i}e^{\textrm{i}(x+y+t)}A^{(2)}+2B^{(1)}, \end{aligned}$$

(24)

in which $A^{(2)}=\dfrac{\Delta A^{(2)}}{\Delta _3}, A^{(1)}=\dfrac{\Delta A^{(1)}}{\Delta _3}, B^{(2)}=\dfrac{\Delta B^{(2)}}{\Delta _3}, B^{(1)}=\dfrac{\Delta B^{(1)}}{\Delta _3}$, where

$$\begin{aligned} \Delta _{3}=\left| \begin{array}{cccccc} \lambda _1^2\varphi ^{(0)} &{} \lambda _1\varphi ^{(0)} &{} \varphi ^{(0)} &{} \lambda _1^2\psi ^{(0)} &{} \lambda _1\psi ^{(0)} &{} \psi ^{(0)} \\ \lambda _1^{2^*}\psi ^{(0)^*} &{} \lambda _1^*\psi ^{(0)^*} &{} \psi ^{(0)^*} &{} -\lambda _1^{2^*}\varphi ^{(0)^*} &{} -\lambda _1^*\varphi ^{(0)^*} &{} -\varphi ^{(0)^*} \\ \lambda _1^2\varphi ^{(1)}+2\lambda _1\varphi ^{(0)} &{} \lambda _{1}\varphi ^{(1)}+\varphi ^{(0)} &{} \varphi ^{(1)} &{} \lambda _1^2\psi ^{(1)}+2\lambda _1\psi ^{(0)} &{} \lambda _1\psi ^{(1)}+\psi ^{(0)} &{} \psi ^{(1)} \\ \lambda _1^{2^*}\psi ^{(1)^*}+2\lambda _1^*\psi ^{(0)^*} &{} \lambda _1^*\psi ^{(1)^*}+\psi ^{(0)^*} &{} \psi ^{(1)^*} &{} -\lambda _1^{2^*}\varphi ^{(1)^*}-2\lambda _1^*\varphi ^{(0)^*} &{} -\lambda _1^*\varphi ^{(1)^*}-\varphi ^{(0)^*} &{} -\varphi ^{(1)^*} \\ \lambda _1^2\varphi ^{(2)}+2\lambda _1\varphi ^{(1)}+\varphi ^{(0)} &{} \lambda _1\varphi ^{(2)}+\varphi ^{(1)} &{} \varphi ^{(2)} &{} \lambda _1^2\psi ^{(2)}+2\lambda _1\psi ^{(1)}+\psi ^{(0)} &{} \lambda _1\psi ^{(2)}+\psi ^{(1)} &{} \psi ^{(2)} \\ \lambda _1^{2^*}\psi ^{(2)^*}+2\lambda _1^*\psi ^{(1)^*}+\psi ^{(0)^*} &{} \lambda _1^*\psi ^{(2)^*}+\psi ^{(1)^*} &{} \psi ^{(2)^*} &{} \lambda _1^{2^*}\varphi ^{(2)^*}+2\lambda _1^*\varphi ^{(1)^*}+\varphi ^{(0)^*} &{} \lambda _1^*\varphi ^{(2)^*}+\varphi ^{(1)^*} &{} \varphi ^{(2)^*} \end{array}\right| , \end{aligned}$$

$\Delta A^{(2)}, \Delta A^{(1)}, \Delta B^{(2)}$ and $\Delta B^{(1)}$ can be uniquely determined by determinant $\Delta _3$ substituting its first, second, fourth and fifth columns by the vector $(-\lambda _1^3\varphi ^{(0)}, -\lambda _1^{3^*}\psi ^{(0)^*}, -\lambda _1^3\varphi ^{(1)}-3\lambda _1^2\varphi ^{(0)}, -\lambda _1^{3^*}\psi ^{(1)^*}-3\lambda _1^{2^*}\psi ^{(0)^*}, -\lambda _1^3\varphi ^{(2)}-3\lambda _1^2\varphi ^{(1)}-3\lambda _1\varphi ^{(0)}, -\lambda _1^{3^*}\psi ^{(2)^*}-3\lambda _1^{2^*}\psi ^{(1)^*}-3\lambda _1^* \psi ^{(0)^*})^{\textrm{T}}$.

Using the expansion of Type-I, according to (24), the third-order bright-dark lump solutions of Eq. (2) can be obtained, it include six arbitrary parameters $g_i, h_i, (i=0,1,2)$, for the third-order lumps, these parameters can not only control the position but also change the arrangement shape.

The propagation characteristics of third-order lumps $q, w, \eta , \nu$ and p are similar to the first and second order lumps, so we merely give the relevant structures of q and $\eta$ in Fig. 7 by selecting various parameter combinations. If $t=g_i=h_i=0$, the strong interactions of the third-order lump are shown in Fig. 7(a1)(b1). Especially, with the increase of time, when $g_i=h_i=0$, the third-order lumps can change their positions and shapes from the strong interactions as shown in Fig. 7(a1)(a2). When $t=g_i=h_i=0$ except $g_1=10^3$, we can see clearly that third-order lumps split into six first-order lumps and arrange into triangles as displayed in Fig. 7(a3)(b3). When $t=g_i=h_i=0$ except $g_2=10^6$ or $h_2=10^6$, the third-order lumps can split into six first-order lumps and arrange into pentagons in Fig. 7(b2)(a4)(b4). Since the propagation of the third-order lumps is similar to the first-order lumps after changing $g_0$ and $h_0$, whose structures are omitted here. Subsequently, we will sum up the main mathematical characteristics of lump solutions related to order N in Table 2.

Fig. 7

Shape (above) and density (below) plots of the bright-dark third-order lump solutions q and $\eta$ via the expansions (24) with different positional parameters at different time: (a1) (b1) $t=g_i=h_i=0, (i=0,1,2)$; (a2) $t=2, g_i=h_i=0$; (b2) $t=g_i=h_i=0$ except $h_2=10^6$; (a3) (b3) $t=g_i=h_i=0$ except $g_1=10^3$; (a4) (b4) $t=g_i=h_i=0$ except $g_2=10^6$

Table 2 Main mathematical characteristics of lump solutions $q_N$, $w_N$, $\eta _N$, $\nu _N$ and $p_N$ related to order N

5 Mixed Breather-Lump Interaction Solutions via the Generalized $(2,N-2)$-Fold DT

In this section, based on the two spectral parameters, we will exhibit the new mixed interaction solutions of lump and breather for Eq. (2) by using generalized $(2,N-2)$-fold DT. In terms of the control of position parameters $g_0, h_0$, we can regulate the interaction between lump and breather. In the following contents, there are two cases: $N=2$ (the generalized (2, 0)-fold DT) and $N=3$ (the generalized (2, 1)-fold DT). For the convenience of calculation, we still discuss the parameters $a=b=\omega =m=\mu =k=\varepsilon _1=\varepsilon _2=w_1=1$.

5.1 Generalized (2,0)-Fold DT

Based on the case of $N=2$, the two spectral parameters $\lambda _1$ and $\lambda _2$ will be used, so there will be three cases: (i) Taylor series expansion is used for both spectral parameters at the same time; (ii) One of the spectral parameters is expanded by using Taylor series and the other is not used; (iii) Taylor series expansion is not used for both spectral parameters.

From the above cases (i) and (ii), we can obtain new formal solutions. For case (i), if we use the expansion of Type-I at $\lambda _1$ and Type-II at $\lambda _2$, we can get mixed interaction solutions for first-order bright-dark lump and first-order PW; If we use the expansion of Type-II at $\lambda _1$ and $\lambda _2$, respectively, the mixed interaction solutions for two first-order PWs will be obtained. For case (ii), if we use the expansion of Type-I at $\lambda _1$ or $\lambda _2$, we will get mixed interaction solutions of one-breather and first-order bright-dark lump; If we use the expansion of Type-II at $\lambda _1$ or $\lambda _2$, the mixed interaction solutions for one-breather and first-order PW will be gotten. For case (iii), this is known as the two-breather and does not constitute the new formal solutions. In this paper, we will only discuss the mixed interaction solutions of one-breather and first-order bright-dark lump in the case (ii), and ignore the other cases. Then, we use the expansion of Type-I at $\lambda _1$ and choose $\lambda _2=-\textrm{i}$.

According to the generalized (2, 0)-fold DT and seed solutions (4), the mixed interaction solutions of first-order bright-dark lump and one-breather can be given as below

$$\begin{aligned}&\widetilde{q}=e^{\textrm{i}(x+y+t)}+2\textrm{i}B^{(1)}, \ \widetilde{w}=1+4\textrm{i}A^{(1)}_y, \nonumber \\&\widetilde{\eta }=\tfrac{1}{2}+\Gamma _1+\Gamma _2 -\textrm{i}A^{(1)}_t+(\textrm{i}e^{\textrm{i}(x+y+t)}-2 B^{(1)})|B^{(1)}|^2\textrm{i}e^{-\textrm{i}(x+y+t)}, \nonumber \\&\widetilde{\nu }=(8\textrm{i}A^{(1)}A^{(1)}_y-8\textrm{i}B^{(1)^*} B^{(1)}_y-4B^{(1)^*}\textrm{i}e^{\textrm{i}(x+y+t)} +4B^{(1)}\textrm{i}e^{-\textrm{i}(x+y+t)}-8\textrm{i} A^{(0)}_y)-4\textrm{i}A^{(1)}_y,\nonumber \\&\widetilde{p}=\textrm{i}e^{\textrm{i}(t+x+y)}+\Xi _1+\Xi _2 +\textrm{i}B^{(1)}_t+(\textrm{i}e^{\textrm{i}(x+y+t)}-2B^{(1)}) A^{(1)^*}-\textrm{i}e^{\textrm{i}(x+y+t)}A^{(1)}+2B^{(0)}, \end{aligned}$$

(25)

where $A^{(1)}, A^{(0)}, B^{(1)}$ and $B^{(0)}$ can be determined by:

$$\begin{aligned} \left\{ \begin{array}{ll} T^{(0)}(\lambda _1)\phi ^{(0)}(\lambda _1)=0,\\ T(\lambda _2)\phi (\lambda _2)=0, \end{array}\right. \end{aligned}$$

(26)

in which $A^{(1)}=\dfrac{\Delta A^{(1)}}{\Delta _2}, A^{(0)} =\dfrac{\Delta A^{(0)}}{\Delta _2}, B^{(1)}=\dfrac{\Delta B^{(1)}}{\Delta _2}, B^{(0)}=\dfrac{\Delta B^{(0)}}{\Delta _2}$, where

$$\begin{aligned} \Delta _{2}=\left| \begin{array}{cccc} \lambda _1\varphi ^{(0)} &{} \varphi ^{(0)} &{} \lambda _1\psi ^{(0)} &{}\psi ^{(0)}\\ \lambda _1^*\psi ^{(0)^*} &{} \psi ^{(0)^*} &{} -\lambda _1^*\varphi ^{(0)^*} &{} -\varphi ^{(0)^*} \\ \lambda _2\varphi _1 &{} \varphi _1 &{} \lambda _2\psi _1 &{} \psi _1 \\ \lambda _2^*\psi _1^* &{} \psi _1^* &{} -\lambda _2^*\varphi _1^* &{} -\varphi _1^* \end{array}\right| , \end{aligned}$$

whereas $\Delta A^{(1)}, \Delta A^{(0)}, \Delta B^{(1)}$ and $\Delta B^{(0)}$ can be uniquely determined by determinant $\Delta _2$ replacing its first, second, third and fourth columns by the vector $(-\lambda _1^2\varphi ^{(0)}, -\lambda _1^{2^*}\psi ^{(0)^*}, -\lambda _2^2\varphi _1, -\lambda _2^{2^*}\psi _1^*)^{\textrm{T}}$, where $\varphi _1=\varphi |_{\lambda =\lambda _2}, \psi _1=\psi |_{\lambda =\lambda _2}$.

According to the solutions (25), which contains two position parameters $g_0$ and $h_0$. Subsequently, we can acquire the mixed interaction solutions of one-breather and first-order bright-dark lump, owing to the analytical expressions are extremely complex, which is leaved out here. In our research, it is found that the interaction characteristics of mixed solutions $q, w, \eta , \nu$ and p are consistent, so we only give the related images of q and $\nu$ as shown in Fig. 8 by selecting various parameter combinations. If $t=g_i=j_i=0$, the strong interaction between the first-order lump and one-breather can be given in Fig. 8(a1) (b1). In particular, as time increases, when $g_0=h_0=0$, the first-order bright-dark lumps q and $\nu$ not only propagate along the positive x and y directions, but also separate from the breather, and the breather propagate along the negative x and positive y directions in Fig. 8(a1)(b1)–(a2)(b2).When the parameters $g_0=8, h_0=0$ or $g_0=0, h_0=6$, the first-order lump propagates in the negative direction of x or negative direction of y, while the position of breather remains unchanged in Fig. 8(a3)(b3)–(a4)(b4). In terms of the generalized (2, 0)-fold DT, we will summarize the interaction structures between localized wave in Table 3.

Table 3 Interaction structures between localized wave via the generalized (2, 0)-fold DT

5.2 Generalized (2,1)-Fold DT

Based on the case of $N=3$, the two spectral parameters $\lambda _1$ and $\lambda _2$ will be used, it will product two cases: (i) Taylor series expansion is used for both spectral parameters simultaneously; (ii) One of the spectral parameters is expanded by using Taylor series and the other is not used.

From the above two cases, we can obtain new formal solutions. For case (i), there are three mixed interaction solutions in the following forms: The first mixed type is first-order bright-dark lump and second-order PW; The second mixed type is the first-order PW and second-order bright-dark lump; The third mixed interaction type is second-order PW and first-order PW. For case (ii), there are two mixed interaction solutions in the following forms: The first mixed mold is one-breather and second-order bright-dark lump; The second mixed mold is one-breather and second-order PW.

Next, we will ignore other cases and only discuss the following two cases:

${{\textbf {Case (a)}}}$ One-breather and second-order bright-dark lump in the case (ii).

${{\textbf {Case (b)}}}$ Second-order PW and first-order lump in the case (i).

In ${{\textbf {Case (a)}}}$, we use the expansion of Type-I at $\lambda _1$ and choose $\lambda _2=-\textrm{i}$. According to the seed solutions (4) and generalized (2, 1)-fold DT, the mixed interaction solutions for one-breather and second-order bright-dark lump can be given as below

$$\begin{aligned}&\widetilde{q}=e^{\textrm{i}(x+y+t)}+2\textrm{i}B^{(2)}, \ \widetilde{w}=1+4\textrm{i}A^{(2)}_y, \nonumber \\&\widetilde{\eta }=\tfrac{1}{2}+\Gamma _1+\Gamma _2 -\textrm{i}A^{(2)}_t+(\textrm{i}e^{\textrm{i}(x+y+t)}-2B^{(2)})| B^{(2)}|^2\textrm{i}e^{-\textrm{i}(x+y+t)}, \nonumber \\&\widetilde{\nu }=(8\textrm{i}A^{(2)}A^{(2)}_y-8\textrm{i} B^{(2)^*}B^{(2)}_y-4B^{(2)^*}\textrm{i}e^{\textrm{i}(x+y+t)} +4B^{(2)}\textrm{i}e^{-\textrm{i}(x+y+t)}-8\textrm{i}A^{(1)}_y) -4\textrm{i}A^{(2)}_y,\nonumber \\&\widetilde{p}=\textrm{i}e^{\textrm{i}(t+x+y)}+\Xi _1+\Xi _2+\textrm{i}B^{(2)}_t +(\textrm{i}e^{\textrm{i}(x+y+t)}-2B^{(2)})A^{(2)^*}-\textrm{i} e^{\textrm{i}(x+y+t)}A^{(2)}+2B^{(1)}, \end{aligned}$$

(27)

where $A^{(2)}, A^{(1)}, B^{(2)}$ and $B^{(1)}$ can be determined by:

$$\begin{aligned} \left\{ \begin{array}{ll} T^{(0)}(\lambda _1)\phi ^{(0)}(\lambda _1)=0,\\ T^{(0)}(\lambda _1)\phi ^{(1)}(\lambda _1)+T^{(1)}(\lambda _1) \phi ^{(0)}(\lambda _1)=0,\\ T(\lambda _2)\phi (\lambda _2)=0, \end{array}\right. \end{aligned}$$

(28)

in which $A^{(2)}=\dfrac{\Delta A^{(2)}}{\Delta _3}, A^{(1)}=\dfrac{\Delta A^{(1)}}{\Delta _3}, B^{(2)}=\dfrac{\Delta B^{(2)}}{\Delta _3}, B^{(1)}=\dfrac{\Delta B^{(1)}}{\Delta _3}$, where

$$\begin{aligned} \Delta _{3}=\left| \begin{array}{cccccc} \lambda _1^2\varphi ^{(0)} &{} \lambda _1\varphi ^{(0)} &{} \varphi ^{(0)} &{} \lambda _1^2\psi ^{(0)} &{} \lambda _1\psi ^{(0)} &{} \psi ^{(0)} \\ \lambda _1^2\varphi ^{(1)}+2\lambda _1\varphi ^{(0)} &{} \lambda _{1}\varphi ^{(1)}+\varphi ^{(0)} &{} \varphi ^{(1)} &{} \lambda _1^2\psi ^{(1)}+2\lambda _1\psi ^{(0)} &{} \lambda _1\psi ^{(1)}+\psi ^{(0)} &{} \psi ^{(1)} \\ \lambda _1^{2^*}\psi ^{(0)^*} &{} \lambda _1^*\psi ^{(0)^*} &{} \psi ^{(0)^*} &{} -\lambda _1^{2^*}\varphi ^{(0)^*} &{} -\lambda _1^*\varphi ^{(0)^*} &{} -\varphi ^{(0)^*} \\ \lambda _1^{2^*}\psi ^{(1)^*}+2\lambda _1^*\psi ^{(0)^*} &{} \lambda _1^*\psi ^{(1)^*}+\psi ^{(0)^*} &{} \psi ^{(1)^*} &{} -\lambda _1^{2^*}\varphi ^{(1)^*}-2\lambda _1^*\varphi ^{(0)^*} &{} -\lambda _1^*\varphi ^{(1)^*}-\varphi ^{(0)^*} &{} -\varphi ^{(1)^*} \\ \lambda _2^2\varphi _1 &{} \lambda _2\varphi _1 &{} \varphi _1 &{} \lambda _2^2\psi _1 &{} \lambda _2\psi _1 &{} \psi _1 \\ \lambda _2^{2^*}\psi _1^* &{} \lambda _2^*\psi _1^* &{} \psi _1^* &{} -\lambda _2^{2^*}\varphi _1^* &{} -\lambda _2^*\varphi _1^* &{} -\varphi _1^* \end{array}\right| , \end{aligned}$$

$\Delta A^{(2)}, \Delta A^{(1)}, \Delta B^{(2)}$ and $\Delta B^{(1)}$ can be determined by determinant $\Delta _3$ substituting its first, second, fourth and fifth columns by the vector $(-\lambda _1^3\varphi ^{(0)}, -\lambda _1^3\varphi ^{(1)}-3\lambda _1^2\varphi ^{(0)}, -\lambda _1^{3^*}\psi ^{(0)^*}, -\lambda _1^{3^*}\psi ^{(1)^*}-3\lambda _1^{2^*}\psi ^{(0)^*}, -\lambda _2^3\varphi _1, -\lambda _2^{3^*}\psi _1^*)^{\textrm{T}}$, where $\varphi _1=\varphi |_{\lambda =\lambda _2}, \psi _1=\psi |_{\lambda =\lambda _2}$.

According to (27) and (28), which contains four position parameters $g_i, j_i, (i=0, 1)$. Subsequently, the mixed interaction solutions for one-breather and second-order bright-dark lump can be acquired. We leave out the complex analytic solution expressions here. Similarly, we found that the interaction characteristics of mixed solutions $q, w, \eta , \nu$ and p are consistent, so we only give the related images of w and $\eta$ as shown in Figs. 9 and  10. In Fig. 9, As time increases, when $g_i=j_i=0$, the second-order bright lump w not only propagates along the positive x and y directions, but also separates from the breather and splits into three first-order lumps that arrange into a triangle, at the same time, the breather propagate along the positive x and y directions as displayed in Fig. 9(a1)–(a3). In particular, if $g_i=j_i=0$, the strong interaction between the second-order lump and one-breather can be given in Fig. 9(a2) (b2). When the parameters $g_i=j_i=0$ except $g_1=10^3$, the second-order lump splits into three first-order lumps clearly as shown in Fig. 9(b1)–(b3), whose propagation characteristics are consistent with Fig. 9(a1)–(a3). Figure 10 shows the mixed interactions between the second-order dark lump and one-breather, whose related properties are the same as Fig. 9.

Based on (27), In ${{\textbf {Case (b)}}}$, we use the Type-II at $\lambda _1$ and Type-I at $\lambda _2$, the mixed solutions for second-order PW and first-order lump can be given, where $A^{(2)}, A^{(1)}, B^{(2)}$ and $B^{(1)}$ can be determined by:

$$\begin{aligned} \left\{ \begin{array}{ll} T^{(0)}(\lambda _1)\phi ^{(0)}(\lambda _1)=0,\\ T^{(0)}(\lambda _1)\phi ^{(1)}(\lambda _1)+T^{(1)}(\lambda _1) \phi ^{(0)}(\lambda _1)=0,\\ T^{(0)}(\lambda _2)\phi ^{(0)}(\lambda _2)=0, \end{array}\right. \end{aligned}$$

(29)

in which $A^{(2)}=\dfrac{\Delta A^{(2)}}{\Delta _3}, A^{(1)} =\dfrac{\Delta A^{(1)}}{\Delta _3}, B^{(2)}=\dfrac{\Delta B^{(2)}}{\Delta _3}, B^{(1)}=\dfrac{\Delta B^{(1)}}{\Delta _3}$, where

$$\begin{aligned} \Delta _{3}=\left| \begin{array}{cccccc} \lambda _1^2\varphi ^{(0)} &{} \lambda _1\varphi ^{(0)} &{} \varphi ^{(0)} &{} \lambda _1^2\psi ^{(0)} &{} \lambda _1\psi ^{(0)} &{} \psi ^{(0)} \\ \lambda _1^2\varphi ^{(1)}+2\lambda _1\varphi ^{(0)} &{} \lambda _{1}\varphi ^{(1)}+\varphi ^{(0)} &{} \varphi ^{(1)} &{} \lambda _1^2\psi ^{(1)}+2\lambda _1\psi ^{(0)} &{} \lambda _1\psi ^{(1)}+\psi ^{(0)} &{} \psi ^{(1)} \\ \lambda _1^{2^*}\psi ^{(0)^*} &{} \lambda _1^*\psi ^{(0)^*} &{} \psi ^{(0)^*} &{} -\lambda _1^{2^*}\varphi ^{(0)^*} &{} -\lambda _1^*\varphi ^{(0)^*} &{} -\varphi ^{(0)^*} \\ \lambda _1^{2^*}\psi ^{(1)^*}+2\lambda _1^*\psi ^{(0)^*} &{} \lambda _1^*\psi ^{(1)^*}+\psi ^{(0)^*} &{} \psi ^{(1)^*} &{} -\lambda _1^{2^*}\varphi ^{(1)^*}-2\lambda _1^*\varphi ^{(0)^*} &{} -\lambda _1^*\varphi ^{(1)^*}-\varphi ^{(0)^*} &{} -\varphi ^{(1)^*} \\ \lambda _2^2\varphi _1^{(0)} &{} \lambda _2\varphi _1^{(0)} &{} \varphi _1^{(0)} &{} \lambda _2^2\psi _1^{(0)} &{} \lambda _2\psi _1^{(0)} &{} \psi _1^{(0)} \\ \lambda _2^{2^*}\psi _1^{(0)^*} &{} \lambda _2^*\psi _1^{(0)^*} &{} \psi _1^{(0)^*} &{} -\lambda _2^{2^*}\varphi _1^{(0)^*} &{} -\lambda _2^*\varphi _1^{(0)^*} &{} -\varphi _1^{(0)^*} \end{array}\right| , \end{aligned}$$

$\Delta A^{(2)}, \Delta A^{(1)}, \Delta B^{(2)}$ and $\Delta B^{(1)}$ can be determined by determinant $\Delta _3$ substituting its first, second, fourth and fifth columns by the vector $(-\lambda _1^3\varphi ^{(0)},-\lambda _1^3\varphi ^{(1)}-3 \lambda _1^2\varphi ^{(0)},-\lambda _1^{3^*}\psi ^{(0)^*}, -\lambda _1^{3^*}\psi ^{(1)^*}-3\lambda _1^{2^*}\psi ^{(0)^*}, -\lambda _2^3\varphi _1^{(0)},-\lambda _2^{3^*}\psi _1^{(0)^*})^{\textrm{T}}$, where $\varphi _1^{(0)}$ and $\psi _1^{(0)}$ are the same as $\varphi ^{(0)}$ and $\psi ^{(0)}$ in (19), respectively.

According to (27) and (29), which contains six position parameters $e_0, d_0, g_0, g_1, h_0, h_1$, for the mixed solutions, these parameters are used to control the position and change the arrangement shape. In Fig. 11, we only show the relevant images of w. The strong interaction for first-order lump and second-order PW can be clearly displayed when the time and parameters are zeroes in Fig. 11(a2). When the parameters are zeroes, with the increase of time, the second-order PW will separate from the first-order lump, and their propagation directions are the same as the the second-order PW and first-order lump, respectively (see Fig. 11(a1)–(a3)). In Fig. 11(b1)–(b3), changing $g_1$ and h1 will split the second-order PW into two first-order PWs, while changing $e_0, d_0, g_0$ and $h_0$ will determine the position change of the lump and PW. Under the control of $e_0, d_0, g_0$ and $h_0$, the position change of the first-order lump and second-order PW are consistent with the first-order lump and first-order PW, respectively. In terms of the generalized (2, 1)-fold DT, we will summarize the interaction structures between localized wave in Table 4.

Table 4 Interaction structures between localized wave via the generalized (2, 1)-fold DT

6 Conclusions

In this paper, we have investigated the nonisospectral $(2+1)$-dimensional Myrzakulov-Lakshmanan-IV equation (2), which may have potential value in applied ferromagnetism and nano magnetism. Compared with the published references [1, 5], the main contributions in this paper are summarized as below:

• (i) MI and the generation mechanism of various localized waves have been analyzed as shown in Fig. 1 for the first time;

• (ii) Generalized $(n,N-n)$-fold DT has been extended for the first time to the nonisospectral $(2+1)$-dimensional Eq. (2);

• (iii) In terms of the generalized $(1,N-1)$-fold DT, location controllable multi-lump and PW solutions for Eq. (2) have been given and discussed, and relevant structures have been shown in Figs. 2 3 4 5 6  and 7;

• (iv) In terms of the generalized $(2,N-2)$-fold DT, the mixed breather-lump and mixed PW-lump interaction solutions for Eq. (2) have been obtained, and relevant structures have been shown in Figs. 8 9 10 and  11;

• (v) It should be specially noted that the positions of these localized waves can be controlled by some special parameters, which allows us to change these control parameters to make them appear at the desired positions. We believe that these results have certain theoretical significance for the parameter control of different localized waves.

These above-mentioned results are first reported. We expect that these achievements and new phenomena in this paper are helpful to understand some physical phenomena in applied ferromagnetism and nano magnetism.

Fig. 8

Shape (above) and density (below) plots of mixed interaction between one-breather and first-order bright-dark lump of solutions q, $\nu$ via the expansions (25) with different positional parameters at different time: (a1) (b1) $t=g_0=h_0=0$; (a2) (b2) $t=3, g_0=h_0=0$; (a3) (b3) $t=h_0=0, g_0=8$; (a4) (b4) $t=g_0=0, h_0=6$

Fig. 9

Shape (above) and density (below) plots of mixed interactions between second-order bright lump and one-breather of solution w via the expansions (27) with different positional parameters: (a1)–(a3) $g_i=h_i=0, (i=0,1)$; (b1)–(b3) $g_i=h_i=0$ except $g_1=10^3$

Fig. 10

Shape (above) and density (below) plots of mixed interactions between second-order dark lump and one-breather of solution $\eta$ via the expansions (27) with different positional parameters: (a1)–(a3) $g_i=h_i=0, (i=0,1)$; (b1)–(b3) $g_i=h_i=0$ except $h_1=10^3$

Fig. 11

Shape (above) and density (below) plots of mixed interactions between second-order PW and first-order lump of solution w via the expansions (27) with different positional parameters: (a1)–(a3) $e_0=d_0=g_0=g_1=h_0=h_1=0$; (b1) $e_0=d_0=g_0=g_1=0$ except $h_0=10, h_1=10^3$; (b2) $e_0=g_0=g_1=h_0=h_1=0$ except $d_0=6$; (b3) $e_0=d_0=g_0=h_0=h_1=0$ except $g_1=10^4$