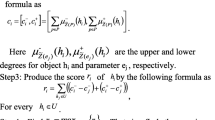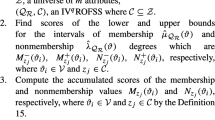1 Introduction

Data in many real-world issues tend to be ambiguous and imprecise, which presents severe difficulties for effective data-driven decision making [1,2,3,4,5, 42]. To deal with uncertainties, Molodtsov [6] developed the idea of a soft set as a universal mathematical tool, which overcame the weaknesses of the classical mathematical tools for dealing with uncertain data such as probability theory, rough sets, and fuzzy sets so on. Active research [7, 8] has been done to improve the definitions and operations of classical soft sets. Soft set theory has been developed and applied to other fields [9,10,11] to solve practical problems.

The soft set theory has no issues with setting the membership function, which promotes the combination of the soft set with other models. There are many extended models such as fuzzy soft sets [13], bipolar complex fuzzy soft sets [14], hesitant fuzzy soft sets [15, 16], vague soft sets [18,19,20], soft rough sets [17, 21, 22], rough soft sets [23,24,25], and intuitionistic fuzzy soft sets [12, 26] so on. The interval-valued fuzzy soft set (IVFSS) is one of the successful extended models of soft set theory. Yang et al. [27] proposed the concept of IVFSS by combining the soft set and interval-valued fuzzy set models. This model has been effectively utilized in decision-making applications. In [28], Ali et al. established interval-valued fuzzy soft pre-sorting and interval-valued fuzzy soft equivalence and proposed two sets of crisp pre-sorting. A scoring function that depends on the comparison matrix was proposed, which showed good performance when solving multi-group decision problems. Qin et al. [29] proposed a decision-making method based on IVFSS using contrast tables. The objective of parameter reduction is to remove those redundant parameters that have little or no effect on the decision. Ma et al. [30] proposed four heuristic parameter reduction algorithms, which were verified in terms of ease of applicability, finding reduction, exact level for reduction, reduction result, applied situation, and computational complexity. The four algorithms retain certain decision-making abilities while reducing redundant parameters. Ma et al. [31] proposed a decision algorithm that is relatively computationally inexpensive and takes into account added objects. The algorithm has higher scalability and flexibility for large-scale datasets. Pairote [32] integrated IVFSS with semigroups. Nor et al. [33] established an axiomatic definition of entropy based on subsets for IVFSS and introduced an entropy measure, which is used to calculate the degree of fuzziness of a particular interval-valued fuzzy soft set. Zhang et al. [34] proposed an improved decision-making method by introducing operators and using a comparable table of IVFSS.

However, a lot of incomplete information will be involved in the actual application process, which is not conducive to decision-makers making correct decisions. Therefore, it is necessary to deal with incomplete information. Among the methods for dealing with missing data, data filling methods have attracted the attention of researchers. In 2008, Zou et al. [35] proposed data analysis methods of soft sets under incomplete information environment. However, which involved high computational complexity and were difficult to understand. To simplify the method, Kong et al. [36] directly proposed the simplified probability to replace incomplete information and proved the equivalence between the weighted average method [35] of all possible choice values and the simplified probability method. In [37], Xia et al. proposed a new decision-making method based on the soft set theory to solve the MCDM problem with redundant and incomplete information, which can be directly used for the original redundant and incomplete dataset. Kong et al. [38] proposed a new method of data filling based on the probability analysis in the incomplete soft set. It also avoids the influence of subjective factors on the threshold and has good objectivity. In [39], Qin et al. proposed a data analysis method for incomplete interval-valued intuitionistic fuzzy soft sets. This method fully considers and utilizes the characteristics of interval-valued intuitionistic fuzzy soft sets.

Due to the particularity of membership in interval-valued fuzzy soft sets (membership degrees are expressed by interval data), the methods in [35,36,37,38,39] for dealing with incomplete data are not suitable for processing interval-valued fuzzy soft sets with incomplete information. Therefore, it is necessary to study data analysis methods based on the interval-valued fuzzy soft sets under incomplete information. Qin et al. [40] proposed a data analysis method for interval-valued fuzzy soft sets under incomplete information. This method deals with missing data through the relationship between the percentage of missing items and the threshold, which provides a new idea for filling incomplete data. However, the method is subjective in setting the threshold of percentage of missing entries and has the weakness of lower accuracy and higher error rate. To address the problems of this method, we propose a KNN data filling method for IVFSS. This method reasonably fills the missing data by introducing K-nearest neighbors (KNN). The main work of this paper is as follows:

  1. (a)

    We discover that the filling results by the existing method in [40] have the probability to dissatisfy the constraints of the interval-valued fuzzy soft set as \(0 \le \mu_{{_{{\tilde{S}(ej)}} }}^{ - *} (h_{i} ) \le \mu_{{_{{\tilde{S}(ej)}} }}^{ + } (h_{i} ) \le 1\).

  2. (b)

    We propose a KNN data filling method based on the interval-valued fuzzy soft sets. The experimental results on the Shanghai five-four star hotel dataset and simulated datasets illustrate that our method has a higher accuracy rate and a significantly lower error rate compared with the existing method in [40].

  3. (c)

    An attribute-based combining rule is proposed to determine whether values containing incomplete data should be ignored or filled which avoids subjectivity.

The rest of the paper is organized as follows. In Sect. 2, we mainly review the basic concepts of this model and the existing data analysis methods based on the incomplete interval value fuzzy soft sets. Section 3 describes the steps of our proposed KNN data filling method based on the incomplete interval-valued fuzzy soft sets. In Sect. 4, experiments are conducted on the Shanghai five-four star hotel datasets and simulated datasets. By comparing with the existing algorithms, the accuracy and feasibility of the method are verified. Section 5 is the conclusion of this paper.

2 Preliminaries and Related Work

In this section, we briefly review some basic definitions of IVFSS. At the same time, the existing data analysis approach of IVFSS under incomplete information is recalled.

2.1 Preliminaries

Let \(U = \{ h_{1} ,h_{2} ,...,h_{n} \}\) be a nonempty initial universe of objects and \(E = \{ e_{1} ,e_{2} ,...e_{m} \}\) be a set of parameters in relation to objects in \(U\) respectively. Let \(P(U)\) be the power set of \(U\), and \(A \subseteq E\). The definition of soft set is given as follows.

Definition 2.1

[1]: A pair \((F,A)\) is called a soft set over U, where \(F\) is a mapping given by F:

$$F:A \to P(U)$$
(1)

Let \(U\) be an initial universe of objects,\(E\) be a set of parameters in relation to objects in U, \(\xi (U)\) be the set of all fuzzy subsets of U. The definition of fuzzy soft set is given as follows.

Definition 2.2

[12]: A pair \((\tilde{F},E)\) is called a fuzzy soft set over \(\zeta (U)\), where \({\tilde{\text{F}}}\) is a mapping given by \({\tilde{\text{F}}}\):

$$\tilde{F}:E \to \zeta (U)$$
(2)

Definition 2.3

[27]: Let \(\hat{X}\) be an interval-valued fuzzy set on a universe \(U\), where \(\hat{X}\) is a mapping such that:

$$\hat{X}:U \to Int([0,1])$$
(3)

where \(\hat{X} \in \xi (U)\) for every \(x \in U\) and \(\xi (U)\) represents the set of all interval-valued fuzzy sets on U. \(Int([0,1])\) represents the set of all closed subintervals of [0, 1].\(\mu_{{\hat{X}}}^{ - } (x)\) and \(\mu_{{\hat{X}}}^{ + } (x)\) represent the lower and upper degrees of membership \(x\) to \(\hat{X}(0 \le \mu_{{\hat{X}}}^{ - } (x) \le \mu_{{\hat{X}}}^{ + } (x) \le 1)\), respectively.

Definition 2.4

[27]: Let \(U\) be an initial universe of objects and \(E\) be a set of parameters in relation to objects in \(U\). A pair \((\varpi ,E)\) is called an interval-valued fuzzy soft set over \(\tilde{\psi }(U)\), where \(\varpi\) is a mapping given by.

$$\varpi :E \to \tilde{\psi }(U)$$
(4)

\(\forall \varepsilon \in E,\varpi (\varepsilon )\) is interpreted as the interval fuzzy value set of parameter \(\varepsilon\). It is actually an interval-valued fuzzy set of \(U\), where \(x \in U\) and \(\varepsilon \in E\), which can be written as \(\varpi (\varepsilon ) = \left\{ {\left\langle {x,\mu_{\varpi (\varepsilon )} (x)} \right\rangle :x \in U} \right\}\). Where \(\varpi (\varepsilon )\) is the interval-valued fuzzy membership degree that object \(x\) holds on parameter \(\varepsilon\).

2.2 The Existing Data Filling Methods for Incomplete Interval-Valued Fuzzy Soft Sets

In this section, we briefly introduce the existing data analysis approach of interval-valued fuzzy soft sets under incomplete information. An example is given to illustrate it.

2.2.1 Average Based Data Filling (ADF) Algorithm for Incomplete Interval-Valued Fuzzy Soft Sets [40]

Input: IVFSS \((\tilde{S},E)\), the parameter set \(E\). The threshold of missing entries and weights \(\lambda_{o} = \lambda_{p} = \frac{1}{2}\).

  1. 1.

    For every parameter, if \(Pe{r}_{S({e}_{a})}^{*}>{r}_{p}\) (\(Pe{r}_{S({e}_{a})}^{*}\) is the percentage of missing entries for parameter ea), the corresponding parameter is ignored. For every object, if \(Per_{{S(h{}_{b})}}^{*} > r_{o}\), the corresponding object is ignored.

  2. 2.

    Find \(\mu_{{\tilde{S}(ea)}}^{*} (h_{b} )\) as the missing degree of membership.

  3. 3.

    Compute \(d_{{\tilde{S}(ea)}}^{ - *} (h_{b} )\) and \(d_{{\tilde{S}(ea)}}^{ + *} (h_{b} )\) as predicted membership degrees for \(e_{a}\).

  4. 4.

    Obtain \(p_{{\tilde{S}(ea)}}^{ - *} (h_{b} )\) and \(p_{{\tilde{S}(ea)}}^{ + *} (h_{b} )\) as predicted membership degrees for \(h_{b}\).

  5. 5.

    Fill the missing degree of membership by

    $$\mu_{{S(e_{a} )}}^{ - *} (h_{b} ) = \lambda_{d} d_{{S(e_{a} )}}^{ - *} (h_{b} ) + \lambda_{p} p_{{S(e_{a} )}}^{ - *} (h_{b} )$$
    $$\mu_{{S(e_{a} )}}^{ + *} (h_{b} ) = \lambda_{d} d_{{S(e_{a} )}}^{ + *} (h_{b} ) + \lambda_{p} p_{{S(e_{a} )}}^{ + *} (h_{b} )$$

Output: a complete interval-valued fuzzy soft set.

One Example is given to present the method in [40].

Example 2.1

Suppose that \(U = \{ h_{1} ,h_{2} ,h_{3} ,...,h_{14} \}\) is a set including 14 objects, \(E = \{ e_{1} ,e_{2} ,e_{3} ,e_{4} ,e_{5} ,e_{6} \}\) involving six parameters. The incomplete interval-valued fuzzy soft set as shown in Table 1. Here is a brief filling process.

Table 1 An incomplete interval-valued fuzzy soft set
Full size table

for parameters and objects as \(r_{p} = r_{o} = 0.8\), and give the weights as \(\lambda_{d} = \lambda_{p} = \frac{1}{2}\). Finally, Table 1 is converted to the complete interval-valued fuzzy soft set shown in Table 2 by the method [40].

Table 2 Converted complete interval-valued fuzzy soft sets
Full size table

Through our observation, it is found that Filling results: \(\mu_{{\tilde{S}(e2)}}^{*} (h_{9} ) = {[0}{\text{.77,}}\,{0}{\text{.75]}}\) and \(\mu_{{\tilde{S}(e4)}}^{*} (h3) = [0.85,0.81]\) do not satisfy the constraints of the interval-valued fuzzy soft set as \(0 \le \mu_{{_{{\tilde{S}(ej)}} }}^{ - *} (h_{i} ) \le \mu_{{_{{\tilde{S}(ej)}} }}^{ + } (h_{i} ) \le 1\). That is, there exist filling results that exceed the limit. Meanwhile, the existing data analysis methods based on the interval-valued fuzzy soft sets have disadvantages such as lower accuracy and more subjectivity. To solve these problems, a new KNN data filling algorithm based on the interval-valued fuzzy soft sets is proposed in this paper.

3 The Proposed Data Filling Algorithm

In this section, we first propose some new related definitions. Subsequently, a new KNN data filling method based on the interval-valued fuzzy soft sets is proposed. An attribute-based combining rule is first designed to determine whether the incomplete data should be ignored or filled. For the remaining incomplete data, it will be filled according to its K complete nearest neighbors. This method avoids subjectivity, and the accuracy of filling results is significantly improved.

3.1 The Related Definitions

Definition 3.1

For an interval-valued fuzzy soft set \((\tilde{F},E)\), \(E = \left\{ {e_{1} ,e_{2} ,...,e_{m} } \right\}\) and \(U = \left\{ {h_{1} ,h_{2} ,...,h_{n} } \right\}\).\(\mu_{{\tilde{S}(e{\text{j}})}}^{{ - *}} (h_{i} )\) and \(\mu_{{\tilde{S}(e{\text{j}})}}^{{ + {*}}} (h_{i} )\) represent the incomplete lower degree of membership and upper degree of membership,respectively. To determine whether incomplete data should be ignored or filled, an attribute-based combining rule is proposed, defined as follows.

$$F_{ej} = \sum\nolimits_{i = 1}^{n} {(\mu_{{\tilde{S}(e{\text{j}})}}^{ - } (h_{i} ) \times \mu_{{\tilde{S}(e{\text{j}})}}^{ + } (h_{i} ))}$$
(5)

where \(\mu_{{\tilde{S}(e{\text{j}})}}^{ - } (h_{i} )\) and \(\mu_{{\tilde{S}(e{\text{j}})}}^{ + } (h_{i} )\) represent the lower degree of membership and upper degree of membership, respectively. \(\mu_{{\tilde{S}(e{\text{j}})}}^{ - } (h_{i} )\) and \(\mu_{{\tilde{S}(e{\text{j}})}}^{ + } (h_{i} )\) of incomplete data are set as 0 in above formula.

  1. (1)

    \(F_{ej} = 0\), ignore filling the incomplete data with attribute \(e_{j}\). (Each object has missing values in the attribute \(e_{j}\)).

  2. (2)

    \(F_{ej} \ne 0\), fill the incomplete data according to our algorithm. (At least one object has a complete degree of membership on attribute \(e_{j}\)).

When \(\mu_{{\tilde{S}(e{\text{j}})}}^{{ - *}} (h_{i} )\) or \(\mu_{{\tilde{S}(e{\text{j}})}}^{{ + {*}}} (h_{i} )\) as missing data are presented in all elements of an attribute, this means that the original dataset contains incomplete data for each object. In other words, no object for the attribute provides complete and accurate information. To avoid amplifying the uncertainty, the filling of incomplete data under this attribute will be ignored. In addition, this rule does not require setting the threshold of missing items, which is different from the existing method, thus avoiding subjectivity.

Inspried by Qi et al. [41], the definition of distance between the object involving incomplete data and the object with complete data is given as follows.

Definition 3.2

The distance between the object \(h_{a}\) involving incomplete data and the object \(h_{b}\) with complete data is defined as.

$${D}_{\mathrm{avg}}({h}_{a},{h}_{b})=\sqrt{{\sum }_{j=1}^{m}\left({\left|{\mu }_{\widetilde{S}(ej)}^{-}({h}_{a})-{\mu }_{\widetilde{S}(ej)}^{-}({h}_{b})\right|}^{2}{I}_{j}^{-}+{\left|{\mu }_{\widetilde{S}(ej)}^{+}({h}_{a})-{\mu }_{\widetilde{S}(ej)}^{+}({h}_{b})\right|}^{2}{I}_{j}^{+}\right)}$$
(6)

\(\mu_{{\tilde{S}(e{\text{j}})}}^{ - } (h_{a} )(\mu_{{\tilde{S}(e{\text{j}})}}^{ - } (h_{b} )\) represents the lower degree of membership of object \(h_{a} (h_{b} )\) and \(\mu_{{\tilde{S}(e{\text{j}})}}^{ + } (h_{a} )(\mu_{{\tilde{S}(e{\text{j}})}}^{ + } (h_{b} )\) represents the upper degree of membership of object \(h_{a} (h_{b} )\).

$$I_{j}^{ - } (I_{j}^{ + } )\, = \,\left\{ \begin{gathered} 1,\,{\text{if}}\,\mu_{{\tilde{S}(ej)}}^{ - } (h_{a} )\,{\text{and}}\,\mu_{{\tilde{S}(ej)}}^{ - } (h_{b} )\,({\text{or}}\,\mu_{{\tilde{S}(ej)}}^{ + } (h_{a} )\,{\text{and}}\,\mu_{{\tilde{S}(ej)}}^{ + } (h_{b} )\,{\text{are}}\,{\text{ not}}\,{\text{missing}} \hfill \\ 0,\,\,{\text{otherwise}} \hfill \\ \end{gathered} \right.$$

for j = 1,2,…,m.

3.2 The Proposed Algorithm

Based on the above definitions, we give our algorithm as follows:

Input: Incomplete interval-valued fuzzy soft set \((\tilde{F},E)\) and parameter set \(E\).

Step 1: Determine \(\mu_{{\tilde{S}(ej{)}}}^{{ - *}} (h_{i} )\) and \(\mu_{{\tilde{S}(ej)}}^{{ + {*}}} (h_{i} )\) as the unknown degree of membership of an element \(h_{i}\) to \(\tilde{S}(e_{j} )\).

Step 2: Judge whether the incomplete data needs to be filled or ignored according to the attribute-based combining rules. If \(F_{ej} = 0\), ignore filling the incomplete data with attribute \(e_{j}\). Else, fill the incomplete data with attribute \(e_{j}\).

Step 3: Use the distance formula (6) to calculate the distance between the object that contains incomplete data and the other objects involving complete data, and sort the distance.

Step 4: Find the optimal K value. In detail, extract incomplete object composition U′ as training dataset, and randomly delete data as missing membership degree values in U′ (that is, choose one membership degree value as training data every row in U′). Repeat steps 1–3 to fill the randomly deleted data in order to find the optimal K value which has the highest average accuracy.

Step 5: Fill the incomplete data which can be calculated according to the following formula:

When the incomplete data is the lower degree of membership:

$$\mu_{{\tilde{S}(ej)}}^{ - *} (h_{i} ) = \frac{{\sum\nolimits_{i = 1}^{k} {\mu_{{\tilde{S}(ej)}}^{ - } (h_{i} )} }}{k}$$
(7)

When the missing value is the upper degree of membership:

$$\mu_{{\tilde{S}(ej)}}^{ + *} (h_{i} ) = \frac{{\sum\nolimits_{i = 1}^{k} {\mu_{{\tilde{S}(ej)}}^{ + } (h_{i} )} }}{k}$$
(8)

\(k\) represents the number of K-nearest neighbors which is obtained in the above step. \(\mu_{{\tilde{S}(e{\text{j}})}}^{ - } (h_{i} )\) and \(\mu_{{\tilde{S}(e{\text{j}})}}^{ + } (h_{i} )\) represent the upper and lower degree of membership of K complete nearest neighbors, respectively.

Output: a complete interval-valued fuzzy soft set.

Figure 1 depicts the flowchart of our proposed new method.

Fig. 1
figure 1

Flow chart of KNN data filling method

Full size image

3.3 Example

The following example is provided to demonstrate this method.

Consider the incomplete interval-valued fuzzy soft set shown in Table 1 and use the KNN data filling method to predict the incomplete data. The prediction steps are as follows.

Input: Incomplete interval-valued fuzzy soft sets, as shown in Table 1.

  • (1) Find

    $$[\mu_{{_{{\tilde{S}(e1)}} }}^{ - *} (h_{5} ),\mu_{{_{{\tilde{S}(e1)}} }}^{ + } (h_{5} )] = [*,0.75]\,[\mu_{{_{{\tilde{S}(e2)}} }}^{ - } (h_{9} ),\mu_{{_{{\tilde{S}(e2)}} }}^{ + *} (h_{9} )] = [0.77,*]$$
    $$[\mu_{{_{{\tilde{S}(e3)}} }}^{ - *} (h_{12} ),\mu_{{_{{\tilde{S}(e3)}} }}^{ + } (h_{12} )] = [*,0.80]\,[\mu_{{_{{\tilde{S}(e4)}} }}^{ - } (h_{3} ),\mu_{{_{{\tilde{S}(e4)}} }}^{ + *} (h_{3} )] = [0.85,*]$$
    $$[\mu_{{_{{\tilde{S}(e5)}} }}^{ - *} (h_{7} ),\mu_{{_{{\tilde{S}(e5)}} }}^{ + } (h_{7} )] = [*,0.78]\,[\mu_{{_{{\tilde{S}(e6)}} }}^{ - } (h_{2} ),\mu_{{_{{\tilde{S}(e6)}} }}^{ + *} (h_{2} )] = [0.78,*]$$

  • (2) Using the combining rules to judge whether the incomplete data needs to be filled or ignored.

Calculate:

$$F_{e1} =\, 0.88 \times 0.9 + 0.74 \times 0.75 + ... + 0.56 \times 0.7 + 0.56 \times 0.83 \ne 0$$

Similarly:

$$F_{e2} \ne F_{e3} \ne F_{e4} \ne F_{e5} \ne F_{e6} \ne 0$$

Therefore, no parameter can be ignored. That is, we keep all parameters, and missing data must be filled.

  • (3) Calculate the distance between objects containing incomplete data and other objects which have the complete data. Taking the example of filling the incomplete data \(\mu_{{\tilde{S}(e{1})}}^{{ - *}} (h_{5} )\):

    $$\begin{gathered} D_{{{\text{avg}}}} (h_{5} ,h_{1} ) = \sqrt {(|0 - 0.88|^{2} \times 0 + |0.75 - 0.9|^{2} \times 1) + ... + (|0.69 - 0.47|^{2} \times 1 + |0.72 - 0.82|^{2} \times 1)} \hfill \\ \quad \quad \quad \quad \quad = \sqrt {0.1168} \hfill \\ \end{gathered}$$

Similarly,

$$D_{avg} (h_{5} ,h_{4} ) = \sqrt {0.1246} \,D_{avg} (h_{5} ,h_{6} ) = \sqrt {0.1334}$$
$$D_{avg} (h_{5} ,h_{8} ) = \sqrt {0.1173} \,D_{avg} (h_{5} ,h_{10} ) = \sqrt {0.1773}$$
$$D_{avg} (h_{5} ,h_{11} ) = \sqrt {0.2002} \,D_{avg} (h_{5} ,h_{13} ) = \sqrt {0.0736}$$
$$D_{avg} (h_{5} ,h_{14} ) = \sqrt {0.1003}$$

And sort the distances as:

\(D_{avg} (h_{5} ,h_{13} ) < D_{avg} (h_{5} ,h_{14} ) < D_{avg} (h_{5} ,h_{1} ) < D_{avg} (h_{5} ,h_{8} ) < D_{avg} (h_{5} ,h_{4} ) < D_{avg} (h_{5} ,h_{6} ) < D_{avg} (h_{5} ,h_{10} ) < D_{avg} (h_{5} ,h_{11} )\)

  • (4) Find the optimal K value.

Extract incomplete objects to form a new incomplete interval-valued fuzzy soft set U′ as training dataset shown in Table 3.

Table 3 Incomplete interval-valued fuzzy soft set U′
Full size table

In U′, delete one data randomly every row and record it as **. Get a new interval-valued fuzzy soft set U′″, as shown in Table 4

Table 4 Incomplete interval-valued fuzzy soft set U′″
Full size table

Calculate the distance between objects containing incomplete data and other objects having complete data. Take filling \(\mu_{{\tilde{S}(e{2})}}^{{ - *}} (h_{9} )\) as an example:

$$\begin{gathered} D_{avg} (h_{9} ,h_{1} ) = \sqrt {(|0.64 - 0.88|^{2} \times 0 + |0.68 - 0.9|^{2} \times 1) + ... + (|0.71 - 0.47|^{2} \times 1 + |0.75 - 0.82|^{2} \times 1)} \hfill \\ \quad \quad \quad \quad \quad = \sqrt {0.2738} \hfill \\ \end{gathered}$$

Similarly,

$$D_{avg} (h_{9} ,h_{4} ) = \sqrt {0.2084} \,D_{avg} (h_{9} ,h_{6} ) = \sqrt {0.1921}$$
$$D_{avg} (h_{9} ,h_{8} ) = \sqrt {0.1981} \,D_{avg} (h_{9} ,h_{10} ) = \sqrt {0.3453}$$
$$D_{avg} (h_{9} ,h_{11} ) = \sqrt {0.2982} \,D_{avg} (h_{9} ,h_{13} ) = \sqrt {0.0774}$$
$$D_{avg} (h_{9} ,h_{14} ) = \sqrt {0.1222}$$

Sorting the distances as:

\(D_{avg} (h_{9} ,h_{13} ) < D_{avg} (h_{9} ,h_{14} ) < D_{avg} (h_{9} ,h_{6} ) < D_{avg} (h_{9} ,h_{8} ) < D_{avg} (h_{9} ,h_{4} ) < D_{avg} (h_{9} ,h_{1} ) < D_{avg} (h_{9} ,h_{11} ) < D_{avg} (h_{9} ,h_{10} )\) Select the K-nearest neighbors and fill the randomly deleted data ** with their average values (Table 5).

Table 5 The filling results of different K values
Full size table

  • (5) Filling the incomplete data: \(\mu_{{\tilde{S}(e{1})}}^{{ - *}} (h_{5} ) = \frac{{\mu_{{\tilde{S}(e1)}}^{ - } (h_{13} ) + \mu_{{\tilde{S}(e1)}}^{ - } (h_{14} )}}{2} = \frac{0.56 + 0.56}{2}\). Repeat step 3 and step 5 to fill all of the missing data.

Output: complete interval-valued fuzzy soft set shown in Table 6.

Table 6 Complete interval-valued fuzzy soft sets
Full size table

We examine the filling results by Average based Data Filling (ADF) Algorithm for incomplete interval-valued fuzzy soft sets [40] in Table 2 and our KNN data filling algorithm in Table 6. It is clear that the algorithm [40] suffers from the error that the filling result does not satisfy the condition \(0 \le \mu_{{_{{\tilde{S}(ej)}} }}^{ - *} (h_{i} ) \le \mu_{{_{{\tilde{S}(ej)}} }}^{ + } (h_{i} ) \le 1\), while our method meets this condition. And there is subjectivity in the setting of the threshold value during the filling process in the method [40]. In our newly proposed KNN data filling method, the attribute-based combining rule avoids subjectivity and makes the filling process more reasonable.

4 Experimental Results and Analysis

In this section, we make the comparison between our method and the idea in [40] from the two evaluation indicators as accuracy and error rate. We perform two methods on five groups experiments. Experiment 1, Experiment 2 and Experiment 3 are constructed on the Five-Four star shanghai hotel dataset in order to validate superiority of our method about accuracy. Experiment 4 and Experiment 5 are based on randomly generated datasets for verifying the good performance of our method in reducing the error rate.

4.1 Evaluation Indicators

Firstly, we present the two evaluation indicators as follows.

4.1.1 Accuracy Verification

To measure the accuracy of the filling results, we give the definitions of accuracy and average accuracy.

Accuracy is defined as:

$$P_{i} = 1 - \frac{{\left| {s_{i} - s_{0} } \right|}}{{s_{0} }}$$
(9)

where S0 is the true value and Si is the predicted value.

Average accuracy rate is defined as:

$$P_{ave} = \frac{{\sum\nolimits_{i = 1}^{t} {P_{i} } }}{t}$$
(10)

where t is the number of missing value.

4.1.2 Error Rate

During the data filling process, the filling value is possible to exceed the limit. That is, some filled results do not satisfy the constraints of the interval-valued fuzzy soft set as \(0 \le \mu_{{_{{\tilde{S}(ej)}} }}^{ - *} (h_{i} ) \le \mu_{{_{{\tilde{S}(ej)}} }}^{ + } (h_{i} ) \le 1\) which is regarded as one error. We use the error rate to measure it.

The error rate is defined as:

$$P^{\prime} = \frac{n}{N}$$
(11)

where n is the number of data which filled value exceeds the limit and N is the number of all incomplete data in the whole dataset that needs to be filled.

4.2 Accuracy Verification

To verify the accuracy of the KNN data filling method, we use the Five-Four star shanghai hotel dataset in [40]. Through multiple experiments, the average accuracy results of our method and the approach in [40] are compared.

4.2.1 Five-Four Star Shanghai Hotel Data Set (14 × 7)

We apply a dataset of Five-Four star shanghai hotel data set in [40] presented in Table 7.

Table 7 Five-Four star shanghai hotel data set
Full size table

In this evaluation system, there are 14 candidate hotels. \(U = \{ h_{1} ,h_{2} ,h_{3} ,...,h_{14} \}\) and seven attributes as diverse as “Staff performance”, “Location”, “Hotel condition/cleanliness”, “Value for Money”, “Room comfort/standard”, “Food/Dining” and “Facilities”.

In this experiment, the missing values are randomly selected from the Five-Four star shanghai hotel dataset. We set up three groups of experiments to verify the accuracy of our method.

4.2.1.1 Experiment 1

We randomly select 5 single degrees of membership (Upper or lower degree of membership) from the initial dataset and note them as *. After performing our proposed KNN data filling method and Average based Data Filling (ADF) Algorithm for incomplete interval-valued fuzzy soft sets [40], we obtain the predicted values. Then, the accuracy and the average accuracy are calculated by using the formula (9) and formula (10).

We take one of the randomized experiments as an example:

$${[}\mu_{S(e2)}^{ - } (h_{9} ),\mu_{S(e2)}^{ + *} (h_{9} ){]} = {[0}{\text{.82,*][}}\mu_{S(e3)}^{ - } (h_{3} ),\mu_{S(e3)}^{ + *} (h_{3} ){]} = {[0}{\text{.66,*]}}$$
$${[}\mu_{S(e6)}^{ - } (h_{10} ),\mu_{S(e6)}^{ + *} (h_{10} ){]}\,{ = }\,{[0}{\text{.81,}}\,{*][}\mu_{S(e7)}^{ - *} (h_{1} ),\mu_{S(e7)}^{ + } (h_{1} ){]} = {[}*{,}\,{0}{\text{.82]}}$$
$$[\mu_{S(e7)}^{ - } (h_{4} ),\mu_{S(e7)}^{ + *} (h_{4} )] = [0.76,*]$$

Applying our proposed KNN data filling method to fill the missing data, we obtain the following predicted values:

$$[\mu_{S(e2)}^{ - } (h_{9} ),\mu_{S(e2)}^{ + *} (h_{9} )] = [0.82,\underline{0.87} ][\mu_{S(e3)}^{ - } (h_{3} ),\mu_{S(e3)}^{ + *} (h_{3} )] = [0.66,\underline{0.86} ]$$
$$[\mu_{{S(e{6})}}^{ - } (h_{{{10}}} ),\mu_{{S(e{6})}}^{ + *} (h_{{{10}}} )] = {[0}{\text{.81,}}\,\underline{{{0}{\text{.86}}}} {][}\mu_{S(e7)}^{ - *} (h_{1} ),\mu_{S(e7)}^{ + } (h_{1} ){]} = {[}\underline{{{0}{\text{.74}}}} {,}\,{0}{\text{.82]}}$$
$$[\mu_{S(e7)}^{ - } (h_{4} ),\mu_{S(e7)}^{ + *} (h_{4} )] = [0.76,\underline{0.83} ]$$

After executing the algorithm [40], we obtain the following predicted values:

$$[\mu_{S(e2)}^{ - } (h_{9} ),\mu_{S(e2)}^{ + *} (h_{9} )] = [0.82,\underline{0.78} ][\mu_{S(e3)}^{ - } (h_{3} ),\mu_{S(e3)}^{ + *} (h_{3} )] = [0.66,\underline{0.85} ]$$
$${[}\mu_{S(e6)}^{ - } (h_{10} ),\mu_{S(e6)}^{ + *} (h_{10} ){]} = {[0}{\text{.81,}}\,\underline{{{0}{\text{.84}}}} {][}\mu_{S(e7)}^{ - *} (h_{1} ),\mu_{S(e7)}^{ + } (h_{1} ){]} = {[}\underline{{{0}{\text{.75}}}} {,}\,{0}{\text{.82]}}$$
$$[\mu_{S(e7)}^{ - } (h_{4} ),\mu_{S(e7)}^{ + *} (h_{4} )] = [0.76,\underline{0.84} ]$$

Applying our proposed KNN data filling method to fill the missing data, the average accuracy of the filling result is 98.65%. By means of ADF, the average accuracy of the filling result is 96.33%, and the missing value \([\mu_{S(e2)}^{ - } (h_{9} ),\mu_{S(e2)}^{ + *} (h_{9} )] = [0.82,\underline{0.78} ]\) does not satisfy the restriction: \(0 \le \mu_{{_{{\tilde{S}(ej)}} }}^{ - *} (h_{i} ) \le \mu_{{_{{\tilde{S}(ej)}} }}^{ + } (h_{i} ) \le 1\).

Repeating this random sampling process 15 times, the missing data are filled using ADF [40] and our method. The comparison on the average accuracy between our method and algorithm [40] are shown in Fig. 2.

Fig. 2
figure 2

Average accuracy rate (single degree of membership)

Full size image

The experimental results show that among 15 groups of randomized experiments: The KNN data filling method has a higher average accuracy in nine groups. ADF [40] has five groups with higher average accuracy and 1 group with equal average accuracy. Overall, the average accuracy of the newly proposed KNN data filling method is 94.35%, and the average accuracy of the algorithm [40] is 91.85%. The KNN data filling method has a higher accuracy rate and the filling results are more reasonable and effective.

4.2.1.2 Experiment 2

We randomly select five data from the initial dataset and note them as [*,*]. After executing our proposed KNN data filling method and ADF [40], we obtain the corresponding predicted values.

Taking one of the randomized experiments as an example, we randomly select the double degree of membership elements as:

$$\mu_{S(e1)} (h_{3} )^{*} = [\mu_{S(e1)}^{ - *} (h_{3} ),\mu_{S(e1)}^{ + *} (h_{3} )] = [*,*]$$
$$\mu_{S(e2)} (h_{14} )^{*} = [\mu_{S(e2)}^{ - *} (h_{14} ),\mu_{S(e2)}^{ + *} (h_{14} )] = [*,*]$$
$$\mu_{S(e3)} (h_{7} )^{*} = [\mu_{S(e3)}^{ - *} (h_{7} ),\mu_{S(e3)}^{ + *} (h_{7} )] = [*,*]$$
$$\mu_{S(e6)} (h_{2} )^{*} = [\mu_{S(e6)}^{ - *} (h_{2} ),\mu_{S(e6)}^{ + *} (h_{2} )] = [*,*]$$
$$\mu_{S(e7)} (h_{12} )^{*} = [\mu_{S(e7)}^{ - *} (h_{12} ),\mu_{S(e7)}^{ + *} (h_{12} )] = [*,*]$$

After executing our proposed KNN data filling method, we obtain the following predicted values:

$$\mu_{{S(e{1})}} (h_{{3}} )^{*} = [\mu_{{S(e{1})}}^{ - *} (h_{{3}} ),\mu_{{S(e{1})}}^{ + *} (h_{{3}} )] = {[0}{\text{.77,}}\,{0}{\text{.85]}}$$
$$\mu_{S(e2)} (h_{14} )^{*} = [\mu_{S(e2)}^{ - *} (h_{14} ),\mu_{S(e2)}^{ + *} (h_{14} )] = [0.79,0.88]$$
$$\mu_{S(e3)} (h_{7} )^{*} = [\mu_{S(e3)}^{ - *} (h_{7} ),\mu_{S(e3)}^{ + *} (h_{7} )] = [0.72,0.86]$$
$$\mu_{S(e6)} (h_{2} )^{*} = [\mu_{S(e6)}^{ - *} (h_{2} ),\mu_{S(e6)}^{ + *} (h_{2} )] = [0.77,0.86]$$
$$\mu_{S(e7)} (h_{12} )^{*} = [\mu_{S(e7)}^{ - *} (h_{12} ),\mu_{S(e7)}^{ + *} (h_{12} )] = [0.76,0.85]$$

After executing ADF, we obtain the following predicted values:

$$\mu_{S(e1)} (h_{3} )^{*} = [\mu_{S(e1)}^{ - *} (h_{3} ),\mu_{S(e1)}^{ + *} (h_{3} )] = [0.69,0.86]$$
$$\mu_{S(e2)} (h_{14} )^{*} = [\mu_{S(e2)}^{ - *} (h_{14} ),\mu_{S(e2)}^{ + *} (h_{14} )] = [0.76,0.83]$$
$$\mu_{S(e3)} (h_{7} )^{*} = [\mu_{S(e3)}^{ - *} (h_{7} ),\mu_{S(e3)}^{ + *} (h_{7} )] = [0.72,0.85]$$
$$\mu_{S(e6)} (h_{2} )^{*} = [\mu_{S(e6)}^{ - *} (h_{2} ),\mu_{S(e6)}^{ + *} (h_{2} )] = [0.75,0.86]$$
$$\mu_{S(e7)} (h_{12} )^{*} = [\mu_{S(e7)}^{ - *} (h_{12} ),\mu_{S(e7)}^{ + *} (h_{12} )] = [0.75,0.85]$$

Applying our proposed KNN data filling method to fill the missing data, the average accuracy of the filling result is 96.85%. The average accuracy of the filling result is 96.61% by the method of ADF [40].

Repeating this random sampling process 15 times, experimental results are shown in Fig. 3.

Fig. 3
figure 3

Average accuracy rate (Double degree of membership)

Full size image

The experimental results showed that the average accuracy of the algorithm [40] is 90.08%, the average accuracy of the KNN data filling method proposed in this paper is 93.82%. When compared with the algorithm [40], the overall performance of KNN data filling method is improved by 3.74%.

4.2.1.3 Experiment 3

We randomly select six data (three double degrees of membership and three single degrees of membership) from the initial dataset noted as * and [*,*]. After executing our proposed KNN data filling method and the algorithm [40], we obtain the corresponding predicted values. Through the true value and the predicted value, the accuracy and average accuracy corresponding to each algorithm are obtained.

Taking one of the randomized experiments as an example, we randomly select unknown degree of membership elements as:

$$[\mu_{S(e3)}^{ - } (h_{3} ),\mu_{S(e3)}^{ + *} (h_{3} )] = [0.66,*][\mu_{S(e3)}^{ - } (h_{13} ),\mu_{S(e3)}^{ + *} (h_{13} )] = [0.6,*]$$
$$[\mu_{S(e7)}^{ - *} (h_{14} ),\mu_{S(e7)}^{ + } (h_{14} )] = [*,0.82][\mu_{S(e2)}^{ - *} (h_{9} ),\mu_{S(e2)}^{ + *} (h_{9} )] = [*,*]$$
$$[\mu_{S(e6)}^{ - *} (h_{1} ),\mu_{S(e6)}^{ + *} (h_{1} )] = [*,*][\mu_{S(e7)}^{ - *} (h_{4} ),\mu_{S(e7)}^{ + *} (h_{4} )] = [*,*]$$

After executing our proposed KNN data filling method, we obtain the following predicted values:

$$[\mu_{S(e3)}^{ - } (h_{3} ),\mu_{S(e3)}^{ + *} (h_{3} )] = [0.66,\underline{0.88} ][\mu_{S(e3)}^{ - } (h_{13} ),\mu_{S(e3)}^{ + *} (h_{13} )] = [0.6,\underline{0.84} ]$$
$$[\mu_{S(e7)}^{ - *} (h_{14} ),\mu_{S(e7)}^{ + } (h_{14} )] = [\underline{0.76} ,0.82]$$
$$\mu_{S(e2)} (h_{9} )^{*} = [\mu_{S(e2)}^{ - *} (h_{5} ),\mu_{S(e2)}^{ + *} (h_{9} )] = [\underline{0.81} ,\underline{0.86} ]$$
$$\mu_{S(e6)} (h_{1} )^{*} = [\mu_{S(e6)}^{ - *} (h_{1} ),\mu_{S(e6)}^{ + *} (h_{1} )] = [\underline{0.81} ,\underline{0.88} ]$$
$$\mu_{S(e7)} (h_{4} )^{*} = [\mu_{S(e7)}^{ - *} (h_{4} ),\mu_{S(e7)}^{ + *} (h_{4} )] = [\underline{0.73} ,\underline{0.85} ]$$

After executing the algorithm [40], we obtain the following predicted values:

$$[\mu_{S(e3)}^{ - } (h_{3} ),\mu_{S(e3)}^{ + *} (h_{3} )] = [0.66,\underline{0.85} ][\mu_{S(e3)}^{ - } (h_{13} ),\mu_{S(e3)}^{ + *} (h_{13} )] = [0.6,\underline{0.85} ]$$
$$[\mu_{S(e7)}^{ - *} (h_{14} ),\mu_{S(e7)}^{ + } (h_{14} )] = [\underline{0.74} ,0.82]$$
$$\mu_{S(e2)} (h_{9} )^{*} = [\mu_{S(e2)}^{ - *} (h_{5} ),\mu_{S(e2)}^{ + *} (h_{9} )] = [\underline{0.70} ,\underline{0.78} ]$$
$$\mu_{S(e6)} (h_{1} )^{*} = [\mu_{S(e6)}^{ - *} (h_{1} ),\mu_{S(e6)}^{ + *} (h_{1} )] = [\underline{0.75} ,\underline{0.86} ]$$
$$\mu_{S(e7)} (h_{4} )^{*} = [\mu_{S(e7)}^{ - *} (h_{4} ),\mu_{S(e7)}^{ + *} (h_{4} )] = [\underline{0.71} ,\underline{0.84} ]$$

The experimental results show that the average accuracy of algorithm [40] is 95.15%. Applying our proposed KNN data filling method to fill the missing data, the average accuracy of the filling result is 97.74%. When compared with algorithm [40], the overall performance of KNN data filling method is improved by 2.59%.

Similarly, the experimental results on fifteen experiments are shown in Fig. 4.

Fig. 4
figure 4

Average accuracy rate (Single and double degree of membership)

Full size image

The experimental results show that the average accuracy of the newly proposed KNN data filling method is 95.24%. While the average accuracy of the algorithm [40] is 90.89%.

From the above three groups experiments, it is obvious that our method outperforms the method in [40] on the accuracy illustrated in Table 8.

Table 8 The comparison result on three groups experiments about average accuracy
Full size table

4.2.2 Error Rate Verification

An interval-valued fuzzy soft set is randomly generated and multiple random experiments are performed on this dataset. The lower the error rate, the higher the reliability of the algorithm and the better the filling effect.

4.2.2.1 Experiment 4

A 14×6 interval-valued fuzzy soft set is randomly generated as shown in Table 9. Six data are randomly selected as missing data from this dataset, and the selection results are shown in Table 9.

Table 9 Interval-valued fuzzy soft set (14 × 6)
Full size table

The missing data are filled using algorithm [40] and our method, respectively. The filling results are shown in Tables 10 and 11.

Table 10 Filling results by algorithm [40] for Table 9
Full size table
Table 11 Filling results by our method for Table 9
Full size table

From the analysis of Table 10, it can be seen that by applying the algorithm [40], the filling results as [0.83, 0.80] and [0.74, 0.71] do not satisfy the constraints of interval-valued fuzzy soft sets: \(0 \le \mu_{{_{{\tilde{S}(ej)}} }}^{ - *} (h_{i} ) \le \mu_{{_{{\tilde{S}(ej)}} }}^{ + } (h_{i} ) \le 1\). The filling results are unreasonable, which can easily lead to decision-makers making wrong decisions.

According to the results in Table 11, the KNN data filling method newly proposed in this paper is used to fill the missing data, and the filling results all satisfy the constraints of the interval-valued fuzzy soft set.

The error rate comparison between our KNN and the method in [40] is show in Table 12.

Table 12 Error rate comparison on Experiment 1
Full size table
4.2.2.2 Experiment 5

To verify the reliability of the results, we randomly generate 30×35 interval-valued fuzzy soft sets, where \(U = \left\{ {h_{1} ,h_{2} ,...,h_{30} } \right\}\) and \(E = \left\{ {e_{1} ,e_{2} ,...,e_{35} } \right\}\) 0.15 data are randomly removed from the initial dataset, which are noted as *. The incomplete data are filled with the algorithm [40] and our KNN data filling method, respectively. This random process is repeated 15 times. The filling results are shown in Fig. 5.

Fig. 5
figure 5

Errors rate comparison

Full size image

Analysis of Fig. 5 shows that using algorithm [40] to fill the missing data, the average error rate of the fill result is 8.89%. By our KNN data filling method to fill the missing data, and the error rate is 2.23% which are shown in Table 13. The lower error rate means that the algorithm is more efficient and reliable.

Table 13 Error rate comparison on 20 simulated experiments
Full size table

Therefore through experiments, it is verified that our proposed KNN data filling method is more accurate and reliable when compared with the existing method.

5 Conclusion

The research on decision making and parameter reduction based on complete interval-valued fuzzy soft sets has become very active. However, in the practical application of interval-valued fuzzy soft sets, we have to deal with a large amount of incomplete data. In this paper, we propose a novel KNN data filling method for incomplete interval-valued fuzzy soft sets. When compared with the current filling technique, the advantages of the proposed KNN method include: (1) Attribute-based combining rule is made to evaluate if missing value data should be filled in or ignored, which avoids subjectivity without setting the threshold. (2) Our method has the higher average accuracy rates when compared with the current technique. (3) Our approach involves the lower error rate which assures the reliability of filling results. Therefore, our method outperforms the existing method.