1 Introduction

Concept lattice [1] is widely used in many fields [2,3,4], such as information retrieval, software engineering, recommendation systems, and knowledge discovery. It has made some achievements in knowledge reduction [1, 5], rule extraction [6, 7], decision analysis [8, 9], and uncertainty reasoning [10, 11], among others [12,13,14]. Concept lattice can be used to discover implicit concepts and their relationships, which can visualize acquired information. Traditionally, concept lattice aims to study the deterministic relationships between objects and their attributes based on formal context. To improve conceptual representation, Burusco et al. [15] combined fuzzy sets with classical concept lattices and extended concept lattices from a classical aspect to a fuzzy one; Krupka et al. [16] proposed an approach to constructing fuzzy concept lattices for incomplete data. Based on an incomplete formal context, Li et al. [17] constructed an approximate concept lattice and proposed an approach to extracting non-redundant approximate decision rules from the incomplete decision context; Li et al. [18] presented K-medoids clustering to compress the approximate concept lattice and clustered the approximate concepts in an incomplete context. In addition, formal concept analysis can be extended to three-way concepts: Yao [19] constructed a framework of three-way concepts in an incomplete formal context, identifying four partially known concepts to study their relationships with existing concepts; Li et al. [20] constructed approximate concepts based on three-way decision and further presented attribute reduction; Wang et al. [21] presented four attribute reduction methods based on SE-ISI concept lattices of incomplete contexts.

When the available information is inaccurate and cannot be calculated with numbers, computing with words becomes necessary, as Zadeh [22] proposed in word computing based on fuzzy sets. However, the calculation method of fuzzy linguistics may lead to information loss, and the fusion results may lack accuracy. Herrera et al. [23] proposed a 2-tuple fuzzy linguistic representation model to overcome this limitation that has been extended in [33], which allows a continuous representation of linguistic information. For discrete and continuous cases, Liao et al. [24] proposed a variety of weighted distances, ordered weighted distances, and similarity measures between hesitant fuzzy linguistic term sets. Liu et al. [25] mainly presented an algorithm of rule extraction using incomplete the multi-expert fuzzy linguistic formal decision context and applied it to multimedia teaching evaluation. To better express comparable or incomparable information in linguistics, Diao et al. [26] proposed a group decision-making method based on LTVIFL. Zou et al. [7] proposed a rule extraction method of LVIFL to meet the needs of experts at different levels and to help people make reasonable decisions. Wang [27] designed a preference decision optimization algorithm with the InPLPR for solving practical problems under the conditions of time pressure and lack of knowledge. In solving the large-scale group decision-making multiple proposals have been done [34] such as in social network (LSGDM-SN), Lu et al. [28] introduced a method of estimating incomplete values in HFPRs, and developed a consensus management process for distrust behaviors. Xu et al. [29] studied the linguistic preference relations with self-confidence which considers the acceptable adjustment range of experts.

To empress incomplete linguistic value information, we introduce linguistic value into an incomplete context inspired by previous works on applying concept lattice to an incomplete formal context. Moreover, we propose both an incomplete fuzzy linguistic formal context and fuzzy linguistic approximation concept for constructing a fuzzy linguistic approximation concept lattice. Overall, our method can improve the representation of uncertain knowledge and better deal with the linguistic-valued information in an uncertain environment.

The rest of this paper is organized as follows. Section 2 briefly reviews some basic notions related to linguistic term set and incomplete context. Section 3 introduces linguistic values into an incomplete context and proposes the incomplete fuzzy linguistic formal context (IFLC). Using a fuzzy linguistic approximation concept (FLAC), we construct a fuzzy linguistic approximation concept lattice (FLAL). In Sect. 4, we design a similarity measure based on IFLC, followed by a practical example to illustrate the feasibility. Finally, Sect. 5 is the summary of this paper.

2 Preliminaries

In this section, we briefly review the concepts of linguistic term set, incomplete context, and approximate concept, as listed in the following definitions for more details.

Definition 1.

[30]. Let \(S=\{{s}_{\alpha }|\alpha =-\tau,\dots,-\mathrm{1,0},1,\dots \tau \}\) a finite ordered set consisting of an odd number of linguistic terms, which \(\tau\) is a positive integer, if S satisfies the following properties:

  1. 1.

    Ordering, \({s}_{\alpha }\le {s}_{\beta }\iff \alpha \le \beta\).

  2. 2.

    Reversibility, \(Neg({s}_{-\alpha })={s}_{\alpha }\), which \(-\alpha +\alpha =0\).

  3. 3.

    Boundedness, \({s}_{-\tau }\) and \({s}_{\tau }\) are the lower and upper bounds of linguistic labels, respectively.

The mid linguistic label \({s}_{0}\) represents an assessment of 'indifference', and the rest are placed symmetrically around it. For example, the linguistic term set S can be represented as \(S = \left\{ {s_{{ - 2}} = {\text{low}},s_{{ - 1}} = {\text{somewhat~low}},s_{0} = {\text{medium}},s_{1} = s{\text{omewhat~high}},s_{2} = {\text{high}}} \right\}\).

In this paper, we transform the 2-tuple representation model [23] of linguistic terms into a symmetric linguistic terms set.

Definition 2.

Let \(S=\{{s}_{\alpha }|\alpha =-\tau,\dots,-\mathrm{1,0},1,\dots \tau \}\) a finite ordered linguistic term set and \(\mu \in [-\tau,\tau ]\) a value representing the result of a symbolic aggregation operation, then the 2-tuple, which expresses the equivalent information to \(\mu\), is obtained with the following function:

$$\Delta \left[ { - \tau,\tau } \right] \to S \times \left[ { - 0.5,0.5} \right)$$
$$\Delta \left( \mu \right) = \left( {s_{\alpha },\delta } \right)$$
$$\left\{ {\begin{array}{*{20}l} {s_{\alpha }, \begin{array}{*{20}c} {\quad \alpha = {\text{round}}\left( \mu \right)} \\ \end{array} } \\ {\delta = \mu - \alpha,\quad \delta \in \left[ { - 0.5,0.5} \right)} \\ \end{array} } \right..$$
(1)

\(\mathrm{round}(\cdot )\) is the usual round operation, \({s}_{\alpha }\) has the closest index label to \(\mu\), and \(\delta\) is the value of the symbolic translation.

Definition 3

[24]. Let \(S=\{{s}_{\alpha }|\alpha =-\tau,\dots,-\mathrm{1,0},1,\dots \tau \}\) a linguistic term set, the discrete linguistic term set S is extended to the continuous linguistic term set \(\overline{S} = \{ s_{\alpha } |\alpha \in \left[ { - q,q} \right]\}\), where \(q(q > \tau )\) is a sufficiently large positive integer. For any two linguistic terms \(s_{\alpha },s_{\beta } \in \overline{S}\), \(\lambda_{1},\lambda_{2},\lambda_{3} \in \left[ {0,1} \right]\), the following operational laws are introduced:

  1. 1.

    \({s}_{\alpha }\oplus {s}_{\beta }={s}_{\alpha +\beta }\);

  2. 2.

    \(\lambda {s}_{\alpha }={s}_{\lambda \alpha }\);

  3. 3.

    \(({\lambda }_{1}+{\lambda }_{2}){s}_{\alpha }={\lambda }_{1}{s}_{\alpha }\oplus {\lambda }_{2}{s}_{\alpha }\);

  4. 4.

    \(\lambda ({s}_{\alpha }\oplus {s}_{\beta })=\lambda {s}_{\alpha }\oplus \lambda {s}_{\beta }\).

Definition 4.

[32]. An incomplete context can be viewed as \((U,A,\{+,?,-\},I)\) consisting of a nonempty and finite set object U, a nonempty and finite attribute set A, the set \(\{+,?,-\}\) of values, and a mapping \(I:U\times A\to \{+,?,-\}\), where \(I(u,a)=+\) means that the object \(u\) has the attribute \(a\), \(I(u,a)=-\) means that the object \(u\) does not have the attribute \(a\), \(I\left(u,a\right)=?\) indicates that it is unknown whether or not the object \(u\) has the attribute \(a\).

Definition 5.

[17]. An incomplete context \((U,A,\{+,?,-\},I)\) with \(X\subseteq U\) is defined:

$$\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{R} \left( X \right) = \left\{ {a \in A|\forall u \in X,I\left( {u,a} \right) = + } \right\}$$
(2)
$$\overline{R}\left( X \right) = \left\{ {a \in A|\forall u \in X,I\left( {u,a} \right) = + \,or\, I\left( {u,a} \right) = ?} \right\}$$
(3)

Definition 6.

[17]. Let \((U,A,\{+,?,-\},I)\) an incomplete context. For \(\forall X\in {2}^{U}\) and\((B,C)\in {2}^{A}\times {2}^{A}\), two operators \(\prec\): \({2}^{U}\to {2}^{A}\times {2}^{A}\) and \(\succ\): \({2}^{A}\times {2}^{A}\to {2}^{U}\) are respectively defined:

$$X^{ \prec } = \left( {\underline {R} \left( X \right),\overline{R}\left( X \right)} \right),$$
(4)
$$(B,C)^{ \succ } = \left\{ {u \in U|\left( {B,C} \right) \le \left( {\underline {R} \left( X \right),\overline{R}\left( X \right)} \right)} \right\}.$$
(5)

\(\underline {R} \left( X \right)\) is a pair \(\left( {\underline {R} \left( X \right),\overline{R}\left( X \right)} \right)\) with \(\overline{R}\left( X \right)\) containing precisely those attributes that are certain to be shared by all the objects in X and \(\overline{R}\left( X \right)\) containing those attributes that are possible to be shared by all the objects in X. \((B,C)^{ \succ }\) is the maximal set of the objects, featuring all the attributes in B with certainty and all the attributes in C with possibility.

Definition 7.

[17]. Let \((U,A,\{+,?,-\},I)\) an incomplete context. For \(\forall X\in {2}^{U}\) and \((B,C)\in {2}^{A}\times {2}^{A}\), if \({X}^{\prec }=(B,C)\) and \((B,C{)}^{\succ }=X\), we say that \((X,(B,C))\) is an approximate concept of \((U,A,\{+,?,-\},I)\). Here, X and \((B,C)\) are called the extension and the intention of the approximate concept \((X,(B,C))\), respectively.

3 Fuzzy Linguistic Approximate Concept Lattice Based on Incomplete Fuzzy Linguistic Formal Context

Based on incomplete context, this section further studies some related concepts of incomplete fuzzy linguistic formal context and constructs the fuzzy linguistic approximate concept lattice.

Definition 8.

Let \((U,A,\{S,\diamond \},{R}^{\diamond })\) an incomplete fuzzy linguistic formal context consisting of a nonempty and finite object set \(U=\{{u}_{i}|i\in \mathrm{1,2},\dots,n\}\), a nonempty and finite attribute set \(A=\{{a}_{j}|j\in \mathrm{1,2},\dots,m\}\),\(S=\{{s}_{\alpha }|\alpha =-\tau,\dots,-\mathrm{1,0},1,\dots,\tau \}\), and a mapping \({R}^{\diamond }:U\times A\to \{S,\diamond \}\). We denote the incomplete fuzzy linguistic formal context \((U,A,\{S,\diamond \},{R}^{\diamond })\) as \(IFLC(U,A,\{S,\diamond \},{R}^{\diamond })\).

Remark.

\(R^{\diamondsuit } \left( {u,a} \right) = \diamondsuit\)indicates that it is unknown whether the object u has the attribute a.\(A_{S}\) is the set of linguistic attribute values, which is the subset of U defined on A, where \(A_{S} = \left\{ {\frac{{s_{a} }}{a}{|}a \in A,s_{a} \in \left\{ {S,\diamondsuit } \right\}} \right\}\). If given a threshold value \(\lambda\), \(R^{\diamondsuit } \left( {u,a} \right) \ge \rlap{--} \lambda\) means that the object u has the attribute a, \(R^{\diamondsuit } \left( {u,a} \right) < \rlap{--} \lambda\) means that the object u does not have the attribute a.

Definition 9.

Let \(IFLC(U,A,\{S,\diamond \},{R}^{\diamond })\) and \(X\subseteq U\). The operators \(^{\prime }\), \(^{\prime \prime }\), \(^{\prime \square }\) and \(^{\prime \prime *}\) are defined as follows:

$${X}^{^{\prime}}=\cap \left\{{R}^{\diamond }\left(u,a\right)|\forall a\in A,{R}^{\diamond }\left(u,a\right)\in S\right\},$$
$$X^{\prime \square } = \left\{ {\frac{{R^{\diamondsuit } \left( {u,a} \right)}}{a} \in A_{S} |\forall R^{\diamondsuit } \left( {u,a} \right) \in X^{\prime },R^{\diamondsuit } \left( {u,a} \right) \ge \rlap{--} \lambda } \right\}.$$
(6)
$${X}^{^{\prime\prime} }=\cap \left\{{R}^{\diamond }\left(u,a\right)|\forall u\in X,a\in A,{R}^{\diamond }\left(u,a\right)\in \left\{S,\diamond \right\}\right\},$$
$$X^{\prime \prime *} = \left\{ {\frac{{R^{\diamondsuit } \left( {u,a} \right)}}{a} \in A_{S} \left| {\forall R^{\diamondsuit } \left( {u,a} \right) \in X^{\prime \prime },R^{\diamondsuit } \left( {u,a} \right) \ge \rlap{--} \lambda \,or\, R^{\diamondsuit } \left( {u,a} \right)} \right||\rlap{--} \lambda } \right\}.$$
(7)

Remark.

If \({R}^{\diamond }(u,a)\) is incomparable to the threshold value \(\rlap{--} \lambda\), that is, \({R}^{\diamond }(u,a)=\diamond\), denoted as \(R^{\diamondsuit } \left( {u,a} \right)\parallel \rlap{--} \lambda\), all the corresponding attribute linguistic values are retained.

Definition 10.

Let \(IFLC(U,A,\{S,\diamond \},{R}^{\diamond })\) and \(X\subseteq U\), \(B,C\subseteq {A}_{S}\). Two operators are defined:

$$X^{\Delta } = \left( {X^{\prime },X^{\prime \prime *} } \right),$$
(8)
$$(B,C)^{\nabla } = \cap \left\{ {u \in U|\forall s_{\alpha } \in C,\forall a \in A,u \in X,\frac{{R^{\diamondsuit } \left( {u,a} \right)}}{a} \ge s_{\alpha },\alpha = - \tau, \ldots, - 1,0,1, \ldots,\tau } \right\},$$
(9)

where \(X^{\prime \square }\) is the intersection set of the linguistic values of attributes that are certain to be shared by all the objects, \(X^{\prime \prime * }\) is the intersection set of the linguistic values of attributes that they have or may have, \((B,C{)}^{\nabla }\) is the intersection set of objects satisfied by the corresponding linguistic values of each attribute.

Definition 11.

Let \(IFLC(U,A,\{S,\diamond \},{R}^{\diamond })\) and \(X\subseteq U\), \(B,C\subseteq {A}_{S}\). If \({X}^{\Delta }=(B,C)\), \({X}^{\Delta }=(B,C)\) and \((B,C{)}^{\nabla }=X\), we say that \((X,(B,C))\) is a fuzzy linguistic approximate concept of \((U,A,\{S,\diamond \},{R}^{\diamond })\). Here, \(X\) and \((B,C)\) are called the extension and the intention of the fuzzy linguistic approximate concept \((X,(B,C))\), respectively.

\(FLAC(U,A,\{S,\diamond \},{R}^{\diamond })\) is used to represent the set of all fuzzy linguistic approximation concepts of \((U,A,\{S,\diamond \},{R}^{\diamond })\). For \(({X}_{1},({B}_{1},{C}_{1}))\), \(({X}_{2},({B}_{2},{C}_{2}))\in FLAL(U,A,\{S,\diamond \},{R}^{\diamond })\), the partial order relation “\(\le\)” can be defined:

$$\left( {X_{1},\left( {B_{1},C_{1} } \right)} \right) \le \left( {X_{2},\left( {B_{2},C_{2} } \right)} \right) \Leftrightarrow X_{1} \subseteq X_{2} \left( { \Leftrightarrow \left( {B_{2},C_{2} } \right) \subseteq \left( {B_{1},C_{1} } \right)} \right).$$
(10)

Proposition 1.

Let \(IFLC(U,A,\{S,\diamond \},{R}^{\diamond })\) and \(X\subseteq U\), \(B,C\subseteq {A}_{S}\), then.

  1. 1.

    \(X\subseteq {X}^{\Delta \nabla },(B,C)\subseteq (B,C{)}^{\nabla\Delta }.\)

  2. 2.

    \({X}^{\Delta }={X}^{\Delta \nabla\Delta },(B,C{)}^{\nabla }=(B,C{)}^{\nabla\Delta \nabla }.\)

  3. 3.

    \(X\subseteq (B,C{)}^{\nabla }\iff (B,C)\subseteq {X}^{\Delta }.\)

Proof.

It is easily obtained by Definition 10 and the proof is omitted.

Proposition 2.

Let \(IFLC(U,A,\{S,\diamond \},\diamond )\) and \(\forall {X}_{1},{X}_{2}\subseteq U\), \({B}_{1},{B}_{2},{C}_{1},{C}_{2}\subseteq {A}_{S}\), then.

  • \(({X}_{1}\cup {X}_{2}{)}^{\Delta }={{X}_{1}}^{\Delta }\cap {{X}_{2}}^{\Delta },(({B}_{1},{C}_{1})\cup ({B}_{2},{C}_{2}){)}^{\nabla }=({B}_{1},{C}_{1}{)}^{\nabla }\cap ({B}_{2},{C}_{2}{)}^{\nabla }.\)

  • \({{X}_{1}}^{\Delta }\cup {{X}_{2}}^{\Delta }\subseteq ({X}_{1}\cap {X}_{2}{)}^{\Delta },({B}_{1},{C}_{1}{)}^{\nabla }\cup ({B}_{2},{C}_{2}{)}^{\nabla }=(({B}_{1},{C}_{1})\cap ({B}_{2},{C}_{2}){)}^{\nabla }.\)

  • \({X}_{1}\subseteq {X}_{2}\Rightarrow {{X}_{2}}^{\Delta }\subseteq {{X}_{1}}^{\Delta },({B}_{1},{C}_{1})\subseteq ({B}_{2},{C}_{2})\Rightarrow ({B}_{2},{C}_{2}{)}^{\nabla }\subseteq ({B}_{1},{C}_{1}{)}^{\nabla }.\)

Proof.

It is easily obtained by Definition 10 and the proof is omitted.

Definition 12.

Let \(IFLC(U,A,\{S,\diamond \},{R}^{\diamond })\) and \(\forall {X}_{1},{X}_{2}\subseteq U\), \({B}_{1},{B}_{2},{C}_{1},{C}_{2}\subseteq {A}_{S}\), the infimum and supremum can be defined respectively:

$$\left( {X_{1},\left( {B_{1},C_{1} } \right)} \right) \wedge \left( {X_{2},\left( {B_{2},C_{2} } \right)} \right) = \left( {\left( {X_{1} \cap X_{2},\left( {B_{1},C_{1} } \right) \cup \left( {B_{2},C_{2} } \right)} \right)^{\nabla \Delta } } \right),$$
(11)
$$\left( {X_{1},\left( {B_{1},C_{1} } \right)} \right) \vee \left( {X_{2},\left( {B_{2},C_{2} } \right)} \right) = \left( {\left( {X_{1} \cup X_{2} } \right)^{{\nabla {\Delta }}},\left( {\left( {B_{1},C_{1} } \right) \cap \left( {B_{2},C_{2} } \right)} \right)} \right).$$
(12)

4 A Similarity Completion Approach Based on Incomplete Fuzzy Linguistic Formal Context

Nowadays, the scale of data collected from real-world applications is enormous, and sometimes data are missing. The incompleteness of data brings specific difficulties to evaluation, interpretation and knowledge discovery. In order to solve this problem, we study a similarity complement approach based on incomplete fuzzy linguistic formal context.

4.1 A Similarity Completion Approach

Definition 13.

An initially filling in \(IFLC(U,A,\{S,\diamond \},{R}^{\diamond })\) with the mean value is:

$$\diamondsuit_{i} = \left( {s_{{\alpha^{\diamondsuit } }},\delta^{\diamondsuit } } \right),\quad i \in 1,2, \ldots,n,\left\{ {\begin{array}{*{20}l} {s_{{\alpha^{\diamondsuit } }}, \begin{array}{*{20}l} {\alpha^{\diamondsuit } = {\text{round}}\left( {\overline{S}_{{A_{c} }}^{{u_{i} }} } \right)} \\ \end{array} } \\ {\delta^{\diamondsuit } = \overline{S}_{{A_{c} }}^{{u_{i} }} - \alpha^{\diamondsuit },\delta^{\diamondsuit } = \left[ { - 0.5,0.5} \right).} \\ \end{array} } \right.$$
(13)

\({\alpha }^{\diamond }=\mathrm{round}(.)\) is the usual round operation. \({A}_{c}\) represents the non-missing attribute set of object \({u}_{i}\), \({S}_{{A}_{c}}\) is the linguistic value set defined by U on \({A}_{c}\), \({S}_{{A}_{c}}=\{{s}_{{a}_{j}}\in S|{s}_{{a}_{1}},{s}_{{a}_{2}},\dots,{s}_{{a}_{m}}\}\), and \(\overline{S}_{{A_{c} }}^{{u_{i} }}\) is the mean value of the linguistic value set of the object \({u}_{i}\) on \({A}_{c}\).

Definition 14.

Let \((U,A,{S}^{*},{R}^{*})\) a fuzzy linguistic formal context after the initial complement consisting of \(U=\{{u}_{i}|i\in \mathrm{1,2},\dots,n\}\) and \(A=\{{a}_{j}|j\in \mathrm{1,2},\dots,m\}\). A mapping \({R}^{*}:U\times A\to {S}^{*}\), \({S}^{*}\) is a linguistic value set. \(FLC\left(U,A,{S}^{*},{R}^{*}\right)\) is used to denote the fuzzy linguistic formal context after the initial complement.

Definition 15.

\({S}_{A}^{*}\) is the linguistic value set of U defined on A in \(FLC\left(U,A,{S}^{*},{R}^{*}\right)\), \({S}_{A}^{*}=\{{s}_{{a}_{j}}\in {S}^{*}|{s}_{{a}_{1}},{s}_{{a}_{2}},\dots,{s}_{{a}_{m}}\}\). For \(\forall {u}_{p},{u}_{q}\in U\), the linguistic value sets are \({S}_{A}^{*{u}_{p}}\) and \({S}_{A}^{*{u}_{q}}\), respectively. The fuzzy linguistic similarity is defined by

$$Sim^{Mixfl} \left( {S_{A}^{{*u_{p} }},S_{A}^{{*u_{q} }} } \right) = \frac{1}{2}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{m} \left| {S_{{a_{j} }}^{{*u_{p} }} \cap S_{{a_{j} }}^{{*u_{q} }} } \right|}}{{\mathop \sum \nolimits_{j = 1}^{m} \left| {S_{{a_{j} }}^{{*u_{p} }} \cup S_{{a_{j} }}^{{*u_{q} }} } \right|}} + \frac{1}{2}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{m} \left( {\alpha_{{a_{j} }}^{{u_{p} }} - \overline{\alpha }_{A}^{{u_{p} }} } \right)\left( {\alpha_{{a_{j} }}^{{u_{q} }} - \overline{\alpha }_{A}^{{u_{q} }} } \right)}}{{\sqrt {\mathop \sum \nolimits_{j = 1}^{m} (\alpha_{{a_{j} }}^{{u_{p} }} - \overline{\alpha }_{A}^{{u_{p} }} )^{2} } \sqrt {\mathop \sum \nolimits_{j = 1}^{m} (\alpha_{{a_{j} }}^{{u_{q} }} - \overline{\alpha }_{A}^{{u_{q} }} )^{2} } }} + 1} \right)} \right)$$
(14)

\({\sum }_{j=1}^{m}\left|{S}_{{a}_{j}}^{*{u}_{p}}\cap {S}_{{a}_{j}}^{*{u}_{q}}\right|\) is the number of intersection elements of the linguistic value set between the objects \({u}_{p}\) and \({u}_{q}\). \({\sum }_{j=1}^{m}\left|{S}_{{a}_{j}}^{*{u}_{p}}\cup {S}_{{a}_{j}}^{*{u}_{q}}\right|\) is the number of union elements in a linguistic value set. \({\alpha }_{{a}_{j}}^{{u}_{p}}\) and \({\alpha }_{{a}_{j}}^{{u}_{q}}\) represent the linguistic value subscripts of attribute \({a}_{j}\) of the objects \({u}_{p}\) and \({u}_{q}\), respectively. \(\overline{\alpha }_{A}^{{u_{p} }}\) and \(\overline{\alpha }_{A}^{{u_{q} }}\) are the mean values of the linguistic value subscripts of attribute \({a}_{j}\) of the objects \({u}_{p}\) and \({u}_{q}\), respectively.

Proposition 3.

For \(\forall {u}_{p},{u}_{q}\in U\) in \(FLC\left(U,A,{S}^{*},{R}^{*}\right)\), the similarity between the linguistic value sets of \({u}_{p}\) and \({u}_{q}\) satisfies the following properties:

  1. 1.

    \(0\le Si{m}^{Mixfl}({S}_{A}^{*{u}_{p}},{S}_{A}^{*{u}_{q}})\le 1\).

  2. 2.

    \(Si{m}^{Mixfl}({S}_{A}^{*{u}_{p}},{S}_{A}^{*{u}_{q}})=Si{m}^{Mixfl}({S}_{A}^{*{u}_{q}},{S}_{A}^{*{u}_{p}})\).

  3. 3.

    \(Si{m}^{Mixfl}({S}_{A}^{*{u}_{p}},{S}_{A}^{*{u}_{q}})=1\) iff \({S}_{A}^{*{u}_{p}}={S}_{A}^{*{u}_{q}}\).

Proof.

The proof can be completed according to Definition 15.

  1. (1)

    Since

    $$0 \le \frac{{\mathop \sum \nolimits_{j = 1}^{m} \left| {S_{{a_{j} }}^{{*u_{p} }} \cap S_{{a_{j} }}^{{*u_{q} }} } \right|}}{{\mathop \sum \nolimits_{j = 1}^{m} \left| {S_{{a_{j} }}^{{*u_{p} }} \cup S_{{a_{j} }}^{{*u_{q} }} } \right|}} \le 1,\quad - 1 \le \frac{{\mathop \sum \nolimits_{j = 1}^{m} \left( {\alpha_{{a_{j} }}^{{u_{p} }} - \overline{\alpha }_{A}^{{u_{p} }} } \right)\left( {\alpha_{{a_{j} }}^{{u_{q} }} - \overline{\alpha }_{A}^{{u_{q} }} } \right)}}{{\sqrt {\mathop \sum \nolimits_{j = 1}^{m} (\alpha_{{a_{j} }}^{{u_{p} }} - \overline{\alpha }_{A}^{{u_{p} }} )^{2} } \sqrt {\mathop \sum \nolimits_{j = 1}^{m} (\alpha_{{a_{j} }}^{{u_{q} }} - \overline{\alpha }_{A}^{{u_{q} }} )^{2} } }} \le 1,$$

    we can easily get.

    $$0 \le \frac{1}{2}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{m} \left| {S_{{a_{j} }}^{{*u_{p} }} \cap S_{{a_{j} }}^{{*u_{q} }} } \right|}}{{\mathop \sum \nolimits_{j = 1}^{m} \left| {S_{{a_{j} }}^{{*u_{p} }} \cup S_{{a_{j} }}^{{*u_{q} }} } \right|}}} \right) + \frac{1}{2}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{m} \left( {\alpha_{{a_{j} }}^{{u_{p} }} - \overline{\alpha }_{A}^{{u_{p} }} } \right)\left( {\alpha_{{a_{j} }}^{{u_{q} }} - \overline{\alpha }_{A}^{{u_{q} }} } \right)}}{{\sqrt {\mathop \sum \nolimits_{j = 1}^{m} (\alpha_{{a_{j} }}^{{u_{p} }} - \overline{\alpha }_{A}^{{u_{p} }} )^{2} } \sqrt {\mathop \sum \nolimits_{j = 1}^{m} (\alpha_{{a_{j} }}^{{u_{q} }} - \overline{\alpha }_{A}^{{u_{q} }} )^{2} } }} + 1} \right) \le 1.$$

    So we can get \(0\le Si{m}^{Mixfl}({S}_{A}^{*{u}_{p}},{S}_{A}^{*{u}_{q}})\le 1\).

  2. (2)

    \(Si{m}^{Mixfl}({S}_{A}^{*{u}_{p}},{S}_{A}^{*{u}_{q}})\)

    $$= \frac{1}{2}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{m} \left| {S_{{a_{j} }}^{{*u_{p} }} \cap S_{{a_{j} }}^{{*u_{q} }} } \right|}}{{\mathop \sum \nolimits_{j = 1}^{m} \left| {S_{{a_{j} }}^{{*u_{p} }} \cup S_{{a_{j} }}^{{*u_{q} }} } \right|}} + \frac{1}{2}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{m} \left( {\alpha_{{a_{j} }}^{{u_{p} }} - \overline{\alpha }_{A}^{{u_{p} }} } \right)\left( {\alpha_{{a_{j} }}^{{u_{q} }} - \overline{\alpha }_{A}^{{u_{q} }} } \right)}}{{\sqrt {\mathop \sum \nolimits_{j = 1}^{m} (\alpha_{{a_{j} }}^{{u_{p} }} - \overline{\alpha }_{A}^{{u_{p} }} )^{2} } \sqrt {\mathop \sum \nolimits_{j = 1}^{m} (\alpha_{{a_{j} }}^{{u_{q} }} - \overline{\alpha }_{A}^{{u_{q} }} )^{2} } }} + 1} \right)} \right)$$
    $$= \frac{1}{2}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{m} \left| {S_{{a_{j} }}^{{*u_{q} }} \cap S_{{a_{j} }}^{{*u_{p} }} } \right|}}{{\mathop \sum \nolimits_{j = 1}^{m} \left| {S_{{a_{j} }}^{{*u_{q} }} \cup S_{{a_{j} }}^{{*u_{p} }} } \right|}} + \frac{1}{2}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{m} \left( {\alpha_{{a_{j} }}^{{u_{q} }} - \overline{\alpha }_{A}^{{u_{q} }} } \right)\left( {\alpha_{{a_{j} }}^{{u_{p} }} - \overline{\alpha }_{A}^{{u_{p} }} } \right)}}{{\sqrt {\mathop \sum \nolimits_{j = 1}^{m} (\alpha_{{a_{j} }}^{{u_{q} }} - \overline{\alpha }_{A}^{{u_{q} }} )^{2} } \sqrt {\mathop \sum \nolimits_{j = 1}^{m} (\alpha_{{a_{j} }}^{{u_{p} }} - \overline{\alpha }_{A}^{{u_{p} }} )^{2} } }} + 1} \right)} \right)$$
    $$= Sim^{Mixfl} \left( {S_{A}^{{{*}u_{q} }},S_{A}^{{{*}u_{p} }} } \right).$$
  3. (3)

    If \({S}_{A}^{*{u}_{p}}={S}_{A}^{*{u}_{q}}\).

We can get

$$\frac{{\mathop \sum \nolimits_{j = 1}^{m} \left| {S_{{a_{j} }}^{{*u_{p} }} \cap S_{{a_{j} }}^{{*u_{q} }} } \right|}}{{\mathop \sum \nolimits_{j = 1}^{m} \left| {S_{{a_{j} }}^{{*u_{p} }} \cup S_{{a_{j} }}^{{*u_{q} }} } \right|}} = 1,\quad \left( {\frac{{\mathop \sum \nolimits_{j = 1}^{m} \left( {\alpha_{{a_{j} }}^{{u_{q} }} - \overline{\alpha }_{A}^{{u_{q} }} } \right)\left( {\alpha_{{a_{j} }}^{{u_{p} }} - \overline{\alpha }_{A}^{{u_{p} }} } \right)}}{{\sqrt {\mathop \sum \nolimits_{j = 1}^{m} (\alpha_{{a_{j} }}^{{u_{q} }} - \overline{\alpha }_{A}^{{u_{q} }} )^{2} } \sqrt {\mathop \sum \nolimits_{j = 1}^{m} (\alpha_{{a_{j} }}^{{u_{p} }} - \overline{\alpha }_{A}^{{u_{p} }} )^{2} } }} = 1} \right)$$

So that

$$\frac{1}{2}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{m} \left| {S_{{a_{j} }}^{{*u_{p} }} \cap S_{{a_{j} }}^{{*u_{q} }} } \right|}}{{\mathop \sum \nolimits_{j = 1}^{m} \left| {S_{{a_{j} }}^{{*u_{p} }} \cup S_{{a_{j} }}^{{*u_{q} }} } \right|}} + \frac{1}{2}\left( {\frac{{\mathop \sum \nolimits_{j = 1}^{m} \left( {\alpha_{{a_{j} }}^{{u_{p} }} - \overline{\alpha }_{A}^{{u_{p} }} } \right)\left( {\alpha_{{a_{j} }}^{{u_{q} }} - \overline{\alpha }_{A}^{{u_{q} }} } \right)}}{{\sqrt {\mathop \sum \nolimits_{j = 1}^{m} (\alpha_{{a_{j} }}^{{u_{p} }} - \overline{\alpha }_{A}^{{u_{p} }} )^{2} } \sqrt {\mathop \sum \nolimits_{j = 1}^{m} (\alpha_{{a_{j} }}^{{u_{q} }} - \overline{\alpha }_{A}^{{u_{q} }} )^{2} } }} + 1} \right)} \right) = 1$$

It means that \(Si{m}^{Mixfl}({S}_{A}^{*{u}_{p}},{S}_{A}^{*{u}_{q}})=1\).

Based on the above discussions, to solve the problem of missing linguistic values in an incomplete fuzzy linguistic formal context, we propose a similarity completion algorithm, which can be described as follows:

figure a

Example 1.

Table 1 shows an incomplete fuzzy linguistic formal context \((U,A,\{S,\diamond \},{R}^{\diamond })\), where \(U=\{{u}_{1},{u}_{2},{u}_{3}\}\),\(A=\{{a}_{1},{a}_{2},{a}_{3}\}\) and \(S=\{{s}_{-2}=\mathrm{low},{s}_{-1}=\mathrm{somewhat low},{s}_{0}=\mathrm{medium},{s}_{1}=\mathrm{somewhat high}, {s}_{2}=\mathrm{high}\}\). Given a threshold value \(\rlap{--} \lambda = s_{0}\), it can be seen from Table 1 that if \(R^{\diamondsuit } \left( {u_{1},a_{1} } \right) = s_{1} > \rlap{--} \lambda\), the object \(u_{1}\) has attribute \(a_{1}\), and the degree is somewhat high. If \(R^{\diamondsuit } \left( {u_{1},a_{2} } \right) = \diamondsuit_{1}\), it is unknown whether the object \(u_{1}\) has the attribute \(a_{2}\). If \(R^{\diamondsuit } \left( {u_{3},a_{1} } \right) = s_{ - 1} < \rlap{--} \lambda\), the object \(u_{3}\) does not have attribute \(a_{1}\).

Table 1 \(IFLC(U,A,\{S,\diamond \},{R}^{\diamond })\)
Full size table

Remark.

\({\diamond }_{1}\)is the missing linguistic value of the object \({u}_{1}\), \({\diamond }_{2}\) is the missing linguistic value of the object \({u}_{2}\).

In Definition 13, the mean values are used to complement the formal context, as shown in Table 2. (The linguistic 2-tuple in bold represents the filling value).

Table 2 \(FLC\left(U,A,{S}^{*},{R}^{*}\right)\)
Full size table

In Definition 15, the similarity between each object’s linguistic value sets is computed after the initial complement. The similarity between \({u}_{1}\) and \({u}_{2}\) is \(Si{m}^{Mixfl}({S}_{A}^{*{u}_{1}},{S}_{A}^{*{u}_{2}})\).

$$Si{m}^{Mixfl}({S}_{A}^{*{u}_{1}},{S}_{A}^{*{u}_{2}})=0.5833.$$

Then, we can get the fuzzy linguistic similarity matrix:

$$Si{m}^{Mixfl}=\left(\begin{array}{ccc}1& 0.5833& 0.4167\\ 0.5833& 1& 0.6036\\ 0.4167& 0.6036& 1\end{array}\right).$$

We can obtain that \({u}_{1}\), \({u}_{2}\) are the most similar to \({u}_{2}\), \({u}_{3}\) respectively. So, the filling values are \({s}_{2}\), \({s}_{0}\), We then get \(FLC\left(U,A,S,R\right)\) as shown in Table 3. (The linguistic value in bold represents the filling value).

Table 3 \(FLC\left(U,A,{S}^{*},{R}^{*}\right)\)
Full size table

4.2 Scenario Analysis

People often need to rent a house when they work or study outside, so how to quickly find a good house and reduce the frequent relocation is a critical issue. Table 4 shows an \(IFLC\left(U,A,\left\{S,\diamond \right\},{R}^{\diamond }\right)\), where \(U=\left\{{u}_{1},{u}_{2},{u}_{3},{u}_{4},{u}_{5}\right\}\) represents five houses, \(A=\left\{{a}_{1},{a}_{2},{a}_{3},{a}_{4},{a}_{5},{a}_{6}\right\}\) represents six attributes: \({a}_{1}\) is "favorable price"; \({a}_{2}\) is "transparent apartment layout"; \({a}_{3}\) is "convenient transportation"; \({a}_{4}\) is "complete facilities"; \({a}_{5}\) is "clean surrounding environment"; \({a}_{6}\) is "convenient shopping". \(S=\{{s}_{-3}=\mathrm{very low},{s}_{-2}=\mathrm{low},{s}_{-1}=\mathrm{somewhat low},{s}_{0}=\mathrm{medium},{s}_{1}=\mathrm{somewhat high},{s}_{2}=\mathrm{high},{s}_{3}=\mathrm{very high}\}\).

Table 4 \(IFLC(U,A,\{S,\diamond \},{R}^{\diamond })\)
Full size table

According to Definition 13, the mean values are used to initially complement the formal context, as shown in Table 5.

Table 5 \(FLC\left(U,A,{S}^{*},{R}^{*}\right)\)
Full size table

After the initial complement, the similarity between each object's linguistic value sets is computed in Definition 15. The similarity between \({u}_{1}\) and \({u}_{2}\) is \(Si{m}^{Mixfl}({S}_{A}^{*{u}_{1}},{S}_{A}^{*{u}_{2}})\).

$$Si{m}^{Mixfl}({S}_{A}^{*{u}_{1}},{S}_{A}^{*{u}_{2}})=0.5177.$$

Then, we can get the fuzzy linguistic similarity matrix:

$$Si{m}^{Mixfl}=\left(\begin{array}{ccccc}1& 0.5177& 0.1300& 0.2349& 0.1306\\ 0.5177& 1& 0.2113& 0.1774& 0.1820\\ 0.1300& 0.2113& 1& 0.5793& 0.5261\\ 0.2349& 0.1774& 0.5793& 1& 0.6537\\ 0.1306& 0.1820& 0.5261& 0.6537& 1\end{array}\right).$$

We can observe that \({u}_{2}\), \({u}_{3}\), \({u}_{5}\) are the most similar options to \({u}_{1}\), \({u}_{4}\), \({u}_{4}\), respectively. So, the filling values are \({s}_{2}\), \({s}_{1}\), \({s}_{2}\). We then get \(FLC\left(U,A,S,R\right)\), as shown in Table 6.

Table 6 \(FLC\left(U,A,S,R\right)\)
Full size table

Given a threshold value \(\uplambda ={s}_{0}\). According to Table 6, we can get 26 FLACs as follows (The linguistic 2-tuple in red bold represents the filling value):

1#\(({u}_{1}{u}_{2}{u}_{3}{u}_{4}{u}_{5},((\varnothing ),(\frac{{{\varvec{s}}}_{0}}{{a}_{3}},\frac{{{\varvec{s}}}_{1}}{{a}_{4}}))),\)

2#\(({u}_{1}{u}_{2}{u}_{3}{u}_{5},((\frac{{s}_{0}}{{a}_{2}}),(\frac{{s}_{0}}{{a}_{2}},\frac{{{\varvec{s}}}_{0}}{{a}_{3}},\frac{{{\varvec{s}}}_{1}}{{a}_{4}})))\),

3#\(({u}_{1}{u}_{2}{u}_{4}{u}_{5},((\frac{{s}_{1}}{{a}_{4}}),(\frac{{{\varvec{s}}}_{2}}{{a}_{3}},\frac{{s}_{1}}{{a}_{4}}))),\)

4#\(({u}_{1}{u}_{3}{u}_{4}{u}_{5},((\frac{{s}_{0}}{{a}_{1}}),(\frac{{s}_{0}}{{a}_{1}},\frac{{{\varvec{s}}}_{0}}{{a}_{3}},\frac{{{\varvec{s}}}_{1}}{{a}_{4}}))),\)

5#\(({u}_{2}{u}_{3}{u}_{4}{u}_{5},((\frac{{s}_{2}}{{a}_{5}}),(\frac{{{\varvec{s}}}_{0}}{{a}_{3}},\frac{{{\varvec{s}}}_{1}}{{a}_{4}},\frac{{s}_{2}}{{a}_{5}}))),\)

6#\(({u}_{1}{u}_{2}{u}_{5},((\frac{{s}_{0}}{{a}_{2}},\frac{{s}_{2}}{{a}_{4}}),(\frac{{s}_{0}}{{a}_{2}},\frac{{{\varvec{s}}}_{2}}{{a}_{3}},\frac{{s}_{2}}{{a}_{4}}))),\)

7#\(({u}_{1}{u}_{3}{u}_{4},((\frac{{s}_{0}}{{a}_{1}},\frac{{s}_{0}}{{a}_{3}}),(\frac{{s}_{0}}{{a}_{1}},\frac{{s}_{0}}{{a}_{3}},\frac{{{\varvec{s}}}_{1}}{{a}_{4}}))),\)

8#\(({u}_{1}{u}_{3}{u}_{5},((\frac{{s}_{0}}{{a}_{1}},\frac{{s}_{0}}{{a}_{2}}),(\frac{{s}_{0}}{{a}_{1}},\frac{{s}_{0}}{{a}_{2}},\frac{{{\varvec{s}}}_{0}}{{a}_{3}},\frac{{{\varvec{s}}}_{1}}{{a}_{4}}))),\)

9#\(({u}_{1}{u}_{4}{u}_{5},((\frac{{s}_{0}}{{a}_{1}},\frac{{s}_{1}}{{a}_{4}}),(\frac{{s}_{0}}{{a}_{1}},\frac{{{\varvec{s}}}_{2}}{{a}_{3}},\frac{{s}_{1}}{{a}_{4}}))),\)

10#\(({u}_{2}{u}_{3}{u}_{5},((\frac{{s}_{0}}{{a}_{2}},\frac{{s}_{2}}{{a}_{5}}),(\frac{{s}_{0}}{{a}_{2}},\frac{{{\varvec{s}}}_{0}}{{a}_{3}},\frac{{{\varvec{s}}}_{1}}{{a}_{4}},\frac{{s}_{2}}{{a}_{5}}))),\)

11#\(({u}_{3}{u}_{4}{u}_{5},((\frac{{s}_{2}}{{a}_{1}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{1}}{{a}_{6}}),(\frac{{s}_{2}}{{a}_{1}},\frac{{{\varvec{s}}}_{0}}{{a}_{3}},\frac{{{\varvec{s}}}_{1}}{{a}_{4}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{1}}{{a}_{6}}))),\)

12#\(({u}_{1}{u}_{2},((\frac{{s}_{2}}{{a}_{2}},\frac{{s}_{3}}{{a}_{4}}),(\frac{{s}_{2}}{{a}_{2}},\frac{{{\varvec{s}}}_{2}}{{a}_{3}},\frac{{s}_{3}}{{a}_{4}}))),\)

13#\(({u}_{1}{u}_{3},((\frac{{s}_{0}}{{a}_{1}},\frac{{s}_{0}}{{a}_{2}},\frac{{s}_{0}}{{a}_{3}}),(\frac{{s}_{0}}{{a}_{1}},\frac{{s}_{0}}{{a}_{2}},\frac{{s}_{0}}{{a}_{3}},\frac{{{\varvec{s}}}_{1}}{{a}_{4}}))),\)

14#\(({u}_{1}{u}_{4},((\frac{{s}_{0}}{{a}_{1}},\frac{{s}_{2}}{{a}_{3}},\frac{{s}_{1}}{{a}_{4}}),(\frac{{s}_{0}}{{a}_{1}},\frac{{s}_{2}}{{a}_{3}},\frac{{s}_{1}}{{a}_{4}}))),\)

15#\(({u}_{1}{u}_{5},((\frac{{s}_{0}}{{a}_{1}},\frac{{s}_{0}}{{a}_{2}},\frac{{s}_{2}}{{a}_{4}}),(\frac{{s}_{0}}{{a}_{1}},\frac{{s}_{0}}{{a}_{2}},\frac{{{\varvec{s}}}_{2}}{{a}_{3}},\frac{{s}_{2}}{{a}_{4}}))),\)

16#\(({u}_{2}{u}_{4},((\frac{{s}_{1}}{{a}_{4}},\frac{{s}_{2}}{{a}_{5}}),(\frac{{{\varvec{s}}}_{2}}{{a}_{3}},\frac{{s}_{1}}{{a}_{4}},\frac{{s}_{2}}{{a}_{5}}))),\)

17#\(({u}_{2}{u}_{5},((\frac{{s}_{0}}{{a}_{2}},\frac{{s}_{2}}{{a}_{4}},\frac{{s}_{2}}{{a}_{5}}),(\frac{{s}_{0}}{{a}_{2}},\frac{{{\varvec{s}}}_{2}}{{a}_{3}},\frac{{s}_{2}}{{a}_{4}},\frac{{s}_{2}}{{a}_{5}}))),\)

18#\(({u}_{3}{u}_{4},((\frac{{s}_{2}}{{a}_{1}},\frac{{s}_{0}}{{a}_{3}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{1}}{{a}_{6}}),(\frac{{s}_{2}}{{a}_{1}},\frac{{s}_{0}}{{a}_{3}},\frac{{{\varvec{s}}}_{1}}{{a}_{4}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{1}}{{a}_{6}}))),\)

19#\(({u}_{3}{u}_{5},((\frac{{s}_{2}}{{a}_{1}},\frac{{s}_{0}}{{a}_{2}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{1}}{{a}_{6}}),(\frac{{s}_{2}}{{a}_{1}},\frac{{s}_{0}}{{a}_{2}},\frac{{{\varvec{s}}}_{0}}{{a}_{3}},\frac{{{\varvec{s}}}_{1}}{{a}_{4}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{1}}{{a}_{6}}))),\)

20#\(({u}_{4}{u}_{5},((\frac{{s}_{2}}{{a}_{1}},\frac{{s}_{1}}{{a}_{4}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{1}}{{a}_{6}}),(\frac{{s}_{2}}{{a}_{1}},\frac{{{\varvec{s}}}_{2}}{{a}_{3}},\frac{{s}_{1}}{{a}_{4}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{1}}{{a}_{6}}))),\)

21#\(({u}_{1},((\frac{{s}_{0}}{{a}_{1}},\frac{{s}_{2}}{{a}_{2}},\frac{{s}_{2}}{{a}_{3}},\frac{{s}_{3}}{{a}_{4}}),(\frac{{s}_{0}}{{a}_{1}},\frac{{{\varvec{s}}}_{2}}{{a}_{2}},\frac{{s}_{2}}{{a}_{3}},\frac{{s}_{3}}{{a}_{4}}))),\)

22#\(({u}_{2},((\frac{{s}_{3}}{{a}_{2}},\frac{{s}_{3}}{{a}_{4}},\frac{{s}_{2}}{{a}_{5}}),(\frac{{s}_{3}}{{a}_{2}},\frac{{s}_{2}}{{a}_{3}},\frac{{s}_{3}}{{a}_{4}},\frac{{s}_{2}}{{a}_{5}}))),\)

23#\(({u}_{3},((\frac{{s}_{3}}{{a}_{1}},\frac{{s}_{0}}{{a}_{2}},\frac{{s}_{0}}{{a}_{3}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{1}}{{a}_{6}}),(\frac{{s}_{3}}{{a}_{1}},\frac{{s}_{0}}{{a}_{2}},\frac{{s}_{0}}{{a}_{3}},\frac{{{\varvec{s}}}_{1}}{{a}_{4}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{1}}{{a}_{6}}))),\)

24#\(({u}_{4},((\frac{{s}_{2}}{{a}_{1}},\frac{{s}_{2}}{{a}_{3}},\frac{{s}_{1}}{{a}_{4}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{1}}{{a}_{6}}),(\frac{{s}_{2}}{{a}_{1}},\frac{{s}_{2}}{{a}_{3}},\frac{{s}_{1}}{{a}_{4}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{1}}{{a}_{6}}))),\)

25#\(({u}_{5},((\frac{{s}_{2}}{{a}_{1}},\frac{{s}_{0}}{{a}_{2}},\frac{{s}_{2}}{{a}_{4}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{2}}{{a}_{6}}),(\frac{{s}_{2}}{{a}_{1}},\frac{{s}_{0}}{{a}_{2}},\frac{{{\varvec{s}}}_{2}}{{a}_{3}},\frac{{s}_{2}}{{a}_{4}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{2}}{{a}_{6}}))),\)

26#\(\left(\emptyset,\left(\left(\frac{{s}_{3}}{{a}_{1}},\frac{{s}_{3}}{{a}_{2}},\frac{{s}_{3}}{{a}_{4}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{2}}{{a}_{6}}\right),\left(\frac{{s}_{3}}{{a}_{1}},\frac{{s}_{3}}{{a}_{2}},\frac{{{\varvec{s}}}_{2}}{{a}_{3}},\frac{{s}_{3}}{{a}_{4}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{2}}{{a}_{6}}\right)\right)\right).\)

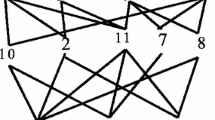
The Hasse diagram of FLAL is depicted in Fig. 1.

Fig. 1
figure 1

FLAL

Full size image

Suppose that a tenant is looking for houses with favorable prices, convenient transportation and a clean surrounding environment, that is, looking for the objects with attributes \({a}_{1}\), \({a}_{2}\) and \({a}_{5}\). After completion, the query is represented by attributes in FLAL as follows:

$$Q=\left\{{a}_{1},{a}_{2},{a}_{5}\right\}.$$

The FLACs, which meet the conditions, are as follows:

19#\(({u}_{3}{u}_{5},((\frac{{s}_{2}}{{a}_{1}},\frac{{s}_{0}}{{a}_{2}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{1}}{{a}_{6}}),(\frac{{s}_{2}}{{a}_{1}},\frac{{s}_{0}}{{a}_{2}},\frac{{{\varvec{s}}}_{0}}{{a}_{3}},\frac{{{\varvec{s}}}_{1}}{{a}_{4}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{1}}{{a}_{6}}))),\)

23#\(({u}_{3},((\frac{{s}_{3}}{{a}_{1}},\frac{{s}_{0}}{{a}_{2}},\frac{{s}_{0}}{{a}_{3}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{1}}{{a}_{6}}),(\frac{{s}_{3}}{{a}_{1}},\frac{{s}_{0}}{{a}_{2}},\frac{{s}_{0}}{{a}_{3}},\frac{{{\varvec{s}}}_{1}}{{a}_{4}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{1}}{{a}_{6}}))),\)

25#\(({u}_{5},((\frac{{s}_{2}}{{a}_{1}},\frac{{s}_{0}}{{a}_{2}},\frac{{s}_{2}}{{a}_{4}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{2}}{{a}_{6}}),(\frac{{s}_{2}}{{a}_{1}},\frac{{s}_{0}}{{a}_{2}},\frac{{{\varvec{s}}}_{2}}{{a}_{3}},\frac{{s}_{2}}{{a}_{4}},\frac{{s}_{3}}{{a}_{5}},\frac{{s}_{2}}{{a}_{6}}))).\)

It can be seen from concept 19# that \({u}_{3}\) and \({u}_{5}\) meet the conditions. The tenant can choose a more appropriate house within all the FLACs that satisfy the conditions. It can be seen from concepts 23# and 25# that if the tenant pays more attention to favorable prices, the tenant can select \({u}_{3}\). And if the tenant has high requirements in all attributes, then he can select \({u}_{5}\).

4.3 Comparative Analysis

Ganter et al. [31] introduced the notion of formal context and concept lattice. The formal concept is defined to be a pair \((X,B)\), where \(X\) and \(B\) are called extension and intension respectively. The family of all the formal concepts forms a complete lattice that is named as the concept lattice of \((U,A,I)\) and is denoted by \(L(U,A,I)\). In the classical formal context, we can definitely infer whether an object has an attribute or not via the relation value. However, uncertainty is full of our life, for which \(L(U,A,I)\) is unable to solve. By contrast, our FLAL is fully capable in representing the uncertainty information (Table 7).

Table 7 Comparison of different concept lattice construction methods
Full size table

To improve \(L(U,A,I)\), Li. et al. [17] proposed AL, a novel method to construct the approximate concept lattice of an incomplete context. In comparison with AL, we introduced linguistic values into concept representation and the fuzzy linguistic approximate concept, which can better interpret the qualitative attributes of a concept.

Liu et al. [25] proposed FLL, the fuzzy linguistic concept lattice, through combining with fuzzy linguistic information for an uncertain linguistic environment. FLAL can improve FLL in many aspects. First, FLAL makes twice complements to avoid information loss caused by only one complement, using the incomplete fuzzy linguistic formal context. It can effectively promote knowledge acquisition. Second, FLAL contains description of attributes. FLAL describes an object from two aspects: one is the essential attribute set; and the other is the nonessential attribute set that the object may have. In an uncertain environment, FLAL may well reduce the information loss caused by uncertain factors. Moreover, it includes a new fuzzy linguistic similarity method to calculate object similarity, which can clearly improve the comparison fairness among different methods. Finally, it can retrieve approximate information, which can greatly increase searching scope and reduce calculation complexity.

5 Conclusions

The problems of uncertainty and incomplete information in real life are difficult to be represented by a certainty concept or relationship. In cognition, decision-making, and implementation, we prefer to use linguistic values to obtain information or knowledge, which can better express qualitative concepts. In this paper, we propose the incomplete fuzzy linguistic formal context and the fuzzy linguistic approximation concept to deal with the incomplete context with linguistic values. The FLAC contains more information and describes the object from two aspects simultaneously. One is an object's essential attributes, and another includes its essential and possible attributes. We constructed the fuzzy linguistic approximate concept lattice. For the problem of missing values in IFLC, a proposed similarity approach can effectively complete the information. After that, we constructed the fuzzy linguistic approximate concept lattice to reduce the loss of missing information, the number of concepts, and the search range. Given the advantages of FLAL, we will continue to study attribute reduction and rule extraction algorithms in the future.