Application of Improved Differential Evolution Algorithm in Solving Equations

Abstract

The problem of finding roots of equations has always been an important research problem in the fields of scientific and engineering calculations. For the standard differential evolution algorithm cannot balance the convergence speed and the accuracy of the solution, an improved differential evolution algorithm is proposed. First, the one-half rule is introduced in the mutation process, that is, half of the individuals perform differential evolutionary mutation, and the other half perform evolutionary strategy reorganization, which increases the diversity of the population and avoids premature convergence of the algorithm; Second, set up an adaptive mutation operator and a crossover operator to prevent the algorithm from falling into the local optimum and improve the accuracy of the solution. Finally, classical high-order algebraic equations and nonlinear equations are selected for testing, and compared with other algorithms. The results show that the improved algorithm has higher solution accuracy and robustness, and has a faster convergence speed. It has outstanding effects in finding roots of equations, and provides an effective method for engineering and scientific calculations.

1 Introduction

To solve a large number of mathematical problems encountered in scientific and engineering calculations [1, 2], it is often necessary to solve the roots of higher-order algebraic equations or nonlinear equations, or even the roots of transcendental equations or equations [3, 4]. In the long-term research, people have summarized some methods, such as dichotomy, Newton's method, secant method, etc. [5]. However, these traditional methods have high requirements for functions: continuous, differentiable, etc., and they are also very sensitive to the selection of initial values, which brings difficulties to practical solutions. To these problems, in recent years, some scholars have proposed some new methods. For example, Long [6] proposed the derivative-free iterative for solving nonlinear equation, this method only needs to calculate the function value, and has a second-order convergence rate. Chen et al. [7] proposed clipping method for computing a root of a polynomial, which leads to a higher approximation order and increases the complexity of the calculation. Swarm intelligence algorithm is a strategy and method for solving problems that is developed by simulating the biological evolution process in nature. It is not restricted by search space constraints (such as differentiate, continuous, etc.) and other auxiliary information, and can effectively deal with complex problems that are difficult to solve with traditional mathematical methods. For example, Wang et al. [8] proposed an improved artificial bee colony algorithm for solving nonlinear equations, Zhao et al. [9] used the improvement of artificial glowworm swarm optimization algorithm to solve nonlinear equations. Fan et al. [10] proposed an improved cuckoo search algorithm for solving nonlinear equations. Yong [11] proposed an improved harmony search for nonlinear equations, etc. These algorithms have improved the convergence speed and accuracy to a certain extent, but there are still some problems, such as insufficient diversity, easy to fall into the local extremum, and unable to efficiently find all solutions.

Evolutionary algorithm is a hot issue currently studied, to overcome the shortcomings of evolutionary algorithms in solving the roots of equations: insufficient population diversity leads to premature convergence, falling into local optimum, and low solution accuracy. This paper proposes an improved differential evolution (IDE) algorithm to solve the roots of the equation, the purpose is to provide effective methods for mathematical calculations in science and engineering.

The paper is organized as follows: The basic principles of the DE algorithm and its convergence are described in Sect. 2. The improvement of DE algorithm and the theory of equation roots are discussed in Sect. 3. The numerical experiments are presented in Sect. 4. Conclusions and further research are discussed in Sect. 5.

2 Differential Evolution Algorithm

The DE algorithm was jointly proposed by R. Storn and K. Price [12] in 1995. It is an optimization algorithm based on the swarm intelligence theory. Compared with other evolutionary algorithms such as GA, DE algorithm has a stronger global search strategy. The algorithm uses real number coding, has few control parameters and do not need to rely on the initial feature information of the problem, it is simple and easy to implement. However, according to the principle that there is no free lunch in the world, no matter how good the algorithm is, it cannot solve all problems. Therefore, the approach of scholars is to improve the algorithm for different problems [13,14,15,16,17,18,19].

The standard DE algorithm includes crossover, mutation, and selection operations. It is different from other swarm intelligence algorithms in population reproduction schemes. The idea of DE algorithm is to obtain a new individual by adding the weighted difference vector of any two individuals to another individual with certain rules. The generated new individual vector and the current target vector are crossed with a certain probability to generate a new individual vector. In addition, in the selection operation, the DE algorithm uses a greedy way of one-to-one elimination mechanism to select the best individual [20,21,22]. If the value of the fitness has better than the old one, the new individual will replace it, otherwise the old individual is kept for next generation.

However, with the increase of evolutionary number, the DE algorithm collectively approaches the current optimal solution, resulting in a decline in population diversity and premature convergence.

To overcome these shortcomings, this paper improves the DE algorithm: (1) In terms of improving population diversity, introduce the one-half rule. Combine differential mutation and evolution strategy reorganization; (2) Change the method of taking fixed values in DE, adopt adaptive mutation and crossover operator, to avoid the rapid crowding of the population to the current optimal solution and lead to premature convergence.

3 Differential Evolution Algorithm for Finding Roots of Equations

In solving scientific and engineering practice, we often encounter the problem of solving roots of higher-order algebraic equations (or systems of equations). In solving these problems, sometimes we have to find the real roots, and sometimes we have to find all the roots. Although many methods have been found to solve these problems. However, most of these methods can only find the real roots, and have strong restrictions on the equation. Therefore, how to quickly find the root of an equation (or systems of equations) has important practical research significance. In this section, we will discuss to solve all the roots of the equations with DE algorithm.

3.1 Distribution Theory of Roots of Algebraic Equations

Given a polynomial equation of degree $n$:

$$f(z) = a_{0} z^{n} + a_{1} z^{n - 1} + ... + a_{n - 1} z + a_{n}$$

(1)

The coefficient ${a}_{i }(i=\mathrm{1,2},\dots ,n)$ is real number or complex number. Suppose ${z}_{k} (k=\mathrm{1,2},\dots ,n)$ is the root of $f(z)$, we can choose $R$ and make it satisfy ${|z}_{k}|<R$ $(k=\mathrm{1,2},\dots ,n)$. There are many methods to choose $R$, according to the usual method, we choose:

$$R = 1 + \max \{ |a_{k} |/|a_{0} |\} \, (k = 1,2, \ldots n)$$

Then suppose $z=Ry$, we can obtain

$$f(Ry) = F(y) = b_{0} y^{n} + b_{1} y^{n - 1} + ... + b_{n - 1} y + b_{n}$$

(2)

If ${y}_{k}(k=\mathrm{1,2},\dots ,n)$ is the root of $F(y)$, then $\left|{y}_{k}\right|<1(k=\mathrm{1,2},\dots ,n)$. After finding the roots ${y}_{k}$ of $F(y)$, we can get the roots ${z}_{k}={Ry}_{k}(k=\mathrm{1,2},\dots ,n)$ corresponding to $f(z)$. After finding a root ${y}_{1}$ of $F(y)$, use comprehensive division to reduce $F(y)$.

$$F(y)/(y - y_{1} ) \to F(y), \, n - 1 \to n$$

The process is repeated until all roots of $f(z)$ can be found.

The following theorems and conclusion can be found in [23].

Theorem 1

(Basic Theorem of Algebra) . Every polynomial with complex coefficients of degree greater than or equal to 1 has one root in the complex number field.

Theorem 2

Every $n$ -degree polynomial of with complex coefficients has exactly n complex roots (multiple roots are calculated by multiplicity).

3.1.1 Conclusion

If the real coefficient polynomial $f\left(\mathrm{x}\right)=0$ has complex root $a+bi$, where $a$ and $b$ are both real numbers and $b\ne 0$, then its conjugate $a-bi$ is also the root of the polynomial.

From the theorems and conclusion above, it can be known that any unary $n$-degree polynomial has n roots in the complex number field. In this paper, an IDE algorithm is used to find all real and complex roots of the polynomial equation.

3.2 Improvement of Differential Evolution Algorithm

The DE generally has premature appearance and slow convergence speed. The main reason is that this algorithm cannot balance the convergence speed and diversity, which is not conducive to the generation of new individuals and dominant individuals. For different stages of evolution, the corresponding optimal parameter values and mutation strategies of DE are also different. To solve these problems. To better develop the performance of the algorithm, an IDE algorithm is designed.

3.2.1 Self-Self-Adaptive Mutation

Mutation is a key operation of DE algorithm. Therefore, the selection of the mutation factor will directly affect the performance of the algorithm. The mutation factor of the basic DE algorithm is to choose a fixed real number between [0, 2]. Numerical experiments have proved that during the evolution of the algorithm, the initial mutation factor should be larger to ensure the diversity of the population and avoid precocity. In the later stage, it should be smaller to retain good information, avoid the optimal solution from being destroyed, and ensure its convergence. This paper proposes a self-adaptive mutation operator, which promotes the balance between global search capabilities and local search capabilities. The self-adaptive mutation operator is designed as follows:

$$\eta =\beta ({e}^{\lambda }-1)$$

(3)

where $\beta \in [\mathrm{0.2,0.6}]$, $\lambda =T/(T+t)$, $T$ is the maximum iterative number, $t$ is the current iterative number.

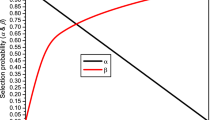
Figure 1 shows the evolution curve of the mutation factor in 200 generations. Where $\beta =0.6$. It can be seen from the figure that the mutation factor $\eta$ gradually decreases exponentially with the increase of evolutionary algebra. It helps to maintain population diversity in the early stage and accelerate the convergence rate in the later stage.

Fig. 1

Self-self-adaptive mutation evolution curve

3.2.2 Recombination of Evolutionary Strategy

The median recombination operator of the evolution strategy can make the new individual compatible with the information of the two parents and increase the convergence speed of the algorithm. Therefore, to better maintain the diversity of the population and improve the convergence speed of the algorithm, this paper introduces the evolutionary strategy's median recombination operation during the evolution of the DE algorithm, and the new individuals will participate in the DE crossover operation.

3.3 Specific Steps to Find the Roots of Equations

Step 1. Initialization. Determine the population size M, the crossover probability ${p}_{c}$. And calculate the modulus of the root of the polynomial (1).

Step 2. Randomly select the initial population within (− 1, 1). Since the root’s modulus of the polynomial (2) is limited to 1, the initial population is randomly generated in (− 1, 1).

Step 3. Calculate the fitness of individuals and sort them, select the half with better fitness to participate in population evolution, and retain the best individual in each generation.

Step 4. Mutation. The DE mutation and the median recombination of the evolution strategy is performed to generate new individuals. The calculation formula is as follows:

$${u}_{ij}\left(t+1\right)={x}_{\mathrm{best}j}\left(t\right)+\eta ({x}_{p1j}\left(t\right)-{x}_{p2j}\left(t\right))$$

$${w}_{ij}\left(t+1\right)=({x}_{p3j}\left(t\right)+{x}_{p4j}\left(t\right))/2$$

(4)

here the subscripts $p1,p2,p3$ and $p4$ are never equal to each other, and $p1,p2,p3$ and $p4$ are arbitrary random integers in $[1,M/2]$. The newly generated individual is denoted as $L$.

Step 5. Crossover. Crossover operation is conducted as follows:

$${v}_{ij}\left(t+1\right)=\left\{\begin{array}{c}{l}_{ij}\left(t+1\right) rand\le {p}_{c} \\ {x}_{ij}\left(t+1\right) rand>{p}_{c}\end{array}\right.$$

(5)

where ${p}_{c}$ is the crossover factor and ${p}_{c}\in (\mathrm{0,1}]$, rand is a random number between [0, 1], $i=\mathrm{1,2},\dots ,M,j=\mathrm{1,2},\dots ,n$.

Step 6. Selection: Among the new individuals produced in step 5 and the old ones, the 50% optimal individual is selected to form the next generation according to the size of the fitness. Selection operation is conducted as follows:

$${X}_{i}^{^{\prime}}=\left\{\begin{array}{c}{V}_{i} f\left({V}_{i}\right)<f({X}_{i}) \\ {X}_{i} otherwise\end{array}\right.$$

(6)

Step 7. Judgment on conditions. The new individual from selection is denoted as follows:

$${X}^{^{\prime}}\left(t+1\right)=({X}_{1}^{^{\prime}}\left(t+1\right),{X}_{2}^{^{\prime}}\left(t+1\right),\dots ,{X}_{M}^{^{\prime}}\left(t+1\right))$$

(7)

The best individual of ${X}^{^{\prime}}(t+1)$ is denoted as ${X}_{\mathrm{best}}(t+1)$. If the given accuracy or the maximum iterative number is satisfied, recording the best individual and outputting ${z}_{k}=R{x}_{\mathrm{best}k}$, at the same time decline the degree of the polynomial and go on step 2, otherwise set $t=t+1$ and then go on step 3. The algorithm continues until all the roots of the equation are found.

4 Numerical Experiments

To test the performance of the IDE algorithm proposed in this paper, 12 classic examples were selected for testing. Among these examples, 5 are for finding all the roots of high-order algebraic equations, and 7 are for finding all the roots of nonlinear systems of equations. These examples are from the corresponding literatures.

4.1 Improved Differential Evolution Algorithm to Find Roots of Equations

To test the capability of IDE, five typical model polynomial equations were tested by MATLAB. In this test, the population size is the same as the comparison algorithm, $M=40$, numerical experiments verify that the effect is best when $\beta =0.6$, ${p}_{c}=0.3$. The fitness function is the modulus of each equation. The biggest iterative number is 200. Some examples are studied in the literature [24], here only the literature results are given. The results are shown from Tables 1, 2, 3, 4 and 5.

Table 1 Comparison of IDE and theoretical solutions

Table 2 Comparison of IDE and theoretical solutions

Table 3 Comparison of calculation solutions with document solutions on $f_{3} (x) = 0$

Table 4 Comparison of calculation solutions with theories solutions on $f_{4} (x) = 0$

Table 5 Comparison of IDE solutions with DE solutions on $f_{5} (x) = 0$

Example 1 [25]

Solving polynomial equation $f_{1} (x) = 0.$

$$f_{1} (x) = x^{8} - 10x^{6} + 33x^{4} - 40x^{2} + 16 = 0$$

Example 2 [26]

Finding all the roots of the polynomial equation $f_{2} (x) = 0$

$$f_{2} (x) = x^{7} + 94.01x^{6} + 4406.44005x^{5} - 29408.4403x^{4} + 26955.695275x^{3} - 12228.972625x^{2} - 123.6375x - 0.625 = 0.$$

Example 3 [27]

Solving polynomial equation $f_{3} (x) = 0.$

$$\begin{gathered} f_{3} (x) = x^{13} + (1 + i)x^{12} + ix^{11} + 3ix^{10} + (7 + 3i)x^{9} + (7 + i)x^{8} + (i - 3)x^{7} + \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} (8i - 3)x^{6} + (8i - 3)x^{5} + (7i - 3)x^{4} + 7ix^{3} - 2ix^{2} - (8 + 2i)x - 8 = 0 \hfill \\ \end{gathered}$$

Table 3 shows the results of the 200 generations of the IDE algorithm in this paper and the results of 2000 generations of IPSO algorithm [27]. As can be seen from the table, the IDE algorithm uses less time to find a more accurate solution. At the same time, when the evolutionary generation is all 200, the solution results are better than that of the parallel GA [4].

Example 4 [28]

Solving polynomial equation $f_{4} (x) = 0.$

$$\begin{gathered} f_{4} (x) = x^{8} - (5.5 - 8.5i)x^{7} + (28 - 47.75i)x^{6} - (78.75 - 114.25i)x^{5} + (142.5 - 58.75i)x^{4} \hfill \\ \begin{array}{*{20}c} {} & { - (23.75 + 134.75i)x^{3} - (151.5 - 126.5i)x^{2} + (108 + 12i)x - (20 + 20i) = 0} \\ \end{array} \hfill \\ \end{gathered}$$

Example 5 [25]

Solving polynomial equation $f_{5} (x) = 0.$

$$f_{5} (x) = x^{41} + x^{3} + 1 = 0$$

From the above calculation results, it can be seen that the IDE algorithm can quickly find the root of the equation in the case of real coefficients and complex coefficients, and requires low initial values. It has strong versatility and can find both single and complex roots. From the data in Table 5, it can also be seen that for higher-order equations, this algorithm has fast calculation speed and stable results, and is significantly better than the standard DE algorithm, it indicates that the algorithm in this paper is robust.

Reference [27] only gives the real root of the problem, and the error of this real root is 10^–12, evolution generation is 2000. Our IDE algorithm not only finds all the roots, but also has an error of 10^–14 corresponding to the real root, which is smaller than the IPSO algorithm [27] and GA [29].

Numerical experiments show that in this paper, the self-adaptive mutation operator and the median recombination operator of the evolution strategy are used in the DE algorithm, and introduce the dichotomy method, greatly improved the performance of the algorithm, and achieved good results in solving all the roots of any high-order algebraic equation with real complex coefficient. It is an effective method for solving all the roots of algebraic equations with real complex coefficients of arbitrary high order.

4.2 Parameter Analysis

This paper analyzes the influence of parameters $\beta$ and ${p}_{c}$ on the algorithm through experiments. According to the parameter setting suggestions of literature [30], use ${f}_{1},{f}_{3},{f}_{4}$ for testing, each set of parameters runs 10 times independently, count the number of times that all solutions are found, it is stipulated that the solution found is regarded as the optimal solution when the error is less than ${10}^{-8}$. The statistical results are as follows:

It can be seen from Table 6 that when ${p}_{c}=0.3$, the number of times to find all the optimal solutions is the most, when $\beta =0.6$, for all values of ${p}_{c}$, the number of times is the most. Therefore, in the first part of the experiment, ${p}_{c}=0.3$, $\beta =0.6$.

Table 6 Comparison of experimental results of each set of parameters

4.3 Improved Differential Evolution Algorithm for Solving Nonlinear Equations

To further verify the effectiveness of the IDE algorithm proposed in this paper, seven nonlinear systems of equations [31, 32] were tested. And compared with the literature solutions, this algorithm is programmed with MATLAB. The parameters are also determined by experimental comparison, the experiment found that when $\beta =0.6$, the crossover operator cannot determine the best value. According to [30], it is set to self-adaptively change between [0, 1]. Therefore, the parameter settings are as follows: $M=40$, ${p}_{c}={e}^{(t-T)/T}$, $\beta =0.6$, the fitness function is the sum of the squares of the equations, maximum number of iterations is 300. Each equation runs 20 times and the error is set to 10^–10. Table 7 shows the true optimal solutions and searched solutions of Eqs. 1 and 2. Figures 2, 3, 4 and 5 show the comparison between the true solutions and the searched solutions from Eqs. 3, 4, 5 and 6.

Table 7 The true optimal solutions and searched solutions

Fig. 2

The true solutions and the searched solutions of Eq. 3

Fig. 3

The true solutions and the searched solutions of Eq. 4

Fig. 4

The true solutions and the searched solutions of Eq. 5

Fig. 5

The true solutions and the searched solutions of Eq. 6

The tested equations are as follows [31]:

$$\left\{ \begin{gathered} x_{1}^{2} - x_{2} + 1 = 0 \hfill \\ x_{1} - \cos \, (0.5\pi x_{2} ) = 0 \hfill \\ \end{gathered} \right.. \, x \in [ - 2, \, 2].$$

(1)

This equation has three true optimal solutions: (− 1/$\sqrt 2$, 1.5), (0, 1) and (− 1, 2) [31].

$$\left\{ \begin{gathered} x_{1}^{2} - x_{2} - 1 = 0 \hfill \\ (x_{1} - 2)^{2} + (x_{2} - 0.5)^{2} - 1 = 0 \hfill \\ \end{gathered} \right.. \, x \in [0, \, 2].$$

(2)

This equation has two true optimal solutions: (1.546342, 1.391174), (1.067412, 0.139460).

For the Eq. 1, the IDE algorithm is better than the HCS algorithm [31], and for the Eq. 2, the two effects are equivalent [31].

$$\left\{ \begin{gathered} x_{{_{1} }}^{2} + x_{{_{2} }}^{2} - 2 = 0 \hfill \\ x_{1}^{2} + x_{{_{2} }}^{2} /4 - 1 = 0 \hfill \\ \end{gathered} \right. \, x \in [ - 2,2].$$

(3)

$$\left\{ \begin{gathered} x_{1}^{4} + 4x_{2}^{4} - 6 = 0 \hfill \\ x_{1}^{2} x_{2} - 0.6787 = 0 \hfill \\ \end{gathered} \right.. \, x_{1} \in [ - 2, \, 2],x_{2} \in [0, \, 1.1].$$

(4)

These two problems all have four solutions. Table 8 shows the true solutions and the searched solutions by the IDE.

Table 8 The true optimal solutions and searched solutions

For Eq. 3, the MMODE algorithm [31] can find all the four solutions, but all the searched solutions cannot completely approach the real optimal solution. To Eq. 4, the MMODE can find all solutions. But for the problem with two variables, our IDE algorithm can solve it very well. The HCS algorithm [31] is the second [32].

$$\left\{ \begin{gathered} \sin \, (x_{1}^{3} ) - 3x_{1} x_{2}^{2} - 1 = 0 \hfill \\ \cos \, (3x_{1}^{2} x_{2} ) - |x_{2}^{3} | + 1 = 0 \hfill \\ \end{gathered} \right. \, x_{i} \in \, [ - 2, \, 2], \, i = 1, \, 2.$$

(5)

This equation has ten true optimal solutions, see literature [29].

$$\left\{ \begin{gathered} 5x_{1}^{9} - 6x_{1}^{5} x_{2}^{2} + x_{1} x_{2}^{4} + 2x_{1} x_{3} = 0 \hfill \\ - 2x_{1}^{6} x_{2} + 2x_{1}^{2} x_{2}^{3} + 2x_{2} x_{3} = 0 \hfill \\ x_{1}^{2} + x_{2}^{2} - 0.265625 = 0 \hfill \\ \end{gathered} \right. \, x_{i} \in [ - 0.6, \, 0.6], \, i = 1, \, 2. \, x_{3} \in [ - 5, \, 5].$$

(6)

This problem has 12 real solutions [32].

From the found solutions analysis, for Eq. 5, both the IDE algorithm and the MMODE [32] algorithm can find ten optimal solutions, HCS [31] algorithm has not tested this equation. For Eq. 6 with three variables, the HCS algorithm only finds 11 solutions, and the MMODE algorithm only finds eight optimal solutions, which is not as good as IDE algorithm can find all the optimal solutions. From the calculation time analysis, a hybrid metaheuristic with Fuzzy Clustering Means [33] took 0.169 s per execution to find all solutions. A generalized bisection based on boxes [35] took 233 s to find all the solutions. Our method was successful in finding all roots in 0.165 s. Figure 5 shows the comparison between the searched solutions by the IDE and the true solutions (Table 9).

Table 9 The searched solutions by the IDE

In terms of computational cost, the IDE algorithm in this paper is obviously superior to other algorithms. Table 10 shows the evolutionary generation and population size of each algorithm.

Table 10 Evolution parameters of each algorithm

Figures 2, 3, 4 and 5 show the comparison between the searched solutions of Eqs. 3, 4 and 5 and the real solutions.

It can be seen from Figs. 2, 3, 4 and 5 that the solution found by the IDE algorithm in this paper can find all the solutions and is consistent with the real solution. This shows that the improvement of the algorithm in this paper is effective [32].

$$\left\{\begin{array}{c}{x}_{1}^{2}+{x}_{2}^{2}-1.0=0 \\ {x}_{3}^{2}+{x}_{4}^{2}-1.0=0 \\ {x}_{5}^{2}+{x}_{6}^{2}-1.0=0 \\ {x}_{7}^{2}+{x}_{8}^{2}-1.0=0 \\ 4.731\times {10}^{-3}{x}_{1}{x}_{3}-0.3578{x}_{2}{x}_{3}-0.1238{x}_{1}+{x}_{7} \\ -1.637\times {10}^{-3}{x}_{2}-0.9338{x}_{4}-0.3571=0 \\ 0.2238{x}_{1}{x}_{3}+0.7623{x}_{2}{x}_{3}+0.2638{x}_{1}-{x}_{7} \\ -0.07745{x}_{2}-0.6734{x}_{4}-0.6022=0 \\ {x}_{6}{x}_{8}+0.3578{x}_{1}+4.731\times {10}^{-3}{x}_{2}=0 \\ -0.7623{x}_{1}+0.2238{x}_{2}+0.3461=0 \end{array}.\right.$$

(7)

Where ${x}_{i}\in [-1, 1]$, $i=1, 2,\dots , 8$. The problem has 16 solutions. For problems 7 with eight decision variables, MMODE algorithm does not solve well, and its 16 optimal solutions are not well searched, which show that MMODE still needs improvement in solving problems with many decision variables. The HCS algorithm finds its 11 solutions, which shows that the HCS algorithm is not perfect for solving nonlinear equations with a large number of solutions, and the coverage of the solutions in the iterative process is not complete, and the diversity of the solutions is not sufficient. A hybrid metaheuristic with Fuzzy Clustering Means [33] took an average time of 0.295 s per execution to find all solutions. Kearfott [34] took 1120 s to find all the roots. Our method was successful in finding all roots taking an average time of 0.276 s per execution. The calculation results show that × 1, × 2, × 3 have four different values, × 4, × 5, × 6 have 16 different values, and × 7, × 8 have eight different values. Due to the dimensional relationship, the corresponding solutions are marked with different signs in Fig. 6. Figure 6 shows the comparison between the 16 solutions found by our IDE algorithm and the real solutions.

Fig. 6

The true solutions and the searched solutions of Eq. 7

For Eqs. 6 and 7 with multiple variables, our IDE algorithm in this paper can also find all the optimal solutions to the problem in a short time. Moreover, the calculation speed is faster than the comparison algorithm. This shows that IDE algorithm can guarantee the diversity of the population in the iterative process, and can also perfectly solve the nonlinear systems of equations with a large number of solutions.

5 Application of Improved Differential Evolution Algorithm in Engineering

Figure 7 is a cross-sectional view of a thin-walled rectangular beam that is common in architectural design. Knowing the load of thin-walled rectangular beams, it is required to determine the size of the beam section.

Fig. 7

Shape of beam section [35]

The nonlinear equation system of this problem is:

$$\left\{\begin{array}{c}A=bh-\left(b-2t\right)\left(h-2t\right) \\ {I}_{y}=b{h}^{3}/12-(b-2t){\left(h-2t\right)}^{3}/12\\ {I}_{n}=2{(h-t)}^{2}{(b-t)}^{2}t/\left(h+b-2t\right)\end{array}\right.$$

Among them, $b$ is the width of the rectangular beam section, $h$ is the height, and $t$ is the thickness.

Although this system of nonlinear equations is only three-dimensional, it is a relatively classic problem, and it hardly converges with Newton's iteration method.

When $A=165,{I}_{y}=9369,{I}_{z}=6835$, each equation of this system of equations is very sensitive to the value of the unknown, as shown in Table 11.

Table 11 The sensitivity of the equation to unknowns

Due to the sensitivity of the equation to unknowns, when using an optimization method to solve this system of equations, the algorithm is required to have strong global search capabilities.

Run 100 times under the same conditions to calculate the success rate, where the success rate is: $\mathrm{error}=\mathrm{max}\left|{f}_{i}\left(x\right)\right|<{10}^{-6}$. Table 12 shows the comparison of the convergence reliability of various algorithms.

Table 12 Contrast of convergence reliability

The optimal solution found by the IDE algorithm that meets the engineering application is: $h$=22.89493803, $b$=12.25651911, $t$=2.78981782.

Through this example, it can be shown that the IDE algorithm can well overcome the defect that the DE algorithm is easy to fall into the local extreme value. The optimization function that is sensitive to variables shows stronger optimization ability, so that the method can also find satisfactory solutions to the equations in engineering applications.

6 Conclusion and Future Work

Solving the roots of high-order real complex coefficient algebraic equations (systems of equations) is of great significance to the analysis and comprehensive design of engineering projects. This paper used self-adaptive mutation operator and cross operation in DE algorithm and introduced the median recombination operator of the evolution strategy. And dichotomy was introduced during evolution. The proposed method is simple to operate and easy to implement. Using the IDE algorithm to solve all roots of high-order algebraic equation with real complex coefficient, some classic equations and nonlinear systems of equations with multiple solutions are tested. The experimental results clearly show that the solutions of all equations and nonlinear systems of equations can be found completely. It shows that the IDE algorithm can effectively enhance the diversity of the population and the robustness of the algorithm. It can deal with equations in engineering applications. In addition, it is an optimized calculation technique, and related mathematical equation models in other fields can also be dealt with.

In the future, we will further enhance the stability of the IDE by employing some advanced strategies and combining other optimization algorithms, and apply our methodology to other nonlinear systems of equations, as for example more real-world examples and the real-world multimodal optimization problems in general.