Evolutionary Social Poisson Factorizationfor Temporal Recommendation

Abstract

Preference-based recommendation systems analyze user-item interactions to reveal latent factors that explain our latent preferences for items and form personalized recommendations based on the behavior of others with similar tastes. Most of the works in the recommendation systems literature have been developed under the assumption that user preference is a static pattern, although user preferences and item attributes may be changed through time. To achieve this goal, we develop an Evolutionary Social Poisson Factorization (EPF$\_$Social) model, a new Bayesian factorization model that can effectively model the smoothly drifting latent factors using Conjugate Gamma–Markov chains. Otherwise, EPF$\_$Social can obtain the impact of friends on social network for user’ latent preferences. We studied our models with two large real-world datasets, and demonstrated that our model gives better predictive performance than state-of-the-art static factorization models.

1 Introduction

The web provides amazing access to products and knowledge, but these choices increasingly overwhelm its consumers. Recommendation systems can reduce this problem, broadly speaking, which use his or her historical data of purchased or ratings to infer uses’ preferences, and then use the inferred preferences to predict which items a user tends to like [25, 26].

One of the most important classes of recommendation methods is collaborative filtering. In collaborative filtering, Poisson factorization (PF) [1] is a recent variant of probabilistic matrix factorization [2] for recommendation, which replaces the usual Gaussian likelihood and real-valued representations with a Poisson likelihood and non-negative representations. So we can also view PF as a type of Bayesian non-negative matrix factorization. A Bayesian treatment of the Poisson model, with Gamma conjugate priors on the latent factors, laid the foundation for the more recent hierarchical Poisson factorization. Poisson factorization demonstrates more efficient inference and better recommendations than both traditional matrix factorization and its variants that adjust for sparse data. The conjugate gamma Poisson structure of Poisson Factorization model ensures computationally tractable approaches for high-dimensional data using variational inference. However, traditional recommendation systems assume that all the users are independent and identically distributed. This assumption ignores the social interactions or connections among users [3]. Through incorporating social network information into the traditional factorization model, Social Poisson Factorization (SPF) enriched the preference-based recommendations [4]. But the time evolving of users’ action is not considered in SPF model, the rate of adopting an item by a user will be increased by any time after her friend adopted this item. Otherwise, most widely-used PF models for collaborative filtering assume that user preferences and item attributes are static over time, while users’ continuously time-varying preferences remain largely under explored [5, 6]. However, in many real-world scenarios, items’ popularity and reception continuously evolve as new items and categories emerging, and users’ preferences and needs drift over time, leading them to interact with items in a time-varying way [7, 8, 27]. We denote the behaviors in these scenarios as dynamic selection. Giving the dynamic selection data, a significant and attractive problem appears: using the historical behavior about what a user clicks as selecting items, how can the items that will be selected by the potential user in the next time period be predicted?

There is a wealth of research to track the aforementioned problem in the context of collaborative filtering frameworks. The first attempt to model time-evolving preference patterns in the context of CF systems can be traced back to the time SVD++ model [9, 10]. This model can effectively capture local changes of user preference, but ignore the drifting nature of item attributes. Similarly, based on imposition of a dynamic hierarchical Dirichlet process [11], dynamic Bayesian probabilistic matrix factorization (dBPMF) is proposed, which focuses mainly on modeling dynamic memberships of users [12]. Nevertheless, the temporal dynamics of latent factors are not modeled across time intervals in dBPMF. In addition to only considering the local effects captured by user group latent factors, item attractiveness is assumed to be slowly changed and item latent factors are thus assumed to be static and capture global effects [13, 21]. Dynamic Poisson Factorization (DPF) captures the time evolving latent factors with a Kalman filter, while modeling the temporal structure using Gaussian techniques under a Poisson likelihood [14]. However, DPF assumes a simple Gaussian state-space model, which lacks the expressive transition structure of the linear dynamical system [15, 22]. In practice, DPF replaces the gamma priors with a Gaussian state space model. However, this model damages the conjugation of the model and leads to the intractability of computation, or in the accurate numerical approximation of posterior inference. In fact, the lack of conjugacy prevents simple closed-form updates and consequently prevents convenient extensions to the model. Furthermore, Gaussian priors at each time step fail to capture the empirical response distribution and the long-tailed Gamma distributions, as demonstrated by Gopalan et al. [1].

In this paper, we focus firstly on addressing the problem of evolving user and item factors within the context of Poisson factorization. Evolutionary Social Poisson Factorization (EPF$\_$Social) model, which models the time evolving latent user and item factors by incorporating multiplicative Gamma–Markov chains, is proposed. EPF$\_$Social has the capacity to eliminate the defects of previously mentioned Gaussian state-space model and assumes the actions of user are either triggered by her intrinsic interests or by previous pleasant experiences of her friends, which can jointly model the dynamic interests of users and popularity of items over time and time-aware peer influence among users in social network. In summary, we have the following main contributions:

• 1. We propose a conjugate Gamma–Markov chain construction with dampened, positively correlated states (i.e., slowly and smoothly evolving in time), which has the capacity to eliminate the defects of Gaussian state-space model and allows us to leverage the long-tailed gamma prior’s better fit to user and item factors in sparse matrices. In addition this conjugate chain construction guarantees a straightforward scalable inference.

• 2. We develop an Evolutionary Social Poisson Factorization (EPF$\_$Social) model, which can incorporate the peer influence and the network of users and obtain the impact of friends on social network for user’s latent preferences.

• 3. We conduct several experiments on two real datasets to demonstrate the performance of our model, where EPF$\_$Social model achieves a higher predictive accuracy than state-of-the-art static and dynamic factorization models.

2 Social Evolutionary Poisson Factorization

2.1 Conjugate Gamma Markov Chain

In order to implement the evolutionary Poisson Factorization, we preserved the gamma-Poisson conjugate structure by placing GMC (Gamma Markov Chain) as prior on each latent factor. The conjugacy makes it possible to design fast inference algorithms for the factors in a flexible and closed form. while the finite items that users consume, most of items that a small number of tail users consume [16, 24] So we place long tail gamma priors on the latent attributes and latent preferences, which controls the average size of the representations of the users and items. In addition, it enables us to capture the diversity of users, some users tend to consume more than others, and the diversity of items, some users are more popular than others.

A straightforward model of GMC as shown in Fig. 1 would generate the ith component of the user’s latent factor at current time slice t by considering previous time slice t − 1 as follows:

$$\begin{aligned} \begin{array}{l} \theta _{n,i}^t|\theta _{n,i}^{t - 1} \sim Gamma({\theta ^a},{\theta ^b}\theta _{n,i}^{t - 1})] \end{array} \end{aligned}$$

(1)

where $\theta _{n,i}^t$ is the ith component of the user n’s latent factor at time t, and Gamma distribution has a fixed shape parameter $\theta ^a$ and a rate parameter ${\theta ^b}\theta _{n,i}^{t - 1}$.

Fig. 1

The dynamic of uses’ preferences and items’ attributes with Gamma Markov Chain

This way defines a discrete state Markov chain where each state encodes a certain regime. However, in this case the full conditional distribution $p\left( {\theta _{n,i}^t\left| {\theta _{n,i}^{t - 1},\theta _{n,i}^{t + 1}} \right. } \right)$ turns out to be non-conjugate since it has $\theta _{i}$, $1/\theta _{i}$ and $\log \theta _{i}$, making inference harder. Therefore, the basic idea is to introduce latent auxiliary variables $P_{n,i}^t$ between $\theta _{n,i}^t$ and $\theta _{n,i}^{t - 1}$, which restore positive correlation between $\theta _{n,i}^{t - 1}$, $\theta _{n,i}^{t + 1}$ while preserving conjugacy. This allows straightforward implementation of a Gibbs sampler or a variational algorithm. Our Conjugate Gamma Markov Chain is defined by:

$$\begin{aligned} \begin{array}{l} p_{n,k}^1 \sim Gamma({\delta ^P},b_u^P)\\ \theta _{u,k}^1|p_{u,k}^1 \sim Gamma({\eta ^P},{\rho ^P}p_{uk}^1)\\ p_{u,k}^t|\theta _{u,k}^{t - 1} \sim Gamma({\delta ^P},{o^P}\theta _{u,k}^{t - 1}) \end{array} \end{aligned}$$

(2)

where p is latent auxiliary variables, the parameter $b_u^P$, used for the initialization of each chain when t = 1, is separated from the transition or chaining parameters $\rho ^P$ and $o^P$.

Through inserting auxiliary variables into GMC, we exploit the transition kernel of Markov Chain. A notable feature here is that we consider separately the parameter $b^{p}_{\mu }$ to initialize the GMC at first time slice, which enables us to capture the static property of latent factor. In order to follow the track of latent factor along with time, we model the temporal corrections by decoupling these parameters. The strength of the correlation is managed by the absolute value of $\eta$ and $\delta$, and ratio ${{{\eta \rho }}{/ { { {\delta o}}}}}$ manages the skewness. When $\mathrm{ratio} <1$ ($\mathrm{ratio} >1$), the probability mass is shifted towards the interval $\theta ^{t}<\theta ^{t-1}$ $(\theta ^{t}>\theta ^{t-1})$ and the chain exhibit a systematic negative (positive drift).

2.2 Time-Evolving Impact of Social Network

Fig. 2

The left represents the actions are triggered by user intrinsic interest on different items. The social relations are also depicted in the right top. Latent triggers are shown by arrows between users in the right bottom

Many applications of recommendation contain an additional source of information: a social network. In order to jointly model the dynamic interests of users and popularity of items over time and peer influence among users in social network, we further consider to model latent Gamma factor for social trust in the user social network, combining all factors in the rate of a Poisson likelihood of the user-item interaction, which assumes the actions of user are either triggered by intrinsic intensity or her friends in social network to engage with some item. The intuition behind the effect of social network is that users tend to interact with items presented by their peers, where items offered through the social network have a positive (or neutral) influence on the user. But we should keep in mind that it is true in real-world scenarios as the impact degree of users’ actions on their friends usually decays over time. We model the effect of previous user-item interactions on the tendency of user u to adopt item i at time t as:

$$\begin{aligned} \chi \left( {t,u,i} \right)= & {} \sum \limits _{v \in N(u,i)} {\sum \limits _{t' = 1}^T {{\lambda _{u,v}}r_{v,i}^{t'}f\left( {t,t'} \right) } } \nonumber \\ f\left( {t,t'} \right)= & {} \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} 0&{}\quad {\mathrm{otherwise}} \end{array}}\\ {\begin{array}{*{20}{l}} {\exp \left( {\frac{{ - (t - t')}}{{\nu /5}}} \right) }&{}\quad {t' \le t \le } \end{array}t' + \nu } \end{array}} \right. \end{aligned}$$

(3)

where N(u) is the set of indices of other users connected to u, $\lambda _{u,v}$ represents the per-neighbor non-negative latent influence of user v on user u and $r_{v,i}^{t'}$ is the number of times user v clicked on item i at time $t'$. The trust factor $\lambda _{u,\upsilon }$ is equal to zero for all users that are not connected in the social network. In order to ensure the effect of interaction decreasing over time, we uses exponential decay function $f(t,t')$ to realize this purpose. Dividing $\nu$ by five means that we can interpret it as the number of time intervals after which the user will have little influence for other users’ action. For example, in Fig. 2, users intrinsic interest contribute partly the adoption of items. The interests of user and attributions of item can be evolved by our conjugate gamma markov chain. Otherwise, the adoption of $item_{1}$ by $user_{2}$ and $user_{3}$ cause also adoption of $item_{1}$ by $user_{1}$.

3 Model Description

Fig. 3

Graphical model of social evolutionary poisson factorization

In this section we will describe Social Evolutionary Poisson Factorization model for recommendation. Data about users, items and neighbors of users are given, where each user u as a vector $\theta$ of K latent preferences and each item i as a vector $\beta$ of K latent attributes. We introduce a set of auxiliary latent variables p and l to preserve the positive correlation for the chains of $\theta$ and $\beta$ while retaining conjugacy, respectively. We use $b^{p}_{u}$ and $b^{l}_{i}$ to parameterize the initial states of the user and item chains.

Instead of introducing a new variable solely to rescale the nonnegative multiplicative gamma chains, independently from the generating distribution, we exploits compound Poisson to draw the variables from exponential dispersion models (EDM) that we can leverage for that purpose, which also provides more flexibility with ratings data types [17]. A random variable that is the sum of $\omega$ independent and identically distributed Gamma random variables is compound Poisson distributed with an element random distribution $p_{\psi (\varepsilon ,\kappa )}$ with fixed scale parameter $\varepsilon$ and natural parameter $\kappa$ [18]. Here, the independent and identically distributed variables are a sequence of additive EDM distributions and $\omega$ is a Poisson-distributed random variable of mean $\Lambda$. By virtue of the additivity property of EDM distributions, a compound Poisson random variable has a distribution $p_{\psi (\varepsilon ,\omega \kappa )}$, which is also an EDM distribution with scale parameter $\omega \kappa$ and natural parameter $\varepsilon$ [2].

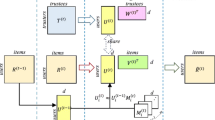
Our model rescales of the contribution of the latent factors towards the generating distributions to ensure the chains don’t grow uncontrollably in time and thus lead to numerical stability during the inference routine. Figure 3 presents the graphical model of our Evolutionary Social Poisson Factorization ($EPF\_Social$) model, and the full generative process of the Evolutionary Social Poisson Factorization ($EPF\_Social$) is detailed in Algorithm 1. This generative process describes the statistical assumptions behind the model.

4 Stochastic Variational Inference

The key computation for Poisson factorization is to infer the posterior distribution of the user preferences $\theta _{uk}^{t}$, item attributes $\beta _{uk}^{t}$ and user trust, given the social network and a set of observed matrix of user ratings for items across time. As for many Bayesian models of interest, however, the posterior is not tractable to compute exactly. We therefore introduce how to efficiently approximate the posterior based on mean-field variational inference [23].

Variational inference is an optimization-based strategy for approximating posterior distributions in complex probabilistic models. Variational inference algorithm introduces a family of distributions over the target latent variable that is indexed by a set of variational parameters, and then optimizing those parameters to find the member of this family that is close to the posterior in terms of Kullback–Liebler (KL) divergence. This inference problem thus becomes an optimization problem that can be scaled to massive data sets using stochastic optimization, leading to stochastic variational inference. By combining stochastic gradient algorithms and variational inference, stochastic variational inference (SVI) provides a new framework for approximating model posteriors with only a small number of passes through the data, enabling such models to be fit at scale.

So the latent variables in the model are user preferences $\theta$, item attributes $\beta$, their corresponding auxiliary chain variables p and l, the rate parameters of the initial states of each chain $b^{p}$ and $b^{l}$, user influences $\lambda$. For convenience, we introduce the auxiliary latent Poisson variables s. Recall that each $s_{u,i}$ is a K-vector of Poisson counts that sum to the observation $\omega _{u,i}$. In mean-field variational inference, each latent variable is assumed to be independent from each other and is governed by its own free variational distribution, which simplifies the optimization procedure. The mean-field variational family for $EPF\_social$ is defined as follows:

$$\begin{aligned}&q\left( \theta _{u,k}^t|\mu _{u,k,t}^\theta \right) q\left( p_{u,k}^t|\mu _{u,k,t}^p\right) q\left( b_u^p|\mu _u^{bp}\right) \nonumber \\&q\left( \beta _{i,k}^t|\mu _{i,k,t}^\beta \right) q\left( l_{i,k}^t|\mu _{i,k,t}^l\right) q\left( b_i^l|\mu _u^{bl}\right) \nonumber \\&q\left( \lambda _{u,v}^t|\mu _{u,v,t}^\lambda \right) q\left( s_{u,i}^t|{\varphi _{u,i,t}}\right) q\left( \omega _{u,i}^t\right) \end{aligned}$$

(4)

where the variational factors for $\theta$, $\beta$, p, l, $b^{p}$, $b^{l}$, and $\lambda$ follow all Gamma distribution, with freely set shape and rate variational parameters. We denote shape with the superscript $s$ and rate with the superscript $r$. For example, the variational distribution for user preferences $\theta$ is $Gamma(\mu ^{\theta }; \mu ^{\theta ,s}, \mu ^{\theta ,r})$. The variational distribution of $s$ is a multinomial distribution.

The $SVI$ algorithm for the general $EPF\_social$ framework is summarized in Algorithm 2. This algorithm is very efficient on sparse matrices. The variational parameter $\varphi$, sums over users and items only need to update over the non-zero observations $\omega$. Otherwise, the update for each user or item parameter is independent of all the other users or items, respectively. Accordingly, this inference routine is easily implemented in parallel. Note the learning rate power $\xi \in (0.5,1]$ controls how quickly old information is forgotten, and the leaning rate delay $\tau \ge 0$ down-weights early iterations. We terminate the algorithm when the variational distribution converges. Convergence is measured by computing the prediction accuracy on a validation set. In this paper, we declare convergence when the change in predictive likelihood is less than $0.0001\%$.

5 Experimental Results

5.1 Datasets

We evaluate the performance of $EPF\_Social$ on two real data sets:

$Netflix{\text {-}}time$ Dataset consists of users’ ratings for movies along with the timestamp of the rating and spans 86 months. We follow a similar procedure as described in Li et al. [19] by filtering users and movies who are active between the first and last time periods(10/01/98 to 12/31/05) and obtain a subset of the Netflix data set. The resulting data set contains 7400 users, 3500 movies, and 2 million non-zero ratings.

Last.fm Dataset is used to make personalized radio and music recommendations for their online radio station. This data set also contains time stamped records of users’ music listening activity with music streaming logs between 1200 users and 3000 artists, which makes it appropriate benchmark for comparing the proposed method to the other state-of-the-art methods.

5.2 Baselines

We compare the performance of our proposed model to three state-of-the-art models in recommendation listed as follows:

DPF  Dynamic Poisson factorization is a new dynamic matrix factorization probabilistic model that based on the Poisson factorization model. The aim is to capture the evolving preferences of users as well as the evolution of item popularity over time [8].

SPF  Social Poisson factorization incorporates social network information into a traditional factorization method, by adding a degree of trust variable and making all user-item interaction conditionally dependent on the user friends [4].

TSR  Time-sensitive recommendation is a convex formulation and an efficient learning algorithm to recommend relevant services, which connects self-exciting point processes and low-rank models to predict the next returning-time of users to existing services in the collection of user-item consumption pairs [20].

5.3 Compare EPF$\_$Social to DPF

To show the performance of our proposed model in capturing the dynamic preferences, we compare the MAP@k and NDCG@k versus our proposed model and DPF. Mean Average Precision at top k (MAP@k) is a metric often used in information retrieval and recommendation system. MAP@k calculates the mean of users’ average precision. MAP@k for user u is equivalent to computing

$$\begin{aligned} \begin{array}{l} MAP@k = \sum \limits _{i = 1}^k {\frac{{precision@i}}{{\min (i,|y_u^{test}|)}}}, \end{array} \end{aligned}$$

(5)

where $y_u^{test}$ is the set of items in the heldout test set for user u.

For each user the NDCG metric is discounted cumulative gain

$$\begin{aligned} \begin{array}{l} DCG@k = \sum \limits _{i = 1}^k {\frac{{{2^{re{l_i}}} - 1}}{{{{\log }_2}(i + 1)}}}, \end{array} \end{aligned}$$

(6)

divided by the ideal DCG value, or

$$\begin{aligned} \begin{array}{l} NDCG@k = \frac{{DCG@k}}{{IDCG@k}}, \end{array} \end{aligned}$$

(7)

where IDCG@k is a normalization factor that ensures NDCG lies between zero and perfect ranking and $rel_{i}$ is the ground-truth relevance of item i for user u.

Table 1 Performance comparison of $EPF\_Social$ and DPF on MAP and NDCG

The Precision@k and NDCG@k results are summarized in Table 1 for each method and data sets. As seen in Table 1, $EPF\_Social$ performs marginally better than DPF in both data sets based on all metrics. We believe this is mostly due to the fact that DPF adopts a simple Gaussian state-space model to replace the gamma priors, which lacks the expressive transition structure of the linear dynamical system. Explicitly, Gaussian priors at each time step fail to capture the empirical response distribution and the long-tailed Gamma distributions. However our conjugate gamma markov chains keep the gamma-Poisson structure to enable us to effect the long-tailed gamma prior’s better fit to user and item factors in sparse matrices.

5.4 Compare EPF$\_$Social to SPF and TSR

In this subsection, our quantitative goal is to predict which test items each user will interact with. We compare the Recall@k and NDCG@k versus our $EPF\_Social$ and SPF. Recall@k is a standard information retrieval measure, which consider user recall given k top-items to recommend. For user u RecallL@ is equivalent to computing

$$\begin{aligned} \begin{array}{l} {\mathop {Re}} call@k = \sum \limits _{i \in y_u^{test}} {\frac{{\mathrm{I}(rank(u,i) \le k)}}{{\min (k,|y_u^{test})}}} \end{array} \end{aligned}$$

(8)

Figure 4a, b show the comparison results of Recall@20 and NDCG@20 for $EPF\_social$, SPF and TSR models over $Netflix{\text {-}}time$, and Fig. 4e, f over Last.fm, respectively. As it can be seen, TSR model performs margin better than SPF because it continue improves the performance by taking information evaporation into consideration, which is a more proper way to treat time. Overall, our $EPF\_social$ exhibits particularly obvious improvements over SPF and TSR model. We believe this is mostly due to the fact that TSR pays more attention to the impact of previous events of the user, and SPF is not able to consider decay degree of users’ actions on their friends over time. These two models pay less or no attention to capture the evolving preferences of users as well as the evolution of item popularity over time. Figure 4c, d show the performance of the NDCG@k and Recall@k with varying k over $Netflix-time$, Fig. 4g, h over Last.fm, respectively. All models show an early increase in NDCG@k and Recall@k with increase of k. Moreover, $EPF\_social$ model consistently being the best one. The results demonstrate further evidence for the importance of modeling jointly the dynamic interests of users and popularity of items over time and peer influence among users in social network.

Fig. 4

Performance comparison of $EPF\_Social$, SPF and TSR on Recall and NDCG

5.5 Returning Time Prediction

we evaluated the performance of different methods in predicting the time when a user will return to the system by computing the mean absolute error (MAE) and root mean squared error (RMSE) between the estimated time and the ground-truth time. Otherwise, Suppose the testing event belongs to the user-item pair (u, i). Ideally item i should rank top at the testing moment. We record its predicted rank among all items. The expressions for MAE and RMSE are defined as follows:

$$\begin{aligned} {\text{MAE}} & = \frac{1}{n}\sum\limits_{{i = 1}}^{N} | (f_{i} - y_{i} )| \\ {\text{RMSD}} & = \sqrt {\frac{{\sum\nolimits_{{i = 1}}^{N} {(f_{i} - y_{i} )^{2} } }}{N}} , \\ \end{aligned}$$

(9)

where $f_{i}$ represents the predicted value, and $y_{i}$ represents the true value.

We report the prediction accuracy results over all users in Fig. 5. Figure 5a, b show that all the Social-based Poisson Factorization methods (EPF$\_$Social to SPF) perform better than the other models (TSRS and DPF). This is due to the fact that the proposed social-based poisson factorization methods model the dynamics of user interests and consider the peer influence of the neighboring users consuming a product. Hence, they are more expressive than other models which do not consider the peer influence among users in social network. Similar results were obtained in Fig. 5c, d. Figure 5 clearly shows that our EPF$\_$Social model can better explain the observed data compared to the other survival analysis models.

Fig. 5

MAE and RMSE of returning-time and predicted rankings

6 Conclusion

In this paper we address the problem of modeling the evolution of user and item factors within the context of Poisson factorization. We have developed $EPF\_Social$, a new Bayesian factorization model, which can effectively model the smoothly drifting latent factors using Conjugate Gamma–Markov chains. Otherwise, $EPF\_Social$ further considers the time-evolving impact of social network for how users consume items. Precision, Recall and NDCG experiments were performed on $Netflix{\text {-}}time$ and Last.fm datasets and showed that our model is superior to other state-of-the-art topic models.