Multi-criteria Optimization Technique with Complex Pythagorean Fuzzy N-soft Information

Abstract

The main objective of this article is to lay the foundations of a novel multi-criteria optimization technique, namely, the complex Pythagorean fuzzy N-soft VIKOR (CPFNS-VIKOR) method that is highly proficient to express a great deal of linguistic imprecision and vagueness inherent in human assessments. This strategy provides a versatile decision-making tool for the ranking-based fuzzy modeling of two-dimensional parameterized data. The CPFNS-VIKOR method integrates the ground-breaking specialities of the VIKOR method with the outstanding parametric structure of the complex Pythagorean fuzzy N-soft model. It is exclusively designed for the specification of a compromise optimal solution having maximum group utility and minimum individual regret of the opponent by analyzing their weighted proximity from ideal solutions. The developed strategy factually permits specific linguistic terms to demystify the individual perspectives of the decision-making experts regarding the efficacy of the alternatives and the priorities of the applicable criteria. We comprehensively assemble these independent appraisals of all the experts using the complex Pythagorean fuzzy N-soft weighted averaging operator. Moreover, we calibrate the ranking measure by utilizing group utility measure and regret measure in order to specify the hierarchical outranking of the feasible alternatives. We demonstrate the systematic methodology and framework of the proposed method with the assistance of an explicative flow chart. We skilfully investigate an empirical analysis related to selection of constructive industrial robots for the modernization of a manufacturing industry which really justifies the remarkable accountability of the proposed strategy. Furthermore, we validate this technique by a comparative study with the existing complex Pythagorean fuzzy TOPSIS (CPF-TOPSIS) method, complex Pythagorean fuzzy VIKOR (CPF-VIKOR) method and Pythagorean fuzzy TOPSIS (PF-TOPSIS) method. The comparative study is exemplified with an illustrative bar chart that visually endorses the rationality of the proposed methodology by interpreting highly compatible and accurate final outcomes. Finally, we holistically analyze the functionality of the developed strategy to enlighten its merits and prominence over other available competent approaches.

1 Introduction

Decision-making is one of the most important and challenging tasks in our day-to-day life. We may describe it as a systematic process of unraveling the real-world problems by identifying an optimum solution after scrutiny of the feasible set of alternatives. Decision-making has become more sophisticated due to the presence of multiple criteria for the assessment of the available alternatives. A new discipline of operation research entitled as multiple criteria decision making (MCDM) process has been developed for coping with such types of arduous problems. A subdiscipline of MCDM is multiple criteria group decision making (MCGDM), by which a number of decision-making experts (usually from various fields) are designated to render their evaluations. Their combined skills guarantee the procurement of more reliable results. The MCGDM strategies have gained prevalence as they are intensively used in sundry disciplines, including robotics, engineering, business management, medical sciences, aeronautics, automotive industries and many other areas of science and information technology. Consequently in the recent few decades, researchers switched their attention to establish a variety of MCGDM strategies, such as VIKOR [1], AHP [2], TOPSIS [3], ELECTRE [4] and PROMETHEE [5].

Although the literature abounds with MCGDM approaches like those mentioned above, the VIKOR method proposed by Opricovic is one of the most renowned and versatile strategies for coping with precise and crisp information. The fundamental principle behind the VIKOR method is the designation of the compromise solution as one that combines two significant characteristics, inclusive of maximum group utility and minimum individual regret of the opponent. It dutifully provides the ranking of alternatives in a hierarchical order. Here ‘compromise’ means an agreement developed by mutual relinquishment. Opricovic resorted to the following form of the $L_{p}$-metric to illustrate the two main peculiarities of the compromise solution:

$$\begin{aligned} L_{p, k}= \left\{ {\sum \limits _{s=1}^{r}}\left[ \mathfrak {I}_{s}\bigg ( \frac{ {\mathfrak {D}}^{*}_{s} - {\mathfrak {D}}_{ks}}{ {\mathfrak {D}}^{*}_{s} - {\mathfrak {D}}_{s}^{'}}\bigg )\right] ^{p}\right\} ^{\frac{1}{p}}, \end{aligned}$$

where $1\le p\le \infty ,$ $s=1, 2, \ldots , r.$

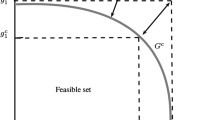
In this expression, $L_{1, k}$ and $L_{\infty , k}$ were employed to produce the group utility measure and individual regret measure, respectively. The graphical representation of the compromise solution $\varvec{\mathfrak {D}}^{c}$ and Ideal solution $\varvec{\mathfrak {D}}^{*}$ is displayed in Fig. 1.

Fig. 1

Ideal and compromise solutions

To justify its many advantages, Opricovic and Tzeng [6] extended the VIKOR method and compared its methodology with ELECTRE, TOPSIS and PROMETHEE methods. Relatedly, Bazzazi et al. [7] modified the VIKOR method by the combination of the entropy method and the analytical hierarchy process (AHP), and they demonstrated the application of this variation for the selection of mine equipment.

However in real-world MCGDM problems, uncertainty and vagueness are deep-rooted in human reasonings and they cannot be entirely addressed by classical decision-making strategies based on crisp lines of thought. Zadeh [8] proposed a solution to such complexity by establishing a novel theory of fuzzy sets (FSs) which captures the imprecise quality of vague data by the appeal to a membership function which can take values from the unit interval [0, 1]. Its implementation led Taylan et al. [9] to investigate the best renewable energy system in Saudi Arabia by using an integrated fuzzy VIKOR method, fuzzy AHP and TOPSIS approaches to manage non-cooperative decisions. Atanassov [10] extended the concept of FS into intuitionistic fuzzy set (IFS) which encapsulates a non-membership degree $(\lambda )$ in addition to the membership degree $(\mu )$ that is already present in FSs. Both degrees are subjected to the joint condition $\mu +\lambda \le 1$ at each element. Krishankumar et al. [11] presented the VIKOR method based on intuitionistic fuzzy information and implemented this method to evaluate personnel in a selection problem. Improving upon Atanassov’s theory, Yager [12] launched Pythagorean fuzzy set (PFS) theory, which admirably relaxes the condition of IFS to $\mu ^{2}+\lambda ^{2} \le 1$ at each element. With its help, Zhou and Chen [13] introduced the Pythagorean fuzzy VIKOR (PF-VIKOR) method which employs risk preference and generalized distance measure to analyze a wider range of MCDM problems. Bakioglu and Atahan [14] integrated the AHP technique with the TOPSIS and VIKOR methods, and they illustrated its potential application for the risk prioritization of self-driving vehicles. Huang et al. [15] developed the Pythagorean fuzzy MULTIMOORA method by setting a novel distance measure and they validated this methodology with a practical application for the selection of disk productions and energy projects. Shete et al. [16] remarkably investigated the sustainable supply chain innovation enablers (SSCIEs) by implementing novel Pythagorean fuzzy AHP method for the accomplishment of viability in supply chains.

All these extended models of fuzzy set theory are admittedly able to capture a large amount of imprecise information. But their capabilities are restricted to model one-dimensional data only. To overcome this deficiency, Ramot et al. [17] developed the theory of complex fuzzy sets (CFSs) that expanded the notion of fuzzy sets in an altogether new way. They suggested that complex membership grades consisting of both amplitude and phase terms would enable the practitioners to address two-dimensional data. Later on, Alkouri and Salleh [18] put forward the concept of complex intuitionistic fuzzy sets (CIFSs) in which both membership $(\mu e^{i\gamma })$ and non-membership $(\lambda e^{i\delta })$ degrees lie inside the complex unit disc, and they are restricted by the conditions $0\le \mu +\lambda \le 1$ and $0\le \frac{\gamma }{2\pi }+\frac{\delta }{2\pi }\le 1.$ Narayanamoorthy et al. [19] presented the VIKOR method based on interval-valued intuitionistic hesitant fuzzy entropy and demonstrated its potential application. Ullah et al. [20] broadened the space of CIFS by establishing a more advanced model, namely, complex Pythagorean fuzzy set (CPFS) which satisfies the refined conditions $0\le \mu ^{2}+\lambda ^{2}\le 1$ and $0\le (\frac{\gamma }{2\pi })^{2}+(\frac{\delta }{2\pi })^{2}\le 1.$ The remarkable ability of CPF theory to capture both aspects of two-dimensional fuzzy information makes it outperform other approaches, especially when it is combined with suitable methodologies. In this regard, Ma et al. [21] integrated the VIKOR method with the complex Pythagorean fuzzy environment and investigated its empirical applications for the selection of renewable energy projects and logistic village locations. Zhou and Chen [22] put forward innovative distance measures of Pythagorean fuzzy information and launched a bi-objective programming technique for the multi-dimensional prioritization of optimal green suppliers. Gul et al. [23] proposed the VIKOR method based on Pythagorean fuzzy information and explicated its methodology with the assistance of practical applications for the risk assessment of mine industry. Rani et al. [24] developed a Pythagorean fuzzy SWARA-VIKOR method and elaborated the MCGDM problem for the selection of a constructive solar panel. Shumaiza et al. [25] extended the VIKOR method under trapezoidal bipolar fuzzy environment and illustrated its methodology with the help of pragmatic applications. Gao et al. [26] proposed the VIKOR method based on q-rung interval-valued orthopair fuzzy information and implemented this method for the assessment of suppliers of medical products. Wang et al. [27] developed a brilliant MCDM technique by deploying novel Pythagorean fuzzy interactive Hamacher power aggregation operators for the judicious appraisement of express service quality.

The aforementioned models such as FS [8], CFS [17], CIFS [18] or CPFS [20] have a common shortcoming, namely, their inability to deal with parameterized scenarios. To resolve this impasse, the theory of soft sets (SS) serves as an alternative mathematical framework that incorporates the parameterization embedded in the description of certain types of data [28]. The appeal of soft set theory increased with its fastest-growing applications in pattern mining [29], rule mining [30] and its interaction with other fuzzy mathematical approaches. From this hybridization, new competent models such as fuzzy soft set (FSS) [31], valuation fuzzy soft set [32], intuitionistic fuzzy soft set (IFSS) [33] and Pythagorean fuzzy soft set (PFSS) [34] were put forward. However, neither of these ideas are designed to encapsulate multinary parameterized information about the alternatives like we often find in real-life problems. Prompted by all these evidences, Fatimah et al. [35] laid the groundwork for a new theory of N-soft sets (NSS). They proposed decision-making algorithms to showcase the significance of ordered grades and ranking-based assessments for empirical applications. Zhao et al. [36] established cumulative prospect theory-based Pythagorean fuzzy TODIM method for the proficient risk assessment of science and technology projects. Later on, the novel N-soft set concept was integrated with additional fuzzy mathematical traits to establish advanced hybrid models inclusive of fuzzy N-soft set (FNSS) [37], hesitant N-soft set (HNSS) [38], hesitant fuzzy N-soft set (HFNSS) [39], multi-fuzzy N-soft set (MFNSS) [40], intuitionistic fuzzy N-soft set (IFNSS) [41], Pythagorean fuzzy N-soft set (PFNSS) [42] and complex Pythagorean fuzzy N-soft set (CPFNSS) [43]. They grant ample room for capturing uncertainty and imprecision of parameterized data along with relative graded appraisals.

To summarize, the following evidences motivate the present study:

• The CPFS theory remarkably models both vagueness and periodicity of given inconsistent data at the same time, but it also has some symmetrical difficulties that arise because of the inadequacy of rating-based parameterized characterization interrelated with this competent approach.

• The proficient idea of NSS skilfully addresses the graded distinctions of the alternatives in a multinary parametric manner. Although this notion submits a robust generalization of soft set theory, still it is unable to represent the 2-dimensional complexity of certain sets of parameterized fuzzy data.

• The PFNSS model provides an effective mathematical tool for capturing the embedded imprecision and obscurity of parameterized ambiguous systems. However, this 1-dimensional theory is unable to illustrate periodical inexact circumstances of uncertain information.

• The traditional VIKOR method is particularly designed for the $L_{p}$-metric-based identification of a compromise solution, which feasibly satisfies all the conflicting criteria. But its advantageous methodology is not sufficient to operate in a context of graded imprecision and indeterminacy of human perspectives.

Inspired by all these facts, this research article establishes an advanced MCGDM technique, namely, the complex Pythagorean fuzzy N-soft VIKOR (CPFNS-VIKOR) method. The term is self-explanatory: this new methodology hybridizes the VIKOR approach with the promising features of CPFNSSs. It enables the panel of decision-making experts to enunciate their linguistic assessments about the characteristics of alternatives with a large degree of freedom. The CPFNSWA operator is employed to construct an aggregated complex Pythagorean fuzzy N-soft decision matrix (ACPFNSDM) from their individual interpretations. Then, the alternatives are categorized in an ascending order on the basis of their corresponding ranking measure. Finally, a compromise solution is identified by focusing on the two pivotal notions of group utility and individual regret of the opponent. The proposed technique is validated by a practical application that consists of prioritizing the industrial robots of a manufacturing company. At the end, a comparative study along with an explicative bar chart is presented to substantiate the flexibility and usefulness of the developed approach.

In a nutshell, the key contributions of this article can be illustrated as follows:

• This research study broadens the literature by developing a productive and most generalized MCGDM technique, namely, the CPFNS-VIKOR method for rating-based fuzzy modeling of two-dimensional parameterized ambiguous data.

• The robust effectuality of the proposed multi-skilled technique is remarkably demonstrated by an empirical analysis in the field of manufacturing industry.

• A comparative analysis with the existing complex Pythagorean fuzzy TOPSIS (CPF-TOPSIS) method, complex Pythagorean fuzzy VIKOR (CPF-VIKOR) method and Pythagorean fuzzy TOPSIS (PF-TOPSIS) method is presented to substantiate the admirable accountability of the established strategy.

• The merits of the developed MCGDM technique are highlighted to shed light on its compatibility, flexibility and advantages over existing decision-making approaches.

The rest of this article is organized as follows: Sect. 2 briefly recalls some basic preliminary concepts and terminologies concerning the proposed strategy. Section 3 illustrates the methodology and offers a flow chart of the proposed CPFNS-VIKOR method to evaluate the practical MCGDM problems. Section 4 demonstrates the expertise of the developed technique by means of a potential application for the selection of constructive industrial robots. Section 5 validates the feasibility and cogency of the proposed strategy by performing its comparative analysis with the existing CPF-TOPSIS, CPF-VIKOR and PF-TOPSIS methods. Section 6 highlights the merits and advantages of the CPFNS-VIKOR method over alternative decision-making strategies. Section 7 presents the concluding remarks of this article and it suggests some future research directions.

2 Preliminaries

In this section, we briefly recall some fundamental definitions and properties required for the competent presentation of the central ideas of the paper.

Definition 2.1

[20] Let ${\mathbb {K}}$ be a universe of discourse. A complex Pythagorean fuzzy set (CPFS) $\mathfrak {Q}$ over the universe ${\mathbb {K}}$ is an object of the form:

$$\begin{aligned} \mathfrak {Q}=\{ \big (k, \mu _{\mathfrak {Q}}(k)e^{i\gamma _{\mathfrak {Q}}(k)}, \lambda _{\mathfrak {Q}}(k)e^{i\delta _{\mathfrak {Q}}(k)}\big )~|~k \in {\mathbb {K}} \}, \end{aligned}$$

where $i=\sqrt{-1},$ the amplitude terms $\mu _{\mathfrak {Q}}(k),$ $\lambda _{\mathfrak {Q}}(k)$ belong to the unit interval [0, 1], and the phase terms $\gamma _{\mathfrak {Q}}(k),$ $\delta _{\mathfrak {Q}}(k)$ belong to the closed interval $[0, 2\pi ],$ satisfying the conditions $0 \le \mu _{\mathfrak {Q}}^{2}(k) + \lambda _{\mathfrak {Q}}^{2}(k) \le 1$ and $0 \le \big (\frac{\gamma _{\mathfrak {Q}}(k)}{2\pi }\big )^{2} + \big (\frac{\delta _{\mathfrak {Q}}(k)}{2\pi }\big )^{2} \le 1$. Then $\mathfrak {I}_{\mathfrak {Q}}(k) = \sqrt{ 1 - \mu _{\mathfrak {Q}}^{2}( k) - \lambda _{\mathfrak {Q}}^{2}( k)}e^{i2\pi \sqrt{ 1 - \bigl (\frac{\gamma _{\mathfrak {Q}}(k)}{2\pi }\bigr )^{2} - \bigl (\frac{\delta _{\mathfrak {Q}}( k)}{2\pi }\bigr )^{2}}}$ represents the degree of indeterminacy, for all $k \in {\mathbb {K}}.$ The pair of membership and non-membership degrees $(\mu _{\mathfrak {Q}}(k)e^{i\gamma _{\mathfrak {Q}}(k)}, \lambda _{\mathfrak {Q}}(k)e^{i\delta _{\mathfrak {Q}}(k)})$ can be referred as a complex Pythagorean fuzzy number (CPFN).

Definition 2.2

[35] Let ${\mathbb {K}}$ be a universe of discourse and L be a collection of attributes. Let $F \subseteq L$ and ${\mathbb {P}} = \{0, 1, \ldots , N-1\}$ be a set of ordered grades, where $N \in \{2, 3, \ldots \}.$ A triplet $\mathfrak {Q}=(t, F, N)$ is said to be an N-soft set over the universe ${\mathbb {K}}$ if $t:F \rightarrow 2^{{\mathbb {K}} \times {\mathbb {P}}}$ is a mapping having the property that for each $f \in F,$ there exists a unique pair $(k, p_{f})\in {\mathbb {K}} \times {\mathbb {P}}$ such that $(k, p_{f})\in t(f),$ $k \in {\mathbb {K}},$ $p_{f}\in {\mathbb {P}}.$ The N-soft set $\mathfrak {Q}$ over the universe ${\mathbb {K}}$ can be characterized as follows:

$$\begin{aligned} \mathfrak {Q}=\{\big ( f_{h}, t(f_{h})\big ) ~|~f_{h}\in F, t(f_{h})\in 2^{{\mathbb {K}} \times {\mathbb {P}}}\}. \end{aligned}$$

Definition 2.3

[43] Let ${\mathbb {K}}$ be a universe of discourse and L be a collection of attributes. Let $F\subseteq L$ and ${\mathbb {P}} = \{ 0, 1,\ldots , N-1 \}$ be a set of ordered grades, where $N\in \{2, 3,\ldots \}.$ A triplet $\mathfrak {Q}=( t, S, N )$ is said to be a complex Pythagorean fuzzy N-soft set (CPFNSS) on ${\mathbb {K}}$ if $S = ( T, F, N )$ is NSS on ${\mathbb {K}}$ and $t : F \rightarrow \mathcal {CPF}^{{\mathbb {K}} \times {\mathbb {P}}},$ where $\mathcal {CPF}^{{\mathbb {K}} \times {\mathbb {P}}}$ is the collection of all complex Pythagorean fuzzy sets (CPFSs) over ${\mathbb {K}} \times {\mathbb {P}}.$ The CPFNSS $\mathfrak {Q}$ can be interpreted as:

$$\begin{aligned} \mathfrak {Q} = \{ \langle f_{h}, t( f_{h} )\rangle | f_{h} \in F, t( f_{h} ) \in \mathcal {CPF}^{{\mathbb {K}} \times {\mathbb {P}}} \}, \end{aligned}$$

where $t(f_{h}) = \{ \bigl (( k_{g}, p_{gh}), \mu _{gh}( k_{g}, p_{gh})e^{i\gamma _{gh}( k_{g}, p_{gh})}, \lambda _{gh}( k_{g}, p_{gh})e^{i\delta _{gh}( k_{g}, p_{gh})}\bigr ) | ( k_{g}, p_{gh})\in {\mathbb {K}} \times {\mathbb {P}} \}$ represents the CPFS over ${\mathbb {K}} \times {\mathbb {P}}.$ The amplitude terms $\mu _{gh}( k_{g}, p_{gh}),$ $\lambda _{gh}( k_{g}, p_{gh})$ belong to unit interval [0, 1] satisfying the condition

$$\begin{aligned} 0 \le \mu _{gh}^{2}( k_{g}, p_{gh}) + \lambda _{gh}^{2}( k_{g}, p_{gh})\le 1 \end{aligned}$$

and phase terms $\gamma _{gh}( k_{g}, p_{gh}),$ $\delta _{gh}( k_{g}, p_{gh})$ belong to closed interval $[ 0, 2\pi ]$ subjected to the condition

$$\begin{aligned} 0 \le \left (\frac{\gamma _{gh}( k_{g}, p_{gh})}{2\pi }\right )^{2}+\left (\frac{\delta _{gh}( k_{g}, p_{gh})}{2\pi }\right )^{2}\le 1, \end{aligned}$$

where $i = \sqrt{-1}.$ For all $(k_{g}, p_{gh}) \in {\mathbb {K}} \times {\mathbb {P}},$ the degree of indeterminacy is represented by $\mathfrak {I}_{gh}( k_{g}, p_{gh}) = \sqrt{ 1 - \mu _{gh}^{2}( k_{g}, p_{gh}) - \lambda _{gh}^{2}( k_{g}, p_{gh})}e^{i2\pi \sqrt{ 1 - \bigl (\frac{\gamma _{gh}( k_{g}, p_{gh})}{2\pi }\bigr )^{2} - \bigl (\frac{\delta _{gh}( k_{g}, p_{gh})}{2\pi }\bigr )^{2}}}.$

Fundamental operations on CPFNSVs can be performed as follows

Definition 2.4

[43] Let $\Omega _{1h} = \langle p_{1h}, ( \mu _{1h}e^{i\gamma _{1h}}, \lambda _{1h}e^{i\delta _{1h}})\rangle$ $( h = 1, 2),$ and $\Omega = \langle p, ( \mu e^{i\gamma }, \lambda e^{i\delta })\rangle$ be any three CPFNSVs and $\eta > 0$ be any real number. Then:

• 1. $\Omega _{11} \oplus \Omega _{12} = \Big \langle \max ( p_{11}, p_{12}), \left( \sqrt{ \mu _{11}^{2} + \mu _{12}^{2} - \mu _{11}^{2}\mu _{12}^{2}} ~e^{i2\pi \sqrt{ (\frac{\gamma _{11}}{2\pi })^{2} + (\frac{\gamma _{12}}{2\pi })^{2} - (\frac{\gamma _{11}}{2\pi })^{2}(\frac{\gamma _{12}}{2\pi })^{2}}}, \lambda _{11}\lambda _{12}~e^{i2\pi (\frac{\delta _{11}}{2\pi }\frac{\delta _{12}}{2\pi })} \right) \Big \rangle ;$

• 2. $\Omega _{11} \otimes \Omega _{12} = \Big \langle \min ( p_{11}, p_{12}), \left( \mu _{11}\mu _{12}~e^{i2\pi (\frac{\gamma _{11}}{2\pi }\frac{\gamma _{12}}{2\pi })}, \sqrt{ \lambda _{11}^{2} + \lambda _{12}^{2} - \lambda _{11}^{2}\lambda _{12}^{2}} ~e^{i2\pi \sqrt{ (\frac{\delta _{11}}{2\pi })^{2} + (\frac{\delta _{12}}{2\pi })^{2} - (\frac{\delta _{11}}{2\pi })^{2}(\frac{\delta _{12}}{2\pi })^{2}}} \right) \Big \rangle ;$

• 3. $\eta \Omega = \Big \langle p, \left( \sqrt{ 1 - ( 1 - \mu ^{2} )^{\eta }}~e^{i2\pi \sqrt{ 1 - ( 1 - (\frac{\gamma }{2\pi })^{2} )^{\eta }}}, \lambda ^{\eta }e^{i2\pi (\frac{\delta }{2\pi })^{\eta }} \right) \Big \rangle ;$

• 4. $\Omega ^{\eta } = \Big \langle p, \left( ( \mu ^{\eta }e^{i2\pi (\frac{\gamma }{2\pi })^{\eta }}, \sqrt{ 1 - ( 1 - \lambda ^{2} )^{\eta }}~e^{i2\pi \sqrt{ 1 - ( 1 - (\frac{\delta }{2\pi })^{2} )^{\eta }}} \right) \Big \rangle .$

Concerning aggregation, the next concept that resorts to operations defined in [43] is useful:

Definition 2.5

Let $\Omega _{h} = \langle p_{h}, ( \mu _{h}e^{i\gamma _{h}}, \lambda _{h}e^{i\delta _{h}})\rangle$ $( h = 1, 2, \ldots , m)$ be a collection of CPFNSVs and $\xi _{h}$ be the relative weighting of $\Omega _{h}$ such that $\xi _{h} \in [0, 1]$ and $\sum \limits _{h=1}^{m}\xi _{h}=1.$ The complex Pythagorean fuzzy N-soft weighted averaging (CPFNSWA) operator is defined by:

$$\begin{aligned}&CPFNSWA_{\varvec{\xi }}(\Omega _{1}, \Omega _{2}, \ldots , \Omega _{m})= \xi _{1}\Omega _{1} \oplus \xi _{2}\Omega _{2} \oplus \ldots \oplus \xi _{m}\Omega _{m}\nonumber \\&\quad =\left\langle \max \big (p_{1}, p_{2}, \ldots , p_{m}\big ),\right. \nonumber \\&\quad \left. \left( \sqrt{ 1 - \prod \limits _{h=1}^{m}\big ( 1 - \mu _{h}^{2}\big )^{\xi _{h}} } e^{i2\pi \sqrt{ 1 - \prod \limits _{h=1}^{m}\big ( 1 - \big (\frac{\gamma _{h}}{2\pi }\big )^{2}\big )^{\xi _{h}}}}, \prod \limits _{h=1}^{m}\lambda _{h}^{\xi _{h}} e^{i2\pi \prod \limits _{h=1}^{m}\big (\frac{\delta _{h}}{2\pi }\big )^{\xi _{h}}}\right) \right\rangle . \end{aligned}$$

(1)

The standard procedure to compare CPFNSVs utilizes the next two definitions:

Definition 2.6

[43] The score function for CPFNSV, $\Omega _{gh} = \langle p_{gh}, ( \mu _{gh}e^{i\gamma _{gh}}, \lambda _{gh}e^{i\delta _{gh}})\rangle$ can be characterized as follows:

$$\begin{aligned} {\mathbb {D}}(\Omega _{gh}) = \big (\frac{p_{gh}}{N-1}\big )^{2} + (\mu _{gh}^{2} - \lambda _{gh}^{2}) + \frac{1}{4\pi ^{2}}( \gamma _{gh}^{2} - \delta _{gh}^{2} ), \end{aligned}$$

(2)

where ${\mathbb {D}}(\Omega _{gh}) \in [ -2, 3 ].$

Definition 2.7

[43] The accuracy function for CPFNSV, $\Omega _{gh} = \langle p_{gh}, ( \mu _{gh}e^{i\gamma _{gh}}, \lambda _{gh}e^{i\delta _{gh}})\rangle$ can be characterized as follows:

$$\begin{aligned} {\mathbb {M}}(\Omega _{gh}) = \big (\frac{p_{gh}}{N-1}\big )^{2} + (\mu _{gh}^{2} + \lambda _{gh}^{2}) + \frac{1}{4\pi ^{2}}( \gamma _{gh}^{2} + \delta _{gh}^{2} ), \end{aligned}$$

(3)

where ${\mathbb {M}}(\Omega _{gh}) \in [ 0, 3 ].$

Armed with these two concepts, we can compare CPFNSVs in the following terms:

Definition 2.8

[43] Let $\Omega _{11} = \langle p_{11}, ( \mu _{11}e^{i\gamma _{11}}, \lambda _{11}e^{i\delta _{11}})\rangle$ and $\Omega _{12} = \langle p_{12}, ( \mu _{12}e^{i\gamma _{12}}, \lambda _{12}e^{i\delta _{12}})\rangle$ be any two CPFNSVs, then the comparison of these two CPFNSVs is performed as follows:

• 1. When ${\mathbb {D}}(\Omega _{11}) < {\mathbb {D}}(\Omega _{12}),$ then $\Omega _{11} \prec \Omega _{12}$ (we declare that $\Omega _{11}$ is inferior to $\Omega _{12}$);

• 2. When ${\mathbb {D}}(\Omega _{11}) > {\mathbb {D}}(\Omega _{12}),$ then $\Omega _{11} \succ \Omega _{12}$ (we declare that $\Omega _{11}$ is superior to $\Omega _{12}$);

• 3. When ${\mathbb {D}}(\Omega _{11}) = {\mathbb {D}}(\Omega _{12}),$ then

  • If ${\mathbb {M}}(\Omega _{11}) < {\mathbb {M}}(\Omega _{12}),$ then $\Omega _{11} \prec \Omega _{12}$ (we declare that $\Omega _{11}$ is inferior to $\Omega _{12}$);

  • If ${\mathbb {M}}(\Omega _{11}) > {\mathbb {M}}(\Omega _{12}),$ then $\Omega _{11} \succ \Omega _{12}$ (we declare that $\Omega _{11}$ is superior to $\Omega _{12}$);

  • If ${\mathbb {M}}(\Omega _{11}) = {\mathbb {M}}(\Omega _{12}),$ then $\Omega _{11} \sim \Omega _{12}$ (we declare that $\Omega _{11}$ is equivalent to $\Omega _{12}$). For other terminologies and applications, the readers are referred to [44–64].

3 CPFNS-VIKOR Method for MCGDM

In this section, we develop an advanced decision-making strategy named CPFNS-VIKOR method. It is designed to capture the formal expression of some MCGDM problems that belong to the CPFNS environment. A multi-criteria optimization strategy is established to determine the compromise solution having maximum group utility and minimum individual regret, evaluated on the basis of “acceptable advantage” and “acceptable stability” of decision-making process. This strategy focuses on the hierarchical ranking of feasible set of alternatives in the presence of conflicting criteria by specifically measuring their weighted proximity to ideal values.

3.1 Mathematical Identification of MCGDM Problem

Consider a decision-making problem having $\mathfrak {L} = \{{\mathfrak {L}}_{1}, {\mathfrak {L}}_{2}, \ldots , {\mathfrak {L}}_{t}\},$ a set of t rational alternatives from which the most favorable alternative has to be identified by thoroughly examining their capabilities and proficiencies on the basis of particular decision-criteria. Let m decision-criteria $\mathfrak {V} = \{{\mathfrak {V}}_{1}, {\mathfrak {V}}_{2}, \ldots , {\mathfrak {V}}_{m}\}$ are determined by the board of decision-making experts for the comprehensive evaluation of inspected MCGDM problem. Let a group of l decision-makers $\mathfrak {E} = \{{\mathfrak {E}}_{1}, {\mathfrak {E}}_{2}, \ldots , {\mathfrak {E}}_{l}\}$ provide their accountable verdict by critically interpreting the proceedings of decision-making problem comprising selection of decision-criteria, determination of their weightage and assessment of the credibility of alternatives regarding specified decisive criteria.

3.2 Methodology of CPFNS-VIKOR Technique

For the constructive analysis of the MCGDM problem under the CPFNS environment stated above, the proposed CPFNS-VIKOR method proceeds by the following steps:

3.2.1 Construction of Independent Decision Matrices of Experts

The appointed decision-making experts rigorously analyze the suitability of each alternative relative to the decision criteria. They produce their assessments by means of linguistic information which is further symbolized in the form of complex Pythagorean fuzzy N-soft values (CPFNSVs). These CPFNS-interpretations of decision-makers corresponding to their evaluated linguistic terms are characterized systematically in the form of l independent complex Pythagorean fuzzy N-soft decision matrices (CPFNSDMs) ${{\mathcal {K}}}^{(f)}=({\mathbb {K}}_{gh}^{(f)})_{t\times m}$ as follows:

$$\begin{aligned} {{\mathcal {K}}}^{(f)}= \begin{pmatrix} \langle p_{11}^{(f)}, ( \mu _{11}^{(f)}, \lambda _{11}^{(f)} ) \rangle &{}~~ \langle p_{12}^{(f)}, ( \mu _{12}^{(f)}, \lambda _{12}^{(f)}) \rangle &{} ~~ \cdots &{} ~~ \langle p_{1m}^{(f)}, ( \mu _{1m}^{(f)}, \lambda _{1m}^{(f)} ) \rangle \\ \\ \langle p_{21}^{(f)}, ( \mu _{21}^{(f)}, \lambda _{21}^{(f)} ) \rangle &{} ~~ \langle p_{22}^{(f)}, ( \mu _{22}^{(f)}, \lambda _{22}^{(f)} ) \rangle &{} ~~ \cdots &{} ~~ \langle p_{2m}^{(f)}, ( \mu _{2m}^{(f)}, \lambda _{2m}^{(f)} ) \rangle \\ \\ \vdots &{} ~~ \vdots &{} ~~ \ddots &{} ~~ \vdots \\ \\ \langle p_{t1}^{(f)}, ( \mu _{t1}^{(f)}, \lambda _{t1}^{(f)} ) \rangle &{} ~~ \langle p_{t2}^{(f)}, ( \mu _{t2}^{(f)}, \lambda _{t2}^{(f)} ) \rangle &{} ~~ \cdots &{} ~~ \langle p_{tm}^{(f)}, ( \mu _{tm}^{(f)}, \lambda _{tm}^{(f)} ) \rangle \\ \\ \end{pmatrix}, \end{aligned}$$

where the subscript g $(g = 1, 2, \ldots , t)$ refers to the considered alternative ${\mathfrak {L}}_{g},$ subscript h $(h = 1, 2, . . . , m)$ corresponds to the selected decision-criterion ${\mathfrak {V}}_{h}$ and superscript f $(f = 1, 2, \ldots , l)$ reflects the judgment of decision-makers ${\mathfrak {E}}_{f}.$ The entries ${\mathbb {K}}_{gh}^{(f)}= \langle p_{gh}^{(f)}, ( \mu _{gh}^{(f)}, \lambda _{gh}^{(f)} ) \rangle =\langle p_{gh}^{(f)}, ( q_{gh}^{(f)}e^{i\gamma _{gh}^{(f)}}, r_{gh}^{(f)}e^{i\delta _{gh}^{(f)}} ) \rangle$ of ${{\mathcal {K}}}^{(f)}$ are the CPFNSVs depicting the evaluations of nominated decision-making experts to illustrate the proficiency of each alternative regarding conflicting criteria.

3.2.2 Assignment of Weightage to Experts

In group decision-making, all the decision-making experts of the panel may not have the same degree of expertise relative to selected decision-criteria. By considering their difference of knowledge and work experiences, the higher authorities subjectively evaluate the relative importance of each decision-maker in terms of linguistic information which are expressed in the form of CPFNSVs. Let $\eta _{f}=\langle p_{f}, ( \mu _{f}, \lambda _{f} ) \rangle =\langle p_{f}, ( q_{f}e^{i\gamma _{f}}, r_{f}e^{i\delta _{f}} ) \rangle$ be the CPFNSV representing the credibility of each appointed decision-maker. Then, the normalized weight $\zeta _{f}$ for each decision-maker can be computed using above evaluated CPFNSVs $\eta _{f},$ as follows:

$$\begin{aligned}&\zeta _{f}=\frac{ \big (\frac{p_{f}}{N ~-~ 1}\big ) + (q^{2}_{f} + r^{2}_{f}) \big (\frac{q_{f}}{q_{f} ~+~ r_{f}}\big ) + \big ( \big (\frac{\gamma _{f}}{2\pi } \big )^{2}+ \big (\frac{\delta _{f}}{2\pi } \big )^{2} \big ) \Big (\frac{\frac{\gamma _{f}}{2\pi }}{ \frac{\gamma _{f}}{2\pi }~ +~ \frac{\delta _{f}}{2\pi } } \Big ) }{\nonumber }\\&\quad \sum \limits _{f=1}^{l} \bigg (\big (\frac{p_{f}}{N ~-~ 1}\big ) + (q^{2}_{f} + r^{2}_{f}) \big (\frac{q_{f}}{q_{f} ~+~ r_{f}}\big )+ \big ( \big (\frac{\gamma _{f}}{2\pi } \big )^{2}+ \big (\frac{\delta _{f}}{2\pi } \big )^{2} \big ) \Big (\frac{\frac{\gamma _{f}}{2\pi }}{ \frac{\gamma _{f}}{2\pi }~+~ \frac{\delta _{f}}{2\pi } } \Big ) \bigg ), \end{aligned}$$

(4)

where $\zeta _{f}\in [0, 1]$ and satisfy the normality condition $\sum \limits _{f=1}^{l}\zeta _{f}=1.$ The weightage $\zeta _{f}$ of decision-making experts are determined on the basis of their proficiency to achieve more accurate and precise decision of considered MCGDM problem.

3.2.3 Formulation of Aggregated Complex Pythagorean Fuzzy N-soft Decision Matrix

The individual reflections of all the decision-makers need to be merged into a cumulative interpretation which is permissible for all experts of the decision-making panel. This leads to the construction of aggregated complex Pythagorean fuzzy N-soft decision matrix (ACPFNSDM) $\tilde{{\mathcal {K}}}=(\tilde{{\mathbb {K}}}_{gh})_{t\times m},$ whose entries $\tilde{{\mathbb {K}}}_{gh}$ can be formulated by utilizing the following CPFNSWA operator:

$$\tilde{{\mathbb {K}}}_{gh} ~~ = ~~ CPFNSWA_{\varvec{\zeta }}({{\mathbb {K}}}_{gh}^{(1)}, {{\mathbb {K}}}_{gh}^{(2)}, \ldots , {{\mathbb {K}}}_{gh}^{(l)}) = \zeta _{1}{{\mathbb {K}}}_{gh}^{(1)} \oplus \zeta _{2}{{\mathbb {K}}}_{gh}^{(2)} \oplus \ldots \oplus \zeta _{l}{{\mathbb {K}}}_{gh}^{(l)} =\left\langle \max \big (p_{gh}^{(1)}, p_{gh}^{(2)}, \ldots , p_{gh}^{(l)}\big ), \left( \sqrt{ 1 - \prod \limits _{f=1}^{l}\big ( 1 - \big (\mu _{gh}^{(f)}\big )^{2}\big )^{\zeta _{f}} } e^{i2\pi \sqrt{ 1 - \prod \limits _{f=1}^{l}\big ( 1 - \big (\frac{\gamma _{gh}^{(f)}}{2\pi }\big )^{2}\big )^{\zeta _{f}}}}, \prod \limits _{f=1}^{l}\big (\lambda _{gh}^{(f)}\big )^{\zeta _{f}} e^{i2\pi \prod \limits _{f=1}^{l}\bigg (\frac{\delta _{gh}^{(f)}}{2\pi }\bigg )^{\zeta _{f}}}\right) \right\rangle , $$

(5)

where $g= 1, 2, \ldots , t$ and $h= 1, 2, \ldots , m.$ The mutual assessment of all the designated experts can be summarized in the following ACPFNSDM:

$$\begin{aligned} \tilde{{\mathcal {K}}}= \begin{pmatrix} \tilde{{\mathbb {K}}}_{11} &{} &{} \tilde{{\mathbb {K}}}_{12} &{} &{} \cdots &{} &{} \tilde{{\mathbb {K}}}_{1m}\\ \\ \tilde{{\mathbb {K}}}_{21} &{} &{} \tilde{{\mathbb {K}}}_{22} &{} &{} \cdots &{} &{} \tilde{{\mathbb {K}}}_{2m}\\ \\ \vdots &{} &{} ~\vdots &{} &{} \ddots &{} &{} \vdots \\ \\ \tilde{{\mathbb {K}}}_{t1} &{} &{} \tilde{{\mathbb {K}}}_{t2} &{} &{} \cdots &{} &{} \tilde{{\mathbb {K}}}_{tm} \end{pmatrix}, \end{aligned}$$

where $\tilde{{\mathbb {K}}}_{gh} = \langle {\tilde{p}}_{gh}, ( \tilde{\mu }_{gh}, {\tilde{\lambda }}_{gh} ) \rangle = \langle {\tilde{p}}_{gh}, ( {\tilde{q}}_{gh}e^{i{\tilde{\gamma }}_{gh}}, \tilde{r}_{gh}e^{i{\tilde{\delta }}_{gh}} ) \rangle$ is obtained by the aggregation of ${{\mathbb {K}}}_{gh}^{(1)}, {{\mathbb {K}}}_{gh}^{(2)}, \ldots , {{\mathbb {K}}}_{gh}^{(l)},$ representing a collaborative perception of all decision-makers about an alternative corresponding to some particular decision-criteria.

3.2.4 Evaluation of Normalized Weights of Decision-Criteria

In multi-criteria analysis, the relative importance of selected criteria may not be identical according to the verdict of all decision-making experts of the panel. By analyzing the needs and requirements of the MCGDM problem under consideration, the appointed experts determine the weightage of each criterion with the help of linguistic information [65, 66]. In our analysis, this can be represented in the form of CPFNSVs $\Omega _{h}^{(f)} = \langle p_{h}^{(f)}, ( \mu _{h}^{(f)}, \lambda _{h}^{(f)} ) \rangle = \langle p_{h}^{(f)}, ( q_{h}^{(f)}e^{i\gamma _{h}^{(f)}}, r_{h}^{(f)}e^{i\delta _{h}^{(f)}} ) \rangle .$ The individual interpretations of all the decision-makers regarding the ranking of each criterion are aggregated to construct the CPFNS weighting vector $\varvec{{\bar{\Omega }}} = ({\bar{\Omega }}_{1}, {\bar{\Omega }}_{2}, \ldots , {\bar{\Omega }}_{m})^{T}$ of decision-criteria. This is achieved by employing the CPFNSWA operator defined above, i.e.:

$$\begin{aligned}&{\bar{\Omega }}_{h} ~~ = ~~ CPFNSWA_{\varvec{\zeta }}(\Omega _{h}^{(1)}, \Omega _{h}^{(2)}, \ldots , \Omega _{h}^{(l)})~~ = ~~ \zeta _{1}\Omega _{h}^{(1)} \oplus \zeta _{2}\Omega _{h}^{(2)} \oplus \ldots \oplus \zeta _{l}\Omega _{h}^{(l)}\nonumber \\&\quad =\left\langle \max \big (p_{h}^{(1)}, p_{h}^{(2)}, \ldots , p_{h}^{(l)}\big ),\right. \nonumber \\&\quad \left. \left( \sqrt{ 1 - \prod \limits _{f=1}^{l}\big ( 1 - \big (\mu _{h}^{(f)}\big )^{2}\big )^{\zeta _{f}} } e^{i2\pi \sqrt{ 1 - \prod \limits _{f=1}^{l}\big ( 1 - \big (\frac{\gamma _{h}^{(f)}}{2\pi }\big )^{2}\big )^{\zeta _{f}}}}, \prod \limits _{f=1}^{l}\big (\lambda _{h}^{(f)}\big )^{\zeta _{f}} e^{i2\pi \prod \limits _{f=1}^{l}\bigg (\frac{\delta _{h}^{(f)}}{2\pi }\bigg )^{\zeta _{f}}}\right) \right\rangle , \end{aligned}$$

(6)

where ${\bar{\Omega }}_{h}=\langle {\bar{p}}_{h}, ( {\bar{\mu }}_{h}, \bar{\lambda }_{h} ) \rangle = \langle {\bar{p}}_{h}, ( {\bar{q}}_{h}e^{i {\bar{\gamma }}_{h}}, {\bar{r}}_{h}e^{i {\bar{\delta }}_{h}} ) \rangle$ is computed by the accumulation of $\Omega _{h}^{(1)}, \Omega _{h}^{(2)}, \ldots , \Omega _{h}^{(l)},$ illustrating the aggregate weight of criterion ${\mathfrak {V}}_{h}.$ The normalized weight $\mathfrak {I}_{h}$ of each decision-criterion can be computed using the CPFNS weight $\Omega _{h}$ of that criterion as follows:

$$\begin{aligned} \mathfrak {I}_{h}=\frac{ \big (\frac{{\bar{p}}_{h}}{N ~-~ 1}\big ) + (\bar{q}^{2}_{h} + {\bar{r}}^{2}_{h}) \big (\frac{{\bar{q}}_{h}}{{\bar{q}}_{h} ~+~ {\bar{r}}_{h}}\big ) + \big ( \big (\frac{{\bar{\gamma }}_{h}}{2\pi } \big )^{2}+ \big (\frac{{\bar{\delta }}_{h}}{2\pi } \big )^{2} \big ) \Big (\frac{\frac{{\bar{\gamma }}_{h}}{2\pi }}{ \frac{\bar{\gamma }_{h}}{2\pi }~+~ \frac{{\bar{\delta }}_{h}}{2\pi } } \Big ) }{ \sum \limits _{h=1}^{m} \bigg (\big (\frac{{\bar{p}}_{h}}{N ~-~ 1}\big ) + ({\bar{q}}^{2}_{h} + {\bar{r}}^{2}_{h}) \big (\frac{{\bar{q}}_{h}}{{\bar{q}}_{h} ~+~ {\bar{r}}_{h}}\big ) + \big ( \big (\frac{{\bar{\gamma }}_{h}}{2\pi } \big )^{2}+ \big (\frac{{\bar{\delta }}_{h}}{2\pi } \big )^{2} \big ) \Big (\frac{\frac{{\bar{\gamma }}_{h}}{2\pi }}{ \frac{\bar{\gamma }_{h}}{2\pi }~+~ \frac{{\bar{\delta }}_{h}}{2\pi } } \Big ) \bigg )}, \end{aligned}$$

(7)

where $\mathfrak {I}_{h}\in [0, 1]$ for each h, and they jointly satisfy the normality condition $\sum \limits _{h=1}^{m}\mathfrak {I}_{h}=1.$ The weight $\mathfrak {I}_{h}$ indicates the relative significance of each selected criterion, and it is determined by the collaborative perception of all decision-making experts allocated to the panel.

3.2.5 Construction of Score Matrix

The formulated CPFNS-entries of AWCPFNSDM are defuzzified into crisp values with the help of a score function to locate the best and worst values of given alternatives regarding the decision-criteria. As a result of this, the score matrix $\mathfrak {D}=({\mathbb {D}}_{gh})_{t\times m}$ is constructed. Its entries ${\mathbb {D}}_{gh}$ can be evaluated as follows:

$$\begin{aligned} {\mathbb {D}}_{gh}= \Big (\frac{\tilde{p}_{gh}}{N-1}\Big )^{2} + (\tilde{q}_{gh}^{2} - \tilde{r}_{gh}^{2}) + \frac{1}{4\pi ^{2}}\big( \tilde{\gamma }_{gh}^{2} - \tilde{\delta }_{gh}^{2} \big), \end{aligned}$$

(8)

where $g=1, 2, \ldots , t$ and $h=1, 2, \ldots , m.$ The formulated score matrix can be displayed in the following manner:

$$\begin{aligned} \mathfrak {D}= \begin{pmatrix} {\mathbb {D}}_{11} &{} &{} {\mathbb {D}}_{12} &{} &{} \cdots &{} &{} {\mathbb {D}}_{1m}\\ \\ {\mathbb {D}}_{21} &{} &{} {\mathbb {D}}_{22} &{} &{} \cdots &{} &{} {\mathbb {D}}_{2m}\\ \\ \vdots &{} &{} \vdots &{} &{} \ddots &{} &{} \vdots \\ \\ {\mathbb {D}}_{t1} &{} &{} {\mathbb {D}}_{t2} &{} &{} \cdots &{} &{} {\mathbb {D}}_{tm} \end{pmatrix}, \end{aligned}$$

where ${\mathbb {D}}_{gh}$ represents the score degree of CPFNS-entry of AWCPFNSDM which is used to determine the best and worst values of the considered alternatives for the MCGDM problem under inspection.

3.2.6 Specification of Best and Worst Values

After the formulation of the score matrix, the best and worst values of alternatives are identified on the basis of cost-benefit analysis, which are further used to evaluate the group utility measure and individual regret measure of alternatives. Let ${\mathfrak {V}}_{\mathfrak {B}}$ denotes the collection of benefit-type criteria and ${\mathfrak {V}}_{\mathfrak {C}}$ denotes the collection of cost-type criteria. Then, the best value ${{\mathbb {D}}}^{+}_{h}$ relative to each decision-criterion ${\mathfrak {V}}_{h}$ can be determined as follows:

$$\begin{aligned} {{\mathbb {D}}}^{+}_{h} = \left\{ \begin{array}{ll} \max \limits _{g}{{\mathbb {D}}}_{gh}, &{} \hbox {if}~ {{\mathfrak {V}}_{h} \in {\mathfrak {V}}_{\mathfrak {B}},} \\ \min \limits _{g}{{\mathbb {D}}}_{gh}, &{} \hbox {if }~ {{\mathfrak {V}}_{h} \in {\mathfrak {V}}_{\mathfrak {C}},} \end{array} \right. \end{aligned}$$

(9)

Likewise, the worst value ${{\mathbb {D}}}^{-}_{h}$ relative to each decision-criterion ${\mathfrak {V}}_{h}$ can be determined as follows:

$$\begin{aligned} {{\mathbb {D}}}^{-}_{h} = \left\{ \begin{array}{ll} \min \limits _{g}{{\mathbb {D}}}_{gh}, &{} \hbox {if}~ {{\mathfrak {V}}_{h} \in {\mathfrak {V}}_{\mathfrak {B}},} \\ \max \limits _{g}{{\mathbb {D}}}_{gh}, &{} \hbox {if}~ { {\mathfrak {V}}_{h} \in {\mathfrak {V}}_{\mathfrak {C}},} \end{array} \right. \end{aligned}$$

(10)

where ${{\mathbb {D}}}^{+}_{h}$ denotes the best value in the sense that it maximizes all the benefit-type criteria and minimizes all the cost-type criteria while ${{\mathbb {D}}}^{-}_{h}$ denotes the worst value which minimizes the benefit-type criteria but maximizes all the cost-type criteria of the MCGDM problem under consideration.

3.2.7 Evaluation of Group Utility, Individual Regret, and Ranking Measure

The next step is to evaluate the functionality as well as ineffectuality of each alternative to identify the best feasible option. For this purpose, we compute the group utility measure ${\mathcal {S}}_{g}$ and individual regret measure ${\mathcal {R}}_{g}$ relative to each considered alternative by using the following formulas.

$$\begin{aligned} {\mathcal {S}}_{g}=\sum \limits _{h=1}^{m}\mathfrak {I}_{h}\bigg (\frac{{{\mathbb {D}}}_{h}^{+} - {{\mathbb {D}}}_{gh} }{{{\mathbb {D}}}_{h}^{+} - {{\mathbb {D}}}_{h}^{-} }\bigg ), \end{aligned}$$

(11)

$$\begin{aligned} {\mathcal {R}}_{g}=\max \limits _{h}\mathfrak {I}_{h}\bigg (\frac{{{\mathbb {D}}}_{h}^{+} - {{\mathbb {D}}}_{gh} }{{{\mathbb {D}}}_{h}^{+} - {{\mathbb {D}}}_{h}^{-} }\bigg ), \end{aligned}$$

(12)

where $\mathfrak {I}_{h}$ is the normalized weight of the decision-criterion, exhibiting their relative importance in the MCGDM problem. Finally, the ranking measure ${\mathcal {Q}}_{g}$ corresponding to each alternative is evaluated with the assistance of ${\mathcal {S}}_{g}$ and ${\mathcal {R}}_{g}$ by utilizing the following relation.

$$\begin{aligned} {\mathcal {Q}}_{g}= \alpha ~\bigg (\frac{{{\mathcal {S}}}_{g} - {{\mathcal {S}}}^{+} }{{{\mathcal {S}}}^{-} - {{\mathcal {S}}}^{+} }\bigg ) + (1 - \alpha )\bigg (\frac{{{\mathcal {R}}}_{g} - {{\mathcal {R}}}^{+} }{{{\mathcal {R}}}^{-} - {{\mathcal {R}}}^{+} }\bigg ), \end{aligned}$$

(13)

where

$$\begin{aligned} {{\mathcal {S}}}^{+}&= \min \limits _{g}{{\mathcal {S}}}_{g}, ~~~~{{\mathcal {S}}}^{-}= \max \limits _{g}{{\mathcal {S}}}_{g},\\ {{\mathcal {R}}}^{+}&= \min \limits _{g}{{\mathcal {R}}}_{g}, ~~~{{\mathcal {R}}}^{-}= \max \limits _{g}{{\mathcal {R}}}_{g}. \end{aligned}$$

The solution formulated by ${{\mathcal {S}}}^{+}$ exhibits the maximum group utility. Likewise, the solution computed by ${{\mathcal {R}}}^{+}$ exhibits the minimum individual regret of the opponent. The parameter $\alpha \in [0, 1]$ indicates the weight of decision-making strategy for maximum group utility, while $(1 - \alpha )$ represents the weight for minimum individual regret. The value of $\alpha$ is determined by analyzing the nature of inspected MCGDM problem, as the required compromise solution can be identified with “veto” $(\alpha < 0.5),$ with “consensus” [67] $(\alpha = 0.5)$, or with “voting by majority” $(\alpha > 0.5).$ Generally, $(\alpha =0.5)$ is preferred to embrace both features of maximum group utility and minimum individual regret in the identified compromise solution.

3.2.8 Ranking of Alternatives

After the evaluation of ${\mathcal {S}},$ ${\mathcal {R}}$ and ${\mathcal {Q}},$ the alternatives are classified by sorting them in an ascending order on the basis of group utility measure, individual regret measure and ranking measure. These computed hierarchical sorting of given alternatives provide three constructive rank-orderings for the identification of compromise solution. The alternative having least value of ${\mathcal {Q}}$ will be interpreted as the feasible alternative of the considered MCGDM problem.

3.2.9 Determination of Compromise Solution

The last step of our strategy is the identification of the required compromise solution of the MCGDM problem. Let ${\mathfrak {L}}^{(1)}$ be the alternative having minimum value of ${\mathcal {Q}}.$ Then, the alternative ${\mathfrak {L}}^{(1)}$ will be interpreted as the optimal compromise solution if the following two conditions are fulfilled:

$\varvec{{\mathcal {C}}}{} \mathbf{1}:$:

“Acceptable advantage” This condition specifies that alternative ${\mathfrak {L}}^{(1)}$ must satisfy the following relation:

$$\begin{aligned} {\mathcal {Q}}({\mathfrak {L}}^{(2)} ) - {\mathcal {Q}}( {\mathfrak {L}}^{(1)} ) \ge DQ, \end{aligned}$$

where ${\mathfrak {L}}^{(2)}$ indicates the alternative which is ranked at second position in the sorting list of ${\mathcal {Q}},$ $DQ=\frac{1}{t - 1}$ and the total number of considered alternatives is t.

$\varvec{{\mathcal {C}}}{} \mathbf{2}:$:

“Acceptable stability in decision-making” According to this condition, the alternative ${\mathfrak {L}}^{(1)}$ will also be ranked best with respect to ${\mathcal {S}}$ or/and ${\mathcal {R}}.$ This proposed compromise solution must be stable within the decision-making process. If any one of the above-stated conditions is not satisfied, then a set of compromise solutions is specified as follows:

• The alternatives ${\mathfrak {L}}^{(1)}, {\mathfrak {L}}^{(2)}, \ldots , {\mathfrak {L}}^{(\sigma )}$ will constitute the proposed set of compromise solutions if only condition ${\mathcal {C}}1$ is not satisfied, where ${\mathfrak {L}}^{(\sigma )}$ is evaluated by the following relation:

  $$\begin{aligned} {\mathcal {Q}}({\mathfrak {L}}^{(\sigma )} ) - {\mathcal {Q}}( {\mathfrak {L}}^{(1)} ) < DQ, \end{aligned}$$

  for maximum value of $\sigma .$

• The alternatives ${\mathfrak {L}}^{(1)}$ and ${\mathfrak {L}}^{(2)}$ will be the only members of the identified set of compromise solutions if only condition ${\mathcal {C}}2$ is not satisfied.

Now, we illustrate the framework of proposed CPFNS-VIKOR strategy with the help of elaborative flowchart, as shown in Fig. 2.

Fig. 2

Flow chart of CPFNS-VIKOR method

4 Application

In this section, we investigate an empirical MCGDM problem related to selection of the most suitable industrial robot for automation, by implementing our developed CPFNS-VIKOR method to demonstrate the versatility and functionality of the proposed decision-making strategy.

4.1 Selection of Industrial Robots for Automation

Robotics and industrial automation is a multi-disciplinary branch of science and technology that provides advanced machinery for the optimization of overall production of industries at lower costs. Globally, the industries have replaced their conventional manufacturing system with the flexible automation system to ensure technological advancements and fulfil the current mass production requirements. The drastically increased utilization of robots has modernized the production processes of automotive industries because of their wide range of industrial applications. The selection of appropriate industrial robotic structure is one of the most crucial decision-making problems due to the availability of a broad spectrum of robotic technologies with various dominant features and specifications. To accomplish the present need, suppose that a renowned manufacturing industry is intended to purchase a constructive robot for the enhancement of their industrial development. The collection of six industrial robots $\mathfrak {L} = \{ {{\mathcal {L}}}_{1}, {{\mathcal {L}}}_{2}, {{\mathcal {L}}}_{3}, {{\mathcal {L}}}_{4}, {{\mathcal {L}}}_{5}, {{\mathcal {L}}}_{6} \}$ is considered after analyzing their diverse capabilities, where

$\mathfrak {L}_{1}:$:

Cartesian robot: This ideal robotic framework has three linear joints that can move along three orthogonal cartesian axes. It is specialized for three-dimensional handling systems such as palletizing, stacking, machine loading, packaging, sorting, and placement of products.

$\mathfrak {L}_{2}:$:

Delta robot: This manipulator is a special type of parallel robot with inverted pyramid structure. This extremely fast robot can perform various tasks such as pick-and-place, sorting and packaging of products. It also has capability to execute minute and precise motions in the multiple industries.

$\mathfrak {L}_{3}:$:

Cylindrical robot: This robotic technology has a cylindrical framework that offers both linear and rotary movements. It is specifically used for spot welding, assembly operations, pick-and-place works, die casting, handling of machine tools and transportation of LCD panels.

$\mathfrak {L}_{4}:$:

Polar robot: This multi-purpose robot has an arm with one linear joint and two rotary joints. It is especially designed for a large number of industrial applications such as material handling, spot welding, die casting, arc welding, fettling, injection molding and gas welding.

$\mathfrak {L}_{5}:$:

Collaborative robot: This automated manipulator has the remarkable ability to interact directly and safely with humans in a collaborative workspace. Its advanced framework is widely used in the automotive industry to perform several tasks such as palletizing, inspection, packaging and material handling.

$\mathfrak {L}_{6}:$:

Articulated robot: This versatile technology has a series of rotary joints, designed on the basis of a human arm. This structure is used for a broad range of applications that include arc welding, pick and place, material handling, assembly, packaging and parts transferring along with many others.

To address this tricky MCGDM problem, the stakeholders of manufacturing industry organize a panel of three decision-making experts $\mathfrak {E} = \{ {\mathfrak {E}}_{1}, {\mathfrak {E}}_{2}, {\mathfrak {E}}_{3} \}$ to thoroughly examine the competency of industrial robots for the exponential growth of the industry under consideration, where

$\mathfrak {E}_{2}:$:

Acquisition manager,

$\mathfrak {E}_{3}:$:

Operation manager,

$\mathfrak {E}_{4}:$:

Technical manager.

All the appointed decision-making experts identify the decisive factors $\mathfrak {V}=\{\mathfrak {V}_{1}, \mathfrak {V}_{2}, \mathfrak {V}_{3}, \mathfrak {V}_{4}\}$ affecting the selection process of industrial robot with the assistance of their certified mutual decisions, where

$\mathfrak {V}_{1}:$:

Repeated positioning accuracy: This measurable characteristic can be regarded as the capability of the robot to reach the exact same orientation each time after the completion of its routine tasks. It directly affects the efficiency of the robots during the execution of its critical operating tasks.

$\mathfrak {V}_{2}:$:

Payload capacity: This remarkable peculiarity refers to maximum load that can be attached or supported by the wrist of the robotic arm of the manipulator. An ideal robot can effectively lift the applied payload during its operating cycle in its given working space.

$\mathfrak {V}_{3}:$:

Investment and maintenance cost: The investment and maintenance cost of the robotic structure have a significant impact on the rapid development of industries. An industrial robot with minimum total cost is preferable as it maximizes the profitability of industries.

$\mathfrak {V}_{4}:$:

Computational efficiency: This significant parameter of robotic manipulator is closely related to each operational user. It is measured by the operating speed at which robot can move in an inertial frame of reference. An efficient robot should support high speed working cycles with minimum vibrations.

The motive of this analysis is to determine the best industrial robotic technology on the basis of cost-benefit analysis, required for the modernization of considered manufacturing industry through automation. The constructive selection of sustainable industrial robots will minimize the overall long-term human interventions, reduce the total cost of production and dramatically accelerate the productivity of the manufacturing industry at large scale, which in turn optimizes the net-profit of the industry.The systematic framework for the identification of the scrutinized MCGDM problem is clearly demonstrated in Fig. 3.

Fig. 3

Specification of investigated problem

The procedure of selecting the optimum industrial robot using proposed CPFNS-VIKOR method is elaborated in following illustrative steps:

Step 1::

The panel of appointed decision-makers critically evaluate the proficiency of six alternative robots relative to selected conflicting criteria with the assistance of particular linguistic terms, as presented in Tables 1 and 2 .

Table 1 Linguistic terms for ranking of industrial robots

Table 2 Rating of industrial robots corresponding to decision-criteria

Step 2::

The individual linguistic reflections of all decision-making experts regarding performance of considered automated industrial robots are expressed in the form of CPFNSVs and encapsulated in Tables 3, 4 and 5 .

Table 3 CPF6SDM of the acquisition manager

Table 4 CPF6SDM of the operation manager

Table 5 CPF6SDM of the technical manager

Step 3::

The linguistic terms specified for the ranking of decision-makers and selected criteria with respect to their importance are symbolized in Table 6. The higher authorities subjectively analyze the credibility and expertise of nominated decision-making experts and assign them weights in terms of linguistic variables which are expressed in the form of CPFNSVs. The allocated CPFNS weights are further normalized by using Eq. (4), as highlighted in Table 7.

Table 6 Linguistic terms for the relative importance of experts and criteria

Table 7 Weightage of experts relative to their importance

Step 4::

The independent evaluations of all the nominated decision-makers of the panel regarding competency of robots are aggregated by utilizing the CPFNSWA operator, as defined in Eq. (5). Then, their accumulated outcomes are presented in Table 8 to summarize their mutual decision in the form of ACPFNSDM.

Table 8 Aggregated complex Pythagorean fuzzy N-soft decision matrix

Step 5::

All the designated decision-makers explicitly identify the relative importance of specified decision-criteria and rank them accordingly with the help of their assigned linguistic terms which are expressed in the form of CPFNSVs, as presented in Tables 9 and 10. These allocated CPFNS weights of criteria are accumulated by employing CPFNSWA operator which are further standardized in the light of Eq. (6), as given in Table 11.

Table 9 Importance of conflicting criteria in terms of linguistic variables

Table 10 Weightage of criteria relative to their importance

Table 11 Normalized weights of decision-criteria

Step 6::

The accumulated complex Pythagorean fuzzy N-soft entries of ACPFNSDM are transformed into crisp numerical entries by using score function, as defined in Eq. (8). The evaluated results are further organized in the form of score matrix, as shown in Table 12.

Table 12 Score matrix $\mathfrak {D}$

Step 7::

The selected decision-criteria such as computational efficiency and payload capacity are identified as benefit type criteria whereas investment cost and repeated positioning accuracy are the cost type criteria. The best and worst values relative to the nature of each decision-criterion are computed using Eqs. (9) and (10), respectively and the corresponding results are presented in Table 13.

Table 13 Best and worst values of decision-criteria

Step 8::

The group utility measure, individual regret measure and ranking measure of considered robots are evaluated using Eqs. (11), (12) and (13), respectively. The value of ${\mathcal {Q}}$ corresponding to each alternative robot is calculated by taking the weight of strategy as 0.5 and all the computed results are assembled in Table 14.

Table 14 Values of ${\mathcal {S}},$ ${\mathcal {R}}$ and ${\mathcal {Q}}$ relative to industrial robots

Step 9::

All the industrial robots of the inspected MCGDM problem are systematically ranked in an ascending order on the basis of their computed group utility measure, regret measure and ranking measure. All these hierarchical orderings of the considered robots are highlighted in Table 15.

Table 15 Hierarchical ranking of industrial robots

Step 10::

The industrial robot ${{\mathcal {L}}}_{5}$ is ranked best having minimum value of ranking measure that satisfies the following two conditions of proposed CPFNS-VIKOR method:

$${\mathcal {Q}}({{\mathcal {L}}}_{1}) - {\mathcal {Q}}({{\mathcal {L}}}_{5})=0.64100 - 0.00000 =0.64100 \ge \frac{1}{6-1} =0.2, $$

where robot ${{\mathcal {L}}}_{1}$ is rated at second position with reference to ranking measure.

The robot ${{\mathcal {L}}}_{5}$ is also ranked best with respect to both group utility measure and regret measure.

Thus, we conclude that collaborative robot $({{\mathcal {L}}}_{5})$ will be preferred as the best industrial robot having maximum group utility and minimum individual regret of the opponent.

5 Comparative Analysis

In this section, a comparative study of our developed CPFNS-VIKOR method with contemporary MCGDM method, namely, complex Pythagorean fuzzy VIKOR method, is presented. We analyze the pragmatic application named “selection of industrial robots for automation” by applying the CPF-VIKOR method to validate the authenticity and rationality of our proposed decision-making technique.

5.1 CPF-VIKOR Method

We now investigate an empirical application 4.1 by implementing the methodology of CPF-VIKOR method, proposed by Ma et al. [21].

Step 1::

The appointed decision-makers scrutinize the competency of industrial robots with the assistance of linguistic variables which can be further expressed in terms of CPFNs, as presented in Table 16, obtained by omitting the grades of CPFNSVs in Table 1 and include hesitancy degree $(\kappa ),$ where $\kappa =\sqrt{1-q^{2}-r^{2}}e^{i2\pi \sqrt{1-(\frac{\gamma }{2\pi })^{2}- (\frac{\delta }{2\pi })^{2} }}.$ The linguistic evaluations of the panel of decision-makers relative to considered robots are already illustrated in Table 2.

Table 16 Linguistic terms for ranking of industrial robots

Step 2::

The individual assessments of all decision-making experts regarding capabilities of industrial robots are summarized explicitly in the form of complex Pythagorean fuzzy decision matrices (CPFDMs) ${{\mathcal {K}}}^{(f)}=({\mathbb {K}}_{gh}^{(f)})_{6\times 4}$, as presented in Tables 17, 18 and 19 , respectively.

Table 17 CPFDM of the acquisition manager

Table 18 CPFDM of the operation manager

Table 19 CPFDM of the technical manager

Step 3::

The linguistic variables identified for the rating of nominated decision-makers and selected criteria are illustrated in Table 20. The supreme authorities assign weights to decision-making experts in terms of linguistic variables which are further represented in the form of CPFNs, $\chi _{f}=(\mu _{f}, \lambda _{f}, \kappa _{f} )=(q_{f}e^{i\gamma _{f}}, r_{f}e^{i\delta _{f}}, s_{f}e^{i\tau _{f}}).$ Then, the normalized weight $\zeta _{f}$ for each decision-maker can be evaluated using following formula:

$$\begin{aligned} \zeta _{f}=\frac{ q_{f} + s_{f} \big (\frac{q_{f}}{q_{f} ~+~ r_{f}}\big ) + \big (\frac{\gamma _{f}}{2\pi } \big ) + \big (\frac{\tau _{f}}{2\pi } \big ) \Big (\frac{\frac{\gamma _{f}}{2\pi }}{ \frac{\gamma _{f}}{2\pi }~+~ \frac{\delta _{f}}{2\pi } } \Big ) }{ \sum \limits _{f=1}^{l} \bigg (q_{f} + s_{f} \big (\frac{q_{f}}{q_{f} ~+~ r_{f}}\big ) + \big (\frac{\gamma _{f}}{2\pi } \big ) + \big (\frac{\tau _{f}}{2\pi } \big ) \Big (\frac{\frac{\gamma _{f}}{2\pi }}{ \frac{\gamma _{f}}{2\pi }~+~ \frac{\delta _{f}}{2\pi } } \Big ) \bigg )}. \end{aligned}$$

(14)

The allocated weights of each decision-maker of the panel relative to their importance and expertise are highlighted in Table 21.

Table 20 Linguistic terms for the relative importance of experts and criteria

Table 21 Weightage of experts relative to their importance

Step 4::

The individual perspectives of all decision-making experts of the panel are assembled in order to construct an aggregated complex Pythagorean fuzzy decision matrix (ACPFDM) $\tilde{{\mathcal {K}}}=(\tilde{{\mathbb {K}}}_{gh})_{6\times 4}$ by utilizing the following CPFWA operator:

$$\begin{aligned}&\tilde{{\mathbb {K}}}_{gh} = CPFWA_{\varvec{\zeta }}({{\mathbb {K}}}_{gh}^{(1)}, {{\mathbb {K}}}_{gh}^{(2)}, \ldots , {{\mathbb {K}}}_{gh}^{(l)})\nonumber \\&\quad = \zeta _{1}{{\mathbb {K}}}_{gh}^{(1)} \oplus \zeta _{2}{{\mathbb {K}}}_{gh}^{(2)} \oplus \ldots \oplus \zeta _{l}{{\mathbb {K}}}_{gh}^{(l)}\nonumber \\&\quad =\left( \sqrt{ 1 - \prod \limits _{f=1}^{l}\big ( 1 - \big (\mu _{gh}^{(f)}\big )^{2}\big )^{\zeta _{f}} } e^{i2\pi \sqrt{ 1 - \prod \limits _{f=1}^{l}\big ( 1 - \big (\frac{\gamma _{gh}^{(f)}}{2\pi }\big )^{2}\big )^{\zeta _{f}}}},\right. \nonumber \\&\quad \left. \prod \limits _{f=1}^{l}\big (\lambda _{gh}^{(f)}\big )^{\zeta _{f}} e^{i2\pi \prod \limits _{f=1}^{l}\bigg (\frac{\delta _{gh}^{(f)}}{2\pi }\bigg )^{\zeta _{f}}}\right) .~~~~~~~~~~~ \end{aligned}$$

(15)

The entries $\tilde{{\mathbb {K}}}_{gh}$ of ACPFDM, computed by Eq. (15) are further encapsulated in Table 22.

Table 22 Aggregated complex Pythagorean fuzzy decision matrix

Step 5::

All the decision-making experts independently determine the relative importance of identified decision-criteria in terms of linguistic variables which are further represented in the form of CPFNs, as presented in Tables 9 and 23 . These assigned CPF-weights $\Omega _{h}^{(f)}$ of selected criteria are assembled by applying the following CPFWA operator:

$$\begin{aligned}&{\bar{\Omega }}_{h} = CPFWA_{\varvec{\zeta }}(\Omega _{h}^{(1)}, \Omega _{h}^{(2)}, \ldots , \Omega _{h}^{(l)})\nonumber \\&\quad = \zeta _{1}\Omega _{h}^{(1)} \oplus \zeta _{2}\Omega _{h}^{(2)} \oplus \ldots \oplus \zeta _{l}\Omega _{h}^{(l)}\nonumber \\&\quad =\left( \sqrt{ 1 - \prod \limits _{f=1}^{l}\big ( 1 - \big (\mu _{h}^{(f)}\big )^{2}\big )^{\zeta _{f}} } e^{i2\pi \sqrt{ 1 - \prod \limits _{f=1}^{l}\big ( 1 - \big (\frac{\gamma _{h}^{(f)}}{2\pi }\big )^{2}\big )^{\zeta _{f}}}},\right. \nonumber \\&\quad \left. \prod \limits _{f=1}^{l}\big (\lambda _{h}^{(f)}\big )^{\zeta _{f}} e^{i2\pi \prod \limits _{f=1}^{l}\bigg (\frac{\delta _{h}^{(f)}}{2\pi }\bigg )^{\zeta _{f}}}\right) . \end{aligned}$$

(16)

The aggregate CPF-weights of specified decisive criteria are further normalized by employing the formula, explicated as follows:

$$\begin{aligned} \mathfrak {I}_{h}=\frac{ {\bar{q}}_{h} + {\bar{s}}_{h} \big (\frac{{\bar{q}}_{h}}{\bar{q}_{h} ~+~ {\bar{r}}_{h}}\big ) + \big (\frac{{\bar{\gamma }}_{h}}{2\pi } \big ) + \big (\frac{{\bar{\tau }}_{h}}{2\pi } \big ) \Big (\frac{\frac{\bar{\gamma }_{h}}{2\pi }}{ \frac{{\bar{\gamma }}_{h}}{2\pi }~ + \frac{\bar{\delta }_{h}}{2\pi } } \Big ) }{ \sum \limits _{h=1}^{m} \bigg ({\bar{q}}_{h} + {\bar{s}}_{h} \big (\frac{{\bar{q}}_{h}}{{\bar{q}}_{h} +~ {\bar{r}}_{h}}\big ) + \big (\frac{{\bar{\gamma }}_{h}}{2\pi } \big ) + \big (\frac{\bar{\tau }_{h}}{2\pi } \big ) \Big (\frac{\frac{{\bar{\gamma }}_{h}}{2\pi }}{ \frac{{\bar{\gamma }}_{h}}{2\pi }~+~ \frac{{\bar{\delta }}_{h}}{2\pi } } \Big ) \bigg )}. \end{aligned}$$

(17)

The aggregate CPF-weights ${\bar{\Omega }}_{h}$ and corresponding normalized weights $\mathfrak {I}_{h}$ of conflicting decision-criteria are summarized in Table 24.

Table 23 Weightage of criteria relative to their importance

Table 24 Normalized weights of conflicting criteria

Step 6::

The complex pythagorean fuzzy entries of ACPFDM are defuzzified into crisp entries with the assistance of score function, defined as follows:

$$\begin{aligned} {\mathbb {D}}_{gh}= \tilde{q}_{gh}^{2} - \tilde{r}_{gh}^{2} + \frac{1}{4\pi ^{2}}( \tilde{\gamma }_{gh}^{2} - \tilde{\delta }_{gh}^{2} ). \end{aligned}$$

(18)

The score degrees of all the entries of ACPFDM are accumulated to construct the score matrix $\mathfrak {D}=({\mathbb {D}}_{gh})_{6\times 4},$ as presented in Table 25.

Table 25 Score matrix $\mathfrak {D}$

Step 7::

The decision-criteria such as computational efficiency and payload capacity are classified as benefit type criteria while investment cost and repeated positioning accuracy are the cost type criteria. The best value ${{\mathbb {D}}}^{+}_{h}$ and worst value ${{\mathbb {D}}}^{-}_{h}$ relative to the nature of each decision-criterion can be identified as follows:

$$\begin{aligned} {{\mathbb {D}}}^{+}_{h} = \left\{ \begin{array}{ll} \max \limits _{g}{{\mathbb {D}}}_{gh}, &{} \hbox {if}~ { {\mathfrak {V}}_{h} \in {\mathfrak {V}}_{\mathfrak {B}},} \\ \min \limits _{g}{{\mathbb {D}}}_{gh}, &{} \hbox {if}~ { {\mathfrak {V}}_{h} \in {\mathfrak {V}}_{\mathfrak {C}},} \end{array} \right. \end{aligned}$$

(19)

$$\begin{aligned} {{\mathbb {D}}}^{-}_{h} = \left\{ \begin{array}{ll} \min \limits _{g}{{\mathbb {D}}}_{gh}, &{} \hbox {if}~ { {\mathfrak {V}}_{h} \in {\mathfrak {V}}_{\mathfrak {B}},} \\ \max \limits _{g}{{\mathbb {D}}}_{gh}, &{} \hbox {if }~ {{\mathfrak {V}}_{h} \in {\mathfrak {V}}_{\mathfrak {C}}.} \end{array} \right. \end{aligned}$$

(20)

The best and worst values corresponding to conflicting decisive criterion, computed by using Eqs. (19) and (20) are organized in Table 26.

Table 26 Best and worst values of decision-criteria

Step 8::

The group utility measure ${{\mathcal {S}}}_{g}$ and individual regret measure ${{\mathcal {R}}}_{g}$ of each industrial robot can be evaluated by using following formulas:

$$\begin{aligned} {\mathcal {S}}_{g}=\sum \limits _{h=1}^{m}\mathfrak {I}_{h}\bigg (\frac{{{\mathbb {D}}}_{h}^{+} - {{\mathbb {D}}}_{gh} }{{{\mathbb {D}}}_{h}^{+} - {{\mathbb {D}}}_{h}^{-} }\bigg ), \end{aligned}$$

(21)

$$\begin{aligned} {\mathcal {R}}_{g}=\max \limits _{h}\mathfrak {I}_{h}\bigg (\frac{{{\mathbb {D}}}_{h}^{+} - {{\mathbb {D}}}_{gh} }{{{\mathbb {D}}}_{h}^{+} - {{\mathbb {D}}}_{h}^{-} }\bigg ). \end{aligned}$$

(22)

The ranking measure ${{\mathcal {Q}}}_{g}$ of considered alternative robots can be formulated with the help of ${{\mathcal {S}}}_{g}$ and ${{\mathcal {R}}}_{g}$ by employing the following relation:

$$\begin{aligned} {\mathcal {Q}}_{g}= \alpha ~\bigg (\frac{{{\mathcal {S}}}_{g} - {{\mathcal {S}}}^{+} }{{{\mathcal {S}}}^{-} - {{\mathcal {S}}}^{+} }\bigg ) + (1 - \alpha )\bigg (\frac{{{\mathcal {R}}}_{g} - {{\mathcal {R}}}^{+} }{{{\mathcal {R}}}^{-} - {{\mathcal {R}}}^{+} }\bigg ), \end{aligned}$$

(23)

where

$$\begin{aligned} {{\mathcal {S}}}^{+}&= \min \limits _{g}{{\mathcal {S}}}_{g}, ~~~~{{\mathcal {S}}}^{-}= \max \limits _{g}{{\mathcal {S}}}_{g},\\ {{\mathcal {R}}}^{+}&= \min \limits _{g}{{\mathcal {R}}}_{g}, ~~~{{\mathcal {R}}}^{-}= \max \limits _{g}{{\mathcal {R}}}_{g}. \end{aligned}$$

The computed values of group utility measure, individual regret measure and ranking measure by setting the weight of strategy $(\alpha )$ as 0.5,  are summarized in Table 27.

Table 27 Values of ${\mathcal {S}},$ ${\mathcal {R}}$ and ${\mathcal {Q}}$ relative to industrial robots

Step 9::

All the industrial robots are further organized in an ascending order relative to their computed group utility measure, regret measure and ranking measure and all these hierarchical rankings are demonstrated in Table 28.

Table 28 Hierarchical ranking of industrial robots

Step 10::

The industrial robot ${{\mathcal {L}}}_{5}$ is outranked best having least value of ranking measure that fulfils the following two conditions of CPF-VIKOR method:

$${\mathcal {Q}}({{\mathcal {L}}}_{1}) - {\mathcal {Q}}({{\mathcal {L}}}_{5})=0.639888 - 0.000001 =0.639887 \ge \frac{1}{6-1} =0.2,$$

where robot ${{\mathcal {L}}}_{1}$ is categorized at second position with respect to ranking measure.

The robot ${{\mathcal {L}}}_{5}$ is also outranked best corresponding to both group utility measure and regret measure.

Thus, we infer that collaborative robot $({{\mathcal {L}}}_{5})$ will be selected as the most productive industrial robot having maximum group utility and minimum individual regret of the opponent.

5.2 Comprehensive Discussion

• 1. We exhibit a comparison of the proposed methodology with existing MCGDM techniques, namely, the complex Pythagorean fuzzy TOPSIS (CPF-TOPSIS) method, complex Pythagorean fuzzy VIKOR (CPF-VIKOR) method and Pythagorean fuzzy TOPSIS (PF-TOPSIS) method. This comparative analysis illuminates the remarkable veracity and reliability of the proposed CPFNS-VIKOR method. The consequences of both the proposed and compared techniques are displayed in Table 29.

Table 29 Comparative study

• 2. Both the compared and proposed strategies prioritize ${\mathfrak {L}}_{5}$ as the most bountiful industrial robot for the modernization of the manufacturing industry, which demonstrates the accountability and effectuality of the decision-making specialities of our proposed technique in practical MCGDM problems.

• 3. An interpretative bar chart is plotted in Fig. 4 to visualize the comparative results of both the proposed and compared MCGDM strategies. This visual summary justifies the reliability and potentiality of our developed methodology at a glance.

• 4. The hierarchical outranking of considered industrial robots differ slightly in both proposed and compared techniques which is due to the scrutinization of distinct fuzzy environments as the compared CPF-VIKOR and CPF-TOPSIS techniques merely tackles the uncertainty of periodic data while our developed strategy addresses the ranking based modeling of imprecise two dimensional graded information. In spite of this, the proposed and compared techniques remarkably decipher the coherent final outcome which illustrates the enforceability of the proposed technique.

• 5. Our developed strategy has an edge over the compared strategies as it convincingly handles the ambiguity of both CPF and PF data by omitting their respective grades and phase terms of CPFNSVs and display the similar end-result as identified by existing compared strategies. This incredible peculiarity of our developed technique models it as the most generalized and productive decision-making strategy for real-world MCGDM problems.

• 6. The compared CPF-TOPSIS and CPF-VIKOR methods have no robust capability to address the complex Pythagorean fuzzy N-soft information because of its shortcomings that arise due to the ineffectuality of multinary assessment grades. However, our proposed CPFNS-VIKOR strategy has potentially resolved these deficiencies of compared techniques by capturing the graded evaluations of imprecise and inaccurate information. Therefore, the flexibility of our developed methodology makes it superior and stronger as compared to the existing strategies.

Fig. 4

Comparative analysis

6 Merits of the Proposed CPFNS-VIKOR Method

Next, we summarize the main assets of the framework that we have presented.

• 1. The methodology of the proposed multi-criteria optimization technique produces an innovative stance of the VIKOR method thanks to the modeling abilities of the hybrid CPFNS model. The fuzziness and periodicity of graded parameterized data can be addressed simultaneously in a convincing manner.

• 2. The CPFNS-VIKOR method makes full utilization of a very general mathematical framework for the identification of compromise solution. To that purpose, it focuses on the maximization of group utility and minimization of individual regret of the opponent. This is done after examining the given set of alternatives, relative to conflicting decision-criteria.

• 3. This strategy analyzes the suitability of the alternatives by independently considering conflicting factors of both cost type and benefit type decision-criteria. Because of this cost-benefit analysis, the end-results and final outcomes are more precise and authentic as compared to existing MCGDM techniques.

• 4. In the modern digital era, ranking systems have gained popularity as they are extensively used for the grading of electronic services, movies, marketing sites, video-games and many other online applications. The technique proposed in this paper is especially designed for the analysis of such ranking-based models of imprecise information of periodic nature to meet the future needs constructively.

• 5. The range of applications of our proposed MCGDM technique is not confined to the case of two-dimensional graded data. This strategy shows similarly accurate results when implemented with one dimensional ranked data inclusive of PFNS-data and IFNS-data. One just need to omit the phase terms accross the specifications. Thus our proposed strategy is a versatile and rational decision-making tool that successfully tackles both traditional and two dimensional fuzzy data with precision.

7 Conclusion

VIKOR is one of the most compelling multi-criteria optimization techniques, which prioritizes the set of alternatives in a rational hierarchical order by analyzing their weighted proximity from ideal solutions. The agenda of this strategy focuses on the specification of a compromise solution that examines the suitability of the available alternatives relative to the conflicting criteria which are pertinent to the problem. It has gained popularity as it is amply used in a wide range of decision-making problems of various disciplines including medical sciences, engineering, business administration, and automotive, logistics and aeronautical industries. In this research article, we have established a novel decision-making technique consisting of a CPFNS-VIKOR method along with an interpretative flow chart. Its target is to analyze the real life MCGDM problems posed in terms of complex Pythagorean fuzzy N-soft information. To this purpose, it determines the optimal feasible alternative by maximizing the group utility and minimizing the individual regret of the opponent on the basis of specific benefit type and cost type decision-criteria. This versatile, quite general strategy takes advantage of a powerful mathematical tool for the modeling of two-dimensional ambiguous information introduced in [43].

In the proposed CPFNS-VIKOR method, we have collected the linguistic individual assessments of the experts regarding the competence of the alternatives and the priorities of decisive criteria. The CPFNSWA operator then merges these linguistic individual appraisals. We have formulated the ranking measure by dint of group utility and regret measures which determine the hierarchical outranking of the alternatives under consideration.

Another substantial contribution of this study is the implementation of the proposed methodology on a heuristic application for the selection of constructive industrial robots. This authenticates the remarkable potentiality and feasibility of this developed technique. In addition, we have conducted a comparative analysis with the existing CPF-TOPSIS, CPF-VIKOR and PF-TOPSIS methods to justify the admirable rationality of the proposed strategy. We have comprehensively discussed the comparative study with the assistance of a bar chart in order to demonstrate the consistency of the results of the developed strategy. Finally, we have dwelled on its merits and advantages over other existing techniques.

This newly established CPFNS-VIKOR method is a robust extension of modern generalized MCGDM strategies that can address the ambiguous human thoughts from more limited perspectives. It has an edge over existing decision-making approaches, as it skilfully resolves their restricted representability abilities by the recourse to the rating-based fuzzy modeling of parameterized data, and with this information it is able to specify the feasible solution that ideally satisfies all conflicting criteria of an optimization problem.

Although the developed methodology has a large ability to capture the graded descriptions of ambiguous knowledge-based systems, it is nonetheless true that this theory has some difficulties that originate when the experts submit evaluations for which the square sum of amplitude and phase terms of both membership and non-membership degrees exceed 1. The decision-making scope of the technique proposed in this work is thus restrained to model real-world MCGDM problems within a confined boundary space. To overcome this issue, in the future we are planning to establish more flexible mathematical structures which should enable us to capture a significantly wider range of evaluations. Additionally, we believe that our research work will allow us to generalize other MCGDM techniques so that we can establish the CPFNS-PROMETHEE method, CPFNS-AHP method, CPFNS-ELECTRE I and CPFNS-ELECTRE II methods. They should provide additional empirical applications of the promising CPFNS model.