1 Introduction

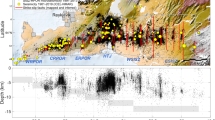
Since the 2018 MW 6.4 (ML 6.2) Hualien earthquake occurred (cf. Rau and Tseng 2019), high seismicity in the Hualien region has persisted for a while (also refer to the Central Weather Bureau (CWB); https://scweb.cwb.gov.tw/en-US). More than a thousand aftershocks (ML ≥ 2) followed the 2018 event within 3 months. Close behind the 2018 event, the Xiulin earthquake with MW 6.2 (ML 6.3) occurred approximately 18 km southeast of the 2018 event, on April 18, 2019 (cf. Lee et al. 2020). Soon after the 2019 event, the Shoufeng earthquake, an MW 5.2 (ML 5.7) event, occurred on February 15, 2020, approximately 22 km south of the 2019 event (see Fig. 1). Approximately 1 year later, on April 18, 2021, an ML 5.8 earthquake occurred again in the Shoufeng region, Hualien; 3 min later, an ML 6.2 earthquake (refined to be 6.26) occurred almost at the same location as the ML 5.8 event (Fig. 1). Subsequently, approximately 500 aftershocks occurred. At first, the aftershocks were distributed around the ML 5.8 and ML 6.2 events; later, the aftershocks were distributed eastwards and became shallower (≤ 10-km depth). The two moderate-sized earthquakes seemed to feature a similar plane along a NE-SW strike based on the focal mechanisms (Fig. 1). The cross-section of the earthquake sequence along line BB′ in Fig. 1 indicated a west-dipping plane, which might be the fault plane for the two 2021 events. In this study, we did not analyze the rupture features of the ML 5.8 and ML 6.2 Shoufeng earthquakes but investigated the source parameters of the earthquake sequence, including the seismic moment (M0), radiated seismic energy (ES), and moment magnitude (MW). Examining the ML 5.8 and ML 6.2 Shoufeng earthquakes’ rupture feature would be a separate issue.

Fig. 1
figure 1

(Left) Map showing the tectonic setting of the Taiwan region. Several moderate and large earthquakes compared with the Shoufeng earthquake sequence are also plotted. (Middle) Seismicity in the Shoufeng region, Hualien County, Taiwan. The red-tone circles denote aftershocks occurring before June 8, 2021; the blue-tone circles show aftershocks occurring after June 8, 2021. The stars indicate the two 2021 Shoufeng earthquakes and several moderate-sized earthquakes occurring around the source area of the 2021 events. Also included are the focal mechanisms reported from the BATS (IES 1996). (Right) AA′ and BB′ profiles reveal that these events are distributed at different depths (< 25 km). The cross-section of these events along line BB′ shows a west-dipping plane, which might be the fault plane of the two 2021 events

Full size image

For earthquakes, ES is one of the key source parameters needed to understand dynamic rupture because ES is strongly related to static stress drop (Δσ), dynamic stress drop (Δσd), and fracture energy (Eg) (cf. Kanamori and Heaton 2000; Kanamori 2001). Here, Δσ and Δσd are defined as σ0–σ1 and σ0–σf, where σ0, σ1, and σf are the initial stress, final stress, and frictional stress, respectively; Eg is the erergy that extends the fault during the earthquake. A derivative parameter called scaled energy, which is defined as the ratio of ES to M0, is often used to indicate the friction drops during the earthquake rupture (Kanamori and Heaton 2000) and also represents the average stress drop on the fault plane (Houston 1990; Kanamori et al. 1993). For large earthquakes, ES/M0 is almost equal to a constant, 5 × 10−5 (Kanamori 1977); however, Ide and Beroza (2001) reported a ES/M0 of 3 × 10−5 for a wide M0 range. For small earthquakes, ES/M0 is approximately 10–100 times smaller than large earthquakes (Abercrombie 1995; Mayeda and Walter 1996; Kanamori and Heaton 2000). Generally, ES can be calculated through the integral of velocity-squared seismograms after certain appropriate corrections are made (cf. Boatwright and Choy 1986; Newman and Okal 1998; Kanamori et al. 1993; Venkataraman et al. 2006). Although ES only represents a portion of strain energy (W) released during an earthquake and is approximately 10% less than W (McGarr 1999), it is a key source parameter for understanding earthquakes’ dynamic ruptures.

Gutenberg and Richter (1956) constructed a relationship between surface magnitude (MS) and logES as logES = 1.5MS + 4.8 (ES in Nm). This indicates that logES is proportional to 1.5MS. Such a relation is capable of being theoretically verified (Kanamori and Anderson 1975). However, most studies have revealed that logES is proportional to 2.0ML (Thatcher and Hanks 1973; Seidl and Berckhemer 1982; Kanamori et al. 1993; Dineva and Mereu 2009). Deichmann (2018a) further confirmed that logES scales as 2.0ML by using numerical simulations. In Taiwan, Huang (2003) first used regional broadband seismic data to establish the relationship between logES and ML, indicating that logES ∝ 2.0ML. Chan et al. (2020) also obtained logES ∝ 2.0ML for the 2019 Xiulin earthquake sequence. In addition, the observed scale between MW and ML (MW:ML) ranges from 1:0.67 to 1:1.5 (Hanks and Kanamori 1979; Margaris and Papazachos 1999; Wu 2000; Wu et al. 2005; Chen et al. 2009; Grünthal et al. 2009; Sargeant and Ottemöller 2009; Bethmann et al. 2011; Zollo et al. 2014; Deichmann 2017; Munafò et al. 2016; Malagnini and Munafò 2018; Mereu 2020). For Taiwan’s earthquakes, Wu et al. (2005) obtained MW ∝ ML; however, Chen et al. (2009) derived MW ∝ 1.25ML. Regarding the Shoufeng earthquake sequence, what is the relation between MW and ML? Hence, in this study, we not only calculated ES for the 2021 Shoufeng earthquake sequence from near-field broadband seismograms but also constructed the logES–ML relationship to infer whether logES ∝ 2.0ML does or does not hold. Furthermore, several relations between source parameters were also discussed, namely the ES–M0, logM0–ML, and MW–ML relations. Such analysis can be used to systemically examine the relationships among source parameters for earthquakes in Taiwan in the future.

2 Data

Velocity seismograms from the Broadband Array in Taiwan for Seismology (BATS; Institute of Earth Sciences (IES), Academia Sinica, Taiwan 1996) were adopted to analyze the radiated seismic energy (ES) of the two moderate-sized earthquakes and their aftershocks occurring in the Shoufeng region, Hualien County, Taiwan. To reduce the effect of complicated structures on wave propagations, we only used data with epicentral distances of less than 50 km. Therefore, the seismic waves propagated approximately within a half-space material (Kanamori 1990). ES is mainly expressed in the S-wave, so ES is generally estimated through the S-wave (cf. Boatwright and Fletcher 1984; Kanamori et al. 1993; Venkataraman et al. 2006). However, it would be not easy to determine the S-wave train when using near-field seismograms. For this reason, we derived ES from only P-waves. Finally, the ES values from P-waves would be corrected to obtain the total energy by introducing energy partitioning between the P and S waves (Boatwright and Choy 1986; Newman and Okal 1998). Because of noise interference, for stably calculating ES, seismograms from various ML were filtered by different frequency bands. Here, a noise test was first made to determine the frequency band for filtering. Figure 2 provides an example of a noise test at station NACB for 2.5 < ML < 4.5 events. We summarized the noise test from each station. Finally, for events with ML ≥ 4.0, the frequency band for filtering was 0.1–10 Hz; for events with 3.5 ≤ ML < 4.0, we used 1–10 Hz to filter these seismograms; the events with 3.0 ≤ ML < 3.5 were filtered from 2 to 10 Hz; for events with 2.5 ≤ ML < 3.0, the band-pass filter with frequencies between 3 and 8 Hz was employed.

Fig. 2
figure 2

Example of noise test at station NACB for 2.5 < ML < 4.5 events to examine the frequency range (FR) used for the follow-up analysis. Obviously, small-sized events have a relatively narrow FR. For ML ≥ 4.0, 3.5 ≤ ML < 4.0, 3.0 ≤ ML < 3.5, and 2.5 ≤ ML < 3.0 events, FR = 0.1–10 Hz, 1–10 Hz, 2–10 Hz, and 3–8 Hz, respectively

Full size image

3 Methods

3.1 Radiated seismic energy (ES)

Radiated seismic energy from the P-wave, called \(E_{S}^{P}\), is measured using the integration of the squared velocity records (\(v\left( t \right)^{2}\)) from a given station (cf. Boatwright and Fletcher 1984; Kanamori et al. 1993), as follows:

$$E_{S}^{P} = 4\pi r^{2} \rho \alpha \frac{{\langle R\rangle^{2} }}{{R^{2} }}\mathop \smallint \limits_{{t_{a} }}^{{t_{b} }} v\left( t \right)^{2} {\text{d}}t,$$
(1)

where \(\alpha\) and \(\rho\) are the P-wave velocity and the density at the source area, respectively; \(r\) is the hypocentral distance, representing the geometrical spreading for seismic-wave propagation; \(t_{a}\) and \(t_{b}\), determined manually, are the time band for integration; \(R\) is the radiation pattern depending on the focal mechanism; \(\langle R\rangle\) is the average radiation pattern over a focal sphere and equates to 0.52 for the P-wave (Aki and Richards 2002). In Eq. (1), \(\frac{{\langle R\rangle^{2} }}{{R^{2} }}\) is assumed to be 1.0 by using the average radiation patterns for all stations, as proposed by Kanamori et al. (1993).

Before calculating \(E_{S}^{P}\), several corrections to the P-waves needed to be made, including correcting the effects of the free surface and attenuation. The free surface effect was calculated using the incident angle of the P-wave to the receiver (cf. Okal 1992; Aki and Richards 2002), and \(t^{*} = 0.029\) was employed to correct the P-wave attenuation from source to receiver following the work of Chan et al. (2020) (also see 5.). Finally, the total radiated seismic energy (ES), the sum of the P-wave energy (\(E_{S}^{P}\)) and the S-wave energy (\(E_{S}^{S}\)) was calculated as follows:

$$E_{S} = E_{S}^{P} + E_{S}^{S} = \left( {1 + q} \right)E_{S}^{P} ,$$
(2)

where \(q\) is the ratio of the S-wave energy to the P-wave energy and is defined as \(1.5\left( {\frac{\alpha }{\beta }} \right)^{5}\) and \(\alpha\) and \(\beta\) are the P-wave and S-wave velocities at the source, respectively. For a Poisson material, \(q\) is equal to 23.4 due to \(\alpha = \sqrt 3 \beta\). Many observations also show \(q\) varying between 9 and 25 (cf. Shearer 2009). In this study, the travel times of the P-waves and S-waves were estimated from source to station for each earthquake to obtain the average \(\alpha\) and \(\beta\) values, which were used to calculate \(q\). Finally, for a given earthquake, we calculated the average of the available ES values from each station to be the ES of the event.

In theory, ES should be estimated over a frequency range of 0–∞ Hz; however, in practice, ES is generally calculated at a finite frequency bandwidth and is apt to be underestimated (Di Bona and Rovelli 1988; Ide and Beroza 2001; Wang 2004). Therefore, the finite frequency bandwidth limitation needs correcting, especially for high-frequency parts. Such correction is dependent on the corner frequency.

3.2 Corner frequency (f c) and seismic moment (M0)

For correcting the finite frequency bandwidth limitation in the calculation of ES, we first derived the corner frequency (fc) from the displacement and velocity P-waves. According to the ω−2 source model (Aki 1967; Brune 1970), Andrews (1986) derived fc as follows:

$$f_{c} = \frac{1}{2\pi }\sqrt {\frac{{I_{v} }}{{I_{d} }}} ,$$
(3)

where \(I_{v} = \mathop \smallint \limits_{{t_{a} }}^{{t_{b} }} v^{2} \left( t \right)dt\) and \(I_{d} = \mathop \smallint \limits_{{t_{a} }}^{{t_{b} }} d^{2} \left( t \right)dt\). \(v\left( t \right)\) and \(d\left( t \right)\) are the observed velocity and displacement P-waves, respectively. \(t_{a}\) and \(t_{b}\) are the time band for integration. In the ω−2 source model, fc is defined as the crossover frequency between the low- and high-frequency spectra. For f < fc, the spectrum is approximately a constant; for f > fc, the spectrum decays with f−2 (also see 5.).

Seismic moment (M0) is expressed in the following form:

$$M_{0} = \frac{{4\pi r\rho \alpha^{3} \Omega_{0} }}{\langle R\rangle},$$
(4)

where \({\Omega }_{0} = 2I_{v}^{ - 1/4} I_{d}^{3/4}\) is the low-frequency spectral level (Andrews 1986); \(\langle R\rangle = 0.52\) for the P-wave; \(\alpha\) and \(\rho\) are the P-wave velocity and density at the source area, respectively. Before calculating \({\Omega }_{0}\), the effects due to the free surface and attenuation on the P-waves were corrected. For a given earthquake, we averaged the available M0 calculated from each station to be the M0 of this event.

3.3 Finite frequency bandwidth correction

On the basis of Parseval’s theorem, the integral of the square of a time function is equivalent to that of the square of its spectrum, that is, \(I_{v} = \mathop \smallint \limits_{ - \infty }^{\infty } v^{2} \left( t \right)dt = \mathop \smallint \limits_{ - \infty }^{\infty } V^{2} \left( f \right)df\), where \(V\left( f \right)\) is the Fourier transform of \(v\left( t \right)\). Because of the finite frequency bandwidth used for the observed P-waves, the real integrals are as follows:

$$I_{v} = \mathop \smallint \limits_{{f_{l} }}^{{f_{u} }} V^{2} \left( f \right)df = \kappa_{v} \mathop \smallint \limits_{ - \infty }^{\infty } V^{2} \left( f \right)df,$$
(5)

where \(f_{l}\) and \(f_{u}\) are the integral range with \(f_{l} < f_{c} < f_{u}\), and \(\kappa_{v}\) (≤ 1.0) is the proportion of finite ES (observation) to full ES. Here, \(\kappa_{v}\) is expressed in the following form (cf. Ide and Beroza 2001; Wang 2004):

$$\kappa_{v} = \frac{2}{\pi }\left[ { - \frac{{\left( {\frac{{f_{u} }}{{f_{c} }}} \right)}}{{1 + \left( {\frac{{f_{u} }}{{f_{c} }}} \right)^{2} }} + \frac{{\left( {\frac{{f_{l} }}{{f_{c} }}} \right)}}{{1 + \left( {\frac{{f_{l} }}{{f_{c} }}} \right)^{2} }} + \tan^{ - 1} \frac{{f_{u} }}{{f_{c} }} - \tan^{ - 1} \frac{{f_{l} }}{{f_{c} }}} \right].$$
(6)

Ide and Beroza (2001) indicated that over 80% of the radiated seismic energy is created from high frequencies larger than the corner frequency. Because ES should be calculated over an infinite frequency, the observed ES from a finite frequency should be corrected by \(\kappa_{v}\), that is \({\text{E}}_{{{\text{SC}}}} = {\text{E}}_{{\text{S}}} /\kappa_{v}\), where ESC is the corrected ES. In other words, through \(\kappa_{v}\), we can restructure ES for a given earthquake.

4 Results and discussion

4.1 ES versus ML

Figure 3 displays a plot of logES versus ML for 2.5 < ML < 5.5 and the ML 5.8 and ML 6.2 events. The ML values were from the earthquake catalog of the CWB, which routinely reports earthquake parameters in Taiwan. From Fig. 3, ES increased with increasing ML, and a linear relationship between logES and ML was present for 2.5 < ML < 5.5 events as logES = 1.99 ML + 2.06 (ES in Nm). The empirical relation initially derived from 2.5 < ML < 5.5 events seemed to be able to predict ES for the ML 5.8 and ML 6.2 events. Therefore, by incorporating the two 2021 events into the regression, we obtained the logES–ML relation as follows.

$$\log {\text{E}}_{{\text{S}}} = (1.98 \pm 0.05){\text{ M}}_{{\text{L}}} + (2.11 \pm 0.17)\left( {{\text{E}}_{{\text{S}}} \;{\text{in}}\;{\text{Nm}}} \right)\;{\text{for}}\;2.5 < {\text{M}}_{{\text{L}}} < 6.3.$$
(7)
Fig. 3
figure 3

Relation between logES and ML, where ES is the radiated seismic energy and ML is the local magnitude. The logES–ML relation has a slope of 1.98; therefore, logES is almost proportional to 2.0ML. For comparison, also included in this plot are the ES of several earthquakes in Taiwan (IRIS DMC 2013; Venkataraman and Kanamori 2004; Wang 2004; Hwang 2012; Hwang et al. 2019, 2022; also see Table 1). The blue dashed lines denote the standard deviations

Full size image

Our results agreed well with logES ∝ 2.0ML and are similar to the logES–ML relation, that is, logES = 1.96ML + 9.05 (Es in erg), proposed by Kanamori et al. (1993) for 1.5 < ML < 6.0 earthquakes in southern California. Likewise, Chan et al. (2020) analyzed ES for the 2019 Xiulin earthquake sequence to reveal logES ∝ 2.0ML for 2.5 < ML < 4.3 events. Many previous studies have also indicated that logES ∝ 2.0ML holds at different ML ranges, from 1 to 7 (Thatcher and Hanks 1973; Seidl and Berckhemer 1982; Kanamori et al. 1993; Dineva and Mereu 2009).

ML is determined using seismograms recorded by Wood–Anderson seismographs (Richter 1935) and proportional to M0 (Randall 1973; Deichmann 2006). Then, logES will scale as 1.5ML following source self-similarity (Aki 1967; Kanamori and Anderson 1975). However, from numerical simulations for − 1 ≤ ML ≤ 6, Deichmann (2018a) further stated what conditions are valid for logES ∝ 2.0ML. For small earthquakes (ML ≤ 3.0), logES ∝ 2.0ML is inevitable because earthquake duration approaches constant; for larger earthquakes, it happens to be consistent with the logES–2.0ML relation because of the effect of the Wood–Anderson response when calculating ML (Deichmann 2018a). Chan et al. (2020, 2021) investigated the logES–ML relation for the 2019 Xiulin aftershocks (2.5 ≤ ML < 4.3) to obtain logES ∝ 2.0ML as well as to find the constant-tending duration for those small events. Although Malagnini and Munafò (2018) noted a crossover magnitude at approximately ML = 4.3 for the MW–ML relation, where MW is the moment magnitude (Kanamori 1977; Hanks and Kanamori 1979), logES was still proportional to 2.0ML for a wide ML range (1–7; Thatcher and Hanks 1973; Seidl and Berckhemer 1982; Kanamori et al. 1993; Dineva and Mereu 2009).

Kanamori et al. (1993) concluded that ML < 6.5 events do not saturate with increasing ES because the derived relationship could not predict the ES of the 1992 ML 6.8 (Mw 7.3) Landers earthquake. Similarly, from the 2019 Xiulin aftershocks, the logES–ML relationship, analyzed by Chan et al. (2020), also failed to predict the ES of the 2019 ML 6.3 Xiulin earthquake (mainshock). Figure 3 also illustrates the ES values for several ML > 6 earthquakes in Taiwan (Venkataraman and Kanamori 2004; Wang, 2004; Hwang 2012; Hwang et al. 2019, 2022; Table 1). The derived ES–ML relation does not seem to satisfactorily predict the ES values for ML larger than 6.3 other than the ES of the 1999 Chi–Chi earthquake from Wang (2004). This also implies that ML saturates for events with ML > 6.3. Besides, whether a difference exists between the eastern and western fault systems for the ES–ML relation is worth investigating further.

Table 1 Source parameters for moderate and large earthquakes in Taiwan
Full size table

4.2 ES versus M0

Figure 4 displays a comparison of M0 from the BATS and M0 from this study for ML > 3.5. The two M0 values have high consistency, indicating that our estimations of M0 through the method of Andrews (1986) are valid (Kao et al. 1998; IES 1996). Such analysis has the advantage of calculating M0 for small earthquakes.

Fig. 4
figure 4

Comparison of M0 from the BATS and M0 from this study for ML > 3.5. M0 derived from the method of Andrews (1986) coincides with that determined from the BATS using moment tensors inversion

Full size image

ES is a dynamic source parameter and can describe the stress state and friction drops during an earthquake (Houston 1990; Kanamori et al. 1993; Kanamori and Heaton 2000). A low ES/M0 shows that the friction drops gradually during faulting; however, a high ES/M0 denotes the fact that the friction drops rapidly. Then, it would result in various stress drops, including static and dynamic stress drops. Therefore, the ES/M0 ratio provides a measurement of the average stress drop on the fault. Figure 5 illustrates the plot of ES vs. M0. As can be seen, ES increases with increasing M0. Additionally, ES/M0 also varies with ML for the earthquake sequence, as displayed in the inset of Fig. 5. On average, for 2.5 < ML < 3.5, 3.5 < ML < 4.5, and ML > 4.5, ES/M0 is 5.3 × 10−6, 6.3 × 10−5, and 2.7 × 10−4, respectively. Except that ES/M0 = 6 × 10–5 for 3.5 < ML < 4.5, the others differ from the global observations of 5 × 10−5 (Kanamori 1977) and 3 × 10−5 (Ide and Beroza 2001). Although the ratio ES/M0 in this study reveals differences to the global values, variations in ES/M0 with ML (or MW) have also been observed in many other studies (e.g., Abercrombie 1995; Mayeda and Walte 1996; Kanamori and Heaton 2000). When ignoring the fracture energy, the corresponding Orowan stress drop, defined as \(\Delta \sigma = 2\mu \frac{{E_{S} }}{{M_{0} }}\), where \(\mu\) is the rigidity (Orowan 1960; Houston 1990; Kanamori et al. 1993), varies from 3 (small events) to 40 and 160 (larger events) bar on average. In other words, the ES/M0 ratio reveals the strength heterogeneities on the fault plane.

Fig. 5
figure 5

The ES–M0 plot. ES increases with increasing M0. ES/M0 = 5 × 10−5 is from Kanamori (1977) for large earthquakes, and ES/M0 = 3 × 10−5 is estimated by Ide and Beroza (2001) for a wide M0 range. The insert illustrates the relation between ES/M0 and ML. On average, ES/M0 = 5.3 × 10−6, 6.3 × 10−5, and 2.7 × 10−4 for 2.5 < ML < 3.5, 3.5 < ML < 4.5, and ML > 4.5, respectively. This reveals that the Orowan stress drops are approximately 3, 40, and 160 bar for different ML range, respectively

Full size image

In theory, the difference in Es/M0 between ML < 4.0 and ML > 4.0 events might be interpreted in a simple stress-drop model (cf. Kanamori and Heaton 2000). Following Kanamori and Heaton (2000), the Es/M0 ratio is proportional to (1 − Dc/D), where Dc is the critical distance and D is the total slip on the fault plane. For small earthquakes, Dc is comparable with D to have a large Dc/D, resulting in a low Es/M0 ratio; by contrast, for large earthquakes, there is a small Dc/D due to the fact that frictional melting or fluid pressurization is likely to occur during an earthquake rupture. Then, it would have a high ES/M0. In other words, for a given M0, a high Dc/D has less ES released; reversely, a low Dc/D has more Es released. In fact, the value of Dc is not apt to be observed, especially for small earthquakes. The discrepancy in ES/M0 shows different rupture dynamics for small and large earthquakes.

4.3 M0 versus ML and MW versus ML

Both M0 and ML represent the earthquake size. Therefore, logM0 should scale as ML. That is, logM0 increases with increasing ML. Figure 6A illustrates logM0 varying with ML for the Shoufeng earthquake sequence. Another scale denoting earthquake size is the moment magnitude (MW), defined as MW = (2/3)logM0 − 6.07 (M0 in Nm; Kanamori 1977; Hanks and Kanamori 1979). Figure 6B displays the relationship between MW and ML. MW is generally smaller than ML, as noted by Wu et al. (2005). Because the M0–ML and MW–ML relations are two sides of a single entity, some interpretations mainly depend on the MW–ML relation. From Fig. 6, a magnitude turning point can be detected at ML = 4.0. Subsequently, the MW–ML relation was determined as follows:

$${\text{M}}_{{\text{W}}} = (0.67 \pm 0.03){\text{M}}_{{\text{L}}} + (0.74 \pm 0.08)\;{\text{for}}\;{\text{M}}_{{\text{L}}} < 4.0,$$
(8)
$${\text{M}}_{{\text{W}}} = (1.00 \pm 0.05){\text{M}}_{{\text{L}}} {-}(0.51 \pm 0.25)\;{\text{for}}\;{\text{M}}_{{\text{L}}} > 4.0.$$
(9)
Fig. 6
figure 6

The plots of A M0 vs. ML and B MW vs. ML. Also shown are several moderate and large Taiwan earthquakes whose M0 and MW are from the U.S. Geological Survey (USGS). A crossover magnitude appears at ML = 4.0, which divides the M0–ML and MW–ML relations into two parts. The relations indicate that ML likely saturates for ML > 6.3

Full size image

Equations (8) and (9) are dissimilar to the MW ∝ 1.25ML from Chen et al. (2009) for ML > 3.5 earthquakes in Taiwan. However, Wu et al. (2005) obtained MW ∝ ML and concluded that ML is, on average, approximately 0.2 units larger than MW for ML > 4.5 earthquakes. This is comparable with Eq. (9), in which ML is 0.5 units larger than Mw. In addition, two studies of Taiwan’s earthquakes with ML > 4.5 expressed the M0–ML relations as logM0 ∝ 1.6ML (Wang et al. 1989) and logM0 ∝ 1.27ML (Chen et al. 2007), corresponding to MW ∝ 1.07ML and MW ∝ 0.85ML. One other study using finite-fault inversion for ML > 5 earthquakes in Taiwan reported logM0 ∝ 1.6ML, that is, MW ∝ 1.07ML (Wu 2000). The MW–ML relations from Wang et al. (1989) and Wu (2000) are similar to Eq. (9). However, using all information, we obtained Mw ∝ 0.82·ML, similar to Chen et al.’s result (Chen et al. 2007) when ignoring the magnitude turning point as addressed in Eqs. (8) and (9). Additionally, a remarkable feature in Fig. 6(A) is that the derived M0–ML relation could not predict the M0 for ML > 6.3 events. This indicates ML saturation beyond ML 6.3.

The MW–ML relation from this study is consistent with that from Malagnini and Munafò (2018), which analyzed the earthquakes of the central and northern Apennines and noted a crossover magnitude at approximately ML = 4.3 for the MW–ML relation. Their results proposed that Mw ∝ 0.67ML for ML < 4.3 and MW ∝ 1.28ML for ML > 4.3. For small earthquakes (below ~ ML 4.0), Mw scaled as 0.67ML, in agreement with Munafò et al. (2016) and our results. By contrast, for larger earthquakes, the results from this study differed from those of Malagnini and Munafò (2018). Munafò et al. (2016) proposed an invariant source duration to interpret MW ∝ 0.67ML for ML < 4.0. Here, we attempted inferring what condition is valid for the derived MW–ML relation. Starting with a simple idea, we assumed an isosceles triangle source time function (moment rate function) with the maximum amplitude A and duration T (also refer to Deichmann 2018b). The integral (area) of the source time function denotes M0; then, M0 ∝ AT; that is, logM0 ∝ logA + logT. Here, two scenarios are considered. First, let M0 ∝ T3, then logM0 ∝ 3logT or logT ∝ (1/3)logM0. These relations result in logM0 ∝ (3/2)logA. Following the definition of ML (Richter 1935), ML is proportional to logA; then, logM0 ∝ (3/2)ML. Finally, ML ∝ MW. Subsequently, if T is assumed to be independent of M0, logM0 will scale as logA, leading to logM0 ∝ ML. Finally, ML ∝ (2/3)MW is obtained. Conversely, if ML ∝ MW is observed, it implies that M0 ∝ T3; if ML ∝ (2/3)MW is obtained, it implies that T is invariant.

As a rule, the M0 ∝ T3 relation is based on the source self-similarity, in which the static stress drop (Δσ) is not related to M0 (cf. Aki 1967; Kanamori and Rivera 2004). Kanamori and Rivera (2004) proposed that the M0 ∝ T3 relation may not necessarily obey the source self-similarity. Another possibility for M0 ∝ T3 is under the condition that ΔσVr3 = constant, where Vr is the rupture velocity (Kanamori and Rivera 2004; Hwang et al. 2020). That is, both source self-similarity and ΔσVr3 = constant can make M0 ∝ T3 hold. Of course, to verify this, it is necessary to probe into how T varies with M0 from observations.

5 Conclusions

By systemically analyzing the source parameters for the 2021 Shoufeng earthquake sequence, we obtained several regression relations among these parameters, including the ES–ML, ES–M0, M0–ML, and MW–ML relations. A crossover magnitude, detected at ML = 4.0, divided the M0–ML and MW–ML relations into two parts, but logES was still proportional to 2.0ML for 2.5 < ML < 6.3. Such results indicated variation between source duration and M0 for the 2021 Shoufeng earthquake sequence. On average, a relatively large ES/M0 ratio and high Orowan stress drop were present for ML > 4.5 events. That is, the stress state at the source area exhibited variation with earthquake size.