1 Introduction

High heat flux thermal management systems are used in various industries such as air conditioning, electronics, and automotive. Two-phase condensing flows are widely used in these systems. For this reason, researchers have paid much attention to estimating heat transfer and pressure drop in condensing flows.

Different models have been used to investigate the pressure drop in condensing and adiabatic flows. Most researchers have used the homogeneous model and the separated-flow model to predict the pressure drop, and some have used the least-squares fitting method. In the homogeneous model, it is assumed that the two phases are well mixed and move at the same velocity; therefore, they can be considered as a single-phase flow. This model works better near the critical point and the mass velocities of two-phase flow larger than 2000 Kg/m2s [1, 2]. In the separate-flow model, it is assumed that each phase has its own properties and velocity. In this model, the two-phase frictional pressure drop is related to the pressure drop of the individual flow of liquid or vapor in the channel [3].

The above methods have been used to develop correlations for two-phase frictional pressure drop. For example, Friedel [4] provided a correlation for frictional pressure drop during the two-phase flows of air-oil, air-water, and refrigerant R12 in channels with diameters larger than 4 mm using a database with 25,000 samples. Müller-Steinhagen and Heck [5] presented a simple frictional pressure drop correlation using 9300 data on two-phase flows of refrigerants, hydrocarbons, water, and air-water in channels with diameters in the range of 4–392 mm. Some researchers have attempted to provide correlations covering a vast range of working fluids, hydraulic diameters, and mass velocities. A universal frictional pressure drop correlation for condensing and adiabatic flows was developed by Kim and Mudawar [6]. The used database included 7115 samples, 17 working fluids, mass velocities in the range of 4–8528 kg/m2s, and hydraulic diameters in the range of 0.0695–6.22 mm.

Since the two-phase frictional pressure drop is a nonlinear function of various variables, new methods have been used based on machine learning to determine the correlation between these variables. Balcilar et al. [7] developed a correlation for predicting the frictional pressure drop during evaporation and condensation of different refrigerants in micro-fin and smooth tubes using artificial neural networks. The used database included 1485 samples, ten refrigerants, and tubes with diameters in the range of 4.39–11.1 mm, and the average error of the model was 7.09%. In another study, Balcilar et al. [8] employed artificial neural networks to estimate the pressure drop of refrigerant R134a during boiling and condensation in corrugated and smooth tubes. The used database included 1177 data points, mass velocities in the range of 200–700 Kg/m2s, tube diameters of 8.1 and 8.7 mm, pressures of 4.5,5.5,10 and 12 bar, and the relative error of the model was ±30%. In a study by Peng and Ling [9], the Colburn and friction factors in compact heat exchangers were predicted using artificial neural network and support vector regression (SVR) models. They used 48 data points for this purpose. The result showed that the SVR model provides better prediction performance with the mean squared errors of 2.64 × 10−4 and 1.251 × 10−3 for Colburn and friction factors, respectively. Zendehboudi and Li [10] used the universal intelligent models including Hybrid-ANFIS, GA-PLCIS, GA-LSSVM, and PSO-ANN to estimate the pressure drop of R134a during condensation in inclined smooth tubes. The database used included 649 data points, tube diameter of 8.38 mm, saturation temperatures of 30, 40, and 50 °C, and mass velocities in the range of 100–400 Kg/m2s. According to the results, GA-PLCIS, GA-LSSVM, and Hybrid-ANFIS models accurately predict the pressure drops. The GA-PLCIS model performs better than the other two models and predicts the pressure drop and frictional pressure drop with mean squared errors of 0.0140 and 0.0126, respectively. Lopez-Belchi et al. [11] used neuro-fuzzy logic neural networks and group method data handling (GMDH) to estimate heat transfer coefficient and pressure drop of condensing flow. They determined the minimum number of variables required to develop the most accurate models using the GMDH method. The database used to predict frictional pressure drop included 1824 data points, hydraulic diameters of 0.71 and 1.16 mm, mass velocities in the range of 175–800 Kg/m2s, and R32, R134a, R290, R410A, and R1234yf refrigerants. The frictional pressure drop was predicted with a MARD of 10.59%. Longo et al. [12] predicted the frictional pressure gradient inside the brazed plate heat exchanger during condensation and boiling using a gradient boosting machine model. The total number of data was 2549, and 16 refrigerants of different types were used. The frictional pressure gradient was predicted with a MARD of 6.6%. Najafi et al. [13] developed an optimal machine learning-based pipeline for two-phase air-water flow using 2021 experimental data points and optimization based on a genetic algorithm. This optimal pipeline, using selected features, estimates training and test sets with MARDs of 6.72% and 7.05%, respectively. Moradkhani et al. [14] presented a general frictional pressure drop correlation for condensing flow in micro, mini and macro channels using genetic programming. The used database included 4000 data points, 22 working fluids, hydraulic diameters in the range of 0.1–19 mm, reduced pressures in the range of 0.03–0.95, and mass fluxes in the range of 32.7–1400 Kg/m2s. The proposed correlation predicted the pressure drop with a MARD of 22.92%. Hughes et al. [15] proposed a universal model to estimate the condensing heat transfer coefficient and frictional pressure drop. The used database included 4000 samples, nine refrigerants, reduced pressures in the range of 0.03–0.96, mass fluxes in the range of 50–800 Kg/m2s, and hydraulic diameters in the range of 0.1–14.45 mm. They developed three machine learning models, including artificial neural networks, random forest, and support vector regression. The results indicated that the random forest model performs better than the other two models and can predict the condensing heat transfer coefficient and frictional pressure drop with a MARD of about 4%.

Many researchers have experimentally investigated the condensing frictional pressure drop for different fluids and a wide range of geometric and flow parameters. Therefore, today there is an acceptable number of databases for the development of universal models based on machine learning. These models are able to estimate the condensing frictional pressure drop with good accuracy. As seen, few studies [14, 15] have been conducted to develop universal models for estimating condensing frictional pressure drop using machine learning methods. Accordingly, this study is performed to develop an accurate and universal machine learning model for estimating the frictional pressure drop during condensing and adiabatic flow in micro, mini and macro channels. In this regard, a large database of 11,411 data points is collected from 80 sources. The database includes a vast range of diameters, working fluids, reduced pressures, and mass velocities. Using this database and taking into account the wide range of dimensionless parameters affecting the frictional pressure drop, important hyperparameters for each machine learning model are tuned. Finally, for the model with the best performance, by considering the trade-off between the model complexity (i.e., the number of used features) and the obtained accuracy, the final model with less complexity is presented.

2 Databases

The database used in this study includes 11,411 data points of frictional pressure drop in condensing and adiabatic flows. These data are collected from 80 sources. Table 1 shows the operating conditions of individual databases. According to the classification proposed by Kandlikar [16], 507 data points concern micro-channels (Dh ≤ 0.2 mm), 6592 data points concern mini-channels (0.2 <Dh≤ 3 mm), and 4312 data points concern macro channels (Dh> 3 mm). The range of various parameters in this database is as follows:

  • Working fluid: R134, R410A, R744, R1234yf, R404A, R290, R32, R1234ze(E), R245fa, R50, R600a, R170, R22, R717, R152a, R601, R14, R407C, R1270, R728, R12, R236ea, R718, R125

  • Hydraulic diameter: 0.069 mm < Dh ≤ 18 mm

  • Mass velocity: 6.3 Kg/m2s < G ≤ 2000 Kg/m2s

  • Flow quality: 0 < x < 1

  • Reduced pressure: 0.001 < Pred < 0.95

Table 1 The database used in this study
Full size table

3 Machine learning models

In this section, data preparation, scaling, and cross-validation are first described, followed by a brief introduction to artificial neural networks (ANN), support vector regression (SVR), gradient-boosted regression trees (GBR), and random forest regression (RFR).

3.1 Data preparation

During machine learning model development, the database is randomly divided into two parts. The part used to build the model is named the training set. The other part is used to evaluate how well the model works; this part is named the test set. In this study, 70% and 30% of the total data were used for training and testing each model, respectively.

The following dimensionless parameters are provided as features to the models:

  • Bo, Pred, Rel, Rev, Relo, Revo, X, Wel, Wev, Frl, Frv, Sul, Suv, DR, Ga, Cal, Cav

Furthermore, the two-phase friction factor and the Chisholm parameter are considered separately as the target. The two-phase friction factor is defined as [15]:

$${f}_{TP}=\frac{2{D}_h{\uprho}_{TP}{\left.\frac{dP}{dz}\right)}_{TP}}{G^2}$$
(1)

The relationship between the Chisholm parameter, the Lockhart-Martinelli parameter, the two-phase frictional multiplier, and the frictional pressure drop for each phase is as follows [97]:

$${\displaystyle \begin{array}{l}{\left.\frac{dP}{dz}\right)}_{TP}={\left.\frac{dP}{dz}\right)}_l{\varphi}_l^2;{\varphi}_l^2=1+\frac{C}{X}+\frac{1}{X^2};\\ {}{X}^2={\left.\frac{dP}{dz}\right)}_l/{\left.\frac{dP}{dz}\right)}_v\\ {}{\left.\frac{dP}{dz}\right)}_l=\frac{2{f}_l{G}^2{\left(1-x\right)}^2}{\uprho_l{D}_h};{\left.\frac{dP}{dz}\right)}_v=\frac{2{f}_v{G}^2{x}^2}{\uprho_v{D}_h}\end{array}}$$
(2)

The phase friction factors are calculated as follows:

$${\displaystyle \begin{array}{l}\ \\ {}\ \\ {}\ \end{array}}{\displaystyle \begin{array}{ll}{f}_k=16{\mathit{\operatorname{Re}}}_k^{-1}& for\ {\mathit{\operatorname{Re}}}_k<2000\\ {}{f}_k=0.079{\mathit{\operatorname{Re}}}_k^{-0.25}& for\ 2000\le {\mathit{\operatorname{Re}}}_k<20000\\ {}{f}_k=0.046{\mathit{\operatorname{Re}}}_k^{-0.2}& for\ {\mathit{\operatorname{Re}}}_k>20000\end{array}}$$
(3)

It should be emphasized that the following equation is used for laminar flow in a rectangular channel [98]:

$${f}_k{\mathit{\operatorname{Re}}}_k=24\left(1-1.3553{\alpha}^{\ast}\right)+1.9467{\alpha^{\ast}}^2-1.7012{\alpha^{\ast}}^3+0.9564{\alpha^{\ast}}^4-0.2537{\alpha^{\ast}}^5$$
(4)

Where α∗ is the aspect ratio of a rectangular cross-section (α∗ ≤ 1). The equation proposed by Sparrow [99] is used for laminar flow in a triangular channel. In Eqs. (3) and (4), the subscript k indicates v or l for the vapor and liquid phase, respectively.

3.2 Scaling and cross-validation

Some models are sensitive to data scaling. In these models, all features must change on a similar scale. Therefore, the features are scaled so that the mean and variance of each feature are zero and unit, respectively. The statistical method k-fold cross-validation is used to assess the generalization performance of the models. In this method, the data is first randomly divided into k approximately equal-size parts, called fold. Then k model is trained. The k-th model is trained using the k-th fold as the test set, and the other folds are used as the training set. The mean of k accuracy values is considered as model accuracy. In this study, three-fold cross-validation was used.

When training set scaling and cross-validation are used together, the data partitioning during cross-validation should be done before scaling to prevent data leakage from the training folds to the validation fold. Therefore, a chain of different processes and models is built and used as a pipeline. The pipeline is generated using the Scikit-learn Python library [100].

3.3 Artificial neural networks (ANN)

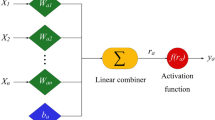
In artificial neural networks, all input variables (features) interact with each other in a complex way. This allows these networks to capture complex relationships in the database. An ANN involves the input layer, hidden layers, an output layer, and an activation function. The following recurrence relations are established between input vector \(\overline{x}\) and output vector \(\overline{y}\), for networks with k hidden layers, and activation function Φ [101]:

$${\displaystyle \begin{array}{l}\textrm{Input}\ \textrm{to}\ \textrm{hidden}\ \textrm{layer}:\\ {}{\overline{h}}_1=\Phi \left({W}_1^T\overline{x}\right)\\ {}\begin{array}{l}\textrm{Hidden}\ \textrm{layer}\ \textrm{to}\ \textrm{hidden}\ \textrm{layer}:\\ {}{\overline{h}}_{p+1}=\Phi \left({W}_{p+1}^T{\overline{h}}_p\right)\forall p\in \left\{1,\dots, k-1\right\}\\ {}\begin{array}{l}\textrm{Hidden}\ \textrm{layer}\ \textrm{to}\ \textrm{output}\ \textrm{layer}:\\ {}\overline{y}=\Phi \left({W}_{k+1}^T{\overline{h}}_k\right)\end{array}\end{array}\end{array}}$$
(5)

In Eq. (5), matrix W1 is the weight between the input and the first hidden layer, matrix Wp is the weight between pth hidden layer and (p + 1)th hidden layer, and matrix Wk + 1 is the weight between the last hidden layer and the output. The goal of network training is to find weight matrices that minimize the error (or loss) function. This process contains two forward and backward phases. In the forward phase, the output and the derivative of the loss function with respect to the output are determined using the current values of the weights. In the backward phase, the gradient of the loss function with respect to different weights is determined using the chain rule. The weights are updated using these gradients.

3.4 Support vector regression (SVR)

The search for function F so that the deviation of this function from target values yi for all training data is less than ε may not be feasible in some cases. Therefore, at some points, the deviation of F from yi is allowed to be ξi + ε. Assuming F is linear:

$$F=\left\langle w,x\right\rangle +b$$
(6)

The problem can be written as an optimization problem [102]:

$${\displaystyle \begin{array}{l}\operatorname{minimize}\ \frac{1}{2}{\left\Vert w\right\Vert}^2+C\sum\limits_{i=1}^n\left({\xi}_i-{\xi}_i^{\ast}\right)\\ {}\textrm{subjected}\ \textrm{to}\ \left\{\begin{array}{c}{y}_i-\left\langle w,{x}_i\right\rangle -b\le \varepsilon +{\xi}_i\\ {}\left\langle w,{x}_i\right\rangle +b-{y}_i\le \varepsilon +{\xi}_i^{\ast}\\ {}{\xi}_i,{\xi}_i^{\ast}\ge 0\ \end{array}\right.\end{array}}$$
(7)

Where 〈∙, ∙〉 denotes the dot product, ‖w‖2 = 〈w, w〉, and C is constant. The solution to the above problem is shown as follows:

$${\displaystyle \begin{array}{l}\hat{w}=\sum\limits_{i=1}^n\left({\hat{\alpha}}_i^{\ast }-{\hat{\alpha}}_i\right){x}_i\\ {}\hat{F}(x)=\sum\limits_{i=1}^n\left({\hat{\alpha}}_i^{\ast }-{\hat{\alpha}}_i\right)\left\langle x,{x}_i\right\rangle +b\end{array}}$$
(8)

Where \({\hat{\alpha}}_i^{\ast }\) and \({\hat{\alpha}}_i\) are the solutions to the following optimization problem:

$${\displaystyle \begin{array}{l}\operatorname{minimize}\ \varepsilon \sum\limits_{i=1}^n\left({\alpha}_i^{\ast }+{\alpha}_i\right)-\sum\limits_{i=1}^n{y}_i\left({\alpha}_i^{\ast }-{\alpha}_i\right)+\frac{1}{2}\sum\limits_{i,j=1}^n\left({\alpha}_i^{\ast }-{\alpha}_i\right)\left({\alpha}_j^{\ast }-{\alpha}_j\right)\left\langle {x}_i,{x}_j\right\rangle \\ {}\textrm{subjected}\ \textrm{to}\ \left\{\begin{array}{c}\sum\limits_{i=1}^n\left({\alpha}_i-{\alpha}_i^{\ast}\right)=0\\ {}{\alpha}_i,{\alpha}_i^{\ast}\in \left[0,C\right]\end{array}\right.\end{array}}$$
(9)

A subset of solutions \(\left({\hat{\alpha}}_i^{\ast }-{\hat{\alpha}}_i\right)\) is commonly nonzero, and the related data values are named the support vectors.

In the nonlinear case, the data is mapped into a higher-dimensional space. In this case:

$$F(x)=H\left[\phi (x)\right]=\left\langle W,\phi (x)\right\rangle +B$$
(10)

The following similar results are obtained by repeating the steps in the linear case:

$${\displaystyle \begin{array}{l}\hat{W}=\sum\limits_{i=1}^n\left({\hat{\alpha}}_i^{\ast }-{\hat{\alpha}}_i\right)\phi \left({x}_i\right)\\ {}\hat{F}\left({x}_i\right)=\sum\limits_{i=1}^n\left({\hat{\alpha}}_i^{\ast }-{\hat{\alpha}}_i\right)\kappa \left({x}_i,{x}_j\right)+B\end{array}}$$
(11)

Where \({\hat{\alpha}}_i^{\ast }\) and \({\hat{\alpha}}_i\) are the solutions to the following optimization problem:

$${\displaystyle \begin{array}{l}\operatorname{minimize}\ \varepsilon \sum\limits_{i=1}^n\left({\alpha}_i^{\ast }+{\alpha}_i\right)-\sum\limits_{i=1}^n{y}_i\left({\alpha}_i^{\ast }-{\alpha}_i\right)+\frac{1}{2}\sum\limits_{i,j=1}^n\left({\alpha}_i^{\ast }-{\alpha}_i\right)\left({\alpha}_j^{\ast }-{\alpha}_j\right)\kappa \left({x}_i,{x}_j\right)\\ {}\textrm{subjected}\ \textrm{to}\ \left\{\begin{array}{c}\sum\limits_{i=1}^n\left({\alpha}_i-{\alpha}_i^{\ast}\right)=0\\ {}{\alpha}_i,{\alpha}_i^{\ast}\in \left[0,C\right]\end{array}\right.\end{array}}$$
(12)

In the above equations, κ(xi, xj) is called the kernel. Various kernel functions such as linear, power, polynomial, sigmoid, and Gaussian radial basis are used in the support vector machine.

3.5 Gradient-boosted regression trees (GBR)

GBR is an ensemble method that combines a large number of simple models (weak learners) such as shallow trees to produce a robust model. In this method, the following equation is established between the estimate of function \({\hat{y}}_i\) and M simple models hm [100]:

$${\hat{y}}_i={F}_M\left({x}_i\right)=\sum_{m=1}^M{h}_m\left({x}_i\right)$$
(13)

This method is made in a greedy fashion, meaning that if a simple model such as hi is selected, the selection will not change, and only new models will be added. Therefore:

$${F}_m(x)={F}_{m-1}(x)+{h}_m(x)$$
(14)

In the above equation, the recently added tree hm is fitted to minimize the total losses Lm of the earlier ensemble Fm-1:

$${\displaystyle \begin{array}{l}{h}_m=\mathit{\arg}\underset{h}{\mathit{min}}{L}_m\\ {}{L}_m=\sum\limits_{\textrm{i}=1}^{\textrm{n}}L\left[{y}_i,{F}_{m-1}\left({x}_i\right)+h\left({x}_i\right)\right]\end{array}}$$
(15)

In the above equation, L[yi, F(xi)] is a loss function. However:

$$L\left[{y}_i,{F}_{m-1}\left({x}_i\right)+h\left({x}_i\right)\right]\approx L\left[{y}_i,{F}_{m-1}\left({x}_i\right)\right]+h\left({x}_i\right){\left.\frac{\partial L}{\partial F}\right|}_{F_{m-1}}$$
(16)

Therefore, by removing the constants and denoting the gradient with gi:

$${h}_m\approx \mathit{\arg}\underset{h}{\mathit{\min}}\sum_{i=1}^nh\left({x}_i\right){g}_i$$
(17)

The simple model is fitted to predict a value proportional to −gi to facilitate the solving of the above minimization problem. Various loss functions such as squared error, least absolute deviation, Huber loss function, and Quantile loss function are used in GBR. In addition, GBR is prone to overfitting, meaning that this method predicts the training set itself rather than the functional dependency between input and output. Regularization techniques such as subsampling, shrinkage, and early stopping prevent overfitting [103, 104].

3.6 Random forest regression (RFR)

Random forest regression is an ensemble method made from a combination of decision trees. Injecting randomness into the tree building reduces the variance and overfitting tendency of the forest estimator relative to the individual decision trees. Trees in the forest are randomized in two ways: by randomly selecting the data points used to build a tree and by randomly selecting the best split from a random subset of features. The average prediction of trees in the forest is considered the final prediction [105].

4 Error analysis

The percentage of samples estimated with an accuracy of 20% (θ20) and 50% (θ50), mean absolute relative deviation (MARD), mean relative deviation (MRD), and R2 score with the following definitions are used to evaluate the accuracy of the models:

$${\displaystyle \begin{array}{l}\textrm{MARD}=\frac{1}{N}\sum \left|\frac{{\left.\frac{dP}{dz}\right|}_{f, pred}-{\left.\frac{dP}{dz}\right|}_{f,\mathit{\exp}}}{{\left.\frac{dP}{dz}\right|}_{f,\mathit{\exp}}}\right|\times 100\\ {}\textrm{MRD}=\frac{1}{N}\sum \frac{{\left.\frac{dP}{dz}\right|}_{f, pred}-{\left.\frac{dP}{dz}\right|}_{f,\mathit{\exp}}}{{\left.\frac{dP}{dz}\right|}_{f,\mathit{\exp}}}\times 100\\ {}{\textrm{R}}^2=1-\frac{\sum {\left[{\left.\frac{dP}{dz}\right|}_{f,\mathit{\exp}}-{\left.\frac{dP}{dz}\right|}_{f, pred}\right]}^2}{\sum {\left[{\left.\frac{dP}{dz}\right|}_{f,\mathit{\exp}}-\overline{{\left.\frac{dP}{dz}\right|}_{f,\mathit{\exp}}}\right]}^2}\end{array}}$$
(18)

An R2 score of 1 corresponds to a perfect prediction, and an R2 score of 0 corresponds to a constant model that predicts only the mean of the data set.

5 Results and discussion

In this section, four universal models for frictional pressure drop in two-phase condensing and adiabatic flows in micro, mini and macro channels are developed and compared using ANN, SVR, GBR, and RFR algorithms and 11,411 data points.

5.1 Models performance comparison

There are hyperparameters in machine learning algorithms that should be tuned. In this study, these parameters are tuned using randomized search, Bayesian search, and grid search [100].

In the ANN model, the number of hidden layers and nodes in each hidden layer is considered important hyperparameters. The number of hidden layers is limited to four, with a maximum of 200 nodes per layer to avoid the over-complexity of the model as well as the high computational cost of searching for the optimal model. The parameters gamma and C in the SVR model, the parameters max-depth, learning-rate, and n-estimators in the GBR model, and the parameters max-features and n-estimators in the RFR model are the most important hyperparameters whose variations are considered. Table 2 shows the range of variation of these hyperparameters, their optimal values, and some other model parameters for predicting the Chisholm parameter (C) and the two-phase friction factor (fTP). Table 3 provides the results of predicting the Chisholm parameter, two-phase friction factor, and frictional pressure drop by four models with optimal parameters. The ANN model predicts the frictional pressure drop with a MARD value of 17.00% using the Chisholm parameter, which is better than the accuracy of conventional models with MARD of about 30%. The model, however, is not very successful in predicting the frictional pressure drop using the two-phase friction factor. The SVR model predicts the frictional pressure drop with a MARD value of 10.83% and a MARD value of 10.86%, respectively, using the Chisholm parameter and the two-phase friction factor. The GBR model predicts the frictional pressure drop with excellent accuracy with a MARD value of 3.09% using the Chisholm parameter. However, this model suffers from overfitting in predicting the two-phase friction factor. The RFR model predicts the frictional pressure drop with a MARD value of 6.93% and a MARD value of 6.16%, respectively, using the Chisholm parameter and the two-phase friction factor.

Table 2 The variation range of the hyperparameters, their optimal values, and some other model parameters for predicting the Chisholm parameter (C), and the two-phase friction factor (fTP)
Full size table
Table 3 The results of predicting the Chisholm parameter, two-phase friction factor, and frictional pressure drop by models with optimal parameters
Full size table

5.2 Sensitivity analysis

As mentioned in Section 5.1, with optimal parameters and 17 dimensionless features (mentioned in Section 3.1), the GBR model has the best performance in predicting the frictional pressure drop. However, the importance of these features in predicting frictional pressure drop varies as can be seen in Table 4. Investigation of the model performance with different numbers of features suggested that the frictional pressure drop can be predicted with a MARD value of 3.24% using six features X, Revo, Ga, Sul, Pred, and DR. In this way, as the number of features decreases from 17 to 6, the frictional pressure drop prediction error increases by only about 5%. The GBR model with these six features is considered the final model and will be used for further analysis.

Table 4 Features importance computed from GBR model
Full size table

5.3 Ascertaining the effectiveness of the present model

The performance of the present model is compared with a homogeneous model [106], three correlations presented for macro channels [4, 5, 107], and four correlations presented for micro, mini and macro channels [6, 14, 49, 108] in all individual databases. Table 5 shows the relative frequency distribution of MARD in predictions of individual databases. As can be seen in the table, the present model performs much better than other models and correlations. The present model predicts the frictional pressure drop in 85% of databases (68 databases) with a MARD value of less than 5%, in 13.75% of databases (11 databases) with a MARD in the range of 5–10%, and only in 1.25% of databases (1 database) with a MARD in the range of 15–20%. The maximum MARD obtained by the present model with a value of 18.78% belongs to the database of Bashar et al. [22]. A comparison of the performance of the present model with previous models and correlations is provided in Table 6 for a total of 11,411 data points. According to the table, the Müller-Steinhagen and Heck model with a MARD value of 29.57% has the best performance following the present model. To visualize the accuracy of the present model, the results are compared with the experimental data in Fig. 1.

Table 5 The relative frequency distribution of MARD in predictions of individual databases by the present model and previous models and correlations
Full size table
Table 6 Comparison of present model prediction with previous models and correlations
Full size table
Fig. 1
figure 1

Comparison of 11,411 experimental data points with predictions of the present model

Full size image

Low overall values of MARD are not sufficient to ascertain the effectiveness and robustness of a new predictive approach. The predictive tool must predict data with uniform accuracy over a relatively wide range of variations of each flow parameter [6, 109]. In this regard, the distribution of MARD in the predictions of the present model and the Müller-Steinhagen and Heck model and the distribution of the number of data relative to working fluids, hydraulic diameters, mass velocities, qualities, and reduced pressures are investigated, and the results are provided in Figs. 2, 3, 4, 5 and 6. The standard deviations of MARD in the predictions of the present model for various working fluids, hydraulic diameters, mass velocities, qualities, and reduced pressures are 0.66%, 0.81%, 1.19%, 0.78%, and 0.58%, respectively, indicating the even distribution of MARD according to the average value of 3.24%. The results also show that the present model predicts the frictional pressure drop much more accurately than the Müller-Steinhagen and Heck model. However, the two models have almost the same accuracy in predicting the frictional pressure drop for a mass velocity range of 1500–1600 Kg/m2s.

Fig. 2
figure 2

Distribution of number of data points and MARD relative to working fluid

Full size image
Fig. 3
figure 3

Distribution of number of data points and MARD relative to mass velocity

Full size image
Fig. 4
figure 4

Distribution of number of data points and MARD relative to hydraulic diameter

Full size image
Fig. 5
figure 5

Distribution of number of data points and MARD relative to quality

Full size image
Fig. 6
figure 6

Distribution of number of data points and MARD relative to reduced pressure

Full size image

The trend of changes in the frictional pressure drop predicted by the present model in terms of mass velocity, quality, saturation temperature, and working fluid is investigated. Figure 7 shows the effect of quality and mass velocity on frictional pressure drop for R134a at a saturation temperature of 31 °C and in a channel with a diameter of 1.1 mm. As the quality and mass velocity increase, the phase interactions and the frictional losses increase [110]. Figure 8 shows the influence of saturation temperature (41 and 31 °C) on the frictional pressure drop at a mass velocity of 500 Kg/m2s in a channel with a diameter of 1.1 mm. As the saturation temperature increases, the vapor density increases, and the liquid density decreases. This reduces the difference in phase velocities, interfacial shear, and frictional pressure drop. Figure 9 compares the frictional pressure drop for the R600a and R1234yf refrigerants at a mass velocity of 400 Kg/m2s and a saturation temperature of 31 °C. At this saturation temperature, the vapor and liquid densities of R1234yf refrigerant are about four and twice that of R600a refrigerant, respectively. Therefore, the difference in phase velocities in the R600a is more remarkable, resulting in higher shear stress between the phases and a more significant frictional pressure drop.

Fig. 7
figure 7

Comparison between experimental [86] and predicted frictional pressure drop by the present model for different mass velocities

Full size image
Fig. 8
figure 8

Comparison between experimental [86] and predicted frictional pressure drop by the present model for different temperatures

Full size image
Fig. 9
figure 9

Comparison between experimental [86] and predicted frictional pressure drop by the present model for different working fluids

Full size image

In order to evaluate the performance of the present model in estimating the frictional pressure drop of a data set that has not been used before in the development of the model, Yang and Nalbandian data [111] is used. They investigated the condensing pressure drop of R134a and R1234yf at a saturation temperature of 15 °C and mass velocities of 200–1200 Kg/m2s. The present model predicts the frictional pressure drop measured by Yang and Nalbandian with a MARD value of 11.82%. Figure 10 shows the comparison between the measured frictional pressure drop and the predictions of the present model. As can be seen in this figure, there is good agreement between the experimental and predicted values, except for R134a data at a mass velocity of 800 Kg/m2s. However, machine learning methods do not perform as well as the data used in model development in predicting previously unseen data. It was recommended that more data be added to the database over time and that a more diverse database be developed to address this shortcoming [109].

Fig. 10
figure 10

Comparison between experimental [111] and predicted frictional pressure drop by the present model for different working fluids and mass velocities

Full size image

6 Conclusions

A new universal machine learning model is developed to predict frictional pressure drop in condensing and adiabatic two-phase flows within micro, mini and macro channels using a database of 11,411 samples from 80 sources. The significant findings are as follows:

  • ANN and GBR models are not very successful in predicting the frictional pressure drop using the two-phase friction factor compared to the Chisholm parameter. SVR and RFR models, however, predict the frictional pressure drop using the two-phase friction factor and the Chisholm parameter with almost equal accuracy.

  • Among the ANN, SVR, GBR, and RFR models, the GBR model has the best performance. This model predicts the frictional pressure drop with a MARD value of 3.09% and an MRD value of 0.81%, using the Chisholm parameter as the target and 17 dimensionless parameters as features.

  • Examination of the features importance suggests that the model can predict the frictional pressure drop with a MARD value of 3.24% and an MRD value of 0.58% using six features X, Revo, Ga, Sul, Pred, and DR.

  • According to the comparison of GBR model performance with several available models and correlations, the MARD value of this model predictions is lower than other models and correlations in all individual databases. The GBR model predicts the frictional pressure drop in 85% of databases with a MARD value of less than 5% and only 1.25% of databases with a MARD value of greater than 10%.

  • The GBR model predicts data with uniform accuracy over a relatively wide range of variations of each flow parameter.

  • The trend of changes in the frictional pressure drop predicted by the GBR model in terms of mass velocity, quality, saturation temperature, and working fluid is consistent with the trend observed in the experimental data.

  • The GBR model is less accurate in predicting the frictional pressure drop of data sets not previously used in model development.

7 Nomenclature

arg min argument of the minimum

Bo Bond number, \({B}_o=\frac{g{D_h}^2\left({\rho}_l-{\rho}_v\right)}{\sigma}\)

C Chisholm parameter

Cal liquid capillary number, \({Ca}_l=\frac{\mu_lG\left(1-x\right)}{\rho_l\sigma }\)

Cav vapor capillary number, \({Ca}_v=\frac{\mu_v Gx}{\rho_v\sigma }\)

Dh hydraulic diameter

DR density ratio, \({DR}=\frac{\rho_l}{\rho_v}\)

f friction factor

Frl liquid Froude number, \({Fr}_l=\frac{G^2{\left(1-x\right)}^2}{{\rho_l}^2g{D}_h}\)

Frv vapor Froude number, \({Fr}_v=\frac{G^2{x}^2}{{\rho_v}^2g{D}_h}\)

g gravitational acceleration

G mass velocity

Ga Galileo number, \(Ga=\frac{\rho_lg\left({\rho}_l-{\rho}_v\right){D_h}^3}{{\mu_l}^2}\)

MARD mean absolute relative deviation

MRD mean relative deviation

Pred reduced pressure

Rel liquid Reynolds number, \({\mathit{\operatorname{Re}}}_l=\frac{G\left(1-x\right){D}_h}{\mu_l}\)

Relo liquid-only Reynolds number, \({\mathit{\operatorname{Re}}}_{lo}=\frac{G{D}_h}{\mu_l}\)

Rev vapor Reynolds number, \({\mathit{\operatorname{Re}}}_v=\frac{G{xD}_h}{\mu_l}\)

Revo vapor-only Reynolds number, \({\mathit{\operatorname{Re}}}_{vo}=\frac{G{D}_h}{\mu_v}\)

Sul liquid Suratman number, \({Su}_l=\frac{\rho_l\sigma {D}_h}{{\mu_l}^2}\)

Suv vapor Suratman number, \({Su}_v=\frac{\rho_v\sigma {D}_h}{{\mu_v}^2}\)

Wel liquid Weber number, \({We}_l=\frac{G^2{\left(1-x\right)}^2{D}_h}{\rho_l\sigma }\)

Wev vapor Weber number, \({We}_v=\frac{G^2{x}^2{D}_h}{\rho_v\sigma }\)

X Lockhart-Martinelli parameter

7.1 Greek symbols

\({\upxi}_{\textrm{i}},{\upxi}_{\textrm{i}}^{\ast }\) slack variables

φ two-phase frictional multiplier

7.2 Subscripts

TP two-phase

l liquid

v vapor