1 Synopsis

Safe natural resource exploration in the Gulf of Eilat (Aqaba) has significant environmental significance and relevance.

2 Introduction

Nowadays novel flexible-scale energy transportation and storage technology OCAES (offshore compressed air energy storage), being applied for marine renewable energy transportation and storage, serving as utility for offshore wind farms, offshore platforms, etc., Fig. 1. To connect floating platforms with its subsea apparatus for deep-water operations, often marine risers being employed. As a result, stability and safety of the overall OCAES system being significantly influenced by marine risers’ dynamic reaction characteristics. In offshore industry risers often being vulnerable to dynamic environmental loads.

Fig. 1
figure 1

Left: marine riser system components; Right: various marine riser applications

Full size image

Marine riser systems being crucial component of any deep-water offshore installation. Marine risers should typically operate and keep their structural integrity for the whole duration of their field's life, and the latter is not a trivial task, due to their intrinsic dynamic nature, as well as lack of access of maintenance options.

Offshore risers may be classified as follows, [1]:

  • ▪ Unbonded flexible risers with continuous sections made of a variety of metallic and polymeric layers, combined to provide pressure resistance, tensile strength, and reduced bending stiffness. These risers can be set up in a variety of subsea configurations, some most popular of which being shown in Fig. 1, right. These flexible marine risers usually have smaller diameters, than rigid lines due to production and operating pressure limitations.

  • ▪ Top tension risers being vertical steel lines, typically being connected by threaded connectors, serving TLPs and Spars for dry tree type of production. Lifter has been tensioned either from tensioner-equipped vessel, or separately using long buoyant cans, restrained inside subsea wellbay. Since well control (tree) being situated at the top of marine riser within wellbay, this form of marine risers is able to withstand high tubing pressures even in the event of a tubing leak.

  • ▪ Top tension risers being vertical steel lines, typically being connected by threaded connectors, serving TLPs and Spars for dry tree type of production. Lifter has been tensioned either from tensioner-equipped vessel, or separately using long buoyant cans, restrained inside subsea wellbay. Since well control (tree) being situated at the top of marine riser within wellbay, this form of marine risers is able to withstand high tubing pressures even in the event of a tubing leak.

  • ▪ Steel pipe pieces being welded together, forming continuous lines, being suspended from the supporting vessel within a catenary arrangement. These marine risers being known as steel lazy wave risers (SLWR), and steel catenary risers (SCR). At hang-off and touchdown locations, risers in this setup may experience substantial degrees of bending and exhaustion. By adding buoyancy components to sustain riser line in a lazy wave arrangement, fatigue damage should be accounted for SLWR.

  • ▪ Free-standing Hybrid Risers (FSHR). Depending on in situ needs, hybrid riser system made up of both solid steel pipes and unbonded pliable pipes. In the case of FSHRs as well as Bundled systems, may either form a vertical stiff line (or bundle), supported by buoyancy can, or SCRs to be supported by underwater pontoon, in the case of Buoyancy supported riser (BSR).

  • ▪ Unbonded flexible riser jumpers being used to establish connection with its host vessel, allowing marine steel riser reaction to be almost independent of vessel movements. Due to a large number of fixed components, these riser systems have robust fatigue performance, but may be quite costly to design, produce, and install offshore.

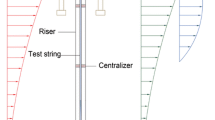
Vortex-induced vibration (VIV) acting on marine risers typically generate a mixture of external, as well as internal excitations, [2, 3], for contemporary methods used to model such phenomena, see [4,5,6,7,8,9,10]. In marine and offshore engineering, riser's extreme response and fatigue damage assessment is necessary, as fatigue damage may cause structural degradation. This study employs extensive laboratory experimental riser dynamic stress data. Information on in situ sea current loads was used to model realistic hydrodynamic loads. Figure 2 presents operating example of marine riser, subjected to sea currents.

Fig. 2
figure 2

Left: example of marine riser, operating in sea currents; Right: sea current profile along with TLP and marine riser

Full size image

Since extreme local events often increase structural damage risks, in situ probability distribution of sea currents is essential. This study utilized local probability distributions of sea currents in a particular offshore area of the Israeli Gulf of Eilat (Aqaba), based on in situ observations, along with available high-frequency radars. As shown in [2], Weibull probability distribution function (PDF) often being good approximation of sea current velocities, with distribution parameters varying over geographic areas, on the scale of few kilometres. The Gulf of Eilat area rarely experiences strong winds during winter storms, [2, 10]. 2 separate 42 MHz HF radars were placed in the Gulf of Eilat (Aqaba), to gather in situ information on surface currents. For details on the science, underlying HF radar data technology, see [2, 8, 9].

Figure 3 shows bathymetry of the Gulf of Eilat (Aqaba) in real time. In the following we provide short introduction to Weibull distributions. For positive values, x > 0, Weibull PDF is

$$f\left(x,k,\lambda \right)=\frac{k}{\lambda }{\left(\frac{x}{\lambda }\right)}^{k-1}{e}^{-{\left(x/\lambda \right)}^{k}}$$
(1)

with \(\lambda\) being the scale parameter, k being the shape parameter of the Weibull distribution. Both \(\lambda\) and k being positive constants. Weibull complementary cumulative distribution function (1-CDF) is

Fig. 3
figure 3

a Map indicating bathymetry of the Gulf of Eilat. b Flow field measured using 2 high-frequency radar sites (1 and 2), [2]. Star marks the position of the selected time series in Fig. 4 (a)

Full size image
$$1-F\left(x,k,\lambda \right)={e}^{-{\left(x/\lambda \right)}^{k}}$$
(2)

Weibull distribution offers reasonable approximation for observed extreme distributions of wind speeds, [10]. There is a clear correlation between wind speeds and sea surface currents speeds, since offshore winds generate sea surface currents. It is also possible to determine distribution moments \(\langle {x}^{m}\rangle\) of the Weibull distribution, given the Weibull distribution's k and parameter

$$\langle {x}^{m}\rangle ={\lambda }^{m}\Gamma \left(1+\frac{m}{k}\right)$$
(3)

with \(\Gamma\) being the Gamma-function. Consequently, it is possible to estimate only the first and second distribution moments, in order to derive related Weibull distribution, given recorded time series of the sea currents, with (k and \(\lambda\)) parameters, [2].

Figure 4a illustrates surface current speeds. Sea current speeds exhibit irregular and reasonably complex variations over the year course. This data series' PDF being displayed in Fig. 4b,c, where the Weibull distribution with \(\lambda\) =14.4 cm s−1 and k = 1.85 being a good match, [2]. The estimated Weibull sea currents distribution will be utilized in this study, as an external input for statistical structural analysis of marine risers, [10].

Fig. 4
figure 4

a Time series of sea surface current speeds (cm \(\bullet\) s−1) obtained using HF radars, covering over one year, indicating mean sea surface currents from the Gulf of Eilat (Aqaba) at 29.4728°N, 34.9358°E. (marked by a star in Fig. 2b). b Time series PDF presented in (a) (solid circles). Solid lines represent Weibull distribution with \(\lambda =\) 14.4 cms−1 and k = 1.85. Weibull distribution with k = 1 (dashed line) is shown just for comparison

Full size image

Figure 5 presents typical multi helical layer marine riser cross-section. Note that when marine riser bends, helical layers slip in nonlinear fashion. Sea wave equation was not considered in this study, as only sea currents were taken into consideration, which is valid assumption for deep water risers. Note that when scaling is done to get from the model scale to the real one, it is important to account for riser flowline operational geometry, as riser’s free span length and shape will affect its oscillations caused by VIV.

Fig. 5
figure 5

Left: right: marine riser typical cross-section, [11]

Full size image

2.1 Laboratory measurements

In offshore industry, risers act as energy carriers, transferring gas or crude oil from subsea wells to producing offshore platform or floating production and storage unit (FPSO). Due to marine riser's distant operating locations, local sea currents will be involved, causing vortex VIV shearing. Lift force, normal to the flow direction, along with drag, parallel to the flow direction being 2 key components of hydrodynamic loading, acting on risers. VIV will be active when flow rate exceeds certain level. Single degree of freedom (1DOF) vibration in riser’s transverse flow direction has been the focus of bulk of our experimental study on VIV forces, acting on marine riser, [3,4,5,6]. To evaluate small-scale models in this study, 1DOF experimental strategy was adopted. Lab experiments were conducted At TU Delft in the Netherlands, using a 14.3-m-long, 0.40-m-wide, and 0.40-m-deep wave tunnel.

Cylinder with a 40 mm diameter and a length of 375 mm served as the trial riser specimen. Velocity distribution across marine riser segment at various sea water depths should be modelled, in order to assess overall drag forces, acting on marine riser (Fig. 6).

Fig. 6
figure 6

a Experimental TU Delft lab facility. b wave tank for free vibration test. c indicator of VIV created by incoming flow of coloured water

Full size image

3 Method

The lifetime distribution (LTD) assessment method for complex nonlinear energy dynamic systems, that are prone to various failure modes during intended service time, being presented in this section. Figure 7 represents example of lifetime distribution, corresponding to Mauna Loa Observatory, where monthly measured CO2 concentration consecutive temporal differences were measured, https://gml.noaa.gov/ccgg/trends/.

Fig. 7
figure 7

Consecutive lifetime distribution illustration. Flashes indicate dynamic system failures

Full size image

Horizontal red line in Fig. 7 indicates the failure/hazard threshold, while inter-consecutive time spans between data-points mark threshold crossings, being denoted here as \(L\), illustrating dynamic system consecutive lifetimes \({L}_{i}\), \(i=\mathrm{1,2},\dots\). Thus \(L\) being a random stochastic variable, representing dynamic system lifetime. When the number of system dimensional components (failure modes) is large, modern offshore engineering reliability methodologies may not readily provide solutions to assess LTD of complex energy systems, [12,13,14,15,16,17,18]. In theory, it is well possible to assess target cumulative density function (CDF)

$$\mathrm{LTD}\left(L\right)=\mathrm{Prob}\left(\mathrm{Lifetime}\le L\right)$$
(4)

using either sufficient observation data, or straight Monte Carlo (MC) models for complex dynamic systems, [19,20,21,22,23]. However, for most complex dynamic energy systems, both numerical as well as experimental costs may be prohibitive. Novel lifespan assessment method for energy systems has been developed here by the authors in order to reduce numerical and measurement costs, during system design phase.

A structural dynamic multi-degree of freedom (MDOF) combined response/load system vector is considered \(\left(X\left(t\right), Y\left(t\right), Z\left(t\right), \dots \right)\), consisting of dynamic system components \(X\left(t\right), Y\left(t\right), Z\left(t\right), ...\), being either measured or simulated, over a sufficiently long (representative) time lapse \((0,T)\). Unidimensional system component’s global maxima being denoted as \({X}_{T}^{\mathrm{max}}=\underset{0\le t\le T}{\mathrm{max}}X\left(t\right)\),\({Y}_{T}^{\mathrm{max}}=\underset{0\le t\le T}{\mathrm{max}}Y\left(t\right)\),\({Z}_{T}^{\mathrm{max}}=\underset{0\le t\le T}{\mathrm{max}}Z\left(t\right), \dots\). By sufficiently long (representative) time span \(T\) we primarily mean here large enough value of \(T\), with respect to environmental/energy dynamic system relaxation, as well as and auto-correlation time scales. With \({X}_{1},\dots ,{X}_{{N}_{X}}\) being temporally consequent dynamic system component’s \(X=X(t)\) local maxima observed at discrete temporally non-decreasing time instants \({t}_{1}^{X}<\dots <{t}_{{N}_{X}}^{X}\) within \((0,T)\). Identical definitions being valid for other MDOF components: \(Y\left(t\right), Z\left(t\right), \dots\) namely \({Y}_{1},\dots ,{Y}_{{N}_{Y}};\) \({Z}_{1},\dots ,{Z}_{{N}_{Z}}\) and so on. For simplicity, all dynamic system component’s local maxima have been assumed to be non-negative, with

$$P=\iiint\nolimits_{\left(0,0,0,,\dots\right)}^{\left(\eta_X,\eta_Y,\eta_Z,\dots\right)}p_{X_T^{\max},Y_T^{\max},Z_T^{\max},\dots}\left(x_T^{\max},y_T^{\max},z_T^{\max},\dots\right)dx_T^{\max} dy_T^{\max} dz_T^{\max}\dots$$
(5)

being target survival probability of dynamic system, given critical values of system components, denoted as \({\eta }_{X}\),\({\eta }_{Y}\),\({\eta }_{Z}\),…; with \(\cup\) being logical unity operator «or»; and \({p}_{{X}_{T}^{\mathrm{max}}, { Y}_{T}^{\mathrm{max}}, { Z}_{T}^{\mathrm{max}} , \dots }\) being the joint PDF of individual system component’s maxima. If riser dynamic system number of degrees of freedom (NDOF) being large, it may not be always practically feasible to directly assess the joint PDF \({p}_{{X}_{T}^{\mathrm{max}}, { Y}_{T}^{\mathrm{max}}, { Z}_{T}^{\mathrm{max}} , \dots }\) along with the target system survival probability \(P\). The latter target system probability \(P\) needs to be assessed according to Eq. (4)

$$\mathrm{LTD}\left(L\right)=\mathrm{Prob}\left(\mathrm{Lifetime}\le L\right)$$
(6)

in an easy manner for a complex environmental/industrial/energy system, employing either available measurement data, or direct numerical MC simulations, [12,13,14,15,16,17,18,19]. For many complex dynamic energy systems, both experimental and numerical costs may be prohibitive. Hence, authors have developed a novel lifespan assessment methodology, especially suitable for energy systems, reducing measurement and calculation costs required at system design phase. If dynamic system’s number of degrees of freedom (NDOF) being large, it will not be practically feasible to directly assess target joint PDF \({p}_{{X}_{T}^{\mathrm{max}}, { Y}_{T}^{\mathrm{max}}, { Z}_{T}^{\mathrm{max}} , \dots }\) and hence the target survival probability \(P\). The latter target dynamic system survival probability \(P\) needs to be assessed according to Eq. (3)

$$\frac{T}{{P}_{\mathrm{failure}}}={L}_{\mathrm{expected}}\equiv E\left[L\right]={{\int}_{0}^{\infty }}L\,d\mathrm{LTD}\left(L\right)$$
(7)

having failure/hazard probability \({P}_{\mathrm{failure}}=1-P\), being complementary to a survival probability \(P\). Dynamic system being regarded as immediately failed (or entered a hazard state), if either system’s component \(X\left(t\right)\) exceeds \({\eta }_{X}\), or \(Y\left(t\right)\) exceeds \({\eta }_{Y}\), or \(Z\left(t\right)\) exceeds \({\eta }_{Z}\), etc. Fixed failure/hazard levels \({\eta }_{X}\), \({\eta }_{Y}\), \({\eta }_{Z}\),… being individually set for each system’s one-dimensional system components\({X}_{{N}_{X}}^{\mathrm{max}}=\mathrm{max }\{{X}_{j}\hspace{0.17em};j=1,\dots ,{N}_{X}\}={X}_{T}^{\mathrm{max}}\), \({Y}_{{N}_{Y}}^{\mathrm{max}}=\mathrm{max }\{{Y}_{j}\hspace{0.17em};j=1,\dots ,{N}_{Y}\}={Y}_{T}^{\mathrm{max}}\), \({Z}_{{N}_{z}}^{\mathrm{max}}=\mathrm{max }\{{Z}_{j}\hspace{0.17em};j=1,\dots ,{N}_{Z}\}={Z}_{T}^{\mathrm{max}}\), … Dynamic system unidimensional components \(X, Y, Z, \dots\) being re-scaled, and non-dimensionalized

$$X\to \frac{X}{{\lambda \eta }_{X}}, Y\to \frac{Y}{{\lambda \eta }_{Y}}, Z\to \frac{X}{{\lambda \eta }_{X}}, \dots$$
(8)

making all dynamic system non-dimensional, having the same target failure/hazard limit. If \(\lambda =1\), target failure probability \(P=P\left(1\right)\) being achieved. Equation (5) may be used now to define \(P\left(\lambda \right)\) as a smooth function of non-dimensional level \(\lambda\). Unidimensional dynamic system component’s local maxima, being now merged into one temporally non-decreasing vector \({\varvec{R}}\left(t\right)\equiv \overrightarrow{R}=\left({R}_{1}, {R}_{2}, \dots ,{R}_{N}\right)\) according with the corresponding merged temporal vector \({t}_{1}\le \dots \le {t}_{N}\), \(N\le {N}_{X}+{N}_{Y}+{ N}_{Z}+\dots\). Each local maxima of \({R}_{j}\) being actual encountered dynamic system component’s local maxima, corresponding to either \(X\left(t\right)\) or \(Y\left(t\right)\), or \(Z\left(t\right)\), or other dynamic system component, [20,21,22,23,24]. Constructed synthetic \(\overrightarrow{R}\)-vector thus having zero data loss, see Fig. 8.

Fig. 8
figure 8

Example of how 2 components, X and Y, being merged, to create 1 new synthetic vector \(\overrightarrow{R}\). Red ellipse highlights case of simultaneous maxima for 2 different system components

Full size image

Having now introduced the temporally non-decreasing synthetic vector \(\overrightarrow{R}\), along with its corresponding temporally non-decreasing occurrence times \({t}_{1}\le \dots \le {t}_{N}\), the lifetime stochastic process \(L=L\left(t\right)\) can be now expressed as follows

$${L}_{i} = {t}_{i} - {t}_{i-1}$$
(9)

for \(i=2,\dots ,N\). Hence composed synthetic process \({\varvec{R}}\left(t\right)\) holds key information related to the target LTD PDF. Survival probability \(P=P\left(1\right)\) may be now expressed via corresponding mean up-crossing rate function

$$P\left(\lambda \right) \approx \mathrm{exp }(-{\nu }^{+}(\lambda )\hspace{0.17em}T);\, {\nu }^{+}\left(\lambda \right)={\int }_{0}^{\infty }\zeta {p}_{R\dot{R}}\left(\lambda ,\zeta \right)d\zeta$$
(10)

with \({\nu }^{+}(\lambda )\) being mean up-crossing rate of a failure threshold level \(\lambda\) for above discussed synthetic non-dimensional vector \(R\left(t\right)\). Mean up-crossing rate function in Eq. (8) being well-known as the Rice's with \({p}_{R\dot{R}}\) being joint PDF for \(\left(R, \dot{R}\right)\) with \(\dot{R}=R{\prime}\left(t\right)\) being a time-derivative. Let failure/hazard limit converge to a target \(\lambda \to 1\)

$${\mathrm{log}}_{ \lambda \to 1}{P}_{\mathrm{failure}}=\frac{T}{{L}_{\mathrm{expected}}}={\nu }^{+}\left(\lambda \right)\hspace{0.17em}T \Rightarrow {L}_{\mathrm{expected}}=\frac{1}{{\nu }^{+}\left(1\right)}$$
(11)

according to Eq. (7). MDOF dynamic energy/environmental system has been assumed to be jointly-stationary, coupled with in-situ environmental scatter diagram, consisting of \(m=1,..,M\) environmental sea states, with each individual short-term environmental sea state having individual probability \({q}_{m}\), with \(\sum_{m=1}^{M}{q}_{m}=1\). According to long-term probability equation

$$\mathrm{LTD}\left(L\right)\equiv \sum\nolimits_{m=1}^{M}{LTD}_{m}\left(L\right){q}_{m}$$
(12)

with \({p}_{k}(\lambda ,m)\) being the same function as in Eq. (7), corresponding to specific short-term environmental sea state, with number \(m\). In the following Section we will illustrate how LTD \(q-\) quantiles of interest

$${L}_{q} = {\mathrm{LTD}}^{-1}\left(q\right)$$
(13)

may be computed, using available EH system measured/simulated underlying time series, with \(q\in \left(0, 1\right)\), and \({\mathrm{LTD}}^{-1}\) being an inverse LTD’s function, namely LTD \(^\circ {\mathrm{LTD}}^{-1}=\boldsymbol{1}\), with \(\boldsymbol{1}\) being the identity operator. Note that for high failure/hazard levels, dynamic system failure/hazard events become almost independent, hence lifetime distribution will follow Poisson distribution with parameter \({\nu }^{+}\left(\lambda \right)\hspace{0.17em}T\). Despite being primarily linked to the Poisson process concept, this research may have broader applications, if system components failures do not constitute impending system failure events. In the latter case data de-clustering should be performed, [25,26,27,28].

4 Results

In this work a bivariate stochastic process \(Z(t)=(X(t),Y(t))\) has been selected for illustration of the above described method, consisting of the horizontal force acting on marine riser, along with its vertical displacement processes \(X(t),Y(t)\), being measured synchronously, across representative time lapse \((0,T)\). Let’s assume that system samples \(({X}_{1},{Y}_{1}),\dots ,({X}_{N},{Y}_{N})\) being taken/recorded at N equidistant discrete time-moments \({t}_{1},\dots ,{t}_{N}\) within measurement/observation period \(\left(0,T\right)\). It should be noted that advocated methodology is equally feasible for any number of system’s dimensions, and 2D has been selected as only an example. This section studies bivariate joint cumulative distribution function (CDF) \(P\left(\xi ,\eta \right):=\mathrm{ Prob }\left({\widehat{X}}_{N}\le \xi ,{\widehat{Y}}_{N}\le \eta \right)\) of the 2D vector \(\left({\widehat{X}}_{N},{\widehat{Y}}_{N}\right)\), with marine riser system components \({\widehat{X}}_{N}=\mathrm{max}\left\{{X}_{j} ;j=1,\dots ,N\right\}\), and \({\widehat{Y}}_{N}=\mathrm{max}\left\{{Y}_{j} ;j=1,\dots ,N\right\}\). In order to unify 2 measured time series \(X, Y\), scaling procedure has been performed, according Eq. (4), making both dynamic system components non-dimensional, and having the same failure/hazard limit, being equal to 1. All system component’s local peaks from two measured time series were then merged into a single time series by keeping them in temporal non-decreasing order \(\overrightarrow{R}=\left(\mathrm{max}\left\{{X}_{1},{Y}_{1}\right\},\dots ,\mathrm{max}\left\{{X}_{N},{Y}_{N}\right\}\right)\) with each set \(\mathrm{max}\left\{{X}_{j},{Y}_{j}\right\}\) being arranged according to the non-decreasing temporal instants of their occurrences.

Dotted lines in Fig. 9 mark extrapolated 95% confidence interval (CI) of the target system survival probability \(P\left(\lambda \right)\), for proofs see for example [12]. Figure 9 exhibits reasonably narrow 95% CI, the latter being an advantage of the advocated approach, [29,30,31,32,33]. Now, as soon as target failure level \(\lambda =1\) up-crossing rate \(P\left(\lambda \right) \approx \mathrm{exp }(-{\nu }^{+}(\lambda )\hspace{0.17em}T)\) have been extrapolated following [16], one may conclude that target dynamic riser system lifetime distribution will follow the Poisson distribution, with temporal parameter \({\nu }^{+}\left(1\right)\), being system’s failure/hazard rate, measured in years−1, having expected system lifetime \({L}_{\mathrm{expected}}=\frac{1}{{\nu }^{+}\left(1\right)}\) IN accordance with Eq. (9).

Fig. 9
figure 9

Extrapolation of \({p}_{k}\left(\lambda \right)\) towards critical/hazard level, corresponding to 1-year return period (marked by red star) and beyond. Extrapolated 95% CI, marked by dotted lines

Full size image

5 Conclusions

Traditional time series reliability methods are not always easily coping with cross-correlation between dynamic system’s components, given a large number of system’s dimensions. Suggested method's capacity to analyze lifetime distributions of high-dimensional nonlinear dynamic systems is thus of paramount importance for engineering design. This study examined dynamic behavior of marine riser systems under random in situ environmental circumstances. Probability distribution of marine riser service life over the course of its specified design lifetime has been assessed, using novel system reliability method. Dynamic systems require development of novel, accurate, yet reliable methods, in order to manage the available data and maximize its value because of their complexity and high dimensionality. Using either direct measurements, or Monte Carlo simulations to evaluate reliability function of dynamic systems is not always affordable. The main goal of this work was to develop the all-purpose, reliable, simple spatio-temporal multi-dimensional marine riser system reliability methodology.

As shown in this study, suggested method produced a fairly narrow confidence intervals. Suggested approach proved to be valuable in a variety of reliability analyses of nonlinear dynamic systems. Potential engineering applications of the introduced methodology are in no way limited by the specified offshore engineering marine riser example.