1 Introduction

According to some, the supply chain is a form of network that is heavily utilised in industrial sectors to meet customer expectations. Producers, distributors, retailers, customers, and traders all make up this framework. Similar to marketing channel management, supply chain management [1] is largely intended for the strategic management of storage materials, components, and procurement in order to improve future profitable growth. The supply chain includes both the intricate creation of goods and their delivery. Depending on the commodities, there are many stages, locations, accounts, payment methods, people, organisations, and forms of transportation. The supply-purchasing process as a result can take months [2]. The parties involved are particularly interested in integrating and developing blockchain technology to improve supply chain logistical operations [3] and increase their profitability due to the inherent complexity and lack of transparency in the logistics process. Although crypto-currencies are where blockchain technology is most frequently used, it offers a considerably wider range of possible uses [4]. There are many uses for the distributed book (ledger) known as blockchain [5].

This SCN is a collection of sequential actions needed by an institution in distributing and transforming raw components and resources into an ultimate product and transporting it to the destined customer [6]. These days, the current increase in the populace global wide and the growing demand for food and diet products, the agricultural business has attained huge significance, particularly in emerging and under emerging nations [7]. Hence, under this circumstance, Agricultural Food Supply Chain (AFSC) plays a crucial part in reducing issues related to food-safety. The AFSC network consists of various shareholders participating in transporting ultimate products to the customer end encompassing the agriculturalists or manufacturers [8], producers or food processors, suppliers, and vendors at the same time adding a particular value to the ultimate products. In the view of logistics, the AFSC scheme can be efficiently improvised by maximizing the site of food manufacturing amenities besides the delivery directions by taking into account the atmospheric aspects in all transportation and supply stages [9]. Consequently, designing an efficient logistic network for farming and diet items can tackle supply-associated problems and thus satisfy interested consumers' needs and hopes.

Constructing and deploying dispersed management, dynamic scheduling, and monitoring schemes of farming actions for product rate anticipation and distribution chains need a crucial effective and safe approach [10]. Artificial Intelligence (AI) is prevalently employed in mathematics and computer science in detailing the formation of ML to the learning procedure, accomplishing transmissions founded on recognition, patterns of extraction, categorization, improvising dynamic viewing and maximizing mechanisms [11]. Metaheuristics are one among the major prevalent approaches for organizing, managing, scheduling, and maximizing data, specifically the ones associated with enterprises [12]. Metaheuristic prototypes were implemented to forecast and organize data/processed records from records in single, greater business data and some transmission managements related to government institutions. Metaheuristic methods are more convolutional and difference by nature, majorly relied on the range of info, particularly genetic protocols in the diet and farming fields [13], and goods price prediction, specifically farming goods like rice. Hence, data handling and maximization are still challenging factors regarded in the metaheuristic-ML area that is being manufactured in real-time [14].

Blockchains are regarded as suitable for application in the logistics and supply chain management sectors for a number of reasons. Data created at each stage of a product's life cycle can be recorded as a transaction as it moves up the value chain and given a permanent historical record.The usage of blockchain, a decentralised, global ledger that is digitally maintained, allows for the permanent storing of transactions. Due to its extensive offering of confidence, openness, and provenance, it is relevant to applications involving transactions. Even non-financial sectors are starting to pay attention to the technology, which was first created to facilitate financial transactions. Some of these sectors include public services, manufacturing, healthcare, and retail. A number of challenges must be overcome before blockchain in supply chain management (SCM) can offer a high level of security. Recently, many innovative optimisation techniques have been created to deal with this problem. The processing of a small number of transactions can be done swiftly while maintaining a high level of security. As a result, it is currently challenging to reconcile security and block size in SCM. Incorporating financial data into blockchain-based SCM could lead to less openness, more expenses, and less effectiveness. In order to create a fresh and efficient SCM privacy framework based on blockchain technology, the proposed work is being made.

This article designs a Hunger Games Search Optimization with Deep Learning Model for Sustainable agricultural and food Supply Chain Management (HGSODL-ASCM) technique. A bidirectional long short-term memory model is created using the HGSODL-ASCM technique to determine how much productivity and storage are needed to generate the most profit. In this work, the HGSO algorithm has been applied to improve the performance of the Bi-LSTM classification process. The presented HGSODL-ASCM technique can independently achieve the SCM policies via interaction with complicated and adaptive environments. A brief set of simulations were performed to ensure the improved performance of the HGSODL-ASCM technique.

2 Related works

Shokouhifar et al. [15], devised a technique termed H-WOA-VNS method (ensemble heuristic–metaheuristic approach using the heuristic data, the WOA, and variable neighbourhood search). For generating a set of near-optimum feasible solutions, a problem-dependent heuristic was projected. Such solutions are inputted in a population-based WAO, which benefitted from exploitation and exploration strategies. Eventually, to enrich the quality of the solution by making use of local search operator, a single-solution variable neighbourhood search is exploited. A method known as novel mixed linear mathematical modelling for ASC was developed by Rajabi-Kafshgar et al. [16] to lower the overall variable and fixed costs of the closed-loop supply chain. Renowned and effectual classical and current meta-heuristic techniques were exploited for addressing the presented model. As well, three hybrid meta-heuristic techniques were advanced to enrich diversification and intensification stages.

Singh and Srivastava [17] intend to overcome the practical and conceptual difficulties in incorporating triple bottom line (TBL) sustainability in ASC. It scrutinizes their causal relations in addition to cross-dimensional interaction under every TBL dimension and finds the key enablers for all 3D of TBL sustainability. Additionally, a decision support framework (DSF) was developed to analyse and assess TBL sustainability practises and policies in ASC. Bhatia and Albarrak [18] introduced a XAI-based Faster RCNN technique, also known as explainable AI -based faster region employing CNN, to assess the components of food items using QR codes and an approachable web-based front-end model. A BC-based elliptic curve integrated encrypted system (ECIES) was used to verify all communication tokens in the network. As well, to register all users, a key artificial rabbit optimization (ARO) was utilized.

Chen et al. [19], devised a BC-related ASC structure to offer product traceability that guaranteed decentralization security for agricultural and food tracing information in ASC. After, for effectual decision-making process on the storage and production of agricultural and food products for profit maximization, a DRL related Supply Chain Management (DR-SCM) technique was devised. Alkahtani et al. [20] this study has combined the BC effect by web design components into the agricultural supply chain management (Agri-SCM). Also, partners in digital marketing SCM (DM-SCM) are met with the problem of detecting web design components –oriented BC technology for obtaining high profits. By applying the fuzzy system, the uncertainty in the technique is managed and to provide cleaner production, carbon emission is considered.

Sachdev looked into how supply chain management systems might be affected by AI and blockchain technologies [21]. The purpose of this project was to apply AI and blockchain models to prevent supply chain disruptions. The blockchain facilitates dependable communication across complex production networks while increasing logistical productivity, legitimacy, and anonymity. Furthermore, it might develop websites where trucking or shipping firms can list their available ships or vehicles.

Salamai et al. [22]. Because tamper-proof smart contracts can be made using blockchain technology, a purchase contract's terms can be automatically enforced. Instead, smart contracts have the potential to independently validate and execute themselves once the correct payments have been paid to the intended receivers. An AI-powered supply chain optimisation solution raises the standard of intelligent assessments by including the optimum course of action into demand estimates. As a result, producers will be able to anticipate how certain events will affect time, costs, and income, which could increase the supply chain’s overall efficiency.

A description of BC technology and its potential for creating a safe and dependable agriculture SCM is provided by Vidhate et al. [23]. To deliver food products from farmers to consumers, Agriculture SCM systems become vital. BC technology is used to attain better payment options and prices, for transparent disbursement of subsidies and land title registration to farmers. Gholian-Jouybari et al. [24], by modelling a stochastic multi-objective programming method and food supply chain system under marketing practices is investigated to boost 3 main pillars of sustainability. The potential of the presented mathematical method was certified by case study on saffron business by making use of the LP-metric approach. To address the NP-hardness of the issues, a metaheuristic-oriented technique composed of a modified Keshtel Algorithm was applied.

Babaeinesami et al. [25]. This model responds to both the demand for finished goods as well as spare parts on the market while simultaneously minimising transportation costs in forward and reverse chains, product purchase costs in the assembly section, costs of renewing collected products, and fixed workplace costs. Suppliers, manufacturing facilities, retail outlets, and customers make up the first player. Collecting sites, refurbishment sites, separation sites, and disposal sites make up the second player. The reward for each actor is the minimization of their own aims, while the model’s (information security’s) objective is for each link in the chain to be unaware of the objectives of the others. The GAMS 24 programme was used to resolve the suggested model. Due to the nested model, the results of the first model are inputted into the second model before the second model is solved.

Babaeinesami et al. [26] provides a mathematical methodology to reduce closed-loop supply chain costs and environmental impacts. Suppliers bring raw timber from forests to industries. Factory-made wood is shipped to retailers. Retailers ship to customers. Customers return items to recovery facilities. After processing, recovery centres ship to industries. Innovations include adapting a genetic solution technique to match the suggested paradigm and developing an environmentally friendly supply network for wood products. 3. Determining the raw materials and finished goods that were sent and received from the flow of forest products. A closed-loop supply chain (CLSC) network, which includes suppliers, assembly sites, retailers, customers, collection sites, refurbishment sites, disassembly sites, and disposal sites, is the subject of [27]. It makes an effort to create a distribution network based on customer requirements in an effort to reduce overall costs and CO2 emissions simultaneously. The self-adaptive non-dominated sorting genetic algorithm II (NSGA-II) is developed and put to the test against the constraint technique in order to address the complexity of the issue.

Adav et al. [28] developed a model for a multi-tiered, sustainable system in the framework of Agriculture and Food Supply Chains (AFSC) that depends on novel Internet of Things (IoT) technology. This study looks at how 14 major components interact, assessing their causal links and implications within an IoT-centered framework for guaranteeing food security. The study uses Interpretive Structural Modeling (ISM) to connect these components, as well as the Fuzzy-Decision-Making Trial and Evaluation Laboratory (F-DEMATEL) to assess the strength of hierarchical cause-and-effect associations. The work makes a theoretical contribution by drawing on Dynamic Capability Theory (DCT) and Information Processing Theory (IPT). This approach gives useful insights for organizational managers engaged in strategy planning by categorizing these aspects into cause and effect groups. Based on the findings of this study, this thorough guide has the ability to motivate managers to integrate IoT technology into AFSC operations.

Dong et al. [29] pioneered cutting-edge Internet of Things (IoT) tracking technologies and conducted extensive supply chain management research. Their approach makes use of machine learning techniques applied to large datasets secured by blockchain technology. This method not only ensures continued expansion, but also allows modern supply chain management, powered by machine learning, to self-improve and stimulate ongoing progress. The incorporation of blockchain technology tackles issues such as insufficient property rights protection, low trust in online transactions, and poor safety and privacy standards. As a result, producers have the capacity to develop flawless production strategies, properly estimate consumer demand, and orchestrate all aspects and linkages within the supply chain, resulting in a cohesive operational framework and efficient oversight. This, in turn, leads to increased revenue.

Radanliev and De Roure [30] concentrated on the ethical design of IoT and updates to IoT design, but they neglected to investigate the interrelated and diverse dangers emerging from IoT systems. Their findings emphasize the importance of adding ethical consideration of cyber threats into supply chains prior to using novel IoT technology. Notably, including IoT into the vaccination supply chain significantly increases security vulnerabilities. The current study assists healthcare practitioners, governments, and medical organizations by providing a comprehensive framework for informed decision-making.

3 The proposed model

In this article, we have focused on the development of the HGSODL-ASCM technique for automated SCM in the agricultural and food supply industries. The goal of the HGSODL-ASCM technique assists in the effectual decision-making process associated to the production and storing of agricultural and food products to optimize profits. In the presented HGSODL-ASCM technique, two stage process is performed namely Bi-LSTM based SCM and HGSO based hyperparameter tuning. SCM is given top attention in corporate organisations since it places a strong emphasis on an industry's effectiveness. Blockchain technology is being used to connect supply chains because the network lacks adequate security. However, there is still a lack of security and privacy protection. In order to safeguard SCM data, this article creates a novel privacy preservation architecture based on blockchain technology. The proposed study's primary objective is to develop a lightweight, privacy-preserving SCM paradigm based on blockchain technology. The fundamental logistics information collected from manufacturers is protected by this approach, which makes use of a cutting-edge optimisation technique.

The development of information and communication technology has made data sharing more practical. The effectiveness of information flow in supply chains has increased thanks to the global framework for long-term coordination and collaboration, enhancing the competitive advantages of businesses. Businesses’ inability to properly coordinate their operations is hampered by a lack of information sharing. The primary objective of the suggested effort is to offer a small and blockchain-based SCM privacy-preserving paradigm. This solution uses a cutting-edge optimisation strategy to safeguard the vital logistics data that was obtained from manufacturers. In order to secure the privacy of supply chain networks, this study suggested creating an innovative blockchain-based architecture. In order to increase the security and privacy of the proposed blockchain-assisted SCM, this study used cutting-edge “data sanitization and data restoration” to protect the data in each block. The optimal key in this situation was chosen using the HGSO optimisation method.

In the literature now available, a variety of optimisation approaches are applied to complicated engineering problems. The HGSO-based optimisation technique is utilised in the proposed study for optimal key generation due to the improved convergence rate and efficacy. Animal behaviour in response to hunger was used to develop the HGSO; this meta-heuristics algorithm was inspired by animal social behaviour and activity-driven behaviour. The creation of a variable weight using the concept of appetite. To increase the effectiveness of their search, the writers took into account the consequences of famine at each stage. Figure 1 illustrates the overall process of HGSODL-ASCM approach.

Fig. 1
figure 1

Overall process of HGSODL-ASCM approach

Full size image

3.1 Problem formulation

The goal of the ASC management challenge is to increase farmer revenue (product profits). Consider a streamlined scenario in which there is a single processor (a corn factory) and numerous retailers on a finite number of occasions, and corn is transported from the manufacturer to the store via distributors (trucks). All the time, the corn quantity must be generated and kept at factory along with corn that shipped to retailer will be determined. A punishment occurred until the requirement met if the retailer could not meet the requirement. For making the problems into reality, there is a limitation on manufacturing ability and memory of the factory in addition limitation on storage capability of retailer.

In terms of this issue, the factory and retailer must be capable of powerfully reconstruct stock based on the corn demand. Particularly, there is one factory, represented as\(v0\), and multiple retailers, represented as\(L=\{\mathcal{V}1, \mathcal{V}2, \dots , {v}_{n}\}\). Firstly, the overall turnover attained by selling corn at retailers can be represented as follows:

$$ TO = p \cdot \mathop \sum \limits_{{i = 1}}^{n} d_{i} $$
(1)

In Eq. (1), \(T\) indicates the number of time periods, \(p\) denotes unit price of corn, and \({d}_{i}={\sum }_{t=1}^{T}{d}_{i,t}\) indicates retailers corn demand. Especially, for the management of ASC, assumes 12 months. In the meanwhile, the use of frozen storage and vacuum packs ensures that the maize will remain fresh for a full year. Therefore, in these circumstances, the corn’s shelf life is disregarded. Due to the seasonal demand for corn at various retailers, Eq. (2) can be used to model the retailer corn demand at any given period.

$$ d_{i,t} = \left[ {\frac{{d_{{\text{max }}} }}{2} + \frac{{d_{{\text{max }}} }}{2} \cdot {\text{ sin }}\left( {\frac{{\left( {2i + t} \right) \cdot \pi }}{6}} \right) + sto_{i,t} } \right] $$
(2)

where \({d}_{\mathrm{max}}\) denotes the predetermined maximal demand at the retailer. \(st{o}_{i,t}\) indicates the stochastic feature which is allocated random value of zero or one at retailer on distinct time periods that was unutilised used for stimulating the rapid rise in demand.

$${C}_{prod}={c}_{pr}\cdot {a}_{0} $$
(3)

In Eq. (3), \({c}_{pr}\) and \(a0\) denotes the unit price of generating corn and the productivity factory level, correspondingly. Next, the transport corn cost can be determined as follows:

$$ C_{{trans}} = \mathop \sum \limits_{{i = 1}}^{n} (c_{{tr,i}} \cdot \left[ {\frac{{a_{i} }}{{t_{ - } cap_{i} }}} \right])~~~~ $$
(4)

In Eq. (4), \({t}_{-}ca{p}_{i}\) indicates the truck capability to the retailer. \({a}_{i}\) shows the transport volume to the retailers, and the overall amount to each retailer must be lesser than factory stock. \({c}_{tr,i}\) denotes truck cost of transport corn to the retailers. Furthermore, corn storage cost was determined as follows:

$$ C_{{store}} = \mathop \sum \limits_{{i = 0}}^{n} (c_{{st,i}} \cdot s_{i} )~ $$
(5)

In Eq. (5), \({c}_{st,i}\) and \({s}_{i}\) indicates corns the storage cost and the stock level of retailer or factory, correspondingly. In addition, the punishment cost takes place while the retailer could not see the corn demand that is shown below:

$$ C_{{punish}} = c_{{pu}} \cdot \mathop \sum \limits_{{i = 1}}^{n} (d_{i} - s_{i} ) $$
(6)

In Eq. (6) \({c}_{pu}\) denotes unit punishment cost. Thus, net profit of selling and producing corn in ASC is computed as follows:

$$Profits =TO-{C}_{prod}-{C}_{trans}-{C}_{store}-{C}_{punish}$$
(7)

3.2 Supply chain management using bi-LSTM model

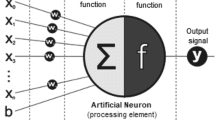
In this work, the Bi-LSTM model is derived to compute the quantity of productivity and storage to accomplish maximum profit. The fundamental RNN cell is not holding long‐term dependence later [28, 29]. It therefore demonstrates the flaws in this cell. If the order is excessively long, preventing the effective upgrading of weights, the backpropagation (BP) gradient tends to fall. Bi-LSTM's architecture is depicted in Fig. 2. The weighted matrix may become unstable if the gradient, however, spreads across a longer sequence if it is strong. Due to the intractable gradient nature, RNN cells are unable to acknowledge or assume responsibility for a long-term connection, which leads to the two problems outlined above. The mathematical equation for RNN structure is defined by Eqs. (8) and (9).

$${h}_{t-1}=\sigma \left({P}_{h}*{h}_{t-1}+{P}_{x}*{x}_{t}+{B}_{a}\right)$$
(8)
$${y}_{t}=\mathrm{ tanh }\left({P}_{o}*{h}_{t}+{B}_{o}\right)$$
(9)

where as \({h}_{t}\) implies the hidden layer (HL), and it is only variety of memory from the RNN cell.\({P}_{h}\) and \({P}_{x}\) exemplify the weighted matrix for HL and \({P}_{o}\) bias vector for cell output correspondingly, \({x}_{t}\) and \({y}_{t}\) portray the input and output of cells at \(t\) time step, respectively, \({B}_{a}\) and \({B}_{o}\) signify the bias vector for HL and cell outputs, correspondingly.

Fig. 2
figure 2

Structure of Bi-LSTM

Full size image

The subsequent HL was reliant on the inputs at hand right now and the HL from the prior time step. The current state and the future state are connected through the cell feedback loop. To take into account past data while altering the current state of the cell, this connection is crucial. In certain circumstances, the sigmoid function has been run, denoted by, to switch on HL, and the Tanh-described hyperbolic tangent function has been triggered on the visible layer. The RNN is a specific ANN method that works well for processing data sequences because it has a cyclic architecture. Large time gaps cause the gradient to disappear and significantly lower learning potential. After these issues were fixed, Hochreiter and Schmidhuber developed the LSTM. The fundamental idea behind the LSTM, which has been extensively applied to time-series data, is that the cell state is connected to one another like a conveyor belt. As a result, as the distance between the states increases, the gradient grows. In LSTM cells, the input, forget, and output gates are employed to regulate the state of the cell.

The GRU was created in 2014 as a network that modified the LSTM approach to increase learning accuracy. The GRU participates in two gating roles and has a quick learning rate compared to LSTM. The parameters are also less than LSTM since the HL and cell state can be integrated into a single HL. As a consequence, the GRU performs very well for long-term reliance on time-series data processing and progresses with a minimum of computation time after being coupled to the LSTM. The GRU formula used to determine the HL is shown below:

$${r}_{t}=\sigma \left({W}_{r}{x}_{t}+{U}_{r}{h}_{t-1}+{b}_{r}\right)$$
(10)
$${z}_{t}=\sigma \left({W}_{z}{x}_{t}+{U}_{z}{h}_{t-1}+{b}_{z}\right)$$
(11)
$${h}_{t}=\left(1-{z}_{t}\right)\odot {h}_{t-1}+{z}_{t}\odot \mathrm{tanh }\left({W}_{h}{x}_{t}+{U}_{h}\left({r}_{t}E\odot {h}_{t-1}\right)+{b}_{h}\right)$$
(12)

whereas, \({r}_{t}\) represents reset gate and \({z}_{t}\) denotes the updating gate at time \(t.\) \({x}_{t}\) stands for input value at \(t\) time, \(W\) and \(U\) signify the weighted, and \(b\) signifies the bias. \({h}_{t}\) defines the HL at time \(t.\) \(\odot \) depicts the component‐wise (Hadamard) multiplication. The LSTM can address RNN's shortcomings; typically, the result of the current time is appropriate for the state data of the previous and future times. By connecting two LSTMs, the Bi-LSTM network has been developed in an effort to address the issue of merging previous and future data. The framework of the Bi-LSTM network includes the front-to-back and back-to-forth LSTM layers. The output of the Bi-LSTM network is created by combining the architectures of the forward and backward layers, which compute the input database:

$${o}_{t}=g({\omega }_{1}{i}_{t}+{\omega }_{2}{0}_{t-1})$$
$${o}_{t}{\prime}=g({\omega }_{3}{i}_{t}+{\omega }_{5}{0}_{t-1}{\prime}),$$
(13)
$${y}_{t}=f({\omega }_{4}{0}_{t}+{\omega }_{6}{0}_{t}$$

In Eq. (13), \(\omega \) signifies the weight parameters in Bi-LSTM network, \({i}_{t}\) illustrates input at \(t\) time\(,\) \({0}_{t}\) stands for the outcome of forward HL at \(t\) time\(,\) \({0}_{t}{\prime}\) refers the resultant of backward HL at \(t\) time, and \({y}_{t}\) indicates the outcome of networks.

3.3 Hyperparameter tuning

For enhancing the performance of the Bi-LSTM classification process, the HGSO algorithm has been utilized in this work. Yang et al. [30, 31] proposed a new optimizer called the HGSO optimization to mimic animals’ starvation‐driven behaviour and activities. They have 2 social behaviours while finding food: at first, the animal behaves as a team. They formulated the mathematical equation of HGS to perform this social manner, as follows:

$${Y}_{i}\left({t}^{\to }+1\right)= \left\{\begin{array}{l}{\mathrm{Game}}_{1} :{Y}_{i}^{\to }(t)(1+randn(1)) {R}_{1}<f, \dots \dots ..(i)\\ Gam{e}_{2} : \overrightarrow{\omega }(t).{Y}_{i}^{\overrightarrow{b}}(t)\to +\widetilde{D}(t).\overrightarrow{\omega }(t).|{Y}_{i}^{b}(t)\to -{Y}_{i}\overrightarrow{(}t)| {r}_{1}>L, {R}_{2}>B(t), \dots \dots ..(ii)\\ Gam{e}_{3} : \overrightarrow{\omega }(t).{Y}_{i}^{b}(t)\to -{D}_{i}(t).\overrightarrow{\omega }(t).|{Y}_{i}^{b}(t)\to -{Y}_{i}\overrightarrow{(}t)| {r}_{1}>L, {R}_{2}<B(t)\dots \dots ..(iii)\end{array}\right.$$
(14)

In Eq. (15), The \({\overrightarrow{\omega }}_{1}\) and \({\overrightarrow{\omega }}_{2}\) denotes the weighted of hungers for implementing the hunger‐driven signal.\({Y}_{i}^{\overrightarrow{b}}(t)\) denotes the position of the better solution at the existing iteration (t), the\(Y(t\)) denotes the location of \({i}^{th}\) animal. The multiplication of\({Y}_{i}\overrightarrow{(}t\)) and \((1+randn(1))\) of Eq. (15) denote the random method of hungry animal while finding the food at the existing location. The \(|{Y}_{i}^{\overrightarrow{b}}(t)\to -{Y}_{i}\overrightarrow{(}t)|)\) of Eq. (14) represent the activity range of the \({i}^{ih}\) animal in\(t\). The weight \(({\overrightarrow{\omega }}_{2})\) is multiplied in that part \((|{Y}_{i}^{\overrightarrow{b}}(t)-{Y}_{i}\overrightarrow{(}t)\) for adjusting the range of activities. Henceforth, the animal could stop finding once it is complete. Subtracting and adding the part of \(\overrightarrow{\omega }.{Y}_{i}^{\overrightarrow{\mathrm{b}}(t)}\) in the 2nd and 3rd lines of Eq. (14) performs the present animal becomes acquainted with its peers when approaching the food position and later continue to find food again at the existing position. \(f\) denotes the constant value selected to be 0.03 depending on the actual article on HGS. \({R}_{1}\) and \({R}_{2}\) denotes random value \(i\) ranges from zero to one. The \(D\) is a ranging controller; whose values within \([-b, b].\) The \(D\) is exploited for managing the range of activities. Thus, it can be reduced gradually to zero. \(randn(1)\) shows the random integer derived from a uniform distribution. The decision making of Eq. (14) can be controlled by the parameter \(B\) that is evaluated as follows.

$${B}_{i}\left(t\right)=sech\left(\left|Fu{n}_{i}\left(t\right)-{G}^{*}\left(t\right)\right|\right)i\in \mathrm{1,2},3, \dots ,N$$
(15)

In Eq. (15),\({G}^{*}\) indicates the optimum obtained objective function at \(t\). \(Fu{h}_{i}\) denotes the main function value of \({i}^{th}\) animal at \(t.\) The \(sech\) \((x)\) denotes the hyperbolic function that equals \(1/Cosh(x)\) and parameter \(N\) denotes the overall number of animals [32].

The first line of the equation represents the application of a self-dependent strategy. Next, 2nd and 3rd lines are emulation of the team cooperation work. The movement of the animal based on the 2nd and 3rd lines is mostly constrained by 3 parameters: \(\overrightarrow{D},{\overrightarrow{\omega }}_{1}\), and \({\overrightarrow{\omega }}_{2}\). Yang et al. adapted those parameters by carrying out the subsequent equation.

  • Tuning the ranging controller\((\overrightarrow{D})\): It is recommended the subsequent formula to perform the animal shrinking strategy through iteration (t):

    $${D}_{i(t)}^{\sim }=2\times shrin{k}_{i}\left(t\right)\times {R}_{3}-shrin{k}_{i}\left(t\right),$$

where,

$$shrin{k}_{\mathrm{i}}\left(t\right)=2\times \left(1-\frac{t}{{M}_{T}}\right)$$
(16)

In Eq. (16), \({M}_{T}\) demonstrates the overall number of iterations, \({R}_{3}\) indicate a random value within [0,1].

  • Tuning the weights \(({\overrightarrow{\omega }}_{1})\) and \(({\overrightarrow{\omega }}_{2})\): it is applied the subsequent equation to increase the animals’ manner when finding the food.

    $${\overrightarrow{\mathrm{w}}}_{1}\left(t\right)=\left\{\begin{array}{ll}Hungr{y}_{i}\left(t\right).\frac{M}{{S}_{-}Hungry\left(t\right)}\times {R}_{4}& {R}_{5}<f\\ 1& {R}_{5}>f\end{array}\right.$$
    (17)
    $${{\overrightarrow{\mathrm{w}}}_{2}}_{\mathrm{i}}(t)=(1-exp(-|Hungr{y}_{i}(t)-{S}_{-}Hungry(t) \times {R}_{6}\times 2 $$
    (18)

where \({S}_{-}Hungry(t)\) represents the sum of hungry feelings of each animal at (t), \({R}_{4},\) \({R}_{5}\), and \({R}_{6}\) the random value, and Hungry(t) denotes the \({i}^{th}\) hungry animal. The equation of Hungry (t) is modelled as follows:

$$Hungr{y}_{\mathrm{i}}(t)=\left\{\begin{array}{ll}0& Fu{n}_{i}(t)=={G}^{*}(t)\\ Hungry (t)+{N}_{-}Hungr{y}_{i}(t)& Fu{n}_{i}(t)={G}^{*}(t)\end{array}\right.$$
(19)

In Eq. (19), \({N}_{-}Hungr{y}_{i}(t)\) denotes the novel hungry animal that is regarded once the main function of \({i}^{th}\) animal isn’t equivalent to the optimal‐obtained objective \({G}^{*}\). The corresponding novel hunger of animals is various. Thus, novel hunger \({N}_{-}\) Hungry equation can be expressed as follows

$${N}_{-}Hungr{y}_{i}(t)=\left\{\begin{array}{ll}{C}_{-}H\times (1+R)& {K}_{-}H<{C}_{-}H\\ {K}_{-}{H}_{i}(t)& {K}_{-}H\ge {C}_{-}H.\end{array}\right.$$
$${K}_{-}{H}_{i}(t)=\frac{Fu{n}_{i}\left(t\right)-{G}^{*}\left(t\right)}{{W}^{*}\left(t\right)-{G}^{*}\left(t\right)}\times {R}_{7}\times 2\times (High-Low)$$

where \({W}^{*}(t)\) denotes the worse value of fitness. \(High\) and \(Low\) represent the searching space upper and lower boundaries, correspondingly. \(C\_H\) indicates a constant value suggested to be \(100\).

4 Results and discussion

The study’s conclusions are presented in this section, along with a blockchain supply chain management concept based on optimization approaches. Blockchains are cutting-edge technological advancements with the potential to alter how people trade today. Blockchain technology is altering actual product safety by improving accountability. Living standards will rise as a result of product traceability, which will also lower application system costs. Additionally, environmental sustainability, social transformation, and environmental preservation have already been impacted by blockchain use. We used the Kaggle Smart Supply Chain dataset to assess how well our solution performed. We took into account a number of optimization approaches for this comparative study, including the particle swarm optimization (PSO), the artificial bee colony (ABC), the grey wolf optimization (GWO), and the jellyfish optimization (JFO). Several metrics, including efficacy, key sensitivity, correlation coefficient, and others, were used to validate the results of our investigation.

The experimental validation of the HGSODL-ASCM technique is investigated in detail. By implementing Hunger Games search optimisation techniques, businesses can align their supply chain management policies with actionable strategies. These techniques facilitate data-driven decision-making, permit organisations to optimise trade-offs, and enhance supply chain performance overall. Throughout the supply chain, they support the implementation of policies that promote sustainability, cost reduction, risk management, operational efficiency, and compliance.

  • Scenario1: A simple scenario with single retailer.

  • Scenario2: A classic scenario with 3 retailers and similar settings.

  • Scenario3: A difficult scenario with 3 retailers and distinct settings.

Table 1 and Fig. 3 examines the reward (profits) analysis of the HGSODL-ASCM technique under scenario 1 with existing models [33]. The experimental outcomes indicate that the HGSODL-ASCM technique reaches increasing rewards over other models. With 1000 time periods, the HGSODL-ASCM technique attains increasing rewards of 66.38 while the heuristic, Q-learning, and DR-SCM models obtain decreasing rewards of 51.19, 31.21, and 55.19 correspondingly. Meanwhile, with 5000 time periods, the HGSODL-ASCM technique attains increasing rewards of 92.77 while the heuristic, Q-learning, and DR-SCM methods attain decreasing rewards of 51.99, 66.38, and 75.98 correspondingly. Moreover, with 10000 time periods, the HGSODL-ASCM technique attains increasing rewards of 96.76 while the heuristic, Q-learning, and DR-SCM methods obtain decreasing rewards of 52.79, 76.78, and 84.77 correspondingly.

Table 1 Reward analysis of HGSODL-ASCM approach with other systems on scenario1
Full size table
Fig. 3
figure 3

Reward analysis of HGSODL-ASCM approach on scenario1

Full size image

Table 2 and Fig. 4 inspects the reward (profits) analysis of the HGSODL-ASCM method under scenario 2 with existing methods. The experimental outcome indicates that the HGSODL-ASCM method obtains increasing rewards over other models. With 1000 time periods, the HGSODL-ASCM method attains increasing rewards of 126.47 while the heuristic, Q-learning, and DR-SCM methods attain decreasing rewards of 104.72, 72.09, and 102.00 correspondingly. Meanwhile, with 5000 time periods, the HGSODL-ASCM technique attains increasing rewards of 190.38 while the heuristic, Q-learning, and DR-SCM methods obtain decreasing rewards of 103.36, 150.95, and 174.06 correspondingly. Furthermore, with 10000 time periods, the HGSODL-ASCM technique attains increasing rewards of 195.81 while the heuristic, Q-learning, and DR-SCM methods obtain decreasing rewards of 108.80, 160.46, and 175.42 correspondingly.

Table 2 Reward analysis of HGSODL-ASCM approach with other systems on scenario2
Full size table
Fig. 4
figure 4

Reward analysis of HGSODL-ASCM approach on scenario2

Full size image

The reward (profits) analysis of the HGSODL-ASCM technique under scenario 3 is examined in Table 3 and Fig. 5 using current models. The results of the experiments demonstrate that the HGSODL-ASCM approach outperforms other models with increasing rewards. With 1000 time periods, the HGSODL-ASCM method attains increasing rewards of 126.10 while the heuristic, Q-learning, and DR-SCM methods obtain decreasing rewards of 128.78, 81.80, and 105.96 respectively. Meanwhile, with 5000 time periods, the HGSODL-ASCM method accomplishes increasing rewards of 190.54 while the heuristic, Q-learning, and DR-SCM method attain decreasing rewards of 118.05, 148.92, and 171.74 correspondingly. Furthermore, with 10000 time periods, the HGSODL-ASCM method attains increasing rewards of 195.91 while the heuristic, Q-learning, and DR-SCM methods attain decreasing rewards of 119.39, 162.35, and 179.80 correspondingly.

Table 3 Reward analysis of HGSODL-ASCM approach with other systems on scenario3
Full size table
Fig. 5
figure 5

Reward analysis of HGSODL-ASCM approach on scenario3

Full size image

Table 4 and Fig. 6 represents the stock analysis of the HGSODL-ASCM technique with other existing techniques such as heuristics, Q-learning, and DR-SCM. The presented HGSODL-ASCM technique is retain the stock of factory accessible for the retailer in majority time periods, then the stock of retailer’s could endure positive. Due to the DR-SCM’s flexibility, production and storage levels at factories and merchants might be modified to accommodate cyclically fluctuating demand over a range of time periods. On the other hand, the current approaches frequently keep factory stock at a level that reflects demand in retailers from a number of perspectives but do not function well once the demand increases. Due to this issue, shops have negative inventories, which suggests that demand cannot be satisfied, resulting in declining profitability. The outcomes demonstrated the benefits of the HGSODL-ASCM technique in managing the difficult problems of ASC management in dynamic environment.

Table 4 Stock analysis of HGSODL-ASCM approach with other systems under varying time periods
Full size table
Fig. 6
figure 6

Stock analysis of HGSODL-ASCM approach with varying time periods

Full size image

Finally, the average training time (ATT) examination of the HGSODL-ASCM technique with recent models in Table 5 and Fig. 7. The experimental values inferred that the HGSODL-ASCM technique accomplishes reduced ATT of 0.20s/episode whereas the DR-SCM, Q-learning, and heuristic techniques attain increasing ATT of 0.43s, 0.68s, and 1.15s for every episodes. Meanwhile, under scenario2, the HGSODL-ASCM technique accomplishes reduced ATT of 1.95s/episode whereas the DR-SCM, Q-learning, and heuristic methods attain increasing ATT of 2.32s, 2.80s, and 3.07s for every episodes.

Table 5 ATT analysis of HGSODL-ASCM approach with recent methods
Full size table
Fig. 7
figure 7

ATT analysis of HGSODL-ASCM approach with recent methods

Full size image

Eventually, under scenario3, the HGSODL-ASCM method accomplishes reduced ATT of 3.19s/episode whereas the DR-SCM, Q-learning, and heuristic techniques attain increasing ATT of 3.54s, 3.91s, and 3.99s for every episodes. These results shown the enhanced performance of the HGSODL-ASCM technique.

5 Conclusion

In this article, we have focused on the development of the HGSODL-ASCM technique for automated SCM in the agricultural and food supply industries. The goal of the HGSODL-ASCM technique assists in the effectual decision-making process related to the production and storage of agricultural and food products to optimize profits. In the presented HGSODL-ASCM technique, the Bi-LSTM model is derived to compute the quantity of productivity and storage to accomplish maximum profit. In order to boost the performance of the Bi-LSTM classification process, the HGSO algorithm has been utilized in this work. The presented HGSODL-ASCM technique can independently achieve the SCM policies via interaction with complicated and adaptive environments. A brief set of simulations were performed to ensure the improved performance of the HGSODL-ASCM technique. The results of the simulation showed how effective the HGSODL-ASCM technique is compared to other methods already in use. The suggested HGSODL-ASCM approach can be expanded in the future to address issues with cold storage in the pharmaceutical sector. In terms of data collecting, storage, and querying capabilities for product identification and monitoring, the proposed HGSODL-ASCM model has a considerable disadvantage. This architecture uses a blockchain, which demands recording all blocks and transactions among network users, placing storage capacity restrictions on this data. The accuracy, security, and privacy of tracking data must be protected, which further reduces the effectiveness and traceability of supply chain management systems. It is suggested that in order to resolve these issues and improve system resilience, central processing should be abandoned and each party should be required to keep a local copy of the whole set of traceable data. The development of sturdy systems will be facilitated by this method. Blockchain architecture places a premium on connecting data across remote data centres, therefore the speed at which that data is shared limits the data’s availability. In other words, the delay makes it harder to communicate the situation as it is. The simulation findings are noteworthy for their speedy convergence, even distribution, and high efficacy and demonstrate the success of the offered approaches. The quality and reliability of the suggested procedures were proven by comparison results with other well-known optimisation techniques. The current work can be improved in the future by putting this technology into a real-time application.