Skip to main content

Advertisement

SpringerLink
Log in

Experimental and numerical analyses on crushing behaviour of drawn cups of laser welded tailored blanks under axial loading

  • Original Article
  • Published:
Archives of Civil and Mechanical Engineering Aims and scope Submit manuscript

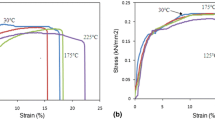
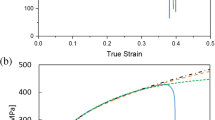
Abstract

It is imperative to characterize the crushing behaviour of deep drawn components of tailor welded blanks for their wide applications in different autobody structures. In the present work, extra deep drawing steel sheets were laser welded to produce welded blanks of similar thickness and dissimilar thickness (LWTBs), and these were deformed using a two stage deep drawing setup to fabricate geometrically similar drawn cups consisting of both hemispherical and cylindrical segments. Subsequently, these drawn cups were axially crushed between two flat platens to study collapse modes, load–displacement responses and energy absorption capabilities. The collapse of the drawn cups was found to onset with an inward dimpling of the hemispherical segment. As deformation progressed, the folding of cylindrical section occurred either axisymmetrically or unevenly based on the extent of non-uniform thickness variations across the weld zone (WZ). It was also found that the load–displacement response and energy absorption of the cups were enhanced because of the presence of WZ and thickness difference in LWTBs. Also, finite element-based numerical models were developed to collate the prediction capabilities of three different anisotropic material models viz. Hill48, YLD89, and Stoughton non-associated flow rule (S-NAFR)-based model. All these material models were successfully calibrated to predict the collapse modes, but the S-NAFR model was found to closely predict the load–displacement curves and energy absorption. Furthermore, the assessment of specific energy absorption and crushing force efficiency suggested that lightweight LWTB components can be fabricated with improved crashworthiness performance using sheet materials of different thickness.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Lokka AM. An economic evaluation of tailor welded blanks in automotive applications. 1997

  2. Song X, Sun G, Li Q. Sensitivity analysis and reliability based design optimization for high-strength steel tailor welded thin-walled structures under crashworthiness. Thin-Walled Struct. 2016;109:132–42. https://doi.org/10.1016/j.tws.2016.09.003.

    Article  ADS  Google Scholar 

  3. Baroutaji A, Sajjia M, Olabi AG. On the crashworthiness performance of thin-walled energy absorbers: recent advances and future developments. Thin-Walled Struct. 2017;118:137–63. https://doi.org/10.1016/j.tws.2017.05.018.

    Article  Google Scholar 

  4. Sen D, Pal SK, Panda SK. Fabrication of longitudinal welded tube of aluminum alloy for structural application using friction stir welding process and its characterization. Arch Civ Mech Eng. 2022. https://doi.org/10.1007/s43452-022-00412-w.

    Article  Google Scholar 

  5. Bartczak B, Gierczycka-Zbrozek D, Gronostajski Z, Polak S, Tobota A. The use of thin-walled sections for energy absorbing components: a review. Arch Civ Mech Eng. 2010;10:5–19. https://doi.org/10.1016/S1644-9665(12)60027-2.

    Article  Google Scholar 

  6. Kumar AP, Mohamed MN, Jusuf A, Dirgantara T, Gunawan L. Axial crash performance of press-formed open and end-capped cylindrical tubes—a comparative analysis. Thin-Walled Struct. 2018;124:468–88.

    Article  Google Scholar 

  7. Tasdemirci A, Sahin S, Kara A, Turan K. Crushing and energy absorption characteristics of combined geometry shells at quasi-static and dynamic strain rates: experimental and numerical study. Thin-Walled Struct. 2015;86:83–93. https://doi.org/10.1016/j.tws.2014.09.020.

    Article  Google Scholar 

  8. Katiyar BS, Panda SK, Saha P. Quasi-static crushing behavior of stretch formed domes of laser welded tailored blanks. Thin-Walled Struct. 2021. https://doi.org/10.1016/j.tws.2020.107288.

    Article  Google Scholar 

  9. Kusuda H, Takasago T, Natsumi F. Formability of tailored blanks. J Mater Process Technol. 1997;71:134–40. https://doi.org/10.1016/S0924-0136(97)00159-3.

    Article  Google Scholar 

  10. Xu F, Wang C. Dynamic axial crashing of tailor-welded blanks (TWBs) thin-walled structures with top-hat shaped section. Adv Eng Softw. 2016;96:70–82. https://doi.org/10.1016/j.advengsoft.2016.02.003.

    Article  Google Scholar 

  11. Basak S, Katiyar BS, Orozco-Gonzalez P, Baltazar-Hernandez VH, Arora KS, Panda SK. Microstructure, forming limit diagram, and strain distribution of pre-strained DP-IF steel tailor–welded blank for auto body application. Int J Adv Manuf Technol. 2019. https://doi.org/10.1007/s00170-019-03938-1.

    Article  Google Scholar 

  12. Xu F, Sun G, Li G, Li Q. Experimental study on crashworthiness of tailor-welded blank (TWB) thin-walled high-strength steel (HSS) tubular structures. Thin-Walled Struct. 2014;74:12–27. https://doi.org/10.1016/j.tws.2013.08.021.

    Article  Google Scholar 

  13. Bandyopadhyay K, Panda SK, Saha P, Padmanabham G. Limiting drawing ratio and deep drawing behavior of dual phase steel tailor welded blanks: FE simulation and experimental validation. J Mater Process Technol. 2015;217:48–64. https://doi.org/10.1016/j.jmatprotec.2014.10.022.

    Article  CAS  Google Scholar 

  14. Choi Y, Heo Y, Kim HY, Seo D. Investigations of weld-line movements for the deep drawing process of tailor welded blanks. J Mater Process Technol. 2000;108:1–7. https://doi.org/10.1016/S0924-0136(00)00536-7.

    Article  CAS  Google Scholar 

  15. Ahmetoglu MA, Brouwers D, Shulkin L, Taupin L, Kinzel GL, Altan T. Deep drawing of round cups from tailor-welded blanks. J Mater Process Tech. 1995;53:684–94. https://doi.org/10.1016/0924-0136(94)01767-U.

    Article  Google Scholar 

  16. Heo YM, Wang SH, Kim HY, Seo DG. The effect of the drawbead dimensions on the weld-line movements in the deep drawing of tailor-welded blanks. J Mater Process Technol. 2001;113:686–91. https://doi.org/10.1016/S0924-0136(01)00672-0.

    Article  Google Scholar 

  17. Abbasi M, Ketabchi M, Labudde T, Prahl U, Bleck W. New attempt to wrinkling behavior analysis of tailor welded blanks during the deep drawing process. Mater Des. 2012;40:407–14. https://doi.org/10.1016/j.matdes.2012.04.015.

    Article  CAS  Google Scholar 

  18. Shi Y, Lin Z, Zhu P, Han S. Impact modeling of the weld line of tailor-welded blank. Mater Des. 2008;29:232–8. https://doi.org/10.1016/j.matdes.2006.12.005.

    Article  CAS  Google Scholar 

  19. Barlat F, Yoon JW, Cazacu O. On linear transformations of stress tensors for the description of plastic anisotropy. Int J Plast. 2007;23:876–96. https://doi.org/10.1016/j.ijplas.2006.10.001.

    Article  CAS  Google Scholar 

  20. Banabic D. Plastic behaviour of sheet metal. In: Sheet metal forming processes. Berlin: Springer; 2010. p. 27–140. https://doi.org/10.1007/978-3-540-88113-1_2.

    Chapter  Google Scholar 

  21. Saunders FI, Wagoner RH. Forming of tailor-welded blanks. Metall Mater Trans A. 1996;27:2605–16. https://doi.org/10.1007/BF02652354.

    Article  Google Scholar 

  22. Zadpoor AA, Sinke J, Benedictus R. Finite element modeling and failure prediction of friction stir welded blanks. Mater Des. 2009;30:1423–34. https://doi.org/10.1016/j.matdes.2008.08.018.

    Article  CAS  Google Scholar 

  23. Padmanabhan R, Baptista AJ, Oliveira MC, Menezes LF. Effect of anisotropy on the deep-drawing of mild steel and dual-phase steel tailor-welded blanks. J Mater Process Technol. 2007;184:288–93. https://doi.org/10.1016/j.jmatprotec.2006.11.051.

    Article  CAS  Google Scholar 

  24. Gaied S, Roelandt JM, Pinard F, Schmit F, Balabane M. Experimental and numerical assessment of Tailor–Welded Blanks formability. J Mater Process Technol. 2009;209:387–95. https://doi.org/10.1016/j.jmatprotec.2008.02.031.

    Article  CAS  Google Scholar 

  25. Barlat F, Aretz H, Yoon JW, Karabin ME, Brem JC, Dick RE. Linear transfomation-based anisotropic yield functions. Int J Plast. 2005;21:1009–39. https://doi.org/10.1016/j.ijplas.2004.06.004.

    Article  CAS  Google Scholar 

  26. Barlat F, Brem JC, Yoon JW, Chung K, Dick RE, Lege DJ, Pourboghrat F, Choi SH, Chu E. Plane stress yield function for aluminum alloy sheets—part 1: theory. Int J Plast. 2003;19:1297–319. https://doi.org/10.1016/S0749-6419(02)00019-0.

    Article  CAS  Google Scholar 

  27. Hariharan K, Nguyen NT, Chakraborti N, Lee MG, Barlat F. Multi-objective genetic algorithm to optimize variable drawbead geometry for tailor welded blanks made of dissimilar steels. Steel Res Int. 2014;85:1597–607. https://doi.org/10.1002/srin.201300471.

    Article  CAS  Google Scholar 

  28. Kohar CP, Brahme A, Imbert J, Mishra RK, Inal K. Effects of coupling anisotropic yield functions with the optimization process of extruded aluminum front rail geometries in crashworthiness. Int J Solids Struct. 2017;128:174–98. https://doi.org/10.1016/j.ijsolstr.2017.08.026.

    Article  Google Scholar 

  29. Ghorbel O, Koubaa S, Mars J, Wali M, Dammak F. Non associated-anisotropic plasticity model fully coupled with isotropic ductile damage for sheet metal forming applications. Int J Solids Struct. 2019;166:96–111. https://doi.org/10.1016/j.ijsolstr.2019.02.010.

    Article  Google Scholar 

  30. Safaei M, Lee MG, Zang SL, De Waele W. An evolutionary anisotropic model for sheet metals based on non-associated flow rule approach. Comput Mater Sci. 2014;81:15–29. https://doi.org/10.1016/j.commatsci.2013.05.035.

    Article  CAS  Google Scholar 

  31. Stoughton TB. A non-associated flow rule for sheet metal forming. Int J Plast. 2002;18:687–714. https://doi.org/10.1016/S0749-6419(01)00053-5.

    Article  Google Scholar 

  32. Basak S, Panda SK, Lee MG. Formability and fracture in deep drawing sheet metals: extended studies for pre-strained anisotropic thin sheets. Int J Mech Sci. 2020. https://doi.org/10.1016/j.ijmecsci.2019.105346.

    Article  Google Scholar 

  33. Banabic D, Aretz H, Comsa DS, Paraianu L. An improved analytical description of orthotropy in metallic sheets. Int J Plast. 2005;21:493–512. https://doi.org/10.1016/j.ijplas.2004.04.003.

    Article  CAS  Google Scholar 

  34. Cazacu O, Barlat F. A criterion for description of anisotropy and yield differential effects in pressure-insensitive metals. Int J Plast. 2004;20:2027–45. https://doi.org/10.1016/j.ijplas.2003.11.021.

    Article  CAS  Google Scholar 

  35. Yoon JW, Yang DY, Chung K, Barlat F. General elasto-plastic finite element formulation based on incremental deformation theory for planar anisotropy and its application to sheet metal forming. Int J Plast. 1999;15:35–67. https://doi.org/10.1016/S0749-6419(98)00059-X.

    Article  CAS  Google Scholar 

  36. Spitzig WA, Richmond O. The effect of pressure on the flow stress of metals. Acta Metall. 1984;32:457–63. https://doi.org/10.1016/0001-6160(84)90119-6.

    Article  CAS  Google Scholar 

  37. Lee JH. Research note on a simple model for pressure-sensitive strain-hardening materials. Int J Plast. 1988;4:265–78. https://doi.org/10.1016/0749-6419(88)90014-9.

    Article  CAS  Google Scholar 

  38. Stoughton TB, Yoon JW. A pressure-sensitive yield criterion under a non-associated flow rule for sheet metal forming. Int J Plast. 2004;20:705–31. https://doi.org/10.1016/S0749-6419(03)00079-2.

    Article  CAS  Google Scholar 

  39. Hill R. A theory of the yielding and plastic flow of anisotropic metals. Proc R Soc Lond Ser A Math Phys Sci. 1948;193:281–97. https://doi.org/10.1098/rspa.1948.0045.

    Article  MathSciNet  CAS  ADS  Google Scholar 

  40. ASTM E-517, Standard test method for plastic strain ratio R for sheet metal. In: ASTM international, pp 1–8, 2010. https://doi.org/10.1520/E0517-00R10.

  41. Hariharan K, Nguyen NT, Chakraborti N, Barlat F, Lee MG. Determination of anisotropic yield coefficients by a data-driven multiobjective evolutionary and genetic algorithm. Mater Manuf Process. 2015;30:403–13. https://doi.org/10.1080/10426914.2014.941480.

    Article  CAS  Google Scholar 

  42. Nguyen NT, Hariharan K, Chakraborti N, Barlat F, Lee MG. Springback reduction in tailor welded blank with high strength differential by using multi-objective evolutionary and genetic algorithms. Steel Res Int. 2015;86:1391–402. https://doi.org/10.1002/srin.201400263.

    Article  CAS  Google Scholar 

  43. Barlat F, Lian K. Plastic behavior and stretchability of sheet metals. Part I: a yield function for orthotropic sheets under plane stress conditions. Int J Plast. 1989;5:51–66. https://doi.org/10.1016/0749-6419(89)90019-3.

    Article  Google Scholar 

  44. Rojek J, Hyrcza-Michalska M, Bokota A, Piekarska W. Determination of mechanical properties of the weld zone in tailor-welded blanks. Arch Civ Mech Eng. 2012;12:156–62. https://doi.org/10.1016/j.acme.2012.04.004.

    Article  Google Scholar 

  45. Mamalis AG, Johnson W. The quasi-static crumpling of thin-walled circular cylinders and frusta under axial compression. Int J Mech Sci. 1983;25:713–32. https://doi.org/10.1016/0020-7403(83)90078-4.

    Article  Google Scholar 

  46. Ghasemabadian MA, Kadkhodayan M, Altenhof W, Bondy M, Magliaro J. An experimental study on the energy absorption characteristics of single- and bi-layer cups under quasi-static loading. Int J Crashworthiness. 2018. https://doi.org/10.1080/13588265.2018.1433348.

    Article  Google Scholar 

Download references

Acknowledgements

The authors are greatly thankful to Prof. Shamik Basak of Department of Mechanical and Industrial Engineering, Indian Institute of Technology Roorkee, India for his help in FE simulations of this study.

Funding

No funding was received for conducting this study.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Indian Institute of Technology Kharagpur, Kharagpur, West Bengal, 721302, India

    Bhupesh Singh Katiyar, Sushanta Kumar Panda & Partha Saha

Authors
  1. Bhupesh Singh Katiyar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sushanta Kumar Panda
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Partha Saha
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Conceptualization: Bhupesh Singh Katiyar, Sushanta Kumar Panda, Partha Saha; methodology: Bhupesh Singh Katiyar, Sushanta Kumar Panda, Partha Saha; formal analysis and investigation: Bhupesh Singh Katiyar, Sushanta Kumar Panda; writing—original draft preparation: Bhupesh Singh Katiyar; writing—review and editing: Bhupesh Singh Katiyar, Sushanta Kumar Panda, Partha Saha; Resources: Sushanta Kumar Panda, Partha Saha; supervision: Sushanta Kumar Panda, Partha Saha.

Corresponding author

Correspondence to Sushanta Kumar Panda.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Katiyar, B.S., Panda, S.K. & Saha, P. Experimental and numerical analyses on crushing behaviour of drawn cups of laser welded tailored blanks under axial loading. Archiv.Civ.Mech.Eng 22, 211 (2022). https://doi.org/10.1007/s43452-022-00537-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s43452-022-00537-y

Keywords

Search

Navigation