1 Introduction

The Ni-Al-Cr ternary system is considered to be well understood nowadays and used as a model system for nickel superalloys [1]. These alloys are used since the 1960’s for high-temperature parts of jet engines and gas turbines [2]. Modern Ni-based superalloys are characterized by developed chemical composition, which is selected so that they can withstand hard working conditions at elevated temperatures and corrosive environments [3]. A very good mechanical strength and resistance to thermal creep deformation superalloys are due to its phase composition obtained by solid solution strengthening. The main strengthening phase γ′ has an ordered FCC structure (L12) and is coherent with the matrix of disordered FCC structure γ phase (A1) [4]. Although the development of superalloys has led to an interest in other strengthening phases, in nickel superalloys γ′-Ni3(Al,Ti) phase is still the basic constituent [5]. Beside chromium as an addition improves anticorrosive properties [6] as well as ductility [7]. The alloys have already found industrial applications or are close to wide commercialization. There are several practical applications, including components of jet engines, turbochargers rotors in diesel-engine trucks, water turbine rotors and water pumps and other [8]. Both γ and γ′ differ considerably in view of mechanical properties. The ratio γ′ to γ in microstructure at a certain temperature determines the strength of modern alloys based on intermetallic phase Ni3Al with Cr addition, which are designated for high-temperature applications. Chromium is an element important in view of resistance to high-temperature corrosion, however, increasing its content at the expense of Al and Ni may modify the phase boundary or change the γ′/γ ratio. Coexistence of the γ and γ′ phases plays a significant role in controlling the strength of the alloys at elevated temperatures. Therefore, it becomes crucial to know precisely the course of phase boundaries γ′ / γ′ + γ / γ. The aim of the study was an investigation of the aforementioned phase boundaries at high-temperature and evaluation of their relationship with the mechanical properties of model alloys from Ni-Al-Cr system.

The complexity of modern nickel-based superalloys requires the use of computer-aided thermodynamic phase diagram calculations to make predictions for the phase behaviour of multi-component alloys [9]. One of the methods for the determination of phase diagrams is the Calphad procedure, which is based on models for the binary and ternary phase diagrams [10]. Therefore reliable experimental data on phase boundaries in these systems are crucial. In the case of the ternary Ni-Al-Cr phase diagram, literature data about phase boundaries γ′/(γ′ + γ) and (γ′ + γ)/γ are based mostly on the investigation of samples subjected to quenching and studied at low temperature [11]. While only at elevated temperature, these alloys reach state close to equilibrium. Figure 1 presents Ni-rich part of Ni–Al–Cr system at 600 °C. The Ni75Al25-Ni87Cr13 section was investigated by DTA thermal analysis [12] and calorimetric method [13]. Points representing γ′/(γ′ + γ) and (γ′ + γ)/γ phase boundaries were determined on the basis of change of alloys formation enthalpy, measured directly at 600 °C with the use of high-temperature calorimetric solution method [13]. Equilibrium solvus curves are results of calculation using the grand canonical Monte Carlo simulation technique [14] and calculation by Thermo-Calc software based on databases for nickel-based superalloys due to Saunders [1] and Dupin et al. [15]. The highest compatibility of mentioned methods can be observed for (γ′ + γ)/γ boundary. In the case of γ′/(γ′ + γ) boundary differences increase but simultaneously result of the calorimetric method is in good agreement with the result of the Monte Carlo simulation.

Fig. 1
figure 1

Ni-rich part of Ni–Al–Cr system at 600 °C. Equilibrium solvus curves are results of GCMC (Grand Canonical Monte Carlo) [14] and Thermo-Calc software calculation [1, 15]. Red line shows Ni75Al25 ÷ Ni87Cr13 section with chemical composition representing alloys studied in this work. Points represent phase boundaries determined by the high-temperature solution calorimetry method [13]

Full size image

With the above remarks in mind, authors of this work decided to present an experimental confirmation of the high-temperature course of phase boundaries γ′/(γ′ + γ) and (γ′ + γ)/γ in Ni–Al-Cr system. The temperature 600 °C has been chosen due to the availability of the comparative data on the tested phase boundaries γ′/γ′ + γ /γ in the literature

[1, 13,14,15]. The second reason for 600 °C was the range of the investigated phases. This is of particular importance in the case of the γ′ ordered phase, in which the field of occurrence drastically decreases with increasing temperature. On the other hand alloys from the nickel-rich part of the Ni-Al-Cr system are model alloys for high-temperature superalloys, which are subjected to heat treatment to stabilize the γ′ reinforcing phase. Therefore, for comparative purposes only, an additional experiment was performed, which consisted of compressing the samples in the as-cast condition at room temperature. Its task was to check what the primary phase composition looks like and whether it affects the mechanical properties of the alloys. For this purpose, alloys with chemical composition from Ni75Al25-Ni87Cr13 section as in work [13] were prepared. Alloys were used to prepare samples subjected to plastic deformation by compression on the universal simulator of metallurgical processes Gleeble 3800. As a result of the experiment, deformation curves of different nature were obtained, which allowed to assign tested alloys to appropriate phase regions: γ′, γ′ + γ and γ. Hardness and X-ray Diffraction (XRD) measurements were also performed, confirming previous results.

2 Materials and methods

The red line in Fig. 1 illustrates the analyzed composition range within the isothermal section of the N-Al-Cr ternary system at 600 °C. Therefore, the eleven alloys corresponding to the indicated composition range were prepared. The nominal and experimentally measured compositions are shown in Table 1. Metals of high purity: Al (99.99%), Ni (99.98%) and Cr (99.90%) were melted in the temperature range 1600–1700 °C using induction vacuum furnace Balzers VSG-02. Alloys were cast into cold ceramic mould under a protective Ar atmosphere. Solidification time did not exceed 10 s. As a result rods with a diameter of approx. 15 mm were obtained. Then the rods were machined to reduce the diameter to 10 mm and cut into 12 mm long pieces. The prepared specimens were used for further research. Chemical composition analysis was carried out on laboratory emission optical spectrometer Foundry-Master Compact by Oxford Instruments. Mean and standard deviation were calculated from six measurements and presented in Table 1. As cast specimens microstructure was analyzed by optical microscopy with the use of a Nikon Eclipse MA200 microscope. Specimens were prepared by grinding, polishing and chemical etching. Reagent containing 25 mL H2O, 50 mL HCl, 15 g FeCl3 and 3 g CuCl2 × NH4Cl2 × H2O was used for etching. Some of the specimens were subjected to mechanical properties research and the rest was forwarded for heat treatment.

Table 1 Chemical composition of studied alloys
Full size table

Mechanical properties were tested on Gleeble 3800 thermomechanical simulator. Cylindrical samples with a diameter of 10 mm and 12 mm height were subjected to a compression test with strain rate 0.001 s−1. First experiment was carried out at room temperature on specimens in the as-cast condition. Specimens in the second experiment were compressed directly at a temperature of 600 °C after being pre-heated to 1100 °C for 300 s in the simulator. This approach was aimed at bringing the alloys closer to thermodynamic equilibrium. Taking into account the device limitations, long-term annealing at 600 °C would not be possible. Therefore, the alloys were heated directly in the device at a temperature in which it was much easier to reach the equilibrium state and cooled to avoid the transition to the metastable state, which is very easy at low temperatures. Resistance heating was carried out in a protective atmosphere of argon. Temperature control was provided by a K-type thermocouple soldered to the sample surface. After the deformation, samples were cooled by blowing with compressed air. Diagram of the Hydrawedge measurement unit used in Gleeble 3800 thermomechanical simulator is shown in Fig. 2.

Fig. 2
figure 2

Diagram of the Hydrawedge system used in Gleeble 3800 thermomechanical simulator: 1 main hydraulic cylinder, 2.transformer, 3 device frame, 4 compression anvil, 5 specimen, 6 anvil, 7 wedge, 8 return spring, 9, 10 pneumatic cylinders, 11. hydraulic piston, 12 moveable shaft, 13 stop, 14 yoke, 15 forming force sensor, 16 hydraulic cylinder of the Hydrawedge system [16]

Full size image

Heat treatment operation was carried out in a laboratory resistance furnace with the Ar protective atmosphere. Solution heat treatment was performed at 1100 °C for 5 h with subsequent quenching in water. Next, part of the solutionized samples were subjected to aging at a temperature of 600 °C for 5 h in the Ar atmosphere with final water quenching. Phase composition of alloys was evaluated by X-ray diffraction method using Phillips X’Pert3 Powder diffractometer. Furthermore, the hardness of specimens was investigated by the Vickers method. Measurements were performed using the ZWICK ZHV TKV5030 Vickers hardness tester using a load of HV10.

3 Results

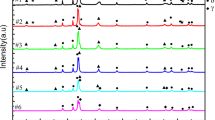
Table 1 shows the chemical composition of tested alloys and their denotation used in this work. Figure 3 shows studied alloys against the ternary Ni-Al-Cr system. Microstructure of the alloys in as-cast condition is shown in Fig. 4. Results of compression tests of samples at room temperature and at temperature 600 °C after pre-heated to 1100 °C in Gleeble 3800 thermomechanical simulator are presented in Figs. 5 and 6. All deformation curves presented in the paper are engineering stress–strain curves. Figure 7 shows a view of the samples after compression tests in reference to the cylinder-shaped base specimen with a diameter of 10 and 12 mm height. XRD analysis results of samples in as-cast condition, samples after solution heat treatment at 1100 °C for 5 h with water quenching and samples subjected to solution heat treatment at 1100 °C for 5 h followed by aging at 600 °C for 5 h with water quenching are presented in Fig. 8, 9 and 10. The reference XRD patern ICDD no. 98-005-8039 was used for identification of the γ′ ordered phase (L12), whereas ICDD no. 98-004-1508 was used to identify the γ disordered phase (A1). Hardness of studied alloys in the above-mentioned conditions is presented in Fig. 11 as an arithmetic mean of five measurements.

Fig. 3
figure 3

Chemical composition of studied alloys against Ni75Al25 ÷ Ni87Cr13 section of ternary Ni-Al-Cr system

Full size image
Fig. 4
figure 4

Microstructure of tested alloys in the as-cast condition

Full size image
Fig. 5
figure 5

Result of compression tests on the Gleeble 3800 thermomechanical simulator at room temperature. Samples in the as-cast condition

Full size image
Fig. 6
figure 6

Result of compression tests on the Gleeble 3800 thermomechanical simulator directly at a temperature of 600 °C after pre-heated to 1100 °C in the device

Full size image
Fig. 7
figure 7

View of the samples after compression tests at room temperature and 600 °C. BS–base sample geometry (cylinder with a diameter of 10 mm and a height of 12 mm)

Full size image
Fig. 8
figure 8

X-ray diffraction patterns with identified phases of samples in as-cast condition

Full size image
Fig. 9
figure 9

X-ray diffraction patterns with identified phases of samples after solution heat treatment at 1100 °C for 5 h with water quenching followed by aging at 600 °C for 5 h with water quenching

Full size image
Fig. 10
figure 10

X-ray diffraction patterns with identified phases of samples after solution heat treatment at 1100 °C for 5 h with water quenching

Full size image
Fig. 11
figure 11

Hardness of studied alloys

Full size image

4 Discussion

The Ni-Al-Cr alloys exhibit γ′-strengthening at elevated temperature. As it was revealed, the Ni-Al-Cr may be characterized by a double-phase microstructure composed of γ-Ni and γ′-Ni3Al phases [17]. The strengthening by the γ′ phase feature substantially improves high creep resistance at an operating temperature [18]. The ternary system Ni–Al–Cr provides the basis for simplifying the complex chemistry of most of Ni-based superalloys [19]. Therefore, the phase boundaries of the Ni-rich part of the system are of special concern. To determine the course of phase boundaries in alloys, various research methods are used, which, due to their limitations and complex chemical compositions of advanced alloys, often require additional experiments to confirm the results [20]. This work presents the results of research aimed at determining the course of the γ′/(γ′ + γ) and (γ′ + γ)/γ phase boundaries in the nickel-rich part of ternary Ni–Al-Cr system at 600 °C. Alloys from Ni75Al25 ÷ Ni87Cr13 section of this system were selected for testing. Temperature of 600 °C was chosen due to the availability of literature data and range of the expected ordered phase γ′. At the same time, such a high temperature facilitates the approach to a state close to thermodynamic equilibrium, which is difficult to achieve at lower temperatures, and practically not achievable at room temperature.

Alloys were prepared using the standard casting method by melting metals in an induction furnace and cast them into a ceramic mold in a protective atmosphere of Ar. Chemical analysis confirmed the lack of significant contamination by other elements that could interfere with the course of the subsequent experiments (Table 1). The obtained chemical compositions are in very good agreement with Ni75Al25 ÷ Ni87Cr13 section of Ni-Al-Cr system (Fig. 3). Tested alloys in the as-cast condition were characterized by a dendritic structure, which is particularly clear in the case of the microstructure of alloy No. 4 (Ni79.8Al15.1Cr5.1) (Fig. 4). The dendrite cores and interdendritic spaces are marked. Qualitative phase analysis performed by the XRD method revealed the presence of the ordered phase γ′ (L12) in alloys from 1 (Ni76.2Al22.4Cr1.4) to 6 (Ni81.8Al11.0Cr7.2). In the remaining alloys, only the disordered phase γ (A1) was identified (Fig. 8). To demonstrate the relationship between phase composition and properties of tested alloys, it was decided to subject them to a compression test carried out on the Gleeble 3800 thermomechanical simulator. Experiments were carried out with a constant deformation rate of 0.001 s−1 on samples in as-cast condition at room temperature and directly at a temperature of 600 °C after pre-heating at 1100 °C in the device. This choice of temperature program was aimed at approaching the conditions of thermodynamic equilibrium. Analysis of performed compression test at room temperature showed differences in the deformability of the tested alloys (Fig. 5). The lowest plasticity was found for alloy No. 1 (Ni76.2Al22.4Cr1.4). In this case, the yield stress reached a value significantly exceeding 1400 MPa. The highest plasticity was observed for alloy No. 10 (Ni85.6Al2.9Cr11.5), for which yield stress was slightly over 800 MPa. Thus, the influence of the increasing chromium content on the increase in the plasticity of tested alloys at room temperature is clearly visible. Only in the case of alloy No. 11 (Ni86.6Al1.0Cr12.4), a higher than expected value of stress and deformation, similar to that of alloy No. 8 (Ni84.0Al6.6Cr9.4), was obtained. This may be due to differences in the alloy phase structure in which chromium begins to play a greater role than aluminum, which can lead to the formation of Ni–Cr phase regions that may be difficult to identify by XRD. Another observation worth noting is the difference in the shape of deformation curves for alloys from 1 (Ni76.2Al22.4Cr1.4) to 6 (Ni81.8Al11.0Cr7.2) compared to alloys from 7 (Ni82.5Al9.5Cr8.0) to 11 (Ni86.6Al1.0Cr12.4) which clearly corresponds with the results of phase analysis of alloys in as-cast state. The γ′ ordered phase was found in the above-mentioned alloys, which is reflected in lower plasticity in relation to alloys containing the γ disordered phase (Fig. 8).

Much greater differentiation in the course of deformation curves was obtained when compressing the alloys directly at 600 °C after pre-heating at 1100 °C (Fig. 6). A common feature for all alloys tested at 600 °C is significantly higher plasticity compared to the samples tested at room temperature, which is also confirmed by the general view of the samples after compression (Fig. 7). Just as in the experiment at room temperature, the highest stress value of approx. 1100 MPa was obtained for sample No. 1 (Ni76.2Al22.4Cr1.4), and the lowest, about 650 MPa for sample No. 10 (Ni85.6Al2.9Cr11.5). Such a large variation in the course of deformation curves was attributed to the variability of the phase composition. Results of a similar nature were distinguished and grouped into four groups (Fig. 12). Alloys with numbers from 3 (Ni78.3Al18.0Cr3.7) to 6 (Ni81.8Al11.0Cr7.2) deserve special attention. Each time during compression tests of alloys from this group, the phenomenon of sample burst was observed, which was most often accompanied by a detachment of soldered thermocouple from the specimen surface (Fig. 13). Measurements were repeated several times, excluding the presence of the contraction cavity as a cause that could affect the occurrence of this phenomenon. Paper presents the most representative compression results at 600 °C for alloys with numbers from 3 (Ni78.3Al18.0Cr3.7) to 6 (Ni81.8Al11.0Cr7.2). A similar behavior was not found for the other alloys, but it is clearly visible that the deformation curves of alloys No. 1 (Ni76.2Al22.4Cr1.4) and 2 (Ni77.4Al20.0Cr2.6) differ from alloys with numbers from 7 (Ni82.5Al9.5Cr8.0) to 11 (Ni86.6Al1.0Cr12.4), which are similar in nature to the results obtained for samples compressed at room temperature. The following part of the discussion presents an attempt to explain the phenomenon of cracking in the compressed samples in relation to the results of phase analysis and hardness measurements of alloys.

Fig. 12
figure 12

Different types of deformation curves recorded during compression of alloys at 600 °C after pre-heating at 1100 °C

Full size image
Fig. 13
figure 13

Alloys for which sample burst was observed during compression at 600 °C after pre-heating at 1100 °C

Full size image

To verify the occurrence of the relationship between the phase structure and the properties of tested alloys, it was decided to perform the XRD phase analysis on samples after heat treatment corresponding to the thermal conditions used during the experiment on the Gleeble 3800 thermomechanical simulator. Alloys in as-cast state were subjected to solution heat treatment at 1100 °C for 5 h in the Ar atmosphere with subsequent quenching in water. Next, samples were subjected to aging at a temperature of 600 °C for 5 h in the Ar atmosphere with final water quenching. Results of the XRD analysis confirmed the presence of ordered phase γ′ in alloys from 1 (Ni76.2Al22.4Cr1.4) to 8 (Ni84.0Al6.6Cr9.4) (Fig. 9). In the remaining alloys, only disordered γ phase was identified, which is consistent with the results obtained for samples compressed at room temperature in the as-cast condition. An additional series of samples for XRD analysis was prepared and subjected only to solution heat treatment at 1100 °C for 5 h in the Ar atmosphere with subsequent quenching in water. Assuming that with increasing temperature the alloy more easily approaches the state of thermodynamic equilibrium, such action was aimed at checking whether the temperature program proposed for compression tests directly at elevated temperature is appropriate. Results of XRD analysis of alloys subjected only to solution heat treatment at 1100 °C for 5 h are presented in Fig. 10. The presence of γ′ ordered phase was confirmed only in alloys from 1 (Ni76.2Al22.4Cr1.4) to 4 (Ni79.8Al15.1Cr5.1).

All results of XRD analysis were compared with the results obtained for analogous alloys by Maciąg et al. who used the calorimetric solution method and Differential Thermal Analysis (DTA) for determination γ′/(γ′ + γ) and (γ′ + γ)/γ phase boundaries [12, 13] (Fig. 14). The calorimetric method, thanks to the use of a high-temperature solution calorimeter, which was equipped with a heated intermediate container, allowed for measurements directly at an elevated temperature. In this method, huge differences in binding energy between ordered (γ′) and disordered (γ) phase were used. Phase boundaries γ′/(γ′ + γ) and (γ′ + γ)/γ at a temperature of 600 °C, 723 °C and 877 °C were determined based on enthalpy of formation of alloys from the range Ni75Al25 ÷ Ni87Cr13 as a function of chromium concentration. Thermal analysis allowed for the determination of phase boundary (γ′ + γ)/γ at temperatures above 900 °C during heating and cooling of alloys, however, it turned out to be too insensitive to identify changes taking place at lower temperatures, in particular related to the γ′/(γ′ + γ) boundary [12]. Similar results can be found in Hong et al. work where authors using DTA thermal analysis method determine (γ′ + γ)/γ phase boundary but not γ′/(γ′ + γ) [21]. Results of XRD analysis presented in this study are in very good agreement with the results obtained by Maciąg et al. in the range of (γ′ + γ)/γ phase boundary at 600 °C and 1100 °C. The difficulty arises in the case of γ′/(γ′ + γ) phase boundary. Due to the fact that the x-ray diffraction pattern of γ′ (L12) phase differs only by the presence of peaks for a few additional angles in relation to γ (A1) phase, we are not able to determine on the basis of the qualitative XRD results whether we are dealing only with the phase γ′ or the two-phase area γ′ + γ. In the case of room temperature, marked in Fig. 14 as 20 °C, we deal with a metastable state, which was confirmed earlier by observations of the microstructure.

Fig. 14
figure 14

Comparison of XRD analysis results obtained in this work for alloys from Ni75Al25 ÷ Ni87Cr13 section of Ni-Al-Cr system with phase boundaries results obtained in other works [12, 13]

Full size image

The last study performed was alloy hardness measurement using the Vickers method under the HV10 load. Samples in as-cast condition, samples after solution heat treatment at 1100 °C for 5 h with water quenching and samples subjected to solution heat treatment at 1100 °C for 5 h followed by aging at 600 °C for 5 h with water quenching were examined (Fig. 11). As-cast state is characterized by higher hardness values, which in the alloy No. 4 (Ni79.8Al15.1Cr5.1) was about 280 HV. There is also a significant decrease in hardness for alloys with numbers from 7 (Ni82.5Al9.5Cr8.0) to 11 (Ni86.6Al1.0Cr12.4). This is in very good agreement with the results obtained during compression tests at room temperature and the results of XRD analysis, which showed in these alloys only the disordered phase γ (Figs. 5 and 8). In general, the course of changes in the hardness of tested alloys takes the shape of a triangle. Chemical compositions on the left and right are closer to single-phase areas, which are characterized by lower hardness than two-phase area in the middle. This is clearly visible in the case of alloys subjected to solution heat treatment at 1100 °C for 5 h followed by aging at 600 °C for 5 h with water quenching, where the highest hardness value of 298 HV was obtained for sample 5 (Ni80.6Al13.2Cr6.2), and according to Fig. 14, chemical composition of this alloy is almost in the middle of the γ′ + γ two-phase area, which can be treated as a disordered γ phase matrix reinforced with ordered γ′ phase particles. It is also worth noting that alloy No. 5 (Ni80.6Al13.2Cr6.2) was the most susceptible to tearing during compression tests at 600 °C (Fig. 13). Further evidence is found in the hardness results for three states of heat treatment, e.g. alloy No. 7 (Ni82.5Al9.5Cr8.0) and alloy No. 8 (Ni84.0Al6.6Cr9.4) at 600 °C lie in the two-phase region γ′ + γ hence their hardness is higher than in samples in as-cast state and samples quenched from 1100 °C. On the other hand, alloy No. 1 (Ni76.2Al22.4Cr1.4), for which we expect a single-phase γ′ structure at 600 °C, after heat treatment and cooling, shows a significant decrease in hardness compared to the alloy in as-cast state, in which we expect also the presence of the disordered γ phase. The alloys with the highest Cr-content exhibit the highest ductility at room temperature. Furthermore, these alloys were characterized by relatively low hardness.

Summing up, the determination of the high-temperature phase boundaries γ′/(γ′ + γ) and (γ′ + γ)/γ in nickel-rich part of the ternary Ni-Al-Cr system based only on the results of a single experimental method is difficult. Each of the experimental methods used in this work has its limitations, but their results showed very good agreement, especially in terms of the (γ′ + γ)/γ phase boundary. This is due to the fact that the appearance of γ′ ordered phase in the system has a clear impact on the mechanical properties of alloy, and at the same time it is possible to identify this phase using XRD analysis. Phase boundary γ'/(γ' + γ) is much more difficult to determine what is reflected in the literature data and the difference between the experiments, and the results of thermodynamic calculations. The results of this work do not allow to unequivocally determine the high-temperature γ′/(γ′ + γ) phase boundary in the ternary Ni-Al-Cr system. Only when they are compared with the results of unconventional methods, such as high-temperature calorimetric solution measurements, they can be interpreted. Presented conclusions can also be extended to other alloys in which ordered phases play a role.

5 Conclusions

  1. 1.

    Series of eleven alloys with chemical composition belonging to the Ni75Al25 ÷ Ni87Cr13 section of ternary Ni-Al-Cr system was subjected to experiments to confirm the course of high-temperature phase boundaries γ′/(γ′ + γ) and (γ′ + γ)/γ.

  2. 2.

    The relationship between the phase structure of studied alloys and their mechanical properties has been proven by the example of compression tests of samples in as-cast condition at room temperature and directly at 600 °C temperature after pre-heating at 1100 °C in Gleeble 3800 thermomechanical simulator.

  3. 3.

    Deformation curves with different courses were recorded. They were grouped and assigned the appropriate phase composition based on the XRD analysis, which confirmed the presence of disordered phase γ and ordered phase γ′ in studied alloys.

  4. 4.

    Hardness measurements of alloys in three states of heat treatment were performed and relationship between hardness and the presence of two or single-phase structure was demonstrated.

  5. 5.

    The results of all research methods described in the paper showed very good agreement when confirming (γ′ + γ)/γ phase boundary. In the case of γ′/(γ′ + γ) phase boundary, the interpretation of results requires the support of unconventional methods results, such as the high-temperature calorimetric solution method.

  6. 6.

    Increase of Cr content in Ni-Al-Cr alloys cause a shift of (γ′ + γ)/γ phase boundary to lower temperatures which is unfavourable in view of their application for heavily loaded components operating at high temperatures. The change in course of phase boundaries is connected with a decrease in strength at high temperatures. The conducted research shows that the determination of high-temperature phase boundaries may allow for estimation of changes in mechanical properties caused by modification of the chemical composition of alloys from Ni-Al-Cr system.