1 Introduction

Nowadays, photovoltaic systems are becoming more popular due to their advantages in terms of unlimited reservation, pollution-free and convenient utilization [1]. As a core piece of equipment for photovoltaic systems, inverters play an important role in reducing output harmonics and improving system efficiency [2]. Compared with traditional two-level inverters, multilevel inverters are more suitable for PV systems due to their unique characteristics [3,4,5]. Multilevel inverters come with the benefits of reduced du/dt, reduced device voltage stress, improved output waveform quality and smaller filter inductance [6,7,8]. These benefits make it easier to meet the demands in photovoltaic applications.

There are a few classics multilevel inverter topologies. These classes are the neutral point clamped topology (NPC) [9,10,11], the flying capacitor topology (FC) [12, 13], and the cascaded H-bridge topology (CHB) [14,15,16]. NPC inverters are widely used in photovoltaic systems due to their characteristics of low switch losses, and freedom from common-mode leakage current. However, all of the NPC inverters need to solve the problem of capacitor voltage balance on dc side. CHB inverters can heighten the voltage rank by series connections. However, CHB converters require multiple sets of isolated dc sources, which is a main drawback of this topology.

Topologies with the multilevel structure have good output characteristics due to their ability to produce staircase-like voltage waveforms. However, multilevel inverters exhibit an important limitation. For an increased number of output levels, they require many power switches, which increases the cost, control complexity and the losses of devices [17]. In photovoltaic applications, the output power of PV cells spans a wide range and varies greatly [18,19,20,21]. Due to the wide input range of inverters, the power levels of the power devices and filter inductor are selected from the maximum output power. This leads to high device cost, high losses and low system utilization.

There is a contradiction between achieving a wide operational range and reducing power losses [22, 23]. For the past few years, efforts have been directed to reduce the cost and losses in multilevel inverters, and many topologies have appeared. In [24] and [25], a T-type inverter with a significant reduction in the number of power devices was described. In addition, this topology can be applied to any number of voltage levels within the switch maximum voltage. The losses are decreased since higher voltage rated switches operate at the fundamental frequency in this topology. In [26], a multilevel inverter using the series/parallel conversion of dc voltage sources was proposed. When the capacitors are connected in series, the voltage of devices is reduced, as well as the total losses of the devices. In [27], a flying capacitor clamped inverter based on a switched-capacitor was proposed. Its modulation strategy reduced the losses of the switch devices by curtailing the switch frequency of certain switches. In [28], an H-bridge inverter with dc side switches was proposed and applied to a PV system. In this topology, the bridge arm switches operate at a low frequency, which reduces the switch losses. The above inverter topologies reduced losses by optimizing the topology structure. However, all of the switches are always under operating state, and the total losses are still large.

Considering the actual conditions in a PV system, the operational range of an inverter should be wide. Different output characteristics of an inverter are needed under different conditions. This paper proposes a cascaded multilevel inverter. Based on a wide operational range, the inverter can provide different output characteristics to adapt to different conditions. Using a bidirectional switch unit, the proposed inverter can change its topology structure to operate in three modes: nine-level mode, five-level mode and three-level mode. When the dc input power is low, the nine-level or five-level mode can provide more output levels to improve the quality of the output waveform. When the dc input power is high, the three-level mode can reduce the number of active switch devices to decrease the inverter losses.

This paper is organized as follows. Section 2 introduces the topology of a cascaded multi-mode inverter, and modulation methods of the three modes are described in detail. In addition, the capacitor voltage balance on the dc side is analyzed. Section 3 analyzes and calculates the losses and the current total harmonic distortion of the inverter during the three modes. Section 4 offers simulation and experimental results. Section 5 provides some conclusions for this paper.

2 Cascaded multimode inverter and its modulation strategy

2.1 Topology structure

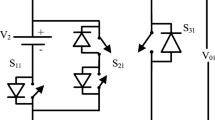
The topology of the proposed cascaded multilevel inverter is presented in Fig. 1a. It consists of twelve switches S1–S12, and a bidirectional switch unit S0. In addition, it also contains four clamping diodes D1–D4, four clamping capacitors C1–C4, and two dc voltage sources. By the bidirectional switch unit, the proposed inverter can change its topology structure to operate in three operation modes. According to different working conditions, different operation modes can be applied.

Fig. 1
figure 1

Diagrams showing: a topology of the proposed inverter; b nine-level mode; c five-level mode; d three-level mode

Full size image

The three working modes are presented as follows. (1) Keep the bidirectional switch S0 off, and the topology is a cascaded nine-level inverter. This mode is called the nine-level mode, as shown in Fig. 1b. (2) Keep the bidirectional switch S0 off, keep the switches S1, S2, S7 and S8 on, and the topology is a cascaded five-level H-bridge inverter. This mode is called the five-level mode, as shown in Fig. 1(c). (3) Keep the bidirectional switch S0 as well as the switches S1, S2, S4, S7, S8 and S9 on. Meanwhile, keep switches S6 and S11 off. The topology becomes one H-bridge inverter composed of the switches S3, S5, S10 and S12. With the switches S1, S2, S4, S7 and S9 and the bidirectional switch S0 kept on, two dc sources are connected in parallel. This mode is called the three-level mode, as shown in Fig. 1d.

2.2 Modulation strategy

When the proposed inverter operates in the nine-level mode, the switches connected to the dc side (S1, S2, S7, S8) are controlled to output required waveforms, and the bridge arm switches (S3–S6, S9–S12) are controlled to change the polarity of output waveforms. Therefore, the dc side switches act at a high frequency while the bridge arm switches act at a low frequency. Taking the upper half of the topology as an example, the voltage of each capacitor is 0.5Udc. When S1 and S2 are switched on, the clamping capacitors C1 and C2 are in the discharge state, and the output voltage is Udc. When S1 is on and S2 is off, or when S1 is off and S2 is on, only one capacitor discharges. Thus, the output voltage is 0.5Udc. When both S1 and S2 are switched off, none of the capacitors discharge. Thus, the output voltage is 0.

The modulation strategy of the nine-level mode of the proposed inverter is shown in Fig. 2. It requires eight carriers (Tri1–Tri8) and one reference signal (Tref) to generate original waveforms. The amplitude of each carrier is 1, the frequency is the same, and the phase difference between adjacent carriers is 90°. Depending on modulation ratio M1, the amplitude of the reference signal Tref changes between 0 and 1. Eight sets of rectangular pulse signals are obtained by comparing the carriers and the reference signal, to control the dc side switches. In addition, the switches (S3–S6, S9–S12) are controlled by the reference signal polarity.

Fig. 2
figure 2

Modulation strategy for the nine-level mode

Full size image

Moreover, the capacitors (C1–C4) clamp the dc voltage when the proposed inverter operates in the nine-level mode. The inverter can output a nine-level voltage when all the capacitor voltage is Udc/2. Thus, it is of great importance to keep the voltage balance of the capacitors. When the inverter outputs a voltage of ± Udc/2, ± Udc, ± 3Udc/2, only parts of the capacitors discharge. As a result, the capacitor voltage balance was broke. The key to achieving voltage balance is to make all of capacitors output the same energy in one cycle.

Figure 3 shows the discharge states of four capacitors, and the colored squares mean the discharge time of each capacitor. Since the carrier frequency is much higher than the modulation frequency, the reference signal in Fig. 3 can be seen as a horizontal line. The amplitude of the carriers is 1. When the reference signal is in the interval of [0, 0.25], the inverter outputs a voltage of 0 or Udc/2. As a result, there are 0 or 1 capacitor discharges at the same time, as shown in Fig. 3a. Similarly, when the reference signal is in the interval of [0.25, 0.5], there are 1 or 2 capacitors discharged at the same time, as shown in Fig. 3b. When the reference signal is in the interval of [0.5, 0.75], there are 2 or 3 capacitors discharged at the same time, as shown in Fig. 3c. In addition, when the reference signal is in the interval of [0.75, 1], there are 3 or 4 capacitors discharged at the same time, as shown in Fig. 3d. Therefore, whatever the value of the reference signal, four capacitors can take turns discharging, and the discharge times of all the capacitors are equal. As a result, each of the capacitors output the same energy, and voltage balance of capacitors is achieved under the carrier frequency. The number of voltage level changes when the modulation ratio M1 changes, and the capacitor voltages are always balanced. Compared with voltage balance strategies under the modulation frequency, the voltage balance strategy proposed in this paper has a smaller voltage ripple and a more stabilized voltage value. Thus, the quality of the output waveform is better.

Fig. 3
figure 3

Capacitor states under different reference signal amplitudes: aTref ∈ [0, 0.25]; bTref ∈ [0.25, 0.5]; cTref ∈ [0.5, 0.75]; dTref ∈ [0.75, 1]

Full size image

When the proposed inverter operates in the five-level mode, the dc side switches (S1, S2, S7, S8) are kept on, and the bidirectional switch S0 is kept off. Then the topology of the proposed inverter changes into a cascaded H-bridge inverter.

The modulation strategy of the five-level mode of the proposed inverter is shown in Fig. 4a. Four carriers (Tri1, Tri3, Tri5, Tri7) and one reference signal (Tref) are required to generate original waveforms. The phase difference between adjacent carriers is 180°. Four sets of rectangular pulse signals are obtained by comparing the carriers and the reference signal, to control the bridge arm switches (S3–S6, S9–S12).

Fig. 4
figure 4

Modulation strategy for: a five-level mode; b three-level mode

Full size image

When the proposed inverter operates in the three-level mode, only four bridge arm switches (S3, S5, S10, S12,) participate in the modulation process. In addition, the topology changes into a three-level H-bridge inverter.

The modulation strategy of the three-level mode of the proposed inverter is shown in Fig. 4b. Two carriers (Tri1, Tri5,) and one reference signal (Tref) are required to generate original waveforms. Two sets of rectangular pulse signals are obtained by comparing the carriers and the reference signal, to control bridge arm switches (S3, S5, S10, S12).

3 Calculations and analysis of losses and current THD

As can be seen from the analysis in Sect. 2, the quality of output waveforms and the losses are quite different when the proposed inverter operates in different modes. In this section, the total losses and current THD of the proposed inverter are calculated and compared under the three modes.

3.1 Calculations of losses

The inverter losses mainly include the conduction losses, the switching losses and the losses of the filter inductor. Since a multilevel inverter has an advantage in terms of reducing the filter inductor, the losses of the inductor are ignored in this paper.

The conduction losses of the proposed inverter are derived first. The conduction losses of one MOSFET device can be approximately calculated as:

$$ \begin{aligned} P_{{{\text{con}\_\text{M}}}} & = (U_{\text{M}} + R_{\text{M}} I)I \\ \, & = U_{\text{M}} I_{\text{m}} \sin \omega t + R_{\text{M}} I_{\text{m}}^{2} \sin^{2} \omega t \\ \end{aligned} $$
(1)

where UM is the conduction voltage drop of the MOSFET (V); RM is conduction resistance (Ω); and I is the current (A), which can be expressed as: I = Im*sin ωt.

Similarly, the conduction losses of one diode can be approximately calculated as:

$$ \begin{aligned} P_{{{\text{con}\_\text{D}}}} & = (U_{\text{D}} + R_{\text{D}} I)I \\ \, & = U_{\text{D}} I_{\text{m}} \sin \omega t + R_{\text{D}} I_{\text{m}}^{ 2} \sin^{2} \omega t \\ \end{aligned} $$
(2)

where UD is conduction voltage drop of the diode (V); and RD is the conduction resistance of the diode (Ω).

The losses of the proposed inverter under the nine-level mode are analyzed first. The number of output levels changes as the modulation radio M1 varies from 0 to 1. When M1 ∈[0.75, 1], the inverter can output a nine-level voltage wave. Since the output waveforms of the inverter have periodic symmetry, the output characteristic can be analyzed in the interval of [0, π/2]. Depending on the voltage of a waveform, three angles are defined to differentiate the output voltage intervals. In a modulation cycle, when the voltage level reaches Udc/2 for the first time, the corresponding angle is defined as θ1. The definitions of θ2 and θ3 are similar to that of θ1. The three angles are defined as:

$$ \theta_{1} = \arcsin \frac{1}{{4M_{1} }},\theta_{2} = \arcsin \frac{1}{{2M_{1} }} ,\theta_{3} = \arcsin \frac{3}{{4M_{1} }} $$
(3)

In the above four intervals, the duty cycles of the switches are different. The duty cycles D11–D14 in the four intervals are expressed as:

$$ \begin{aligned} D_{11} & = 4M_{1} \sin \omega t\quad \omega t \in \left[ {0,\theta_{1} } \right] \, \\ D_{12} & = 4M_{1} \sin \omega t - 1\quad \omega t \in \left[ {\theta_{1} ,\theta_{2} } \right] \\ D_{13} & = 4M_{1} \sin \omega t - 2\quad \omega t \in \left[ {\theta_{2} ,\theta_{3} } \right] \\ D_{14} & = 4M_{1} \sin \omega t - 3\quad \omega t \in \left[ {\theta_{3} ,\pi /2} \right] \\ \end{aligned} $$
(4)

Moreover, in the four intervals above, the conduction losses are different when the inverter output voltage changes. To calculate the conduction losses, the number of conductive switch devices with different output voltages is analyzed, as shown in Table 1.

Table 1 Number of conductive switches of the nine-level mode
Full size table

According to (1), (2), (4) and Table 1, the conduction losses of a MOSFET in the nine-level mode (Pcon_M9) and the conduction losses of a clamp diode in the nine-level mode (Pcon_D9) can be obtained as:

$$ \begin{aligned} P_{{{\text{con}\_\text{M9}}}} & = \frac{2}{\pi }\left\{ {\begin{array}{*{20}l} {\int_{0}^{{\theta_{1} }} {[4P_{{{\text{con}\_\text{M}}}} (1 - D_{11} ) + 5P_{{{\text{con}\_\text{M}}}} } D_{11} ]{\text{d}}\omega t} \hfill \\ { + \int_{{\theta_{1} }}^{{\theta_{2} }} {[5P_{{{\text{con}\_\text{M}}}} } (1 - D_{12} ) + 6P_{{{\text{con}\_\text{M}}}} D_{12} ]{\text{d}}\omega t} \hfill \\ { + \int_{{\theta_{2} }}^{{\theta_{3} }} {[6P_{{{\text{con}\_\text{M}}}} (1 - D_{13} ) + 7P_{{{\text{con}\_\text{M}}}} D_{13} ]} {\text{d}}\omega t} \hfill \\ { + \int_{{\theta_{3} }}^{{\frac{\pi }{2}}} {[7P_{{{\text{con}\_\text{M}}}} (1 - D_{14} ) + 8P_{{{\text{con}\_\text{M}}}} D_{14} } ]{\text{d}}\omega t} \hfill \\ \end{array} } \right\} \\ \, & = \left( {\frac{8}{\pi } + 2M_{1} } \right)U_{\text{M}} I_{m} + \left( {2 + \frac{{16M_{1} }}{3\pi }} \right)R_{\text{M}} I_{m}^{2} \\ \end{aligned} $$
(5)
$$ \begin{aligned} P_{{{\text{con}\_\text{D9}}}} & = \frac{2}{\pi }\left\{ {\begin{array}{*{20}l} {\int_{0}^{{\theta_{1} }} {[4P_{{{\text{con}\_\text{D}}}} (1 - D_{11} ) + 3P_{{{\text{con}\_\text{D}}}} } D_{11} ]{\text{d}}\omega t} \hfill \\ { + \int_{{\theta_{1} }}^{{\theta_{2} }} {[3P_{{{\text{con}\_\text{D}}}} } (1 - D_{12} ) + 2P_{{{\text{con}\_\text{D}}}} D_{12} ]{\text{d}}\omega t} \hfill \\ { + \int_{{\theta_{2} }}^{{\theta_{3} }} {[2P_{{{\text{con}\_\text{D}}}} (1 - D_{13} ) + P_{{{\text{con}\_\text{D}}}} D_{13} ]{\text{d}}\omega t} } \hfill \\ { + \int_{{\theta_{3} }}^{{\frac{\pi }{2}}} {[P_{{{\text{con}\_\text{D}}}} (1 - D_{14} } )]{\text{d}}\omega t} \hfill \\ \end{array} } \right\} \\ \, & = \left( {\frac{8}{\pi } - 2M_{1} } \right)U_{\text{D}} I_{\text{m}} + \left( {2 - \frac{{16M_{1} }}{3\pi }} \right)R_{\text{D}} I_{\text{m}}^{ 2} \\ \end{aligned} $$
(6)

Then the switching losses in the nine-level mode are calculated. The switching losses are caused by the non-ideal state of the switch device. It takes time for the switch device to go from fully on to fully off, and this process produces losses. The switching loss of one MOSFET in a single switch motion can be calculated as:

$$ E_{\text{s}} = \frac{1}{2}V_{\text{D}} I_{\text{D}} \times (t_{\text{S(on)}} + t_{\text{S(off)}} ) $$
(7)

where Es is the energy of the switching loss of one switch motion (J); VD is the voltage stress of the switch (V); ID is the conduction current of the switch (A); and tS(on) and tS(off) are the on delay time and the off delay time of the switch (s).

When the proposed inverter operates in the nine-level mode, there are 12 switches participate in modulation. S1, S2, S7, S8 operate at the carrier frequency in one cycle. The bridge arm switches act only one time in one cycle, and can be ignored. The total switching losses can be obtained by summing the losses of all the switches.

$$ \begin{aligned} P_{{{\text{sw}\_ 9}}} & = \frac{1}{T}\sum\limits_{s = 1}^{12} {E_{\text{s}} f_{\text{s}} } \\ \, & = \frac{2}{T}f_{\text{c}} I_{\text{out}} U_{\text{dc}} \times (t_{\text{S(on)}} + t_{\text{S(off)}} ) \\ \end{aligned} $$
(8)

where, Psw_9 is power of the switching losses (W); T is the modulation period (s); fs is the motion frequency of one switch (Hz); and fc is the carrier frequency (Hz).

To sum up (5), (6), (8), the total losses of the inverter in the 9-level mode is:

$$ P_{9} = P_{{{\text{con}\_\text{M9}}}} + P_{{{\text{con}\_\text{D9}}}} + P_{{{\text{sw}\_ 9}}} $$
(9)

Similarly, the losses of the proposed inverter under the five-level mode is calculated. The conduction losses of the MOSFET (Pcon_M5) and the conduction losses of the antiparallel diode (Pcon_D5) can be expressed as:

$$ \begin{aligned} P_{{{\text{con}\_\text{M5}}}} & = \frac{2}{\pi }\left\{ {\begin{array}{*{20}l} {\int_{0}^{{\theta_{1} }} {[2P_{{{\text{con}\_\text{M}}}} (1 - D_{21} ) + 5P_{{{\text{con}\_\text{M}}}} D_{21} } ]{\text{d}}\omega t} \hfill \\ { + \int_{{\theta_{1} }}^{{\frac{\pi }{2}}} {[5P_{{{\text{con}\_\text{M}}}} \left( {1 - D_{22} } \right) + 8P_{{{\text{con}\_\text{M}}}} D_{22} ]{\text{d}}\omega t} } \hfill \\ \end{array} } \right\} \\ \, & = \left( {\frac{4}{\pi } + 3M_{2} } \right)U_{M} I_{\text{m}} + \left( {1 + \frac{{24M_{2} }}{3\pi }} \right)R_{M} I_{\text{m}}^{2} \\ \end{aligned} $$
(10)
$$ \begin{aligned} P_{{{\text{con}\_\text{D5}}}} & = \frac{\pi }{2}\left\{ {\begin{array}{*{20}l} {\int_{0}^{{\theta_{1} }} {[2P_{{{\text{con}\_\text{D}}}} (1 - D_{21} ) + P_{{{\text{con}\_\text{D}}}} D_{21} ]{\text{d}}\omega t} } \hfill \\ { + \int_{{\theta_{1} }}^{{\frac{\pi }{2}}} {P_{{{\text{con}\_\text{D}}}} (1 - D_{22} ){\text{d}}\omega t} } \hfill \\ \end{array} } \right\} \\ \, & = \left( {\frac{4}{\pi } - M_{2} } \right)U_{D} I_{\text{m}} + \left( {1 - \frac{{8M_{2} }}{3\pi }} \right)R_{\text{D}} I_{\text{m}}^{ 2} \\ \end{aligned} $$
(11)

The total switching losses in the five-level mode can be expressed as:

$$ \begin{aligned} P_{{{\text{sw}\_ 5}}} & = \frac{1}{T}\left( {\sum\limits_{s = 3}^{6} {E_{\text{s}} f_{\text{s}} } + \sum\limits_{s = 9}^{12} {E_{\text{s}} f_{\text{s}} } } \right) \\ \, & = \frac{2}{T}f_{\text{c}} I_{\text{out}} U_{\text{dc}} \times (t_{\text{S(on)}} + t_{\text{S(off)}} ) \\ \end{aligned} $$
(12)

To sum up (10), (11), (12), the total losses of the inverter in the five-level mode is:

$$ P_{5} = P_{{{\text{con}\_\text{M5}}}} + P_{{{\text{con}\_\text{D5}}}} + P_{{{\text{sw}\_ 5}}} $$
(13)

The losses of the proposed inverter under the three-level mode are calculated as follows. The conduction losses of the MOSFET (Pcon_M3) and the conduction losses of the antiparallel diode (Pcon_D3) can be expressed as:

$$ \begin{aligned} P_{{{\text{con}\_\text{M3}}}} & = \frac{2}{\pi }\int_{0}^{{\frac{\pi }{2}}} {[2P_{{{\text{con}\_\text{M}}}} (1 - D_{31} ) + 5P_{{{\text{con}\_\text{M}}}} D_{31} } ]{\text{d}}\omega t \\ \, & = \left( {\frac{4}{\pi } + \frac{{3M_{3} }}{2}} \right)U_{M} I_{m} + \left( {1 + \frac{{4M_{3} }}{\pi }} \right)R_{M} I_{m}^{2} \\ \end{aligned} $$
(14)
$$ \begin{aligned} P_{{con}\_\text{D3}} & = \frac{\pi }{2}\int_{0}^{{\frac{\pi }{2}}} {[2P_{{con}\_\text{D}} (1 - D_{31} ) + P_{{con}\_\text{D}} D_{31} ]{\text{d}}\omega t} \\ \, & = \left( {\frac{4}{\pi } - \frac{{M_{3} }}{2}} \right)U_{D} I_{m} + \left( {1 - \frac{{4M_{3} }}{3\pi }} \right)R_{D} I_{m}^{2} \\ \end{aligned} $$
(15)

The total switching losses under the three-level mode can be expressed as:

$$ \begin{aligned} P_{{{\text{sw}\_ 3}}} & = \frac{1}{T}\left( {E_{\text{s3}} f_{\text{s3}} + E_{\text{s5}} f_{\text{s5}} + E_{\text{s10}} f_{\text{s10}} + E_{\text{s12}} f_{\text{s12}} } \right) \\ \, & = \frac{1}{T}f_{\text{c}} I_{\text{out}} U_{\text{dc}} \times (t_{\text{S(on)}} + t_{\text{S(off)}} ) \\ \end{aligned} $$
(16)

To sum up (14), (15), (16), the total losses of the inverter in the three-level mode is:

$$ P_{3} = P_{{{\text{con}\_\text{M3}}}} + P_{{{\text{con}\_\text{D3}}}} + P_{{{\text{sw}\_ 3}}} $$
(17)

To analyze and compare the losses under different modes, specific data was substituted into the equations and a function diagram was obtained, as shown in Fig. 5. To simplify the calculations, the parameters of the antiparallel diode and the clamping diode are the same. The parameters used in the calculation are shown in Table 2.

Fig. 5
figure 5

Total losses of the three modes

Full size image
Table 2 Parameters used in the calculations
Full size table

As can be seen from Fig. 5, the total losses increase with an increase of the current. When the current is the same, the losses of the nine-level mode are the largest, and the losses of the three-level mode are the lowest. The larger the current is, the more obvious the difference is. An increase of the level number leads to an increase of the losses.

3.2 Calculations of current THD

Total harmonic distortion (THD) plays an important role in the detection and evaluation of a power system. It is an important index to evaluate the characteristics of an inverter. It is not easy to calculate the current THD by its definition. However, the output current of an inverter can be seen as a combination of the current fundamental wave and the current ripple. Therefore, the current ripple can be approximately regarded as the sum of harmonic currents. Thus, the current THD is approximately expressed by the ratio of the current ripple to the fundamental wave as:

$$ {\text{THD}} \approx \frac{{\Delta I_{\text{RMS}} }}{{I_{1} }} = \frac{{\sqrt 2 \Delta I_{\text{m}} }}{{2\sqrt 3 I_{\text{M}} }} $$
(18)

where ∆IRMS is the RMS value of the current ripple (A); ∆Im is the peak–peak value of the current ripple wave (A); and IM is the peak value of the output current fundamental wave (A).

When the proposed inverter operates in the nine-level mode, the current ripple in different intervals is calculated first. Following the rules in Sect. 2.1, interval [0, π/2] is divided into four parts. Thus, the peak–peak values of the current ripple in the four intervals are:

$$ \left\{ {\begin{array}{*{20}l} {\Delta I_{\text{m91}} = \frac{1}{{4Lf_{\text{c}} }}\left( {\frac{{U_{\text{dc}} }}{2} - U_{\text{out}} } \right)\left( {4M_{1} \sin \omega t} \right)} \hfill \\ {\Delta I_{\text{m92}} = \frac{1}{{4Lf_{\text{c}} }}\left( {U_{\text{dc}} - U_{\text{out}} } \right)\left( {4M_{1} \sin \omega t - 1} \right)} \hfill \\ {\Delta I_{\text{m93}} = \frac{1}{{4Lf_{\text{c}} }}\left( {\frac{{3U_{{{\text{d}}c}} }}{2} - U_{\text{out}} } \right)\left( {4M_{1} \sin \omega t - 2} \right)} \hfill \\ {\Delta I_{\text{m94}} = \frac{1}{{4Lf_{\text{c}} }}\left( {2U_{\text{dc}} - U_{\text{out}} } \right)\left( {4M_{1} \sin \omega t - 3} \right)} \hfill \\ \end{array} } \right. $$
(19)

RMS values of the current ripple are obtained by integrating the peak–peak values of the current ripple in the four intervals. Thus, the RMS values of the current ripple in the nine-level mode are expressed as:

$$ \Delta I_{{{\text{RMS}}9}} = \frac{1}{2\sqrt 3 }\sqrt {\frac{2}{\pi }\left( {\begin{array}{*{20}l} {\int_{0}^{{\theta_{1} }} {\Delta I_{{{\text{m}}91}}^{2} } {\text{d}}\omega t + \int_{{\theta_{1} }}^{{\theta_{2} }} {\Delta I_{{{\text{m}}92}}^{2} } {\text{d}}\omega t} \hfill \\ { + \int_{{\theta_{2} }}^{{\theta_{3} }} {\Delta I_{{{\text{m}}93}}^{2} } {\text{d}}\omega t + \int_{{\theta_{3} }}^{\pi /2} {\Delta I_{{{\text{m}}94}}^{2} } {\text{d}}\omega t} \hfill \\ \end{array} } \right)} $$
(20)

Hence, the current THD of the proposed inverter in the nine-level mode is obtained as:

$$ {\text{THD}}_{9} = \frac{{\sqrt 2 \Delta I_{\text{RMS9}} }}{{I_{\text{M}} }},\quad M_{1} \in [0.75,1] $$
(21)

Similarly, when the inverter operates in the five-level mode, the interval [0, π/2] is divided into two parts. In addition, the peak–peak value of the current ripple in the two intervals are:

$$ \left\{ {\begin{array}{*{20}l} {\Delta I_{\text{m51}} = \frac{1}{{4Lf_{\text{c}} }}\left( {U_{\text{dc}} - U_{\text{out}} } \right)\left( {2M_{2} \sin \omega t} \right)} \hfill \\ {\Delta I_{\text{m52}} = \frac{1}{{4Lf_{\text{c}} }}\left( {2U_{\text{dc}} - U_{\text{out}} } \right)\left( {2M_{2} \sin \omega t - 1} \right)} \hfill \\ \end{array} } \right. $$
(22)

The RMS value of the current ripple in the five-level mode can be obtained as:

$$ \Delta I_{{{\text{RMS}}5}} = \frac{1}{2\sqrt 3 }\sqrt {\frac{2}{\pi }\left( {\int_{0}^{{\theta_{21} }} {\Delta I_{{{\text{m}}51}}^{2} } {\text{d}}\omega t + \int_{{\theta_{21} }}^{\pi /2} {\Delta I_{{{\text{m}}52}}^{2} } {\text{d}}\omega t} \right)} $$
(23)

Thus, the current THD of the proposed inverter in the five-level mode is expressed as:

$$ {\text{THD}}_{5} = \frac{{\sqrt 2 \Delta I_{\text{RMS5}} }}{{I_{\text{M}} }},\quad M_{2} \in [0.5,1] $$
(24)

In a similar way, when the inverter operates in the three-level mode, the peak–peak value of the current ripple in the interval [0, π/2] is:

$$ \Delta I_{{{\text{m}}31}} = \frac{1}{{2Lf_{\text{c}} }}\left( {U_{\text{dc}} - U_{\text{out}} } \right)\left( {M_{3} \sin \omega t} \right) $$
(25)

The RMS values of the current ripple in the three-level mode is calculated as:

$$ \Delta I_{{{\text{RMS}}3}} = \frac{1}{2\sqrt 3 }\sqrt {\frac{2}{\pi }\left( {\int_{0}^{\pi /2} {\Delta I_{{{\text{m}}31}}^{2} } {\text{d}}\omega t} \right)} $$
(26)

The current THD of the proposed inverter in the five-level mode is expressed as:

$$ {\text{THD}}_{3} = \frac{{\sqrt 2 \Delta I_{{{\text{RMS}}3}} }}{{I_{\text{M}} }},\quad M_{3} \in [0,1] $$
(27)

To intuitively analyze the difference of the current THD in the three modes, specific data was substituted into the above equations. Take a grid-connected application as an example, ‘Uout’ in (19), (22) and (25) is replaced with ‘Em sinωt’, and its value is 311 V. For comparison purposes, Udc in both the nine-level mode and the five-level mode is 200 V; and Udc in the three-level mode is 400 V. The other parameters used in the calculations are shown in Table 2. Figure 6 shows different current THDs under the three operation modes. As can be seen from Fig. 6, the current THD decreases along with the increase of the current. When the current is the same, the current THD of the nine-level mode is the lowest, and that of the three-level mode is the highest.

Fig. 6
figure 6

Current THD of the three modes

Full size image

4 Simulation and experimental results

4.1 Simulation results

To verify the correctness and feasibility of the proposed inverter, simulation models are established on a MATLAB/Simulink platform. The parameters used in the simulations are shown in Table 3.

Table 3 Simulation and experimental parameters
Full size table

The steady-state performance of the inverter under each mode was simulated first. The proposed inverter has three modes. Simulation results of the nine-level mode are shown in Fig. 7. Figure 7b shows the current waveform with a 25 Ω resistive load and an 18mH inductive load. It can be seen from Fig. 7 that the inverter can output a nine-level voltage waveform with a frequency of 50 Hz as required.

Fig. 7
figure 7

Simulation waveforms of the nine-level mode: a output voltage; b output current

Full size image

Simulation results of the five-level mode are shown in Fig. 8. Figure 8b shows the output current with the same load as the nine-level mode. The inverter can output a five-level voltage waveform and the switching frequency of the output voltage is halved when compared with Fig. 7a.

Fig. 8
figure 8

Simulation waveforms of the five-level mode: a output voltage; b output current

Full size image

Simulation results of the three-level mode are shown in Fig. 9. Comparing the above three simulation results, the quality of the output current under the nine-level mode is the best, and the quality of the output current under the three-level mode is the worst. Simulation results can confirm the theoretical analysis in this paper.

Fig. 9
figure 9

Simulation waveforms of the three-level mode: a output voltage; b output current

Full size image

When the inverter works in the nine-level mode, the capacitor voltage must be balanced. Figure 10 shows the voltage waveforms of the four capacitors. The obtained simulation results indicate that the voltages of the four capacitors are well balanced under the modulation strategy proposed in this paper.

Fig. 10
figure 10

Voltage waveforms of four capacitors

Full size image

The dynamic performance of the proposed inverter was also simulated. Figure 11 shows the simulation results of the online transition process with different modes. With the given control signals at 0.3 s and 0.6 s, the inverter changes from the nine-level mode to the five-level mode at 0.3 s, and from the five-level mode to the three-level mode at 0.6 s. The output waveform is correct and good during the transition process.

Fig. 11
figure 11

Voltage waveform among the different modes

Full size image

Simulation results of THD corresponding to different currents are obtained by an FFT analysis. In addition, simulation results of the current THD curve are obtained, as shown in Fig. 12. The colored points are simulation values of different currents. By comparing the THD simulation results with the THD calculation results in Fig. 6, it can be seen that the simulation results are in accord with the calculation curves, which verifies the correctness of calculations in this paper.

Fig. 12
figure 12

Simulation curves of the current THD

Full size image

4.2 Experimental results

An experimental platform was implemented to further validate the proposed inverter and its modulation strategy. The parameters in the experiment are the same as those used in the simulation, as shown in Table 3.

Firstly, the steady-state performance of the inverter was tested. Experiments of the inverter working in different modes were conducted, and output voltage and current waveforms were observed. Figure 13 shows signal waveforms of twelve switches in the nine-level mode. It can be seen from this figure that the four dc side switches work at a high frequency and the eight bridge arm switches work at a low frequency. The obtained experimental signals are consistent with modulation signals.

Fig. 13
figure 13

Switching signals of the nine-level mode: a signals of S1–S4; b signals of S5–S8; c signals of S9–S12

Full size image

Figure 14 shows output voltage waveforms and current waveforms of the proposed inverter in the nine-level mode. Figure 14a shows output waveforms with a 60 Ω resistive load, and Fig. 14b shows output waveforms with a 25 Ω resistive load and an 18mH inductive load.

Fig. 14
figure 14

Output waveforms of the inverter in the nine-level mode: a resistive load; b inductive load

Full size image

Figure 15 shows dc side capacitor voltage waveforms when the inverter works in the nine-level mode. It can be seen from this figure that the voltage of each capacitor is half of the dc side voltage. The voltage values are stable and the voltage ripple is small. This shows that the voltage balance strategy in this paper is effective.

Fig. 15
figure 15

Capacitor voltage waveforms: a voltage of C1 and C2; b voltage of C3 and C4

Full size image

Figure 16 shows switching signal waveforms of the five-level mode. As can be seen, eight switches participated in the modulation. The obtained experimental switching signals are consistent with the modulation signals.

Fig. 16
figure 16

Switching signals of the five-level mode: a signals of S3–S6; b signals of S9–S12

Full size image

Figure 17 shows output voltage waveforms and current waveforms of the proposed inverter in the five-level mode. Figure 17a shows output waveforms with a 60 Ω resistive load, and Fig. 17b shows output waveforms with a 25 Ω resistive load and an 18 mH inductive load.

Fig. 17
figure 17

Output waveforms of the inverter in the five-level mode: a resistive load; b inductive load

Full size image

Figure 18 shows switching signal waveforms of the three-level mode. Four bridge arm switches participated in the modulation. The obtained experimental switching signals are consistent with the modulation signals.

Fig. 18
figure 18

Switching signals of the three-level mode

Full size image

Figure 19 shows output voltage waveforms and current waveforms of the proposed inverter in the five-level mode. Figure 19a shows waveforms with a 60 Ω resistive load, and Fig. 19b shows waveforms with a 25 Ω resistive load and an 18mH inductive load. It can be observed from Figs. 14, 17 and 19 that the inverter has the best output characteristics under the nine-level mode, and that the voltage waveform has the highest switching frequency. With the same load, the output characteristics under the three-level mode are the worst. The obtained voltage waveform has a lower switching frequency. These experimental results are consistent with the theoretical analysis and simulation results in this paper.

Fig. 19
figure 19

Output waveforms of the inverter in the three-level mode: a resistive load; b inductive load

Full size image

Then the dynamic performance of the proposed inverter was tested. The inverter changes its working modes online by given control signals. Figure 20 shows experimental results of an online transition between the different modes of the inverter.

Fig. 20
figure 20

Output voltage waveforms with inverter mode transitions: a nine to five-level mode; b five to three-level mode

Full size image

In Fig. 20a, the inverter changes from the nine-level mode to the five-level mode, and t1 is the moment to give a switch signal. In Fig. 20b, the inverter changes from the five-level mode to the three-level mode, and t2 is the moment to give a switch signal. Since the circuit structure changes from cascade to parallel, the output voltage of the three-level mode is halved. The obtained experimental results are in agreement with simulation results. It can be seen from these results that the working modes can switchover online and that the output waveforms is good during the transition process.

5 Conclusions

To achieve a wide operational range and to reduce the power losses, a flexible cascaded multilevel inverter is proposed in this paper. According to the actual working conditions, the inverter can change its topology structure to work in three modes. The proposed inverter can reduce the number of active switch devices to decrease the inverter losses in the three-level mode. In addition, the inverter can provide more output levels to improve the quality of its output waveforms in the nine-level mode. Furthermore, its modulation strategies and voltage balance method were analyzed. Simulations and experiments were conducted. The obtained results indicate that the topology and modulation strategy of the inverter are correct and valid. In addition, the online transition process between the different modes is effective and favorable. The proposed inverter can achieve a wide operational range and decreased total losses.