Introduction

Heart failure

The impact of an application of mechanical replacement to heart failure has attracted scientists’ attention in the last decade. The main symptoms of heart disease can be classified into four main categories: dyspnea, fatigue, dizziness, and irregular heartbeat (Cohn et al. 2015). Currently, cardiac failure is one of the most common diseases affecting at least 26 million population throughout the world, and its prolonged effect leads to renal failure (Deyranlou et al. 2021; Deyranlou et al. 2020; Schmack et al. 2018), amongst other diseases. In the early 2000s, support for hemolysis reduction has been dramatically increased, and left ventricular assist devices to solve this problem have been changed over the past decades; Accordingly, ventricular assist devices (VADs) were designed to decrease such effects (Abraham and Smith, 2013; McElroy et al. 2020; 2016).

Based on their applications, VADs are generally classified into two categories (Harris and Kuppurao 2012):

  1. 1.

    Left ventricular assist devices (LVADs): Similar to the function of left ventricles, LVADs pump the blood into the aorta.

  2. 2.

    Right ventricular assist devices (RVADs): In comparison to LVADs, the application of RVADs is low and only used for short periods.

Centrifugal blood pump

Left ventricular assist devices (LVADs) are an established form of treatment for patients with heart failure and result in clear survival benefit. Although LVADs demonstrate significant survival improvements, they are also associated with postoperative complications such as ischemic and hemorrhagic stroke due to abnormal hemodynamics (Boyle et al. 2014; Menon et al. 2012; Parikh et al. 2016). With a growing proportion of LVADs being implanted as a destination therapy, the associated risk of stroke (especially for women) remains too high (Kirklin et al. 2015; Kirklin et al. 2014; Kirklin et al. 2013; Parikh et al. 2016).

One of the most common blood pumps, used as LVADs, is a centrifugal blood pump (CBP). The main reasons for using an CBP are to improve stability and durability of left ventricle. Therefore, a great deal of research has been designed to investigate the performance of blood pumps as an utmost procedure for curing the patients suffering from heart failure (Bozkurt et al. 2015; Horobin et al. 2018; Ozturk et al. 2018; Petrou et al. 2017; Song et al. 2004; Wiegmann et al. 2018; Wu et al. 2017). With all these features, the risk of thrombosis is well identified (Wu et al. 2016). So far, the precision of new CBPs application have not been tested through relevant medical experiments. At present, although the adrenergic inotropes are considered as a remarkable problem bringing about heartbeat and hemolysis, CBP not only unloads the heart, but also boosts the coronary and systemic of blood flow (Westaby et al. 2012).

An inducer represents a turbomachinery unit which is mounted upstream of the inlet to the main impeller of the centrifugal pump to reduce the negative effects of pressure drops, mechanical corrosion, and instability in the fluid inlet to the pump and convert rotational energy into flow and head of the pump. Inducers have been utilized in other applications such as rocket pump feed systems, water jet propulsion, high-speed ship, and auxiliary power units for aircraft due to their simplicity and compact design (Japikse 2001). Using inducers is a promising way to prevent hemolysis in pumps. In order to reduce the rate of wall shear stress (WSS) in a given pump, an inducer is positioned upstream of the inlet to the main impeller with an aim of increasing the inlet pressure to the pump (Shojaeefard et al. 2019).

As mentioned above, due to the importance of CBPs, their performance has been the subject of many studies. In this regard, computational fluid dynamics (CFD) have also served as an important tool to predict WSS (Keshmiri and Andrews 2015) and the efficiency of CBPs. Some examples of application of CFD to CBPs are given below.

In order to improve the efficiency of centrifugal blood pump and hemolysis index (HI), Ghadimi et al. (2018) studied an optimum design of a centrifugal blood pump and found that non-dominated sorting genetic algorithm II (NSGA-II) and artificial neural network were suitable to find the Pareto front, and also using multi-objective optimization could enhance the efficiency of centrifugal blood pumps by 11.9% and improve the HI by 7.2%. Through employing three different rates of fluid flow, Telyshev et al. 2018) evaluated the characteristics of an implantable pediatric CBP, both experimentally and numerically, and concluded that if the flow rate reaches to 1 L/min, backflows and stagnation zones appear.

Thamsen et al. 2015) compared two pumps (HeartMate II and HeartWare HVAD) regarding their potential blood trauma using CFD, and it was found that the gap zone has regions of high WSS.

In order to assess the effect of axial and radial clearances on the hydrodynamic performance of a CBP, Rezaienia et al. (2018) performed a Reynolds-Averaged Navier–Stokes (RANS) computation with a direct attention to the hemolysis and hydrodynamic efficiency. They found that large clearances cannot reduce blood trauma.

Kido et al. 2006) evaluated the effect of the blood circulation on the tiny CBP in children and infants and accordingly employed two different types of bearing clearance numerically and experimentally; and his results revealed that smaller bearing clearance acted better in lower WSS.

The performance of trans-valve LVAD was conducted experimentally by Okamoto et al. 2020). Also, studying the effect of pulsatility of LVAD showed that the trans-valve LVAD has an ability to preserve pulsatility with a simple mechanism. In this way, numerical studies were carried out to explore the influence of the pulse-modulated speed on the performance of CBP (Chen et al. (2019). A minor effect of modulated speed on the blade of CBP was investigated. Also, it was proposed that the pulse-modulated speed of VAD have an ability to restore the vascular pulsatility.

Gross-Hardt et al. (2019) modeled the effect of a centrifugal blood pump and compared numerical results with experimental data. The most suitable blood flow rates were selected because of the importance of hemolysis. The results showed that when flow rates decrease below 1L/min, not only hydraulic efficiency drops, but also adverse effects increased.

Kannojiya et al. (2020) reported the effect of numbers, profile, tip width, and splitter of blades on the hydraulic performance of a centrifugal blood pump. They proposed an optimum design based on non-Newtonian characteristics of the blood. Also, they concluded installing splitter blades on the blood pump leads to raises in the head pressure.

Jing et al. 2020) analyzed the effects of the variable speed on the steady cavitating flow and stated that an increase of the impeller speed generates the vortex cavitation which affects the sheet cavitation on the impeller. It also increases the blockage effect near the hub and impeller.

Miyamoto et al. (2020) examined the effect of blood pump orientation on an advanced ventricular assist device performance. Four variable speeds of impeller were used, and it was found that the orientation of the VAD had a minor influence on the hydraulic performance of the VAD.

Zhang et al. 2006) implemented a test to evaluate an CBP, both experimentally and numerically, and found that the relatively large gap passages between the outer rotor walls and the lower housing cavity walls result in adequate efficiency over a range of physiological operating conditions.

Shi et al. 2010) conducted computational modeling of cardiovascular response to heart failure, and their findings improved the efficiency of CBP under a constant rotational speed.

In general, there are different procedures such as employing a pump or control mechanism (Crow et al. 2009; Gokce et al. 2003; Ootaki et al. 2008) to reduce the rate of arterial pulsatility, and so far, different HI, WSS, and turbulence models have been used to explain a pump mechanism (Molteni et al. 2018) (Mozafari et al. 2017) (Nammakie et al. 2017) (Rezaienia et al. 2017) (Thamsen et al. 2016).

Aims and objectives

While to date there are numerous experimental and computational works on the performance of blood pump, not much information is available about the role of different geometrical and operational parameters involved in blood pump performance. Therefore, the present research aims to investigate the effect of temperature, surface roughness, and an inducer on the CBP performance. More specifically, based on the literature review presented above, there is a clear lack of research on the role of an inducer in CBPs. The present study was designed primarily to determine the effects of working fluid temperature and rotational speed on the CBP performance. In order to simulate the flow characteristics, the constitutive equations of the fluid as well as additional transport equations were solved computationally, and the results were validated by our own experimental data. Finally, the effect of an inducer on the CBP is numerically assessed.

Methods

The experimental procedure

The CBP tests have been performed within a closed flow loop during the 3-h period (Figs. 1–2). To ensure the accuracy of the results and repeatability, the tests were scheduled to be performed on four different days in terms of LVAD and analysis of hemolysis assessment (ASTM 2005). Each test was conducted at both constant (4.7 L/min) and variable flow rate to evaluate the effects of rotational speed and fluid temperature. The schematic of the experimental apparatus is given in Fig. 2. A catheter-type pressure transducer with 0.1% measurement error was used for calculating the inlet and outlet pressure of CBP. Using an ultrasonic flow meter, the flow was measured at the inlet of the CBP, and its systematic measurement uncertainty is 0.2%. In order to take control of flow, a throttle valve was used. Also, the temperature of the fluid at the inlet and outlet was measured using a thermometer

Fig. 1
figure 1

Representative photographic samples of the present CBP from different angles

Full size image
Fig. 2
figure 2

Schematic of the experimental setup of the CBP

Full size image

The geometric models

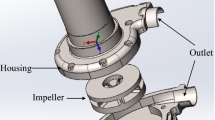
The CBP tested in the present work consists of a volute (i.e., upper and downer casing), an impeller, two motors, two flow probes, and a microcontroller needed to be implanted outside the body. It is worth mentioning that this model resembles a bearing-less motor technology in which an impeller, without any mechanical contact, will be suspended in a given pump. The blood circulation is directed into the volute by an inlet and then rotated by an impeller for a while and finally driven to the outlet. In reality, an impeller is the only moving element of the pump. An overview of the dimensions and the operational parameters of the model as well as a schematic of the CBP utilized in the simulation are given in Table 1 and Fig. 3. The impeller of the CBP consists of a four-bladed suspension with design speed and mass flow rate of 2800 rev/min and 4.7 L/min, respectively. It is worth mentioning that the gaps between the top and the bottom surfaces in our model are 50 and 160 μm, respectively. A coil winding was utilized to provide a magnetic field and also a controller circuit to drive the system.

Table 1 Operational and design characteristics of the present CBP
Full size table
Fig. 3
figure 3

Schematic of the present CBP model: a 3D view of assembly, b cross-sectional view, and c impeller

Full size image

Mesh generation and grid independence check

Since the geometries investigated in this study are rather complicated, the unstructured tetrahedral and prismatic elements, generated by ANSYS ICEM (Version 16.1), were used for modeling CBP. Also, due to the small gap between the impeller and casing zones, mesh refinements were applied to these regions so that more accurate flow details can be captured. The schematic of the mesh used in this study is given in Fig. 4. In order to ensure the results are mesh independent, different meshes with different number of elements and refinement levels were tested, and eventually, a mesh consisting of approximately 13.8 million cells was selected and was deemed to be fine enough.

Fig. 4
figure 4

Schematic of the unstructured mesh of the whole computational domain: (a) impeller and (b) planar cut through the middle of the pump (c)

Full size image

Governing equations

The governing equations for numerical simulation are based on the assumptions of incompressible fluid. The time-averaged equations used for determining the mass and momentum are as follows:

$$\frac{\partial p}{\partial t}+\nabla .\left(pU\right)=0$$
(1)
$$\frac{\partial (pU)}{\partial t}+\nabla .\left(pU\times U\right)=-\nabla p+\nabla .\tau +{S}_{m}$$
(2)

where the stress tensor, τ, is related to the strain rate by:

$$\tau =\mu \left(\left(\nabla U+{\nabla U}^{T}\right)-\frac{2}{3}\delta \nabla .U\right)$$
(3)

where µ is the fluid viscosity, ρ is the density of fluid, U is velocity, and p is pressure. The Boussinesq, 1887) concept which relates the Reynolds stresses to the mean velocity gradients with the eddy viscosity (μt) as the proportionality factor is used to model the stress tensor (\(-\rho \overline{{u}_{i}^{^{\prime}}{u}_{j}^{^{\prime}})}\):

$$-\rho \overline{{u}_{i}^{\mathrm{^{\prime}}}{u}_{j}^{\mathrm{^{\prime}}}}=\left[{\mu }_{t}(\frac{{\partial U}_{i}}{{\partial x}_{j}}+\frac{{\partial U}_{j}}{{\partial x}_{i}})\right]-\frac{2}{3}{\rho k\delta }_{ij}a$$
(4)

where k is the kinetic energy of turbulence, µt is turbulent viscosity, and δij is Kronecker delta.

Finally, based on the comparison results, complex flow behavior, and also available data in literature, the shear stress transport (SST) k-ω model was selected as the most appropriate model. The transport equations for the kinetic energy of turbulence (k) and its turbulent frequency (ω) are obtained from the following equations (Rodi 2017):

$$k=\frac{1}{2}\sum_{i=1}\overline{{{u}_{i}^{\mathrm{^{\prime}}}}^{2}}$$
(5)
$$\omega ={\mu }_{t}\overline{\left(\frac{{\partial u}_{i}}{{\partial x}_{j}}\right)\left(\frac{{\partial u}_{i}}{{\partial x}_{j}}\right)}/\rho k$$
(6)

where \(u^{\prime}_{i}\) is fluctuating velocity. The kinetic energy of turbulence deformation tensor is determined by:

$$\frac{\partial \rho k}{\partial t}+\frac{\partial }{{\partial x}_{i}}\left({\rho u}_{i}k\right)=\frac{\partial }{{\partial x}_{i}}\left((\mu +\frac{{\mu }_{turb}}{{\sigma }_{k}})\frac{\partial k}{{\partial x}_{i}}\right)+{P}_{k}-{\beta }^{*}\rho \omega k$$
(7)

where μturb is turbulent viscosity and Pk is production of turbulent kinetic energy due to interaction between relative flow and flow field:

$${P}_{k}={\tau }_{ij}\frac{{\partial u}_{i}}{{\partial x}_{j}}=\left[{\mu }_{turb}\left(\frac{{\partial u}_{i}}{{\partial x}_{j}}+\frac{{\partial u}_{j}}{{\partial x}_{i}}-\frac{2}{3}\frac{{\partial u}_{k}}{{\partial x}_{k}}{\delta }_{ij}\right)-\frac{2}{3}{\rho k\delta }_{ij}\right]\frac{{\partial u}_{i}}{{\partial x}_{j}}$$
(8)

In which \(\beta^{ * } \rho \omega k\) is turbulent kinetic depreciation. The turbulent frequency deformation tensor is given by:

$$\frac{\partial \rho \omega }{\partial t}+\frac{\partial }{{\partial x}_{i}}\left({\rho u}_{i}\omega \right)=\frac{\partial }{{\partial x}_{i}}\left\{(\mu +\frac{{\mu }_{turb}}{{\sigma }_{\omega }})\frac{\partial \omega }{{\partial x}_{i}}\right\}+\frac{\rho \gamma }{{\mu }_{turb}}{\tau }_{ij}\frac{{\partial u}_{i}}{{\partial x}_{j}}-{\rho \beta \omega }^{2}+2\rho \left(1-{F}_{1}\right){\sigma }_{w2}\frac{1}{\omega }\frac{\partial k}{{\partial x}_{j}}\frac{\partial \omega }{{\partial x}_{j}}$$
(9)

where \(\phi = F_{1} \phi_{1} + (1 - F_{1} )\phi_{2}\) is constant. The model constants are listed in Table 2.

Table 2 Constants of set 1(\(\phi_{1}\)) and set 2(\(\phi_{2}\))
Full size table

F1 is a blending function composition (based on distance from nearest wall) which is given by:

$${F}_{1}=\mathrm{tanh}({\mathrm{arg}}_{1}^{4})$$
(10)

Also:

$${\mathrm{arg}}_{1}=\mathrm{min}\left[\mathrm{max}\left(\frac{\sqrt{k}}{0.09\omega y},\frac{500\mu }{{y}^{2}\omega \rho }\right),\frac{{4\rho \sigma }_{w2}k}{{CD}_{k\omega }{y}^{2}}\right]$$
(11)

where y is a distance to the nearest wall and CDkω is the positive portion of the cross-diffusion term of Eq. 11:

$${CD}_{k\omega }=\mathrm{max}({2\rho \sigma }_{w2}\frac{1}{\omega }\frac{\partial k}{{\partial x}_{j}}\frac{\partial \omega }{{\partial x}_{j}},{10}^{-20})$$
(12)

The turbulent viscosity is obtained using a limiter. Menter (1994) has argued that the use of this limiter does not increase the turbulent viscosity in regions close to the stagnation point:

$${\mu }_{turb}=\frac{0.31\rho k}{\mathrm{max}(0.31\omega ,{\Omega F}_{2})}$$
(13)

where Ω is the absolute value of vorticity given by \(\Omega =\sqrt{{2W}_{ij}{W}_{ij}}\) where \({W}_{ij}=\frac{1}{2}\left(\frac{{\partial u}_{i}}{{\partial x}_{j}}-\frac{{\partial u}_{j}}{{\partial x}_{i}}\right)\) The blending function F2 can be expressed by:

$$\begin{array}{l}{F}_{2}=\mathrm{tanh}({\mathrm{arg}}_{2}^{2})\\ {\mathrm{arg}}_{2}=\mathrm{max}(\frac{2\sqrt{k}}{0.09\omega y},\frac{500\mu }{{y}^{2}\omega \rho })\end{array}$$
(14)

Boundary conditions

In the present computational framework, the rotor–stator interface is used which utilizes a rotational domain for the rotor and a stationary domain for the volute. A static pressure is applied at the inlet of the volute, while a constant mass flow rate is prescribed at the outlet. All other boundaries are treated as no-slip wall.

Solver settings

The governing equations were numerically simulated using a finite-volume method, implemented in the commercial code, ANSYS-CFX (Version 16.1). In order to couple the velocity pressure, the SIMPLE scheme was used, and a high-resolution second-order scheme was utilized for discretizing the advection term. The results were obtained by applying a total time of 6 s and the time step size of 0.02 s. Also, the convergence criterion in this investigation was set to 10−6. Although blood is a non-Newtonian fluid, it generally behaves as a Newtonian fluid when the shear rate was low (less than 100 s−1). Therefore, in the present study, the blood is assumed to be an incompressible Newtonian fluid with a density of 1050 kg/m3 and a viscosity of 0.0035 Pa s (Fraser et al. 2012; Pirbodaghi et al. 2014; Schenkel et al. 2013; Su et al. 2012; Untaroiu et al. n.d.; Yang et al. 2011; Zhang et al. 2008; 2006).

Results

In this section, the results from experimental testing and numerical simulations including performance of CBP in different conditions are carried out. The measured experimental data were validated with numerical results. Then, an inducer is installed in front of CBP for reducing WSS which has been shown to be associated with myocardial infarction and progression of atherosclerosis.

Experimental results

In order to determine the characteristics of LVAD, a series of experimental tests were carried out to study the effects of the working fluid temperature and the rotational speed on the CBP performance. The effects of the rotational speed on the pressure difference and power of the CBP was briefly evaluated based on the data given in Fig. 5. The tests were chosen to examine various rotational speeds (2400, 2600, 2800, 3000, and 3200 rev/min) at blood temperature of 28 °C. The results in Fig. 5 were obtained at a constant inlet pressure by varying the mass flow rate. The results of the rotational speed revealed that the trend of all curves was somewhat similar, in such a way that an increase in the rate of rotational speed led to a decrease in the CBP’s pressure difference and power. Therefore, the CBP performance strongly depends on the rotational speed. Typically, volumetric losses occur at part load, and frictional losses prevail for higher flow rates.

Fig. 5
figure 5

The effects of rotational speed on the (a) pressure difference and (b) power of the CBP at the blood temperature of 28 °C

Full size image

Due to a strong correlation between the CBP performance and the working fluid temperature, the effect of the blood temperature at different levels (16, 22, 28, and 34 °C) was assessed next.

The change in the pumped fluid’s temperature obviously affects the density and dynamic viscosity. Therefore, the influence of the working fluid temperature on a performance curve of the CBP was determined at the rotational speed of 2800 rev/min and is show in Fig. 6. It can be seen that the CBP performance was improved slightly as the blood temperature was elevated. However, given the difference between the curves in Fig. 6, the blood temperature is found not to have significant effects on the CBP performance, particularly at low flow rates.

Fig. 6
figure 6

Effects of the working fluid temperature on the CBP’s pressure difference at the rotational speed of 2800 rev/min

Full size image

Numerical results and validation

To validate our numerical results against the experimental data, a series of 3D numerical simulations were carried out. In our numerical tests, five common turbulence models (namely, k-ε, k-ω standard, RNG k-ε, k-ω SST, and Spalart–Allmaras) were employed, and the results for the pressure head were compared against the experimental data, as shown in Fig. 7. As can be seen in the figure, there is a wide variation between in the performance of each turbulence, while the shear stress transport (SST) turbulence model is found to have the best agreement with the experimental data. The maximum difference between other turbulence models and the data are as follows: 6.02% (k-ε), 2.38% (k-ω standard), 6.26% (RNG k-ε), 0.57% (k-ω SST), and 13.17% (Spalart–Allmaras turbulence model).

Fig. 7
figure 7

Comparison of different turbulence models against the experimental data for pressure difference under nominal flow coefficient (Q = 4.7 L/min) and rotational speed of 2800 rev/min

Full size image

The variation of the pressure difference against flow coefficient for CBP obtained by both experimental and numerical techniques are given in Fig. 8. The results were obtained at a constant pressure through changing the rate of mass flow. The numerical results are in very good agreement with the experimental data, which demonstrates the efficacy of a two-equation RANS model in re-producing experimental data. In Fig. 8, at lower mass flow rates, a small discrepancy can be seen between the results and the data, with the CFD results, slightly over predicting the pressure head. This discrepancy is expected due to different values of velocity downstream. The maximum and average difference between the CFD and experimental results are as follows: 4% and 1.21% at 3000 rev/min, 5.038% and 1.66% at 2800 rev/min, and 3.51% and 1.13% at 2600 rev/min, respectively.

Fig. 8
figure 8

Comparison of the experimental and numerical results on the effects of rotational speed on the pressure difference at the blood temperature of 28 °C

Full size image

The effects of three rotational velocities on the hydraulic efficiency are shown in Fig. 9. The hydraulic efficiency here is defined as:

Fig. 9
figure 9

Effects of the rotational velocity on the CBP’s hydraulic efficiency

Full size image
$$\upeta =\frac{{Q\Delta P}_{t}}{\tau\Omega }$$
(15)

where Q is flow rate, ΔPt is total pressure difference, τ is torque, and Ω is rotational speed.

Undoubtedly the main challenging aspect of the blood trauma is managing the hydraulic efficiency. Figure 9 shows that the hydraulic efficiency increases as the rotational velocity is increased. It can be seen obviously that the hydraulic efficiency increases firstly and then decreases with discharge flow increment. In general, an increase in the flow coefficient leads to an increase in rate of volumetric flow, and this enhancement was found to be higher rather than that was observed by decreasing total pressure difference to impeller torque ratio. The figure also shows that for all 3 rotational velocities, the maximum hydraulic efficacy is achieved at the volumetric rate of 5.6 L/min.

Effect of surface roughness

In this section, the effects of surface roughness on the CBP performance is discussed. Once again, the effects of surface roughness is assessed in terms of pressure head and hydraulic efficiency against the volumetric flow rate. In addition to a “slip surface” case, five levels of surface roughness, ks (0, 10, 20, 30, 40 µm), are tested. The results are shown in Fig. 10, and as before, the rotational velocity and blood temperature are kept fixed at 2800 rev/min and 28 °C, respectively.

Fig. 10
figure 10

Effects of surface roughness on (a) pressure difference and (b) hydraulic efficiency, at the rotational speed of 2800 rev/min and blood temperature of 28 °C

Full size image

The results in Fig. 10a show that the pressure head is highly dependent on the impeller roughness, and as the surface roughness increases, the pressure head decreases. The effect of surface roughness on the CBP’s impeller is moderately distinctive at high flow coefficients as friction losses are dependent on the Reynolds number. As expected, the highest value of pressure difference is attributed to the case of “slip surface.” It is worth noting that when the mass flow rate increases, the effect of surface roughness on the pressure difference is also increased.

The hydraulic efficiency of different surface roughness is shown in Fig. 10b. As seen in previous figures, the hydraulic efficiency tends to peak at around Q = 5.6 L/min, followed by a drop. As expected, the highest hydraulic efficiency corresponds to the slip surface case.

CBP with inducer

In order to reduce the rate of hemolysis, an increase in the diameter of the impeller and a decrease in the rotating velocity of the pump on the ordinary heart ventricular assist devices have been proposed (Hubbard and Clausen, 1995). In this section, the influence of mounting inducer on the overall performance of CBP is discussed, given that an inducer is installed at the inlet of the CBP.

Based on the data given in Fig. 11, inducers with three blades are installed at the entrance of an impeller. In this section, the CBP is assumed to be equipped with an inducer with a taper-shaped hub and a variable-pitch. The rotational velocity and blood flow temperature are taken as 2800 rev/min and 28 °C, respectively. The parameters involved in the design of the present inducer are given in Table 3.

Fig. 11
figure 11

3D model of the inducer and the impeller in the present CBP

Full size image
Table 3 Geometrical and operational characteristics of the inducer
Full size table

The effects of including an inducer in the CBP are shown in Fig. 12 in terms of pressure head and hydraulic efficiency. It is evident that there is no significant difference between the two cases in the range of volumetric flow rates tested here (i.e., 1.4–6.4 L/min). Hence, it can be said that an inducer has small effects on the pressure head and hydraulic efficiency (Japikse 2001).

Fig. 12
figure 12

Effects of including mounting an inducer on the (a) pressure difference and (b) hydraulic efficiency

Full size image

It should also be noted that in the application of LVAD, an inducer is a type of axial blood pump. Clearly, this inducer and axial blood pump need higher rotational velocity than the CBP to give designers the opportunity of improving the performance of inducer and the axial blood pump. Due to the fact that the nominal rotational speed of CBP is 2800 rev/min, the static pressure and torque of an inducer is lower than the impeller of CBP.

In the high viscosity environment, an inducer pumps bulk liquid to the first stage of CBP, and also it is a positive displacement device which can provide adequate flow and pressure into the impeller’s eye, especially when there is a blockage at intake of the impeller.

Wall shear stress (WSS)

WSS and other WSS-based hemodynamic parameters play an important role in studying blood flow in cardiovascular diseases, designing medical devices including CBP and many other applications Kabinejadian et al. 2016; McElroy et al. 2021; McElroy and Keshmiri, 2018; Ruiz-Soler et al. 2017). In this section, the WSS distributions are presented in Fig. 13 where it provides an isometric view of the WSS distribution, under a constant rate of rotational speed of 2800 rev/min, throughout CBP impeller and inducer at nominal flow rate. The results of the two models (CBP equipped with and without inducer) are presented at six different timing including 0.24, 1.16, 2.48, 3.68, 4.12, and 5.48 s.

Fig. 13
figure 13

WSS distributions at the rotational speed of 2800 rev/min at 28 °C. (a) CBP equipped with inducer, (b) CBP equipped without inducer, and (c) inducer

Full size image

As expected, a high shear zone was found in CBP’s impeller being symmetrical in both models. It is worth mentioning that the highest WSS was obtained in the blade channel of the impeller and tip blade of the inducer. As the time point reached to 5.48 s, the magnitude of the highest WSS gradually enhanced. Hence, the lowest WSS is observed at 0.24 s.

The results of our research demonstrated that WSS in an CBP, equipped with an inducer, was lower than the CBP without inducer, especially in timing range of 3.68 s and 5.48 s. Therefore, installing an inducer is able to reduce the surface of the blood’s contact with the impeller and the time of the lower blood residence in the high WSS zones at same time.

As shown in Fig. 13c, a high shear zone is visible in the hub surface at > 3.68 s. It is necessary to say that the highest WSS of an inducer was observed at 35 Pa in terms of the overall timing, but the resultant was not significant as compared to the highest WSS in the impeller. High shear rates flow through the pumps (due to the high rotation rates), and cavitation can lead to disagreeable the aggregation of red bloods cells.

Discussion

Effect of rotational velocity and fluid temperature

Generally, VAD is a device to support and control the cardiomyopathy and increase the blood pressure based on the blood damage which is the main parameter in the stability of pumps. These useful devices are, of course, widely used for improving output pressure of heart to deliver nutrition and oxygen to the organs. Typically heart failure occurs at the left ventricular, while LVADs are designed to work with the volume flow rate of 4.5L/min and pressure head of 80 mm Hg (Thamsen et al. 2015). However, rotational velocity has profusion impact on the performance of CBP (as shown in Figs. 8 and 9). The overall efficiency of CBP significantly depends on blood trauma and loss in the pump. The most important losses in the pump are mechanical losses, which are related to bearing and shaft seal, and hydraulic losses, which are caused by recirculation, flow separation, and leakage and occur in various parts within CBPs such as the volute. Nevertheless, the impeller and the casing have significant effects on hydraulic efficiency. In fact, the hydraulic efficiency increases as the rotational velocity increases when the discharge flow is lower than 5.6 L/min. At the same time, the trend of curve turns reversed when flow discharge is between 5.6 and 7.21 L/min. It can be clearly seen that lower rotational velocity returns slightly higher efficiency which is due to the existence of larger losses and rotational speed.

The present results also show that high rotational velocity in these pumps exposes the impeller wall to a higher range of WSS, which can cause the membrane rupture of the erythrocyte. On the other hand, as rotational velocity decreases, the blood will remain through the pump for longer duration, and this could increase the possibility of thrombus formation (Fig. 13).

The results in Fig. 6 suggest that the effect of working fluid temperature affects the pressure head. In the design point, when temperature increases, the head pressure also increases too. Therefore, one could conclude that the blood temperature of the patients could play a role in the performance of CBPs.

Effect of surface roughness

As shown in Fig. 10, surface roughness can play an important role in the performance of CBPs. It would be possible to consider an impeller without roughness. Needless to say that measurement of pressure drop has great clinical significance for the treatment of heart failure. Therefore, when surface roughness increases on the CBP’s impeller, both pressure head and hydraulic efficiency drop dramatically. Due to the dependency of the hydraulic efficiency on the ratio of total pressure difference/torque, a reduction in surface roughness at a certain flow coefficient is presumed to bring about a reduction in the total pressure difference/torque ratio. Of course, this ratio will be reduced in higher and lower flow coefficients.

Effect of an inducer

Inducers can be viewed as a type of turbomachinery which are mounted upstream of the inlet to the main impeller. in the context of centrifugal pumps, inducers are being used to prevent cavitation (Shojaeefard et al. 2019). Cavitation is the formation of vapor cavities in the liquid due to the rapid change of pressure. This phenomenon occurs where the pressure is relatively low which is an undesirable occurrence that might take place in LVADs. Although cavitation instability in CBP is an important issue that should be considered, the aggregation of red bloods cells or hemolysis by the cavitation is more of a concern (Brennen 2015). The present results demonstrated that higher WSS is found in the suction eye of CBP. Therefore, installing an inducer in front of CBP has a significant impact on decreasing WSS. As a result, the presence of an inducer in the structure of an CBP helps to reduce WSS. In general, mounting an inducer upstream of an impeller moderately declines hemolysis (Hubbard and Clausen 1995), especially on the impeller surfaces. This is due to the velocity of the blade being at its minimum at the center of the impeller, probably because the first point of blood contact with the surfaces of the impeller occurs in the regions having a fairly low tangential velocity in terms of the rotational axis. As the blood continues to travel into the housing, it is accelerated to the maximum velocity, tangential to the axis of rotation, which happens towards the outer blade. The moderate acceleration declines the flow turbulence through the housing and results in smaller WSS in comparison to that before entering the CBP (Fig. 13). As a caveat, the type of inducer studied here (i.e., helical or three-bladed) may not be appropriate for all types of CBPs.

Conclusion

Based on the fact that the development of a centrifugal blood pump is a very difficult task, describing some important geometrical parameters can help designers in order to improve the efficiency of LVAD. In the present work, 3D numerical simulation and experimental tests were carried out to evaluate the effect of surface roughness, working fluid temperature, and incorporating an inducer on the performance of a centrifugal blood pump. In summary, the following main conclusions can be drawn from the present study:

  • The typical disagreement obtained between the numerical simulations and experimental data for the pressure difference was 1.66% at the rotational speed of 2800 rev/min, suggesting high level of accuracy in the present numerical techniques.

  • The k-ω-SST (shear stress transport) turbulence model is found to have the best agreement with the experimental data due to the fact that minimum deviation of the k-ω-SST between experimental data and numerical results is 0.57%.

  • Increasing the surface roughness causes the pressure difference and the hydraulic efficiency to decrease in the CBP performance. In fact, at nominal flow rate, if the surface of impeller was slip, the performance and efficiency of the CBP improved by 2.5% and 1.2%.

  • The pressure difference in the pump increases with increasing the working fluid temperature. Additionally, the pressure head locally increases between Q = 4 and 6 L/min. The pressure head of the CBP with fluid temperature of 34 °C at nominal flow rate is 6.01% and 7.51% higher than the CBP with fluid temperature of 22 °C and 16 °C, respectively.

  • While adding an inducer does not significantly impact the pressure difference and the hydraulic efficiency of the pump, it can considerably reduce the WSS of the impeller, highlighting a need for conducting further design optimization on the inducer.