A hybrid genetic local and global search algorithm for solving no-wait flow shop problem with bi criteria

Abstract

This paper addresses the m-machine no-wait Flow Shop Scheduling with Setup Times (NW-FSSWST). Two performance measures: total flow time and makespan are considered. The objective is to find a sequence that minimizing total flow time ($\sum C_{j}$) and makespan ($C_{j}$) simultaneously. A Hybrid Genetic Local and Global Search Algorithm (HGLGSA) is proposed to solve the NW-FSSWST for two performance criteria. The hybrid genetic algorithm is constructed by insert-search and self-repair algorithm with self-repair function. The proposed HGLGSA is tested on 192 benchmark problems of NW-FSSWST in the literature. A full factorial experimental design is made for determined the best parameter sets that improve the performance of the proposed algorithm. The computational results are compared with the benchmark solutions from the literature. The experimental results demonstrate the effectiveness and efficiency of the proposed HGLGSA for solving NW-FSSWST.

1 Introduction

Scheduling is a highly effective method for modeling industrial production processes [1]. No-wait flow shop problems are specific forms of flow shop problems. In flow shop problems, parts flow through serial machines. While some parts are processed in a certain machines, others might be skipped those machines. In a no-wait flow shop scheduling problem, a certain process of a job needs to be conducted uninterruptedly from the beginning of the process to the end of the process [2]. No-wait scheduling has many applications in real-world such as flight, train, and surgery problems.

Minimizing total flow time in a no-wait flow shop environment attracts the attention of many researchers. To minimize the work-in-process inventory by using the total flow time as a criterion in no-wait scheduling problems is meaningful for today’s production environment due to stabilizing usage of resources [3]. Besides, the makespan criterion is directly related to resource utilization. The makespan performance is the most commonly used as a criterion for the no-wait scheduling problems. In this paper, two performance measures: total flow time and makespan are considered. The makespan is defined as the completion time of the last job on the last machine. The total flow time is defined as a sum of the completion times of all jobs.

The no-wait flow shop scheduling is an NP-hard problem with a single objective if the number of machines is more than two. In this research, total flow time and makespan performance measures are considered for NW-FSSWST problems. For solving the NW-FSSWST problems, the genetic algorithm is hybridized. A genetic algorithm (GA) is an effective population-based meta-heuristic method for solving combinatorial optimization problems. But, GA has got some disadvantages steps during the run time. For example, GA can sticks into local optima, after a few solution steps. To eliminate this disadvantage of GA, improve its performance, and reducing search time a hybrid method is proposed. The GA is hybridized by the insert-search and self-repair method. These hybridize methods are refining the search space and performing local exploration. Insertion-search is used as a local search procedure. It searches a small neighborhood. The self-repair is used as a global search method. Also, it searches a large neighborhood in a search space. The aims of the insert-search and self-repair method are to find out better fitness value by inserting a chosen gene to other possible locations on the chromosome and repairing the chromosome itself.

It can be seen in the literature review section, there is no published paper about the no-wait flow shop scheduling problem with setup times to minimizing total flow time and makespan simultaneously. The contributions of this paper are summarized as follows.

• This is the first study to use the total flow time and makespan performance criteria simultaneously for no-wait flow shop scheduling problems with setup times.

• The proposed hybrid genetic local and global search algorithm is first used to solve the no-wait flow shop scheduling with setup times problems for two criteria.

• A full factorial experimental design is done for determining the best parameter sets of the proposed hybrid genetic algorithm for solving the no-wait flow shop scheduling problems with setup times.

• The proposed HGLGSA is calibrated for NW-FSSWST by some benchmark problems in the literature.

• The NW-FSSWST benchmark problems in the literature are solved by the proposed HGLGSA with two criteria.

The experimental results showed that the proposed HGLGSA provides better makespan and total flowtime values for the NW-FSSWST problems.

The remaining contents of the paper are organized as follows. The literature review related to no-wait scheduling problems is given in Sect. 2. Section 3 defines the NW-FSSWST formulation. Section 4 provides the hybrid genetic local and global search algorithm. Section 5 gives the computational results. Section 6 gives the conclusion and future researches.

2 Literature review

This section is devoted to the literature review related to the no-wait flow shop scheduling problems. The no-wait flow shop scheduling (NW-FSS) problem has been addressed widely in the literature. Some of them are given as follows. Hall and Sriskandarajah [4] provided literature reviews with no-wait in process from 1970 to 1993. Allahverdi [5] provided second literature reviews with no-wait in process from 1993 to 2016. Grabowski and Pempera [6] suggested and compared different local search algorithms like descending search algorithms with multi-moves and tabu search algorithms for minimizing C_max. They also proposed dynamic tabu lists to avoid trapped at a local optimum. Wang et al. [7] compared simulating annealing and genetic algorithm in an environment of 10–300 jobs on 2–3 machines on account of scheduling efficiency for no-wait scheduling problems. Liu et al. [8] suggested a hybrid particle swarm optimization algorithm for the no-wait scheduling problem. In their study, a meta-lamarckian simulating annealing algorithm was used as a local search algorithm for hybridizing their particle-swarm optimization algorithm. Laha and Chakraborty [9] suggested a heuristic for minimizing C_max in case of job insertion. They also compared their algorithm with well-known methods in the literature. Pan et al. [10] proposed a hybrid discrete particle swarm optimization to solve NW-FSS problems with the criterion of C_max. Tseng and Lin [11] improved a hybrid genetic algorithm to minimize total completion time. They hybridized the genetic algorithm and a novel local search schema. An orthogonal-array-based crossover operator was designed to enhance the capability of intensification in the genetic algorithm. They proposed a local search schema that combines two local search methods: the insertion search and a novel local search method for makespan performance criterion. Engin and Gunaydin [12] studied an adaptive learning approach to obtain total completion time in NW-FSS problems with setup times. Chaudhry and Khan [13] presented a general GA methodology for no-wait flow shop scheduling and compared it with other well-known meta-heuristics. Allahverdi and Aydilek [14] tried to minimize total completion time in NW-FSS with constrained C_max value which must be less than a certain time. Panwalkar and Koulamas [15] considered two-machine no-wait open shop scheduling with minimum makespan objective. An optimal algorithm was proposed to solve two-machine no-wait open shop scheduling problems. Lin and Ying [16] designed a no-wait flow shop as an asymmetric traveling salesman problem and suggested two metaheuristics algorithms to solve it for minimizing the makespan criterion. Ye et al. [17] proposed a heuristic that was named “average departure time” to minimize makespan. Ye et al. [18] introduced an average idle time heuristic to minimize makespan in no-wait flow shop production. An initial sequence algorithm was proposed in which current and future idle times were taken into consideration. They used insertion and neighborhood exchanging methods to improve solution quality. Shao et al. [19] suggested an iterated greedy algorithm for distributed no-wait flow shop scheduling problems with the makespan criterion. Engin and Güçlü [20] developed a Hybrid Ant Colony Optimization (HACO) algorithm for no-wait flow shop scheduling problems with setup times. Zhao et al. [21] proposed a discrete water wave optimization algorithm to solve no-wait flow shop scheduling problems.

No-wait flow shop scheduling with the total flow time performance criteria has been addressed in the literature by a limited number of researchers. Some of these studies are given as follows: Filho et al. [22] improved an evolutionary algorithm for minimizing total flow time in the NW-FSS problem. Also, they compared their algorithm with Olivera and Lorana’s evolutionary clustering search algorithm. Akhshabi et al. [23] proposed a hybrid particle swarm optimization algorithm for the NW-FSS problem to minimize the total flow time. Laha et al. [24] proposed a penalty-based construction algorithm for the NW-FSS problem with the minimum makespan and total flow time objectives. Originally, it was derived from Hungarian penalty method to generate an initial schedule of jobs. Koulamas and Panwalkar [25] offered an index priority rule for NW-FSS with makespan criterion for specially-structured job processing times. Moreover, they derived an index priority rule for two machine NW-FSS with the minimum weighted total completion time criterion. Zhu et al. [26] presented a novel quantum-inspired cuckoo co-search algorithm for solving the NW-FSS problem with the makespan criterion. Allahverdi and Allahverdi [27] developed a two-machine NW-FSS problem with the total completion time performance criteria. They developed eight algorithms for the processing and setup times on both machines, convert the two machine problem into a single machine one.

In the no-wait literature, multi-criteria scheduling problems have been addressed by using different criteria. There are a few studies in the literature. Some of these studies are given as follows: Allahverdi and Aldowaisan [28] suggested a hybrid genetic algorithm and hybrid simulated annealing algorithm to minimize just T_max and both of T_max and C_max in no-wait flow shop scheduling. Tavakkoli-Moghaddam et al. [29] suggested an artificial immune system algorithm to minimize means of T_max and C_max. Rahimi-Vahed et al. [30] presented a search algorithm for minimizing weighted completion time and weighted mean tardiness time simultaneously. Pan et al. [31] improved a multi-objective particle swarm optimization algorithm for solving no-wait flow shop scheduling problems with C_max and T_max criteria. Aydilek and Allahverdi [32] proposed several algorithms, including a simulated annealing algorithm for solving no-wait flow shop scheduling problems to minimize C_max and Total Completion Time (TCT) performance criteria. Aydilek and Allahverdi [33] developed two improved simulated annealing algorithms for solving the no-wait flow shop scheduling problem to minimize C_max and TCT criteria. Allahverdi and Aydilek [34] generated different versions of insertion in genetic algorithm in the no-wait flow shop to minimize TCT and C_max. Allahverdi et al. [2] proposed an algorithm that was a combination of simulated annealing and insertion algorithm for solving the no-wait flow shop scheduling problem with two criteria: total tardiness and C_max.

3 No-wait flow shop scheduling with setup times

This paper considers m-machine, n-job no-wait flow shop scheduling with setup times for total flow time and makespan performance criteria. The m-machine no-wait flow shop with setup times for makespan performance measure, denoted by $Fm/ {\text{no}} - {\text{wait}}$, $sj,i/ C_{\max } ,$ where $Fm$ denotes the flow shop with m machines; no-wait indicates the no-wait processing characteristic, $sji$ denotes the setup time of job j on machine i, and $C_{\max }$ (makespan) indicates the performance criterion [20].

Some preconditions in the NW-FSSWST are as follow [20]:

• All jobs and machines are available,

• All jobs have a setup and processing times,

• The setup and processing times of each job on each machine are given before,

• The setup time is dependent on both job and machine,

• A job can be only processed on a single machine at a moment,

• Each machine can process only one job at a time,

• Before processing a job on a machine, its setup must be completed

• Jobs are independent,

• Jobs must be processed without waiting time,

• The target of the scheduling is to find out minimum total flow time and makespan values simultaneously.

The m-machine no-wait flow shop with setup times for total flow time performance measure, denoted by $Fm/ {\text{no}} - {\text{wait}}$, $sj,i/\sum C_{j}$, where $\sum C_{j}$ indicates the performance criterion, total flow time of job j.

In this study, two performance criteria: total flow time and makespan are considered. This problem is denoted by F_m/no-wait, s_j,i/C_max, $\sum C_{j}$. Several approaches have been developed for bi-criteria and multi-criteria scheduling problems in the literature. In this type of problem, some conflicting criteria have to be optimized simultaneously. The existing approaches for solving bi-criteria or multi-criteria no-wait scheduling problems do not integrate explicitly a manager’s preferences [35, 36]. Thus, we proposed an aggregation procedure for two performance criteria. Total flow time and total completion time combined as a satisfaction function in the proposed procedure to solve no-wait flow shop scheduling problems. Also, this procedure was used by Allouche et al. [35] for multi-criteria flow shop scheduling problems in the literature. To the best of our knowledge, this is the first study that combined total flow time and total completion time performance criteria combined as the satisfaction function for the no-wait scheduling problem.

The NW-FSSWST consists of a set of n jobs (j = 1,2,…,n) to be processed on a set of m machines (i = 1,2,…,m) with an s_j,i setup time of job j on machine i.

The NW-FSSWST is formulated as follow;

n:

Job number

m:

Machine number

$\pi$:

Permutation of job $\pi = \left\{ {\pi_{1 } ,} \right.\pi_{2 } , \ldots ,\left. {\pi_{n } } \right\}$

$ST\left( {\pi_{j} ,i} \right)$:

Setup time of the job j on machine i.

$PT\left( {\pi_{j} ,i} \right)$:

Processing time of the job j on machine i.

$MinD\left( {\pi_{j - 1} ,\pi_{j} } \right)$:

Minimum delay on the first machine between starting time of job $\pi_{j}$ and $\pi_{j - 1}$

$MCT$:

Minimum completion time.

$\sum C_{j}$:

Total flow time (TFT) of job j.

The ${\text{Min}}D$ calculated from the following Eqs. 1, 2, 3 [6, 10, 20].

$$\begin{aligned} {\text{Min}}D\left( {\pi_{j - 1} , \pi_{j} } \right) & = {\text{ST}}\left( {\pi_{j - 1 } , 1} \right) + {\text{PT}}\left( {\pi_{j - 1 } , 1} \right) \\ & \quad + \max \left[ {0, \mathop {\max }\limits_{2 \le i \le m} \left\{ {\mathop \sum \limits_{i = 2}^{m} \left( {{\text{ST}}\left( {\pi_{j - 1} , i} \right) + {\text{PT}}\left( {\pi_{j - 1} , i} \right)} \right) - \mathop \sum \limits_{i = 1}^{m - 1} \left( {{\text{ST}}\left( {\pi_{j} , i} \right) + {\text{PT}}\left( {\pi_{j} , i} \right)} \right)} \right\}} \right] \\ \end{aligned}$$

(1)

$${\text{Makespan}} = C_{\max } \left( \pi \right) = {\text{MCT}}\left( { \pi } \right) = \mathop \sum \limits_{j = 2}^{n} {\text{Min}}D\left( {\pi_{j - 1,} \pi_{j} } \right) + \mathop \sum \limits_{i = 1}^{m} \left( {{\text{ST}}\left( {\pi_{n} , i} \right) + {\text{PT}}\left( {\pi_{n} , i} \right)} \right)$$

(2)

$${\text{MCT}}\left( {\pi^{*} } \right) \le M\left( {\pi_{n } ,m} \right)\forall_{\pi } \in \pi$$

(3)

$$\sum C_{j} = \mathop \sum \limits_{j = 2}^{n - 1} \left( {n - j} \right){\text{Min}}D\left( {\pi_{j - 1} , \pi_{j} } \right) + \mathop \sum \limits_{i = 1}^{m} \left( {{\text{ST}}\left( {\pi_{n} , i} \right) + {\text{PT}}\left( {\pi_{n} , i} \right)} \right)$$

(4)

$${\text{TFT}}\left( {\pi^{*} } \right) \le {\text{TFT}}\left( {\pi_{n } ,m} \right)\forall_{\pi } \in \pi$$

(5)

4 Hybrid genetic local and global search algorithm

4.1 Genetic algorithm

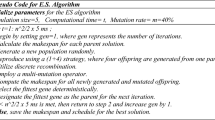
The genetic Algorithm which was proposed by Holland in 1975 firstly, is a method commonly used in the solution of combinatorial optimization problems [37]. A genetic algorithm is a population-based meta-heuristic method. It tries to find an optimum or closer solution for NP-hard problems [38, 39]. Fundamental parts of genetic algorithms are chromosome, population, and gen which is the smallest meaningful element of a chromosome. Every gen represents a job in a scheduling problem. Thus, multiple gens come together to generate a chromosome. Similarly, a population consists of a set of chromosomes [40]. The basic steps of a genetic algorithm are presented below [37, 41].

Step 1 All possible solutions must be presented as an array of gens in the solution space. So, all solutions are coded as a set of arrays in this study.

Step 2 An initial population is created by random generally.

Step 3 A fitness value is calculated for every array.

Step 4 A certain number of arrays are selected for the process of breeding randomly.

Step 5 Fitness values of every individual in the new generation are calculated. Then, they are crossed over and mutated.

Step 6 Step 3 to Step 5 is repeated up to reach a predetermined generation number.

Step 7 The arrow which has the best fitness value is selected.

Operators of genetic algorithm are explained in below;

4.1.1 Breeding operator

The intention of breeding operators in genetic algorithms is that the individuals that have better fitness values are more likely to be in the next generation. Hence, the fitness value of those individuals is normalized by the mean of the population.

4.1.2 Crossover operator

Crossover operator exchanges information between arrays and produces better individuals. Randomly (generally) selected at least two gens from two arrays are interchanged. In other words, it generates two possible solutions. Although, there are many types of crossover in the literature, single-point crossover, and multi-point crossover are used widely [42]. Position-based, order-based, partial-mapped crossover, linear order-based crossover are well-known multi-point crossovers.

4.1.3 Mutation operator

The mutation is a sudden change in a parent’s genotype which is caused by an alteration in a gene or a chromosome. The number of genes is constant in a process of mutation. Mutation occurs just on one array (chromosome). Reverse mutation, exchanging randomly chosen two genes, exchanging randomly chosen three genes, and gene insertion are widely used mutation operators in the literature.

4.1.4 Elitism strategy

After breeding, crossover, and mutation operators, the individuals which have the best fitness value in their population might not be transferred to the next generation. To avoid this undesirable condition, the individuals which have better fitness value are exchanged with other individuals those have worse fitness value in their population by the elitism process [43].

4.1.5 Crossover and mutation probability

Crossover and mutation probabilities are used as parameters of the genetic algorithm. These may have a value between 0 and 1. Thus, they are considered probabilities. If the “0” value is given to an operator, it means none of the individuals will be changed in this population as a result of that operator. Similarly, if “1” is given as a parameter, that means all the individuals, in other word, all populations will be changed. Both of those values are not to be given generally since they don’t contribute efficiency of the algorithm. So, we choose a value between 0 and 1 for crossover and mutation probabilities in this study.

4.2 Hybrid genetic local and global search

The genetic algorithm uses a selection and recombination operator for global exploration in the search space. During the run time, the genetic algorithm converges slowly toward the local optimum. After a few solution steps, the genetic algorithm sticks to a local optimum. Therefore, the proposed algorithm hybridizes the genetic algorithm for refining the search space and performing local exploration. The insertion search is used as a local search algorithm. The local search method plays important role in the search spaces. The insertion search is used for searching a small neighborhood. Also, the self-repair algorithm is used as a global search algorithm. The self-repair algorithm is responsible for searching a large neighborhood in a search space.

The flow chart of the HGLGSA is given in Fig. 1. Local and global search procedures were likewise utilized in addition to a hybrid genetic algorithm. After initialization, insert-search and self-repair algorithms are integrated into 3rd step. While insert search algorithm works as a local search algorithm, self-repair algorithm addresses to repair the chromosomes itself. Additionally, when the self-repair algorithm is executed, it sends a₂ cut point parameter to the insert-search algorithm instead of a₁. We avoid designing a too greedy algorithm for preventing the trap of local optimal point. Thus, P₁ and P₂ chromosomes are chosen randomly rather than utilizing the best pair of chromosomes in the initial population.

Fig. 1

Flow chart of proposed HGLGSA

The proposed insert search and self-repair algorithm are given in Figs. 2 and 3, respectively. Also, flow chart of the self-repair function is given in Fig. 4.

Fig.2

Insert-search algorithm

Fig.3

Self-repair algorithm

Fig. 4

Self-repair function

The insert-search is a kind of local search method which aims to find better fitness values by inserting a chosen gene to other possible location on the chromosome. It doesn’t check all possible neighborhoods of all genes in the chromosome, but it searches different neighborhoods of a chosen genes in the chromosome.

Self-repair method, repeats to run self-repair function and insert-search methods up to reach a pre-assigned loop number. The main purpose of the self-repair function is to find out better fitness value by repairing the chromosome itself. The function chooses the most problematic gene pair, where makes the biggest difference in total completion time as a repair location. Then, it explores to find better fitness values by inserting those genes into several locations on the chromosome. Also, it has a random chromosome selection process to prevent overpressure of elitist strategies.

5 Computational results

In this study, we suggested a self-repaired multi-objective hybrid genetic algorithm for NW-FSSWST. Moreover, we have tried to optimize the goals in Tseng and Lin [3]’s study which are C_max and $\sum C_{ji}$ in a flow shop environment. Total flow time and total completion time were combined as a satisfaction function of Allouche et al. [35] to reflect the manager’s preferences. The manager’s preferences can explicitly express any deviation of the achievement from the aspiration level of each objective. The model that explicitly incorporates the manager’s preferences through the satisfaction functions for objectives of makespan and total flow time is given in Eq. 6 [35].

$${\text{Maximize}} \mathop \sum \limits_{c = 1}^{2} {\text{SR}}_{C} \left( {{\text{RPD}}_{c} } \right)$$

(6)

where c is defined as the number of criteria (Makespan and total flow time); SR_c is defined as satisfaction rate for criterion c, and RPD_c is defined as relative percentage deviation for criterion c.

According to Allouche et al. [35]’s study, the best value of every goal could deviate a certain rate in a multi-objective based algorithm. Similarly, we built a satisfaction function. When the RPD is between 0 and 1%, the manager is completely satisfied. If the rate goes between 1 and 3%, SR is reducing from 100 to 0%. When the satisfaction rate gets a “0” value, there is no satisfaction but the solution is still acceptable up to %5 of deviation. After “0” satisfaction and 5% RPD, the solutions of the multi-objective model will be rejected. The satisfaction function is presented in Fig. 5.

Fig. 5

The satisfaction function

In this study, 192 no-wait flow shop, n jobs {n = 8, 10, 12, 50, 100, 150, 200, and 250} and a set of m machines {m = 2, 3, 5, 8, 10, 15, 20, and 25}, with setup times problems that were generated by Engin and Günaydın [12], were used as benchmark instances. According to the processing times on each machine, these problems are classified a, b, and c type problems. These problems are commonly used in the literature [12, 20, 44,45,46].

Thus, 192 problems were solved by proposed HGLGSA with two-performance measures Total Flow Time (TFT) and makespan (C_max).

Minimize TFT

Subject to C_max

5.1 Parameter optimization of HGLGSA for NW-FSSWST

The operating parameters of the HGLGSA are playing important role in the quality of the NW-FSSWST problem’s solution. The parameters of HGLGSA are initial population number, crossover and mutation rates, local and global terminators, loop quantity, cut point, a range for insert-search local terminator (α₁), and search range of global terminator (α₂). The parameter levels are shown in Table 1.

Table 1 The SRMOHGA’s parameter levels used for the parameter optimization

A full factorial experimental design was performed for obtaining a set of the best parameters, which are given in Table 2.

Table 2 Parameters of NW-FSP

5.2 Calibration of proposed HGLGSA for NW-FSSWST

The proposed HGLGSA was calibrated by Engin and Günaydın [12]’s benchmark instances.

The performance of the HGLGSA is compared with the GEN-2 (Aldowaisan and Allahverdi’s genetic algorithm for no-wait flow shop problems [44]), ALA (Engin and Günaydın’s Adaptive Learning Algorithm [12]), and HACO (Engin and Güçlü’s Hybrid Ant Colony Optimization [20]) as a Relative Percentage Deviation (RPD). The RPD is given in Eq. 7 [47].

$${\text{RPD}} = \frac{{{\text{Heuristic Algorithm}} \left( {C_{\max } } \right) - {\text{Best}} \left( {C_{\max } } \right)}}{{{\text{Best}} \left( {C_{\max } } \right)}} \times 100$$

(7)

At Eq. 7, Best (C_max) is the minimum makespan-C_max of the Engin and Günaydın [12]’s benchmark instances the best values found by CPLEX solutions [12, 20, 44]. Also, the heuristic algorithms are defined as the proposed HGLGSA, GEN-2 [44], ALA [12], and HACO [20].

Solution performance of the proposed HGLGSA, GEN-2 [44], ALA [12], and HACO [20] is given in Table 3 for 48 problems totally.

Table 3 RPD of HGLGSA, GEN-2, ALA and HACO

Average Relative Percentage Deviation (ARPD) of proposed HGLGSA is compared to the GEN-2 [44], ALA [12], and HACO [20] algorithms. The ARPD is defined with Eq. 8. For each problem group, the number of instances is given as I (L = 1,…, I) notation at Eq. 8 [20].

$${\text{ARPD}} = \frac{{\mathop \sum \nolimits_{L = 1}^{I} {\text{ARPD}}\left( L \right)}}{I}$$

(8)

The 48-benchmark instances, ARPD for proposed HGLGSA, GEN-2, ALA, and HACO are calculated as 0.0233; 2.3679; 2.3282, and 1.2543, respectively. The proposed HGLGSA has found a smaller ARPD than GEN-2, ALA, and HACO. These results showed that the proposed HGLGSA has better solution performance on NW-FSSWST. Also to better understand the performance of the proposed HGLGSA, the t-test is done with 95% significance for m (2, 3, 5, 8, 10, 15, 20, 25)—machines instances. The results are given in Table 4. The average RPD values, in Table 4, are analyzed on a box plot in Fig. 6.

Table 4 The results of the t-test for proposed HGLGSA and HACO [20]

Fig. 6

Box plots for the average RPD values

In Fig. 6, for average HACO-RPD and HGLGSA-RPD box plots are given. Also, minimum, first quartile (Q1), median, third quartile (Q3), maximum, mean, and range values were calculated. It can be seen in Table 4 and Fig. 6, the proposed HGLGSA performance is better than HACO.

The CPU time of the proposed HGLGSA is compared with the GEN-2 [44], ALA [12], and HACO [20] algorithms. The results are given in Table 5.

Table 5 The maximum CPU times of the proposed HGLGSA, GEN-2 [44], ALA [12], and HACO [20]

It can be seen in Table 5, the CPU time of the proposed HGLGSA is shorter than GEN-2, ALA, and HACO.

5.3 Computational results of two performance measures

The 192 NW-FSSWST benchmark instances, which were created by Engin and Gunaydin [12], were solved by proposed HGLGSA for minimizing C_max and $\sum C_{j}$ values. Computational results are given in Table 6.

Table 6 Computational results of HGLGSA in case of satisfaction function

When we are analyzing Table 6, we see that deviation values of C_max and $\sum C_{j}$ are raised generally if the amount of machines and jobs are increased. There are just 3 positive $\sum C_{j}$ deviation values for 2 machines; on the other hand, there are 12 positive $\sum C_{j}$ deviation values for 25 machines. Similarly, while there are 16 “0” C_max deviation values for 8 jobs, there is just one “0” C_max deviation value for 250 jobs.

Satisfaction status based on C_max and $\sum C_{j}$ of HGLGSA is given in Table 7 for “completely satisfied” “satisfaction level” and “acceptance borders” to minimize $\sum C_{j}$ and C_max values of every job-machine combination.

Table 7 Satisfaction status based on $\sum C_{j}$ and C_max objectives

Also, the satisfaction status based on $\sum C_{j}$ and C_max objectives is given in Fig. 7 by graphical results.

Fig.7

The satisfaction status based on $\sum C_{j}$ and C_max objectives

As seen in Table 7 and Fig. 7, full satisfaction is obtained in 156 of 192 problems based on $\sum C_{j}$ objective deviation. While 29 of 192 deviations are satisfaction levels, 6 deviations are acceptance borders. One deviation is rejected.

Also, 56 of 192 fully satisfied deviations are found regarding to C_max objective value. While 11 of 192 are satisfaction levels, 6 of 192 are acceptance borders. 119 of 192 are rejected.

According to those results, multi-objective problem structure does not affect $\sum C_{j}$ values deeply. Calculated deviation values are distributed in a narrow interval.

Because of the multi-objective structure, we could have obtained better $\sum C_{j}$ values in some cases. Also, the most of $\sum C_{j}$ values have taken place in the full satisfaction area.

6 Conclusions and future research

In this study, we suggested an insert-search algorithm and self-repair algorithm with a self-repair function to develop our HGLGSA. HGLGSA was proposed to solve the NW-FSSWS, which are well-known NP-hard problems in the literature. Firstly, the proposed HGLGSA was calibrated by GEN-2, ALA, and HACO in the literature for no-wait flow shop scheduling problems. Secondly, a full factorial design was performed to determine the best parameter sets in the HGLGSA for NW-FSSWST with two criteria that enhance the performance of the algorithm. Then Engin and Gunaydin [12]’s benchmark NW-FSSWST problems were solved by the proposed HGLGSA for two performance measures which are total flow time and makespan. The parameters of the proposed HGLGSA are the number of initial populations, the rates of crossover and mutation, execution times of local and global search, loop quantity, cut point (N), the levels of α₁ and α₂. Finally, Engin and Gunaydin [12]’s 192 test benchmark instances were solved based on the satisfaction function for bicriteria by using the best parameter set of the proposed HGLGSA. A full satisfaction was obtained in 156 of 192 problems based on $\sum C_{j}$ objective deviation and 11 of 192 problems based on C_max objective value.

Experimental results showed that the proposed HGLGSA is a highly effective meta-heuristic algorithm for solving NW-FSSWST with two performance criteria. Moreover, the multi-objective structure has not affected $\sum C_{j}$ objective values dramatically but, it has caused to obtain longer C_max values relatively.

Future studies are suggested to focus on different meta-heuristic methods to get fully satisfied C_max values in the multi-objective environment for NW-FSSWST problems.