Power and energy system oscillation damping using multi-verse optimization

Abstract

Power system oscillations are the primary threat to the stability of a modern power system which is interconnected and operates near to their transient and steady-state stability limits. Power system stabilizer (PSS) is the traditional controller to damp such oscillations, and flexible AC transmission system (FACTS) devices are advised for the improved damping performance. This paper suggests a technique for controller parameters tuning of PSS and a shunt connected FACTS device to be operated in coordination. A static synchronous compensator (STATCOM) connected in a two-machine system is considered as a test power system for the system studies. A recent meta-heuristic algorithm, Multi-Verse optimizer (MVO) has been suggested and compared with the other state-of-the-art algorithms. Improvement in system damping has been achieved by minimizing the oscillating nature of the system states by framing the objective function as a function of damping ratio and location of poles of the system. The Phillips-Heffron model of the test system has been designed by considering the system dynamics. The coordinated system behavior under the perturbation in system parameters has been observed satisfactory with the tuned controller parameters obtained from the suggested algorithm.

1 Introduction

In the present day by day growing open-access power system regime, damping of power network oscillations playing a vital role for trustworthy power transfer to the load ends. Power networks are experiencing electromechanical oscillations due to inconsistent conditions prevailing in the network. In damping the electromechanical oscillations, power system stabilizers (PSS) are conventionally used [1]. The increase in power demand necessities the interconnection of various power systems via transmission lines. Due to the expansion in the power network, perturbations in system parameters introduces the oscillations in the whole system [2]. In an extensive power system, weakening in stabilizer performance takes place due to system latency [3]. To balance the load requirements and to run reliably, PSS are operating to their maximum limits and to maintain the whole system in a stable and safe operating mode is becoming a challenging task [4].

In promoting the utilization of renewable energy sources in power generation, rapid growth in solar and wind energy generation has been observed [5]. The new non-conventional energy sources which are integrated into the power grid introduce fluctuations into the existing system. The system uncertainties are modeled using inverse output additive perturbation structure from the study of DFIG effect on low-frequency oscillations to show the performance characteristics of PSS in improving transient stability [6]. The concept of reducing multiple machine control into multiple single machine control has been introduced by decentralized nonlinear model predictive control approach, and power system oscillation damping has been achieved [7]. An ant-colony based STATCOM has been suggested for the power system stability enhancement in a multi-machine power system [8]. The proposed optimization method has been tested for the different system disturbances and the successful oscillation damping has been achieved. A multi-objective grasshopper algorithm has been proposed for the stability enhanced by the authors [9]. A STACOM has been suggested with higher order sliding mode controller for the stability enhancement [10]. The low-frequency oscillations and forced oscillations mitigation have been done with FACTS devices with energy source [11], by shifting the resonating frequency of the system using UPFC [12]. The oscillations injected into the system due to the installation of wind farm and PV plant have been controlled by facts devises and coordinated with PSS using adaptive velocity update relaxation particle swarm optimization (AVURPSO) algorithm and compared with genetic algorithm (GA) and gravitational search algorithm (GSA) [13] and by using energy-storage unit based on the supercapacitor (SC) [14]. For the power system stability improvement, a fuzzy lead‐lag controller for a coordinated structure combining SSSC and PSS has been designed, and the parameters have been tuned by modified whale optimization algorithm (WOA) [15]. The lightning search algorithm has been applied in coordinating IPFC and PSS in the combined two‐area restructured ALFC and AVR system [16].

The applications of different meta-heuristic algorithms in the tuning of PSS parameters have been increasing, namely firefly algorithm [17], backtracking search algorithm (BSA) [18], hybrid particle swarm optimization algorithm [19] to minimize the settling time and overshoot of the low-frequency oscillations to improve the system stability. Frequency deviation and tie-line power deviation of an interconnected power system have been minimized by the biogeography‐based optimization (BBO) in a system with fractional order fuzzy PID control [20]. The applications of GWO [21], WOA [22], PSO and modified PSO [23,24,25] are getting increased in the recent time in the field of power systems. GWO algorithm shows better performance characteristics in small-signal stability of a power system [26], and in transmission line expansion problem [27]. The contribution of WOA also predominant and proven as efficient optimization technique in optimal reactive power dispatch [28], in performance improvement of photovoltaic power systems [29] and distribution systems [30]. PSO with time-varying acceleration coefficients (PSO-TVAC) has been extensively used in achieving optimal parameters and efficient performance characteristics in generation schedule [31] and in other recent applications in power systems [32,33,34].

From the literature presented above, it has been identified that the necessity of different power oscillation damping devices is more in the present scenario. Also, various FACTS devices have been proposed by various researchers to enhance the performance of a power network. Hence, the installation of the newly proposed controllers with the existing traditional PSS is much needed without creating any king of incoordination among the controllers. By keeping all these concerns, the need for an appropriate technique to obtain the controller parameters of various devices is essential. The present manuscript includes these objectives and highlighted as follows:

• This paper considers a STATCOM as power system oscillation damping device alone with the existing PSS for a power network.

• A two-machine system connected with STACOM has been mathematically modeled by considering all system dynamics for the purpose of analysis.

• The objective of this paper is to derive an optimal solution for the controller variables in damping power system oscillations and is achieved by installing and coordinating the PSS and STATCOM.

• Different object functions on the basis of system eigenvalues have been proposed and examined.

• A recently developed multi-verse optimization (MVO) has been suggested for finding the optimal controller parameters by incorporating superior features over other methods in the literature.

• The system model has been built with lesser number of control parameters and proposed MVO have faster convergence characteristics to achieve the objective.

• The implementation of MVO is not complex and results in consistent optimal solution over several trails. The proposed method includes exploration, exploitation and local search for achieving the best solution.

The organization of the paper is as follows: Briefing the severity of power system oscillations and present approaches in damping those in Sect. 1. Section 2 deals with the detailed system modeling and objective function to be minimized with constraints have been explained. Section 3 explains the proposed optimization algorithm and assessment made by comparing with other popular methods in Sect. 4. Section 5 gives the detailed system performance under different loading conditions followed by the conclusions made in the study. Finally ends with appendixes and references considered in the paper.

2 Research methodology

2.1 STATCOM mechanism in damping power system oscillations

A STATCOM is a shunt connected FACTS device primarily used to provide reactive power support in a power system. It is widely employed to improve the voltage stability of a system. During the abnormalities in the system, the reactive power magnitude and direction varies in the transmission line based on the location of the abnormality. The installation of STATCOM in an appropriate location will provide the necessary reactive power in either direction. The reactive power absorption or delivery at the utility bus depends on the direction of the current provided by the voltage source converter (VSC) of the STATCOM. This further depends on the voltage difference between the converter terminal and utility bus. So, it mainly used for dynamic compensation for providing voltage support, transient stability enhancement and to increase damping [35]. The valve switching action of the VSC is controlled by the pulse width modulation technique with the modulation index (m_e), and the phase angle (d_e). The magnitude of current depends on the DC voltage of the VSC, usually a capacitor or energy-storage device (C_dc). Hence, the selection of m_e and d_e will define the purpose of STATCOM installation, which can be further performed as the controlling variable of STATCOM.

2.2 Mathematical modeling of test system

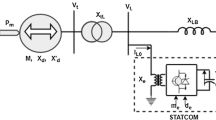
The considered test system is depicted as Fig. 1. The main components in each generator side are represented, and dynamics have been considered for the complete system modeling [36].

Fig. 1

Test power system with STATCOM and PSS controllers

The magnitude of current and voltage at the generator can be represented as (1), (2).

$$I_{iL} \, = \,I_{iLd} \, + \,jI_{iLq}$$

(1)

$$V_{tj} \, = \,V_{tjd} \, + \,jV_{tjq;} V_{tj} \, = \,V_{tj} (\sin \delta_{j} \, + \,j\cos \delta_{j} )$$

(2)

where δ_j = ∠(E′_qj, V_tj), i: is the generator; j: is the area 1, 2.

From Fig. 1, the d, q components of the STATCOM current can be expressed as in (3), (4).

$$\begin{gathered} I_{L0d} = x_{e} \left[ {\frac{{E^{^{\prime}}_{q1} }}{{x_{dee1} }} + \frac{{E^{^{\prime}}_{q2} }}{{x_{dee2} }}} \right] - meV_{dc} \sin de\left[ {\frac{{x_{2L} }}{{x_{dee1} }} + \frac{{x_{1L} }}{{x_{dee2} }}} \right] + x_{e} \left[ {\frac{{V_{t2} \cos (\delta_{1} - \delta_{2} )}}{{x_{dee1} }} + \frac{{V_{t1} \cos (\delta_{2} - \delta_{1} )}}{{x_{dee2} }}} \right] \hfill \\ \hfill \\ \end{gathered}$$

(3)

$$I_{L0q} = meV_{dc} \cos de\left[ {\frac{{x_{2L} }}{{x_{qee1} }} + \frac{{x_{1L} }}{{x_{qee2} }}} \right] + x_{e} \left[ {\frac{{V_{t1} \sin (\delta_{2} - \delta_{1} )}}{{x_{qee2} }} + \frac{{V_{t2} \sin (\delta_{1} - \delta_{2} )}}{{x_{qee1} }}} \right]$$

(4)

The mechanism of reactive power flow control with m_e, d_e at the STATCOM can be realized from Eqs. (3) and (4).

2.3 Power system dynamics

The analysis of the test system can be done by the location of system eigenvalues. For finding the system eigenvalues, the dynamic behavior of the generator–excitation system can be represented by (5)–(8) [37].

$$\Delta \mathop \delta \limits^{.} = \omega_{b} \Delta \omega$$

(5)

$$\Delta \mathop \omega \limits^{.} = \frac{{( - \Delta P_{e} - D\Delta \omega )}}{M}$$

(6)

$$\Delta \mathop {E^{^{\prime}}_{q} }\limits^{.} = \frac{{( - \Delta E_{q} + \Delta E_{fd} )}}{{T^{^{\prime}}_{d0} }}$$

(7)

$$\Delta \mathop {E_{fd} }\limits^{.} = - \frac{1}{{T_{A} }}\Delta E_{fd} - \frac{{K_{A} }}{{T_{A} }}\Delta V_{t}$$

(8)

where $\Delta \omega = (\omega - \omega_{0} )/\omega_{0}$ and system parameters are explained in Nomenclature.

The system state equations with the STATCOM can be represented as (9).

$$\mathop X\limits^{.} = Ax + Bu$$

(9)

where A is the state matrix, B is the STATCOM control input matrix. With $\left[ {\Delta \mathop \delta \limits^{{}}_{1} \Delta \mathop {\omega_{1} }\limits^{{}} \mathop {\Delta E^{^{\prime}}_{q1} }\limits^{{}} \mathop {\Delta E_{fd1} }\limits^{{}} \mathop {\Delta V_{dc} }\limits^{{}} \Delta \mathop {\delta_{2} }\limits^{{}} \Delta \mathop {\omega_{2} }\limits^{{}} \Delta \mathop {E^{^{\prime}}_{q2} }\limits^{{}} \Delta \mathop {E_{fd2} }\limits^{{}} } \right]_{{}}^{T}$ are the state variables and $\left[ {\Delta me\,Delta de} \right]^{T}$ are the control variables.

2.4 PSS mechanism in damping power system oscillations

The conventional PSS consists of a compensation block which is comprised of a first-order lead-lag system with gain, and a reset block. It is represented, as shown in Fig. 2. The mechanism of PSS is to provide a lead or lag signal depending on the rotor speed deviations. The signal is provided to the excitation control unit to balance the speed of the rotor based on the rotor speed variation. Hence, in PSS, the time constants and the gain of the compensation block acts as the controlling parameters to damp the system oscillations. However, in the normal operation, the washout block functions to avoid the compensation effect in the system, which can be achieved by choosing a large value of T_w.

Fig. 2

PSS representation

By considering the effect of PSS, Eq. (9) can be modified as in (10).

$$\mathop X\limits^{.} = Ax + Bu + B_{E} u_{E}$$

(10)

where A is system state matrix, B is STATCOM control input matrix and B_E is the supplementary control matrix.

$$A_{c} \, = \,\left[ {\begin{array}{*{20}c} {A_{11} } & \ldots & {A_{113} } \\ \vdots & \ddots & \vdots \\ {A_{131} } & \cdots & {A_{1313} } \\ \end{array} } \right]\;{\text{and}}$$

$$B_{c} \, = \,\left[ {0 \, 0;B_{21} B_{22} ;B_{31} B_{32} ;B_{41} B_{42} ;B_{51} B_{52} ;B_{61} B_{61} ;B_{71} B_{72} ;0 \, 0;B_{91} B_{92} ;B_{101} B_{102} ;B_{111} B_{112} ;B_{121} B_{122} ;B_{131} B_{132} } \right]$$

where A₁₂ = w₀; A₂₁ = -K₁₁/M₁; A₂₂ = -D₁/M₁; A₂₃ = -K₂₁/M₁; A₂₅ = -Kpd₁/M₁; A₃₁ = -K₄₁/Td0₁₁; A₃₃ = -K₃₁/Td0₁₁; A₃₄ = 1/Td0₁₁; A₃₅ = -Kqd₁/Td0₁₁; A₄₁ = -Ka₁*K₅₁/Ta₁; A₄₃ = -Ka₁*K₆₁/Ta₁; A₄₄ = -1/Ta₁; A₄₅ = -Ka₁*Kvd₁/Ta₁; A₄₇ = Ka₁/Ta₁; A₅₁ = K₇₁; A₅₃ = K₈₁; A₅₅ = -K₉; A₅₈ = K₇₂; A₅₁₀ = K₈₂; A₆₁ = -K₁₁/M₁; A₆₂ = -D₁/M₁; A₆₃ = -K₂₁/M₁; A₆₅ = -Kpd₁/M₁; A₆₆ = -1/T_w; A₇₁ = -KA₁₁*K₁₁*T₁₁/(M₁*T₂₁); A₇₂ = -D₁*KA₁₁*T₁₁/(M₁*T₂₁); A₇₃ = -KA₁₁*T₁₁*K₂₁/(M₁*T₂₁); A₇₅ = -Kpd₁*KA₁₁*T₁₁/(M₁*T₂₁); A₇₆ = (KA₁₁/T₂₁)*(1-(T₁₁/T_w)); A₇₇ = -1/T₂₁; A₈₉ = w₀; A₉₅ = -Kpd₂/M₂; A₉₈ = -K₁₂/M₂; A₉₉ = -D₂/M₂; A₉₁₀ = -K₂₂/M₂; A₁₀₅ = -Kqd₂/Td0₁₂; A₁₀₈ = -K₄₂/Td0₁₂; A₁₀₁₀ = -K₃₂/Td0₁₂; A₁₀₁₁ = 1/Td0₁₂; A₁₁₅ = -Ka₂*Kvd₂/Ta₂; A₁₁₈ = -Ka₂*K₅₂/Ta₂; A₁₁₁₀ = -Ka₂*K₆₂/Ta₂; A₁₁₁₁ = -1/Ta₂; A₁₁₁₃ = Ka₂/Ta₂; A₁₂₅ = -Kpd₂/M₂; A₁₂₈ = -K₁₂/M₂; A₁₂₉ = -D₂/M₂; A₁₂₁₀ = -K₂₂/M₂; A₁₂₁₂ = -1/T_w; A₁₃₅ = -Kpd₂*KA₁₂*T₁₂/(M₂*T₂₂); A₁₃₈ = -KA₁₂*K₁₂*T₁₂/(M₂*T₂₂); A₁₃₉ = -D₂*KA₁₂*T₁₂/(M₂*T₂₂); A₁₃₁₀ = -KA₁₂*T₁₂*K₂₂/(M₂*T₂₂); A₁₃₁₂ = (KA₁₂/T₂₂)*(1-(T₁₂/T_w)); A₁₃₁₃ = -1/T₂₂; And zero for the remaining elements.

B₂₁ = -Kpe₁/M₁; B₂₂ = -Kpde₁/M₁; B₃₁ = -Kqe₁/Td0₁₁; B₃₂ = -Kqde₁/Td0₁₁; B₄₁ = -Ka₁*Kve₁/Ta₁; B₄₂ = -Ka₁*Kvde₁/Ta₁; B₅₁ = K_Ae; B₅₂ = K_Ade; B₆₁ = -Kpe₁/M₁; B₆₂ = -Kpde₁/M₁; B₇₁ = -KA₁₁*T₁₁*Kpe₁/(M₁*T₂₁); B₇₂ = -KA₁₁*T₁₁*Kpde₁/(M₁*T₂₁); B₉₁ = -Kpe₂/M₂; B₉₂ = -Kpde₂/M₂; B₁₀₁ = -Kqe₂/Td0₁₂; B₁₀₂ = -Kqde₂/Td0₁₂; B₁₁₁ = -Ka₂*Kve₂/Ta₂; B₁₁₂ = -Ka₂*Kvde₂/Ta₂; B₁₂₁ = -Kpe₂/M₂; B₁₂₂ = -Kpde₂/M₂; B₁₃₁ = -KA₁₂*T₁₂*Kpe₂/(M₂*T₂₂); B₁₃₂ = -KA₁₂*T₁₂*Kpde₂/(M₂*T₂₂);

The system constants are further defined in Appendix B.

2.5 Objective function and constraints

The detailed system model with STATCOM has been explained, and the complete model has been presented in the form of state-space representation with state variables and control variables mentioned above. The eigenvalues obtained from the designed test system can be represented as in (11).

$$\lambda_{i} = \, {\text{Re}} \, \left[ {\lambda_{i} } \right] + j \, {\text{Im}} \left[ {\lambda_{i} } \right]$$

(11)

where Re [λ_i], Im [λ_i] are the real and imaginary parts of the ith eigenvalue.

The damping ratio for the given eigenvalue can be calculated using (12).

$$Damping \, Ratio \, (\xi_{i} )\, = \frac{{ - {\text{Re}} \, \left[ {\lambda_{i} } \right]}}{{\sqrt {({\text{Re}} \, \left[ {\lambda_{i} } \right])^{2} + ({\text{Im}} \left[ {\lambda_{i} } \right])^{2} } }}$$

(12)

where i = 1, 2….s; and s = Number of system states.

Any system with eigenvalues located in the LH-side of s-plane and higher magnitude of damping ratio represents the desired features of a stable system. These two features can be framed as the objective function for the considered research problem as given in (13), (14).

$$J_{1} \, = \,\sum\limits_{i = 1}^{s} {(\sigma_{0} - {\text{Re}} \, \left[ {\lambda_{i} } \right])^{2} }$$

(13)

$$J_{2} \, = \,\sum\limits_{i = 1}^{s} {(\xi_{0} - \xi_{i} )^{2} }$$

(14)

where s = No. of system state variables, limiting values of decrement ratio (σ₀) and damping factor (ξ₀) are considered as -3 and 0.3, respectively [38]. The common features of (13), and (14) can be achieved with the objective function framed as given in (15).

$$J_{3} \, = \,\left\{ {\sum\limits_{i = 1}^{s} {(\sigma_{0} - {\text{Re}} \, \left[ {\lambda_{i} } \right])^{2} } + \alpha \sum\limits_{i = 1}^{s} {(\xi_{0} - \xi_{i} )^{2} } } \right\}$$

(15)

where the selection of multiplication coefficient (α) is based on the magnitudes of individual portions J₁ and J₂, as the magnitude of the square of the low damping ratios is comparatively less than the square of the real parts, the α is selected as 1000 [39]. The considered objective functions and their operating regions are represented in Fig. 3.

Fig. 3

Desired location of system eigen values with objective function a J₁, b J₂, and c J₃

The controller parameters of the PSS and STATCOM can be selected by employing the proposed objective functions and meta-heuristic technique within limits as mentioned in (16) and Table 1.

$$\left. \begin{gathered} T_{11,min} \le \, T_{11} \le T_{11,max} \hfill \\ T_{21,min} \le \, T_{21} \le T_{21,max} \hfill \\ Kc_{11,min} \le \, Kc_{11} \le Kc_{11,max} \hfill \\ T_{12,min} \le \, T_{12} \le T_{12,max } \hfill \\ Kc_{12,min} \le \, Kc_{12} \le Kc_{12,max} \hfill \\ \begin{array}{*{20}l} {T_{22,min} \le \, T_{22} \le T22,max} \hfill \\ {m_{e,min} \le \, m_{e} \le m_{e,max} } \hfill \\ {d_{e,min} \le \, d_{e} \le d_{e,max} } \hfill \\ \end{array} \hfill \\ \end{gathered} \right\}$$

(16)

where T₁₁, T₂₁, T₁₂, T₂₂ are the time constants and K_c11, and K_c12 are the gains of PSS of generator 1 and generator 2, and m_e and d_e are the modulation index and phase angle of VSC based STATCOM.

Table 1 Limits of control parameters

3 Multi-verse optimization

Multi-verse optimization [40] is a national inspired meta-heuristic algorithm, from the big bang theory, which says that the universe is formed in a highly dense and hot condition and there exist multiple universes in the space. The features and methodology of MVO are further explained in the following subsections.

3.1 Features

The multi-verse theory says that there are multiple universes exist and they interact and might collide with each other. The main components involved in the interaction of universes are Black holes, White holes and Wormholes. Black holes are formed when there is a run out of hydrogen or other nuclear fuel to burn and begin to collapse in a giant star. This giant start, which is of around 20 times bigger in size that of sun, forms a region of space from which nothing can escape, including light. White holes behave in contrast to the black holes that nothing including light can enter inside it. A wormhole is a kind of passageway that connects very distant points in space as if there is no or very less distance between them. Every universe can cause its growth through space by means of its inflation rate [41].

3.2 Methodology

The MVO explore the search space with the concept of white holes and black holes, whereas exploits the search space with the concept of a wormhole. The fitness function value is analogous to the inflation rate, and the following rules are applied for the solutions of MVO:

• The larger fitness function value/inflation rate, then the universe will have a greater probability of possessing white holes and lesser probability of possessing black holes.

• A universe with the greater inflation rate, rise to move objectives through white holes and universe with lower inflation rate rise to accept more objects through black holes.

• Irrespective of inflation rates, the objects approach the best universe through wormholes in all universes.

Where each solution and variables are analogous to the universe and objects, respectively.

3.3 Mathematical interpretation of MVO

The mathematical interpretation of object exchange between the universe via white holes and black holes has been implemented by adopting the Roulette Wheel Mechanism. Based on fitness function value/ inflation rate, the sorted white holes for the best universe have been obtained by roulette wheel theory as,

$$a\, = \,\left( {\begin{array}{*{20}c} {a_{11} } & \ldots & {a_{1n} } \\ \vdots & \ddots & \vdots \\ {a_{m1} } & \cdots & {a_{mn} } \\ \end{array} } \right)$$

(17)

where a is the universe; m = Number of universes (or solutions); n = Number of Parameters (Variables) and

$$a_{ij} = \left\{ \begin{gathered} a_{kj} ,r1 < NI(U_{i} ) \hfill \\ a_{ij} ,r1 \ge NI(U_{i} ) \hfill \\ \end{gathered} \right.$$

(18)

where a_ij represents the jth parameter of the ith universe, r1 denotes a random number in [0, 1], NI(Ui) denotes a normalized inflation rate of the ith universe. And a_kj is selected by the roulette wheel selection mechanism.

Considering two coefficients wormhole existence probability (WEP) and traveling distance rate (TDR) as,

$$WEP = WEP\_\min + ite \times \left( {\frac{WEP\_\max - WEP\_\min }{{max\_ite}}} \right)$$

(19)

$$TDR = 1 - \frac{{ite^{1/acc} }}{{max\_ite^{1/acc} }}$$

(20)

where ‘WEP_min' is the minimum and ‘WEP_max’ is the maximum values of wormhole existence probability, ‘ite’ denotes the present iteration, and ‘max_ite’ denotes the total number of iterations, ‘acc’ defines the accuracy of exploitation during the iterations.

As explained in the methodology, the exchange of objects between two universes will take place through space by means of wormholes. This exchange will take place until the objects move to the best universe. In the MVO algorithm, the formation of the wormhole to exploit the searchability is defined by,

$$a_{ij} = \left\{ \begin{gathered} \left\{ \begin{gathered} X_{j} + TDR \times ((ub_{j} - lb_{j} ) \times r4 + lb_{j} );r3 < 0.5 \hfill \\ X_{j} - TDR \times ((ub_{j} - lb_{j} ) \times r4 + lb_{j} );r3 \ge 0.5 \hfill \\ \end{gathered} \right.;r2 < WEP \hfill \\ a_{ij} ;r2 \ge WEP \hfill \\ \end{gathered} \right.$$

(21)

where X_j specifies the jth parameter of best universe formed so far, lb_j indicates the lower limit of jth parameter, ub_j is the upper limit of jth parameter, and r2, r3, r4 are arbitrary values in [0, 1].

3.4 MVO in Damping power system oscillations

Step 1 model the power system with the controllers mathematically, as explained in Sect. 2.

Step 2 define the constants for all the components of the power system as given in Appendix A.

Step 3 define the number of universes (Search Agents) and time (maximum iterations) as given in Appendix A.

Step 4 assign the minimum and maximum limits for the unknown parameters (PSS and STATCOM parameters) as mentioned in Table 1 and create a universe given in (17) and (18).

Step 5 initialize the parameters within the search space randomly and calculate the inflation rate (Objective Functions) by using Eq. (13) to (15).

Step 6 initialize minimum and maximum WEP, best universe, best universe inflation rate, as mentioned in Appendix A.

Step 7 compute WEP and TDR using (19) and (20), respectively.

Step 8 check whether the generated solutions are within the search limit or not (16) and Table 1.

Step 9 update the position of the universe from best to worst based on the inflation rate (Objective function value) from (21).

Step 10 check for maximum iteration condition and go to step 5 with the updated universe.

Step 11 optimal values of variables and the best inflation rate gives the solution of MVO.

4 Performance analysis of MVO

For the modeled power system and objective functions considered in Sect. 2, the MVO algorithm has been implemented as explained in Sect. 3 within the limits of control parameters. To demonstrate the supremacy of the proposed optimization algorithm, the analysis on the considered system under the same operating environment has been performed and compared with the widespread optimization algorithms in the present scenario namely, WOA, GWO and PSO-TVAC. The optimal controller settings for the considered optimization algorithms are tabulated in Fig. 4, and the corresponding convergence characteristics for the objective functions with respect to the number of iterations is shown in Table 3. All the optimization algorithms that are proposed to damp out the power system oscillations have been analyzed for three different loading conditions and three choices in the selection of objective functions. The minimization of the considered objective functions for the considered algorithms has been presented for a total number of 500 iterations.

Fig. 4

Convergence characteristics under various case studies

From Table 2, it has been observed that for the objective function J1, as explained above, all the optimization algorithms have given satisfactory controller parameters in the prescribed boundary limits, whereas all the proposed algorithms gave comparable value for the objective function. And from the convergence characteristics shown in Fig. 4, it has been observed that MVO has given better convergence characteristics in objective function minimization in less number of iteration whereas GWO has shown the next better convergence characteristics followed by WOA and PSO-TVAC.

Table 2 Controller parameters under different loading conditions

For the objective function J2, the performances of different algorithms can be observed from Table 2 and convergence characteristics in Fig. 4. For light load condition, GWO minimized the objective function to the minimum values followed by MVO, WOA and PSO-TVAC optimization algorithms. Whereas for the nominal load condition, all the four algorithms have minimized to the almost similar value of the objective function of which GWO has given the better result. In case of heavy loading condition, unlike the other loading conditions, a certain difference in the performance of proposed algorithms can be observed. The optimization algorithm PSO-TVAC resulted in a relatively higher value of the minimized objective function in comparison with other optimization methods. However, the convergence characteristics for the given minimized value of objective function show that MVO and GWO algorithms have been converged in the lesser number iterations for the minimized value.

For the objective function J3, the performance characteristics have been analyzed similarly as above, and it has been inferred that the performance of different algorithms has been variant for the different operating conditions. And in concise, with reference to the minimized value of objective function and number of iterations taken, MVO and GWO have shown better performance characteristics over WOA and PSO-TVAC. In all the similar cases that have been analyzed, the minimized value of the objective function has upturned in stabilizing the power networks toward the damping of power oscillations for the considered objective function.

However, the analysis based on the optimization and number of iterations is no longer be sufficient for the selection of the optimal algorithm in designing the controller parameters for the complex systems like power systems. So, the study is further carried to comment on the better algorithm in controller selections by considering the behavior of system states under different system operating conditions.

5 Results and analysis

Based on the convergence characteristics and boundary limits, a primary analysis has been prepared for the considered power system in the previous section. Further, the analysis of the system stability has been carried out in this section to comment on the efficiency of the considered optimization algorithms for the corresponding objective function. The preliminary eigenvalue investigation is presented in Table 3 with all the combinations of the optimization algorithm, objective functions and system loading conditions. The study and analysis on the system have been further extended for behavior of system states under perturbations and oscillation damp out characteristics under different loading conditions. The concise analysis will lead to the selection of a suitable combination of optimization algorithm and objective function. The basic idea of analyzing the system performance based on location of system eigenvalues is the magnitude of real and imaginary parts of eigenvalues define the oscillating behavior of the corresponding system state. The eigenvalues of complete system consist the oscillating and non-oscillating modes. Where the imaginary part of non-oscillating eigenvalues is zero, which in turn has damping ratio as 1. The oscillating eigenvalues can be classified as positively damped or negatively damped poles based on the location of eigenvalue either in RH-side or in LH-side to the imaginary axis. The system with negative damping ratio eigenvalues is highly unstable for any perturbations in the system operating conditions. However, the weekly positive damped eigenvalues also to be taken care for the effectual system operation. Hence, the proposed objective functions will contribute toward the improvement of system performance, which can be analyzed as below.

Table 3 Eigenvalues and corresponding damping ratios under different case studies

In Table 3, the system eigenvalues comparison of the proposed optimization algorithms has been presented for different loading conditions. As explained in Sect. 2, the functioning of objective function J1 is to drift all the critical or oscillatory mode of eigenvalues toward the prescribed value of real part (σ = −3), and with objective function J2, the system eigenvalues should have prescribed value of damping ratio (ξ = 0.3). The pooled performance characteristics of functions J1 and J2 should be resulted by the multi-objective function J3. From Table 3, the proposed algorithms in the majority of system operating conditions resulted in locating the eigenvalues in the left half of the s-plane with positive damping ratio, which represents the stable system operating conditions. But in case of heavy loading condition, the optimization algorithm PSO-TVAC with objective function J2 and multi-objective function J3 has unable to locate the eigenvalues with satisfactory damping ratio, and in result, the eigenvalue for a particular system state has been situated in the right half of the s-plane with negative damping ratio. In the previous section, the similar performance for the stated algorithm and loading conditions has been observed with relatively high magnitude in the minimized value of the objective function in contrast with the other optimization methods. However, for the modeled power network with challenging system constants, the proposed optimization algorithms are not completely succeeded to place the eigenvalues with the deserved characteristics as estimated as considered objective functions. Still, the eigenvalue analysis shown in Table 3 expresses the stable system mode of operation for the different loading conditions under a steady-state with the proposed optimization algorithms in tuning the system control parameters. As the practical power network is prone to handle the complex operating conditions in critical cases, the system study under the adverse operating conditions will recommend the better optimization method with a suitable objective function.

Figures 5, 6, 7 and 8 gives a rigorous analysis of the behavior of system states by considering perturbation in it. The system analysis under perturbation will give a summary on the considered objective function impact in stabilizing the system under various system loading conditions. For the purpose of analysis and design, the study has been made on system states with 10% perturbations and presented as, Fig. 5 illustrates the variation in the angular velocities of both machines, Fig. 6 shows the variation in delta angle of both the areas, Fig. 7 shows the variation in internal voltage of both alternators and Fig. 8 shows the variation in the field excitation voltage of both machines. All the above characteristics are presented as a comparison of optimization algorithms under different system loading conditions.

Fig. 5

Damping nature of angular speed deviation under different loading conditions

Fig. 6

Damping nature of torque angle deviation under different loading conditions

Fig. 7

Damping nature of generators internal voltage deviation under different loading conditions

Fig. 8

Damping nature of field voltages deviation under different loading conditions

The functioning of PSS is to control the field excitation in response to the variations in the rotor angular velocity corresponding to the load variations. The tuned parameters with the proposed optimization algorithms should preserve the stable system operating environment for the predictable abnormalities/fluctuations. From Figs. 5, 6, 7 and 8, the response of system states under perturbation can be observed and it has been observed that the response corresponding to the objective function J1 is leading to the more oscillations but its characteristics are analogous to the underdamped system and settling to the zero-deviation value after a time period depending on the algorithm employed and loading condition. Whereas corresponding to the objective function J2, the system states are taking comparatively more time to get the zero variations in its states for some operating conditions. But, the multi-objective function leading to the much more satisfactory responses by resulting in less settling time and less number of oscillations, which leads to the higher possible stability level of the system in abnormal system operating conditions. Though the system analysis is satisfactory in all these cases with respect to the eigenvalue analysis, system study during abnormalities will suggest multi-objective function rather than the single objective function that have been explained in this paper. Based on the all the analysis made on the system for the proposed optimization methods (Tables 2 and 3, Figs. 4, 5, 6, 7 and 8), MVO and GWO have been showing better performance characteristics, and in detail, MVO with multi-objective function leads to the efficient performance characteristics under different loading conditions.

6 Conclusion and future scope

In this paper, a rigorous stability analysis has been presented on a sample power system model connected with STATCOM. The coordination among the auxiliary device STATCOM and supplementary controller PSS has been achieved by implementing four meta-heuristic algorithms namely WOA, GWO, MVO and PSO-TVAC on the modeled system and the same has been analyzed by considering different objective functions for the optimal system operating conditions. For choosing the best combination of objective function and algorithm, a detailed analysis has been performed on the sample system based on the minimized value of objective function achieved, system eigenvalues for the corresponding combination. The robustness of the system controller parameters has been determined by conducting the whole analysis under different loading conditions. The assessments have been derived from the analysis made by observing the system parameter stabilization under perturbation in its states, and the suitable algorithm has been suggested. Based on the rigorous analysis made on the considered sample system model, MVO with the multi-objective function has been suggested for the robust system operating condition.

The inferences derived from the present work highly suggests the application of MVO in the stability enhancement of a multi-machine power system. The system analysis can also be performed under the contingency conditions that suits the practical implementation of the suggested technique.

Appendices

Appendix A

1.1 Power system parameters

M1 = M2 = 6.0; D1 = D2 = 0;

Vt₁ = 1.0; Vt₂ = 0.89;

Ka₁ = Ka₂ = 50; Ta₁ = Ta₂ = 0.01; Td0₁₁ = Td0₁₂ = 6.3;

x_e = 0.15; x_1L = 0.3; x_2L = 0.3;

1.2 Load parameters

Light Load: Pe₁ = Pe₂ = 0.3; Qe₁ = Qe₂ = 0.1;

Nominal Load: Pe₁ = Pe₂ = 0.8; Qe₁ = Qe₂ = 0.6;

Heavy Load: Pe₁ = Pe₂ = 1.3; Qe₁ = Qe₂ = 1.0;

1.3 Software specifications

The study has been conducted in Matlab 2016A platform with the computer having specifications of windows 10 operating system, 6-bit, Intel core-i7 8^th gen. processor 16 GB DDR4 RAM.

1.4 Optimization algorithm parameters

Appendix B

2.1 System constants

$K_{11} = \frac{{(V_{t1d} - x^{^{\prime}}_{d1} I_{1Lq} )(x_{de1} - x_{dt1} )V_{t2} \sin (\delta_{1} - \delta_{2} )}}{{x_{dee1} }} + \frac{{(V_{t1q} + x_{q1} I_{1Ld} )(x_{qt1} - x_{qe1} )V_{t2} \cos (\delta_{1} - \delta_{2} )}}{{x_{qee1} }}$; $K_{21} = (I_{1Lq} + \frac{{V_{t1d} (x_{2L} + x_{e} )}}{{x_{dee1} }})$$K_{31} = 1 + \frac{{(x^{^{\prime}}_{d1} - x_{d1} )(x_{2L} + x_{e} )}}{{x_{dee1} }}$; $K_{41} = \frac{{ - (x^{^{\prime}}_{d1} - x_{d1} )(x_{de1} - x_{dt1} )V_{t2} \sin (\delta_{1} - \delta_{2} )}}{{x_{dee1} }}$$K_{pe1} = \frac{{(V_{t1d} - x^{^{\prime}}_{d1} I_{1Lq} )(x_{bd1} - x_{de1} )V_{dc} \sin de}}{{2x_{dee1} }} + \frac{{(V_{t1q} + x_{q1} I_{1Ld} )(x_{bq1} - x_{qe1} )V_{dc} \cos de}}{{2x_{qee1} }}$$K_{pde1} = \frac{{(V_{t1d} - x^{^{\prime}}_{d1} I_{1Lq} )(x_{bd1} - x_{de1} )meV_{dc} \cos de}}{{2x_{dee1} }} + \frac{{(V_{t1q} + x_{q1} I_{1Ld} )( - x_{bq1} + x_{qe1} )meV_{dc} \sin de}}{{2x_{qee1} }}$$K_{pd1} = \frac{{(V_{t1d} - x^{^{\prime}}_{d1} I_{1Lq} )(x_{bd1} - x_{de1} )me\sin de}}{{2x_{dee1} }} + \frac{{(V_{t1q} + x_{q1} I_{1Ld} )(x_{bq1} - x_{qe1} )me\cos de}}{{2x_{qee1} }}$$K_{51} = \frac{{(V_{t1d} /V_{t1} )x_{q1} (x_{qt1} - x_{qe1} )V_{t2} \cos (\delta_{1} - \delta_{2} )}}{{x_{qee1} }} - \frac{{(V_{t1q} /V_{t1} )x^{^{\prime}}_{d1} (x_{de1} - x_{dt1} )V_{t2} \cos (\delta_{1} - \delta_{2} )}}{{x_{dee1} }}$; $K_{61} = \frac{{(V_{t1q} /V_{t1} )(x_{dee1} + x^{^{\prime}}_{d1} (x_{2L} - x_{e} ))}}{{x_{dee1} }}$$K_{71} = (\frac{3}{{4C_{dc} }})\left\{ {\frac{{meV_{t2} \sin (\delta_{1} - \delta_{2} )(\cos de)x_{de1} }}{{x_{dee1} }} - \frac{{meV_{t2} \cos (\delta_{1} - \delta_{2} )(\sin de)x_{qe1} }}{{x_{qee1} }}} \right\}$; $K_{81} = ( - \frac{3}{{4C_{dc} }})\frac{{x_{2L} me\cos de}}{{x_{dee1} }}$ similarly constants with respective to generator 2 can also be written.

$$K_{9} = (\frac{3}{{4C_{dc} }})\left\{ \begin{gathered} \frac{{me\sin de(me\cos de)x_{bd1} }}{{2x_{dee1} }} + \frac{{me\cos de(me\sin de)x_{bq1} }}{{2x_{qee1} }} \hfill \\ + \frac{{me\sin de(me\cos de)x_{bd2} }}{{2x_{dee2} }} + \frac{{me\cos de(me\sin de)x_{bq2} }}{{2x_{qee2} }} \hfill \\ \end{gathered} \right\}$$

$$K_{ce} = (\frac{3}{{4C_{dc} }})\left\{ \begin{gathered} \frac{{V_{dc} sinde(me\cos de)x_{bd1} }}{{2x_{dee1} }} + \frac{{V_{dc} \cos de(me\sin de)x_{bq1} }}{{2x_{qee1} }} + \hfill \\ \frac{{V_{dc} sinde(me\cos de)x_{bd2} }}{{2x_{dee2} }} + \frac{{V_{dc} \cos de(me\sin de)x_{bq2} }}{{2x_{qee2} }} \hfill \\ \end{gathered} \right\}$$

$$\begin{gathered} K_{cde} = (\frac{3me}{{4C_{dc} }})(I_{L0q} \cos de - I_{L0d} \sin de) \hfill \\ + (\frac{3}{{4C_{dc} }})\left\{ \begin{gathered} \frac{{meV_{dc} \cos de(me\cos de)x_{bd1} }}{{2x_{dee1} }} - \frac{{meV_{dc} \sin de(me\sin de)x_{bq1} }}{{2x_{qee1} }} \hfill \\ + \frac{{meV_{dc} \cos de(me\cos de)x_{bd2} }}{{2x_{dee2} }} - \frac{{meV_{dc} \sin de(me\sin de)x_{bq2} }}{{2x_{qee2} }} \hfill \\ \end{gathered} \right\} \hfill \\ \hfill \\ \end{gathered}$$