1 Introduction

Rivers are the most important fresh water resources where have historically been vital role to develop communities. Owing to population growth, water demand would be increased in future years. In other words, it means offstream flow of rivers will be increased [1]. Conversely, instream flow would be reduced that lead to unsuitability of aquatics’ habitats. This conflict caused for defining concept of environmental flow requirements in the river. As a description on available methods for assessment of environmental flow, they can be categorized in three main classes including historic flow method, hydraulic rating method and habitat methods [2]. Due to lack of focus on regional ecological values by older methods, they have been replaced by habitat methods as robust methods to finalize assessed environmental flow though historic flow methods and hydraulic rating method may be in used for initial assessments [3]. Habitat methods might include a long list of approaches. For example, instream flow incremental methodology (IFIM) and building block methodology (BBM) as holistic methods are the most known accessible methods that highlight regional ecological values [4, 5]. Physical habitat simulation is the most important and a key component in IFIM. Historically, univariate habitat models are the oldest method to assess physical habitat suitability of river that include evaluation of depth, velocity and substrate in microhabitats of rivers [6]. This method has however been criticised due lack of sufficient accuracy and validity in assessment of habitat hydraulics. Previous studies corroborated univariate habitat models with any combining method including product, geometric mean and arithmetic would generate poor results compared with observed redds [7]. Multivariate methods such as generalized linear model, generalized additive model, logistic regression, ridge regression may be some solutions to improve accuracy of physical habitat models [8, 9]. Moreover, fuzzy logic multivariate model is a known method to simulate physical habitats that has been applied by development of CASIMIR software [10]. Previous studies indicated robustness of fuzzy logic multivariate compared with univariate methods. Development of fuzzy habitat rules is a serious challenge for many species due to unavailability of ecological knowledge on physical habitat selection process.

Powerful computers had tremendous effect on application of computational methods in many branches. Environmental and river basin management were not an exception in this regard that means data-driven models have been utilized as robust methods to find the best fitness or a map between inputs and outputs [11]. For instance, neural networks or artificial neural networks (ANNs) are one of the mostly used models in river basin engineering and management. The most important advantage of ANNs is their ability for training by observed data. However, lack of suffcient interpretability is a weakness point for these models. Because, they act as black box [12]. Neuro fuzzy inference systems (NFISs) were a remarkable progressive step to apply data-driven models. Because, they have both advantages of fuzzy systems and neural network. Adaptive neuro fuzzy inference system (ANFIS) generates a map between input–output based on Sugeno fuzzy approach and stipulated data pairs. Previous studies authenticated ability of this method to model different phenomena in environmental engineering [13]. It should be noted that ANFIS has been used in many branches. For example, estimating the Heat Capacity of Non-Newtonian fluid Systems [14], estimating effect of inhibitors on Asphaltene precipitation [15], forecasting oil flocculated asphaltene weight percentage [16], estimating thermal conductivity enhancement of metal and metal oxide based nanofluids [17]. It should also be noted that coupled evolutionary algorithms-ANFIS methods demonstrated efficiency in other problem of environmental engineering. For example, optimizing equations for Estimation of Dispersion Coefficient in Natural Streams [18], improvements of the Explicit Estimation of Pollutant Dispersion Coefficient in Rivers [19], forecasting models for immediate-short-term to long-term influent flow prediction [20], Improving one-dimensional pollution dispersion modelling in rivers [21] and Optimizing sediment transport in open channels [22].

Evolutionary algorithms that are called metaheuristic algorithms were another powerful computational method to find the best solution in a searching space. These methods such as genetic algorithms as the most known method have broadly been used in optimization problems [23]. As a known example of applying evolutionary algorithms, a long list of meta-heuristic algorithms have been employed to optimize reservoir operation in river basin management [24]. It should be noted that training process of ANFIS based model is the most momentous step to develop data-driven model. Different algorithms may be useable regarding process of training that may have different methodology. Hence, coupling ANFIS model with evolutionary algorithms may improve results of data-driven model.

As a more description on theory of applying data-driven models to simulate physical habitat, some points should be noted. Previous studies demonstrate relationship between physical factors may be complex [25]. Hence, using improved models such as data-driven model is essential. In other word, fish may follow a complex pattern to select physical habitats in river. Therefore, using simple mathematical relationship would not be precise method to assess habitats. ANFIS has been utilized to develop physical habitat data-driven models [26,27,28]. However, effectiveness of improving training methods is ambiguous. In other words, traditional solutions for training ANFIS may not be efficient in all of the cases. Hence, applicability and ability of coupled evolutionary algorithm-data driven model for physical habitat simulation must be noted. Present study contributes to improve physical habitat model as one of the main effective factors for suitable river habitats by development and evaluation of a coupled invasive weed optimization (IWO) as a robust evolutionary algorithm and ANFIS as applicable and known data-driven model. Furthermore, present study highlights application of coupled proposed method and two-dimensional hydraulic model in a practical habitat simulation compared with field observations.

As a description on paper structure, we described background and improvements by the present study at the present section. Section 2 states methodology of this study including introduction on study area, field study methods, structure of developed data-driven model and testing process of model. Section 3 presents results of modelling and relevant discussion. Finally, Sect. 4 presents conclusions of research that might be a useful summarization.

2 Methods

2.1 Study area and field studies

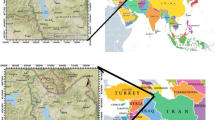
Present study was carried out based on extensive ecological studies in the Lar national park as one of the undisturbed habitats in southern Caspian Sea basin where includes plentiful rivers and stream as habitats of many aquatic species. It should be noted that this park was an exceptional habitat for the Brown trout as native species in this large basin as sub-catchment at upstream of Haraz river. A large dam where is named Lar has been constructed at upstream of this beautiful river. This dam has separated habitats on upstream and downstream of river. Lar national park has been located at upstream of dam where is included some streams for feeding dam reservoir. Area of this park where has been embellished by mountainous streams is approximately 27,000 ha. This park has been introduced as protective natural area by department of environment as a main responsible organization to manage natural aquatic and terrestrial habitats. Hence, available aquatic habitats were not disturbed and polluted which means physical parameters were mainly effective to select habitat by fish. Given that main inhabited species in river habitats was the Brown trout who did not have any serious competitor in river habitats, we selected Brown trout as target species in the present study. All of the streams at the upstream of Lar dam were main habitats of target species that means it could be observed in all of the streams. Location of Lar national park at southern Caspian Sea basin and upstream tributaries of Lar dam where are located at park have been displayed in Fig. 1.

Fig. 1
figure 1

Location of Lar national park

Full size image

Moreover, it is essential to review methodology of field studies. First section of our field studies was fish sampling in habitats. A long field studies approximately in 11 years had been carried out by research team of present study to investigate and sample physical habitats. Main part of this long-term field studies was to identify characteristics of used microhabitats by Brown trouts with focus on physical parameters consist of depth and velocity. In other words, we simultaneously sampled fish, depth and velocity. Several methods have been proposed to observe or sample fish in microhabitats that may categorize in two main classes include direct and indirect methods. As an in illustration, direct methods would contain methodologies that are able to observe fish in their actual habitats such as video telemetry. Conversely, indirect methods would sample fish out of actual habitats where would enable us to carry out precise biometric measurements such as electorfishing [29]. Conspicuously, each method may have its own strength and drawbacks. For instance, direct methods are able to recognize accurate features of habitats though they are not good solutions for high turbid water. Furthermore, precise biometric measurements may not be possible. Moreover, their implementation may be such expensive. In contrast, indirect methods such as electorfishing may injury fish due to using electricity power to shock. It is however more inexpensive method with possibility of using in higher turbid waters. Several reasons convinced us to utilize electorfsihing method in the present study including proper cost, accurate biometric measurement and dexterity of research team for using related devices in mountainous streams. What is more, we measured velocity by propeller and depth by metal ruler [29]. It should be noted that river habitats of Lar national park were mainly weadable, hence walking in streams and measurement were possible.

Secondly, we surveyed and measured a representative reach to implement physical habitat simulation to investigate accuracy of proposed method to assess physical habitats. This part mainly includes qualitative assessment of presence/absence of fish in microhabitats which means actual biometric measurement was not carried out. In other words, exact location of point was recorded. Then, they were categorized as high density and low density areas based on absence or presence. Moreover, measurement of flow in different cross sections were carried out by sub-division method. It should be noted that precise digital elevation model with high resolution have been provided previously by department of environment that has been used in the present study.

2.2 Structure of data-driven model

Data-driven model includes coupled invasive weed optimization- adaptive neuro fuzzy inference systems (IWO-ANFIS) which might generate a robust framework to simulate and analyse physical habitats. Due to main purpose of present study that was focused on efficiency of IWO-ANFIS method to model physical habitats of rivers, physical effective parameters were confined to depth and velocity In other words, observed data were recorded in relatively the same bed river particle size as well as selected simulated reach. Main characteristics of data-driven model has been displayed in Table 1. In other words, a combination of inputs including depth and velocity may generate a specific level of physical habitat suitability in river habitats. Developed data-driven model would generate a map between combined depth and velocity as inputs and physical habitat suitability as output.

Table 1 Characteristic of developed ANFIS
Full size table

Moreover, we used invasive weed optimization to enhance robustness of data-driven physical habitat model. This meta-heuristics algorithm was selected due to high efficiency to solve engineering optimization problems compared with other algorithms [30]. Weeds are such adaptive to change of environmental features. Hence, using their properties could lead to development of a robust optimization algorithm. Its flowchart as brief description on methodology has been displayed in Fig. 2.

Fig. 2
figure 2

Flowchart of IWO [30]

Full size image

2.3 Testing process

Due to complexities of habitat hydraulic simulation that may be pertaining to impact of unknown ecological factors to select physical habitats by fish, we considered two stages of testing process for the developed model. First, model was tested based on recorded data in observed microhabitats in Lar national park that makes it possible to compare model’s result and observed habitats. Thus, measurement of system performance was indispensable by robust and clear indices. We applied several known indices to measure system performance including root means square error (RMSE), mean absolute error (MAE), reliability index (RI), vulnerability index (VI) and Nash–Sutcliffe model efficiency coefficient (NSE) that have been described as follows.

Equation (1) indicates designated form of reliability index for physical habitat analysis where MMHS is modelled mean habitat suitability and OMHS is observed mean habitat suitability in data series.

$$\alpha_{E} = \frac{MMHS}{{OMHS}}$$
(1)

Second index that has been used to measure system performance is vulnerability index. Similar to reliability index, It has also originally been developed and used for analysis of water systems such as reservoirs [31]. Equation (2) proposes designated form of this index for physical habitat analysis where MHS and OHS are respectively modelled and observed habitat suitability in each point.

$$\gamma_{E} = Max_{t = 1}^{T} \left( {\frac{{OHS_{t} - MHS_{t} }}{{OHS_{t} }}} \right)$$
(2)

Max means maximum function in Eq. (2). Root mean square error (RMSE) is another index as system performance in the present study that has been displayed in Eq. (3). Another useful and applicable index to measure system performance was mean absolute error (MAE) which is displayed in Eq. (4) [32]

$$RMSE = \sqrt {\mathop \sum \limits_{t = 1}^{T} \frac{{\left( {OHS_{t} - MHS_{t} } \right)^{2} }}{T}}$$
(3)
$$MAE = \frac{{\mathop \sum \nolimits_{t = 1}^{T} \left| {OHS_{t} - MHS_{t} } \right|}}{T}$$
(4)

Moreover, we used NSE that is initially used to assess the predictive power of hydrological models [33]. Equation (5) displays definition of NSE in the present study. Subscript m is mean of observed habitat suitabilities.

$$NSE = 1 - \frac{{\mathop \sum \nolimits_{t = 1}^{T} \left( {MHS_{t} - OHS_{t} } \right)^{2} }}{{\mathop \sum \nolimits_{t = 1}^{T} \left( {OHS_{t} - OHS_{m} } \right)^{2} }}$$
(5)

As a more description on recorded data, it should be noted that recorded data includes three main factors in each microhabitat. The first and second factor are measured depth and velocity in each microhabitat. Area of each microhabitat may be 1 to 2 square metre. We measured depth and velocity by stated methods in few points, then by averaging depth and velocity were estimated in microhabitat. Third measured factor was number of adult fish which was sampled based on electrofishing method. Number of sampled fish was normalized based on maximum number of fish observed in surveyed microhabitats. Therefore, final recorded data was used for testing process including depth, velocity and normalized number of fish that was considered as habitat suitability index (HSI) between zero and 1.

Second stage of testing process was practical physical habitat simulation in a representative reach. In fact, coupled habitat-hydrodynamic modelling has been carried in this stage. Due to considerable advantages of two-dimensional hydraulic modelling, we used two-dimensional hydraulic model by application of HEC-RAS 2D as reliable hydraulic model which has extensively been used in different studies. More detail on hydraulic modelling is presented in next section.

2.4 2D hydraulic model

We applied HEC-RAS 2D as one of the recent developed two-dimensional hydraulic model. One-dimensional HEC-RAS has been applied to implement other environmental flow assessment methods such as hydraulic rating method [3]. Hence, it could be an efficient hydraulic model for physical habitat simulation applications. It is a depth averaged hydraulic model. In other words, it is able to estimate depth and velocity in 2D domain of river plan. Figure 3 displays flowchart of HEC-RAS 2D as methodology which has been used in the present study. This model has specifically been utilized to simulate habitat physical habitats that demonstrated it is sufficiently efficient to simulate habitat hydraulics [34]. Due to comprehensive description on its method to simulate velocity and depth in the literature, presenting more details on two-dimensional hydraulic model has been neglected. We compared results of habitat hydraulic simulation by qualitative observations in river habitats. It should be noted that special condition of streams in Lar national park makes it possible to have this exceptional comparison. Because, not only was population density very high, but also turbidity was very low which means movement of fish could easily be seen. Related results have been presented in the further section.

Fig. 3
figure 3

Methodology for 2D hydraulic modelling by HEC-RAS 2D

Full size image

3 Results and discussion

In the first step, results of testing process by sampled data has been presented as follows. Figure 4 displays calculated habitat suitability index by model and recorded data. Figure 5 shows frequency of habitat suitability in ten classes that would be helpful to evaluate results by model. Differences between model and recorded field data could be observed in all of the classes. Because, no model could not be a perfect tool to simulate nature. It could however be seen, performance of model is close to recorded physical habitats. It seems that as general judgement with some exceptions, IWO-ANFIS habitat model may have underestimation in physical habitat assessment which means model would assess habitat suitability lower than actual habitat suitability though differences are not remarkable. It would be an advantage for proposed habitat model, because results demonstrate not only model is able to assess physical habitat with negligible difference compared with actual habitats but also habitat assessment would be highly reliable in practical projects due to minor underestimations.

Fig. 4
figure 4

Habitat suitability distribution for sampled data

Full size image
Fig. 5
figure 5

Habitat suitability frequency for sampled data

Full size image

Table 2 displays computed indices that are applicable to compare model and recorded data. RI indicates mean habitat suitability computed by model is very close to observations that implies IWO-ANFIS model is generally very robust to assess physical habitats. Moreover, RMSE and MAE corroborate our conclusion on robustness of model. NSE is the most important index to compare model and observations. Proposed threshold values to demonstrate a model of sufficient quality have been suggested at NSE > 0.5. Computed NSE based on results of present study is 0.78 that means considerable proximity between model and observations may authenticate robustness of proposed model. VI however indicates inability of model to simulate physical habitat in some points. It should be noted that by review on habitat suitability distribution, it seems that number of samples with high inaccurate physical habitat assessment are rare which means it is negligible. A point must be noted regrading developed data-driven model technically. Owing to complexities for selecting physical habitats by fish, it is not technically possible to achieve the same results with natural observations. Because, in selecting physical habitats by fish other ecological factors may be effective which would not be considered in physical habitat models. In other words, proximity between results by model and observations is considerable based on computed NSE. Hence, developed model was able to consider effect of unknown factors to predict habitat suitability. Based on review on previous researches, they were not as robust as developed IWO-ANFIS model [26, 27]. In other words, application of evolutionary algorithm could improve results of habitat model or enhance proximity between results by model and observations. Moreover, it is required to discuss on displayed result in Fig. 5. As stated, this figure displays difference between results of model and observation for different habitat classes. In other words, deviations by model could be discussed. Model predicted highly suitable habitats in observations as suitable habitats. In other words, in the first glance, the situations for suitability classes 0.9 and 1 are seen to be problematic. However, if we consider the magnitude (not the percentages) of deviations for situations of suitability classes 0.4, 0.5, 0.6, 0.7, 0.8 the deviations for 0.9 and 1 is seen to be acceptable. Average magnitude of deviation is approximately 4 units (but < 4 units) for all of the classes except 0.9 and 1 where the deviation for 0.9 is seen to be 4 units and for 1 is 3 units. In other words, the deviation for the cases of 0.9 and 1 is seen to be nearly acceptable. To sum up, model is able to predict habitat suitability with an acceptable deviation for all of the suitability classes. Due to same deviation for all of the habitat suitability classes, developed model might be highly reliable for further studies.

Table 2 System performance measurement
Full size table

Recorded microhabitats authenticated results of proposed model. However, it is indispensable to test performance of model in a practical habitat simulation due to complexities of ecological status in aquatic habitats. It should be noted that practical habitat simulation would aid us to observe performance of model to assess habitat suitability distribution map where may be a certification on applicability of model in practical projects. Two flow rates were considered for simulations including low flow and high flow. In other words, we considered one simulation for lower flow rate and one simulation for higher flow. Conspicuously, observations on natural habitat may be difficult and tedious, our maximum effort was to observe habitats in two mentioned status, it was only however possible in higher rate of flow due to technical issues. Although recording velocity and depth in some points was carried out that was used to verify two-dimensional hydraulic model. Hence, habitat simulation has been carried out in low and high rate of flow. Actual qualitative observations of fish in streams was mainly however carried out in high flow. As an illustration on results of hydraulic simulation, Figs. 6 and 7 displays depth and velocity in low and high flow respectively. Seemingly, alteration of depth and velocity due to change of flow is considerable. For example, depth has been changed between 0 and 0.6 m in low flows though high flows indicates depth range between 0 and 1.3 m as well as velocity. In other words, significant change of range would demonstrate that simulated stream is ideal case for investigating impact of physical parameters on habitat suitability.

Fig. 6
figure 6

Depth (left) and velocity (right) distribution map for simulated river reach in low flow

Full size image
Fig. 7
figure 7

Depth (left) and velocity (right) distribution map for simulated river reach in high flow

Full size image

As a general classification on physical habitat suitability, it has been classified in three classes including avoided, indifferent and preferred [35]. We used this fundamental definition in the present study. As could be observed in Fig. 8, assessed habitat suitability has been calculated in a wide range by IWO-ANFIS model that seems reasonable. Because, even most suitable streams might have some unsuitable habitats due to change of velocity and depth in each cross sections. Most of habitats are suitable. It however demonstrated close physical habitats to centerline might suffer from lack of enough suitability. Classification of habitats shows that centerline and close habitats to this line are mainly avoided habitats, whereas by moving toward riverbanks, fish could experience favorite habitats. To complete measuring robustness of proposed model for physical river habitat analysis, it is essential to investigate suitability status of high flow in studied stream. As discussed, our observations were sufficient in different points which means it was possible to determine fish population density in each point qualitatively. In other words, we evaluated absence/presence of fish in each cell of river with precise surveying X and Y of each point that makes it possible to implement points in geographical information system. Figure 10 displays result of observations by inverse distance weighting interpolation for different points, hence a complete absence/presence map has been produced which is useable for further comparisons. Based on observations, some habitats where are close to centerline of stream were categorized as avoided habitats. In other words, we could not directly observe presence of fish in these areas. Due to high suitability of select reach even in high flows, area of suitable habitats close to riverbanks are remarkable which affirms selected reach is an exceptional habitat for Brown trout.

Fig. 8
figure 8

Habitat suitability (left) and habitat classification (right) distribution map for simulated river reach in low flow

Full size image

According to Fig. 9 where displays result of physical suitability modeling in high flow, it seems that performance of model in practical habitat hydraulic simulation is robust. Because, model mainly recognizes habitats as preferred or indifferent which means they are useable for fish. In other word, in definition of habitat classes, suitability of habitats in indifferent class is between 0.4 and 0.6 that implies it is not completely physical suitable for fish. They are however useable for biological activities such as searching for food or reproduction. Hence, evaluation of habitats as indifferent in high flow could not deteriorate robustness of model. As complement explanation, it was possible for us to evaluate habitats by observation as presence/ absence. Conspicuously, actual number of fish in presence points could be varied compliance with suitability, which was not considered in qualitative observations. Hence, not all of the presence points would indicate highest suitability, but due to limitations for actual observations, we considered them in suitable class as could be observed in Fig. 10.

Fig. 9
figure 9

habitat suitability (left) and habitat classification (right) distribution map for simulated river reach in high flow

Full size image
Fig. 10
figure 10

Qualitative observations on fish population density in simulated reach in high flow

Full size image

To sum up, IWO-ANFIS physical habitat model is sufficiently robust to simulate habitat hydraulic in streams. Accurate prediction of suitability in different habitats and practical habitat simulation could corroborate abilities of proposed model for further studies. In other words, either observed microhabitats or practical physical habitat simulation could demonstrate reliability of model. Some points must be considered to finalize our discussion on results. Previous studies demonstrated univariate habitat model is not sufficiently robust to simulate habitat hydraulics, which means it must be excluded from list of proper methods to simulate habitat hydraulic. As one of the remarkable efforts for improvement, fuzzy logic multivariate method has been proposed and applied in some areas especially in European rivers. However, there are some challenges in application of this method. In fact, development of fuzz rules of physical habitat suitability based on expert’s knowledge would not be possible. Because, enough information is not available for many species in the world that means ecological experts could not judge on requirement of physical habitat suitability correctly. What is more, using ANFIS has been rarely addressed in the literature; however, training methods need to be improved by applying evolutionary algorithms. By a brief review on drawbacks of previous methods, we claim that our method could propose a reliable model that could be an alternative for inefficient. In other words, we improved ANFIS method by coupling it by IWO as training method. Moreover, present study could provide two stages for verification of physical habitat model that ensure us for applicability of method in practical projects.

4 Conclusion

Present study proposed a novel habitat model by coupling IWO-ANFIS model to simulate physical habitat in rivers. Depth and velocity were considered as main physical parameters that may be effective on habitat hydraulic suitability remarkably. Two stages for test of model have been considered. In the first stage, by application of frequency analysis and using different indices, performance of model was measured. We used root means square error, mean absolute error, reliability index and vulnerability index. Although vulnerability index indicated that model may not be efficient for rare points, but other indices demonstrated model is generally very robust to assess physical habitats. Furthermore, practical physical habitat simulation demonstrated that proposed model is sufficiently efficient for application in practical projects. Low and high flow rates were considered to simulate physical habitat by a coupled habitat hydraulic method. Results indicated proximity between results by model and observations is unquestionable. We recommend using proposed physical habitat model in further practical projects as reliable method that combined a robust evolutionary algorithm as training method with adaptive neuro fuzzy inference system. In other words, proposed method may be considered as valuable progressive step to improve river habitat analysis.