1 Introduction

The very high-frequency (VHF) transmission has varied prominence in civilian and military application. The characteristics of the VHF frequency band have the potential to cover large areas and support reliable communication systems [1]. VHF wireless propagation is far less complicated compared to the higher band due to reduced scattering and reflection [2]. Over the decade, numerous works have stressed the prospect of exploiting the vacant band using cognitive radio access (CR) and television white space (TVWS) [3,4,5,6,7,8,9].

The low VHF band and the upper VHF band are underutilized in most of the countries. [10,11,12,13], and it is considered a potential solution for bridging digitally divided regions. In India, digital switchover is still underway [14], and this switchover will generate a vacant band, creating a prospect for providing low-cost wireless facility to the remote rural areas. In this light, understanding signal variability of the same frequency spectrum in the study area poses a vital aspect.

Terrestrial mobile radio propagation can roughly be characterized as the variation of signal strength due to propagation loss through distance, shadowing, and multipath fading. A diverse primary physical principle causes each of these nearly independent phenomena. Propagation path loss is the weakening of power radiated as it spreads out in space and the counterproductive effects of the propagation channel. The base station and the mobile station antenna height greatly influenced the propagation mechanism and the losses involved, but the primary contributor to propagation loss is its propagation environment. This attenuation limits the rate of the data transmission which needs to be accounted for when designing a communication network.

In wireless communication, path loss models aim to forecast the mean deviation of signal strength received at a particular setting and formulate the parameters or the variables that affect the signal variations. To model propagation loss, conversely, is challenging, which requires vast data over diverse channel parameters and apprehend their impact on various signal frequencies. The other substitute is to exploring existing empirical propagation loss model. In practice, due to attenuation and fading (depending on the environment), even a decent performing model for one location does not work for another [15] and hence requires adjustment. Furthermore, our measurement data have indicated model imprecision when traversing two different cluttered environments with varying topography. Therefore, we need to fine-tune the selected path loss models to apprehend the loss based on the variation in the propagation channel.

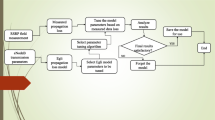
The vast majority of loss reports for a diverse propagation scenario consists of fine-tuning the propagation loss models. Techniques like genetic algorithm optimization method of path loss model are discussed in [16], while the literature like [17] has reported the success of particle swarm over the genetic algorithm optimization of Hata model with improved results. Authors in [18] have presented the success of an RMSE-based tuning method for the Hata path loss model. Notwithstanding these methods, the least-square approximation method is also another indispensable tool for minimizing errors due to its simplistic design, which has been incorporated in a number of studies for the optimization of path loss models [19,20,21,22]. In the literature, the majority of the tuning method lean toward the Hata model, and little attention is given to the Egli model. Nonetheless, it is worthwhile to note that in all of the technique mentioned above, paramount concepts are to diminish the errors associated with the model prediction. In this paper, we employ path loss models to consider the terrestrial VHF signal variations of an elevated base antenna propagating over a hilly forested scenario in an outdoor environment. An initial small sample test of measured data [23] has shown that Egli, Hata, and Perez perform decently. We focus this paper on correcting the model prediction for the different scenarios using the least-square regression fitting method. We estimated the loss using the Egli model [24], Hata model [25], and Perez Vega et al. model [26] using the parameters specified by our study area in Sect. 2. We performed the least-square regression analysis for the Egli and Hata model and applied a modification for the two models based on this analysis in Sect. 4. We learned that though expressed differently, the optimized model of Egli and Hata model predicts the equal loss with improved performance and we evaluated these findings by performing R-squared (\(r^2\)) test for all the models. This study will help in tuning existing propagation models using the least-square approximation method for different scenarios over a large signal coverage area.

2 Path loss models

2.1 Egli loss model

To understand the characteristics of electromagnetic propagation over irregular terrain, Egli [27] developed graphs and correcting curves based on a statistical analysis of wide-range measurements made between 40 and 1000 MHz in a different region of the USA. This model fundamentally is the theoretical plane earth propagation model with added terrain factor (dependent on frequency) and an evaluation of position [28]. Some of the literature works [24, 29, 30] provide a distinctive mathematical expression of Egli’s graphs, which approximately gives the same result when compared. Egli model is expressed in the form [24]:

$$\begin{aligned} \begin{aligned} L_p ({\rm{dB}})=20\log _{10}(f_c )+40\log _{10}(R)-20\log _{10}(h_b) \\ + {\left\{ \begin{array}{ll} (76.3-10\log _{10}(h_m) &{} h_m<10 \\ (85.9-20\log _{10}(h_m) &{} h_m\ge 10\\ \end{array}\right. } \end{aligned} \end{aligned}$$
(1)

\(f_c\) is the frequency (MHz), \(h_b\) is the base antenna (Tx) height in meter (m), \(h_m\) is mobile antenna (Mx) height (m), and R is Tx and Mx separation in kilometers (km).

2.2 Okumura–Hata loss model

The first comprehensive field strength measurement was done in 1968 by Okumura et al. for the Japanese environments [31]. The Okumura prediction method is one of the most referenced models applicable within the frequency − 150 to 2000 MHz. The underlying principle of the model is that path loss consists of free space loss plus the attenuation factor relative to this open space, which is a function of distance and frequency [32]. The model provides sets of curves [30, 33, 34] for estimating the propagation losses. The Okumura method requires complex graphical interpretations to determine the propagation loss. To reduce this complication, Hata [25] developed a model from Okumura’s curves applicable between 150 and 1500 MHz. Hata model offers three terrain-based mathematical expressions with urban area propagation loss as the standard expression in each terrain type and also provided a correction factor to account for the different terrain types.

$$\begin{aligned}&\begin{aligned} L_{u}({\rm{dB}})&=69.55+26.16\log _{10}f_c+(44.9-6.55\log _{10}h_t)\log _{10}R \\&-13.82\log _{10}h_t-\bigl (\underbrace{1.1\log _{10}f_c-0.7)h_m -(1.56\log _{10}f_c-0.8}_{{{\rm medium-small \ city \ correction}}}\bigr ) \end{aligned} \end{aligned}$$
(2)
$$\begin{aligned}&\begin{aligned} L_{\rm{suburb}}(\rm{dB})&=L_{u}-2\log _{10}(f_c/28)^2-5.4 \\ L_{\rm{open}}~({\rm{dB}})&=L_{u}-4.78(\log _{10}(f_c))^2+18.33\log _{10}(f_c)-40.94 \end{aligned} \end{aligned}$$
(3)

where \(f_c\) is the frequency (MHz), \(h_t\) is the Tx height (m), \(h_m\) is the Mx height (1 m to 10 m), R is Tx and Mx separation (1 km to 20 km) and the ‘medium–small city correction’ factor is the mobile antenna height correction for the concerned area.

In (2) and (3) \(L_u\) is the urban area propagation loss with medium–small area correction, \(L_{\rm{suburb}}\) and \(L_{\rm{open}}\) are the respective Suburban and Open area loss. Comparisons of the three area correction factors show insignificant differences for 203.25 MHz frequency and 1.8-m mobile antenna, and the Suburban and the Open area model with medium–small city correction gives the best fit prediction with our measured data.

2.3 Perez Vega and Zamanillo loss model

In theoretical and experimental-based studies [31, 33,34,35] there are clear indications of the logarithmic variation of the average received signal with distance.

$$\begin{aligned} L_p(\rm{dB})=10n\log _{10}(R)+ L_0 \end{aligned}$$
(4)

R is the Tx and Mx separation (m), \(L_o\) is the propagation loss at 1 m in free space, and n is the path loss exponent.

This relationship is one consistent model for significant area propagation path loss where the power could vary as a function of the transmission factors. Based on this Perez-Vega [26] developed a simple propagation model for estimating the average propagation loss in the VHF and UHF band where the exponent of distance n is extracted from the F(50, 50) graph and given in SI unit as graphs [32].

2.4 Signal loss

To calculate the loss (dB) associated with our measured signal strength (dB\(\mu\)V/m) we employ the relation given in [25].

$$\begin{aligned} L (\rm{dB})=P_t-E_{f}-10\log _{10}(\lambda ^2/4\pi )+145.8 \end{aligned}$$
(5)

Where \(P_t\) is the power transmitted (dBw) and \(E_f\) is the received signal strength (dB\(\mu\)V/m), and \(\lambda\) is the wavelength of the 203.25 MHz signal.

3 Signal measurement survey

3.1 Study area

We performed signal measurements in Aizawl, Mizoram India. Mizoram is one of the North-Eastern states of India comprising of rugged valleys and steep hills with dense forest cover, which accounts for 86.27 % of its total area. The base antenna (Tx) location is Aizawl, the capital of Mizoram (Fig. 1). The measurement site topography of the North (Kolasib) and the South (Thenzawl) is a hilly terrain region with a blend of both open and moderate-dense forest. For both the northern and southern part, forest cover ranges from low to moderate within an approximate 10 km away from Tx. Beyond 10 km, we have moderate–heavy forest cover in the majority of the sites with low forest cover in some locations. Both forest ecosystem appears almost the same; however, the topology of both measurement direction (North and South) is entirely different.

Table 1 Experimental details
Full size table
Fig. 1
figure 1

Map showing the location of Aizawl, Mizoram (North-East India), and the extended view of the North (Kolasib) and South (Thenzawl) direction with each measurement sites

Full size image

3.2 Signal strength measurement

In Aizawl Mizoram, there is only two frequency 182.25 MHz and 203.25 MHz in the Band III channel propagating across the city. At the time of the survey, we measured a continuous wave propagation for 203.25 MHz only as there are irregularities in the 182.25 MHz measurements. Table 1 provides the experimental parameters of the survey details.

We noted down the coordinates of Tx location and using Google Map. We mark points at a regular interval of an approximate 2 km aerial distance away from Tx. We navigate to these points using the Google navigation system, available in Google map application, and in each of these sites, different sets of signal strength measurements were taken using a spectrum analyzer (Anritsu Sitemaster) coupled with the standard dipole antenna. We mount the dipole antenna on a tripod stand on clear ground and set the dipole antenna length accordingly to match our measured frequency (203.25 MHz). Following this procedure, we took signal strength measurements (in dB\(\mu\)V/m) at 32 sites (64 km aerial distance approximate) and 28 places (56 km aerial distance approximate) for the Northern and Southern regions of Tx, respectively, as shown in Fig. 1.

4 Methodology

4.1 Graphical analysis

Fig. 2
figure 2

Plot showing the loss dataset as a function of Tx–Mx separation (km) for the two directions

Full size image

A scatter plot provides a useful insight into the data [36]. After evaluating the loss associated with different sets of signal measurements taken at each point using (5), we obtained a scatter plot of this as a function of transmitter (Tx)–receiver (Mx) separation for both directions. We observed that the southern data showed a higher loss, as shown in Fig. 2, and that both the losses showed a positive correlation with the Tx–Mx separation. From the averaged loss, we calculated a linear fit for both. We noted that the fit lines are almost parallel to one another, which signifies that the signal propagation loss, although different, shows a similar trend.

4.2 Least-square optimization

Different studies have widely referenced the Hata model and performed optimization for different region. In our study, we presented a correction to the Egli and the Hata model based on least-square regression analysis, while we neglected the Perez Vega model as there is no simple optimization process.

We express the error between the measured field strength and prediction made by the model as

$$\begin{aligned} {\rm{Erro}}(\epsilon )={\rm{Measured}}(Y_i)-{\rm{Predicted}}(Z_i). \end{aligned}$$
(6)

Using a basic regression analogy, the predictor variable \(X_i\) and the dependent variable \(Z_i\) (Predicted Model) are related as

$$\begin{aligned} (Z_i)=(A+BX_i) \end{aligned}$$
(7)

where A and B are the regression parameters. We can subsequently write the errors in the form

$$\begin{aligned} \begin{aligned} \sum _{i=1}^n\epsilon ^2&= \sum _{i=1}^n(Y_i-(A+BX_i))^2 \\ \sum _{i=1}^n\epsilon ^2&= \sum _{i=1}^n(Y_i-A-BX_i)^2 \\ \end{aligned} \end{aligned}$$
(8)

According to the least-square method, the estimators A and B are those respective values of \(\alpha\) and \(\beta\), which minimizes the error \(\epsilon\) for the given observation sample [37]. The minimum value of \(\epsilon\) (minimum error between the measured and predicted model) can be obtained by equating the first-order derivative of \(\epsilon\) concerning for \(\alpha\) and \(\beta\) to zero.

$$\begin{aligned}&\begin{aligned}&\frac{\partial }{\partial \alpha } \sum _{i=0}^n \epsilon ^2 = 2 \sum _{i=0}^n(Y_i-\alpha -\beta X_i)(-1)=0 \\&- \sum _{i=0}^nY_i+ \sum _{i=0}^n\alpha +\beta \sum _{i=0}^nX_i=0 \\ \end{aligned} \end{aligned}$$
(9)
$$\begin{aligned}&\begin{aligned} \sum _{i=0}^nY_i&=n\alpha +\beta \sum _{i=0}^nX_i \\ \text {where}~n\alpha&=\sum _{i=0}^n\alpha \end{aligned} \end{aligned}$$
(10)

Again taking derivatives with respect to the \(\beta\) term and equating it to zero, we obtain:

$$\begin{aligned}&\frac{\partial }{\partial \beta } \sum _{i=0}^n \epsilon ^2 = 2 \sum _{i=0}^n(Y_i-\alpha -\beta X_i)(-X_i) \end{aligned}$$
(11)
$$\begin{aligned}&\sum _{i=0}^n X_iY_i=\alpha \sum _{i=0}^nX_i+\beta \sum _{i=0}^nX_i^2 \end{aligned}$$
(12)

(10) and (12) are called normal equations, and \(\alpha\) and \(\beta\) are the respective point estimators of A and B.

$$\begin{aligned} \begin{aligned} \sum _{i=0}^nY_i&=n\alpha +\beta \sum _{i=0}^nX_i \\ \sum _{i=0}^n X_iY_i&=\alpha \sum _{i=0}^nX_i+\beta \sum _{i=0}^nX_i^2 \end{aligned} \end{aligned}$$
(13)

Rearranging (10) and (12), we can write them as a set of equation (13) and solve the \(\alpha\) and \(\beta\) associated using a matrix method.

$$\begin{aligned}&\begin{bmatrix} n &{} \sum X_i \\ \sum X_i &{} \sum X_i^2 \end{bmatrix} \begin{bmatrix}\alpha \\ \beta \end{bmatrix} = \begin{bmatrix}\sum Y_i \\ \sum X_iY_i \end{bmatrix} \end{aligned}$$
(14)
$$\begin{aligned}&\alpha = \frac{\sum Y_i-\beta \sum (X_i)}{n } \end{aligned}$$
(15)
$$\begin{aligned}&\beta = \frac{n\sum (X_iY_i)-\sum X_i \sum Y_i}{n\sum (X_i)^2-(\sum X_i)^2 } \end{aligned}$$
(16)

In the predicted value \((Z_i)\) if we assume \(\alpha\) to be constant and \(\beta\) as the variable that is changing with some parameters, then optimization of the models could be made. Based on the methods discussed, we corrected the errors associated with Egli and Hata models.

4.3 Egli model optimization

Egli model for (\(h_m <\)10 m) is

$$\begin{aligned} \begin{aligned} L_{\rm{Egli}} {\rm{(dB})}&=20\log _{10}(f_c )-20\log _{10}(h_b)+76.3 \\&-10\log _{10}(h_m)+40\log _{10}(R) \\ \end{aligned} \end{aligned}$$
(17)

Separating the term for the intercept and the slope, we can write

$$\begin{aligned} \begin{aligned} L_{\rm{Egli}}&=E_a+E_bX_i \end{aligned} \end{aligned}$$
(18)

Here \(X_i\) term is the (\(\log _{10}R\)) term, where

$$\begin{aligned} \begin{aligned} E_a=20\log _{10}(f_c )-20&\log _{10}(h_b)+76.3-10\log _{10}(h_m) \\&E_b = 40 \end{aligned} \end{aligned}$$
(19)

Comparing this with (7) in \(\alpha\) and \(\beta\) term, we can write

$$\begin{aligned}&\begin{aligned} L_{\rm{Egli}}&=E_a+E_b~\log _{10}R \\ L_{\rm{Egli}}(Z_E)&=~\alpha ~+~\beta X_i \end{aligned} \end{aligned}$$
(20)
$$\begin{aligned}&L_{\rm{Egli}}(Z_E)=\bigl (\overbrace{E_a\pm C_{\alpha }}^{\alpha } \bigr )+\bigl (\overbrace{E_b\pm C_{\beta }}^{\beta }\bigr ) \bigl ( \overbrace{\log _{10}R}^{X_i}\bigr ) \end{aligned}$$
(21)

where \(C_{\alpha }\) and \(C_{\beta }\) are the respective correction needed for \(E_a\) and \(E_b\)

Comparing with the normal equations (10,12)

$$\begin{aligned} \begin{aligned} X_i&=\log _{10}R \\ Y_i&=L_m~(\rm{Measured~loss}) \end{aligned} \end{aligned}$$
(22)

and substituting in (15) and (16), we obtain:

$$\begin{aligned} \alpha= & {} \frac{ \sum L_m-\beta \sum (\log _{10}R)}{n} \end{aligned}$$
(23)
$$\begin{aligned} \beta= & {} \frac{n\sum (L_m \log _{10}R)-\sum (L_m)\sum (\log _{10}R)}{n\sum (\log _{10}R)^2-(\sum \log _{10}R)^2} \end{aligned}$$
(24)

When we solve (23) and (24) (i.e., the \(\alpha\) and \(\beta\) equation), a condition arises that \(E_a\pm C_{\alpha }\) cannot be higher than \(\alpha\) and \(E_b\pm C_{\beta }\) cannot be higher than \(\beta\), i.e.,

$$\begin{aligned} \begin{aligned} E_a\pm C_{\alpha }&<\alpha \\ E_b\pm C_{\beta }&<\beta \end{aligned} \end{aligned}$$
(25)

4.4 Hata model optimization

In the Hata model, we have used the Suburban area loss model for the Southern region and the Open area model for the North. In both of these, we have used ‘medium–small city’ correction factors. Therefore, we estimated a separate fit model for the North and Southern regions in the case of Hata model analysis. To find the fit for the Hata Suburban and Open area we rearranged (3) as

$$\begin{aligned}&\begin{aligned} H_{a({\rm{Suburb}})}&=64.15+26.16\log _{10}f_c-[(1.1\log _{10}f_c-0.7)h_m \\&-(1.56\log _{10}f_c-0.8)]-2{\log _{10}(f_c/28)}^2-13.8\log _{10}h_b \\ H_{a({\rm{Open}})}&=29.05+26.16\log _{10}f_c-[(1.1\log _{10}f_c-0.7)h_m \\&-(1.56\log _{10}f_c-0.8)]-4.78(\log _{10}(f_c))^2 + 18.33\log _{10}(f_c) \\&-13.8\log _{10}h_b \end{aligned} \end{aligned}$$
(26)
$$\begin{aligned}&H_b=(44.9-6.55\log _{10}h_b ) \end{aligned}$$
(27)
$$\begin{aligned}&\begin{aligned} L_{\rm{Hata}}&=H_a+H_b~\log _{10}R \\ L_{\rm{Hata}}(Z_H)&=~\alpha ~+~\beta X_i \end{aligned} \end{aligned}$$
(28)
$$\begin{aligned}&L_{\rm{Hata}}(Z_H)=\bigl (\overbrace{H_a\pm C_{\alpha }}^{\alpha } \bigr )+\bigl (\overbrace{H_b\pm C_{\beta }}^{\beta }\bigr ) \bigl ( \overbrace{\log _{10}R}^{X_i}\bigr ) \end{aligned}$$
(29)

where \(C_\alpha\) and \(C_\beta\) are the respective correction needed for \(H_a\) and \(H_b\). Following the Egli model optimization concept, we evaluated the fit for the Hata Suburban and Open area model separately. As in Egli calculations, we have

$$\begin{aligned} \alpha= & {} \frac{ \sum L_m-\beta \sum (\log _{10}R)}{n} \end{aligned}$$
(30)
$$\begin{aligned} \beta= & {} \frac{n\sum (L_m \log _{10}R)-\sum (L_m)\sum (\log _{10}R)}{n\sum (\log _{10}R)^2-(\sum \log _{10}R)^2} \end{aligned}$$
(31)

The condition of \(\alpha\) and \(\beta\) as we ensured in the Egli model (25) correspondingly applies here, and the values of \(\alpha\) and \(\beta\) are calculated separately for both directions.

4.5 Statistical evaluation

To compare the measured loss with the optimized model and the models presented, we used the coefficient of determination (\(r^2\)) for the evaluation of each model’s performance. We have to note that the models shown are logarithmic, and we cannot evaluate the correlation coefficient, which identifies the strength of linear association [38] between the models and the measured data, without transforming the variables. There are different transformation methods to linearize a dataset [39], but a data transformation can introduce a bias leading to erroneous reports [40]. Therefore, instead we used the modified coefficient of determination for evaluating the nonlinear dataset which is given by the relation [41, 42]

$$\begin{aligned}&{{r}^{2}}=1-\frac{\rm{SSres}}{\rm{SStot}} \end{aligned}$$
(32)
$$\begin{aligned}&\begin{aligned} {\rm{SSres}}&=\sum {(\kappa -\hat{\kappa }})^2 \\ {\rm{SStotal}}&=\sum {(\kappa -\bar{\kappa }})^2 \end{aligned} \end{aligned}$$
(33)

where \(\hat{\kappa }\) and \(\bar{\kappa }\) represent the predicted data and the mean of the measured loss data, respectively, while \(\kappa\) represents the measured loss data. The result \(r^2\) analysis is given in Table 2, the value of \(r^2\) ranges from 0 to 1, where a value closer to 1 suggests a stronger relationship.

5 Result

Based on the least-square fitting method discussed, we calculated \(\alpha\), \(\beta\), \(C_{\alpha }\), and \(C_{\beta }\) in the Egli and Hata model individually for the North and South, as shown in Table 3.

Table 2 Coefficient of determination (\(r^2\)) of the Egli, Perez, Hata models (\(L_{u}, L_{\rm{suburb}}, L_{\rm{open}}\)), and the optimized model (Egli or Hata) for the North and the South
Full size table
Fig. 3
figure 3

Plot of Egli and Hata optimized loss estimate. Here straight line indicates equal loss estimated from the two different corrected model

Full size image
Fig. 4
figure 4

Plot showing comparison of Egli, Hata, Perez, and the optimized Egli/Hata model for the North. Optimized fit line \(r^2 = 0.47\)

Full size image
Fig. 5
figure 5

Plot showing comparison of Egli, Hata, Perez, and the optimized Egli/Hata model for the South. Optimized fit line \(r^2 = 0.55\)

Full size image

5.1 Optimized Egli and Hata model

As explained in Sect. 4.4, we adjusted the Hata Suburban area model for the Southern area and the Hata Open area model for the Northern region of our study area while we used the same model for the North and the South in the Egli model optimization.

Using the correction factors calculated and provided in Table 3, we estimated the least-square fitted Egli and Hata model, respectively, for both North and South.

Optimized model for the North

$$\begin{aligned}&\begin{aligned} L_{\rm{hata~open}}&= 42.16+44.49\log _{10}(f_c)-13.82\log _{10}(h_b)-\gamma \\&-4.78(\log _{10}(f_c))^2+(43.47-6.55\log _{10}(h_b))\log _{10}R \\ \end{aligned} \end{aligned}$$
(34)
$$\begin{aligned}&\begin{aligned} L_{\rm{Egli}}&=85.16 + 20\log _{10}(f_c)-20\log _{10}(h_b)-10\log _{10}(h_m) \\&+32.98\log _{10}R \end{aligned} \end{aligned}$$
(35)

Optimized model for the South

$$\begin{aligned}&\begin{aligned} L_{\rm{hata~suburban}}&=68.55 + 26.16\log _{10}(f_c) - 13.82\log _{10}(h_b) - \gamma \\&- 2(\log _{10}(f_c/28))^2+(47.65 - 6.55\log _{10}(h_b))\log _{10}R \\ \end{aligned} \end{aligned}$$
(36)
$$\begin{aligned}&\begin{aligned} L_{\rm{Egli}}&=87.83 + 20\log _{10}(f_c) - 20\log _{10}(h_b) - 10\log _{10}(h_m) \\&+ 37.161\log _{10}R \end{aligned} \end{aligned}$$
(37)

where \(\gamma =(1.1\log _{10}(f_c) - 0.7)h_m - (1.56\log _{10}(f_c) - 0.8)\) is the Hata model medium–small city correction factor

In arrears to the same least-square correction method employed, we observed that, although Egli and the Hata model expressions are entirely different from one another, they provide equal prediction value, as presented in Fig. 3. This equality attributes from the fact that we used the same least-square correction factor (\(\alpha\) and \(\beta\)) for the Egli and Hata models w.r.t the same measurement loss data. We denote this Egli and Hata corrected model as the Optimized model. Although we did not obtain the plot, to further assess the performance of the Optimized model, we conduct an \(r^2\) test for all the Hata model (open area, suburban area, and an urban area) for North and South w.r.t to the loss data. A plot of the optimized model compared with the measured loss, Egli, Hata, and Perez model is shown in Figs. 4 and 5.

Table 3 Least-squared fit correction factors for Egli and Hata model
Full size table

Our results showed that the optimized model of Egli and Hata showed an equal prediction, and therefore, we present a single optimized model for both the models. The coefficient of determination (\(r^2\)) showed that \(47\%\) of the loss data accounted for by the optimized model in the North while accounting for \(55\%\) of the loss data in the South. Thus, the rest \(53\%\) and \(45\%\) of the respective North and Southern region is still unexplained. Since the propagation models presented do not consider the environmental factor, we could attribute this to the fading, scattering, diffraction, and reflection [43] that the radio signal tends to suffers along the propagation channel. The original models with Perez model presented a lower performance compared to this tuned model. This coefficient of determination (\(r^2\)) is the explanatory power of the model, and from this analysis, we learned that the model before and after optimization has higher explanatory power compared to their original models.

6 Discussion

The global analog-to-digital television migration practice has led many countries to look into the cognitive radio access or the so-called white space vacancy opportunity in the TV’s VHF and UHF band [7,8,9]. With the rising demand for bandwidth, there is a prospect of utilizing this VHF spectrum as this band is underutilized across India [4]. Though wireless technology and optical fiber technology can coexist, the idea of wireless services is preferable to high-speed optical fiber services in terms of the cost and the location settings. Furthermore, taking into account the coverage area and the cost-effectiveness, lower frequency transmission could still play an important role, parallel to those high-frequency transmissions.

From the model analysis, we learned that the empirical irregular terrain Egli model [27] and quasi smooth terrain Hata model [25] gives a different extrapolation since both are modeled from different measurement regions (the USA and Japan). Both models acquire the probability of prediction through the fittings of the specific-region measurement data [44]. Although the Hata model provides three different area prediction curves, both models did not incorporate the impact of geodata factors explicitly. As such, our data taken in the hilly forested region contrast with these empirical reproductions to a certain extent. From this examination, we learned the importance of considering the impact of geodata to get a complete picture of signal propagation loss.

In wireless communication, to model a loss, one requires a vast amount of data and their dependence on different propagation parameters (frequency, Tx and Mx height, transmitted power, gain, etc.). And the generalization of a loss model pertinent to every region would require exploiting the effect of the different region-specific channel influencing factors like terrain diffraction, line of sight, vegetation attenuation, etc., to be more deterministic [45]. This method, however accurate, is again inefficient. In this light, tuning of the existing empirical loss model tends to be one practical approach alternative to modeling. It is worthwhile mentioning that the optimized model does not pose to be better than the original models. Instead, it is the same model with the least-square approximated minimum errors-based model to consider the additional loss or gain due to the differences in the attenuation of each measurement region.

Our study aims at understanding the VHF signal variation across the hilly terrain region of one of the North-Eastern states of India and test the existing path loss models. We learned that our study area propagation channel differs from the selected empirical model measurement region. Furthermore, we learned that the least-square optimization correction method is a simple and effective method for loss model tuning. This optimized model is based on an actual in-site measurement survey, with a minimized error. Therefore, the adjusted model could be used as an optimal prediction model for future loss estimation across the study area or other areas with similar topographical backdrops. This will benefit broadcasters in the proper forecasting, performance analysis, and the deployment of wireless service across the region.

7 Conclusion

In this paper, we use Egli and Hata model to consider the terrestrial VHF signal variations of an elevated base antenna propagating over a hilly forested scenario in an outdoor environment. An initial small sample test of measured data has shown that Egli, Hata, and Perez perform decently for our study area. Our primary focus is on correcting the model prediction variance for the different scenarios using the least-square regression fitting method and obtaining the best-fitted model for future signal prediction across the study area or areas with similar topography. Based on this least-square regression analysis, we modified the Egli and Hata original model and presented a correction factor for the respective North and South composed of different topography. We observed that the optimized Egli and Hata model predicts the same result although expressed differently. A coefficient of determination (\(r^2\)) analysis showed that the optimized model explained 47% of loss variation for the North and 55% for the South. Finally, we presented a separate optimized model for the Northern and Southern regions. This method of model tuning is not region-specific or model-specific. However, we need to recalculate the correction coefficients for different areas composed of changeable attenuation parameters to obtain a minimal error for a given expanse.