1 Introduction

Advancement in technology has led to a renewed interest in the investigation of non-Newtonian fluids because several important fluids available for engineering and industrial processes possess some flow properties that are not captured by Newtonian fluid model. As a result, various models have been proposed. Some of these are third grade fluid, couple stress fluid, micropolar fluid-a subclass of microfluids which was first investigated by Eringen [1]. Micropolar fluids have distinguishing features such as the local structure effects, which are microscopic and micro-motion of the fluid elements, stresses due to couple, and so on. It has important applications in exotic lubricants [2], animal blood [3], liquid crystals with rigid molecules [4], and some biological fluids [5]. Excellent research analysis on the significance and applications of this type of fluid has been investigated over the past few decades. Boundary layer flow solution of a polar fluid was considered by Ebert [6]. Heruska et al. [7] considered micropolar flow past a porous stretching sheet. Khonsari and Brew [8] presented the study on finite journal bearing with micropolar fluid used as a lubricant. Chemical reaction effect on micropolar fluid through vertical surface was studied by Gorla [9], Desseaux and Kelson [10] presented micropolar fluid flow through a stretching sheet. Nazar et al. [11] discussed the stagnation point flow of a micropolar fluid towards a stretching sheet.

In recent times, research work in this direction has attracted the attention of investigators such as Mahmoud and Waheed [12] who presented hydromagnetic flow and heat transfer of a micropolar fluid. Oahimire and Olajuwon [13] discussed the mixed convection hydromagnetic micropolar fluid. Perturbation technique was applied to tackle the dimensionless equations obtained from the governing equations. Olajuwon et al. [14] also investigated the unsteady case of viscoelastic mixed convection micropolar fluid with thermal radiation and Hall current effects.

Attention of several researchers has been drawn to the significance of Hall current and Ion slip in the past few decades, due to the fact that several physical situations such as magnetohydrodynamic generators, Hall accelerators, flight magnetohydrodynamics, electrostatic precipitation require the inclusion of Hall current. It occurs in the presence of strong magnetic field or low density in an electrically conducting fluid.

In Hall current, the induced current in the fluid is conducted by electrons and collide vigorously with other neutral or charged particles. The collision of these charged particles resulted in the reduction of conductivity parallel to the electric field while it enhances the conductivity in the direction normal to both electric and magnetic fields.

Meanwhile studies have revealed that Coriolis force cannot be ignored due to its significant influence on fluid dynamics of the system. It induces secondary flow in the flow field. Its applications are found in the estimation of the flight path of rotating wheels and spin-stabilized missiles, monitoring the movement of oil and gas through the reservoirs, rotating heat exchangers, manufacturing of turbines and turbo mechanics. Further applications are in the studies of maintenance and secular variations in Earth’s magnetic field due to motion of Earth’s liquid core, internal rotation rate of the Sun, structure of the magnetic stars, solar and planetary dynamo problems, turbo machines, rotating MHD generators and rotating drum separators for liquid metal.

In view of the above, several investigations have been conducted. The first significant work on Hall-magnetohydrodynamic was carried out by Sato [15], the result shows that fluid flow becomes secondary in nature. Seth [16] presented the influence of Hall currents on unsteady hydromagnetic flow in a rotating channel with oscillating pressure gradient. Furthermore, Linga and Rao [17] considered the effect of Hall current on temperature distribution in a rotating ionized hydromagnetic flow between parallel walls. Bég et al. [18] studied the combined effects of Ohmic dissipation, Hall current and ionslip on transient MHD flow in a porous medium channel. Recently, Seth et al. [19] investigated the effects of Hall current and rotation on unsteady MHD couette flow in an inclined magnetic field. Very recently, Animasun et al. [20] investigated the significance of Lorentz force and thermoelectric on the flow of 29 nm cuo–water nanofluid on an upper horizontal surface of a paraboloid of revolution. It was posited that at higher values of Hall parameter the domain of cross-flow velocity can be significantly reduced. Other related studies are [21,22,23,24,25].

However, the irreversibility analysis of micropolar fluid has not been adequately considered despite the fact that the performance of thermal devices is always affected by fluid irreversibility which usually results in the enhancement of entropy generation and reduction of thermal efficiency. Since the introduction of second law of thermodynamics for irreversibility analysis by its proponent, Bejan [26], the approach has found application in several fluids flow such as third grade fluid [27–29], couple stress fluid [30,31,32,33], nanofluid [34], Couette flow [35], Poiseuille flow [36] and even micropolar fluid [37, 38], others are found in Refs. [39,40,, 40]. Motivated by Srinivasacharya and Bindu [38], this work seeks to analyse the entropy generation due to Hall-magnetohydrodynamics and Coriolis effects on micropolar fluid flow. The solutions of the governing equations are obtained by an efficient and rapidly convergent differential transform method (DTM). The convergence of this technique is addressed in the following references [41,42,43].

1.1 Mathematics analysis

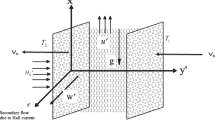
A steady magnetohydrodynamic incompressible, viscous and electrically conducting micropolar fluid between two infinite vertical plates of distance \(2h\) is investigated. The coordinate system chosen is such that the \(x\)-axis is along the vertical upward direction, the \(y\)-axis is along the width of the plate and the \(z\)-axis is taken normal to the plane of the plate, as depicted in Fig. 1. Assumption that the physical quantities depend on \(y\) only is also taken. In addition, a magnetic field of constant strength \(B_{0}\) is introduced in a direction parallel to \(z\)-axis in a perpendicular direction to the fluid flow. The effect of fluid polarization is not significant due to the assumption that applied or polarized voltage is not introduced corresponding to case where there is no addition or removal of energy from the fluid by any electrical means. It is further assumed that the entire system rotates about the normal axis to the plate with an angular velocity of \(\Omega^{*}\) and the plate is subjected to a constant suction such that \(v_{0} > 0\) is the velocity for suction and \(v_{0} < 0\) is the velocity of injection. The equations governing the flow of fluid under the usual Boussinesq approximation are given by

Fig. 1
figure 1

Diagrammatic representation of the problem

Full size image

Continuity equation

$$\frac{\partial v}{\partial y} = 0$$
(1)

Momentum equation in x -direction

$$(\mu + \kappa )\frac{{\partial^{2} u}}{{\partial y^{2} }} - \rho v_{0} \frac{\partial u}{\partial y} - 2\Omega^{*} w + \kappa \frac{\partial \xi }{\partial y} + \rho g\beta (T - T_{1} ) + \frac{{\sigma B_{0}^{2} }}{{(1 + m^{2} )}}(u + mw) - \frac{\partial p}{\partial x} = 0$$
(2)

Momentum equation along y -direction

$$(\mu + \kappa )\frac{{\partial^{2} w}}{{\partial y^{2} }} - \rho v_{0} \frac{\partial w}{\partial y} + 2\Omega^{*} u - \kappa \frac{\partial \xi }{\partial y} - \frac{{\sigma B_{0}^{2} }}{{(1 + m^{2} )}}(mu - w) = 0$$
(3)

Angular momentum equation

$$\gamma \frac{{\partial^{2} \xi }}{{\partial y^{2} }} - \rho j^{*} v_{0} \frac{\partial N}{\partial y} - 2\kappa \xi - \kappa \frac{\partial u}{\partial y} = 0$$
(4)

Energy equation

$$k_{f} \frac{{\partial^{2} T}}{{\partial y^{2} }} - \rho c_{p} v_{0} \frac{\partial T}{\partial y} + (\mu + \kappa )\left[ {\left( {\frac{\partial u}{\partial y}} \right)^{2} + \left( {\frac{\partial w}{\partial y}} \right)^{2} } \right] + 2\kappa \left( {\xi^{2} + \xi \frac{\partial u}{\partial y}} \right) + \gamma \left( {\frac{\partial \xi }{\partial y}} \right)^{2} + \sigma B_{0}^{2} \left( {u^{2} + w^{2} } \right) = 0$$
(5)

and the boundary conditions:

$$u(h) = w(h) = \xi (h) = 0,\;\;T^{\prime } (h) = \frac{q}{{k_{f} }},\;\;u( - h) = w( - h) = \xi ( - h) = 0,\;\;T( - h) = T_{1}$$
(6)

The following dimensionless variables are introduced

$$\begin{aligned} \eta & = \frac{y}{d},\;\;u = U_{0} f,\;\;w = U_{0} g,\;\;\xi = \frac{{U_{0} }}{d}h,\;\;\theta (\eta ) = \frac{{T - T_{1} }}{{\frac{qd}{{k_{f} }}}}, \\ N & = \frac{\kappa }{\kappa + \mu },\;\;{\text{Pr}} = \frac{{\rho C_{p} }}{{k_{f} }}\;\;,{\text{Re}} = \frac{{\rho U_{0} d}}{\mu }, \\ R & = \frac{{\rho v_{0} d}}{\mu },\;\;{\text{Gr}} = \frac{{\rho^{2} g\beta qd^{4} }}{{\mu^{2} k_{f} }},M^{2} = \frac{{\sigma B_{0}^{2} d^{2} }}{\mu }, \\ A & = \frac{{d^{2} }}{{\mu U_{0} }}\frac{\partial p}{\partial x},\;\;a_{j} = \frac{{j^{*} }}{{d^{2} }},\;\;n^{2} = \frac{{d^{2} \kappa (2\mu + \kappa )}}{\gamma (\mu + \kappa )},Br = \frac{{\mu U_{0}^{2}}}{k_{f} (T_{2}-T_{1})} \\ \end{aligned}$$
(7)

It is obvious that the continuity Eq. (1) is satisfied by using (7) and (2)–(6) yield

$$\frac{1}{1 - N}f^{\prime \prime } + Rf^{\prime } + K^{2} g - \frac{N}{1 - N}h^{\prime } + \frac{{\text{Gr}}}{{\text{Re}}}\theta - A + \frac{{M^{2} }}{{\left( {1 + m^{2} } \right)}}(f + mg) = 0$$
(8)
$$\frac{1}{1 - N}g^{\prime \prime } + Rg^{\prime } - K^{2} f + \frac{N}{1 - N}h^{\prime } + \frac{{M^{2} }}{{\left( {1 + m^{2} } \right)}}(mf - g) = 0$$
(9)
$$\frac{2 - N}{{n^{2} }}h^{\prime \prime } - a_{i} R\left( {\frac{1 - N}{N}} \right)h^{\prime } - 2h - f^{\prime } = 0$$
(10)
$$\theta^{\prime \prime } - {\text{Re}}\, {\text{Pr}} \theta^{\prime } + \frac{\text{Br}}{1 - N}\left[ {f^{\prime 2} + g^{\prime 2} + 2N\left( {h^{2} + hf^{\prime } } \right) + \frac{N(2 - N)}{{n^{2} }}h^{\prime 2} + M^{2} \left( {f^{2} + g^{2} } \right)} \right] = 0$$
(11)
$$f = 0,\;\;g = 0,\;\;h = 0,\;\;\theta^{\prime } = 1;\;\;\eta = 1:f = 0,\;\;g = 0,\;\;h = 0,\;\;\theta^{\prime } = 0;\;\;\eta = - 1$$
(12)

In this work, primes are used to denote differentiation with respect to \(\eta\).

1.2 Differential transform solution procedure

The basic principle of differential transformation method (DTM) is introduced in this section. Consider a function, \(f(y)\), then the differential transform of the \(k\)th derivative of \(f(y)\) is given by

$$F(s) = \frac{1}{{\text{s}}!}\left[ {\frac{{d^{s} f(y)}}{{dy^{s} }}} \right]_{y = 0}$$
(13)

The inverse differential transform of \(F(s)\) is given by

$$f(y) = \sum\limits_{s = 0}^{\infty } {y^{s} F(y)}$$
(14)

Some of the basic DTM theorems that are applicable in this paper are as follows:

Theorem 1

If \(f(y) = p(y) \pm q(y)\), then \(F(s) = P(s) \pm Q(s)\).

Theorem 2

If \(f(y) = \tau p(y)\), then \(F(s) = \tau P(s)\), where \(\tau\) is a given constant.

Theorem 3

If \(f(y) = \frac{{d^{n} p(y)}}{{dy^{n} }}\), then \(F(s) = (s + 1)(s + 2) \ldots (s + n)P(s + n)\).

Theorem 4

If \(f(y) = p(y)q(y)\), then \(F(s) = \sum\nolimits_{r = 0}^{s} {P(r)Q(s - r)}\).

By applying DTM and relevant theorems from Theorems 1, 2, 3 and 4, one obtains the following iterative schemes:

$$\begin{aligned} F(s + 2) & = - \frac{1 - N}{(s + 1)(s + 2)}\left[ {R(s + 1)F(s) + K^{2} G(s) - \frac{N}{1 - N}(s + 1) + \frac{{\text{Gr}}}{{\text{Re}}}\Theta (s)} - A + \frac{{\text{Gr}}}{{\text{Re}}}\Theta (s) + \frac{{M^{2} }}{{\left( {1 + m^{2} } \right)}}\left\{ {F(s) + mG(s)} \right\} \right] \\ \end{aligned}$$
(15)
$$\begin{aligned} G(s + 2) & = - \frac{1 - N}{(s + 1)(s + 2)}\left[ {R(s + 1)G(s + 1) - K^{2} F(s) + \frac{N}{1 - N}(s + 1)H(s)} + \frac{{M^{2} }}{{\left( {1 + m^{2} } \right)}}\left\{ {mF(k) - G(s)} \right\} \right] \\ \end{aligned}$$
(16)
$$H(s + 2) = \frac{{n^{2} }}{(2 - N)(s + 2)!}\left[ {a_{i} R\left( {\frac{1 - N}{N}} \right)(s + 1)H(s + 1) + 2H(s) + (s + 1)F(s + 1)} \right]$$
(17)
$$\begin{aligned} \Theta (s + 2) & = \frac{1}{(s + 1)(s + 2)}\left[ {\text{Re} {\text{Pr}} (s + 1)\Theta (s + 1) - \frac{{\text{Br}}}{1 - N}\left\{ {\sum\limits_{r = 0}^{s} {(r + 1)(s - r + 1)} F(r + 1)F(s - r + 1)} \right.} \right. \\ & \quad + \sum\limits_{r = 0}^{s} {(r + 1)(s - r + 1)G(r + 1)G(s - r + 1) + 2N\left( {H(r)H(s - r) + \sum\limits_{r = 0}^{s} {H(r)(s - r + 1)} F(s - r + 1)} \right)} \\ & \left. \left. {\quad + \frac{N(2 - N)}{{n^{2} }}\sum\limits_{r = 0}^{s} {(r + 1)(s - r + 1)} H(r + 1)H(s - r + 1) + M^{2} \left( {F(r)F(s - r) + G(r)G(s - r)} \right)}\right\} \right] \\ \end{aligned}$$
(18)

where \(F(s)\), \(G(s)\), \(H(s)\) and \(\Theta (s)\) are the differential transformed functions of \(f(\eta )\), \(g(\eta )\), \(h(\eta )\) and \(\theta (\eta )\) respectively.

Let us designate

$$\begin{array}{*{20}c} {F(0) = a_{1} ,} & {F(1) = a_{2} ,} \\ {G(0) = b_{1} ,} & {G(1) = b_{2} ,} \\ {H(0) = c_{1} ,} & {H(1) = c_{2} ,} \\ {\Theta (0) = d_{1} } & {\Theta (1) = d_{2} ,} \\ \end{array}$$
(19)

whose values are to be determined using \(f = g = h = 0,\;\;\theta^{\prime } = 1,\;\;\eta = 1\) and \(f = g = h = \theta^{\prime } = 0,\;\;\eta = - 1\).

The approximants for \(f(\eta )\), \(g(\eta )\), \(h(\eta )\) and \(\theta (\eta )\) can now be obtained using the iterative formulas in Eqs. (15)–(18).

The entropy generation expression for an incompressible micropolar fluid can be stated as [26]

$$E_{G} = \frac{{k_{f} }}{{T_{1}^{2} }}\left( {\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right)^{2} + \frac{\mu + k}{{T_{1} }}\left[ {\left( {\frac{\partial u}{\partial y}} \right)^{2} + \left( {\frac{\partial w}{\partial y}} \right)^{2} } \right] + \frac{2k}{{T_{1} }}\left( {\xi^{2} + \xi \frac{\partial u}{\partial y}} \right) + \frac{\gamma }{{T_{1} }}\left( {\frac{\partial \xi }{\partial y}} \right)^{2} + \frac{{\sigma B_{0}^{2} }}{{T_{1} }}\left( {u^{2} + w^{2} } \right) = 0$$
(20)

and the dimensionless form is obtained by using (7) in (20) to give

$$N_{S} = \left( {\theta^{\prime } } \right)^{2} + \frac{{\text{Br}}}{1 - N}\left[ {f^{\prime 2} + g^{\prime 2} + 2N\left( {h^{2} + hf^{\prime } } \right) + \frac{{N\left( {2 - N} \right)}}{{n^{2} }}h^{\prime 2} + M^{2} \left( {f^{2} + g^{2} } \right)} \right]$$
(21)

The entropy generation distribution is determined by Bejan number \(({\text{Be}})\), this is stated as

$${\text{Be}} = \frac{{N_{1} }}{{N_{s} }} = \frac{1}{1 + \Phi },\quad \Phi = \frac{{N_{2} }}{{N_{1} }},$$
(22)

where

$$N_{1} = \left( {\frac{\partial \theta }{\partial \eta }} \right)^{2} ,\;\;N_{2} = \frac{{\text{Br}}}{1 - N}\left[ {\left( {\frac{\partial f}{\partial \eta }} \right)^{2} + \left( {\frac{\partial g}{\partial \eta }} \right)^{2} + 2N\left( {h^{2} + hf^{\prime } } \right) + \frac{N(2 - N)}{{n^{2} }}h^{\prime 2} + M^{2} \left( {f^{2} + g^{2} } \right)} \right]$$
(23)

The Bejan number ratio in Eq. (22) is an indication of Bejan number variation from \(0\) to \(1\) which reveals that viscous dissipation irreversibility is dominant when \({\text{Be}} = 0\) and heat transfer irreversibility dominates entropy production at \({\text{Be}} = 1\). However, equal contribution from viscous dissipation irreversibility and heat transfer irreversibility to entropy production is noted when \({\text{Be}} = 0.5\).

To validate the results obtained using the differential transform technique described above, the results are compared with Srinivasacharya and Bindu [38] as shown in Table 1 at \(N = 0.1\), \(n = 1\), \(A = - 1\), \(R = 0\), \(\alpha = 0\), \(K = 0\), \({\text{Gr}} = 0\), \(M = 0\) are presented. The approximate solutions for the velocity (8) and micrototation (10) profiles are obtained as

Table 1 Comparison of the solution of the velocity and microtation profiles with Srinivasacharya and Bindu [38] at \(N = 0.1\), \(n = 1\), \(A = - 1\), \(R = 0\), \(\alpha = 0\), \(K = 0\), \({\text{Gr}} = 0\), \(M = 0\)
Full size table
$$\begin{aligned} f(\eta ) & = 0.45179445044303724 - 0.45353088643367002\eta^{2} + 1.7543859649122807 \times 10^{ - 20} \eta^{3} \\ & \quad + 0.0016794436743871474\eta^{4} + 8.7719298245614035 \times 10^{ - 22} \eta^{5} + 0.000055981455812904913\eta^{6} \\ & \quad { + 2} . 0 8 8 5 5 4 7 2 0 1 3 3 6 6 7 5\times 1 0^{ - 23} \eta^{7} + 9.9966885380187337 \times 10^{ - 7} \eta^{8} + 2.9007704446300936 \times 10^{ - 25} \eta^{9} + \ldots \\ \end{aligned}$$
(24)

and

$$\begin{aligned} h(\eta ) & = - 1 \times 10^{ - 18} + 0.070617728673400420\eta - 5.2631578947368422 \times 10^{ - 19} \eta^{2} \\ & \quad - 0.057177746975485895\eta^{3} - 4.3859649122807017 \times 10^{ - 20} \eta^{4} - 0.0033588873487742948\eta^{5} \\ & \quad - 1.4619883040935672 \times 10^{21} \eta^{6} - 0.000079973508304149875\eta^{7} - 2.606934001670843 \times 10^{ - 23} \eta^{8} \\ \end{aligned}$$
(25)

2 Results and discussion

The equations governing the motion of a micropolar fluid as shown in Eqs. (7)–(11) are analytically tackled using differential transform technique. The effects of various physical parameters governing the flow on primary velocity, secondary velocity, temperature, microrotation, entropy generation and Bejan number are carried out for \(1 \le M \le 2\), \(0.1 \le N \le 0.5\), \(1 \le K \le 6\) and \(0.3 \le m \le 1\) while \(n = 2\), \(A = - 1\), \({\text{Gr}} = 1\), \(s = 1\), \(a_{j} = 0.001\), \({\text{Pr}} = 0.71\), \({\text{Br}} = 0.5\) are fixed.

In Fig. 2 the response of fluid velocity to variation in Hall current parameter, ion-slip parameter, coupling number and magnetic field parameter is displayed. In Fig. 2a, b primary velocity decelerates and reached minimum at \(\eta = 0\) while secondary velocity is enhanced and attained maximum at \(\eta = 0\). The boost in secondary velocity is due to the reduction in the damping effect of magnetic field as the values of Hall parameter rise. This implies that higher values of Hall parameter reduce the resistive force imposed by the applied magnetic field. It is observed in Fig. 2c, d that primary velocity decelerates while secondary velocity receives a boost as rotation parameter increases in magnitude. This observation is attributed to the dominance effect of Coriolis in the area close to the wall of rotation which consequently accelerates secondary fluid velocity. Figure 2e, f, g, h depict that fluid motion decelerates as both coupling number and magnetic field parameter increase. The reduction in fluid motion is caused by the resistive force produced as a result of the applied magnetic field to the electrically conducting fluid which tends to slow down fluid velocity as displayed in Fig. 2g, h.

Fig. 2
figure 2

Velocity profiles for Hall curent (m), ion-slip (K), coupling number (N) and magnetic field (M) parameter

Full size image

Fluid temperature behaviour to variation in Hall parameter, ion slip parameter, coupling number and magnetic parameter are illustrated in Fig. 3. A significant reduction in fluid temperature as Hall parameter, coupling number and magnetic parameter increase in values as displayed in Fig. 3a, c, d while ion slip parameter enhances fluid temperature considerably in Fig. 3b. Furthermore, Fig. 4a illustrates that increase in coupling number reduces mirorotation profile. This observation is attributable to the reduction in fluid Newtonian viscousity since N represents the coupling of the Newtonian viscousity \((\mu )\) and rotational viscousity \((\kappa )\) \(\left( {N = \frac{\kappa }{\kappa + \mu }} \right)\) such that \(0 < N < 1\).

Fig. 3
figure 3

Temperature profiles for Hall curent (m), ion-slip (K), coupling number (N) and magnetic field parameter (M)

Full size image
Fig. 4
figure 4

Microrotation profile for coupling number (N)

Full size image

The effects of magnetic parameter and coupling number on the entropy generation and Bejan number are presented in Figs. 5 and 6. It is noted in Fig. 5a that there is no significant change in entropy generation as Hall parameter values vary. However, reduction in entropy generation is observed as Ion-slip parameter, magnetic parameter and coupling number increase in magnitude as depicted in Fig. 5b, c, d. The result of this work could be utilised to scale down entropy generation rate in systems design and manufacturing industries. It further reveals that entropy generation minimisation (EGM) goal is realisable. Finally, in Fig. 6a, b the Bejan number is enhanced as magnetic field parameter and coupling number increase. However, the rise in Bejan number is more significant at the channel walls region, this indicates the dominance of heat transfer irreversibility over fluid friction irreversibility. Generally, it is observed that the plots for the entropy generation and Bejan number are parabolic and as \(N \to 0\) the entropy generation is drastically reduced at the channel walls but becomes less pronounced at the centre line.

Fig. 5
figure 5

Entropy generation for Hall curent (m), ion-slip (K), coupling number (N) and magnetic field parameter (M)

Full size image
Fig. 6
figure 6

Bejan number for magnetic parameter (M) and coupling number (N)

Full size image

3 Conclusion

In this study, investigation has been conducted on the entropy generation of Hall and ion-slip effects on MHD micropolar flow past a vertical plate. The differential transform technique was employed to obtain the solutions of the velocity, temperature and microrotation profiles. The solutions are substituted in the expressions for the entropy generation and Bejan number. The results are presented and explained using Figs. 2, 3, 4, 5 and 6. The main findings of this present investigations are outlined below.

  1. (i)

    Increase in Hall effect, ion-slip parameter, coupling number and magnetic parameter increase primary velocity;

  2. (ii)

    Secondary velocity increases with Hall and ion-slip effects while coupling number and magnetic field reduce secondary velocity;

  3. (iii)

    Temperature profile is reduced as Hal parameter, coupling number and magnetic parameters are increased while ion-slip e parameter increased fluid temperature;

  4. (iv)

    Coupling number reduced microrotation;

  5. (v)

    Entropy generation is reduced as coupling number and magnetic parameter are increased;

  6. (vi)

    Bejan number is enhanced with increase in coupling number and magnetic parameter;

  7. (vii)

    Heat irreversibility is more dominant than entropy generation due to fluid friction at the region close to the wall channels than at the centreline.