1 Introduction

Cognitive robotics is described as “the study of knowledge representation and reasoning problems, faced by an autonomous robot (or agent) in a dynamic and uncertain world” [1]. The efficient control of robots, operating in remote environments, has long proved to be a challenge, especially when the robot operates in a dynamic environment. In a typical remote-controlled, semi-autonomous robot, elementary knowledge is stored in a knowledgebase (KB), which is augmented by a domain expert. The KB is used for the generation of inference models (controllers) for decision-making by the robot.

Arguably, the most widely used statistical formalism for the high-level control of robots is the use of finite state automata (FSA) as high-level controllers. In FSA, Markov decision processes (MDPs) represent the states and state-action pairs of each state-transition. The state-action pairs are referred to as the policies of the FSA and it is the policies which governs the behaviour of the robot. The objective is to find an optimum policy for each state-transition. However, the generation of inference models in dynamic and remote environments is not trivial.

1.1 Problem description

  • Augmenting or modifying the KB of a remotely-deployed robot becomes more convoluted, error-prone and computationally expensive if the structure of the KB is complex. Limited communication bandwidth also restricts the maintenance of the KB.

  • High-level controllers are often generated through machine learning techniques, where an FSA is generated for all states. These techniques progressively learn the policies of the FSA, using user-defined parameters, which are often selected subjectively or derived through experimentation. For example, Q-learning uses a user-defined probability state-transition matrix (STM) and reinforcement learning (RL) uses a user-defined discounted reward to statistically determine the best policies for the FSA. Changes in the environment, is likely to lead to the re-optimization of the parameters and re-learning of the model.

  • When machine learning is used to generate models as high-level controllers, the controller (FSA) is learnt in its entirety. For dynamic environments, a large number of models have to be learnt to handle different scenarios. However, when the underlying knowledgebase changes or the environment changes, learnt models may become obsolete and need to be replaced. Due to the time it takes to relearn a model, re-generation of high-level controllers in real-time operation becomes infeasible.

1.2 Proposed solution

The solution proposed in this research study aims to reduce and simplify the “cognitive world” of the robot (UAV in this study). In this study, cognitive reasoning is defined as decision-making, based on current knowledge which is optimized using real-time evidence. The solution introduces a cognitive reasoning process (CRP) for the UAV in order to govern its behaviour in real-time. This process is similar to that of the human cognitive framework [2] and intuitively provides the UAV with some intelligence in decision-making. Figure 1, gives an overview of the CRP:

Fig. 1
figure 1

Cognitive reasoning process (CRP)

Full size image

A domain expert provides all the knowledge, i.e. the KB, mission definitions and evidence definitions, to be used by the CRP. The KB is the set of all state-transitions (policies) between the states of the UAV. Each state-transition has a trigger formula which is composed of a set of conjunctive propositions. The mission definition is defined as a set of tasks to be completed in order to successfully complete the specified mission. The evidence definition is a set of variables, representing environmental observations, received in real-time. The KB, mission definitions and evidence definitions are used by the CRP to find the optimal policy, given the evidence. The CRP will be discussed in detail in Sect. 4.

Since the KB is a set of discrete elements, the problem is defined as a constrained, set-based knowledge optimization problem. Therefore, the CRP uses the AE-SPSO and AEFQ algorithms to find, quantify and evaluate each potential policy for optimality. The best policy is then selected and its action is passed as a command to the UAV.

To the best of our knowledge, there has been no attempt to affect high-level robot control through dynamic and real-time policy optimization using a particle swarm optimization approach.

The main contributions of this research study are the following:

  1. 1.

    The introduction of a novel adaptive entropy fitness quantification (AEFQ) algorithm for the statistical quantification of state-transitions (policies) of a FSA as high-level controller.

  2. 2.

    The introduction of an improved set-based PSO which uses the AEFQ, to produce an optimized KB*, which contains the optimal policies for selection.

  3. 3.

    The generation of re-usable high-level controllers (FSAs) as a result of the real-time, evidence-based, policy optimization and execution of the CRP.

The remainder of the research study is organized as follows: Sect. 2 reviews related work on high-level autonomous control in robotics; Sect. 3 provides some theoretical background on the methodologies used in the study. Section 4 introduces the methodology for the CRP and discusses the novel AEFQ algorithm and AE-SPSO algorithms in detail. Sections 5, 6 describes the experiment setup, results and analysis, respectively. Section 7 concludes the work of this research study and proposes relevant future work on autonomous high-level control through knowledge optimization in the CRP.

2 Related work

Improving the cognitive ability of robots has received a considerable amount of attention over the last decade. As described in the introduction, the two key factors of cognitive robotics, are knowledge representation and cognitive reasoning [3]. Although the problem of improving autonomy is non-trivial, it is relevant to a variety of robotic applications, for example, in humanoid robotics [4, 5], human–robot interaction [6,7,8,9], Search and Rescue (SAR) [10] and multi-robot systems [11].

2.1 Knowledge representation

In order to perform efficient inference, the structure and content of the KB is very important, especially if the KB has to be maintained remotely.

For many years various machine learning approaches, such as statistical relational learning (SRL) [12], inductive logic programming (ILP) [13, 14] and knowledge-based model construction (KBMC) [15, 16] have been used to derive expert knowledge from existing data sources. Some machine learning systems have been developed to learn and formulate knowledge: FOIL [17] learns Horn clauses from relational data and MADDEN [16] performs statistical knowledge extraction from textual data. CLAUDIEN [14] is an ILP engine which computes a set of logically valid clauses from data sets.

Horn clauses are particularly useful, as its form is similar to programmatic conditional statements, and therefore easier to implement.

More recent approaches are proving more suitable for cognitive robotics. Linear temporal logic (LTL) is used as a formal language to define the tasks of a robot, as applied in [18], where LTL is combined with Petri Nets to determine optimal movement planning for multiple robots.

The problem of high-dimensionality in the relationship between task planning, using LTL and robot motion is investigated by Shoukry et al. [19]. Here, LTL is used to define a set of propositions, applicable to all robots, for each region of the workspace. The robots’ movements across regions are controlled by the LTL propositions.

2.2 Cognitive reasoning

A lot of research have been focussed on the low-level control of robots, for example improving path planning in dynamic environments, where obstacles are avoided by prioritizing and predicting the future behaviour of the object [20]. However, cognitive robotics is concerned with cognitive reasoning, using current knowledge. In [9], a semi-autonomous high-level controller is proposed for the semi-autonomous control of robot teams in urban search and rescue missions. The objective of the controller is to reduce the workload of the robot operator. Other cognitive robotic approaches, for example, inductive logic programming (ILP) which is used for predicate generation, is combined with reinforcement learning (RL) to learn optimal behavioural policies in [21].

A popular approach used for cognitive robotics is the combination of (LTL) and MDPs, where the LTL formulae provide a formal definition of tasks for the robot and the MDPs are used to synthesize high-level controllers. However, synthesizing high-level controllers in a, dynamic environment remains a challenge. Meyer and Dimarogonas [22] introduces a framework to increase the adaptability of the synthesis process, by using a 3-layer top-down hierarchical decomposition of the control problem. A three step-approach is used to firstly, solve the LTL problem on a FSA, secondly, find the best policy for transitioning and thirdly, synthesize a controller.

Reinforcement learning (also referred to as Q-learning) of MDP type controllers are increasingly being combined with other methodologies to learn high-level controllers to accomplish some task. Generally, the objective of Q-learning is to iteratively select the best policy, i.e. state-action, which maximizes the expected discounted reward (Q-value), given the current state, the user-defined STM and user-defined rewards. The most popular approach is the use of the Bellman equations [23], which calculates the optimal Q-value over all policies. In [24], Q-learning is used in combination with a Deep Deterministic Policy Gradients (DDPG) algorithm for a UAV to learn a landing task in simulation. In [25], the effectiveness of the Q-learning algorithm for robot path planning, is improved by using a flower pollinating algorithm to initialize the q-values of the algorithm.

2.3 Critical review

For semi-autonomous robots, remotely deployed in unknown and dynamic environments, the complexity of the formulation of expert knowledge is critical. The methods discussed in Sect. 2.1 may prove to be sufficient for discovery and formulation of knowledge for high-level robot control in a controlled or well-defined environment. However, in an unknown or highly dynamic environment, the knowledge needs to be maintained in real-time, often over vast distances. For these types of environments, the methods discussed will prove to be computationally expensive and error-prone and may be constrained by communication bandwidths.

Similarly, learning high-level controllers using machine learning techniques, such as Q-learning mentioned in Sect. 2.2, will be sufficient in well-defined or controlled environments. For environments such as these, effective models can be learned. A degree of dynamism may be catered for by learning a large number of models to cater for as many scenarios as possible. However, if the environment is unknown or highly dynamic, the accuracy of the models will be sub-optimal. Moreover, it is infeasible to relearn a model in real-time, every time the environment changes.

The AE-SPSO/AEFQ methodology introduced in this study follows a real-time optimization approach, while a machine learning methodology follows an a priori learning approach. The main differences between the two methodologies are:

  • The modification and updating of the expert-knowledge (missions, states and rules), which is used in the optimization process is simplified, and therefore uses less bandwidth and is less error-prone.

  • No subjective user-defined state-transition probabilities are required; instead probabilities are accurately calculated from real-time evidence, received from the environment.

  • An open world assumption (OWA) (c.f. Sect. 3.1) is used in the quantification process.

  • State-transitions can be composite, i.e. multiple state-transitions between the same two states, each statistically quantified using its own rules and with its own actions.

  • A re-usable high-level controller (FSA) is dynamically created, step-by-step in real-time.

These differences are too significant to do a fair empirical comparison between a machine learning approach and the AE-SPSO/AEFQ approach proposed in this study. This is mainly due to the differences between the learning approach followed by a machine learning methodology and a real-time optimization approach followed the AE-SPSO/AEFQ approach.

Therefore, the performance of the AE-SPSO/AEFQ methodology will be evaluated experimentally, on two simulated UAV benchmark problems.

3 Background

In this section, some characteristics of the knowledgebase are discussed and an overview of the standard particle swarm optimization algorithm and the set-based particle swarm optimization algorithms is given.

3.1 Knowledgebase characteristics

The KB contains domain-specific and relevant knowledge, required for decision-making, i.e. inference. In this study, the KB is composed of the set of all state-transitions with a trigger formula for each state-transition. The trigger formula is composed of a conjunctive set of logic propositions. Inference, is defined as the CRP which uses the KB to find the optimal policy to control the the UAV. The CRP is directly influenced by the completeness and consistency of the KB.

The KB is considered to be complete, if all possible knowledge needed for inference is formulated within the KB. This means each trigger formula is completely defined.

The KB is considered to be consistent, if there are no changes made to any of the ground propositions during inference. While consistency is not a requirement for the representation of the knowledge in the KB, it is important for efficient reasoning.

In addition, inference is performed, using either a closed world assumption (CWA) or an open world assumption (OWA) [26, 27]. The CWA assumes the knowledge about the environment is complete and consistent. This means that, unless it is known that a trigger formula is true, it must be assumed to be false.

The OWA on the other hand, assumes that the knowledge representing the environment is incomplete or inconsistent. This means that if all knowledge is not explicitly specified, the truth of the trigger formula is considered unknown, but not false. Therefore, a probability (“degree of belief”) is statistically allocated to the trigger formula.

In a dynamic environment, the KB can never be complete, as the domain expert could update the KB with new or updated state-transitions or trigger formulae at any time.

Also, the KB can never be consistent, as the evidence, which will be applied to the trigger formula for fitness quantification, constantly changes in real time.

Clearly, for a robot functioning in a dynamic and uncertain environment, the OWA is the preferred approach to follow. Therefore, the solution must enable simple, dynamic and efficient maintenance of the KB and dynamic and real-time reasoning for high-level robot control. Section 4 below discusses the proposed methodology to achieve this, in more detail.

3.2 Overview of standard particle swarm optimization

Particle swarm optimization (PSO) is a stochastic optimization algorithm, which has been successfully applied to optimization problems in the fields of engineering and robotics [28,29,30]. PSO has been successfully applied to problems where the search space is either continuous or discrete.

Inspired by the movement and behaviour of a flock of birds searching for food, Eberhart and Kennedy introduced the standard particle swarm optimization (StdPSO) algorithm [31]. The swarm of particles moves through a D-dimensional solution space. The position of particle \(i\) in the solution space represents a candidate solution, which is defined as a solution vector, \({\mathbf{X}}_{i} \in {\mathbb{R}}^{D}\). The optimality of the candidate solution is determined by a fitness function, \(f\left( {{\mathbf{X}}_{i} } \right) \in {\mathbb{R}}\). The particle’s velocity represents the step size and direction of its movement and is defined by a vector \({\mathbf{v}}_{i} \in {\mathbb{R}}^{D}\). StdPSO iteratively updates each particle’s velocity and position using the following equations:

$$v_{ij} \left({t + 1} \right) = \fancyscript{w}v_{ij} \left(t \right) + c_{1} r_{1j} \left({y_{ij} \left(t \right) - x_{ij} \left(t \right)} \right) + c_{2} r_{2j} \left({\hat{y}_{j} \left(t \right) - x_{ij} \left(t \right)} \right)$$
(1)
$$x_{ij} \left( {t + 1} \right) = x_{ij} \left( t \right) + v_{ij} \left( {t + 1} \right)$$
(2)

where \(v_{ij} \left( t \right)\) represents the jth element of the velocity vector of particle \(i\), at the tth iteration. An inertia weight \(\fancyscript{w}\) is applied to the particle velocity. Two key components of the velocity equation are, the cognitive component, \(c_{1} r_{1j} \left( {y_{ij} \left( t \right) - x_{ij} \left( t \right)} \right)\), and the social component, \(c_{2} r_{2j} \left( {\hat{y}_{j} \left( t \right) - x_{ij} \left( t \right)} \right)\), where \(y_{ij} \left( t \right)\) represents the jth element of the personal best vector of particle \(i\) at the tth iteration and \(\hat{y}_{j} \left( t \right)\) represents the jth element of the global best vector of the swarm at the tth iteration. The term, \(x_{ij} \left( t \right)\), represents the jth element of the current position of particle \(i\) at the tth iteration. The two positive real numbers \(c_{1}\) and \(c_{2}\) are acceleration constants, used to scale the contributions of the cognitive and social components. The random values, \(r_{1j} , r_{2j} \sim U\left( {0,1} \right)\), add a stochastic element to the cognitive and social components. A user-defined inertia weight, \(\fancyscript{w}\), is added to the current velocity [32], which, along with the acceleration constants, balances the effect between global search and local search.

The general fitness function for the PSO is defined as:

$$f : {\mathbb{R}}^{{n_{\phi } }} \to {\mathbb{R}}$$
(3)

For a minimization problem, the personal best position at the next iteration is calculated as,

$$y_{i} \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}l} {y_{i} \left( t \right)} \hfill & {if\;f\left( {X_{i} \left( {t + 1} \right)} \right) \ge f\left( {y_{i} \left( t \right)} \right)} \hfill \\ {X_{i} \left( {t + 1} \right)} \hfill & {if\;f\left( {X_{i} \left( {t + 1} \right)} \right) < f\left( {y_{i} \left( t \right)} \right)} \hfill \\ \end{array} } \right.$$
(4)

and for a maximization problem, the personal best position at the next iteration is calculated as,

$$y_{i} \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}l} {y_{i} \left( t \right)} \hfill & {if\;f\left( {X_{i} \left( {t + 1} \right)} \right) \le f\left( {y_{i} \left( t \right)} \right)} \hfill \\ {X_{i} \left( {t + 1} \right)} \hfill & {if\;f\left( {X_{i} \left( {t + 1} \right)} \right) > f\left( {y_{i} \left( t \right)} \right)} \hfill \\ \end{array} } \right.$$
(5)

For a minimization problem, the global best position at the next iteration is calculated as,

$$\hat{y}\left( {t + 1} \right) = \left\{ {\begin{array}{*{20}l} {\hat{y}\left( t \right)} \hfill & {if\;f\left( {X_{i} \left( {t + 1} \right)} \right) \ge f\left( {\hat{y}\left( t \right)} \right)} \hfill \\ {X_{i} \left( {t + 1} \right)} \hfill & {if\;f\left( {X_{i} \left( {t + 1} \right)} \right) < f\left( {\hat{y}\left( t \right)} \right)} \hfill \\ \end{array} } \right.$$
(6)

and for a maximization problem, the global best position at the next iteration is calculated as,

$$\hat{y}\left( {t + 1} \right) = \left\{ {\begin{array}{*{20}l} {\hat{y}\left( t \right)} \hfill & {if\; f\left( {X_{i} \left( {t + 1} \right)} \right) \le f\left( {\hat{y}\left( t \right)} \right)} \hfill \\ {X_{i} \left( {t + 1} \right)} \hfill & {if\;f\left( {X_{i} \left( {t + 1} \right)} \right) > f\left( {\hat{y}\left( t \right)} \right)} \hfill \\ \end{array} } \right.$$
(7)

On conclusion of all iterations, all (or most) of the particles have converged on the best solution, which is represented by the global best vector.

3.3 Overview of set-based particle swarm optimization

When the search space is discrete, the velocity and position update Eqs. (1) and (2) cannot be used without re-definition. Langeveld and Engelbrecht [33] introduced a generic, set-based PSO (SPSO), suitable for optimization problems with a discrete search space. To remain in accordance with standard PSO, velocity and position update equations, are redefined in terms of set-based operators. The set-based velocity equation is:

$$V_{i} \left( {t + 1} \right) = \left( {c_{1} r_{1} \otimes \left( {Y_{i} \left( t \right){ \ominus }X_{i} \left( t \right)} \right)} \right) \oplus \left( {c_{2} r_{2} \otimes \left( {\hat{Y}\left( t \right){ \ominus }X_{i} \left( t \right)} \right)} \right) \oplus \left( {c_{3} r_{3} \odot_{k}^{ + } A_{i} \left( t \right)} \right) \oplus \left( {c_{4} r_{4} \odot^{ - } S_{i} \left( t \right)} \right)$$
(8)

where \(\left( {c_{1} r_{1} \,\otimes\, \left( {Y_{i} \left( t \right)\,{ \ominus }\,X_{i} \left( t \right)} \right)} \right)\) is the cognitive component and \(\left( {c_{2} r_{2} \,\otimes\, \left( {\hat{Y}\left( t \right)\,{ \ominus }\,X_{i} \left( t \right)} \right)} \right)\) is the social component. Two additional components are added to the standard PSO equation: \(c_{3} r_{3} \odot_{k}^{ + } A_{i} \left( t \right)\) and \(c_{4} r_{4} \odot^{ - } S_{i} \left( t \right)\), where \(A_{i} \left( t \right) = U\backslash \left( {X_{i} \left( t \right) \cup Y_{i} \left( t \right) \cup \hat{Y}\left( t \right)} \right)\) and \(S_{i} \left( t \right) = \left( {X_{i} \left( t \right) \cap Y_{i} \left( t \right) \cap \hat{Y}\left( t \right)} \right)\). The parameters are \(c_{1} , c_{2} \in \left[ {0, 1} \right]\) and \(c_{3} , c_{4} \in \left[ {0, \left| U \right|} \right]\). The random numbers, \(r_{1}\) to \(r_{4}\), are random values sampled from a uniform distribution, i.e. \(r_{1} ,r_{2} ,r_{3} ,r_{4} \sim \varOmega \left( {0,1} \right)\).

The set-based position update equation is:

$$X_{i} \left( {t + 1} \right) = X_{i} \left( t \right)\; { \boxplus }\; V_{i} \left( {t + 1} \right)$$
(9)

While the movement of particles through the search space is governed by Eqs. (1) and (2) for a continuous search space, Eqs. (8) and (9) govern the movement of particles (sets) through a discrete set-based search space. The knowledge optimization process of the CRP will be implemented using an improved SPSO algorithm.

4 Methodology

This CRP of an autonomous UAV (illustrated in Fig. 1), have two main functions: cognition and reasoning. The cognition component is tasked with the statistical optimization of the knowledge from the KB, given the environmental evidence. The reasoning component is tasked with selecting the optimal action \(\pi^{*}\), from the optimized knowledgebase, KB. The methodology is implemented in Algorithms 1–3.

4.1 Evidence definitions

Environmental evidence is defined as two sets, representing the mission parameters and evidence parameters. The former is provided by the domain expert in relation to a specific mission and the latter is sensory information observed by the robot.

The runtime parameter is defined as,

$$\varPhi^{r} = \left\{ {\varphi_{1}^{r} ,\varphi_{2}^{r} , \ldots ,\varphi_{{n_{{\varPhi^{r} }} }}^{r} } \right\}$$
(10)

where \(\varphi_{i}^{r}\), \(i = 1,..,n_{{\varPhi^{r} }}\) is the runtime parameter representing the evidence observed in the environment.

The mission parameters are defined as,

$$\varPhi^{m} = \left\{ {\varphi_{1}^{m} ,\varphi_{2}^{m} , \ldots ,\varphi_{{n_{{\varPhi^{m} }} }}^{m} } \right\}$$
(11)

where \(\varphi_{j}^{m} \in \left[ {lb^{{m_{j} }} , ub^{{m_{j} }} } \right]\), \(j = 1,..,n_{{\varPhi^{m} }}\) defines the mission parameter, constrained to specified lower and upper boundaries. Both the mission and evidence parameters are used in the calculation of constraint averages, and represent the dynamic environmental information received by the robot’s CRP.

4.2 Knowledgebase definitions

The KB is defined as the set of state-transitions which governs the behaviour of the UAV:

$$KB = \left\{ {\tau_{1} ,\tau_{2} , \ldots ,\tau_{{n_{{\left| {KB} \right|}} }} } \right\}$$
(12)

where \(\tau_{k} \in KB\), \(k = \left( {1, \ldots ,\left| {KB} \right|} \right)\) represents a state-transition in the KB.

The state-transition is a tuple,

$$\tau_{k} = \left({\fancyscript{v}, \eta,{\mathcal{A}},{\mathcal{F}}} \right)$$

where \(\fancyscript{v} = \left\{{0,1} \right\}\) indicates whether the transition is valid, \(\eta \in {\mathbb{Z}}^{ + }\) is an objective identifier assigned to the transition, \({\mathcal{A}} = \left\{ {a_{1} , \ldots ,a_{{n_{{\mathcal{A}}} }} } \right\}\) is a set of actions and \({\mathcal{F}} = \left\{ {p_{1} ,p_{2} , \ldots ,p_{{n_{{\mathcal{F}}} }} } \right\}\) is the trigger formula for the transition, consisting of a set of simple logic propositions.

Each proposition \(p_{l} \in {\mathcal{F}}\), \(l = \left( {1, \ldots ,n_{{\mathcal{F}}} } \right)\) is defined by a domain expert and is a tuple,

$$p_{l} = \left( {\varphi_{i}^{r} , logical\_operator,\varphi_{j}^{m} } \right)$$
(13)

where the runtime and mission parameters are related by a \({\text{logical}}\_{\text{operator}}\), from the set \(\left\{ { > , < , = } \right\}\), to form simple propositions of the form:

$$\left( {\varphi_{i}^{r} > \varphi_{j}^{m} } \right),\left( {\varphi_{i}^{r} < \varphi_{j}^{m} } \right)\;{\text{and}}\;\left( {\varphi_{i}^{r} = \varphi_{j}^{m} } \right)$$
(14)

(Any non-numeric argument is discretized to a numeric value, prior to quantification of \({\mathcal{F}}\)).

The indicator \(\fancyscript{v}\), the objective identifier \(\eta\), the actions \({\mathcal{A}}\) and all the propositions \(p_{l}\) are defined and maintained by the domain expert.

4.3 Adaptive entropy fitness quantification

4.3.1 Model construction

In order to perform the quantification of a state-transition \(\uptau_{\text{k}}\), a problem-specific model is constructed before it is presented to the MEP equation for quantification. Given a state-transition \(\uptau_{\text{k}} \in {\text{KB}}\) the model is formally defined as a tuple,

$${\mathcal{M}}_{{\tau_{k} }} = \left( {{\mathbf{V}},{\mathbf{X}}, {\mathbf{F}}, {\varvec{\Lambda}}} \right)$$
(15)

The set of variables are represented by \({\mathbf{V}} = \left\{ {\left\{ {v^{{\mathbb{Q}}} } \right\} \cup ,\left\{ {v_{1}^{{\mathbb{P}}} ,v_{2}^{{\mathbb{P}}} , \ldots v_{{n_{{\mathbb{P}}} }}^{{\mathbb{P}}} } \right\} \cup \left\{ {v_{1}^{{\mathbb{A}}} ,v_{2}^{{\mathbb{A}}} , \ldots v_{{n_{{\mathbb{A}}} }}^{{\mathbb{A}}} } \right\}} \right\}\) where \(v^{{\mathbb{Q}}}\) is the query variable, \(v_{p}^{{\mathbb{P}}}\), \(p = 1, \ldots ,n_{{\mathbb{P}}}\) is a predictor variable, representing a proposition in the trigger formula and \(v_{l}^{{\mathbb{A}}}\), \(l = 1, \ldots ,n_{{\mathbb{A}}}\) is an association variable. Note that, since the propositions are independent, they will not have any effect on the query variable, unless relevant associations are defined between the query variable and appropriate predictor variables. The associations are problem-specific and are defined by the user.

Let \(m_{{ \tau_{k} }} = \left| {\left\{ {v^{{\mathbb{Q}}} } \right\} \cup \left\{ {v_{1}^{{\mathbb{P}}} ,v_{2}^{{\mathbb{P}}} , \ldots v_{{n_{{\mathbb{P}}} }}^{{\mathbb{P}}} } \right\}} \right|\), and \(n_{{\tau_{k} }} = 2^{{m_{{ \tau_{k} }} }}\), then a \(m_{{\tau_{k} }} \times n_{{\tau_{k} }}\) constraint matrix. \({\mathbf{X}}\) is the state space of the trigger formula and defines all the joint statements of \(\left\{ {v^{{\mathbb{Q}}} } \right\} \cup \left\{ {v_{1}^{{\mathbb{P}}} ,v_{2}^{{\mathbb{P}}} , \ldots v_{{n_{{\mathbb{P}}} }}^{{\mathbb{P}}} } \right\}\). A binary constraint function, \(F\left( {X = x_{ij} } \right)\), \(i \in n_{{\tau_{k} }}\) and \(j \in m_{{\tau_{k} }}\) assigns a boolean constraint to each variable in the state space. Let \(n_{V} = \left( {1 + n_{{\mathbb{P}}} + n_{{\mathbb{A}}} } \right)\), then vector \({\mathbf{F}} = \left( {F_{1} , F_{2} , \ldots ,F_{{n_{F} }} } \right)\), \(n_{F} = n_{V}\) are constraint averages for each of the variables in \({\mathbf{V}}\). The vector \({\varvec{\Lambda}} = \left( {\lambda_{1} ,\lambda_{2} , \ldots \lambda_{{n_{\varLambda } }} } \right)\), \(n_{\varLambda } = n_{V}\), represents the Lagrange multipliers, calculated for each variable in \({\mathbf{V}}\), using (25).

Each constraint average \(F_{{n_{F} }} \in {\mathbf{F}}\) represents the degree of belief in a proposition and is derived from real-time information (evidence) received from the environment. The constraint average follows the OWA, and is crucial for the accurate quantification of the state-transition.

In this research study, the constraint average is calculated by interpreting a proposition as a degree of believe, (probability), derived from a distance calculation. For example, Fig. 2 illustrate two example state-transitions:

Fig. 2
figure 2

Example state-transitions with corresponding propositions

Full size image

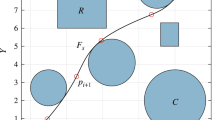
A constraint average for the proposition is calculated by measuring the progress of the current runtime parameter \(\varphi_{i}^{r}\), relative to the operational bounds of the mission task. The result is a probability assigned to the proposition. Figure 3 illustrates the approach:

Fig. 3
figure 3

Method for constraint average assignment to propositions

Full size image

This approach ensures that the constraint average accurately reflects relevant environmental evidence. This also ensures that the fitness quantification of the trigger formula for the state-transition is based on relevant and correct environmental evidence.

The rule is translated into a probability as follows:

Firstly, given the proposition \(p_{l}\), calculate the total operation distance \(d_{j}^{m} ,\) using the upper and lower bounds of the mission argument:

$$d_{j}^{m} = ub_{j}^{m} - lb_{j}^{m}$$
(16)

Calculate the current distance \(d_{i}^{r}\) of the runtime argument, \(\varphi_{j}^{r}\) with respect to the upper and lower bounds of the mission parameter, \(\varphi_{i}^{m}\), according to the logical operation of the proposition:

$$d_{i}^{r} = \left\{ {\begin{array}{*{20}l} {\varphi_{i}^{r} - lb_{j}^{m} ;} \hfill & { if\;p_{l} = \left( {\varphi_{i}^{r} \le \varphi_{j}^{m} } \right) } \hfill \\ {ub_{j}^{m} - \varphi_{{\begin{array}{*{20}c} i \\ \end{array} }}^{r} ; } \hfill & {if\;p_{l} = \left( {\varphi_{i}^{r} \ge \varphi_{j}^{m} } \right)} \hfill \\ {0;} \hfill & {if\;p_{l} = \left( {\varphi_{i}^{r} \ne \varphi_{j}^{m} } \right)} \hfill \\ {1;} \hfill & {if\;p_{l} = \left( {\varphi_{i}^{r} = \varphi_{j}^{m} } \right)} \hfill \\ \end{array} } \right.$$
(17)

Use (16) and (17) to calculate a real valued distance, in the range \(\left[ {0,1} \right]\), for the proposition:

$$Pr\left( {p_{l} } \right) = \frac{{d_{i}^{r} }}{{d_{j}^{m} }}$$
(18)

where \(Pr\left( {p_{l} } \right)\) represent the relative remaining distance of \(\varphi_{i}^{r}\), within the boundaries \(lb_{j}^{m}\) and \(ub_{j}^{m}\) as a probability. Once the distances for each proposition have been calculated, the distances for each of the joint statements can be calculated. To illustrate, let \(v^{{\mathbb{Q}}} = p_{0}\), \(v_{1}^{{\mathbb{P}}} = p_{1}\) and \(v_{2}^{{\mathbb{P}}} = p_{2}\), then the state space consists of \(2^{3} = 8\) joint statements. The joint distances, for the predictor variables are calculated as follows:

$$d_{{p_{1} p_{2} }} = d_{{p_{1} }} + d_{{p_{2} }}$$
(19)
$$d_{{p_{1} \overline{{p_{2} }} }} = d_{{p_{1} }} + \left( {1 - d_{{p_{2} }} } \right)$$
(20)
$$d_{{\overline{{p_{2} }} p_{2} }} = \left( {1 - d_{{p_{1} }} } \right) + d_{{p_{2} }}$$
(21)
$$d_{{\overline{{p_{1} }} \overline{{p_{2} }} }} = \left( {1 - d_{{p_{1} }} } \right) + \left( {1 - d_{{p_{2} }} } \right)$$
(22)

The overall distance \(d_{f}\), represented by the probability distribution over all the propositions of the trigger formula, is calculated by:

$$d_{f} = \left( {d_{{p_{1} p_{2} }} + d_{{p_{1} \overline{{p_{2} }} }} + d_{{\overline{{p_{2} }} p_{2} }} + d_{{\overline{{p_{1} }} \overline{{p_{2} }} }} } \right)$$
(23)

With all the joint distances of the joint statements available, the respective constraint averages can now be calculated. Firstly, the constraint average \({\text{F}}_{1}\) of the query variable \({\text{p}}_{0}\) is set to 1.0. The constraint averages for the predictor and association variables are then set as follows:

$${\mathbf{F}} = \left( {d_{{p_{0} }} ,\frac{{\left( {d_{{p_{1} p_{2} }} + d_{{p_{1} \overline{{p_{2} }} }} } \right)}}{{d_{f} }}, \frac{{\left( {d_{{p_{1} p_{2} }} + d_{{\overline{{p_{1} }} p_{2} }} } \right)}}{{d_{f} }}, \frac{{\left( {d_{{p_{1} p_{2} }} + d_{{p_{1} \overline{{p_{2} }} }} } \right)}}{{d_{f} }},\frac{{\left( {d_{{p_{1} p_{2} }} + d_{{\overline{{p_{1} }} p_{2} }} } \right)}}{{d_{f} }}, \frac{{d_{{p_{1} p_{2} }} }}{{d_{f} }}} \right)$$
(24)

Next, the Lagrange multipliers are determined.

The duality between the Lagrange multipliers and the user-defined constraint averages, allows the Legendre transform to be used to derive the Lagrange multipliers:

$${\mathcal{L}}_{trans} = {\varvec{\Lambda}} = \mathop {\hbox{min} }\limits_{{\lambda_{k} }} \left( {\ln Z\left( {\lambda_{1} ,\lambda_{2} , \ldots \lambda_{k} } \right) - \mathop \sum \limits_{j = 1}^{{{\text{m}}_{{\uptau_{\text{k}} }} }} \lambda_{j} F_{j} } \right)$$
(25)

The multipliers are derived by varying the values of \(\lambda_{k}\) while keeping the constraint average, \(F_{j}\) fixed, until \({\mathcal{L}}_{trans}\) reaches a minimum. Table 1 shows an example of a model for a trigger formula containing two propositions, B and C, including associations with the query variable A, i.e. AB, AC, ABC. The model contains a \(m_{{\tau_{k} }} \times n_{{\tau_{k} }}\) boolean constraint matrix, where \(m_{{\tau_{k} }} = 3\) and \(n_{{\tau_{k} }} = 8\).

Table 1 Model of illustrative example
Full size table

Once the model is complete, the fitness quantification can be performed.

4.3.2 Fitness quantification

Given the model \({\mathcal{M}}_{{\tau_{k} }}\), the probability distribution, \({\mathbf{Q}} = \left( {q_{1} ,q_{2} , \ldots q_{{n_{{\mathbf{Q}}} }} } \right)\), \(n_{{\mathbf{Q}}} = n_{{\tau_{k} }}\) over the variables (propositions) of the trigger formula can now be calculated. Given the \(m_{{\tau_{k} }} \times n_{{\tau_{k} }}\) constraint matrix and let \(i \in n_{{\tau_{k} }}\) and \(j \in m_{{\tau_{k} }}\), the MEP is then formally defined as:

$$\left( {q_{i} |{\mathcal{M}}_{{\tau_{k} }} } \right) = \frac{1}{{Z\left( {\lambda_{1} ,\lambda_{2} , \ldots \lambda_{k} } \right)}}e^{{ - \mathop \sum \limits_{j = 1}^{{{\text{m}}_{{\uptau_{\text{k}} }} }} \lambda_{j} F_{j} \left( {X = x_{i} } \right)}}$$
(26)

where \(Z\left( {\lambda_{1} ,\lambda_{2} , \ldots \lambda_{k} } \right) = \mathop \sum \limits_{i = 1}^{{\uptau_{\text{k}} }} e^{{\mathop \sum \limits_{j = 1}^{{{\text{m}}_{{\uptau_{\text{k}} }} }} \lambda_{j} F_{j} \left( {X = x_{i} } \right)}}\)

\(Z\) is the partition function which ensures the probabilities are assigned between 0 and 1. The Lagrange multipliers are represented by \(\lambda_{j}\), \(j = 1, \ldots ,k\) and \(F_{j} \left( {X = x_{i} } \right)\) assigns a real-world, domain-specific constraint, to the state \(i\) of variable \(j\).

(Refer to [34], chapters 24 and 25 for a detailed discussion on the mathematical derivation of the Legendre transformation and the MEP formula).

Finally, the fitness of the state-transition \(\tau_{k} \in KB\) is calculated as,

$$f\left({\tau_{k}} \right) = \fancyscript{v} \times \text{ }q_{1}$$
(27)

where \(\fancyscript{v} \in \tau_{k}\) and \(\fancyscript{v} = 1\) indicate a valid state-transition and \(\fancyscript{v} = 0\) indicate an invalid state-transition.

Note that any of the resulting probabilities (including marginal probabilities) in the distribution \({\mathbf{Q}}\) may now be used in the fitness quantification. However, in this study, only \(q_{1}\) will be used for fitness quantification, since its value is conditioned on all the predictor variables, i.e. propositions.

4.4 The AE-SPSO algorithm

The AE-SPSO algorithm is an improved variant of the SPSO (c.f. Sect. 3.3). The AE-SPSO algorithm eliminates the random removal of (potentially good) solutions from the personal best- and global best sets. Moreover, an elitism approach is added to the AE-SPSO to ensure the best performing elements are retained in a scalable manner. The AE-SPSO algorithm uses the same cognitive, social and positioning components as those in Eqs. (1) and (2). However, since the particle is a set of state-transitions, each with a trigger formula, the algebraic operations of Eqs. (1) and (2) are not suitable and have to be redefined as set-based operations:

Let:

  • \(X_{i}\) be the current position of particle \(i\), (i.e. the set of state-transitions, \(\tau_{k}\)).

  • \(Y_{i}\) be the personal best position of particle \(i\), (i.e. the personal best set of state-transitions).

  • \(\hat{Y}\) be the global best position of the swarm (i.e. the global best set of state-transitions).

  • \(c_{1} , c_{2}\) be the cognitive and social accelerators respectively.

then

$$V_{i} \left( {t + 1} \right) = r_{1} c_{cog} \left( {d_{cog} } \right) \cup r_{2} c_{soc} \left( {d_{soc} } \right)$$
(28)
$$X_{i} \left({t + 1} \right) = max_{\varepsilon} \left({X_{i} \cup v_{i} \left({t + 1} \right)} \right)$$
(29)

where

$$Cognitive\;difference :\;d_{cog} :Y_{i} \cup \left( {X_{i} \backslash Y_{i} } \right)$$

The difference between the particle’s personal best set \(y_{i}\) and the particle’s current set \(X_{i}\) is defined as the unification of \(Y_{i}\) and the set-theoretic difference between \(Y_{i}\) and \(X_{i}\). That is, all the elements in the particle’s personal best set are retained and the elements in \(X_{i}\) which are not in \(Y_{i}\) are included in the difference set.

$$Social\;difference :\;d_{soc} :\hat{Y} \cup \left( {X_{i} \backslash \hat{Y}} \right)$$

The difference between the swarm’s global best set \(\hat{Y}\) and particle’s current set \(X_{i}\) is defined as the unification of \(\hat{Y}\) and the set-theoretic difference between \(\hat{Y}\) and \(X_{i}\). That is, all the elements the swarm’s best set is retained and the elements in \(X_{i}\) which are not in \(\hat{Y}\) are included in the difference set.

$$Cognitive\;velocity :\;v_{cog} :f\left( {{\text{KB}},r_{1,} c_{1} } \right) \cup \left( {d_{cog} } \right)$$

The cognitive velocity is derived by the union of \(c_{1}\) random elements selected from the \({\text{KB}}\) and the cognitive difference set. For each \(c_{1}\), a random integer value \(r_{1}\) is selected from the range \(\left[ {1,\left| {\text{KB}} \right|} \right]\) and the element (state-transition) at index \(r_{1}\) is added to \(d_{cog}\).

$$Social\;velocity :\;v_{soc} : f\left( {{\text{KB}},r_{2,} c_{2} } \right) \cup \left( {d_{soc} } \right)$$

The social velocity is derived by the union of \(c_{2}\) random elements from the \({\text{KB}}\) and the social difference set. For each \(c_{2}\), a random integer value \(r_{2}\) is selected from the range \(\left[ {1,\left| {\text{KB}} \right|} \right]\) and the element (state-transition) at index \(r_{2}\) is added to \(d_{soc}\).

$$Particle\;velocity :\;V_{i} \left( {t + 1} \right) = v_{cog} \cup v_{soc}$$

The resulting velocity \(V_{i} \left( {t + 1} \right)\) is the union of the elements of cognitive velocity \(v_{cog}\) and the elements of the social velocity \(v_{soc}\).

$$Particle\;position :\;X_{i} \left({t + 1} \right) = max_{\varepsilon} \left({X_{i} \cup V_{i} \left({t + 1} \right)} \right)$$

Using the AEFQ algorithm (Algoritm 1), the fitness \(f\left( {\tau_{k} } \right)\), where \(\tau_{k} \in X_{i}\), is calculated. In order to preserve the fittest elements from one iteration to the next, an elitism parameter \(\varepsilon\), is introduced [48]. The elitist parameter \(\varepsilon\) specifies the number of fittest elements to include in the particle’s new position set. The new position \(X_{i} \left( {t + 1} \right)\) is derived by selecting the top \(\varepsilon\) (fittest) elements from the union of the current position \(x_{i}\) and the velocity \(V_{i} \left( {t + 1} \right)\). The selection of the top \(\varepsilon\) elements is denoted by \(max_{\varepsilon} \left(\cdot \right)\).

Note the absence of the inertia weight applied to the particle’s current velocity. In the standard PSO, the inertia weight \(\fancyscript{w}\), along with the accelerator constants \(c_{1} , c_{2}\) control the granularity of the exploration. In set-based PSO, the accelerator constants \(c_{1} , c_{2}\) control the granularity by specifying the size of the random set of new elements to be added. Similarly, the inertia weight \(\fancyscript{w}\), would specify the size of the subset of elements (the inertia set) to be selected from the velocity set. However, it would serve no purpose to add the inertia set again, because when calculating the new position set, the velocity set is already added in full to the current position set. Therefore, when calculating the difference sets \(d_{cog}\) and \(d_{soc}\) at the next iteration, the new position already includes the velocity elements.

figure a

The CRP is implemented according to the logical processes defined by Algorithms 1–3. Algorithm 1 shows the implementation of the adaptive entropy fitness quantification method.

Note that, for simplicity, the sensory input is processed as single set, rather than each individual input element. Prior to the constraint average calculation (line 9), the arguments of the trigger formula of the state-transition are ground using the corresponding sensory input parameters. This automation of the grounding process simplifies modification or creation of new propositions.

Algorithm 2 shows the process for finding the optimal solution (state-transition), based on the fitness of the particle, determined by the AEFQ (Algorithm 1).

figure b

The CRP uses the optimal set of solutions (state-transitions) found by the AE-SPSO to select and execute the relevant actions.

figure c

5 Experiment setup

The methodology is experimentally evaluated by simulation, where a UAV autonomously execute two benchmark missions, one simple and one more complex. The performance measures for each of the benchmark missions are:

  1. 1.

    Success—measured by inspecting the completeness of the learned FSA (digraph), for each mission and;

  2. 2.

    Reasoning—measured by inspecting the level of velocity control of the UAV, based on reasoning about the statistical fitness of each state-transition.

Hardware: The experiments were executed on an Intel i7 laptop computer with 2.97 GHz quad core CPU, 16 Gb RAM and an Intel HD Graphics 4000 video adapter.

Software: The experiments were performed using the AirSim/Unity simulation environment, running on the Microsoft Windows 8.1 operating system.

Figure 4 illustrates the simulation’s software architecture:

Fig. 4
figure 4

Experiment platform architecture

Full size image

The code base of the AirSim/Unity simulator is C++ and the CRP were implemented using C#/NET (providing simpler memory management and easier data structure manipulation). To simplify future deployment of the CRP on a UAV platform, the CRP was functionally abstracted from the simulation environment. Integration between the AirSim/Unity simulator and the CRP was performed using a Redis Cache database. Expert data, such as mission data, were entered in extensible markup language (XML) format.

5.1 Benchmark mission 1

From the Home (I) location, arm the motors, ascend to a specified operational height and fly to the Charging point (IV). Descend on the charging point and disarm the motors (Fig. 5).

Fig. 5
figure 5

Benchmark mission 1

Full size image

5.2 Benchmark mission 2

From the Home (I) location, arm the motors, ascend to a specified operational height and fly to the Collection point (II). Descend and collect the cargo, then ascend to the specified operational height and fly to the Delivery point (III). Descend at the delivery point and deliver the cargo. Ascend to a new operational height and fly to the Charging point (IV) for recharging. Descend on the charging point and disarm the motors (Fig. 6).

Fig. 6
figure 6

Benchmark mission 2

Full size image

The UAV platform has nine states (Table 2).

Table 2 UAV states
Full size table

The nine UAV states yields a KB of 81 possible state-transitions (Table 3).

Table 3 UAV state-transitions
Full size table

The KB is constructed as a square matrix, assuming a transition from every state to every other state. Valid states are defined by the domain expert, by setting an indicator on the state-transition as well as defining a trigger formula for each valid state-transition. Although some state-transitions can never be valid [e.g. from S5 (flying) to S1 (Motors Off)], this approach makes it simpler for the domain expert to activate new transitions. Valid state-transitions for the experiments are marked in Table 3 as shaded/italic/bold cells.

For each of the benchmark missions, an annotated video of the simulation is recorded and published to YouTube:

  1. 1.

    UAV benchmark mission 1 [35]

  2. 2.

    UAV benchmark mission 2 [36]

6 Experiment results

6.1 Benchmark mission 1: results

Figure 7 shows the resulting FSA for benchmark mission 1, dynamically learned by the CRP from the KB (Table 3), during the execution of mission 1. The node in bold shows the start state, i.e. Motors Off.

Fig. 7
figure 7

FSA learned for benchmark mission 1

Full size image

Figure 8 provides a “zoomed” view showing the “fly” state-transitions, and corresponding fitness of each, generated by the CRP.

Fig. 8
figure 8

A “zoomed” image of the iterative “fly” transition generated during mission 1

Full size image

The learned FSA can be saved and, provided the mission and operational conditions remain the same, may be used as high-level controller to execute similar, subsequent missions.

Figure 9 shows the dynamic control of the velocity, derived from the state-transition fitness. The graph shows the reduction in velocity, in accordance with the reduction in fitness of the “fly” state-transition, as the UAV nears its destination.

Fig. 9
figure 9

Dynamic velocity adjustment during mission 1

Full size image

On the graph, the target destination (charging) of mission 1 can be seen at task 18. The graph shows that the UAV proportionally reduces its velocity as it approaches its destination.

Figures 10 and 11 show some key stages in the simulation for benchmark mission 1. The window at the bottom shows the CRP finding the optimal state-transitions and sending the corresponding actions to the simulator. The window on the left shows the results of the simulator as it performs the actions received from the CRP.

Figure 10, shows the dynamic velocity adjustment of the UAV, derived from the fitness probability, as the UAV approaches its target. This behaviour is used to evaluate performance measure 2.

As the UAV approaches its target, \({ \Pr }\left( {{\varphi }_{\text{i}}^{\text{r}} < {\varphi }_{\text{j}}^{\text{m}} } \right)\) is reduced from 0.3 to 0.25 and the velocity of the UAV (indicated in the window left) is adjusted accordingly from 8.00 to \(2.00 \;{\text{m/s}}\).

Figure 11, shows the successful completion of the mission. This behaviour is used to evaluate performance measure 1.

When the UAV reached its target destination (the charging point), it descends and successfully completes the mission.

6.2 Benchmark mission 2: results

Figure 12 shows the resulting FSA for benchmark mission 2, dynamically learned by the CRP from the KB (Table 3), during the execution of the mission. The node in bold shows the start state, i.e. Motors Off.

Figure 13 provides a “zoomed” view showing the “fly” state-transitions, and corresponding fitness for each, generated by the CRP.

The graph in Fig. 14 shows the dynamic velocity control, derived from the state-transition fitness. The graph shows the corresponding reduction in velocity every time the UAV near its target.

On the graph, the three target destinations (collection, delivery and charging) of the missions can be seen at tasks 7, 15, and 21. The graph shows that the UAV proportionally reduces its velocity as it approaches each of the destinations.

Figures 15 and 16 shows some key stages in the simulation for benchmark mission 2. Figure 15 shows the UAV in process of collecting its cargo.

Figure 16 shows the UAV adjusting its velocity in accordance with the fitness of the state-transition, fly.

Figure 17 shows the UAV successfully delivering its cargo.

6.3 Discussion

6.3.1 Performance

Overall, the experimental results (Figs. 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17) shows that our approach works well for real-time knowledge optimization for high-level control in cognitive robotics.

Fig. 10
figure 10

UAV reducing its velocity as it approaches its target destination

Full size image
Fig. 11
figure 11

UAV reaching its destination and completing the mission

Full size image
Fig. 12
figure 12

FSA learned for benchmark mission 2

Full size image
Fig. 13
figure 13

A “zoomed” image of the iterative “fly” transition generated during mission 2

Full size image
Fig. 14
figure 14

Dynamic velocity adjustment during mission 2

Full size image
Fig. 15
figure 15

UAV collecting its cargo at the collection point

Full size image
Fig. 16
figure 16

UAV reducing its velocity as it approaches its target destination

Full size image
Fig. 17
figure 17

UAV successfully delivering its cargo

Full size image

The simulation was executed repeatedly, with consistent results. Figures 7 and 8 (for benchmark mission 1) and Figs. 12 and 13 (for benchmark mission 2) shows that the approach successfully executed the expert-defined missions. This success was also observed during the simulation. Figures 9 and 14, for benchmark mission 1 and 2 respectively, shows the successful reasoning for velocity control, using statistical reasoning. The figures show the corresponding velocity adjustment, based on the fitness (probability) which is also shown in the zoomed Figs. 8 and 13 for the “fly” action.

In addition, conducting the experiments also showed the following general benefits:

  • The approach is less error prone and requires less bandwidth to maintain because, in our approach, knowledge and missions are defined using a simple structure. The trigger formula of state-transitions is constructed as a simple conjunction of propositions, and is therefore more intuitive to the domain expert. Moreover, the knowledgebase and missions can be modified independently, reducing errors during the updating process.

  • There is no re-learning of complex statistical reasoning models or networks whenever the knowledge or evidence changes because, in our approach, potential solutions are evaluated in real-time and a statistical model for reasoning is generated in real-time by the MEP.

  • Autonomous behaviour can be controlled more effectively because in our approach, the probabilities and marginal probabilities provided by the AEFQ algorithm enables a finer control of the statistical fitness evaluations of the state-transitions.

  • The high-level control provided by the CRP is more representative of human cognition, because in our approach, the OWA is followed. This means the action of a state-transition may be less probable, but not impossible. This gives the CRP powerful reasoning capabilities.

  • The fitness of a state-transition is a true representation of the environment because, the MEP applied in our approach, guarantees an accurate probability assignment, based only on the constraint averages derived from the mission constraints and environmental evidence. There are no other subjective control parameters or bias in the fitness quantification.

6.3.2 Time efficiency

The objective of this study is the real-time, high-level control provided by the CRP. Therefore, the time efficiency of the CRP, i.e. the time taken by the AE-SPSO to find an optimal solution for a mission task, is evaluated. Optimization algorithms, including the PSO algorithm, is known for the extensive time it takes to converge on an optimum. This is especially true for large, multi-dimensional and real search spaces. However, in our approach, the search space is finite and discrete, allowing the AE-SPSO to find optimal solutions in acceptable and sufficient time. Moreover, the control parameters of the AE-SPSO makes it easy to scale the performance of the PSO when the search space increases.

Figure 18 shows the time the CRP took to find an optimal solution for each of the tasks of each mission.

Fig. 18
figure 18

CRP time of benchmark missions

Full size image

The average CRP time for benchmark mission 1 was 0.0785 s and for benchmark mission 2, the average CRP time was 0.1477 s. These times were found to be completely suitable for the high-level control of the UAV, while executing its missions.

The behaviour of the UAV in both benchmark missions is demonstrated in the accompanying videos [35, 36].

6.3.3 Simulation constraints

The performance of the UAV may appear slow in the videos. This is because the complex integration architecture of the AirSim simulator and the Unity games engine is not optimal and causes a considerable time lag between the simulator and the games engine. It was observed that, at high velocity, the UAV would overshoot its target destination in the Unity games engine. This resulted in the target position parameters reported by the AirSim to be inconsistent from that reported by the games engine. This caused the UAV to wrongly interpret its position and therefore miss its objectives.

To improve the performance, a delay was explicitly implemented between the execution of mission tasks, in order to give the games engine and simulator time to synchronise. Assisted by the explicit delay, the UAV would autonomously correct its positioning, by repeating the task (see Figs. 8 and 13), while constantly reducing its velocity according to the fitness of the task. At low velocity, the positioning of the UAV was quite accurate and it could achieve its objectives. With the autonomous velocity control, the UAV was able to successfully reach the charging station in benchmark mission 1 and was able to successfully collect and deliver its cargo in benchmark mission 2. It should be noted that this is a simulation problem which, is unlikely to occur in a real-world scenario.

7 Conclusion and future work

In real-world scenarios, semi-autonomous systems, such as exploratory robots, operate in environments which may constantly change. Therefore, it must be trivial and computationally inexpensive to alter a robot’s behaviour, by updating its KB and/or mission objectives in real-time. This is especially important for remotely deployed robotic systems, such as extra-terrestrial exploration robots, where communication time and bandwidth are at a premium.

In this research study, an approach which combines expert knowledge and a cognitive reasoning process was introduced. The approach simplifies the management of the knowledgebase by domain experts, while providing the system with autonomous reasoning, by optimizing the knowledge, given the real-time environmental knowledge. The approach presented here introduces a simple knowledgebase structure, which is easy to maintain and less error-prone. The results of the research also show that, the robot can successfully execute its missions by optimizing the expert-provided knowledge and dynamically and progressively generating and executing a high-level controller.

Further study could extend this approach by investigating multi-objective knowledge optimization in order to generate parallel FSA’s with specific sub-task objectives. This will be useful for high-level control of a robotic system with multiple capabilities. For example, a FSA for flight-control, a FSA for camera control and a FSA for gripper control.