1 Introduction

Rolling element bearings are widely used in rotating machinery as supporting components, it has the functions of bearing support, guiding positioning, reducing resistance and energy saving, eliminating vibration and noise reduction, etc. but it is also one of the most commonly fault sources of mechanical equipment [1]. The smooth and quiet running of rolling bearings will directly affect the precision, performance and the reliability of the mechanical system [2], if the fault features information can be effectively extracted at the early stage, and accurately identifying the running state of the bearing, timely replace or repair the damaged bearings, effectively avoid cascading failures, has a great significance for reducing economic losses [3,4,5].

The defects of rolling bearings can be divided into two categories: distributed defects and localized defects [6]. The distributed defects are mainly surface roughness, waviness, misalignment of raceway and off-size rolling elements, etc. These defects are mainly caused by manufacturing errors, improper installation or abrasive wear, which are difficult to monitor [7]. The localized defects mainly include cracks, concave points and peeling off on the surface of balls or raceways. The main reason of these faults is the long-term running of roller bearings, which can be diagnosed by monitoring in the early stage of the faults [8]. When the local defect on the bearing interacting with their matching elements, the contact stress at the interface changes abruptly, resulting in a very short duration of pulse, the pulse generates vibration and noise [9], and it can monitor the existence of defects in bearings. Then the localized defects can be diagnosed and monitored in the early stage. The dominant mode of failure of the rolling bearing is spalling, that a fatigue crack begins the subsurface of the metal and propagates towards the surface until a piece of metal block breaks away from the raceways or ball to produce a small pit or spall, that is, the fatigue spalling. The data source for the bearing condition-monitoring (CM) program can be classified as vibration information, temperature information, noise information, voltage information, lubricating oil information, etc. [10, 11], and the vibration information data has been the most widely used for fault diagnosis of bearing.

The dynamic modeling of the bearing can be used to predict the dynamic performance of the bearing system, and the theoretical model of the bearing with local defects can improve our understanding of the vibration generated when the incipient fault occurs [12]. The contact force and contact deformation between the ball and the inner and outer raceways satisfy the Hertz contact theory [13]. Nonlinear restoring force between ball and raceways can be changed due to the change of bearing clearance, due to the existence of local defects, when the local defect on the bearing element is interacting with their matching elements, the clearance at the interface will changes abruptly, and the nonlinearity of the clearance will bring complex nonlinear response to the system; the stiffness of the bearing changes when each of the balls enters and leaves the load area, the vibration induced by time-varying stiffness is usually called VC vibration [14], which can cause time-varying stiffness parametrically excited vibration. Therefore, ball bearing contains three basic nonlinear factors, namely, bearing clearance, varying compliance and Hertz contact between balls and raceways, which bring complex nonlinear dynamic behavior to the system [15]. Shock vibration will occur when the bearing is damaged locally. Researchers usually use pulse sequence to simulate vibration shock, and the mechanism of vibration caused by defects is rarely studied [16]. This article is based on contact dynamics, deeply studied the mechanism of nonlinear vibration, taking the three nonlinear relationships as the vibration sources, to established a dynamic model when the bearing outer race, inner race or the ball with local damage. The validity of the model is verified by comparing the time-domain and frequency-domain characteristics of the simulated vibration signals with the experimental vibration signals.

2 Dynamic model of faultless bearing

No matter what kind of defect it is, the impact force occurs only when the defect is exposed to a certain pressure and contact with other contact surfaces, moreover, the frequency of the impact force produced by the surface defects of the inner race corresponds to the frequency of the ball passing through the inner race. The frequency of the impact force generated by the surface defect of the outer race corresponds to the frequency of the ball passing through the outer race. When the surface of the ball has defects, rotation and revolution occur simultaneously, the frequency of the impact force generated by the ball surface defect is more complex, where assumed that the center of the ball defect is always in the revolution plane, they are always contacted with the inner/outer raceways. When the bearing is running, assumed that the outer race is fixed in a rigid support and the inner race rotates with the rotating shaft, the fault frequencies are given by the following expressions:

Ball-pass frequency at outer race (BPFO)

$$f_{o} = \frac{Z}{2}\frac{n}{60}\left( {1 - \frac{D}{{d_{m} }}\cos \alpha } \right).$$
(1)

Ball-pass frequency at inner race (BPFI)

$$f_{i} = \frac{Z}{2}\frac{n}{60}\left( {1 + \frac{D}{{d_{m} }}\cos \alpha } \right).$$
(2)

Ball-spin frequency (BSF)

$$f_{b} = \frac{{d_{m} }}{D}\frac{n}{60}\left( {1 - \left( {\frac{D}{{d_{m} }}\cos \alpha } \right)^{2} } \right).$$
(3)

Fundamental train frequency (FTF)

$$f_{c} = \frac{1}{2}\frac{n}{60}\left( {1 - \frac{D}{{d_{m} }}\cos \alpha } \right).$$
(4)

The above frequencies are called defect frequency of bearings, and the defects will cause the increase of vibration energy at the defects frequencies. Bearings running at normal speeds, the frequency of defects is generally located in the low-frequency range [17]. In the actual working, the frequency of the ball slipping or slipping in the raceway may be slightly different from the calculated value [18].

2.1 Calculating the contact force

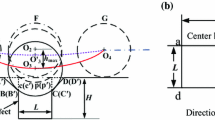
The rolling element bearing is composed of inner race, outer race, rolling element and the cage, assuming that the outer race of the bearing is fixed in a rigid support, and the inner race rotates with the rotating shaft. Due to the existence of radial load in the bearing, there will be contact deformation between the ball and the inner/outer raceways, it can be considered as a pair of series spring–damper system [19], the simplified model of the bearing is shown in Fig. 1.

Fig. 1
figure 1

Simplified model of bearing

Full size image

When the bearing running, the deflections of the bearing in the x- and y-axis directions is x and y respectively, assumed that the initial radial clearance is \(P_{d}\), the depth of the rolling body falling into the defect is u, the angular speed of bearing rotor is \(\omega_{s}\), the initial azimuth angle of the first ball is \(\theta_{o0}\), the radial deflection of the contact between the i-th ball and the race at angle \(\theta_{i}\) is \(\delta_{i}\).

$$\delta_{i} = x\cos (\theta_{i} ) + y\sin (\theta_{i} ) - P_{d} - u,$$
(5)
$$\theta_{i} = \omega_{s} t + \frac{2\pi (i - 1)}{Z} + \theta_{o0} .$$
(6)

According to the Hertz contact deformation theory [20], the contact load produced by i-th ball and the raceway is

$$\left\{ {\begin{array}{*{20}l} {F_{i} = K\delta_{i}^{n} } \hfill & {\quad \delta_{i} > 0,} \hfill \\ {F_{i} = 0} \hfill & {\quad \delta_{i} \le 0.} \hfill \\ \end{array} } \right.$$
(7)

where \(\delta_{i}\) is the radial contact deflection, n is the load–deflection exponent, n = 3/2 for ball bearing and n = 10/9 for roller bearing. The load–deflection factor K depends on the contact geometry.

$$K = \left[ {\frac{1}{{\left( {1/k_{i} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 n}}\right.\kern-0pt} \!\lower0.7ex\hbox{$n$}}}} + \left( {1/k_{o} } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 n}}\right.\kern-0pt} \!\lower0.7ex\hbox{$n$}}}} }}} \right]^{n} .$$
(8)

When the rolling element and the raceway are the same material,

$$K_{i} = K_{o} = \frac{2\sqrt 2 E}{{3\left( {1 - \upsilon^{2} } \right)}} \times \sum {\rho^{{\frac{1}{2}}} } \times \left( {\rho^{*} } \right)^{{ - \frac{3}{2}}} .$$
(9)

where \(\upsilon\) Poisson ratio, \(E\) is the modulus of elasticity, \(\sum \rho\) is the curvature sum. The components of the contact pressure \(F_{i}\) in the X and Y directions are respectively.

$$\left\{ \begin{aligned} F_{ix} = F_{i} \cos (\theta_{i} ), \hfill \\ F_{iy} = F_{i} \sin (\theta_{i} ). \hfill \\ \end{aligned} \right.$$
(10)

The total bearing force produced by rolling bearings in x and y directions are as follows:

$$\left\{ \begin{array}{ll} F_{x} = \mathop \sum \nolimits_{i = 1}^{Z} K[x\cos (\theta_{i} ) + y\sin (\theta_{i} ) - P_{d} - u_{i} ]^{3/2} \cos (\theta_{i} ), \hfill \\ F_{y} = \mathop \sum \nolimits_{i = 1}^{Z} K[x\cos (\theta_{i} ) + y\sin (\theta_{i} ) - P_{d} - u_{i} ]^{3/2} \sin (\theta_{i} ). \hfill \\ \end{array} \right.$$
(11)

3 Outer race defect modeling

If there is a local defect in the bearing, the contact stress between the contact surfaces will change abruptly when the defect comes into contact with the contact element, and then impact vibration will occur. A local fault produces a pulse with the same repetition rate as the characteristic frequency of the bearing: ball-pass frequency at outer race (BPFO), ball-pass frequency at inner race (BPFI), and twice the ball-spin frequency (2 * BSF). When there is a fault in the outer race of the bearing, the size of the early surface damage is usually very small, assumed that the damage of the outer race is a pitting, with the width of W, depth of d and the injury angle is \(\theta_{0}\), the outer race fault model is shown in Fig. 2.

Fig. 2
figure 2

Simplified model of defect on outer race

Full size image

When a ball passing over the local defect, compared with the normal bearing, the clearance of the bearing will increase rapidly. This will cause the contact load between the ball and the inner/outer raceways suddenly decreases or even unloaded. At this point the bearing will release a certain amount of deformation u, and the maximum deformation is

$$u_{\mathrm{max} } = \frac{D}{2} - \sqrt {\left( {\frac{D}{2}} \right)^{2} - \left( {\frac{w}{2}} \right)^{2} } .$$
(12)

When the depth d is less than the maximum deformation \(u_{max}\), the bearing will release a certain amount of deformation d. When the depth of d is greater than the maximum deformation of \(u_{max}\), the bearing will release a certain amount of deformation \(u_{max}\).

$$\tilde{u} = \left\{ {\begin{array}{*{20}l} {\text{d}} \hfill & {\quad {\text{d}} < u_{\mathrm{max} } ,} \hfill \\ {\frac{D}{2} - \sqrt {\left( {\frac{D}{2}} \right)^{2} - \left( {\frac{w}{2}} \right)^{2} } } \hfill & {\quad {\text{d}} \ge u_{\mathrm{max} } .} \hfill \\ \end{array} } \right.$$
(13)

When the difference between the angular position of the i-th ball and the position of the outer race damage within the range of \(\theta_{0}\), there will be a change in the bearing clearance.

$$u_{o} = \left\{ {\begin{array}{*{20}l} {\tilde{u}} \hfill & {\quad 0 < \bmod \left( {\frac{{\theta_{\mathrm{i}} }}{2\pi }} \right) - \theta_{\mathrm{out}} < \theta_{ 0} ,} \hfill \\ 0 \hfill & {\quad {\text{others}} .} \hfill \\ \end{array} } \right.$$
(14)

The total contact load of the ball acting on the outer race is

$$\left\{ \begin{array}{l} F_{box} = \mathop \sum \nolimits_{i = 1}^{Z} K[x\cos (\theta_{i} ) + y\sin (\theta_{i} ) - P_{d} - u_{oi} ]^{3/2} \cos (\theta_{i} ), \hfill \\ F_{boy} = \mathop \sum \nolimits_{i = 1}^{Z} K[x\cos (\theta_{i} ) + y\sin (\theta_{i} ) - P_{d} - u_{oi} ]^{3/2} \sin (\theta_{i} ). \hfill \\ \end{array} \right.$$
(15)

When the bearing is running, the contact deformation occurs in the load area due to the existence of the radial load. According to Newton’s second law, the equation of motion for a two degree of freedom system is

$$\left\{ \begin{aligned} m_{0} \ddot{x} + C_{x} \dot{x} + F_{box} = F_{r} , \hfill \\ m_{0} \ddot{y} + C_{y} \dot{y} + F_{boy} = mg. \hfill \\ \end{aligned} \right.$$
(16)

The second order nonlinear differential equations are converted into the first order differential equations through the state space variable method to obtain the solution of the equations.

$$\begin{aligned} {\text{Let}} & \quad p_{1} = x,\, p_{2} = \dot{x},\, p_{3} = y,\, p_{4} = \dot{y}. \\ & \quad \dot{p}_{1} = \dot{x} = p_{2} ,\, \dot{p}_{2} = \ddot{x},\, \dot{p}_{3} = \dot{y} = p_{4} ,\, \dot{p}_{4} = \ddot{y}. \\ \end{aligned}$$

Then

$$p = \left\{ {\left. \begin{array}{l} p_{1} \\ p_{2} \\ p_{3} \\ p_{4} \\ \end{array} \right\}} \right. = \left\{ {\left. \begin{array}{l} x \\ {x^{\prime}} \\ y \\ {y^{\prime}} \\ \end{array} \right\}} \right.\quad {\text{and}}\quad p^{\prime} = \left\{ {\left. \begin{array}{l} p^{\prime}_{1} \\ p^{\prime}_{2} \\ p^{\prime}_{3} \\ p^{\prime}_{4} \\ \end{array} \right\}} \right. = \left\{ {\left. \begin{array}{l} p_{2} \\ p^{\prime}_{2} \\ p_{4} \\ p^{\prime}_{4} \\ \end{array} \right\}} \right. = \left\{ {\left. \begin{array}{l} {x^{\prime}} \\ {x^{\prime\prime}} \\ {y^{\prime}} \\ {y^{\prime\prime}} \\ \end{array} \right\}} \right..$$

In order to verify the validity of the proposed model, the simulation results of pitting corrosion on outer race surface are compared with experimental data. In this paper the analysis applied to a 6205-2RS JEM SKF deep groove ball bearing, the bearing geometry, velocity of movement and the size of each defect are listed in Table 1. The mechanical model equations are solved by ODE 45 solver in Matlab–Simulink environment.

Table 1 Geometric and physical properties used for the rolling element bearings
Full size table

According to the formula for calculating the frequency of rolling through the outer race,

$$f_{o} = \frac{Z}{2}\left( {1 - \frac{D}{{d_{m} }}\cos (\alpha )} \right)*f_{s} = \frac{9}{2}\left( {1 - \frac{7.94004}{39.0398}\cos (0)} \right)*\frac{1797}{60} = 107.293.$$
(17)

There are many nonlinear factors in the dynamic model of rolling bearings, therefore, the RKF (Runge–Kutta–Fehlberg) method with variable step-size is used to solve the numerical integration of differential equations, to obtain the dynamic response of the system, use it to study the regularity of rolling bearing vibration with local defects, and the simulation results obtained are shown in Fig. 3.

Fig. 3
figure 3

Simulation results of the outer race with a single-point defect

Full size image

Figure 3 shows the time-domain and the frequency-domain of the vibrations due to outer race with a defect. In the frequency domain, the ball passes frequency of outer race (107.4 Hz) and its harmonic frequency (214.7 Hz, 322.1 Hz, etc.) appeared. In the time domain waveform that in the 0.1 s there are 11 equal intervals of the vibration waveform, is exactly equal to the frequency of rolling through the outer race.

In order to further verify the correctness of the mechanical model, this paper uses the experimental data of Case Western Reserve University electronic engineering laboratory [21] for comparative analysis, and the CWRU bearing test rig is shown in Fig. 4.

Fig. 4
figure 4

Test-rig of the rolling bearing

Full size image

Figure 4 shows the basic layout of the test rig, a 2 horsepower (1 hp = 735 W) reliance electric motor driving a shaft mounted with a torque transducer and encoder, and the torque applied to the shaft obtained by a dynamometer and electronic control system (not shown), the acceleration value was measured along the vertical direction on the housing of the fan end bearing and the drive end bearing (SKF deep-groove ball bearings: 6205-2RS JEM and 6203-2RS JEM). The single point faults diameters of 7 mils, 14 mils, 21 mils, 28 mils, and 40 mils were seeded on the bearings using electro-discharge machining (EDM) at the inner raceway, rolling element and outer raceway, respectively. For fault depth, please refer to fault specifications. When testing, the motor running at a constant speed of 0–3 horsepower (approximate motor speeds of 1797–1720 rpm),and the sample sampling frequency, some tests are 12 kHz, and the others are 48 kHz.

The accuracy of the mechanical model is further verified by comparing the time-domain and frequency-domain characteristics of the vibration signals obtained by the model simulation with the experimental results. The time domain diagram and frequency domain diagram of the outer race fault vibration obtained through the experimental data, as shown in the following Fig. 5.

Fig. 5
figure 5

Experimental results of the outer race with a single-point defect

Full size image

The amplitude of the vibration waveform obtained by the theoretical model and the actual test is quite different, which is because it is difficult to take into account the effects of the whole rotating system and the influence of the external environment on the bearing system in the theoretical model. Within the acceptable range, after comparing, the vibration waveform is basically uniformity, and the frequency is almost the same, which further validates the correctness of the model established in this article.

4 Inner race fault modeling

The modeling method of the inner race fault is similar to that of the outer race fault, except that when the inner race contains local defect, the defect will rotate with the inner race. Therefore, the frequency of the vibration signal obtained by the model should include following frequencies: ball-pass frequency at inner race (BPFI) and its frequency multiplication, the rotation frequency of the inner race, and the side frequency formed by the modulation of the signal.

In order to establish the inner race fault model more conveniently, where assumes that the inner race is stationary, the outer race is rotated with an angular velocity of \(\omega_{s}\) and opposite to the actual rotation direction of the inner race; the revolution angle speed of the ball is \(\omega_{s} - \omega_{c}\), and the direction is opposite to the actual rotation direction of the inner race. In this paper, the vibration of the bearing is regarded as the vibration of the outer race relative to the inner race, and the center of the inner race is set as the coordinate origin, and the two-dimensional bearing coordinate system is set up as shown in Fig. 6.

Fig. 6
figure 6

Simplified model of defect on inner race

Full size image

The revolution angular velocity of a ball is

$$\omega_{s} - \omega_{c} = \frac{1}{2}\left( {1 + \frac{D}{{d_{m} }}\cos (\alpha )} \right)\omega_{s} .$$
(18)

The angle of the i-th ball is

$$\theta_{i} = \left( {\omega_{s} - \omega_{c} } \right)t + \frac{2\pi (i - 1)}{Z} + \theta_{i0} .$$
(19)

The \(\theta_{i0}\) is the initial position angle of the first rolling body, when the inner race with a defect, the x and y directions act on the total contact load of the outer race, and the method is the same as the outer race fault, which is no longer repeated. The two degree of freedom dynamic differential equation of bearing outer race is

$$\left\{ \begin{array}{l} m_{0} \ddot{x} + C_{x} \dot{x} + F_{box} = F_{r} \cos (\omega_{s} t), \hfill \\ m_{0} \ddot{y} + C_{y} \dot{y} + F_{boy} = F_{r} \sin (\omega_{s} t) - mg. \hfill \\ \end{array} \right.$$
(20)

The frequency of the ball passing through the inner race is

$$f_{i} = \frac{Z}{2}\left( {1 + \frac{D}{{d_{m} }}\cos (\alpha )} \right)*f_{s} = 162.185.$$
(21)

Inner race rotation frequency

$$f_{s} = \frac{n}{60} = \frac{1797}{60} = 29.95.$$
(22)

According to the established mechanical model, the time-domain and-frequency domain responses are obtained as shown in Fig. 7.

Fig. 7
figure 7

Simulation results of the inner race with a single-point defect

Full size image

As shown in Fig. 7 that the frequency domain waveform, the ball passing through the outer race frequency of 162.2 Hz and its frequency doubling 324.4 Hz; The rotation frequency of the inner race is 29.88 Hz; the side frequency of the signal modulation is 30 Hz, almost equal to the frequency of the inner race rotation 29.95 Hz. When the outer race of the rolling bearing has a single point defect, there are 8 equal vibration waveforms within the 0.05 s, which is equal to the frequency of the rolling element passing through the inner race.

Using the experimental data analysis, the vibration waveform and its frequency spectrum of the outer race fault obtained from the experimental data are shown in the following Fig. 8.

Fig. 8
figure 8

Experimental results of the inner race with a single-point defect

Full size image

During the actual operation of the bearing, there are many external factors, within the realm of acceptable, after comparing, the waveform is basically uniformity, and the frequency is almost the same, which further validates the correctness of the model established in this article.

5 Rolling element fault modeling

When there is a defect on the rolling element surface, the defect may be contacted with the inner and outer races separately in the rotation of the ball, resulting in two shocks in the loaded area per revolution of the ball about its own axis. However, in practice, it is difficult to establish a real dynamic model with ball faults because of the unpredictability of ball rotation path. In this paper, to simplify the model, it is assumed that the center of the rolling defect is always in the center of the raceway region. In the model, the i-th ball of the rolling bearing has a pitting, where the span angle is \(\theta_{R}\), the angle between the ball and the X axis is \(\theta_{i}\), the position of the fault rolling body in the bearing and the contact between the defect of the rolling body and the inner and outer race are shown in the Fig. 9.

Fig. 9
figure 9

Simplified model of defect on rolling element

Full size image

The angular position \({\uptheta}_{\mathrm{i}}\) of the i-th ball is a function of the angular speed of the cage. Let the initial reference position be \({\uptheta}_{1}\), and the time elapsed t, \({\uptheta}_{\mathrm{i}}\) can be expressed as

$$\theta_{i} = \frac{2\pi (i - 1)}{Z} + \omega_{c} t + \theta_{1} .$$
(23)

Span angle of defect:

$$\theta_{R} = 2*\arcsin (w/D) .$$
(24)

When the rolling defect passes through the inner race, if the inner race surface can exposed to the bottom of the defect, the maximum contact deformation is the fault depth d, if the bottom of the defect cannot be contacted, the maximum contact deformation \(H_{maxi}\) is the sum of the deformation \(H_{ri}\) and the inner deformation \(H_{i}\) of the inner race, assume that the radius of the outer race is \(r_{i}\), and the outer race radius is \(r_{o}\), according to the geometric relation:

$$H_{\mathrm{max} i} = H_{ri} + H_{i} ,$$
(25)
$$H_{ri} = \frac{D}{2} - \sqrt {\left( {\frac{D}{2}} \right)^{2} - \left( {\frac{w}{2}} \right)^{2} } ,$$
(26)
$$H_{i} = r_{i} - \sqrt {r_{i}^{2} - \left( {\frac{w}{2}} \right)^{2} } .$$
(27)

Similarly, when the rolling defect passes through the outer race, if the outer race surface can be exposed to the bottom of the defect, the maximum contact deformation is d of the fault depth; if it cannot contact the bottom of the defect, the maximum contact deformation \(H_{maxo}\) is the difference between the rolling deformation \(H_{ro}\) and the outer race deformation \(H_{o}\), according to the geometric relation:

$$H_{\mathrm{max} o} = H_{ro} - H_{o} ,$$
(28)
$$H_{ro} = \frac{D}{2} - \sqrt {\left( {\frac{D}{2}} \right)^{2} - \left( {\frac{w}{2}} \right)^{2} } ,$$
(29)
$$H_{o} = r_{o} - \sqrt {r_{o}^{2} - \left( {\frac{w}{2}} \right)^{2} } .$$
(30)

Therefore, when the defect is in contact with the inner and outer races, the amount of contact deformation is:

$$\tilde{u} = \left\{ {\begin{array}{*{20}l} d \hfill & {\quad d \le H_{\mathrm{max} k} ,} \hfill \\ {H_{\mathrm{max} k} } \hfill & {\quad d > H_{\mathrm{max} k} ,} \hfill \\ \end{array} } \right.$$
(31)

where \(k = i,o\). The speed of ball about its own axis is

$$\omega_{b} = \frac{{d_{m} }}{2D}\left( {1 - \left( {\frac{D}{{d_{m} }}\cos (\alpha )} \right)^{2} } \right)\omega_{s} ,$$
(32)
$$f_{b} = \frac{{d_{m} }}{2D}\left( {1 - \left( {\frac{D}{{d_{m} }}\cos (\alpha )} \right)^{2} } \right)f_{s} = 70.583815.$$
(33)

The initial position angle of the rolling defect center is \(\theta_{p}\), the center position angle of the rolling defect center is \(\theta_{pt}\), and the rolling body rotates clockwise:

$$\theta_{pt} = \omega_{b} t + \theta_{p} .$$
(34)

When the ball defect is in contact with the outer race

$$u = \left\{ {\begin{array}{*{20}l} {\tilde{u}} \hfill & {\quad 2n_{i} \pi + \theta_{i} \le \omega_{b} t \le 2n_{i} \pi + \theta_{i} + \theta_{R} ,} \hfill \\ 0 \hfill & {\quad others.} \hfill \\ \end{array} } \right.$$
(35)

When the ball defect is in contact with the outer race

$$u = \left\{ {\begin{array}{*{20}l} {\tilde{u}} \hfill & {\quad \left( {2n_{i} \pi + 1} \right) + \theta_{i} \le \omega_{b} t \le \left( {2n_{i} \pi + 1} \right) + \theta_{i} + \theta_{R} ,} \hfill \\ 0 \hfill & {\quad others.} \hfill \\ \end{array} } \right.$$
(36)

When the defect is contacted with the outer race, the number of the self-rotation circles of the ball is

$$n_{i} = {\text{int}} (\omega_{b} t/2\pi ) .$$
(37)

When the defect is contacted with the outer race, the number of the self-rotation circles of the ball is

$$n_{i} = \left\{ {\begin{array}{*{20}l} {\text{int} (\omega_{b} t/2\pi )} \hfill & {\quad \theta_{i} < \pi ,} \hfill \\ {\text{int} (\omega_{b} t/2\pi ) - 1} \hfill & {\quad \theta_{i} \ge \pi .} \hfill \\ \end{array} } \right.$$
(38)

Assumed that the cage is stationary, the outer race rotates in a positive direction with the angular velocity \({\upomega}_{\mathrm{c}}\), so the radial load Fr acting on the outer race also rotates in the positive direction with the angular velocity \({\upomega}_{\mathrm{c}}\). According to Newton’s second law, the vibration differential equation of two degrees of freedom for rolling bearing with single local fault is

$$\left\{ \begin{array}{l} m_{0} \ddot{x} + C_{x} \dot{x} + F_{obx} = F_{r} \cos (\omega_{c} t), \hfill \\ m_{0} \ddot{y} + C_{y} \dot{y} + F_{oby} = F_{r} \sin (\omega_{c} t) - mg. \hfill \\ \end{array} \right.$$
(39)

In the case of both sides are in contact, the theoretical shock frequency of the rolling defect is

$$f_{b} = \frac{{d_{m} }}{D}\left( {1 - \left( {\frac{D}{{d_{m} }}\cos (\alpha )} \right)^{2} } \right)*f_{s} = 141.0751.$$
(40)

Revolution frequency of the ball is

$$f_{c} = \frac{1}{2}\left( {1 - \frac{D}{{d_{m} }}\cos (\alpha )} \right)*f_{s} = 11.9285.$$
(41)

Revolution period of the ball is

$$T_{c} = \frac{1}{{f_{C} }} = 0.08383.$$
(42)

From the picture above

$$T_{\mathrm{half beat}} = X_{O2} - X_{O1} = 0.042,$$
(43)
$$f^{\prime}_{b} = X_{O5} - X_{O3} = 141.1,$$
(44)
$$f^{\prime}_{c} = X_{O5} - X_{O4} = 12.$$
(45)

According to the mathematical model, the dynamic response of the bearing is obtained, the time domain and frequency domain waveform that simulation of the rolling element with a single-point defect is shown in Fig. 10.

Fig. 10
figure 10

simulation results of the rolling element with a single-point defect

Full size image

As is shown on the left of the Fig. 10, when the rolling element has a single point defect, within 0.1 s, there are 14 pairs of equal interval vibration waveform; this is exactly equal to the shock frequency of the rolling body theory; And from the diagram appears the beat, this is due to the results of synthesis of vibration waves at different frequencies, the beat frequency is about 0.084 s, which is equal to the revolution period of the ball.

As can be seen from Fig. 10, the damage frequency of the ball is 141.6 Hz, which is substantially equal to the theoretical value. There are also frequency-doublings, such as 282 Hz for the second-harmonic and 432.6 Hz for the third-harmonic. The side-band frequency is 12 Hz, which is basically equal to the rotational frequency of the ball. The side frequencies also occur in frequency doubling.

The vibration waveform and its frequency spectrum of the outer race fault obtained from the experimental data are shown in the Fig. 11.

Fig. 11
figure 11

Experimental results of the rolling element with a single-point defect

Full size image

When the rolling bearing is in actual work, if the ball fails, the contact between the pitting and the inner and outer race is uncertain, and the external environment has a great impact on the vibration data, so the time domain waveform and frequency domain waveform are very complex, in the acceptable range verified the accuracy of the model. It is noteworthy that some researchers have found that the main response of the system under rolling body fault is the cage frequency and its harmonics [22].

Based on contact dynamics, the mechanism of nonlinear vibration of bearings is analyzed in this manuscript, and the effect of local faults on bearing vibration is obtained. Considering the main factors affecting bearing vibration and neglecting the secondary factors, the nonlinear dynamic model of bearing with local defects is established, which provides a theoretical basis for dynamic analysis and fault vibration of bearing system. The introduction of the local defect into the theoretical model of the bearing can improve our understanding of the vibration caused by the initial fault and provide a reference for the early fault identification.

6 Conclusions

When there is a local defect in the bearing, researchers usually used a short term impulses to represent the reaction when the local defect is interacting with their matching elements, without further study of the structural mechanism that causes vibration. This paper deeply studied the nonlinear vibration mechanism based on the Hertz contact dynamics when there is an internal defect in the inner race, outer race or the ball of rolling element bearing, obtained the relationship between the geometric shape of defects and the deformation that is produced. The ball-raceway contact pair in ball bearing is regarded as a spring–damping system, and the nonlinear dynamic model of bearing is established by considering the nonlinear factors such as bearing clearance, varying compliance and Hertz contact between balls and raceways. Comparison of time-domain and frequency-domain parameters obtained from the mode and the experimental data, verified the validity of this model.