1 Introduction

Water pollution causes serious human health hazards and environmental implications. These heavy metal ions may enter into humans through different routes via water, air or food. Small concentrations of these heavy metal ions have severe toxic effects in living organisms. Cd(II) is one of the toxic heavy metal, whose occurrence is natural and is most extensively concerned because of its non-degradable nature. Cd(II) may exist in aqueous solution as the hydrated ion, as organic complex with humic acid, or as inorganic complexes such as sulphates, carbonates, chlorides [1]. It may enter into aquatic biomes through direct release from industrial operations, seepage from contaminated sites, weathering and erosion of soil and bedrock. The permissible Cd(II) concentration as per the Environmental Protection Agency [2] and World Health Organization [3] in drinking water is 0.005 and 0.003 mg/L respectively.

Kidney and gastrointestinal tract mainly gets affected by oral exposure of cadmium. The half life of cadmium in the kidneys is expected in the range of 10–40 years. The major toxic effect which occurs in kidney is renal tubular proteinuria after long-term exposure of cadmium [4]. Abdominal cramps, headache, muscle cramps, irritation, vomiting, nausea, and diarrhea may be caused by high levels of cadmium. Ingestion of cadmium in human body also leads to itai–itai disease. In bones and joints, it alters calcium and phosphorus metabolism [5]. Cadmium metal is also found to be carcinogenic in nature [6,7,8,9]. However, there is not adequate data to state that cadmium has the potential to cause cancer from chronic exposure through drinking water. Cadmium causes hyperactivity of the nervous system and damages nerve cells. In cardiovascular system, it replaces zinc in arteries, leads to brittle and inflexible arteries [10]. In men, it lowers the sperm counts, causes prostate problems and impotency [11].

The detrimental and toxic effect of heavy metals on living beings and environment has forced the researchers across the world to explore new methods or develop highly efficient adsorbent for the toxic metal ions adsorption from water. Various techniques have been used for heavy metal adsorption from environmental samples such as precipitation, ion exchange, cementation, coagulation, sedimentation, and adsorption [12,13,14]. Among these methods, adsorption is found to be the best technique due to its simple process and economical nature for heavy metals adsorption from solution. A wide variety of adsorbents have been used for cadmium ion removal in past years, however, they have low sorption efficiency and capacity limits [15, 16].

Now-a-days, mesoporous materials have been widely used for adsorption of heavy metal [17, 18]. Mesoporous materials structures can be easily tailored by various surfactants, different reaction conditions, organic chemicals and additives. MCM-41 is a mesoporous silicate having hexagonally packed arrays of uniform distribution of cylindrical pores, large pore volume and specific surface area [19]. This study has been undertaken to optimize the adsorption behaviour of gemini incorporated mesoporous silica (G-MCM-41) for cadmium ions. Response Surface Methodology (RSM) is used for optimizing the adsorption conditions of cadmium ions by G-MCM-41. RSM analyze the interactions between the independent variables and response [20, 21]. The effect of different physiochemical parameters such as pH, heavy metal ion initial concentration and contact time was examined using Box–Behnken design (BBD).

2 Materials and methods

2.1 Optimization of adsorption process

Optimization is a mathematical programming for maximizing or minimizing one or more functions with any possible constraints. It’s an alternative to find best performance by maximizing desired variables and minimizing the undesired one under given constraints. The main purpose of using optimization techniques is to improve the performance by running less number of experiments that reduce the overall cost of experimental work [22, 23].

2.2 Response surface methodology (RSM)

RSM involves a set number of designed experiments to attain a response using a limited number of trials. It is a statistical technique which is appropriate for multi-factor experiments and gives the relationship between various parameters for optimal operation conditions [24, 25]. The number of experiments runs (N) in RSM is given by following equations

$${\text{N}} = 2{\text{K }}\left( {{\text{K}} - 1} \right) \, + {\text{ C}}_{\text{o}}$$
(1)

where K = Number of variables and Co = Centre-point.

The behavior of the system is explained by the following quadratic equation:

$${\text{Y }} = \,\upbeta_{0} + \, \sum^{\text{k}}_{{{\text{i}} = 1}}\upbeta_{\text{i}}\, {\text{x}}_{\text{i}} + \sum^{\text{k}}_{{{\text{i}} = 1}}\upbeta_{\text{ii}}\, {\text{x}}_{\text{i}}^{2} + \, \sum^{\text{k}}_{{1 \le {\text{i}} \le {\text{j}}}}\upbeta_{\text{ij}}\, {\text{x}}_{\text{i}} \,{\text{x}}_{\text{j}} +\upvarepsilon$$
(2)

where Y = Predicted response, β0 = Constant coefficient, βi = Linear coefficient, βii = Quadratic, βij = Interactive coefficients and ε = Error of the model [26].

The response is represented graphically by contour plots and surface plots which shows the interaction effects between the main factors and optimal conditions of the system. Experimental design was generated using Design Expert 7.0.0 software to study the collective effect of four independent input variables by sets of experiments (29), including five replications at the center points. Process parameters had three levels as specified in Table S1. The four mentioned parameters were selected as independent variables while the maximum adsorption capacity was the output response variable. This method helps us to find out the effects of different process parameters on adsorption with minimum number of experiments.

2.3 Preparation of materials

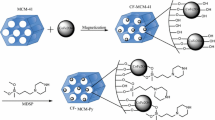
Gemini surfactant 16-6-16 was prepared from N,N-dimethylhexadecylamine with 1,4-dibromobutane at 353.15 K. Mesoporous material based on gemini surfactant, 16-6-16 was prepared by mixing of 0.06 surfactant: 0.65 NaOH: 150 H2O with tetraethoxysilane (TEOS) [27]. Final adsorbent was calcinated in oven at 523 K for 6 h to remove the unwanted materials from the pores of the surfactant based mesoporous material. Stock solution of cadmium concentrations of 20 mg/L, 60 mg/L and 100 mg/L, was prepared using cadmium nitrate. The cadmium concentrations were observed by an atomic adsorption spectrophotometer (AA-6200, Shimadzu). Amount of cadmium adsorbed, qe (mg/g) was calculated using the Eq. (3):

$${\text{q}}_{\text{e}} = \left( {{\text{C}}_{\text{o}} - {\text{C}}_{\text{e}} } \right)\,{\text{V}}/{\text{m}}$$
(3)

where C0 = Initial cadmium amount (mg/L); Ce = Equilibrium cadmium amount (mg/L); V = Volume of cadmium solution (L); and m = Mass of G-MCM-41 (g).

3 Results and discussion

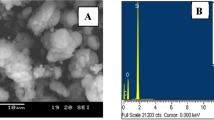
Batch experiments using G-MCM-41 for cadmium ions adsorption has been carried out earlier using conventional method [27]. Scanning electron microscopy (SEM) and X- ray diffraction (XRD) analysis were carried out in previous study for surface structure and crystallinity of G-MCM-41. SEM image showed the vacant sites on the surface of G-MCM-41 which are not uniform in size. After adsorption almost all the adsorption sites are filled confirmed by SEM image [27]. XRD graph shows two sharp peaks at 2θ of 0.5 and 2 indicating the well-ordered hexagonal mesoporous structure. Infra red spectrum shows characteristics bands for the identification of the compounds. The band at 3,436 cm−1 is a characteristic band of Si–OH vibration in micelle templated MCM-41. The sharp peaks at 2922 cm−1, 2855 cm−1 and 1483 cm−1 are the characteristic peaks of asymmetric and symmetric stretching of –CH2 groups in the micelle template. There are considerable changes were observed in the peaks after adsorption of cadmium ions [28].

Traditional method of optimization does not show the combined effects of different input variables. So, the current study used RSM to optimize different variables and to find out the combined effect of different input parameters [29, 30]. Experiments were conducted according to the BBD as given in Table 1 in order to find out the optimum combination of variables for the adsorption of cadmium using G-MCM-41. The experimental domains for different variables with their coded and actual values are shown in Table S1. BBD was applied to analyse the interactive effect of four factors on adsorption capacity. The four factors studied were pH, initial concentration, temperature and contact time for cadmium ions adsorption in the solution. 29 trials were runs according to Box–Behnken design as shown in Table 1.

Table 1 Experimental design in terms of actual factors of Cd(II) ions
Full size table

3.1 Statistical analysis

The quadratic equation for finding the optimal value was attained according to the BBD. The empirical model’s equations between adsorption capacity and input factors in coded terms are given as Eq. (4).

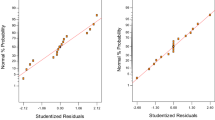
$$\begin{aligned} \% \,{\text{removal}}\,\left( {\text{Cd}} \right) \, & = \, 97 - 18.904{\text{A}} - 4.376{\text{B}} + 14.98{\text{C}} + 5.11{\text{D}} + 9.55{\text{AB}} - 1.5{\text{AD}} - 1.15{\text{AC}} \\ & + \,6.7{\text{BC}} - 3.28{\text{BD}} + 9.54{\text{CD}} - 25.95{\text{A}}^{2} - 25.21{\text{B}}^{2} - 20.25{\text{C}}^{2} - 9.91{\text{D}}^{2} \\ \end{aligned}$$
(4)

The adequacy of the model is determined by the ANOVA. The results from the ANOVA for removal of metal ions are shown in Table S2. The results show that the regression was statistically significant at the F-value 212.15 for cadmium ions and the values of prob > F was < 0.0001 for cadmium ions. Quadratic model was the suggested model with p value > 0.001. Summary statistics shows that the predicted R2 of 0.972 and adjusted R2 of 0.990 was in reasonable agreement with each other (Table 2). Signal to noise ratio was measured by adequate precision. A ratio < 4 is enviable that shows the fitness of the model. The data was also analyzed to check the normal plot of residuals between percentage probability and internally studentized residuals (Fig. 1). The data was also examined to verify the relationship between the experimental and predicted qe as shown in Fig. 2. It is shown in Fig. 2 that the data points were allocated near to the line. It indicates a good correlation between the experimental and predicted qe value. The result also proposed that the quadratic model was most suitable in predicting the response.

Table 2 Model summary statistics
Full size table
Fig. 1
figure 1

Normal plot of residuals

Full size image
Fig. 2
figure 2

Predicted versus actual plot

Full size image

3.2 Response surface plots

The graphical illustration of the response surface of the adsorbed amount of cadmium ions relative to the four variables was used to attain understanding of interactions between variables and validate the optimal level of each variable to a maximum adsorption value [31,32,33]. The surface plots of percentage removal of cadmium versus the pH, contact time, temperature and initial concentration are shown in Figs. 3, 4 and 5. Figure 3a, b illustrates the effect of initial concentration and pH on cadmium ions adsorption by keeping contact time constant at 70 minutes and temperature at 30 °C. There was increase in cadmium ions adsorption with increase in initial concentration up to 60 mg/L and pH 4.5.

Fig. 3
figure 3

Response surface plots a, b initial concentration (mg/L) and pH (contact time = 70 min; temperature = 30 °C); c, d contact time (min) and pH (initial concentration = 60 mg/L; temperature = 30 °C) for cadmium adsorption onto G-MCM-41

Full size image
Fig. 4
figure 4

Response surface plots a, b temperature (°C) and pH (initial concentration = 60 mg/L; contact time = 70 min); c, d temperature (°C) and initial concentration (mg/L) (pH = 5.50; contact time = 70 min) on cadmium adsorption on G-MCM-41

Full size image
Fig. 5
figure 5

Response surface plots a, b temperature (°C) and contact time (min) (pH = 5.50; initial concentration = 60 mg/L); c, d contact time (min) and initial concentration (mg/L) (pH = 5.50; temperature = 30 °C) on cadmium adsorption on G-MCM-41

Full size image

Figure 3c, d represents the effect of contact time and pH on cadmium ions adsorption by keeping initial Cd(II) ions concentration constant at 60 mg/L and temperature at 30 °C. Figure 4a, b represents the effect of pH and temperature on cadmium ions adsorption by keeping initial concentration constant at 60 mg/L and contact time constant at 70 minutes. Figure 4c, d represents the effect of temperature and initial concentration on cadmium ions adsorption by keeping initial pH 5.5 and contact time constant at 70 minutes. Figure 5a, b represents the effect of temperature and contact time on cadmium ions adsorption by keeping initial concentration constant at 60 mg/L and pH 5.5. Figure 5c, d represents the effect of contact time and initial concentration on cadmium ions adsorption by keeping initial pH 5.5 and temperature at 30 °C. It is important to highlight that response surface plots depict the removal up to 98% and can be achieved at initial concentration up to 60 mg/L at pH range 5–5.5, contact time 70–79 minutes, and temperature of 26–30 °C. Desirability function was applied to get optimal conditions for maximum metal ions adsorption. The optimal parameters were obtained for 97.99% removal of cadmium ions at initial concentration 60.16 mg/L, pH 5.09, contact time 78.95 minutes and temperature 26.66 °C (Fig. 6).

Fig. 6
figure 6

Desirability graphs

Full size image

3.3 Comparison study

Comparison of optimization of cadmium adsorption onto different adsorbents using RSM is presented in Table 3. It is practically complicated to evaluate and compare efficiency of one adsorbent to another adsorbent because of different experimental conditions. However, Table 3 gives the general suggestion about the adsorption nature of adsorbent at pH (5–8) and temperature (293–318 K). It is clear from the table that G-MCM-41 showed maximum percentage removal capacity compared to other adsorbents. In other words, it can be concluded that G-MCM-41 possesses good adsorption properties at normal temperature conditions and can be applied as a promising adsorbent for removal of cadmium ions from water.

Table 3 Comparison study of various adsorbents for removal of cadmium ions from water
Full size table

4 Conclusion

Box Behnken design model was successfully applied to find out the effects of important process parameters on the adsorption and then to facilitate the optimization of cadmium ions adsorption by G-MCM-41. Quadratic model was the suggested model by the Box Behnken design model. The predicted and experimental values obtained were showing good agreement between the values with relatively small errors. Process optimization was performed and the optimal parameters were obtained for 97.99% removal of Cd(II) ions at pH 5.09, contact time 78.95 minutes, initial concentration of 60.16 mg/L and temperature of 26.66 °C.