Heat transfer enhancement from an inclined plate through a heat generating and variable porosity porous medium using nanofluids due to solar radiation

Abstract

This work involves the numerical simulation of heat transfer enhancements by magnetohydrodynamic natural convection over an inclined, semi-infinite, non-reflecting, ideally transparent plate embedded in a variable-porosity, heat generating porous medium using nanofluid in the presence of solar radiation effect. The Brinkman extended Darcy model with the Forchheimer inertia term is assumed for the porous medium, while a single-phase model is used for the nanofluid model. Non-similar transformations are used to convert the governing equations to non-similar forms, and then a local non-similar technique is applied to solve the resulting system. Wide ranges of the governing parameter, namely, the heat loss coefficient, the Darcy number, the heat generation/absorption parameter, the magnetic field parameter, the nanoparticle volume fraction and the inclination angle are considered and a validation test is performed. The results show that among all the variable porosity models, M4 is found to be having a largest rate of fluid flow and temperature distributions, while M3 has the lowest. Also, the local Nusselt number is an increasing function of the heat loss coefficient and nanoparticle volume fraction.

1 Introduction

In the recent years, there are great aspects for modeling the non-Darcian transport through the porous media. Transport through the porous media has numerous practical applications including electronic cooling, thermal insulation, petroleum industries and geothermal systems. Vafai and his co-authors have presented early works on the porous media for the convective heat transfer. Vafai and Tien [1] presented the boundary and inertial effects in the fluid flow and convective heat transfer through the porous media. In addition, Vafai and Tien [2] presented the convective mass transfer through the porous media under the effects of the inertial effects. Vafai and Kim [3] obtained a solution for the flow in a porous channel using Brinkman–Forcheimer-extended Darcy model.

In the literature, there are several studies concern the enhanced models of the porous media. The enhanced models were used for simulating flow through packed and fluidized beds. Vafai [4] employed the model of the variable porosity media for the convective flow and heat transfer. Vafai et al. [5] investigated experimentally the heat transfer in the variable porosity media. Poulikakos and Renken [6] studied the effects of the variable porosity, flow inertia and Brinkman friction on the forced convection in a channel filled with porous media. Renken and Poulikakos [7] investigated the effects of the variable porosity on the forced convective heat transfer in the porous media. Hunt and Tien [8] studied the forced convection in fibrous media under the effects of thermal dispersion. Also, Hunt and Tien [9] investigated the non-Darcian convection in the cylindrical packed beds. The non-uniform porosity and thermal dispersion effects on the natural convection has been studied by Hsiao et al. [10]. Hong et al. [11] investigated the effect of the non-Darcian non-uniform porosity on the natural convection in porous media over the vertical-plate. They showed that the heat transfer is enhanced by the increase in dispersion parameter.

In the recent years, there are extensive studies on the hydromagnetic flows and heat transfer in porous media. The reason returns to their several engineering processes including casting, filtration of liquid metals, fusion control and cooling of nuclear reactors. Takhar and Bèg [12] summarized the effects of the magnetic field on the mixed convection flow over a vertical plate saturated with porous medium. Their results indicated that for the positive values of Eckert number, the magnetic field enhances the heat transfer. Chamkha [13] introduced the effects of Hall current on the hydromagnetic free convection on a vertical plate saturated with a porous medium. In addition, there are several studies focus on the natural convection due to the solar radiation. Fathalah and Elsayed [14] considered the natural convection flow due to the solar radiation in view of its possible application in the solar collectors. Chamkha [15] introduced a porous medium for the natural convection flow due to the solar radiation. In addition, Chamkha et al. [16] introduced a variable porosity for the natural convection due to the solar radiation.

Due to the low thermal conductivity of the traditional fluids compared to that of crystalline solids [17]. Hence, there are ideas to enhance thermal conductivity of the base fluid by adding small solid particles in the base fluid. This idea backs Maxwell’s study [18]. Choi and Eastman [19] were firstly introduced the term of the nanofluid. Eastman et al. [20] used nanofluids to enhance heat transfer coefficients of 10–40%. Xuan et al. [21] investigated the thermal conductivity of the nanofluids using the thermal Lattice Boltzmann model. Nield and Kuznetsov [22] studied the problem of Cheng and Minkowycz [23] for the natural convective flows over a vertical flat plate filled with nanofluid and saturated with a porous medium. Chamkha and Aly [24] studied the boundary layer flow of a nanofluid near a porous vertical plate under the effects of magnetic field and heat generation/absorption.

Bhatti et al. [25,26,27,28,29,30] introduced many analytical and numerical studies related to the enhancement heat transfer using nanofluid. Bhatti and Lu [25] introduced analytical study for heat on collision between hydro-elastic solitary waves. Sheikholeslami and Bhatti [29, 30] studied the nanofluid forced convection under the effects of Coulomb force in a porous semi-annulus in the presence of uniform magnetic field. In addition, using the nanofluids in investigation the heat transfer in cases of external and internal flows can be found in [31,32,33,34,35]. Here it should be mentioned that there are semi-analytical methods that can solve this problem [36].

On the other hand, by examinations the study that reported by Fathalah and Elsayed [14], it is found that they neglected the cases of variable porosity, inclined plate, heat generation effects, nanofluids and presence of magnetic field. Also, Chamkha [15] generalized the study of Fathalah and Elsayed [14] by considering the case of the porous media but he neglected the cases of the variable porosity, inclined plate, nanofluids, presence of the magnetic force and heat generation effects. Moreover, according to our knowledge, there are no published studies related to the effect of the solar radiation on the magnetohydrodynamic natural convection over an inclined plate embedded in a variable-porosity with nanofluid. Hence, the purpose of this study is to involve the numerical simulation of the heat transfer enhancements by the magnetohydrodynamic natural convection over an inclined, semi-infinite, ideally transparent plate embedded in a variable-porosity in the presence of the solar radiation effect. The Brinkman extended Darcy model with the Forchheimer inertia term is assumed for the porous medium, while a single-phase model is used for the nanofluid. The governing equations have been transformed to the non-similar forms using Non-similar transformations. Wide ranges of the governing parameter, namely, the heat loss coefficient, Darcy number, heat generation/absorption parameter, nanoparticle volume fraction, magnetic field parameter and an inclination angle are considered. The results show that among all of the variable porosity models, M4 is found to be having the largest rate of the fluid flow and temperature distributions, while M3 has the lowest. In addition, the local Nusselt number is an increasing function of the heat loss coefficient and nanoparticle volume fraction. A validation test is performed compare to the previous published result with well agreement.

2 Problem assumptions and mathematical model

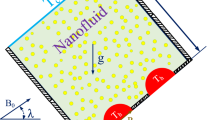
Consider the boundary layer of the flow of magnetohydrodynamic nanofluid over a plate inclined with the angle $\Phi$ embedded in a porous medium. Figure 1 shows the physical model and Cartesian coordinates of the problem. It shows that the x-axis is along the plate and y-axis is normal to it. In the current simulation, the following assumptions are considered:

Fig. 1

Physical model of the problem and coordinates system

• The flow is laminar, two dimensional and steady.

• The nanofluid is viscous, incompressible and electrically conducting.

• The plate is inclined with angle $\Phi$, semi-infinite, non-reflecting, ideally transparent and non-absorbing.

• The intensity of the solar radiation flux is $q^{{\prime \prime }}$ and it penetrates the wall to be absorbed in a homogeneous nanofluid of the absorption coefficient $a_{e}$.

• The heat of the plate is lost to the surroundings by the heat transfer coefficient $R.$

• There is a heat source inside the flow domain with dimensional heat generation/absorption parameter $Q_{0}$.

• All times, there is a magnetic field of strength $\beta_{0}$ affects in the negative $y$ direction.

• For the porous medium, we considered the Darcy model of Brinkman extended with the Forchheimer inertia term.

• The porous medium is isotropic and homogenous and the local thermal equilibrium model between the porous medium and the fluid is applied.

• The non-uniform porosity of the porous medium is considered, while the Joule heating and viscous dissipation effects are ignored.

• The single phase nanofluid model is applied and the LTEM (local thermal equilibrium model) between the fluid and suspended nanoparticle is applied.

• The base fluid is water with $Pr = 6.2$ at 20 °C and copper is the nanoparticles.

• The nanofluid thermophysical properties are presented in Table 1.

  Table 1 Thermo-physical properties for the base fluid and the nanoparticles

• The density of the fluid is approximated via Boussinesq approximation, and all other properties of the fluid are constants.

Taking into account all these assumptions, the continuity, momentum and energy equations can be written as (see Vafai and Tien [1] and Gebhart et al. [37])

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0$$

(1)

$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = \nu_{nf} C_{1} \frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{{\nu_{nf} }}{K\left( y \right)}u - C\left( y \right)u^{2} - \frac{{\sigma_{nf} \beta_{0}^{2} }}{{\rho_{nf} }}u + g\frac{{\left( {\rho \beta } \right)_{nf} }}{{\rho_{nf} }}\left( {T - T_{\infty } } \right)\cos\Phi$$

(2)

$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \frac{{k_{eff} }}{{\left( {\rho C_{p} } \right)_{nf} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{Q_{0} }}{{\left( {\rho C_{p} } \right)_{nf} }}\left( {T - T_{\infty } } \right) + \frac{{a_{e} q^{{\prime \prime }} }}{{\left( {\rho C_{p} } \right)_{nf} }}\exp \left( { - a_{e} y} \right)$$

(3)

Subjected to the following boundary conditions:

$$\begin{aligned} u\left( {x,0} \right) & = v\left( {x,0} \right) = 0, k_{eff} \frac{{\partial T\left( {x,0} \right)}}{\partial y} = R\left( {T\left( {x,y} \right) - T_{\infty } } \right), \\ u\left( {x,\infty } \right) & = 0, T\left( {x,\infty } \right) = T_{\infty } \\ \end{aligned}$$

(4)

In Eqs. (1)–(4), $u$ and $v$ are the velocity components in the $x$- and $y$-directions, $g$ is the gravity acceleration, $T$ is the temperature, $K$ is the permeability, $\nu$ is the kinematic viscosity, $\sigma$ is the electrical conductivity, $\rho$ is the density, $\beta$ is the thermal expansion, $C_{p}$ is the specific heat, and the subscripts $nf, eff$ refer to the nanofluid and effective, respectively.

2.1 Properties of the porous medium

Different models of variable porosity are summarized by Alazmi and Vafai [38] and in this study, it is needed to compare among these models to present a comprehensive study. The following table displays the forms of these models in which the porosity is variable:

Model	$C_{1}$	$\frac{1}{K\left( y \right)}$	$C\left( y \right)$
$M_{1}$	1	$\frac{{150\left( {1 - \varepsilon } \right)^{2} }}{{\varepsilon^{3} d_{p}^{2} }}$	$\frac{{1.75\left( {1 - \varepsilon } \right)}}{{\varepsilon^{3} d_{p} }}$
$M_{2}$	$\frac{1}{\varepsilon }$	$\frac{{150\left( {1 - \varepsilon } \right)^{2} }}{{\varepsilon^{3} d_{p}^{2} }}$	$\frac{{1.75\left( {1 - \varepsilon } \right)}}{{\varepsilon^{3} d_{p} }}$
$M_{3}$	$\frac{1}{\varepsilon }$	$\frac{{150\left( {1 - \varepsilon } \right)^{2} }}{{\varepsilon^{3} d_{p}^{2} }}$	$\frac{{1.75\left( {1 - \varepsilon } \right)}}{{\varepsilon^{2} d_{p} }}$
$M_{4}$	1	$\frac{{150\left( {1 - \varepsilon } \right)^{2} }}{{\varepsilon^{2} d_{p}^{2} }}$	$\frac{{1.75\left( {1 - \varepsilon } \right)}}{{\varepsilon^{2} d_{p} }}$

where $\varepsilon$ is the porosity of the porous medium and in this study it is assumed to be a function of the Cartesian coordinates y as follows:

$$\varepsilon \left( y \right) = \varepsilon_{\infty } \left( {1 + a\,\exp \left[ {\frac{ - by}{{d_{p} }}} \right]} \right)$$

(5)

In Eq. (5) $\varepsilon_{\infty }$ is ambient porosity and a and b are empirical constants that depend on the ratio of the porous bed to particle. In addition, Eq. (5) is an approximate representation of the experimental data reported by Benenati and Brosilow [39] for their study on void fraction distribution in packed beds.

To give a good approximation to the data reported by Benenati and Brosilow [39] for a particle diameter of 4 mm, we chose the values of $\varepsilon_{\infty }$, a, and c employed in the present work as 0.5, 0.98, and 1, respectively.

2.2 Nanofluid properties

Here, a single-phase nanofluid model is employed to the present simulation. In this model the nanoparticle volume fractions is taken as independent variable and the thermophysical properties are taken as function of it. Following Daniel Makinde [40], the nanofluid density, the thermal diffusivity, the dynamic viscosity, the thermal expansion, the heat capacitance, the electrical conductivity, and the thermal conductivity of nanofluid are given as follows:

$$\rho_{nf} = \phi \rho_{p} + \left( {1 - \phi } \right)\rho_{f}$$

(6)

$$\alpha_{nf} = \frac{{k_{eff} }}{{\left( {\rho C_{p} } \right)_{nf} }}$$

(7)

$$\mu_{nf} = \frac{{\mu_{f} }}{{(1 - \phi )^{2.5} }}$$

(8)

$$\left( {\rho \beta } \right)_{nf} = \phi \left( {\rho \beta } \right)_{p} + \left( {1 - \phi } \right)\left( {\rho \beta } \right)_{f}$$

(9)

$$\left( {\rho C} \right)_{nf} = \phi \left( {\rho C} \right)_{p} + \left( {1 - \phi } \right)\left( {\rho C} \right)_{f}$$

(10)

$$\sigma_{nf} = \sigma_{f} \left[ {1 + \frac{{3\left[ {\frac{{\sigma_{s} }}{{\sigma_{f} }} - 1} \right]\phi }}{{\left[ {\frac{{\sigma_{s} }}{{\sigma_{f} }} + 2} \right] - \left[ {\frac{{\sigma_{s} }}{{\sigma_{f} }} - 1} \right]\phi }}} \right]$$

(11)

$$k_{nf} = k_{f} \frac{{\left( {k_{p} + 2k_{f} } \right) - 2\phi (1 + \gamma )^{3} (k_{f} - k_{p} )}}{{\left( {k_{p} + 2k_{f} } \right) + \phi (1 + \gamma )^{3} (k_{f} - k_{p} )}}$$

(12)

In the previous equations, $\phi$ is the solid volume fraction and $\gamma$ is the ratio of nanolayer thickness to nanoparticle radius and thereby accounts for the size dependent nature of thermal conductivity of nanofluids. Here, a nanolayer thickness of 1 nm is considered which corresponds to $\gamma = 0.1$. Also, the subscripts $f, nf$, and $p$ refer to the base fluid, nanofluid and nanoparticles, respectively.

3 Solution of the problem

In this section, non-similar solutions are used to the governing equations. These solutions required to introduce the following transformations as well as the stream functions as:

$$\begin{aligned} &\Psi = \nu_{f} G_{x} F\left( {\xi ,\eta } \right),\quad T = T_{\infty } - \frac{{5xq^{{\prime \prime }} }}{{k_{f} G_{x} }}\theta \left( {\xi ,\eta } \right),\quad \xi = \frac{{G_{x} }}{{G_{a}^{5} }},\quad \eta = \frac{{yG_{x} }}{5x},\quad G_{x} = 5\left[ {\frac{{g\beta_{f} q^{{\prime \prime }} x^{4} }}{{5k_{f} \nu_{f}^{2} }}} \right]^{{\frac{1}{5}}} \\ & \quad G_{a} = 5\left[ {\frac{{g\beta_{f} q^{{\prime \prime }} }}{{5k_{f} \nu_{f}^{2} a_{e}^{4} }}} \right]^{{\frac{1}{5}}} ,\quad u = \frac{{\partial\Psi }}{\partial y},\quad v = - \frac{{\partial\Psi }}{\partial x}. \\ \end{aligned}$$

(13)

where $G_{x}$ is the local Grashof number based on the distance along the plate $x$ and $G_{a}$ is the $G_{a}$ is the Grashof number based on the effective absorption coefficient $a_{e}$. Here, the velocity components take the forms:

$$u = \frac{{\nu_{f} G_{x}^{2} }}{5x}F^{{\prime }}$$

(14)

$$v = - \nu_{f} \frac{{G_{x} }}{5x}\left[ {4F + 4\xi \frac{\partial F}{\partial \xi } - \eta \frac{\partial F}{\partial \eta }} \right]$$

(15)

Substituting Eqs. (13)–(15) into Eqs. (1)–(3), the continuity equation is satisfied identically, while the momentum and energy equations take the following forms:

$$\begin{aligned} & \frac{{\nu_{nf}}}{{\nu_{f}}}F^{{{\prime\prime \prime}}} - 3F^{{{\prime}2}} + 4FF^{{\prime \prime}} + 4\xi \left[{F^{{\prime \prime}} \frac{\partial F}{\partial \xi} - F^{{\prime}} \frac{{\partial F^{{\prime}}}}{\partial \xi}} \right] - 25\xi^{{\frac{1}{2}}} \frac{{\nu_{nf}}}{{\nu_{f}}}\left[{\frac{{150\left({1 - \varepsilon} \right)^{2}}}{{Da^{2} \varepsilon^{3}}} + M^{2} \frac{{\sigma_{nf}}}{{\sigma_{f}}}\frac{{\mu_{f}}}{{\mu_{nf}}}} \right]F^{{\prime}} \\ & \quad - 5\xi^{{\frac{5}{4}}} \left[{\frac{{1.75\left({1 - \varepsilon} \right)G_{a}^{5}}}{{\varepsilon^{3} Da}}} \right]F^{{{\prime}2}} - \frac{{\left({\rho \beta} \right)_{nf}}}{{\rho_{nf} \beta_{f}}}\theta \cos\Phi = 0 \\ \end{aligned}$$

(16)

$$\begin{aligned} & \frac{{k_{eff}}}{{k_{f}}}\frac{{\left({\rho C_{p}} \right)_{f}}}{{\left({\rho C_{p}} \right)_{nf}}}\theta^{{\prime \prime}} + Pr\left[{4F\theta^{{\prime}} - F^{{\prime}} \theta - 4\xi \left[{F^{{\prime}} \frac{\partial \theta}{\partial \xi} - \frac{\partial F}{\partial \xi}\theta^{{\prime}}} \right]} \right] \\ & \quad + \,25\xi^{{\frac{1}{2}}} \frac{{\left({\rho C_{p}} \right)_{f}}}{{\left({\rho C_{p}} \right)_{nf}}}Q\theta - 5\xi^{{\frac{1}{4}}} \frac{{\left({\rho C_{p}} \right)_{f}}}{{\left({\rho C_{p}} \right)_{nf}}}\exp \left({- 5\xi^{{\frac{1}{4}}} \eta} \right) = 0 \\ \end{aligned}$$

(17)

where $Da = a_{e} d_{p}$ is the Darcy number, $M^{2} = \sigma_{f} \beta_{0}^{2} /a_{e} \mu_{f}$ is the magnetic field parameter and $Q = \frac{{Q_{0} }}{{\alpha_{f} a_{e}^{2} \left( {\rho C_{p} } \right)_{f} }}$ is the heat generation absorption parameter, $Pr = \frac{{\nu_{f} }}{{\alpha_{f} }}$ is the Prandtl parameter. Moreover, the non-similar form of the boundary conditions (Eq. 4) is:

$$F\left( {\xi ,0} \right) = F^{{\prime }} \left( {\xi ,0} \right) = 0, \frac{{k_{eff} }}{{k_{f} }}\theta^{{\prime }} \left( {\xi ,0} \right) = 5Rc\xi^{{\frac{1}{4}}} \theta \left( {\xi ,0} \right)$$

(18a)

$$F^{{\prime }} \left( {\xi ,\infty } \right) = 0, \theta \left( {\xi ,\infty } \right) = 0$$

(18b)

In Eq. (18), $Rc = \frac{R}{{k_{f} a_{e} }}$ is the heat loss coefficient. It should be mentioned that wide ranges for $\xi$ and $Rc$ are considered in this study, where, $\xi$ ranging from 0.0001 to 10 and $Rc$ is ranging from 0 to 10. These ranges are due to cover the wide range of the absorption coefficient $a_{e}$ as well as the measurements of Dorsey for the absorption of radiation in water layers with different thickness as stated by Cooper [41]. Note, the absorption coefficient $a_{e}$ depends on the type of absorbing fluid and its degree of colouring or contamination. Also, as mentioned by Fathalah and Elsayed [14], the Dorsey’s data was analyzed using the Beer’s law which takes the form:

$$q_{abs}^{{\prime \prime }} = q^{{\prime \prime }} \left( {1 - exp\left( { - a_{e} y} \right)} \right)$$

(19)

Justification of the ranges of $a_{e}$ and the radiation flux intensity $q^{{\prime \prime }}$ are introduced in the studies presented by Cooper [29] and Fathalah and Elsayed [14].

4 Local Nusselt number

The local Nusselt number based on the absorption parameter is defined by:

$$Nu = \frac{h}{{k_{f} a_{e} }}$$

(20)

where $h$ is the heat transfer coefficient which based on the maximum temperature [14] and it is given by:

$$h = \frac{{q_{u}^{{\prime \prime }} }}{{T_{max} - T_{\infty } }}$$

(21)

Here $q_{u}^{{\prime \prime }}$ is the useful heat gain collected by the absorbing fluid and it can be expressed as:

$$q_{u}^{{\prime \prime }} = q^{{\prime \prime }} - R\left[ {T_{p} - T_{\infty } } \right]$$

(22)

where $T_{p}$ is the plate temperature. Substituting Eq. (22) into Eq. (21), the following form for $h$ is obtained:

$$h = \frac{{q^{{\prime \prime }} }}{{T_{max} - T_{\infty } }} - R\frac{{T_{p} - T_{\infty } }}{{T_{max} - T_{\infty } }}$$

(23)

Inserting Eq. (23) in Eq. (20) and using the non-similar transformations (Eq. 13), the local Nusselt number takes the form:

$$Nu = - \frac{1}{{\theta_{max} }}\left[ {\frac{1}{{5\xi^{1/4} }} + R_{c} \theta_{p} } \right]$$

(24)

5 Numerical solutions and validation

The non-similar Eqs. (16) and (17) with the boundary conditions (18) are solved numerically using the MATLAB function bvp4c. All the details of this method are found in Ahmed and Mahdy [42] and Mahdy and Ahmed [43]. The step size is set as $\Delta \eta = 0.05$ and the convergence criterion of the solution required that the relative difference between two successive iterations be $10^{ - 5}$. The accuracy of this method is checked by valuable comparisons with previously published results in special cases of the current study. Figure 2 shows a comparison of the velocity profiles and temperature distributions for different values of the loss coefficient $Rc$ with those obtained by obtained by Fathalah and Elsayed [14] at $Pr = 6.5, Da = \infty , Q = 0,M = 0,\phi = 0\% ,\Phi = 0,\xi = 0.1$. It is observed that the present results are much closed to those of Fathalah and Elsayed [14].

Fig. 2

comparison of the present results (left) and those obtained by Fathalah and Elsayed [14] (right) at $Pr = 6.5, Da = \infty , Q = 0,M = 0,\phi = 0\% ,\Phi = 0,\xi = 0.1.$

6 Results and discussion

In order to get a clear physical insight, a set of graphical figures is presented and discussed here. The obtained results are plotted in terms of velocity profiles, temperature distributions and local Nusselt number; those are presented for wide ranges of the governing parameters. As stated later, the range of the loss coefficient $Rc$ is chosen between 0 and 10 and this selection to cover the high velocities of wind. Also, the range of heat generation/absorption parameter Q is chosen between − 2 and 3 to represent both the heat generation and the heat absorption cases inside the porous medium. Regarding the ranges of the inclination angle $\Phi$ ($0 \le\Phi \le\uppi/6)$, magnetic field parameter M ($0 \le {\text{M}} \le 5)$ and Darcy number Da ($0.5 \le {\text{Da}} \le 5)$, those are chosen according to the studies reported by Chamkha et al. [16] and Chamkha [15]. The value of $Pr = 6.7$ is selected to represent water at 20 °C and the range of the nanoparticle volume fraction $\phi \left( {0\% \le\upphi \le 6\% } \right)$ to be suitable for the nanofluid thermal conductivity correlation. Additionally, the value of $Ga = 1.25$ is chosen to correspond the radiation flux of 900 W/${\text{m}}^{2}$.

Figure 2 shows the distributions of the porosity of the porous medium along the boundary layer. It is found that the range of $\varepsilon$ considered in this study is between 0.98 at the wall and 0.5 far away from the wall. This figure helps the reader in understanding the behavior of velocity and temperature. In addition Yu and Choi [44] presented a modification for the Maxwell model [45] by including the ratio of nanolayer thickness to nanoparticle radius. Figure 2 displays a comparison between these two models. It is observed that the thermal conductivity obtained by model [44] is greater than that of [45] (Figs. 3, 4).

Fig. 3

Distributions of the porosity through the boundary layer at $\xi = 0.1, Da = 2$

Fig. 4

Comparison of the present model (Yu and Choi model [44]) and Maxwell–Garnett model [45] for the considered range of $\phi .$

Figures 5 and 6 show the velocity profiles and temperature distributions for the different models used for the variable-porosity porous medium. The results indicated that among all these models, M4 gives the high behavior of the velocity and nanofluid temperature and M3 gives the low one. Also, the profiles of M2 and M1 are closed to each other but M2 gives the high rate comparing with M1. These behaviors are attributed to the resistance force resulting from the elements of the porous medium that damps the convective flow and this force in M4 is the smallest one compared with the other model, see Table 1.

Fig. 5

Velocity profiles for different models at $Rc = 5, Ga = 1.25,Da = 5, Q = 1,M = 1,\phi = 2\% ,\Phi = \frac{\pi }{6},\xi = 0.1$

Fig. 6

Temperature distributions for different models at $Rc = 5, Ga = 1.25,Da = 5, Q = 1,M = 1,\phi = 2\% ,\Phi = \frac{\pi }{6},\xi = 0.1$

The influence of the heat loss coefficient $Rc$ on the velocity profiles, temperature distributions and local Nusselt number are depicted in Figs. 7, 8 and 9, respectively. It is clear that in the absence of solar radiation, the maximum value of the temperature occurs at the wall but when the radiation effect is considered, the maximum temperature occurs inside the nanofluid not on the wall. The physical explanations of this effect are due to absorption of the radiation by the nanofluid and the ideally transparent wall can only heated via the absorbing nanofluid. Also, this description interprets the overshot in the velocity behavior near the wall in which occurs the maximum temperature. In addition, it is observed that the increase in $Rc$ causes a reduction in the velocity profiles and the maximum temperature. Consequently the local Nusselt number is enhanced for all models as Rc increases.

Fig. 7

Velocity profiles for different values of $Rc$ at $M1, Ga = 1.25,Da = 2, Q = 1,M = 1,\phi = 2\% ,\Phi = \frac{\pi }{6},\xi = 0.1$

Fig. 8

Temperature distributions for different values of $Rc$ at $M1, Ga = 1.25,Da = 2, Q = 1,M = 1,\phi = 2\% ,\Phi = \frac{\pi }{6},\xi = 0.1$

Fig. 9

Effects of the heat loss coefficient on the local Nusselt number for different models at $Da = 2, Ga = 1.25, Q = 1,M = 1,\phi = 2\% ,\Phi = \frac{\pi }{6},\xi = 0.1$

Figures 10 and 11 determine the velocity profiles and temperature distributions for the variations of the nanoparticle volume fraction $\phi$. It of noted that the increase in $\phi$ reduces both the velocity and temperature. This is because the viscosity of the nanofluid increases by addition the nanoparticles (i.e. increase of $\phi$) which slowdown the velocity. Like the effect of $\phi$ on the velocity profiles, the presence of magnetic field acts as a retarding force to the fluid flow. As it can be seen in Fig. 12, the increase in M reduces the profiles of F′. However, the maximum temperature increases, slightly, as M increases, as it can be observed in Fig. 13. This is because of the Lorentz force resulting from the presence of magnetic field which heated up the nanofluid.

Fig. 10

Velocity profiles for different values of $\phi$ at $M1, Rc = 5,Ga = 1.25,Da = 2, Q = 1,M = 1,\Phi = \frac{\pi }{6},\xi = 0.1$

Fig. 11

Temperature distributions for different values of $\phi$ at $M1, Rc = 5,Ga = 1.25,Da = 2, Q = 1,M = 1,\Phi = \frac{\pi }{6},\xi = 0.1$

Fig. 12

Velocity profiles for different values of $M$ at $M1, Rc = 5,Ga = 1.25,Da = 2, Q = 1,M = 1,\phi = 2\% ,\Phi = \frac{\pi }{6},\xi = 0.1$

Fig. 13

Temperature distributions for different values of $M$ at $M1, Rc = 5,Ga = 1.25,Da = 2, Q = 1,\phi = 2\% ,\Phi = \frac{\pi }{6},\xi = 0.1$

Figures 14 and 15 illustrate the profiles of velocity and temperature for different values of the heat generation/absorption parameter Q. The results revealed that both the velocity and temperature increase gradually as Q increases indicating to a good natural convection by increasing Q. This behavior is anticipated because the increase in Q means an additional heat in the nanofluid which makes the fluid flow rapidly.

Fig. 14

Velocity profiles for different values of $Q$ at $M1, Rc = 5,Ga = 1.25,Da = 2, Q = 1,M = 1,\phi = 2\% ,\Phi = \frac{\pi }{6},\xi = 0.001$

Fig. 15

Temperature distributions for different values of $Q$ at $M1, Rc = 5,Ga = 1.25,Da = 2, Q = 1,M = 1,\phi = 2\% ,\Phi = \frac{\pi }{6},\xi = 0.001$

The effects of the inclination angle of the plate on the velocity and temperature are examined with the help of Figs. 16 and 17. It is found that the increase in the inclination angle causes an increase in the thermal buoyancy effect and hence the velocity profiles and maximum temperature are enhanced. This behavior is observed for $\Phi \le \pi /4$, however more increase in $\Phi$ leads to reduce the velocity and temperature profiles.

Fig. 16

Velocity profiles for different values of $\Phi$ at $M1, Ga = 1.25,Da = 2, Q = 1,M = 1,\phi = 2\% ,\Phi = \frac{\pi }{6},\xi = 0.1$

Fig. 17

Velocity profiles for different values of $\Phi$ at $M1, Ga = 1.25,Da = 2, Q = 1,M = 1,\phi = 2\% ,\Phi = \frac{\pi }{6},\xi = 0.1$

Figure 18 focuses on the effect of variation of Darcy number Da on the velocity profiles. It observed that the behavior of $F^{{\prime }}$ at the values of $Da < 1$ larger than those of $Da \ge 1$. Also, the behaviors correspond the values of $Da \ge 1$ are closed to each other. On the other hand the increase in Da causes a decrease in the behaviors of velocity pointing an enhancement in rate of heat transfer. To explain these behaviors, it should be mentioned to the definition of Da ($Da = a_{e} d_{p} )$. It depends on the diameter of the porous medium’s element. Therefore the increase in $Da$ means the increase in $d_{p}$ which brings much resistance to the flow and hence F’ decreases.

Fig. 18

Velocity profiles for different values of $Da$ at $M1, Ga = 1.25,Da = 2, Q = 1,M = 1,\phi = 2\% ,\Phi = \frac{\pi }{6},\xi = 0.2.$

7 Conclusions

Steady-state natural convection and heat transfer over an inclined plate through a heat generating and variable porosity porous medium in the presence of solar radiation using nanofluids have been, numerically, investigated in this study. The used nanofluid consists of Cu-nanoparticles suspended in water at 20 °C. The Brinkman extended Darcy model was considered to simulate the porous medium and four models for the variable porosity were taken into account. Based on the findings of this study, it can be concluded that:

• M4 gives the largest values of the velocity and temperature while M3 gives the lowest values.

• The increase in the loss coefficient decreases the velocity profiles while it increases the local Nusselt number.

• The increase in the nanoparticles volume fraction causes a reduction in the profiles of velocity and temperature while it enhances the local Nusselt number.

• As the magnetic parameter increases, the velocity profiles decreases but the local temperature is enhanced.

• The local Nusselt number is an increasing function of Darcy number, heat generation/absorption parameter, inclination angle and magnetic field parameter.