1 Introduction

The intelligent transportation system is a popular research topic to deal with the traffic congestion. Several applications are proposed, e.g., variable speed limits [1], intelligent intersection control [2], cooperative lane change control [3]. Those applications benefit from the popularity of connected vehicle technology, such as vehicle to vehicle (V2V) and vehicle to infrastructure (V2I). Cooperative adaptive cruise control (CACC) based on vehicle connectivity is a valuable technology that can significantly improve traffic throughput [4, 5]. Compared with the adaptive cruise control (ACC), the CACC controller has access to more information about the surrounding environment. Several communication topological structures are designed in the literature to improve the performance of the CACC, e.g., leader-predecessor following [6], two-predecessor following [7] and bidirectional following [8]. CACC technology decreases the time headway while ensuring comfort and safety.

When multiple vehicles equipped with CACC are following each other in the same lane, two requirements should be fully considered in the design process: keeping a suitable distance with the preceding vehicle and attenuating the disturbance along with the platoon.

To the best knowledge of the authors, three following distance strategies are commonly applied in the literature. References [9, 10] utilize the constant headway to design the CACC controller. This distance strategy improves the traffic efficiency to some extent, but it is unsafe to use the constant headway at high speeds, and it is proved that the constant headway following strategy cannot guarantee the string stability. References [11, 12] adopt the nonlinear following strategy. This following strategy reflects the requirement at different speeds well and guarantees the string stability with suitable control parameters. Its disadvantage is that this strategy is more complex than the constant time headway following strategy. The constant time headway strategy guarantees safety at a high speed and ensures traffic efficiency at a low speed [13,14,15]. Furthermore, the drivers can choose the preferred time headway conveniently. After selecting the following strategy, internal stability is required to keep the desired distance with acceptably small following errors. Routh–Hurwitz is adopted in Ref. [9], which guarantees internal stability by making sure that poles have negative real part. However, this approach ignores the convergence performance. Reference [16] replaces the left half of the s-plane by the designed \({\mathcal{D}}\)-region, which proposes the bandwidth, damping ratio and desired settling time instead of only absolute stability. Another shortcoming of most literature is that they ignore the effect of feedforward control on reducing the following errors [13, 17, 18], and the feedforward gain is selected as a constant. To sum up, two steps are adopted in this paper to follow at the desired distance with acceptably small following errors: optimizing the feedforward loop to reduce the matching errors and optimizing the feedback loop to guarantee \({ \mathcal{D}}\)-stability.

The most critical difference between CACC and ACC is that CACC can attenuate the disturbance along with the platoon, which is guaranteed by string stability design. Contrary to traditional stability definitions for dynamic systems concentrating on the evolution of system responses over time, string stability of a vehicular platoon mainly depends on the propagation of system states along with the platoon. Consequently, string stability is interpreted as asymptotic stability of interconnected systems in References [19]. Various definitions of string stability have been proposed in the literature using time-domain, frequency-domain and z-domain frameworks. The most famous approach is Lp string stability, which is borrowed from the networked control system literature [20, 21]. String stability is defined as the amplification or attenuation of signals along with the platoon, which can be quantified by the magnitude of transfer functions between the leading vehicle and its followers. Thus, to keep the string stability of the platoon the following expression has to be satisfied

$$\left| {\varGamma \left( {j\omega } \right)} \right| = \left| {\frac{{X_{i} \left( {j\omega } \right)}}{{X_{i - 1} \left( {j\omega } \right)}}} \right| \le 1, \forall \omega$$
(1)

Here, the term \(X_{i} \left( {j\omega } \right)\) denotes the Laplace transform of acceleration at time t. To deal with string stability, \({\mathcal{H}}_{\infty }\) approach is applied in Ref. [22], and some optimization approaches are adopted in Refs. [11, 13]. These approaches only give one set of suitable or optimized control parameters. In the real-world application, it is difficult to co-design with the low-level controller. The parameter space approach overcomes this disadvantage by giving room to adjust the trade-offs at the low-level controller design phase [17, 23]. This approach reflects the design requirements in the s-plane and gives the feasible region in the parameter space.

In this study, the hierarchical structure is applied, where the CACC controller is designed to determine the desired acceleration and the longitudinal tracking controller is applied to control the throttle and brake of the visual vehicle in the CarSim. Furthermore, the mode switching strategy is proposed in the longitudinal tracking controller to achieve smooth and suitable mode switch between the throttle and brake adjustment. The main contribution of this paper is that the parameter space approach is applied to optimize the CACC controller considering the effect of communication time delay. The feasible region of control parameters is graphically represented in the parameter space, where the internal stability and the string stability are guaranteed. This method gives the selection range of control parameters diagrammatically and demonstrates the effect of communication time delay intuitively. The effectiveness of this approach is verified in the simplified acceleration/stop scenario. Another realistic evaluation contribution is that a CarSim/Simulink co-simulation is introduced to verify the rationality of the CACC controller with the impact of the complex longitudinal dynamic and the performance of the longitudinal tracking controller.

The rest of this paper is organized as follows. Section 2 illustrates the hierarchical control framework, which includes the CACC controller and the longitudinal tracking controller. Section 3 builds the control block with simplified vehicle dynamic and analyzes the internal stability and string stability of the CACC controller using the parameter space approach. Section 4 verifies the effectiveness of the CACC controller in a simplified speed-up and stop scenario and introduces a CarSim/Simulink co-simulation to verify the rationality of the CACC controller in the real vehicular platoon application. Section 5 ends this study with conclusions.

2 Control Framework

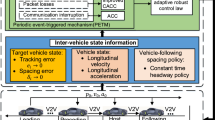
The hierarchical structure is widely used in control, as it simplifies the design process and reduces the interaction. The hierarchical control structure is applied in this paper to achieve homogenous platoon control. As shown in Fig. 1, CACC controller is designed to determine the desired acceleration, and longitudinal tracking controller is designed to follow the desired acceleration accurately.

Fig. 1
figure 1

The control framework of the homogeneous platoon control

Full size image

2.1 CACC Controller Design

The primary objective of the CACC controller is determining the desired acceleration to follow the preceding vehicle with the designed headway.

When the constant time headway strategy is applied to decide the desired following distance \(d_{i}^{*}\) of vehicle i, the following errors can be expressed as

$$e_{i} = d_{i} - d_{i}^{*} = d_{i} - \left( {r + h*v_{i} } \right)$$
(2)

where r is the desired space when the vehicle is stationary; h is the headway-time constant;\(v_{i}\) is the velocity of the considered vehicle; and \(d_{i}\) is the distance between vehicle i and its proceeding vehicle.

Owing to the simultaneous requirements of following the state of the preceding vehicle and keeping the desired distance, the onboard sensor is used to detect the distance with the preceding vehicle and the vehicular ad-hoc networks (VANET) is adopted to receive the acceleration of the preceding vehicle. Then, the desired acceleration of the ego vehicle can be projected by the feedforward of the acceleration of the preceding vehicle \(a_{i - 1}\) and the feedback of the following errors \(e_{i}\), as given in Eq. (3).

$$u_{i} \left( {\text{t}} \right) = k_{\text{p}} e_{i} \left( t \right) + k_{\text{v}} \dot{e}_{i} \left( t \right) + k_{\text{a}} a_{i - 1} \left( {t - \sigma } \right)$$
(3)

in which \(u_{i}\) is the desired acceleration of the ego vehicle; \(\sigma\) is the communication time delay of the VANET; and \(k_{\text{p}} , k_{\text{v}} , k_{\text{a}}\) are the control gains which are designed in Sect. 3.

The commonly used CACC controllers in the literature transmit the position, velocity and acceleration all by VANET. This method has three disadvantages:

  1. (1)

    It has high requirements for GPS accuracy or needs the support of high-resolution maps.

  2. (2)

    It brings the communication time delay and other bad influence of nonideal communication conditions into the detecting of the following errors.

  3. (3)

    It owns a variety of limited communication resources.

However, in the CACC controller designed in this paper, the advantages of the autonomous vehicles and the connected vehicles are well combined. The following errors detected by radar has tiny time delay and high reliability, and the acceleration transmitted by VANET improves the response speed.

2.2 Longitudinal Tracking Controller Design

The longitudinal dynamic of the vehicle contains several nonlinear factors, such as motor characteristics, braking characteristic and aerodynamics. And the longitudinal tracking is achieved by the coordination between the throttle control and the brake control. In order to track the desired acceleration, the desired torque \(T_{\text{des}}\) of wheels can be calculated by combining the air resistance, slope resistance, acceleration resistance and friction resistance. Then, the inverse engine model and inverse brake model are introduced to produce the desired torque.

$${{\alpha }} = f^{ - 1} \left( {\frac{{T_{\text{des}} }}{{i_{\text{g}} i_{0} \eta }},\omega } \right)$$
(4)
$${{\beta }} = \frac{{T_{\text{des}} }}{{K_{\text{b}} }}$$
(5)

in which \(i_{\text{g}} , i_{0} ,\eta ,\omega ,K_{\text{b}}\) are the transmission ratio, final drive ratio, efficiency of the drive system, engine speed and braking coefficient, respectively; \(\alpha\) and \(\beta\) are the throttle angle and the braking pressure, respectively; \(f\) represents the nonlinear engine model.

To reduce the influence caused by the inaccuracy of the inverse model, a feedback PI controller is designed to adjust the throttle angle and the braking pressure. A threshold is adopted in the switching strategy, then, to avoid switching between modes too frequently. The whole longitudinal tracking controller is shown in Fig. 2.

Fig. 2
figure 2

The longitudinal tracking controller

Full size image

3 Parameter-Space-Approach-Based CACC Controller Design

To simplify the CACC controller design, the linearized third-order state-space is adopted to model the longitudinal dynamic of every vehicle, which is widely used in much literature for theoretical analysis [7, 12]. Then, the vehicle is modeled as

$$\left\{ {\begin{array}{*{20}l} {\dot{x}\left( t \right) = v\left( t \right)} \\ {\dot{v}\left( t \right) = a\left( t \right)} \\ {\dot{a}\left( t \right) = \frac{1}{\tau }u\left( {t - \varphi } \right) - \frac{1}{\tau }a\left( t \right)} \\ \end{array} } \right.$$
(6)

in which \(x,v,a\) denote the position, the velocity and the acceleration, respectively; \(\tau\) is the time lag; \(u\) expresses the desired acceleration; and \(\varphi\) is the signal transmission delay.

Therefore, the longitudinal dynamics of vehicle i are described in the Laplace domain by the transfer function \(G_{i} \left( s \right)\) as

$$G_{i} \left( s \right) = \frac{{a_{i} \left( s \right)}}{{u_{i} \left( s \right)}} = \frac{1}{{\left( {\tau s + 1} \right)}}e^{ - \varphi s}$$
(7)

Then, the overall control block diagram of vehicle i is shown in Fig. 3; where \(D = e^{ - \zeta s} , H = hs + 1,M = 1/s^{2}\); \(G_{\text{F}}\) is the feedforward gain; \(G_{\text{B}}\) is the feedback gain as \(G_{\text{B}} = k_{\text{p}} + k_{\text{v}} s\); and \(G_{i}\) is the longitudinal dynamics of vehicle i.

Fig. 3
figure 3

The control block diagram of vehicle i

Full size image

To select the feedforward gain and the feedback gain, the following two objectives should be satisfied:

  1. (1)

    Internal stability: keeping the following errors \(e\left( t \right)\) convergent.

  2. (2)

    String stability: attenuating the disturbance along with the platoon.

3.1 Internal Stability

For the system described in Fig. 3, the input is the acceleration of the preceding vehicle and the transfer function \({ \mathcal{J}}\) from the input to the following errors is formulated as

$${\mathcal{J}}\left( s \right) = \frac{e\left( s \right)}{{a_{i - 1} \left( s \right)}} = \frac{{M - G_{\text{F}} DGHM}}{{1 + G_{\text{B}} G_{i} H}}$$
(8)

The internal stability can be achieved by selecting suitable feedforward gain to keep the numerator convergent (\(M - G_{\text{F}} DGHM = 0\)) and selecting suitable feedback gain to adjust convergence performance.

As the feedforward loop gain is designed to reduce the model matching errors, it is established as

$$G_{\text{F}} = \frac{1}{GHD} = \frac{\tau s + 1}{hs + 1}e^{{\left( {\sigma + \varphi } \right)s}}$$
(9)

After ignoring the influence of time delay, the feedforward gain is selected as

$$k_{\text{a}} = \frac{1}{GHD} = \frac{\tau s + 1}{hs + 1}$$
(10)

Pole region assignment is then applied to control the convergence characteristic, and the system is \({\mathcal{D}}\)-stability if and only all the poles are located in the specified region \({\mathcal{D}}\). Figure 4 shows a pole region \({\mathcal{D}}\). The boundary \(\vartheta_{1}\) corresponds to the desired settling time and the boundary \(\vartheta_{2}\) corresponds to the minimum value of damping. And its bandwidth is bounded by a circular arc \(\vartheta_{3}\). Then, the boundary of the pole region \({\mathcal{D}}\) can be described as

$$\partial {\mathcal{D} := }\left\{ {s |s = \sigma \left( \alpha \right) + j\omega \left( \alpha \right),\alpha \in \left[ {\alpha^{ - } ,\alpha^{ + } } \right]} \right\}$$
(11)

Defining q as the parameter of the feedback loop. The roots of \(p\left( {s,\varvec{q}} \right)\) are continuous in \(\varvec{q}\), and it is impossible to step out the region \({\mathcal{D}}\) without crossing the boundary \(\partial {\mathcal{D}}\). Consequently, by extending the parameter space approach to the \({\mathcal{D}}\)-stability [24], the region \({\mathcal{D}}\) in the s-plane can be transferred to the q-plane.

Fig. 4
figure 4

Pole region \({\mathcal{D}}\) in the s-plane with specifications

Full size image
$$\partial {\mathcal{Q}}_{\text{CRB}} \left( \alpha \right)\text{ := }\{ \varvec{q}|p\left[ {\sigma \left( \alpha \right) + j\omega \left( \alpha \right),\varvec{q}} \right] = 0,\alpha \in \left[ {\alpha^{ - } ,\alpha^{ + } } \right]\}$$
(12)
$$\partial {\mathcal{Q}}_{\text{RRB}} \text{ := }\left\{ \varvec{q}|p\left( {\sigma_{0} ,\varvec{q}} \right) = 0\right\}$$
(13)

Equations (12) and (13) give the complex root boundary (CRB) that crosses region \({\mathcal{D}}\) at \(s = \sigma \pm j\omega\) and the real root boundary (RRB) that crosses region \({\mathcal{D}}\) on real axis at \(s = \sigma\), respectively. The pole region \({\mathcal{D}}\) is defined as no roots can be closer than − 0.1 \({{\uppi }}\) in real part and further than − 3 \(\uppi\) in magnitude, which corresponds to \(\vartheta_{1}\) and \(\vartheta_{3}\), respectively. The damping ratio should be smaller than \(\zeta = 0.707\), which is expressed by \(\theta = 45^\circ\).

Figure 5 shows the boundary ∂\({\mathcal{D}}\) in the \(\varvec{q}\)-plane when the other parameters are defined as given in Table 1. When the feedback gains are selected from the region bounded by these five boundaries, they guarantee the \({\mathcal{D}}\)-stability of the platoon and the following errors are convergent with desired convergence performance.

Fig. 5
figure 5

\({\mathcal{D}}\)-stable boundary in parameter space

Full size image
Table 1 The parameters used in the paper
Full size table

3.2 String Stability

The string stability means that the disturbance should be attenuated along with the platoon. The most commonly used definition of string stability is \({\mathcal{L}}_{2}\) string stability. It is proved that the following expression has to be satisfied to guarantee \({\mathcal{L}}_{2}\) string stability.

$$\left| {\varGamma \left( s \right)} \right| = \left| {\frac{{X_{i} \left( s \right)}}{{X_{i - 1} \left( s \right)}}} \right| \le 1$$
(14)

\(X_{i} \left( s \right)\) denotes the Laplace transform of acceleration at time t.

For the system described in Fig. 3, the transfer function between the ego vehicle and its preceding vehicle can be expressed as

$$\left( {1 + HMG_{\text{B}} G} \right)a_{i} = \left( {DG_{\text{F}} G + MG_{\text{B}} G} \right)a_{i - 1}$$
(15)

Combining Eqs. (14) and (15), the boundary of the \({\mathcal{L}}_{2}\) string stability transfer to

$$\left| {{{\varGamma }}\left( {j\omega } \right)} \right| = \left| {\frac{{D\left( {j\omega } \right)G_{\text{F}} \left( {j\omega } \right)G\left( {j\omega } \right) + M\left( {j\omega } \right)G_{\text{B}} \left( {j\omega } \right)G\left( {j\omega } \right)}}{{1 + H\left( {j\omega } \right)M\left( {j\omega } \right)G_{\text{B}} \left( {j\omega } \right)G\left( {j\omega } \right)}}} \right| = 1,\quad \forall \omega$$
(16)

Rearranging Eq. (16) yields

$$\xi \left( {j\omega } \right) = \text{Re} \left( {\varGamma \left( {j\omega } \right)} \right)^{2} + \text{Im} \left( {\varGamma \left( {j\omega } \right)} \right)^{2} - 1 = 0$$
(17)

To map the boundary of Eq. (17) in the parameter space, it suffices to consider two mathematical conditions, the point condition and the tangent condition.

The point condition is applied when \(\xi \left( {j\omega } \right)\) starts or ends at the boundary. For the boundary defined by Eq. (17), while \(\omega \to 0^{ + }\), it can be calculated that \(\xi \left( {j\omega } \right) \to 0\). And when \(\omega \to \infty\), it can be calculated that \(\xi \left( {j\omega } \right) \to - 1.\) Therefore, it is clear that the point condition is satisfied for every control parameter.

The tangent condition allows for the mapping of touching points, i.e., the points where \(\xi \left( {j\omega } \right)\) becomes tangent to a smooth branch of the boundary. The tangent condition can be stated as follows.

For a fixed \(\omega = \omega^{*}\), find the control parameter \(\varvec{ q}\) such that

$${{\xi }}\left( {{\text{j}}\omega^{*} ,\varvec{q}} \right) = 0$$
(18)
$$\partial \frac{{\partial {{\xi }}\left( {{\text{j}}\omega^{*} ,\varvec{q}} \right)}}{{\partial \omega^{*} }} = 0$$
(19)

Then, the boundary of the parameter of the feedback loop is mapped in the parameter space by gridding the \(\omega\) and finding the corresponding \(\varvec{q}\).

As the control block includes the communication time delay, it shows that the communication condition can obviously affect the string stability and it is necessary to consider the influence of the communication time delay in the design process. Figure 6 shows the string stable region of the feedback control gain under different communication time delay. The grey region in Fig. 6 is the string stable region when the communication time delay is 0.1 s. Other three string stable boundaries are also shown in Fig. 6. It demonstrates that with the increase in the communication time delay, a larger \(k_{\text{v}}\) is required to guarantee the string stability.

Fig. 6
figure 6

The string stability region in the parameter space

Full size image

Then feedback gains of the CACC controller are selected as \(k_{\text{p}}\) = 1.6, \(k_{\text{v}}\) = 1.7, which are located in both \({\mathcal{D}}\)-stable region and string stable region. It shows that these feedback gains are still located in the string stable region when the communication time delay is 0.3 s.

4 Numerical Simulation

To verify the effectiveness of the platoon controller, two different scenarios are applied.

  1. (1)

    Simplified speed-up and stop scenario: A six-vehicular platoon is simulated in this scenario, where the third-order vehicle longitudinal dynamic is applied.

  2. (2)

    Highway fuel economy test (HWFET) scenario: A CarSim/Simulink co-simulation is designed to compare the performance of CACC and ACC.

4.1 Verification of the Internal Stability and String Stability

In order to verify whether the internal stability and string stability are satisfied by the design approach proposed in this research, the location of poles and the frequency response magnitude of the transfer function \(\varGamma\) are given for the selected parameters.

As shown in Fig. 7, there are one real pole and one numerator set of conjugate complex poles. And these poles are located in the desired \({ \mathcal{D}}\) region, which means the convergence performance is guaranteed by the selected parameters. As the internal stability is determined by the design of feedback loop of the CACC controller, the communication time has no effect on internal stability.

Fig. 7
figure 7

The location of the poles

Full size image

As for the string stability, the influence of communication time delay should be well considered. Figure 8 shows the frequency response magnitude of the transfer function \(\varGamma\) under different communication time delay.

Fig. 8
figure 8

The frequency response magnitude of the transfer function \(\varGamma\) under different communication time delay

Full size image

The selected control parameters ensure the string stability when the communication time delay is 0.1 s. This phenomenon proves the correctness of the previous process, as shown in Fig. 6, which is calculated for the communication condition with 0.1-s time delay. To further discuss the influence of communication time delay, four other values of communication time delay are proposed as shown in Fig. 8. It illustrates that only when the communication time delay is selected as 0.4 s, the vehicular platoon cannot guarantee string stability, as the frequency response magnitude is larger than one at some frequencies. And when the communication time delay is selected as 0.34 s, the frequency response curve is tangent to the critical line at \(\omega_{1}\). Then, the designed CACC controller does not only guarantee the string stability when the communication time delay is 0.1 s, but also works when the communication time delay is up to 0.34 s.

4.2 Simplified Speed-Up and Stop Scenario

The objective of this scenario is to test the convergence performance and the string stability of the platoon with the ideal vehicle dynamic. In this sense, the vehicle can follow the desired longitudinal commands after a constant time lag. This assumption only considers the performance of CACC controller without the influence of the longitudinal tracking controller.

Figure 9 shows the simulation results of simplified acceleration and stop scenario. It shows that the initial velocity of every vehicle is 10 m/s. The leader vehicle accelerates first and then decelerates until stop. Figure 9a demonstrates that the vehicles in the platoon can follow the preceding vehicle after a little time delay. And the amplitude of acceleration fluctuation attenuates along with the platoon, which is marked by the red arrow. This phenomenon proves that string stability is achieved by the selected control parameters. Owing to the ideal acceleration-following performance, the vehicles follow the velocity of the preceding vehicle without overshoot, which highly improves the drive comfort. Another proof of the string stability is that the following errors also attenuates along with the platoon marked in Fig. 9c. Furthermore, with the acceleration disturbance of the leader vehicle, the following errors are convergent without fluctuations and overshoot. This is a benefit of the \({\mathcal{D}}\)-stability design.

Fig. 9
figure 9

The simulation results during the simplified acceleration and stop scenario

Full size image

To sum up, the simulation results illustrate that the \({\mathcal{D}}\)-stability and string stability are achieved with the selected control parameters.

4.3 HWFET Scenario

To further verify the effectiveness of the hierarchical control framework and the rationality of the CACC controller in a realistic vehicular platoon application, a co-simulation is designed with a CarSim/Simulink model. CarSim is applied to simulate the vehicle dynamic, and Simulink is applied to simulate the controller. It is recognized that highway driving is the most suitable condition for the application of V2X technology and CACC control has great benefits to improve traffic flow efficiency and safety on the highway. As a consequence, the HWFET standard driving cycle is used to assess the performance of the designed controller. To verify the effectiveness of the designed CACC controller, another vehicle controlled by the ACC algorithm is simulated for comparison. The control strategy of the ACC algorithm is selected as follows [25], which is wildly applied in the literature.

$$u_{i} \left( {\text{t}} \right) = k_{1} e_{i} \left( t \right) + k_{2} \left( {v_{i - 1} \left( t \right) - v_{i} \left( t \right)} \right)$$
(20)

Specifically, the time headway of the ACC algorithm is 1.1 s and \(k_{1} = 0.23\), \(k_{2} = 0.07\).

Figure 10 shows the throttle and brake control commands of the vehicle equipped with CACC controller. It indicates that the vehicle controlled by the longitudinal tracking controller can follow the desired acceleration determined by the CACC controller accurately. Using the simulation results between 50 and 100 s for example, the vehicle does not switch between drive and brake mode frequently, benefiting from the application of threshold.

Fig. 10
figure 10

The simulation results of the longitudinal tracking controller during the HWFET cycle

Full size image

Figure 11 shows the acceleration and velocity profiles of the vehicle equipped with CACC controller or ACC controller, respectively. In the detailed picture of Fig. 11a, it is clear that the vehicle of CACC follows the acceleration of the preceding vehicle accurately. But the vehicle with ACC amplifies the acceleration fluctuations of the preceding vehicle; besides affecting the following accuracy, it also deteriorates the comfort. Table 2 gives the statistical data of the acceleration of HWFET drive cycle. It shows that the root mean square (RMS) of the vehicle with CACC is a little smaller than the proceeding vehicle. The magnitude of the reduction is not as obvious as that in Fig. 9 because of the complex dynamic of the vehicle. Furthermore, the threshold in the switching strategy and the tracking performance also have a negative effect on the following accuracy. Then, string stability is guaranteed for the real vehicle dynamic even with the influence of the low-level controller. On the other hand, the vehicle with ACC controller fails to follow the acceleration of the preceding vehicle without overshoot, and the RMS value of the acceleration is about 17.97% higher than that of the preceding vehicle. It illustrates that the disturbance is expanded along with the platoon and this phenomenon gets worse with the increase in the size of the platoon. Owing to the different acceleration-following performance of the vehicle with CACC or ACC, the velocity profiles are also totally different. The vehicle with CACC follows the velocity of the preceding vehicle without overshoot, while the vehicle with ACC shows severe over-acceleration and over-braking. This comparison result proves that the CACC improves the drive comfort significantly.

Fig. 11
figure 11

The simulation results of the vehicles with different controllers during the HWFET cycle

Full size image
Table 2 The RMS of the acceleration profile of HWFET drive cycle
Full size table

Another advantage of the CACC controller is that it keeps a desired following distance with a small following errors. In the simulation result shown in Fig. 12, the maximum following errors of the vehicle with CACC is 0.1865 m. When these two vehicles are completely stopped, the distance between them is about 1.96 m. These two findings illustrate that CACC control achieves better following errors and safety performance during the whole drive cycle. On the other hand, the following errors of the vehicle with ACC reaches the peak at 10.32 m and the vehicle fails to stop at the desired position after the preceding vehicle. It shows that a collision occurs during deceleration. Consequently, ACC control is only suitable for the cruising scenario, and the following errors is relatively large.

Fig. 12
figure 12

Following characteristics of vehicle with CACC controller and ACC controller

Full size image

Based on the above comparison results, the following three conclusions can be summarized.

  1. (1)

    The feedforward loop of the acceleration of the preceding vehicle improves the response speed, and reduces the following errors by selecting suitable feedforward gain.

  2. (2)

    The feedback gains selected from the feasible region shown in Figs. 5 and 6 guarantee the string stability of the CACC controller, and the following errors is quite small which is the benefit of the well-designed convergence performance.

  3. (3)

    The application of the CACC significantly improves driving comfort and safety and can be used in all scenarios considered here, i.e., starting scenario, cruising scenario and stopping scenario.

5 Conclusions

A hierarchical framework is designed for the distributed homogeneous platoon with communication time delay in this paper. The CACC controller is proposed to determine the desired acceleration by utilizing the feedforward loop of the acceleration of the preceding vehicle and the feedback loop of the following errors. Then, the longitudinal tracking controller is designed to control the throttle and brake system of the ego vehicle. To achieve well-designed convergence performance and attenuation of the disturbance along with the platoon, the parameter space approach is introduced to visualize the feasible region of the controller parameter, where the \({\mathcal{D}}\)-stability and string stability are guaranteed.

The simulation results with simplified vehicle dynamic show that amplitude of acceleration fluctuation attenuates along with the platoon and the following errors are convergent without fluctuations and overshoot. To further consider the influence of the complex vehicle dynamic and the performance of the longitudinal tracking controller, a CarSim/Simulink co-simulation is carried out under the HWFET drive cycle. Comparison of the simulation results of the vehicle with ACC control demonstrates that the application of the CACC significantly improves driving comfort and safety. Specifically, the vehicle with CACC controller follows the acceleration profile of the preceding vehicle accurately and smoothly and the following errors is quite small which is one of the benefits of the well-designed convergence performance.

Future work should pay more attention to the robust control of the vehicular platoon, considering the communication delay, packet dropout and even the possibility of cyber-attack.