Solid-State Electrochemistry and Solid Oxide Fuel Cells: Status and Future Prospects

Abstract

Solid-state electrochemistry (SSE) is an interdisciplinary field bridging electrochemistry and solid-state ionics and deals primarily with the properties of solids that conduct ions in the case of ionic conducting solid electrolytes and electrons and/or electron holes in the case of mixed ionic and electronic conducting materials. However, in solid-state devices such as solid oxide fuel cells (SOFCs), there are unique electrochemical features due to the high operating temperature (600–1 000 °C) and solid electrolytes and electrodes. The solid-to-solid contact at the electrode/electrolyte interface is one of the most distinguished features of SOFCs and is one of the fundamental reasons for the occurance of most importance phenomena such as shift of the equipotential lines, the constriction effect, polarization-induced interface formation, etc. in SOFCs. The restriction in placing the reference electrode in solid electrolyte cells further complicates the SSE in SOFCs. In addition, the migration species at the solid electrode/electrolyte interface is oxygen ions, while in the case of the liquid electrolyte system, the migration species is electrons. The increased knowledge and understanding of SSE phenomena have guided the development of SOFC technologies in the last 30–40 years, but thus far, no up-to-date reviews on this important topic have appeared. The purpose of the current article is to review and update the progress and achievements in the SSE in SOFCs, largely based on the author’s past few decades of research and understanding in the field, and to serve as an introduction to the basics of the SSE in solid electrolyte devices such as SOFCs.

Graphical abstract

1 Introduction

Solid-state electrochemistry (SSE) is an interdisciplinary field bridging electrochemistry and solid-state ionics and has been extensively covered by a number of monographs and reviews [1,2,3,4,5]. By definition, SSE is a discipline dealing with the properties of solids that conduct ions and electrons or electron holes in ionic and/or electronic conducting materials [2]. In materials science, SSE is similar to solid-state ionics dealing with the preparation, characterization, theory and application of solid ionic conducting materials [6] but also refers to the electrochemical activity and behavior of materials in solid states such as the density and mobility of charge carriers associated with the defect chemistry, intercalation and redox changes [7,8,9,10,11,12]. The SSE principle is particularly relevant to the development of solid electrolyte-based devices such as solid-state sensors, solid oxide electrolysis and fuel cells (SOECs and SOFCs) and solid-state batteries. In solid-state Li-ion batteries, the solid electrolytes belong to a class of composite solid electrolytes, which consist of heterogeneous mixtures of single-phase solid electrolytes or other components such as inorganic and polymer-based composites. The SSE and the ion conduction mechanism of composite solid electrolytes are most critical for solid-state devices such as Li-ion batteries and have recently been extensively studied and reviewed [13].

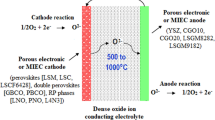
Among the single-phase solid electrolyte systems, high-temperature SOFCs are the most represented and extensively investigated solid-state devices. SOFCs are energy conversion technologies that electrochemically convert the chemical energy of hydrogen and hydrocarbon fuels into electrical energy with the highest efficiency among the fuel cell family [14,15,16,17,18]. A basic solid oxide cell consists of only ceramic materials and operates in the temperature range of 600–1 000 °C. The most common ceramic materials in a typical SOFC are the dense oxide ion conducting yttria-stabilized zirconia (YSZ) electrolyte, porous lanthanum strontium manganite (LSM) cathode and porous nickel/YSZ (Ni/YSZ) cermet anode [18, 19]. The working principle of an SOFC can be illustrated in a H₂-O₂ fuel cell. In this fuel cell, oxygen molecules, O₂, are ionized to oxygen ions, O²⁻, by taking two electrons and are incorporated into the oxygen lattice site of an oxide ion conducting electrolyte by occupying an oxygen vacancy. This O₂ reduction reaction (ORR) can be expressed as follows in Kröger–Vink notation:

$$\frac{1}{2}{\mathrm{O}}_{2(\mathrm{cathode})}+2{\mathrm{e}}^{-}+{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot }= {\mathrm{O}}_{\mathrm{O}({\mathrm{electrolyte},}\mathrm{cathode})}^{x}$$

(1)

where ${\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}$ is a vacant oxygen lattice site or oxygen vacancy and ${\mathrm{O}}_{\mathrm{O}}^{x}$ is an oxygen ion at a regular oxygen site in the electrolyte lattice. At the same time, oxygen ions flow from the LSM cathode to the Ni/YSZ cermet anode through the dense YSZ electrolyte via oxygen vacancies:

$${\text{O}}_{{{\text{O}}({\text{electrolyte}},{\text{cathode}})}}^{x} \xrightarrow{{{\text{V}}_{{\text{O}}}^{{ \cdot \cdot }} }}{\text{O}}_{{{\text{O}}({\text{electrolyte}},{\text{anode}})}}^{x}$$

(2)

At the anode, the H₂ oxidation reaction (HOR) occurs through the combination of H₂ molecules with the oxygen ions that migrated from the cathode, forming H₂O and releasing two electrons and an oxygen vacancy back to the electrolyte:

$${\mathrm{H}}_{2(\mathrm{anode})}+{\mathrm{O}}_{\mathrm{O}({\mathrm{electrolyte},}\mathrm{anode})}^{x}= {\mathrm{H}}_{2}{\mathrm{O}}_{(\mathrm{anode})}+2{\mathrm{e}}^{-}+ {\mathrm{V}}_{\mathrm{O}(\mathrm{electrolyte})}^{\cdot \cdot}$$

(3)

The overall reaction is thus the combination of hydrogen from the anode and oxygen from the cathode via oxygen vacancy migration through the electrolyte to form water on the anode side:

$${\mathrm{H}}_{2(\mathrm{anode})}+\frac{1}{2}{\mathrm{O}}_{2(\mathrm{cathode})}\xrightarrow{{\mathrm{V}}_{\ddot{\mathrm{O}}(\mathrm{electrolyte})}}{\mathrm{H}}_{2}{\mathrm{O}}_{(\mathrm{anode})}$$

(4)

The electrons flow from the anode (the negative electrode) to the cathode (the positive electrode) to produce an electrical energy output. Figure 1 illustrates the scheme of and electrode reactions occurring in an SOFC.

Fig. 1

Scheme and working principle of an SOFC

As shown above, both the ORR and HOR require the supply and release of oxygen ions and electrons. Thus, the oxidation/reduction efficiency critically depends on the ionic conductivity of the solid electrolyte and mixed ionic and electronic conductivity of the electrodes, i.e., the SSE of the materials. In addition, SOFC devices are characterized by high operating temperatures, solid-state electrodes, solid-state electrolytes, and gaseous reactants and products. The gaseous phase reaction occurs at the porous electrode/dense electrolyte interface, and the ionic/electronic transport properties are critically related to the microstructure of the cell, such as the tortuosity and three- or triple-phase boundary (TPB) areas [20], and to the surface chemistry, such as segregation [21, 22]. The solid-to-solid (StS) contact between the porous electrode and dense electrolyte is in general not necessarily continuous and may be restricted to only a fraction of the interface. Such restriction in the contacted interface will cause misalignment and asymmetric contact between the working and counter electrodes and result in a significant change in the equipotential line. Such a change in the potential distribution across the solid electrolyte is further complicated by the limitation of the placement and positioning of the reference electrode (RE) due to the use of solid electrolytes. In contrast to aqueous electrolyte systems, incorporating the RE into the electrolyte bulk is extremely difficult and inconvenient, and instead, in most cases, the RE can only be placed on an external surface of the solid electrolyte. This not only restricts the electrochemical techniques that can be used in high-temperature SOFCs but also significantly affects the electrical potential line distribution in cells, which in turn affects the electrochemical behavior of the reaction at the interface. Additionally, very different from the interface in liquid-state electrochemistry (LSE), the physical boundary between the porous electrode and dense electrolyte cannot be clearly defined due to the MIEC properties of the electrodes. For example, in the case of the Ni/YSZ anode and the YSZ electrolyte, the interface is extended into the electrode bulk due to the YSZ-to-YSZ network in the cermet (see Fig. 1).

As is well known, the peak power performances or densities obtained in stacks are generally lower than those observed in single cells [23]. The cause for the differences in the power performances can be attributed to the contacts between the electrode coating and current collector, particularly between the cathode and current collector or interconnect interface [24,25,26,27]. An early study showed that increasing the contact area between the Pr_0.8Sr_0.2MnO₃ cathode and current collector from 4.6% to 27.2% resulted in a reduction in the cell resistance from 1.43 to 0.19 Ω cm² and a decrease in the overall cell overpotential from 225 to 119 mV at 250 mA cm⁻² and 800 °C [25]. Such a significant effect of the contact area on both the cell ohmic and polarization resistances is also called the constriction effect in SOFCs. More recently, this constriction effect on the ohmic and polarization resistances in a stack was further confirmed in a detailed analysis of the cathode contact in the temperature range of 650–800 °C [28]. The results showed that the cell ohmic resistance increases with decreasing temperature, while the cell polarization resistance shows a minimum at 700 °C for the stack with a 35% reduction in the contact area. The fundamental reason for this contact area effect is related to the intrinsic relationship between the StS contact and the location of the equipotential line in the solid electrolyte.

In SOFCs, the microstructure and phase change, particularly at the electrode and electrolyte interfaces, are interrelated with the operation parameters, such as the polarization current, temperature, fuel type, oxygen partial pressure, deposition and poisoning of contaminants. Some changes are intrinsically related to the defect chemistry of the materials involved, such as enhanced grain boundary diffusion, deposition and poisoning of contaminants, and correlation between the oxygen ion conductivity and reactivity for the ORR [17, 29,30,31]. However, some of the microstructural changes and interfacial phenomena are not particularly related to the classic defect chemistry and are unique to solid-state electrolyte cells such as SOFCs. For example, polarization-induced microstructure changes and reactions at electrode/electrolyte interfaces occur under SOFC operating conditions and critically influence the performance and durability of SOFCs [32, 33]. The knowledge and understanding of the unique features and phenomena of the SSE in SOFCs, including the constriction effect, RE placement and reliability, and, most recently, surface segregation effect, have been significantly increased, which has guided the development of SOFC technologies in the last 30–40 years. However, there appear to be no comprehensive and up-to-date reviews on the SSE despite its importance in solid-state electrolyte devices such as SOFCs.

The purpose of the current article is twofold: to summarize the progress and achievements in the SSE in SOFCs, viewed from a prospective angle and largely based on the author’s past few decades of research and understanding in the field, and to serve as an introductory note to anyone interested in this interdisciplinary and important field. This review will start with a brief introduction to the defect chemistry in electrode and electrolyte materials in SOFCs. Then, the issues related to the cell configuration and RE placement, the electrical potential line distribution and its implication for the polarization and impedance separation in solid oxide cells, the constriction effect, surface segregation and polarization-induced interface formation under SOFC operating conditions will be discussed.

2 Basic Defect Chemistry in Electrode and Electrolyte Materials of SOFCs

The conduction of charge carriers such ions in a liquid electrolyte occurs through a distinct diffusion mode known as “vehicular”, in which a solvation sheath or cloud of polar molecules travels with the ion. Such a diffusion mode is also possible in the polymer-based electrolytes used in polymer electrolyte or proton exchange membrane fuel cells (PEMFCs) [34, 35]. The presence of a solvation sheath changes the effective radius of charge carriers and imposes certain characteristics on the electrochemical reaction at the interface. In solid electrolytes, no solvation sheath or cloud exists, and conduction of charged ions is usually mediated by hopping between adjacent lattice sites. In SOFCs, the major charged particles are electrons (or electron holes) and oxide ions. In the case of proton conducting electrolyte-based solid oxide cells or protonic ceramic fuel cells, the charged species also include protons, H⁺. The proton conduction issues in solid proton conducting electrolytes in SOFCs have been recently reviewed [36]. The ionic species are transported through the electrolyte between the two electrodes, and the electrodes carry the electrons to and from the reactive sites where the electrochemical reactions occur. The interconnect transfers electrons from the anode of one cell to the cathode of another cell to form a stack. Thus, the current caused by the flow of electrons is called electronic conduction, while the current due to the net motion of ions is termed ionic conduction. However, ceramic conductors have an intrinsic resistance to charge flow, and this resistance to charge flow leads to polarization loss for fuel cells. The polarization loss due to the resistance is generally termed ohmic loss or ohmic polarization. In fuel cells, the electrical conductivity, σ, is often used, which is the reciprocal of the electrical resistivity, ρ:

$$\sigma \, = \,{1}/\rho$$

(5)

The conductivity for most materials can be expressed as the product of the concentration and mobility of charge carriers:

$$\sigma =(nz\mathrm{e})\frac{v}{\xi }=(nz\mathrm{e})\mu$$

(6)

where n is the number of charge carriers, electrons (electron holes) or oxide ions in carriers per cm³; ze is the charge per carrier, where z is the valence and e is the electronic charge; v is the velocity (cm s⁻¹) of charge carriers; and ξ is the electric field. The term v/ξ can be defined as the mobility of the charge carriers, μ (cm² V⁻¹ s⁻¹). Thus, material conductivity is characterized by two major factors: the number of carriers available and the mobility of these carriers. For materials with more than one carrier, this is expressed as:

$${\sigma }_{\mathrm{i}}=F\sum {|z}_{\mathrm{i}}|{c}_{\mathrm{i}}{\mu }_{\mathrm{i}}$$

(7)

where c_i is the mole number of charge carriers per unit volume, z_i is the charge number (or valence) for the carrier (|z_i| is always positive), and F is Faraday’s constant. The subscript i can refer to electrons, electron holes, ions, or vacancies.

In ceramic materials, electronic and ionic defects are charge carriers that enable the conduction of an electric current. These charge carriers can be formed within the material (intrinsic charge carriers), thus increasing the entropy of the system, or can be introduced into the material by doping (extrinsic charge carriers). Examples of ionic point defects are vacancies and interstitials. Electronic defects are negatively charged electrons and positively charged electron holes.

2.1 Electronic Conduction in Perovskite-Type Oxides

In a metallic conductor, valence electrons associated with atoms of the metal become detached, i.e., they are excited and promoted to the low-lying empty and available energy state above the Fermi level of electrons and become free electrons for electronic conduction. This occurs because for metals, the band structure is such that there are vacant energy states adjacent to the highest filled state at the Fermi level. Thus, very little energy is needed to excite electrons to the low-lying empty state.

Prior to a discussion of the conduction properties of oxide materials, a brief introduction to the perovskite structure is beneficial, as perovskites are the most common structured oxides in SOFCs. Figure 2 shows a typical perovskite structure. A perovskite is any material with the same type of crystal structure as calcium titanium, CaTiO₃, with the general chemical formula of ABO₃, where A and B are two cations of very different sizes, and O is an oxygen anion. The ideal cubic perovskite has the B cation in sixfold octahedral coordination (the coordination number or CN = 6), surrounded by an octahedron of oxygen anions, and the A cation in 12-fold cuboctahedral coordination (CN = 12). The A-site cations are typically from the alkaline earth or rare earth group, and B-site cations are generally transition metal group elements. The combination of the redox properties of transition metals with the acid–base properties of alkaline earth metals is fundamental to many interesting applications, including catalysis and fuel cells. In SOFCs, undercoordinated transition metal sites are considered vital in the ORR [31, 37]; nevertheless, the active sites on perovskite oxides for the ORR are much more complicated due to the critical role of the surface structure and composition in the reaction.

Fig. 2

Typical perovskite structure with the general chemical formula of ABO₃

The deviation from the ideal cubic perovskite structure is governed by the Goldschmidt tolerance factor, t:

$$t=\frac{\left({r}_{\mathrm{A}}+{r}_{\mathrm{O}}\right)}{\sqrt{2}\left({r}_{\mathrm{B}}+{r}_{\mathrm{O}}\right)}$$

(8)

where r_A, r_B and r_O are the ionic radii of A, B and O ions, respectively. Cubic symmetry is observed for 0.95 $\leqslant$ t $\leqslant$ 1.04, while perovskite structures with lower-symmetry distorted versions, such as orthorhombic and rhombohedral symmetries, are observed for 0.75 $\leqslant$ t $\leqslant$ 0.90. The ionic radii are related to the CN.

Most ceramics or, more precisely, ionic ceramics are generally insulating materials at room temperature due to the relatively large band gap between the filled valence band and the empty conduction band. Thus, at room temperature, only very few electrons may be excited across the band gap by the available thermal energy, resulting in a very low conductivity. Increasing the temperature will increase the conductivity of oxide materials in general; however, in the case of oxide materials with metallic behavior, the conductivity will decrease with increasing temperature, as shown later in this review. For the ceramic oxide components used in SOFCs, there are different ways to increase the ionic and electronic conductivity by tailoring the defect chemistry.

The electronic conductivity of oxide materials of SOFCs can be either n- or p-type, with p-type materials being commoner. Taking the perovskite lanthanum chromite (LaCrO₃) as an example, LaCrO₃-based oxides are commonly used as ceramic interconnects in SOFCs. LaCrO₃ is a p-type conductor from room temperature to high temperature (> 1 000 °C) and becomes nonstoichiometric through the reaction of oxygen with LaCrO₃, resulting in the formation of cation vacancies or defects [38, 39]. This can be written as:

$$\frac{3}{2}{\mathrm{O}}_{2}={\mathrm{V}}_{\mathrm{La}}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}+{\mathrm{V}}_{\mathrm{Cr}}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}+3{\mathrm{O}}_{\mathrm{O }}^{x}+6{\mathrm{h}}^{\cdot }$$

(9)

where ${\mathrm{V}}_{\mathrm{La}}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}$ and ${\mathrm{V}}_{\mathrm{Cr}}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}$ are La and Cr cation vacancies, respectively, and ${\mathrm{h}}^{\cdot }$ is an electron hole. The negatively charged cation vacancies are electrically compensated by the concomitant appearance of positively charged electron holes. Electronic conduction in LaCrO₃ occurs by small polaron hopping via transport of electron holes. However, the electronic conductivity of undoped LaCrO₃ is very low. To improve the p-type electronic conductivity, divalent cations such as strontium (Sr) and calcium (Ca) are used as dopants to substitute trivalent La cations. Divalent Sr on a trivalent La site creates a negatively charged point defect, ${\mathrm{Sr}}_{\mathrm{La}}^{\mathrm{^{\prime}}}$. To maintain electroneutrality, a positive electron hole is formed:

$$\mathrm{SrO}\xrightarrow{{\mathrm{LaCrO}}_{3}}{\mathrm{Sr}}_{\mathrm{La}}^{\mathrm{^{\prime}}}+{\mathrm{O}}_{\mathrm{O}}^{x}+{\mathrm{Cr}}_{\mathrm{Cr}}^{\cdot }$$

(10)

${\mathrm{Cr}}_{\mathrm{Cr}}^{\cdot }$ is Cr⁴⁺ on a Cr³⁺ site and represents an electron hole localized on a Cr site. ${\mathrm{Cr}}_{\mathrm{Cr}}^{\cdot }$ has the same function as ${\text{h}}^{\cdot }$. The introduction of a positively charged electron hole to a cation site will lead to the attraction of anions and the repulsion of cations at the same time. Such polarization of the surroundings of a localized electron hole due to the attraction and repulsion of ions is called a polaron [40]. This is schematically shown in Fig. 3. For small polarons, the polarization is of the size of one unit cell, while for large polarons, the polarized volume is much larger than a unit cell.

Fig. 3

Charge compensation of the Sr²⁺ dopant in a La³⁺ site by the formation of positively charged electron holes via the Cr³⁺ → Cr⁴⁺ transition in Sr-doped LaCrO₃. For simplicity, the arrangement of cations and anions is not to scale. Arrows indicate the attractive and repulsive electrostatic forces between ions

The transport of electron holes (polaron conductivity) can be formulated as charge transfer via a hopping mechanism, in which an electron is transferred from a Cr ion in one oxidation state to a neighboring Cr ion in a higher/lower oxidation state, possibly via an oxygen ion.

Electroneutrality can also be maintained by the formation of oxygen vacancies:

$${\mathrm{O}}_{\mathrm{O}}^{x}+{2\mathrm{Cr}}_{\mathrm{Cr}}^{\cdot }={\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}+\frac{1}{2}{\mathrm{O}}_{2}+{2\mathrm{Cr}}_{\mathrm{Cr}}^{x}$$

(11)

At equilibrium, we have:

$${K}^{\mathrm{o}}=\frac{\left[{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}\right]\times {[{\mathrm{Cr}}_{\mathrm{Cr}}^{x}]}^{2}\times {{p}}_{{\mathrm{O}}_{2}}^{1/2}}{[{\mathrm{O}}_{\mathrm{O}}^{x}]\times {[{\mathrm{Cr}}_{\mathrm{Cr}}^{\cdot }]}^{2}}$$

(12)

where K^o is the equilibrium constant of Eq. (11). This equation does not explicitly include the extrinsic point defect, but the concentration of point defects is involved in the charge neutrality condition:

$$\left[{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}\right]+2\left[{\mathrm{Cr}}_{\mathrm{Cr}}^{\cdot }\right]=2[{\mathrm{Sr}}_{\mathrm{La}}^{\mathrm{^{\prime}}}]$$

(13)

This means that under reducing conditions, the lattice oxygen transforms into a doubly charged oxygen vacancy, consuming two electron holes simultaneously. Thus, for Sr-doped LaCrO₃, La_1−xSr_xCrO₃ should be expressed as La_1−xSr_xCrO_3−δ due to the formation of oxygen vacancies, where the subscript δ is used to represent the oxygen nonstoichiometry. The drop in electronic conductivity with decreasing oxygen partial pressure is a reflection of the reduced electron hole concentration, $[{\text{h}}^{\cdot }]$. Nevertheless, under an oxidizing environment (${p}_{{\mathrm{O}}_{2}}$>10⁻⁸ atm, 1 atm = 1.013 × 10⁵ Pa), oxygen vacancies are negligible. Therefore, all charge compensation occurs primarily via a Cr³⁺ → Cr⁴⁺ transition, and the neutrality condition can be simply described as:

$$\left[{\mathrm{Sr}}_{\mathrm{La}}^{\mathrm{^{\prime}}}\right]=[{\mathrm{Cr}}_{\mathrm{Cr}}^{\cdot }]$$

(14)

The p-type (hole) electronic conductivity increases with the concentration of ${\mathrm{Sr}}_{\mathrm{La}}^{\mathrm{^{\prime}}}$ and becomes independent of oxygen partial pressure beyond a pressure threshold. At low oxygen partial pressure, ionic compensation becomes a dominant mechanism through the formation of oxygen vacancies, resulting in a significant drop in the electrical conductivity. Figure 4 gives the conductivity isotherms of Ca-doped LaCrO₃ at 1 000 °C [39], showing the electronic compensation mechanism at high ${p}_{{\mathrm{O}}_{2}}$ > 10⁻¹⁰ atm ($[{\mathrm{h}}^{\cdot }]$ is constant) and ionic compensation mechanism at low ${p}_{{\mathrm{O}}_{2}}$<10⁻¹⁰–10⁻¹⁵ atm ($[{\mathrm{h}}^{\cdot }]$ decreases). Nevertheless, the magnitude of the pressure threshold scales with the doping level.

Fig. 4

Copyright 1993, IOP Publishing

Conductivity isotherms at 1 000 °C for three different compositions, x = 0.1, 0.2 and 0.3, in La_1−xCa_xCrO_3−δ as a function of oxygen partial pressure. Modified with permission from Ref. [39].

However, LaCrO₃-based perovskites are well known to be characterized by a unique densification process and a unique surface/interface structure. The poor sinterability of LaCrO₃ can be ascribed to the formation of a thin layer of Cr₂O₃ condensed at the interparticle neck from CrO₃ vaporized from the convex parts of LaCrO₃ particles during the initial stage of sintering in air [41]. Sintering in reducing atmospheres and/or doping at the A and/or B sites can prevent the formation of a Cr₂O₃ layer by decreasing the CrO₃ vapor pressure without precipitation of La₂O₃. Yokokawa et al. showed that Ca doping enhances the LaCrO₃ sinterability due to the formation of unique surface/interface structures of Cr₂O₃, La₂O₃ and CaO compared to nondoped LaCrO₃ [41]. In addition to the sinterability, both experimental and theoretical results reveal that the electronic conductivity of LaCrO₃ is significantly increased by partial substitution of La ions in A sites by Ca, Sr, and Ba ions and reaches a maximum value with the Ca dopant [42].

The electronic conductivity through hopping of small polarons is thermally activated and is generally expressed as:

$$\sigma T={A}_{\mathrm{o}}\mathrm{exp}\left(-\frac{{E}_{\mathrm{a}}}{kT}\right)$$

(15)

where A_o is the pre-exponential constant and E_a is the activation energy, which can be obtained from the slope of the plots of log(σT) versus 1/T.

The strontium titanate perovskite SrTiO₃ provides an example of an n-type conductor. In contrast to LaCrO₃, where the Sr²⁺ cation on a La³⁺ site creates a negatively charged defect, trivalent La on a divalent Sr site creates a positively charged point defect, ${\mathrm{La}}_{\mathrm{Sr}}^{\cdot }$. The excess positive charge is compensated by the formation of a negatively charged electron:

$${\text{La}}_{2} {\text{O}}_{3} \xrightarrow{{{\text{SrTiO}}_{3} }}2{\text{La}}_{{{\text{Sr}}}}^{ \cdot } + 3{\text{O}}_{{\text{O}}}^{x} + 2{\text{Ti}}_{{_{{{\text{Ti}}}} }}^{\prime }$$

(16)

${\mathrm{Ti}}_{\mathrm{Ti}}^{\mathrm{^{\prime}}}$ is Ti³⁺ on a Ti⁴⁺ site and represents an electron localized on a Ti site. At low oxygen partial pressure and high temperature, the primary compensation mechanism is the reduction of Ti⁴⁺ to Ti³⁺. Different from the electron holes located in the valence band of Cr in Sr-doped LaCrO₃, electrons formed in ${\mathrm{Ti}}_{\mathrm{Ti}}^{\mathrm{^{\prime}}}$ are located in the conduction band formed by the overlap of the Ti 3d orbitals. As expected, the electronic conductivity of doped SrTiO₃ increases with decreasing oxygen partial pressure and decreases with temperature, behaving like a metallic conductor.

2.2 Electronic Structure and Defect Chemistry of Perovskite Electrodes

In SOFCs, the cathode is one of the most critical components and becomes a limiting factor for operation at intermediate to low temperatures due to the large energy barrier (i.e., activation energy) of the reaction compared to the ionic conductivity of the electrolyte [43,44,45]. Among the most common and extensively investigated perovskite electrodes are electronic conducting (La, Sr)MnO₃ (LSM) and MIEC (La, Sr)(Co, Fe)O_3−δ (LSCF) [46, 47]. The electrochemical activity and stability of perovskite electrodes are closely related to their electronic structure and defect chemistry [31].

2.2.1 LSM

LSM is the best known electronic conducting electrode material in SOFCs due to its high electrocatalytic activity for the ORR at high temperatures, high electronic conductivity, high structural stability and chemical compatibility with the YSZ electrolyte [46]. The electrical conductivity of LSM varies significantly with Sr doping and increases with temperature, a typical p-type conductor behavior, as shown in Fig. 5 [48]. The activation energies determined from the slope decrease with the Sr doping level, varying in the range of 24 to 3 kJ mol⁻¹. This suggests the predominant small polaron hopping mechanism for electrical conduction. The maximum conductivity was observed for LSM with a Sr doping level of x = 0.5. However, La_1−xSr_xMnO₃ with x = 0.1–0.2 is commonly used in SOFCs due to its sufficiently high conductivity (~ 200 S cm⁻¹ at 900 °C) and the compatible thermal expansion coefficient (11 × 10⁻⁶–12 × 10⁻⁶ K⁻¹) with the YSZ electrolyte.

Fig. 5

Reproduced with permission from Ref. [48]. Copyright 2000, Elsevier

Arrhenius plots of the electronic conductivity (σ) of La_1−xSr_xMnO_3+δ (0 $\leqslant$ x $\leqslant$ 0.7) in pure oxygen ($p_{{{\text{O}}_{{2}} }}$ = 1 bar, 1 bar = 100 000 Pa).

A detailed density functional theory (DFT) study by Pavone et al. showed that Sr substitution of A-site La leads to the formation of electron holes in the LSM electronic structure [49]. At SOFC operating temperatures, the electron holes are localized onto specific Mn ions, forming Mn⁴⁺ ions, ${\mathrm{Mn}}_{\mathrm{Mn}}^{\cdot }$, or electron holes, ${\mathrm{h}}^{\cdot }$, and causing local distortion of the LSM lattice. Due to the high oxygen vacancy formation energy [49,50,51,52], the oxygen vacancy concentration is too low to allow efficient oxygen ion diffusion in LSM. The neutrality condition can be simply described as:

$$\mathrm{SrO}\xrightarrow{{\mathrm{LaMnO}}_{3}}{\mathrm{Sr}}_{\mathrm{La}}^{\mathrm{^{\prime}}}+{\mathrm{Mn}}_{\mathrm{Mn}}^{\cdot }+{\mathrm{O}}_{\mathrm{O}}^{x}$$

(17)

LSM is somewhat unusual compared to most perovskite oxides in that it can have oxygen-excess as well as oxygen-deficient nonstoichiometries. One of the best examples is the oxygen nonstoichiometry of La_1−xSr_xMnO_3±δ as a function of oxygen partial pressure, ${p}_{{\text{O}}_{2}}$, temperature and composition reported by Mizusaki et al.; see Fig. 6 [53]. An oxygen-deficient region and an oxygen-excess region are observed (a typical example is given for La_0.9Sr_0.1MnO_3±δ). The oxygen content depends strongly on the oxygen partial pressure, exhibiting two plateaus: the oxygen-excess (3 + δ) region at high ${p}_{{\mathrm{O}}_{2}}$ and the stoichiometric (δ = 0) region at intermediate ${p}_{{\mathrm{O}}_{2}}$. With decreasing oxygen partial pressure, the oxides become oxygen deficient (3 − δ), and the formation of the positively charged ${\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}$ is compensated by the reduction of B-site Mn cations.

Fig. 6

Copyright 2000, Elsevier

Oxygen nonstoichiometry of La_0.9Sr_0.1MnO_3±δ as a function of oxygen partial pressure, clearly showing the oxygen-excess and oxygen-deficient regions. Modified with permission from Ref. [53].

Under normal SOFC operating conditions, LSM is in the oxygen-excess region and only becomes oxygen deficient at very low ${p}_{{\mathrm{O}}_{2}}$, e.g., < 10⁻¹⁰ Pa at 900 °C for x = 0.2. In the oxygen-excess region, there are two possibilities for maintaining the electrical neutrality disrupted by the oxidation of B-site Mn cations: formation of cation vacancies or interstitial oxide ions. The close-packed nature of the perovskite lattice implies that the structure cannot accommodate an excess of oxygen as interstitial oxygen ions. Thus, cation vacancies, rather than oxygen interstitials, are responsible for the oxygen-excess nonstoichiometry of LSM [50]. The oxygen-excess nonstoichiometry of LSM-based oxides is probably the most unique and interesting, as it is rarely observed in other perovskite-structured oxides. This is probably the main reason for the dominant electronic conductivity of doped LaMnO₃ cathode materials under SOFC operating conditions.

In the oxygen-deficient region, the predominant ionic defect is the oxygen vacancy, and charge compensation occurs by Mn reduction. Since electronic conduction in LSM is a hopping p-type mechanism irrespective of the oxygen content (δ < 0 and δ > 0), disproportion of Mn ions into Mn²⁺, Mn³⁺, and Mn⁴⁺ occurs [54]. This can be written as:

$$\frac{1}{2}{\mathrm{O}}_{2}+{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}+2{\mathrm{Mn}}_{\mathrm{Mn}}^{x}=2{\mathrm{Mn}}_{\mathrm{Mn}}^{\cdot }+{\mathrm{O}}_{\mathrm{O}}^{x}$$

(18)

$$\frac{1}{2}{\mathrm{O}}_{2}+{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}+2{\mathrm{Mn}}_{\mathrm{Mn}}^{\mathrm{^{\prime}}}=2{\mathrm{Mn}}_{\mathrm{Mn}}^{x}+{\mathrm{O}}_{\mathrm{O}}^{x}$$

(19)

where ${\mathrm{Mn}}_{\mathrm{Mn}}^{\cdot }$ is Mn⁴⁺ on a Mn³⁺ cation site and ${\mathrm{Mn}}_{\mathrm{Mn}}^{\mathrm{^{\prime}}}$ is Mn²⁺ on a Mn³⁺ site. Compared to the electronic conductivity, the ionic conductivity of LSM is much smaller. The oxygen ion conductivity of LSM materials was reported to be approximately 5.9 × 10⁻⁸ S cm⁻¹ under ${p}_{{\mathrm{O}}_{2}}$ of 10⁻¹ to 10⁻³ atm at 800 °C [55].

As the oxygen ion conductivity of LSM is very low, the TPB region is the dominant reaction site for the ORR. In addition to the very low ionic conductivity, the high activation energy of the reaction is also considered to be a limiting factor in the application of LSM-based cathodes for the ORR at reduced operating temperatures. For example, for the ORR on an LSM electrode, R_E is 0.4 Ω cm² at 900 °C and dramatically increases to 56 Ω cm² at 700 °C [56]. Thus, pristine LSM is not suitable for intermediate temperature (IT) SOFCs.

2.2.2 LSCF

Similar to LSM, LSCF is the best known MIEC ABO₃ perovskite electrode in SOFCs, and the most representative composition is La_0.6Sr_0.4Co_0.2Fe_0.8O_3−δ (or LSCF6428) [47]. LSCF is a typical acceptor-doped (acceptor dopants are cations with a lower oxidation state than the host cation) cobaltite perovskite-type oxide and is characterized by enhanced lattice oxygen vacancy formation, particularly at increased temperatures. For example, La_0.8Sr_0.2Co_0.2Fe_0.8O_3−δ is stoichiometric (i.e., δ = 0) at room temperature, whereas at 800 °C, δ is 0.02 in air [57] and increases to 0.07 at a low ${p}_{{\mathrm{O}}_{2}}$ of 1.4 × 10⁻³ atm [58]. The high concentration of oxygen vacancies in conjunction with the relatively high mobility allows LSCF-based oxides to exhibit high oxide ion conductivity. LSCF has a high electrical conductivity and shows metallic conduction behavior at high temperatures.

For acceptor-doped perovskite oxides such as LSCF, charge compensation can occur by both ionic and electronic defects. Thus, the charge compensation due to the dissolution of SrO in the La(Fe, Co)O₃ perovskite lattice can be described by a valence change of the B-site cations, e.g., Fe cations:

$$\mathrm{SrO}\xrightarrow{\mathrm{La}(\mathrm{Fe},\mathrm{Co}){\mathrm{O}}_{3}}{\mathrm{Sr}}_{\mathrm{La}}^{\mathrm{^{\prime}}}+{\mathrm{Fe}}_{\mathrm{Fe}}^{\cdot }+{\mathrm{O}}_{\mathrm{O}}^{x}$$

(20)

where ${\mathrm{Fe}}_{\mathrm{Fe}}^{\cdot }$ is the Fe⁴⁺ ion in a normal Fe³⁺ ion lattice site with a positive charge (similar to ${\mathrm{Cr}}_{\mathrm{Cr}}^{\cdot }$, functioning as an electron hole). Electrical neutrality can also be maintained by the formation of positively charged oxygen vacancies:

$$2\mathrm{SrO}\xrightarrow{\mathrm{La}(\mathrm{Fe},\mathrm{Co}){\mathrm{O}}_{3}}2{\mathrm{Sr}}_{\mathrm{La}}^{\mathrm{^{\prime}}}+{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}+{2\mathrm{O}}_{\mathrm{O}}^{x}$$

(21)

Since ionic compensation and electronic compensation occur simultaneously and compete with each other, the charge neutrality condition, assuming that only localized electronic charge carriers are present and charge compensation also occurs by the valence change of cobalt ions, can be expressed as:

$$\left[{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}\right]+\left[{\mathrm{Fe}}_{\mathrm{Co}}^{\cdot }\right]+\left[{\mathrm{Co}}_{\mathrm{Co}}^{\cdot }\right]=4\left[{\mathrm{Sr}}_{\mathrm{La}}^{\mathrm{^{\prime}}}\right]$$

(22)

The oxygen nonstoichiometry (δ) of LSCF is known to vary almost linearly with the logarithm of ${p}_{{\mathrm{O}}_{2}}$, indicating that the predominant defects in LSCF are oxygen vacancies, ${\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}$, i.e., the charge compensation in LSCF is dominated by Eq. (21) rather than Eq. (20). DFT calculations show that Sr substitution reduces the oxygen vacancy formation energy, ${\Delta G}_{\mathrm{f},\mathrm{vac}}$ [59]. ${\mathrm{Sr}}_{\mathrm{La}}^{\mathrm{^{\prime}}}$ defects produce electron holes that are partially delocalized across the oxygen sublattice, causing the oxygen sublattice to become susceptible to forming ${\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}$.

The electronic structure of LSCF is considered to be a combination of La_1−xSr_xCoO_3−δ (LSC) and La_1−xSr_xFeO_3−δ (LSF) perovskites. LSC and LSF have very different electronic structures, although their crystal structures are similar. In LSC, the conduction electrons are delocalized, and electrical conduction occurs with more band-like conduction via Co 3d/O 2p hybridization states. This is supported by the metal-like high conductivity of LSC [60]. In LSF, electrons and holes are localized with an adiabatic hopping-type conductivity of small polarons (through Fe³⁺ and Fe⁴⁺ sites) [61]. Thus, the electronic conduction in LSCF is a mixed conduction with band-like conduction by the Co 3d/O 2p hybridized orbital and hopping of small polarons [62]. The electrical conductivity of LSCF depends critically on the composition, as a change in composition changes both the crystal structure and the orbital configuration of valence electrons. The conductivity of LSCF increases with temperature up to a maximum and then decreases (see Fig. 7) [63, 64]. The temperature of the maximum conductivity of LSCF is affected by the Sr and Co contents at the A and B sites of LSCF. The electronic and ionic conductivities of LSCF-based materials critically depend on the defect chemistry of the materials, which is in turn closely related to the Co and Fe contents in the B-site lattice. Ritzmann et al. used DFT plus U (DFT + U) analysis to investigate the effect of Co addition at the B site of LSCF and reported a significant change in the electronic structure of the materials with a mixture of Co and Fe [65]. The electronic conduction changes from the p-type semiconducting behavior of La_0.5Sr_0.5FeO₃ to semimetallic behavior for the Co-containing compounds. The decrease in conductivity at high temperatures can be due to the metal-like conducting behavior, and the increase in oxygen vacancies at high temperatures also reduces the number of p-type electronic carriers.

Fig. 7

Copyright 1995, Elsevier

Electrical conductivity of a La_1−xSr_xCo_0.2Fe_0.8O₃ and b La_0.8Sr_0.2Co_1−yFe_yO₃ as a function of temperature in air, showing the change from semiconducting to metallic conducting behavior with the maximum conductivity temperature changing as a function of Sr and Co contents. Lines are added as a guide only. Modified with permission from Ref. [63, 64].

In such a mixed conductivity model, the conductivity of hybridized bands changes with changing oxygen vacancy concentration, while the hopping-type conductivity is more or less constant. Thus, regardless of the temperature, the conductivity decreases with decreasing ${p}_{{\mathrm{O}}_{2}}$ due to the decrease in the number of carrier holes with the increasing number of electrons in the Co 3d/O 2p hybridized orbital [66]. With the decrease in ${p}_{{\mathrm{O}}_{2}}$, Co³⁺ is preferentially reduced to Co²⁺, while Fe remains at a higher valence above 3 [67]. This indicates that the formation of oxygen vacancies is the dominant charge compensation mechanism in LSCF.

The oxide ion conductivity depends on the formation of oxygen vacancies. In LSCF, there are three possible oxygen vacancy formation sites, depending on the adjacent Co or Fe ions, $\mathrm{Co}-{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}-\mathrm{Co}$, $\mathrm{Co}-{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}-\mathrm{Fe}$, and $\mathrm{Fe}-{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}-\mathrm{Fe}$. The oxygen vacancy formation reactions can be expressed as:

$${\mathrm{O}}_{\mathrm{O}}^{x}+2{\mathrm{Co}}_{\mathrm{Co}}^{x}\to {\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}+2{\mathrm{Co}}_{\mathrm{Co}}^{\mathrm{^{\prime}}}+\frac{1}{2}{\mathrm{O}}_{2}$$

(23)

$${\mathrm{O}}_{\mathrm{O}}^{x}+{\mathrm{Co}}_{\mathrm{Co}}^{x}+{\mathrm{Fe}}_{\mathrm{Fe}}^{x}\to {\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}+{\mathrm{Co}}_{\mathrm{Co}}^{\mathrm{^{\prime}}}+{\mathrm{Fe}}_{\mathrm{Fe}}^{\mathrm{^{\prime}}}+\frac{1}{2}{\mathrm{O}}_{2}$$

(24)

$${\mathrm{O}}_{\mathrm{O}}^{x}+2{\mathrm{Fe}}_{\mathrm{Fe}}^{x}\to {\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}+2{\mathrm{Fe}}_{\mathrm{Fe}}^{\mathrm{^{\prime}}}+\frac{1}{2}{\mathrm{O}}_{2}$$

(25)

The preferable position for the formation of oxygen vacancies depends on the formation energy of oxygen vacancies, which is closely related to the local environment. Mastrikov et al. showed that oxygen vacancy formation preferably occurs at oxygen sites between Co ions, $\mathrm{Co}-{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}-\mathrm{Co}$ [68], while Ritzmann et al. indicated that the ${\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}$ defects prefer to form between one Fe³⁺ ion and one Co³⁺ ion, $\mathrm{Co}-{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}-\mathrm{Fe}$, based on a calculation on a supercell with 80 atoms [65]. Nevertheless, oxygen vacancy formation due to the increase in the Co content at the B site of the LSCF perovskite structure also simultaneously leads to increased electron defects. This is consistent with the increase in the electronic conductivity and the reduction in the peak temperature of the metallic conductivity behavior with the Co content (Fig. 7b) [63].

The electrochemical activity of the LSCF electrode for the ORR significantly decreases with decreasing temperature due to its high activation energy for the ORR (e.g., 135–150 kJ mol⁻¹). At temperatures below 600 °C, the reaction is increasingly driven to the electrode/electrolyte interface region due to the substantial decrease in the ionic conductivity of LSCF below 600 °C.

However, replacing La with Ba at the A site of LSCF can substantially enhance its oxygen ion conductivity and thus the electrochemical activity for the ORR at intermediate temperatures. Since the presence of Ba with a large ionic radius (Ba³⁺—0.16 nm; La³⁺—0.136 nm for CN = 12 [69]) is beneficial to forming a large lattice spacing for oxide ion movement, a higher Ba content in the perovskite leads to an enhanced ORR rate. Barium strontium cobalt ferrite (BSCF)-based materials are characterized by high oxygen deficiency, i.e., oxygen vacancy concentration, and thus high oxygen mobility due to their low oxygen vacancy formation energy and low oxygen vacancy migration barrier [70, 71]. The best example is Ba_0.5Sr_0.5Co_0.8Fe_0.2O₃, which has been reported to show a high activity for the ORR and high oxygen exchange kinetics with high oxygen exchange coefficient and surface exchange coefficient [72, 73].

2.3 Oxide Ion Conductivity in Fluorite-Type Oxides

Fluorite-type oxides are the main ionic conductors and are used as electrolyte materials in SOFCs. The fluorite-type structure (CaF₂) is a face-centered cubic structure and has the general formula MO₂, where M is a large tetravalent cation, e.g., Zr⁴⁺, Ce⁴⁺, and Th⁴⁺, and the anion is an oxygen ion (see Fig. 8). To form the fluorite structure in MO₂, the minimum ionic radius ratio (i.e., the ratio of the M ion radius to the O anion radius) is 0.732. This structure is rather open, which is beneficial for rapid ion diffusion.

Fig. 8

Fluorite structure and the scheme of replacement of Zr⁴⁺ by Y³⁺, forming oxygen vacancies

The oxide ion conductivity is generally related to the lattice defect structure in metal oxides. There are three probable defect models in this case: (i) an oxygen vacancy model with all metal ions fixed at their lattice sites, (ii) a cation interstitial model with all oxygen ions fixed at their lattice sites (Frenkel type), and (iii) a mixed oxygen vacancy and cation interstitial model (the Schottky type). In the case of stabilized ZrO₂, the defect structure is the oxygen vacancy model. This also applies for stabilized ceria and other fluorite-type oxide ion conductors.

The best known example is Y₂O₃-stabilized ZrO₂ or YSZ. Dissolution of Y₂O₃ in ZrO₂ results in incorporation of Y³⁺ on the Zr⁺⁴ cation sites with concomitant formation of positively charged oxygen vacancies, ${\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}$, as charge compensation defects. The defect formation reaction can be written as:

$${\mathrm{Y}}_{2}{\mathrm{O}}_{3} \xrightarrow{{\mathrm{ZrO}}_{2}}{\to } 2{\mathrm{Y}}_{\mathrm{Zr}}^{\mathrm{^{\prime}}}+3{\mathrm{O}}_{\mathrm{O}}^{x}+{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}$$

(26)

where ${\mathrm{Y}}_{\mathrm{Zr}}^{\mathrm{^{\prime}}}$ is the Y³⁺ ion in the Zr⁴⁺ lattice site with a negative charge and ${\mathrm{O}}_{\mathrm{O}}^{x}$ is a normal oxygen lattice site. The oxygen vacancy concentration is given simply by the electroneutrality condition. In this case, for every two Y³⁺ occupations of the Zr⁴⁺ cation lattice site, one oxygen vacancy is generated.

$$2\left[{\mathrm{Y}}_{\mathrm{Zr}}^{\mathrm{^{\prime}}}\right]= \left[{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}\right]$$

(27)

Thus, oxide ion conduction occurs through oxygen vacancies. The oxide ion conductivity increases with temperature and dopant concentration. The conductivity of YSZ increases with increasing Y₂O₃ content, reaching a maximum for YSZ with 8 mol% (mol% means the mole percentage) Y₂O₃ and then decreasing with a further increase in Y₂O₃ content. A similar dependence of the conductivity on the dopant concentration has been observed for other dopants (see Fig. 9) [74]. The Y₂O₃ content that corresponds to the maximum conductivity is nearly independent of temperature. The decrease in conductivity is attributed to the formation of dopant-vacancy pairs or defect clusters according to:

Fig. 9

Reproduced with permission from Ref. [74]. Copyright 1999, Elsevier

Dependence of the conductivity of (ZrO₂)_1−x(Ln₂O₃)_x on the dopant concentration, measured at 1 000 °C.

$${\mathrm{Y}}_{\mathrm{Zr}}^{\mathrm{^{\prime}}}+ {\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}={\left({\mathrm{Y}}_{\mathrm{Zr}}^{\mathrm{^{\prime}}}-{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}\right)}^{\cdot }$$

(28)

$${2\mathrm{Y}}_{\mathrm{Zr}}^{\mathrm{^{\prime}}}+ {\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}={\left({\mathrm{Y}}_{\mathrm{Zr}}^{\mathrm{^{\prime}}}-{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}-{\mathrm{Y}}_{\mathrm{Zr}}^{\mathrm{^{\prime}}}\right)}^{x}$$

(29)

in which the superscript ⋅ indicates the defect cluster with a positive charge and x the neutral defect cluster. These defect clusters trap oxygen vacancies, reducing the defect mobility and thus the conductivity.

The formation of such defect clusters or associates is due to Coulombic and elastic attractive forces between ${\mathrm{Y}}_{\mathrm{Zr}}^{\mathrm{^{\prime}}}$ and ${\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}$ and is affected by the binding enthalpy, E_a, which is more dominant at low temperatures. Based on Eq. (6), the oxide ion conductivity can be expressed by:

$$\sigma =(nze)\mu =ze\mu \left[{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}\right]$$

(30)

The mobility µ is given by:

$$\mu =\frac{B}{T}\mathrm{exp}\left(-\frac{{E}_{\mathrm{m}}}{RT}\right)$$

(31)

where E_m is the enthalpy for the motion and B is a constant. The activation energy for oxide ion conduction E_i is also related to the valence of the dopant due to the association effects between dopant cations and their charge compensation defects, and it can be expressed in a more general form as follows [75]:

$${E}_{\mathrm{i}}={E}_{\mathrm{m}}+\frac{2}{n}{E}_{\text{a}}$$

(32)

where n is equal to 1 or 2 for a di- or trivalent dopant, respectively. At higher temperatures, defect clusters tend to dissociate, forming free ${\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}$, while at lower temperatures, defect clusters or associates prevail, significantly affecting the population of free vacancies. This is reflected by the distinctive curvature of the Arrhenius curves (activation energy plots) of the electrical conductivity of doped ZrO₂ systems [74]. YSZ shows a higher activation energy at lower temperatures, and the activation energy at low temperatures increases with dopant concentration, which is characteristic of dopant ions acting as nucleating agents for the formation of dopant-vacancy pairs or defect clusters.

The minimum dopant content necessary to stabilize ZrO₂ in the cubic structure is close to the composition that gives the highest conductivity: 8 mol% Y₂O₃, 10 mol% Sc₂O₃, 15 mol% Nd₂O₃, 10 mol% Sm₂O₃, and 10 mol% Gd₂O₃. This maximum corresponds to the minimum dopant level required to fully stabilize the high-temperature cubic phase. A further increase in the dopant content results in the formation of oxygen vacancy-dopant clusters, as discussed above. The conductivity and activation energy for oxygen ion conduction depend strongly on the dopant ionic size for the ZrO₂-Ln₂O₃ system (Fig. 10) [74].

Fig. 10

Reproduced with permission from Ref. [74]. Copyright 1999, Elsevier

Maximum conductivities, oxygen ion migration enthalpy and association enthalpy of doped ZrO₂ for a specific dopant concentration as a function of the dopant ionic radius.

Sc-doped ZrO₂ shows the lowest ion migration enthalpy and highest conductivity. ZrO₂ doped with 9.0 to 9.3 mol% Sc (ScSZ) has a conductivity of 0.34–0.36 S cm⁻¹ at 1 000 °C [76], higher than that of YSZ. The higher oxide ion conductivity of ScSZ is attributed to the smaller mismatch in size between Zr⁴⁺ (0.084 nm) and Sc³⁺ (0.087 nm) ions compared to that between Zr⁴⁺ (0.084 nm) and Y³⁺ (0.101 9 nm) ions. The ion migration enthalpy increases with increasing dopant ionic radius due to the elastic strain energy induced by the size difference on the cation lattice. This indicates that the diffusion of oxygen ion vacancies is closely related to the elastic strain energy, i.e., the size mismatch between the dopant and host cations.

Similar to the case of stabilized ZrO₂, the conductivity of the doped CeO₂ electrolyte increases with the dopant concentration to a maximum and then decreases with a further increase in the dopant concentration [77]. The maximum conductivity with the doping level is also due to the interaction between the dopant and oxygen vacancies, leading to the formation of dopant-vacancy clusters, ${(\mathrm{M}}_{\mathrm{Ce}}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}-{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot})\mathrm{ or }(2{\mathrm{M}}_{\mathrm{Ce}}^{\mathrm{^{\prime}}}-{\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot})$, where M is a dopant with divalent or trivalent charge.

3 Equipotential Line Distribution and RE Placement

In SOFCs, the position of the RE and its effect on the measurement of the equipotential line have been extensively studied by computational modeling and experimental approaches [78,79,80,81,82,83,84,85,86,87,88,89,90]. This issue is important because it is essentially related to the cell configuration design and reliability of the accurate measurement of the polarization losses and impedances of individual electrode and electrolyte processes. Despite the great effort, there are considerable discrepancies regarding the reliability and suitability of the RE in polarization and impedance measurements in SOFCs. We will examine the issue from idealized cell and experimental aspects of the studies.

3.1 Idealized Cell

Figure 11 shows a thin flat-plate cell with a thin dense oxygen ion conducting electrolyte sandwiched by two active working and counter electrodes (the WE and the CE) and an RE placed on the surface of the inactive region of the electrolyte [91]. The distance between the edge of the active electrodes and the inactive region of the electrolyte is approximately three electrolyte thicknesses [92]. Under these idealized conditions, the cell voltage measured between the WE and the CE (V_Cell) can be divided into V₁ and V₂. V₁ contains the overpotential of the WE plus some fraction of the cell iR drop, and V₂ contains the overpotential of the CE plus the remaining fraction of the cell iR drop (Fig. 11b). Similarly, the cell impedance (Z_Cell) can be separated into Z_CE and Z_WE (Fig. 11d). In such ideal cells, the equipotential line will be in the middle of the solid electrolyte.

Fig. 11

Reproduced with permission from Ref. [91]. Copyright 2020, Elsevier

Ideal electrolyte cell with an RE in a thin electrolyte. a Cell geometry, b separation of cell potential, c equivalent circuit of the idealized cell, and d separation of cell impedances.

The separation of the polarizations and impedances of electrode reactions in an idealized cell, as shown in Fig. 11, can be validated on symmetric cells in which the WE and CE are identical not only in the electrode/electrolyte contact interfaces but also in their electrochemical behavior (resistance and capacitance). Figure 12 shows an example of symmetric cells with a La_0.8Sr_0.2MnO₃ (LSM) electrode on a YSZ electrolyte measured at 800 °C in air. The polarization performance of the cell can be divided into the polarization losses for the ORR that occurred at the WE and for the O₂ evolution reaction (OER) that occurred at the CE (Fig. 12a). For the reaction at 800 °C under open-circuit conditions, i.e., overpotential or dc bias = 0 mV, the impedance responses on the WE and the CE are identical and characterized by a slightly depressed semicircle (Fig. 12b). The polarization resistance for the ORR in the reaction is 3.9 Ω cm², very close to 3.83 Ω cm² for the reaction on the CE. The sum of electrode polarization resistances measured for the ORR and OER is 7.73 Ω cm², which is also close to the value of 8.0 Ω cm² obtained for the full cell. This indicates the excellent separation of the individual electrode processes at the WE and the CE via the RE due to the fact that in such symmetric cells, the equipotential line is in the middle of the solid electrolyte. This is consistent with the computational calculations that cell configurations with symmetric electrodes and similar electrochemical characteristics introduce little distortion into electrode impedance responses [79, 87]. In fact, symmetric cells are commonly used to investigate the electrode performance, performance degradation, and reaction mechanism and kinetics of the ORR in SOFCs [93,94,95,96,97,98,99,100,101] and the OER in SOECs [102,103,104,105,106,107,108,109].

Fig. 12

Polarization and impedance curves of the oxygen reaction on symmetric LSM electrode/YSZ electrolyte cells, measured between the WE and the CE (the cell), on the WE and on the CE at 800 °C in air. Impedance responses were measured under open-circuit conditions

Caution should be taken in that the reversibility of symmetric cells is a strong function of both the operating conditions (e.g., dc bias and operating temperature) and electrode materials. A recent study on the reversibility of the symmetric cell configuration for Pt, La_0.8Sr_0.2MnO₃ (LSM) and La_0.6Sr_0.4Co_0.2Fe_0.8O₃ (LSCF) electrodes showed that the reversibility of the ORR at the WE and the OER at the CE strongly depends on the reversibility of the electrode/electrolyte interface in the oxygen incorporation/exsolution process, which in turn is closely related to the oxygen ion conductivity of the electrode and to a lesser extent to the ionic conductivity of the electrolyte [91]. Figure 13 shows a typical example of the impedance responses of a symmetric cell with LSM electrodes, measured at different temperatures and dc biases [91]. The reversibility of the LSM symmetric cells decreases with decreasing temperature and increasing dc bias. In contrast, the LSCF electrode shows a much higher degree of reversibility than LSM, indicating that the MIEC properties of the electrode materials enhance the reversibility. In the case of the Pt electrode, the oxygen reaction is essentially not reversible, consistent with the poor electrocatalytic activity of Pt electrodes for the ORR and OER at high temperatures [91, 110,111,112]. Nevertheless, the symmetric cell configuration is a useful tool for the investigation of oxygen electrodes in solid oxide cells. Tao et al. studied the ORR/OER performance of LSCF/samaria-doped ceria (SDC) composite electrodes on SDC interlayer/YSZ electrolyte cells with a porous LSCF current collector layer [113]. By controlling the SDC content, as well as the thickness and porosity of the LSCF catalyst layer, the gas diffusion rate and the conduction networks for electrons and oxide ions could be optimized, resulting in a marked reduction in the overpotential for the ORR and OER.

Fig. 13

Reproduced with permission from Ref. [91]. Copyright 2020, Elsevier

Impedance spectra of the full cell, the WE and the CE for the reaction in an LSM symmetric cell with a YSZ electrolyte, measured under various dc biases at 800 °C, 750 °C and 700 °C.

In reality, achieving perfect alignment is almost impossible, particularly for small and thin electrolyte button cells. In 1998, Winkler et al. [86] theoretically showed that minor misalignment of the WE and the CE can cause significant errors in the measured polarization resistance of the WE, and the major reason for the impedance distortions is the change in the potential distribution inside the electrolyte. Adler used finite element calculations to simulate the half-cell impedance responses and showed that an electrode misalignment of only 11% of the electrolyte thickness can cause a measurable difference in the ohmic resistance and a ~ 10% error in the electrode polarization resistance of half-cells [78].

Cimenti et al. studied in detail the impedance distortions as a function of the position and geometry of the electrodes in solid electrolyte cells [79, 87]. The results indicate that the distortion increases with increasing misalignment, i.e., the differences in the electrode area, as shown in Fig. 14 [87]. With increasing difference in the electrode areas (i.e., r = A_CE/A_WE), both the size and high frequency intercept of the WE impedance (Z_WE) increase, while the cell impedance (Z_TOT) decreases, leading to merged Z_WE and Z_TOT. The overlap of Z_TOT and Z_WE indicates that Z_WE contains a contribution from the CE, leading to overestimation of the WE impedance. At high frequencies (ω → ∝), the equipotential line is shifted toward the CE/electrolyte interface (Fig. 14c). Differences in the two active electrode areas are commonly observed, particularly in the case of anode-supported thin electrolyte cells, in which the area of the anode is much larger than that of the cathode. For example, McIntosh et al. [114] showed that the cathode impedance is very close to the total cell impedance of anode-supported cells, indicating the limitation of the RE in impedance separation for electrode reactions of anode-supported thin electrolyte cells. Similar observations were also reported by others [115, 116].

Fig. 14

Reproduced with permission from Ref. [87]. Copyright 2007, WILEY‐VCH Verlag GmbH & Co. KGaA, Weinheim

a Asymmetric cell geometry with different WE and CE areas, b Z_WE and Z_TOT changes with the change in the ratio of the CE to WE area and c equipotential lines probed by the RE in the primary (ω → ∝) and secondary (ω → 0) potential distributions.

Misalignment between two active electrodes can also be caused by the significant differences in the microstructure and electrochemical characteristics of the electrodes. One of the best examples is cells with LSM cathodes and Ni/YSZ cermet anodes. LSM is a dominant electronic conductor with negligible ionic conductivity, and the reaction is restricted mainly to the TPB (where electrode, electrolyte and oxygen gas molecules meet) [46]. In contrast, the Ni/YSZ cermet is a two-phase composite with an electronic conducting Ni phase and an oxygen ion conducting YSZ phase, i.e., an MIEC material. Thus, during the fuel oxidation reaction on Ni/YSZ cermet anodes, the fuel reaction sites will be extended into the electrode bulk due to the presence of an ion-to-ion conducting YSZ network in the cermet and the formation of a TPB of the electronic conducting Ni phase, ionic conducting YSZ phase and fuel reactant [117, 118]. The differences in the electronic and ionic conductivities of the electrode materials will cause significant differences in the location of the TPB, i.e., the electrode/electrolyte interface contacts. Such asymmetries in the interfacial contacts lead to distortion of the potential distribution and a change in the equipotential line, which does not depend on the electrolyte thickness.

In addition to the alignment of active electrodes, the contact between the electrode coating and current collector also affects the equipotential line/surface in a cell [25]. The contact areas affect both the ohmic and polarization resistances of the cell. This will be discussed in detail in the Constriction section.

3.2 Experimental Approaches

Symmetric cells with two identical electrodes on both sides of the electrolyte have the advantage of simplicity in cell configuration without the complications associated with the position of the RE. However, this is an indirect method that allows the measurement of the electrode impedance of only one kind of interface. Symmetric cells also have limitations in the polarization performance under dc bias due to the significant deviation of the cells from reversibility under dc bias or overpotential. As the majority of the cells in SOFCs are unsymmetrical in nature, i.e., cells with different types of anodes and cathodes, three-electrode cells with an additional RE are required to allow the separation of the individual interface impedance and polarization losses. Small-sized cells with diameters of 10–20 mm are commonly used in SOFCs, in which the ring-shaped RE is placed on the electrolyte surface of the CE side or the edge of the electrolyte disc to minimize the effect of changing gas partial pressure of the WE on the RE potential [119,120,121,122]. Other types of RE were also reported. Hashibon et al. suggested a patterned RE very close to the WE with negligible ohmic contribution from the electrolyte [123]; however, in reality, such a patterned RE in thin electrolyte cells is difficult to fabricate, and making good electronic contact with micron-scale electrodes is also difficult. Ostergard et al. presented a Luggin-type RE for thick electrolyte cells [124], which is considered to be analogous to using a Luggin capillary in an aqueous electrolyte. However, this is a complex design, and thick pellets with an internal channel for the Luggin-type RE are not easy to fabricate. The thick electrolyte (~ 20 mm) may also limit the practical and technologically meaningful current density that can be achieved. Figure 15 shows a typical thick electrolyte cell with a Luggin-type RE and a planar cell configuration commonly used in performance measurement and isolation in SOFCs. Small button cells with circular WE and CE with diameters of 10–20 mm or relatively large planar cells with large sizes (e.g., 50 mm × 50 mm) are often used.

Fig. 15

Cell configurations used in performance measurements in SOFCs. a Thick electrolyte pellet cells with a Luggin-type RE, b two-electrode symmetric cell, c three-electrode cell with an RE, and d three-electrode cell with two REs for large planar cells

Various designs and approaches have been suggested to improve the accuracy and reliability of REs in solid electrolyte cells [80, 123,124,125,126,127]. Barfod et al. presented a method to accurately separate the impedance responses measured on a full cell into the contributions from the anodic hydrogen oxidation and cathodic oxygen reduction reactions [125]. However, this method requires prior knowledge of the frequency domains of the different processes of the anodic and cathodic reactions. A similar subtraction method was also used by Birss et al. to derive the polarization performance of Ni/YSZ anodes deposited using electrophoretic methods on the inner YSZ electrolyte surface of microtubular SOFCs by first performing two-electrode impedance measurements of the symmetric cell [128]. Offer et al. also reported an indirect method using electrochemical impedance spectroscopy to correct for errors in the measurement of the WE overpotential during polarization arising from a shift in the electrolyte current distribution under load [126]. However, from the performance point of view, the most straightforward solution is to design a special cell configuration that has the capability to directly measure and assess the individual electrode processes.

Before the design of such a special cell configuration, we need to examine the equipotential line distribution in an idealized thin, flat-plate cell, as shown in Fig. 11. In this case, the electric field between the cathode and anode is uniform. Therefore, the equipotential line will be present within the electrolyte between the active anode and cathode (see Fig. 16). The requirement of the RE being on an inactive surface of the electrolyte is satisfied for a specific aspect ratio (e.g., > 3), which is defined as the distance between the RE and the edge of the active electrode divided by the electrolyte thickness.

Fig. 16

Equipotential line/surface location (the dotted line) and partitioning of the cell resistances in a thin electrolyte cell with symmetric contacts at both electrode/electrolyte interfaces

Let us start by examining the resistance distribution and measurement in an SOFC. In a solid electrolyte cell, based on Fig. 16, the total cell resistance, R₁, can be obtained by:

$${R}_{1}={R}_{\mathrm{A}1}+{R}_{\mathrm{C}1}$$

(33)

where R_A1 and R_C1 are the anodic and cathodic partitioning resistances of R₁ measured by a conventional voltage probe (VP1) against the RE, respectively. R_A1 includes the contact resistance between the anode and current collector, anode resistance and part of the electrolyte resistance, and R_C1 includes the contact resistance between the cathode and current collector, cathode resistance and remaining electrolyte resistance. The anodic and cathodic partitioning resistances can also be measured through an imaginary voltage that is not in contact with the current collector, VP2. In this case, the measured resistance will mainly be the electrolyte resistance, R₂:

$${R}_{2}={R}_{\mathrm{A}2}+{R}_{\mathrm{C}2}$$

(34)

As the reference potential samples on average the equipotential line in the cell, the partitioning of the cell resistances can be used to indicate the location/position of the equipotential line. Therefore, the resistance partitioning results measured by VP1 and VP2 should give the same assessment of the equipotential line. Under idealized conditions, the equipotential line lies within the electrolyte, and thus, the cell voltage (V_Cell) and cell impedance can be separated into two half-cell voltages and impedances.

3.3 Assessment of the Equipotential Line with Special Voltage Probes

Thus, to independently separate the polarization losses and impedances of individual electrode processes, measuring the resistance fraction or partitioning of the associated electrode processes is clearly essential. A conventional voltage probe cannot accurately separate the anodic and cathodic partitioning resistances due to the large contribution of the contact resistance between the electrode and the current collector (CC). To overcome this problem, we designed a special cell configuration in which VP1 is the conventional voltage probe attached to the CC and VP2 is a special voltage probe that is electrically isolated from the CC (Fig. 17) [90, 129]. For the benefit of the readers, the functions of VP1 and VP2 and the corresponding measured resistances are summarized in Table 1 [90].

Fig. 17

Copyright 2001, IOP Publishing

Cell configuration and arrangement of conventional and special voltage probes (VP1 and VP2) with REs. A and C represent the anode and cathode sides, respectively, and the cell typically has an area of 5 cm × 5 cm. An optical image of a Pt woven mesh CC is shown in the figure. Modified with permission from Ref. [129].

Table 1 Resistances measured by VP1 and VP2

Figure 18 shows an example of polarization curves measured on a YSZ electrolyte cell with a Pt anode and a Pt cathode by a galvanostatic current interruption (GCI) technique at 900 °C [90]. The total cell resistance measured by VP1, R₁, is 1.23 Ω cm², which is much higher than the electrolyte resistance measured by VP2, R₂ = 0.61 Ω cm², indicating the existence of significant contact resistance between the electrode and the electrolyte. The GCI curves measured between VPs on the same electrode sides primarily consist of iR losses, which are characteristics of the contact resistance [129]. From the curves, the electrode/CC contact resistances of the anode and cathode sides (R_A/C and R_C/C) are 0.34 and 0.29 Ω cm², respectively. The very high polarization losses, ~ 230 mV at 25 mA cm⁻², measured between voltage probes are actually due to the fact that Pt is a very poor electrode for both the HOR and ORR at high temperatures. The cathodic resistance measured between CVP1 and A_ref is very small, R_C1 = 0.08 Ω cm². In contrast, the anodic resistance measured between AVP1 and C_ref, R_A1, is 1.17 Ω cm². The most interesting observation is the GCI curves measured between CVP2 and A_ref on the Pt cathode side, showing an unusual and depressed GCI curve. However, from the instantaneous potential drop immediately after the current interruption, the resistance between CVP2 and A_ref can be measured, and R_C2 is 0.24 Ω cm². In contrast, a normal GCI curve is observed between AVP2 and C_ref, giving R_A2 = 0.82 Ω cm².

Fig. 18

Copyright 2017, IOP Publishing

GCI curves measured between various VPs and REs on a cell with a Pt anode and a Pt cathode at 25 mA cm⁻² and 900 °C. The thickness of the 3 mol% Y₂O₃-doped ZrO₂ (3YSZ) electrolyte plate is approximately (108 ± 4) μm. The circle indicates the depressed polarization decay. Modified with permission from Ref. [90].

Let us briefly discuss the physical significance of resistance components R₁, R₂, R_A/C and R_C/C. R₁ is the total cell resistance, as shown by the arrangement of VP1, while R₂ is dominantly the electrolyte resistance because VP2 is isolated from the current collect with no current passing through the probe. R_A/C and R_C/C are physically the contact resistances between the electrode and CC, as they are measured from VPs on the same electrode side.

With respect to the resistances, we can also identify the positions of various VPs. For example, AVP2 would be positioned between R_A/C and R₂, and CVP2 would be positioned between R_C/C and R₂. Similarly, AVP1 and CVP1 would be positioned outside R_A/C and R_C/C, respectively. The equipotential line can be estimated based on the anodic and cathodic partitioning resistances of the cell, R_A1 and R_C1. Based on the resistance values, the resistance distribution in the cell with a Pt anode and a Pt cathode along with the estimated equipotential line location can be obtained, as shown in Fig. 19.

Fig. 19

Copyright 2017, IOP Publishing

Resistance distribution and partitioning of the cell resistances in a YSZ electrolyte cell with a Pt cathode and a Pt anode at 900 °C, showing the equipotential line location (the dotted line) within the Pt cathode. The scanning electron microscopy (SEM) micrographs show asymmetric contacts at the electrode/electrolyte interface, showing that the Pt anode/electrolyte interface contact is much smaller than that at the Pt cathode/electrolyte interface. The unit for R is Ω cm^-2. Modified with permission from Ref. [90].

From the resistance partitioning, the total resistance in a solid electrolyte cell consists of three components:

$$R_{1} = R_{{{\text{A}}/{\text{C}}}} + R_{2} + R_{{{\text{C}}/{\text{C}}}} = R_{{{\text{A}}1}} + R_{{{\text{C}}1}} = 0.34 + 0.61 + 0.29 \approx 1.17 + 0.08 \approx 1.23\;\;(\Omega {\text{cm}}^{2})$$

(35)

For the cell with a Pt anode and a Pt cathode, the measured anodic partitioning resistance, R_A1, is 1.17 Ω cm², very close to the cell resistance, R₁ = 1.23 Ω cm². Additionally, the cathodic partitioning resistance, R_C1, is 0.08 Ω cm², which is much smaller than the cathode contact resistance, R_C/C = 0.29 Ω cm². This indicates that the partitioning of the electrolyte resistances cannot be within the electrolyte bulk and that the equipotential line is located inside the Pt cathode in the vicinity of the Pt cathode/YSZ electrolyte interface region. This may be the reason for the depressed GCI responses observed for CVP2 against the RE. This in turn indicates that the cathodic resistance fraction, R_C2, measured between CVP2 and A_Ref. becomes negative, as it is outside the electrolyte. By the definition of Eq. (34), we have:

$$R_{2} = R_{{{\text{A}}2}} + R_{{{\text{C}}2}} = 0.82 + \left( { - 0.24} \right) = 0.58\;\;\Omega\,{\text{cm}}^{-2}$$

(36)

This is very close to the measured value of 0.61 Ω cm². The shift of the equipotential line for the cell with Pt electrodes is consistent with the microstructure of the cell, showing a highly porous Pt anode in comparison with the Pt cathode. Thus, the contact areas at the Pt anode/YSZ electrolyte interface would be much smaller than the contact area between the Pt cathode and the YSZ electrolyte. This will push the equal potential line toward the Pt cathode side, as shown in Fig. 19.

The same tests were also carried out for a thin YSZ electrolyte cell with a Ni/YSZ cermet anode and a La_0.8Sr_0.2MnO₃ (LSM) cathode, and based on the results, the resistance distribution with estimation of the equipotential line location was observed, as shown in Fig. 20 [90]. Similar to the cell with Pt electrodes, R_C1 and R_A1 are also far from equal, but R_C1 is much higher than R_A1 and is close to the total cell resistance, R₁. The results indicate that the location of the equipotential line is inside the Ni/YSZ cermet anode rather than inside the LSM cathode. This is consistent with the much higher interface contact area between the Ni/YSZ cermet anode and the YSZ electrolyte due to the existence of an ionic conducting YSZ-to-YSZ network in the cermet. In the case of the LSM cathode, the interface contact is restricted to the cathode/YSZ electrolyte interface. The resistance values measured on both cells are given in Table 2. However, different from the cell with a Pt cathode and a Pt anode, the anodic resistance fraction, R_A2, measured between AVP2 and C_ref becomes negative, as it is outside the electrolyte. By the definition of Eq. (34), we also have:

Fig. 20

Copyright 2017, IOP Publishing

Resistance distribution and partitioning of the cell resistances in a YSZ electrolyte cell with an LSM cathode and a Ni/YSZ cermet anode at 800 °C, showing the equipotential line location (the dotted line) within the Ni/YSZ cermet anode. The SEM micrographs show asymmetric contacts at the electrode/electrolyte interface, showing that the Ni/YSZ cermet anode/electrolyte interface contact area is much higher than that at the LSM cathode/electrolyte interface due to the presence of YSZ-to-YSZ networks in the cermet. The Ni phase in the Ni/YSZ cermet was removed by acid treatment. The unit for R is Ω cm^-2. Modified with permission from Ref. [90].

Table 2 List of resistances measured on a cell with a Pt cathode and a Pt anode in Ω cm², measured at 900 °C, and a cell with an LSM cathode and a Ni/YSZ cermet anode, measured at 800 °C

$$R_{2} = R_{{{\text{A}}2}} + R_{{{\text{C}}2}} = \left( { - 0.32} \right) + 1.07 = 0.75\;\;(\Omega\, {\text{cm}}^{2})$$

(37)

This is very close to the measured electrolyte resistance of 0.77 Ω cm².

Ciucci et al. studied the distribution of the electrochemical equipotential and transport interaction, i.e., the flux of both ionic and electronic species, through a mixed ionic and electronic conductor (e.g., SDC in this case) with an electrochemically active surface in a uniform gas environment (H₂-H₂O-Ar) using an adaptive finite element method [130]. SDC serves as both the active electrocatalyst for the reaction and the electrolyte through which ions are transported. In addition to the ionic flux that flows through the SDC electrolyte, there are two currents: a cross-plane (CP) current that flows in a general direction as the ionic current and an in-plane (IP) current that flows between the redox-active SDC surface and the metal CCs, as shown in Fig. 21 for a typical set of conditions. The ionic (i.e., oxygen vacancy) equipotential and flux lines bend gently around the metal/SDC interface but are linear through the bulk of the cell. In contrast, the equipotential and flux lines for electrons are not linear even at some distance from the termination of SDC. In addition to the flow of an electronic current between metal electrodes, an electronic current flows laterally between the metal electrode and the SDC redox-active surface (i.e., the IP current). The termination of the ionic current at the metal electrode/SDC electrolyte interface is based on the assumption that the metal/MIEC interface blocks the ionic species. However, if the electrode is MIEC or ionic conductivity develops in the vicinity of an electronically dominant electrode such as LSM under polarization conditions in SOFCs [131, 132], then the ionic current could propagate into the electrode bulk, i.e., ionic equipotential and flux lines will be within the electrode bulk of solid electrolyte cells. This is experimentally demonstrated by the measurement of the presence of ionic equipotential lines within the cathode in the case of the cell with Pt cathode and anode and within the anode for the cell with an LSM cathode and a Ni/YSZ cermet anode, as shown in Figs. 19 and 20.

Fig. 21

Reproduced with permission from Ref. [130]. Copyright 2011, Royal Society of Chemistry

Electronic and ionic electrochemical equipotential lines (thin) and corresponding current flux lines (thick) computed for a typical set of conditions (T = 650 °C, ${p}_{{\mathrm{O}}_{2}}$ = 4.1 × 10⁻²⁶ atm, at which the electronic transfer number is 0.86) for three representative reaction rate constants: a, b k⁰ = 3 × 10⁻⁷ Ω⁻¹ cm⁻² atm^−1/4, c, d k⁰ = 6 × 10⁻⁷ Ω⁻¹ cm⁻² atm^−1/4, and e, f k⁰ = 3 × 10⁻⁵ Ω⁻¹ cm⁻² atm^−1/4. Only the region close to the interface is shown; the potentials and fluxes are essentially linear beyond the plotted region. The hatched area in (a) is the surface-influence zone.

Due to the StS contact at the electrode/electrolyte interface, the electric field is not uniform. Charge transfer can occur at the physical interface between the electrode and the electrolyte as well as within the solid electrode, depending on the migration of charge carriers such as ions and electrons. This is particularly the case for MIEC materials and composite electrodes [133,134,135]. Considering the experimental results of Fig. 20, the contact at the LSM/YSZ interface is not continuous and is primarily restricted to the physical boundary between LSM and YSZ due to the electronically dominant LSM electrode materials. In contrast, the Ni/YSZ cermet is a two-phase system with an electronic conducting Ni phase and an ionic conducting YSZ phase. In Ni/YSZ cermet anodes, the established electron-to-electron and ion-to-ion conducting networks are responsible for the high structural stability and high electrochemical activity of the HOR [136, 137]. Therefore, electrode reactions occur beyond the physical boundary of the solid electrode and solid electrolyte interface [131, 133, 138]. This is very different from the uniform distribution of the electric field in the aqueous electrolyte and restriction of the charge transfer to the physical solid electrode and liquid electrolyte interface in the case of aqueous electrochemical systems. Consequently, the reactive areas on the Ni/YSZ cermet anode/YSZ side will be significantly larger than those on the LSM cathode/YSZ electrolyte side. This implies that the electrochemical contacts at the anode/YSZ electrolyte are larger than those at the LSM/YSZ electrolyte, resulting in a nonuniform distribution of the electric field (i.e., ionic and electronic flux lines) within the solid electrolyte between the two electrodes. Such asymmetric contact in terms of electrochemical reaction areas would push the equipotential line to the anode side close to the YSZ electrolyte, as shown experimentally in Fig. 20. Therefore, the equipotential lines being located within the Ni/YSZ cermet anode are theoretically possible due to the continuous YSZ phase in the anode arising from the YSZ-to-YSZ ionic conducting network within the cermet.

3.4 Equipotential Line Distribution vs. Electrolyte Thickness

Theoretical calculations on the effect of the solid electrolyte thickness on changes in the equipotential line have not yet been performed. However, experimentally, the effect of the solid electrolyte thickness on changes in the equipotential line can be assessed. In a carefully designed experiment, planar cells with a large WE area of 10.88 cm² were used with a model LSM cathode and a Ni/YSZ cermet anode, and the anodic and cathodic fraction or partitioning resistances, R_A1 and R_C1, of the cell were measured by using conventional VP1 (see Fig. 22) [83]. The YSZ electrolyte thickness varied between 65 and 247 µm, the same Pt mesh CCs were used on both sides of the cells to ensure equal contact resistance, and large cells were used to increase the accuracy. As shown above [90], the relative change in the R_A1 and R_C1 values can be used as an indication of the change in the position of the equipotential line. The relative electrode resistance partitioning strongly depends on the electrolyte thickness. For example, for thin electrolyte cells with electrolyte thicknesses in the range of 65 to 75 µm, the relative percentage of R_C1 with respect to the cell resistance is 90%–95%, indicating a significant distortion of the electrochemical potential distribution in the cell. In this case, the equipotential line is most likely shifted to the cathode/electrolyte interface side. This indicates that for thin electrolyte cells, the use of an RE is no longer reliable. This is consistent with the observed distortion of the polarization measurements in anode-supported thin electrolyte cells [114,115,116, 128]. However, the difference between R_C1 and R_A1 decreases as the electrolyte thickness increases. This implies a shift of the equipotential line to the middle region of the electrolyte with increasing electrolyte thickness. This in turn indicates that increasing the electrolyte thickness effectively diminishes the distortion effect of asymmetric contact at the interface on the electrochemical polarization measurements of solid electrolyte cells. For cells with electrolyte thicknesses larger than ~ 125 μm, the anodic and cathodic partitioning resistances, R_C1 and R_A1, fall within the range of 20%–80%. In this case, the anodic and cathodic polarization losses can be accurately separated under the conditions of this study [83].

Fig. 22

Copyright 2004, Springer Nature

Resistance partitioning/fraction measured based on the relative anodic and cathodic fraction resistances of the cell. Cell—50 mm × 50 mm; cathode—LSM; anode—Ni/YSZ; YSZ electrolyte—65–247 µm in thickness. Lines are a guide only. Symbols: (•) R_A1 at 1 000 °C, (ο) R_C1 at 1 000 °C, (closed triangle) R_A1 at 900 °C, and (open triangle) R_C1 at 900 °C. The shaded area indicates the validity of the RE in the separation of anodic and cathodic polarization resistances based on the resistance partition ratio. Modified with permission from Ref. [83].

The shift of the equipotential line away from the electrolyte bulk will lead to significant errors in and distortion of the polarization and impedance measurements in thin electrolyte cells, as shown in the literature. Clearly, the uniformity of the electric field within the solid electrolyte improves with increasing thickness of the solid electrolyte, resulting in a shift of the equipotential line. Thus, the equipotential line shifts toward the solid electrolyte with increasing electrolyte thickness, as shown schematically in Fig. 23. Numerous studies have demonstrated that in thick electrolyte cells, the polarization and impedance responses of individual electrode reactions at the electrode/electrolyte interface can be accurately separated and measured with a properly positioned RE [114, 119, 122, 139,140,141,142,143,144]. Nevertheless, the location of the equipotential line is not necessary in the middle of the solid electrolyte.

Fig. 23

Shifting of the equipotential line (the dotted line) with increasing electrolyte thickness, taking a porous LSM cathode and Ni/YSZ cermet anode with the YSZ electrolyte cell as an example

Despite the fact that the cell partitioning resistances are measured on LSM cathode and Ni/YSZ anode cells with significant asymmetric electrode/electrolyte contacts, the trend of the change in the relative partitioning resistances of the cell as a function of the electrolyte thickness is very clear, demonstrating a significant implication for the assessment of the equipotential line in solid electrolyte cells. With an electrolyte thickness equal to or higher than 250 µm, the equipotential line moves to the middle region of the electrolyte, indicating a substantially reduced effect of the physical misalignment between the anode and cathode on the distortion of the potential distribution in the electrolyte cell. This in turn indicates that the reliability of the RE in polarization and impedance measurement of the electrode/electrolyte interface is a strong function of the electrolyte thickness. As the misalignment between the WE and CE increases with decreasing electrode area, therefore, as a general guideline, the use of electrolytes with a thickness of at least 250 µm for planar cells with electrode areas of ~ 10 cm² is recommended for accurate separation of the cathode and anode polarizations. In the case of small button cells with electrode areas of ~ 1 cm², the minimum electrolyte thickness should be 0.5 mm or higher with the ring-shaped or point RE for accurate electrochemical activity measurements.

4 Current Constriction Effect

4.1 Current Constriction Effect on the Resistance/Resistivity of Solid Electrolyte Cells

The current constriction or constriction effect is a common phenomenon associated with electrode and electrolyte resistance measurements in SOFCs [145,146,147,148]. In SOFCs, the constriction effect affects the polarization behavior (i.e., the polarization resistance) and, in particular, the ohmic resistance of the cell [25, 28, 146]. The measured electrolyte resistance is generally larger than the electrolyte resistance calculated from the electrolyte thickness and electrolyte ionic conductivity [25, 148, 149]. The higher value of the measured resistance is evidently related to the nonuniform contact at the interface, as shown in the SEM micrographs of the Pt electrode/YSZ electrolyte interface. In solid electrolyte cells, the StS contact is usually not continuous, and electrodes (e.g., Pt and LSM) are only active at some discrete contact points. This effectively leads to loss of the cross-sectional area for the current flow through the electrolyte and thus a nonuniform distribution of the current line density across the cell. The result is that the measured resistance is higher than the resistance calculated based on electrolyte thickness. This phenomenon of an increased resistance of the electrolyte due to a reduction in the active contact/transport area at the interface is generally called the constriction effect. The constriction effect can be represented by a cell/electrolyte resistivity or cell/electrolyte resistance ratio:

$$\lambda =\frac{{\rho }_{\mathrm{cell}}}{{\rho }_{\mathrm{electrolyte}}} {\text{or}}=\frac{{R}_{\mathrm{cell}}}{{R}_{\mathrm{electrolyte}}}$$

(38)

where ρ_electrolyte and R_electrolyte are the resistivity and resistance of the electrolyte material, respectively, and ρ_cell and R_cell are the measured cell resistivity and resistance, respectively. As ρ_electrolyte is the property of an electrolyte and does not change with the electrolyte thickness, the change in λ with the electrolyte thickness is an indication of the constriction effect. λ is equal to or greater than 1.

For example, for a YSZ electrolyte cell with a Pt cathode and a Pt anode (see Fig. 19), the conductivity of the YSZ electrolyte (3 mol% Y₂O₃-ZrO₂ in this case) at 900 °C is 0.039 S cm⁻¹ [150]. For the cell with a 108-µm-thick YSZ electrolyte, the electrolyte resistance, R₂, measured via the special voltage probe is 0.61 Ω cm², more than 2 times higher than the electrolyte resistance, 0.28 Ω cm², calculated based on the electrolyte thickness (λ = 2.2). The cell resistance, R₁, measured by the conventional voltage probe is 1.23 Ω cm², with λ = 4.4. This indicates that the StS contact between the electrode and CC has a significant effect on the constriction effect. Due to advancements in 3D imaging techniques such as focused ion beam-SEM (FIB-SEM) and X-ray computed tomography (CT), the constriction effect is considered to be part of the microstructure effect, or the M-factor, consisting of the geometric tortuosity, the percolation factor and the constriction factor in solid electrolyte devices such as solid-state Li-ion batteries and the transport properties of SOFC anodes [151, 152].

In SOFCs, the constriction effect is fundamentally related to the StS contact between the electrode and the CC and between the electrode and the electrolyte. We quantitatively investigated the effect of the contact area between the electrode and the CC on the cell performance, and the results are shown in Fig. 24a [25]. In this experiment, the ohmic and polarization resistances of Ni/YSZ cermet anode-supported cells with a Pr_0.80Sr_0.20MnO₃ (PSM) cathode were measured as a function of the cathode contact area between the CC and the PSM electrode with a constant anode Ni mesh contact layer at 800 °C. Both the cell resistance and polarization performance strongly depend on the contact area between the PSM cathode and the CC. The overall cell resistance and overpotential at 250 mA cm⁻² decrease from 1.43 Ω cm² and 225 mV for the cell with a cathode contact area of ~ 5% to 0.19 Ω cm² and 119 mV for the cell with a cathode contact area of 27%, respectively. The peak power density (PPD) of the cell increases with increasing cathode contact area. The high sensitivity of the cell performance to the contact area can be ascribed to the constriction effect, and the reason for the high constriction effect is the low conductivity of the porous PSM electrode, 3–4 S cm⁻¹ at 800 °C in this case. Kennouche et al. investigated the effect of the cathode contact area on the contact resistance of short stacks and observed an average increase of 57% in the high contact resistance for stacks with a 35% reduced contact area [28]. The contact resistance has an activation energy of 0.82 eV, close to the value of 0.91 eV for the electrolyte resistance (Fig. 24b). This indicates that contact resistance induced by the constriction effect is actually part of the electrolyte resistance, although the contact resistance is measured between the electrode and current-collecting layer.

Fig. 24

Copyright 2003, Elsevier. b Arrhenius plots of the electrolyte resistance and the contact resistance. The electrolyte resistance was obtained by subtracting the resistance of thin and thick electrolyte cells. Reproduced with permission from Ref. [28]. Copyright 2018, IOP Publishing

a Plots of cell resistance and PPD of Ni/YSZ cermet-supported cells with a PSM cathode as a function of the contact area between the CC and the PSM cathode at 800 °C in 97% H₂/3% H₂O and air. Modified with permission from Ref. [25].

The constriction effect is also related to the conductivity of the electrolyte because the nonuniform current distribution within the electrolyte caused by discrete and asymmetric contacts at the electrode/electrolyte interface is related to the conductivity of the electrolyte. Kenjo and Nojiri [153] systematically studied the polarization behavior of Ag electrodes on doped zirconia electrolytes with different resistivities by using different dopants and observed that the polarization resistance increases with increasing doped zirconia electrolyte resistivity. A nonuniform electrode model was proposed to explain the dependence of the electrode polarization resistance on electrolyte resistivity. With the increase in the electrolyte resistivity, the polarization for the reaction becomes distorted, probably due to the locally nonuniform current distribution in the electrolyte in the TPB region. This is essentially a constriction effect-related polarization phenomenon. The current collection method and contact area have a significant effect on the power performance and performance stability [154, 155]. Jin et al. studied the effect of the cathode contact area on the power performance and stability and observed an increase in the power density and stability of the stack with an optimum contact area of ~ 45% [156]. Thus, to reduce the contact resistance, particularly at the cathode side in SOFC stacks, an additional cathode contact layer or cathode current-collecting layer (CCCL) is often added to ensure satisfactory electrical contact. A CCCL is a critical component in SOFC stacks[157,158,159,160]. This layer not only ensures electrical contact between the interconnect and cathode but also compensates for the dimensional tolerances of various parts of the stack.

Because the constriction effect originates in the StS contact, the constriction effect in SOFCs also strongly depends on the electrolyte thickness, electrochemical activities of the electrodes and operating temperature. Figure 25 shows the results of a carefully designed experimental study of the constriction effect as a function of electrolyte thickness and electrochemical activities of the electrodes [161]. In this experiment, planar cells with a relatively large cell area (~ 10 cm²) were used under consistent and carefully controlled test conditions. A YSZ electrolyte was prepared from 3 mol% Y₂O₃-doped ZrO₂ (3YSZ) powder with a thickness in the range from 70 to 200 μm. LSM and Ni/YSZ cermet were used as the cathode and anode, respectively, but prepared by three different processes. Based on the performance, three groups of cells were obtained. Under typical test conditions, the overpotentials of the cell 1, 2 and 3 groups are (186 ± 13), (130 ± 18), and (89 ± 6) mV, measured at 900 °C and 250 mA cm⁻². The electrochemical activity of the cells follows the sequence of cell 1 < cell 2 < cell 3. However, within each group, the activities of the LSM cathodes and Ni/YSZ cermet anodes are close.

Fig. 25

Copyright 2008, Elsevier

Plots of the apparent cell resistivity and resistance of the cell 1, cell 2 and cell 3 groups as a function of YSZ electrolyte thickness measured at 900 °C and 800 °C. Modified with permission from Ref. [161].

The measured cell resistivity or apparent cell resistivity is a significant function of the electrolyte thickness. In contrast to the constant electrolyte resistivity, the measured apparent cell resistivity increases almost linearly with decreasing electrolyte thickness regardless of the cell group, while the apparent cell resistance shows a maximum with the electrolyte thickness. The slope of the increase in the apparent cell resistivity increases with decreasing temperature. This indicates that the constriction effect is more serious with a reduction in the cell operating temperature. With the enhancement in the electrochemical activities of cells, the apparent cell resistivity line moves to the left. With increasing electrolyte thickness, both the apparent cell resistivity and resistance approach the calculated value, indicating a reduced constriction effect with increasing electrolyte thickness. This is consistent with the improved electric field distribution with a thick electrolyte, as shown in [83].

Nielsen et al. used the finite element method (FEM) to estimate the current constriction effect at the Ni/YSZ cermet anode/YSZ electrolyte interface based on FIB-SEM tomography reconstruction of the interface [162]. The calculation indicates that depending on the asymmetric contacts between two electrodes, the area specific resistance (ASR) of the cell associated with the constriction effect approaches infinity or a maximum as the electrolyte layer thickness approaches zero, instead of reaching zero as in the case of no constriction effect. The constriction effect becomes increasingly significant with decreasing electrolyte thickness. This indicates that the constriction effect is most detrimental for thin electrolyte cells; therefore, good contact and high electrical conductivity of the electrode coatings are particularly critical to reduce the constriction effect on the power output of thin electrolyte-based IT-SOFCs. Improvement in the cell performance is due to increased electrochemical activities of the LSM cathode and Ni/YSZ cermet anodes and improved interfacial contact at the electrode/electrolyte interface. This indicates that the most effective way to reduce the constriction effect on thin electrolyte cells is to increase the electrode electrochemical activity.

4.2 Constriction Effect on the Scalability of the Electrode Performance

As the constriction effect affects both the ohmic and polarization resistances of the cells, the power performance measured on small button cells or single cells is not necessarily equal to that measured on the large cells or stack in SOFCs, and the peak power performances or densities obtained in stacks are generally lower than those observed in single cells [23, 163]. This is particularly the case for small button cells, as evaluating the performance and activity of electrode materials and cells using small button cells is a common practice due to the convenience and ease of the test rig setup. Such a dependence of the performance on the cell size or scalability of the electrode performance depends on a number of factors, including the conductivity of the porous electrode coating, the electrical contact and contact area between the CC and electrode, and the test conditions, such as the load used in the test station. The scalability was quantitatively studied by comparing the electrode performances of LSM cathodes and Ni/YSZ cermet anodes measured on both small button cells and large planar cells under similar test conditions (see Fig. 26) [163]. The measurements were carried out at 250 mA cm⁻² and 900 °C in air and in 97% H₂/3% H₂O, respectively. Small button cells and large 50 mm × 50 mm planar cells were prepared using the same electrode inks. The CCs for the LSM cathode and Ni/YSZ cermet anode were Pt and Ni woven meshes, respectively. Despite the similar contact and identical test conditions, there are significant differences in the electrochemical performances of LSM cathodes measured on small button cells and large planar cells. However, for Ni/YSZ cermet anodes, the differences are much smaller.

Fig. 26

Plots of overpotentials (η) measured at 250 mA cm⁻² and 900 °C for the ORR on an LSM cathode and the HOR on a Ni/YSZ cermet anode in small button cells (0.44 cm²) and planar cells (10 cm²) under identical test conditions

We can define the scalability as the ratio of the performances or activities measured on small button cells and large planar cells based on the overpotential, η:

$$\varepsilon =\sum_{i=1}^{i=n}\frac{{\eta }_{i,\text{Large\, planar\, cell}}}{{\eta }_{i,\text{Button \, cell}}}$$

(39)

For practical electrodes, ε is equal to or greater than 1. The higher ε is, the poorer the scalability. Based on the data given in Fig. 26, the scalability of LSM electrodes and Ni/YSZ cermet anodes is 3.44 ± 1.71 and 0.91 ± 0.16, respectively. The high scalability of the LSM electrode indicates that the performance losses measured on large planar cells with an electrode area of 10 cm² are more than three times higher than those measured on small button cells. In contrast, ε is very close to unity for Ni/YSZ cermet anodes, indicating an excellent scalability and good reproducibility of the performance measured between small and large cells. The effect of cell size on the performance scalability is most pronounced on LSM cathodes but is negligible on Ni/YSZ cermet anodes.

The significantly reduced performance of the LSM cathode in large cells is most likely caused by the low conductivity of the porous LSM coating in this case. In this experiment, the electronic conductivity of the porous LSM electrode coating and Ni/YSZ cermet anode coating is 45 and 254 S cm⁻¹ at 800 °C, respectively [25] (please note that the electronic conductivity of a porous electrode coating is generally much lower than the corresponding material conductivity). The low electronic conductivity will lead to a high contact resistance between the electrode coating and CC. This in turn will result in increased polarization losses at the electrode/electrolyte interface for the reaction. With increasing cell size, the load on the cell will be reduced, and the pressure between the electrode coating and CC will become increasingly uneven. This will increase the contact resistance between the electrode coating and the CC, which in turn will lead to an increase in the polarization loss at the electrode/electrolyte interface [25]. The fundamental reason for the effect of the electronic contact between the electrode and CC on the activity of the electrode is the constriction effect. The much higher electronic conductivity of Ni/YSZ cermet anodes improves the contact between the cermet and the CC and substantially reduces the constriction effect on the polarization performance of the anode.

Another complication in the scalability of the power performance and stability of electrodes is the issue related to metal deposition at the electrode/electrolyte interface typically associated with small button cells. The deposition of precious metal elements at the interface, such as Pt, Ag, and Au, will affect the microstructure, local electronic conductivity and thus electrochemical activity of electrodes for the reaction [164,165,166,167,168,169,170,171,172]. Xiong et al. examined Pt and Au deposition at the interface region of an LSM/scandia-stabilized zirconia (ScSZ) cell after cathodic polarization at 800 °C and observed a rapid improvement in the cathode performance (see Fig. 27)[168]. The enhancement of the performance was ascribed to the considerable amount of Pt particles deposited in the vicinity of the TPB (Fig. 27b). Such improvement in the performance was not observed in the cell using a Au CC, and no Au particles were found at the interface. This indicates that a small button cell may not be suitable for stability studies of the electrodes of SOFCs.

Fig. 27

Reproduced with permission from Ref. [168]. Copyright 2009, IOP Publishing

a Long-term current data of LSM cathodes by using a platinum CC or a gold CC at a fixed potential of − 0.5 V vs. the air RE at 1 073 K. b Element mapping in the LSM/ScSZ interface region after the cell test by using a platinum CC.

5 Polarization-Induced Interfacial and Surface Segregation Phenomena

5.1 Polarization-Induced Interface Change and Formation

Due to the nature of the ceramic components in SOFCs, the solid electrode and electrolyte interface is generally formed by high-temperature sintering, e.g., 1 300–1 400 °C for Ni-based cermet anodes [173,174,175], 1 100–1 150 °C in the case of LSM/YSZ cells or ~ 900 °C for LSCF/Gd-doped ceria (GDC) cells [46, 56, 176]. In the case of LSM electrodes, the cathode/electrolyte interface formed during high-temperature sintering is generally characterized by the formation of convex rings on the YSZ or GDC electrolyte surface and interdiffusion of cations (Mn²⁺/Mn³⁺) during high-temperature sintering [177,178,179,180,181]. Ni interdiffusion and segregation were also reported at the anode/electrolyte interface of Ni-based cermet anodes during high-temperature sintering at 1 400 °C [182]. Electrode reactions occur at the electrode/electrolyte interface, similar to in liquid electrochemical systems or cells. However, very different from the LSE, the electrode/electrolyte interface in SOFCs is dynamic, constantly changing and evolving under fuel cell operating conditions [183]. Typical phenomena and changes are associated with the solid electrode/solid electrolyte interface, such as interfacial reactions [184,185,186,187], micropore formation [178, 180], element segregation and diffusion [187, 188], delamination [189, 190], and impurity poisoning and deposition[191, 192]. These phenomena that occur at the electrode/electrolyte interface substantially impact the electrochemical activity and stability of the cell. For example, the interfacial reaction between an LSCF cathode and a YSZ electrolyte increases the interfacial resistance as a result of the formation of insulating layers such as SrZrO₃ and La₂Zr₂O₇ [193, 194]. In contrast, the reaction between a Ni-BZCY anode and a ceria electrolyte has been reported to promote the formation of a BaCeO₃ layer at the interface, preventing electronic current leakage across the ceria electrolyte and thus improving the cell performance [195]. In addition, the Sr segregation in the case of an LSCF electrode and Mn²⁺ segregation in the case of LSM under cathodic polarization conditions are detrimental to the electrochemical activity of the electrodes due to the segregated species facilitating Cr deposition [196, 197]. The discussion of interface-related issues is beyond the scope of the present review, and there are a number of good reviews devoted to specific topics in the literature [30, 198,199,200]. In this article, we will only concentrate on the polarization-induced interface and interface change because the fundamental reason for such a change can originate from the StS contact in the SSE.

Electrochemical polarization has a significant effect on the microstructure and morphology of the electrode/electrolyte interface. Our early studies showed a significant effect of polarization on the microstructure and morphology of LSM electrodes [177, 201, 202]. Electrochemical polarization treatments (cathodic or anodic polarization) cause microstructural changes in the as-prepared LSM particles. The reason for the change in the microstructure of the LSM particles is most likely the valence change of the manganese species, which is related to oxygen vacancy formation under cathodic polarization conditions. Electrochemical polarization not only causes a microstructure change in the LSM particles but also induces a morphology change at the interface between the LSM electrode and YSZ electrolyte, as shown in Fig. 28 [177]. The cathodic polarization treatment causes a morphological change in the convex contact rings, characterized by the disappearance of the sharp edge of the convex rings and growth of the ring width to (0.15 ± 0.05) μm (Fig. 28b). The cathodic polarization-induced interfacial changes cannot be reversed by the subsequent anodic polarization (Fig. 28c). A similar microstructural change of the LSM/YSZ interface is also observed under anodic polarization treatment (Fig. 28d). The microstructural change of the convex contact rings under cathodic and anodic polarization treatment provides conclusive experimental evidence indicating that oxygen reactions, either reduction or oxidation, occur in the O₂/LSM/YSZ TPB region, a well-known and accepted theory in SOFC communities, although there are significant discrepancies in the individual reaction steps of the oxygen reactions at the cathodes of SOFCs [131, 133].

Fig. 28

Copyright 2005, IOP Publishing

Atomic force microscopy (AFM) images of the YSZ electrolyte surface after removal of the LSM electrode by HCl treatment. a Before polarization, b after cathodic polarization treatment for 3 h, c after cathodic and anodic polarization treatment for 6 h, and d after anodic polarization treatment for 3 h. All polarization treatments were carried out at 200 mA cm⁻² and 800 °C in air. The scale bar applies to all AFM micrographs. Modified with permission from Ref. [177].

The microstructural change at the interface between an LSM cathode and a YSZ electrolyte after polarization was also studied in detail by Matsui et al. using the FIB-SEM technique [33, 203, 204]. Discharge operation led to a reduction in the electrode ASR for the ORR and caused a change in the YSZ electrolyte surface. The extent of the change significantly depends on the duration of cathodic current passage. Quantitative analysis by 3D reconstruction of the LSM/YSZ interface showed that the increase in the active TPB length after cathodic polarization at 200 mA cm⁻² and 1 000 °C for 5 h is ~ 7%, while the ASR is initially 0.33 Ω cm² and is reduced to 0.15 Ω cm² after polarization at 200 mA cm⁻² and 1 000 °C for 5 h, a 54% decrease in the ASR[33]. This indicates that the TPB increase due to the cathodic polarization is just one of the factors for the observed activation phenomena of LSM cathodes for the ORR. The microstructure at the LSM/YSZ interface, e.g., densification and micropore formation at the interface, is significantly affected by the La/Sr ratio of the LSM composition [204], indicating the critical role of the oxygen nonstoichiometry, i.e., cation vacancy formation, of LSM in the interface change under polarization conditions.

In addition to the effect on the microstructure of the electrode/electrolyte interface, polarization can also induce the formation of an interface. Figure 29 shows the change in the electrode impedance for the ORR on LSM/YSZ and LSM/GDC measured at 1 000 mA cm⁻² and 800 °C and the corresponding interface formed [32]. The initial R_E for the directly assembled LSM cathode is 38 Ω cm², much higher than that on presintered LSM electrodes measured under identical conditions (14–17 Ω cm²). Very different from the constant ohmic resistance (R_Ω) of the presintered LSM electrode, R_Ω is reduced from the initial 3.1 Ω cm² to 1.4 Ω cm² after cathodic current passage at 1 000 mA cm⁻² for 15 min, a reduction of 1.7 Ω cm² (ΔR_Ω = 1.7 Ω cm²). The reduction in R_Ω indicates an improvement in the interface contact of the LSM electrode directly assembled on a YSZ electrolyte. Similar to the presintered LSM electrode, the directly assembled LSM electrode also shows a significant decrease in electrode polarization resistance (R_E) with cathodic polarization, a typical activation behavior of LSM cathodes. A similar reduction in electrode impedance is also observed for LSM directly assembled on a GDC electrolyte. The reduction in R_Ω (ΔR_Ω) is 0.9 Ωcm² after polarization at 1 000 mA cm⁻² for 3 h. The R_E for the reaction also decreases with cathodic polarization. In both electrodes, a significant number of contact marks or clusters form on the YSZ and GDC electrolyte surface, and the number of contact marks/clusters increases with the polarization current density.

Fig. 29

Copyright 2015, IOP Publishing

Impedance curves for the ORR on the LSM electrode directly assembled on YSZ and GDC electrolytes, LSM/YSZ and LSM/GDC as a function of polarization time at 1 000 mA cm⁻² and 800 °C. AFM images of YSZ and GDC electrolyte surfaces in contact with directly assembled LSM after polarization for 3 h. The LSM electrode was removed by HCl treatment. Modified with permission from Ref. [32].

Since there is no preformed convex ring-type interface contact between the electrode and electrolyte, as in the case of the presintered LSM electrode, the initial contact resistance between the directly assembled electrode and electrolyte is high due to the isolated StS contacts at the interface. When passing a cathodic current, the localized current density will be very high due to the limited localized contact points between the LSM particles and the electrolyte. This will in turn generate Joule heating, causing localized sintering at the contact points and effectively leading to the formation of an interface. The formation of such contact clusters/marks is indicated by the reduction in R_Ω. Despite the significant differences in the morphology of the LSM/YSZ interface, the polarization-induced LSM/YSZ interface shows an electrochemical performance comparable to that of the high-temperature sintered LSM/YSZ interface, indicating that the polarization-induced electrode/electrolyte interface is electrochemically identical to that formed by high-temperature sintering [32, 205]. The fundamental reason for the formation of the contact mark/cluster-shaped interface is most likely oxygen migration from the oxygen electrode and incorporation into the oxygen ion conducting electrolyte. This is also due to the fact that in the case of oxide ion conducting electrolyte fuel cells the species involved at the interface is oxygen ions and in the case of the aqueous electrolyte system, migration species at the solid electrode and aqueous electrolyte interface is electrons. The mass of an oxygen atom is 2.656 10–26 kg, 29 158 times the mass of an electron, 9.109 10–31 kg. The size of an oxygen ion is more than 50 000 times the size of electrons based on the classical electron radius of electrons (2.817 910–15 m). This is supported by the observation of oxygen vacancy formation on the LSM cathode using X-ray nanotomography to in situ reconstruct the 3D microstructure of the LSM electrode under cathodic polarization [206]. Figure 30 shows a scheme of the formation of the interfaces induced by high temperature and polarization. Using FIB-scanning transmission electron microscopy (FIB-STEM), the interface induced by polarization is identical to that formed under high-temperature sintering; see Fig. 28c [181].

Fig. 30

Reproduced with permission from Ref. [205]. Copyright 2016, Royal Society of Chemistry. The LSM/YSZ interface induced by polarization is shown in c. Reproduced with permission from Ref. [181]. Copyright 2018, Elsevier

Schematic diagrams of the LSM electrode/YSZ electrolyte interfaces formed a by high-temperature sintering, e.g., 1 150 °C, and b by cathodic polarization under SOFC operating conditions, e.g., 800 °C.

The polarization-induced interface is a relatively new phenomenon in SOFCs and has significant implications for the interface formation and evolution in solid-state devices in general. Recent developments in this area indicate migration and diffusion of active phases such as doped bismuth at the electrode/electrolyte interface under polarization conditions [207,208,209,210]. The in situ formed active bismuth layer not only substantially enhances the electrocatalytic activity and stability of the electrode for the reversible ORR and OER but also functions as an effective barrier layer to prevent the interfacial reaction between the electrolyte and electrode in the case of a cobaltite cathode and a YSZ electrolyte.

5.2 Polarization-Induced Surface Segregation, Incorporation and Inhibition

Surface segregation is a phenomenon generally associated with the redistribution and accumulation of a specific cation at the oxide surface due to a loss of symmetry at the surface relative to the bulk. Surface segregation is inherently related to the defect chemistry of solid-state ionic materials and plays a very important role in the electrochemical activities of solid electrolyte cells such as SOFCs [22]. Cation segregation, Sr in particular, frequently occurs on Sr-containing perovskite-based electrodes such as LSM and LSCF annealed under an oxidizing atmosphere and/or under SOFC operating conditions. The segregated species occupy the active surface sites and thus degrade the electrocatalytic activity and durability for the oxygen reduction and oxidation reactions [47, 188, 198, 199, 211, 212]. In the case of surface-segregated SrO, the species is highly mobile and can diffuse through the GDC barrier layer, forming a SrZrO₃ insulating layer on the YSZ electrolyte [213, 214]. The segregated SrO on the LSCF surface also actively interacts with volatile impurities, forming inert and nonreactive reaction products such as SrCrO₄, SrSO₄ and SrCO₃, leading to significant poisoning of the oxygen electrodes [30, 215,216,217].

The internal strain in the perovskite lattices caused by cation size mismatch between dopant and host cations can be relaxed through surface migration of larger dopant cations. Elastic interactions have been proposed as one of the main driving forces for SrO surface segregation in perovskites such as LSM and LSCF [212, 218,219,220,221]. The surface polarity and electrostatic interactions between positively charged oxygen vacancies and negatively charged point defects due to the substitution of Sr²⁺ for La³⁺ in perovskite lattices, ${\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}\, \mathrm{and} \,{\mathrm{Sr}}_{\mathrm{La}}^{\mathrm{^{\prime}}}$, are also important factors in cation surface segregation processes [222,223,224]. Lee et al. [219] provided a good example of cation surface segregation using (La, D) MnO₃ (D = Ca, Sr and Ba) as a model system. The tendency to segregate to the surface increases with increasing dopant size (the radii of Ca²⁺, Sr²⁺, Ba²⁺ and La³⁺ with CN = 12 are 0.134, 0.144, 0.161 and 0.136 nm, respectively [69]). Here, a smaller size mismatch between the host and dopant cations suppresses dopant segregation due to reduced elastic interactions. The negatively charged ${\mathrm{D}}_{\mathrm{La}}^{\mathrm{^{\prime}}}$ defects due to substitution of A-site La³⁺ by D²⁺ in the perovskite lattice can be compensated by the formation of positively charged oxygen vacancies, ${\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}$, on the surface. The electrostatic interaction between ${\mathrm{D}}_{\mathrm{La}}^{\mathrm{^{\prime}}}$ and ${\mathrm{V}}_{\mathrm{O}}^{\cdot \cdot}$ can then drive the substituted D²⁺ cations toward the surface. Figure 31 shows both elastic and electrostatic interactions as driving forces for surface segregation [219].

Fig. 31

Reproduced with permission from Ref. [219]. Copyright 2013, American Chemical Society

Schematic diagram showing the driving forces for A-site segregation in a perovskite (La, D)MnO₃ (D = Ca, Sr and Ba) system.

The extent of surface segregation of cations, in particular Sr, is subject to various factors, including the stoichiometric composition, strain, temperature, oxygen partial pressure, nature of the oxide samples, type of cations in the B site and electrochemical polarization conditions [199, 225]. Among them, polarization-induced surface segregation is most relevant to the electrochemical activity and durability of oxygen electrodes of SOFCs. Such surface segregation is closely related to the polarization-induced defect chemistry of the materials, i.e., the coupling of point defects and oxygen nonstoichiometry. To illustrate the role of polarization in the surface segregation processes, LSM and LSCF perovskites are used as model electrodes in this article with an emphasis on Sr segregation.

5.2.1 Polarization-Induced Surface Segregation/Incorporation on LSM Electrodes

Early studies on LSM electrodes showed that the electrocatalytic performance of LSM for the ORR is highly sensitive to the electrochemical polarization. The performance of an as-prepared LSM electrode is significantly enhanced by cathodic polarization but deteriorated by anodic polarization [201, 212, 221, 226, 227]. Figure 32 gives an example of the activation and deactivation processes on an LSM electrode for the ORR as a function of the cathodic and anodic polarization processes measured at 800 °C and 200 mA cm⁻² in air [221]. From the R_E curve, we can see that the deactivation process is much slower than the activation process. The R_E of the LSM cathode also increases with the subsequent holding time in open-circuit conditions, indicating the deactivation of LSM electrodes under open-circuit conditions [21, 221]. Activation under cathodic current passage and deactivation under subsequent open-circuit conditions were also reported by Matsui et al.[33] for the ORR on LSM electrodes at 1 000 °C.

Fig. 32

Copyright 2007, Springer Nature

Change in the impedance responses of an as-prepared La_0.72Sr_0.18MnO₃ electrode for O₂ reduction as a function of a cathodic, b anodic and c cathodic polarization time at 200 mA cm⁻² and 800 °C in air. The change in electrode polarization resistance, R_E, as a function of the polarization process is given in d. Arrows show the change in the impedance arcs or R_E with the polarization time. Modified with permission from Ref. [21].

Various mechanisms have been proposed for the activation of LSM electrodes for the ORR under cathodic polarization, including oxygen vacancy formation at the TPB[228, 229], decomposition of insulating phases such as La₂Zr₂O₇ [230], migration of manganese ions from LSM to the YSZ electrolyte surface[231] and removal and/or incorporation of segregated SrO species [212, 221], but few studies have investigated the deactivation mechanism. The activation and deactivation processes are largely reversible under cathodic and anodic polarization conditions, whereas the interface change induced by the polarization is not reversible [177]. Therefore, proposing that the removal and/or incorporation of segregated Sr species are probably the most applicable mechanisms for the activation of the reaction on an LSM electrode under cathodic polarization and the deactivation of the reaction due to the resegregation of Sr species under anodic polarization or open-circuit conditions is reasonable. The hypothesis of the Sr incorporation and segregation mechanism of LSM under cathodic and anodic polarization conditions has been validated by numerous in situ characterization techniques. Chang et al.[232] used grazing incidence X-ray diffraction (GIXRD) to in situ probe the cation concentration of LSM films during annealing and under an applied cathodic potential at 800 °C. After annealing, SrO segregation occurred uniformly over the LSM surface, while after applying the cathodic potential, the Sr amount was reduced on ~ 70% of the LSM surface. Huber et al.[233, 234] in situ studied the surface chemistry of LSM and La_0.75Sr_0.25Cr_0.5Mn_0.5O₃ (LSCM) electrodes under polarization by X-ray photoelectron spectroscopy (XPS) and time of flight-secondary ion mass spectrometry (ToF–SIMS). The results indicate that cathodic polarization leads to depletion of Sr on the surfaces, while anodic polarization accelerates Sr surface segregation (see Fig. 33). A similar phenomenon was reported on an LSCM film by Rohnke et al. [235]. Significant Sr segregation on the surface of LSM electrodes under anodic polarization has also been supported by the observation of SrCrO₄ formation on LSM electrodes in the presence of gaseous Cr contaminants under anodic polarization conditions [236], in contrast to the (Cr, Mn)₃O₄ spinel phase formation on LSM electrodes under cathodic polarization[196]. Segregation of B-site Mn cations to the surface of LSM under cathodic polarization was observed by Backhaus-Ricoult et al. [231] by photoelectron microscopy. The anodic polarization accelerates Sr surface segregation and at the same time inhibits the generation of manganese species such as Mn²⁺.

Fig. 33

Reproduced with permission from Ref. [234]. Copyright 2012, Royal Society of Chemistry

Scanning X-ray photoelectron microscopy (SPEM) images of the Sr 3d component measured on the La_0.75Sr_0.25Cr_0.5Mn_0.5O₃ surface for different applied voltages. In the images, bright colors denote high Sr concentrations, and dark colors characterize areas with low Sr concentrations.

Under cathodic polarization, oxygen vacancies are generated in the interface region between the LSM electrode and the YSZ electrolyte, and the subsequent positive charge of oxygen vacancies can be compensated by the reduction of B-site manganese ions, i.e., Mn³⁺ to Mn²⁺ and Mn⁴⁺ to Mn³⁺, as shown in Eqs. 18 and 19 [54, 228]. Valence changes of cations will inevitably cause lattice volume changes. The effective ionic radii for the Mn ions in octahedral coordination (CN = 6) are Mn²⁺  = 0.067 (LS) and 0.083 (HS); Mn³⁺  = 0.058 (LS) and 0.064 5 (HS); and Mn⁴⁺  = 0.053 nm (LS), in which LS and HS refer to low and high spin [69]. Thus, if the electroneutrality is maintained by the reduction of B-site Mn cations, then the average Mn size would increase and cause lattice expansion. This in turn would increase the internal stress and drive the substituted Sr and/or Mn cations to the surface, similar to the elastic interaction due to the size mismatch between the Sr dopant and La host. Experimentally, B-site Mn cation segregation to the LSM surface under cathodic polarization has been observed by Backhaus-Ricoult et al. [231] using photoelectron microscopy techniques. The segregation and subsequent migration of Mn species to the TPB region of the LSM/YSZ interface have been well documented by deposition and poisoning of Cr studies and the formation of (Cr, Mn)₃O₄ spinels [30, 196, 237]. However, Sr segregation under cathodic polarization contradicts the reduction of segregated SrO on the LSM surface, as shown by in situ studies on the LSM surface using XPS and ToF–SIMS [233], and the significant enhancement of the electrochemical activity of LSM under cathodic polarization [33, 201, 212, 221, 226]. This indicates that the charge compensation mechanism for oxygen vacancy formation under cathodic polarization conditions through the reduction of B-site Mn cations cannot explain the observed Sr incorporation.

This may bring up a situation in which the oxygen vacancies generated under cathodic polarization conditions can also be electronically compensated by a different mechanism. This is possible because the generated positively charged oxygen vacancies are enriched at the LSM surface in the vicinity of the TPB, denoted as ${\mathrm{V}}_{\mathrm{O},\mathrm{LSM},\mathrm{surface}}^{\cdot \cdot}$. This implies that the concentration of the oxygen vacancies in the electrode bulk would not change even under cathodic polarization conditions. Considering the high concentration of positively charged oxygen vacancies on the LSM surface, electroneutrality can be established by attracting segregated SrO to the La lattice, forming negatively charged ${\text{Sr}}_{\text{La}}^{^{\prime}}$. The presence of such point defects close to the surface region could stabilize oxygen vacancies. Such incorporation of SrO through the electrostatic attractive interaction can be expressed as:

$$2{\text{SrO}}_{{{\text{surface}}}} \xrightarrow{{{\text{Cathodic}}\;{\text{polarization}},{\text{LaMnO}}_{3} }}2{\text{Sr}}_{{{\text{La}},{\text{surface}}}}^{\prime } + {\text{V}}_{{{\text{O}},{\text{LSM}},{\text{surface}}}}^{{ \cdot \cdot }} + 2{\text{O}}_{{\text{O}}}^{x}$$

(40)

We must note here that in this case, oxygen vacancies are formed under the influence of cathodic polarization and not due to Sr substitution. The observed fast activation effect and rapid reduction of Sr species at LSM electrode surfaces [212, 232,233,234] indicate that the incorporation of segregated SrO species can be a fast process due to the strong electrostatic attractive force between the positively charged ${\mathrm{V}}_{\mathrm{O},\mathrm{LSM},\mathrm{surface}}^{\cdot \cdot}$ and negatively charged ${\mathrm{Sr}}_{\mathrm{La}}^{\mathrm{^{\prime}}}$. The electrostatic interaction force is high enough to overcome the relatively weak elastic interaction due to the size mismatch to push the substituted Sr to the surface. This is possible due to the relatively weak elastic interaction in LSM compared to that in LSCF.

Under anodic polarization conditions, oxygen excess occurs, similar to the oxygen excess of LSM materials at high oxygen partial pressures [48, 54]. Due to the compact nature of the LSM perovskite structure, excess oxygen would exist as negatively charged cation vacancies (most likely as A-site cation vacancies, ${\mathrm{V}}_{\mathrm{La}}^{\mathrm{^{\prime}}\mathrm{^{\prime}}\mathrm{^{\prime}}}$). However, they would function similarly in electrostatic interactions, as they are both negatively charged point defects. The presence of excess oxygen in the form of negatively charged ${\mathrm{O}}_{\mathrm{excess}}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}$ ions (or negatively charged cation vacancies) would push the negatively charged ${\mathrm{Sr}}_{\mathrm{La}}^{\mathrm{^{\prime}}}$ out of the lattice to the surface by the electrostatic repulsive force. The Sr segregation due to the excess oxygen in LSM under anodic polarization can be expressed as follows:

$${\text{Sr}}_{{{\text{La}}}}^{\prime } \xrightarrow{{{\text{Anodic\,polarization}},{\text{O}}_{{{\text{excess}}}}^{{\prime \prime }} }}{\text{SrO}}_{{{\text{surface}}}}$$

(41)

This anodic polarization-induced electrostatic interaction can subsequently drive Sr segregation to the LSM surface. Therefore, the driving force for Sr segregation at LSM electrode surfaces under polarization is most likely the result of the oxygen nonstoichiometry-modulated electrostatic interaction on the LSM surface induced by cathodic/anodic polarization. This also implies that elastic interactions due to the reduction of B-site Mn cations (see Eqs. 18 and 19) would drive the surface segregation of Mn species but not Sr species under cathodic polarization conditions. The electrostatic interactions modulated through the oxygen nonstoichiometry under polarization conditions play a critical role in Sr segregation to and incorporation on the LSM surface. The Sr segregation/incorporation processes on LSM under dynamic polarization conditions are schematically shown in Fig. 34.

Fig. 34

Reproduced from Ref. [22] under Creative Common CC BY License

Segregation and incorporation (or inhibition) processes of Sr species on the LSM electrode surface under cathodic and anodic polarization conditions.

5.2.2 Polarization-Induced Surface Segregation/Inhibition on LSCF Electrodes

The electrochemical polarization also has a remarkable impact on cation segregation on the surface of LSC-based electrodes. However, different from that observed on LSM electrodes, cathodic polarization generally increases the cation, in particular Sr, segregation. Vovk et al. [238] studied the surface chemistry of LSC film surfaces under polarization using in situ XPS and reported an irreversible increase of 5% in the Sr/(La + Co) ratio at the LSC surface under cathodic polarization and no change in the La/Co ratio. Baumann et al. [239] also observed an increase in surface Sr and Co on LSCF films under cathodic polarization but not under anodic polarization conditions. Mutoro et al. [240] probed the surface composition of LSC films using synchrotron XPS and observed SrO surface segregation by applying cathodic polarization and Sr incorporation and Co segregation by applying anodic polarization. A similar reversible change in the surface Sr content was reported on the LSC/(La, Sr) ₂CoO₄ bilayer film [240].

We investigated the effect of cathodic and anodic polarization currents on Sr segregation on LSCF oxygen electrodes directly assembled on Ni-YSZ hydrogen electrode-supported YSZ electrolytes without the conventional high-temperature sintering step [241,242,243]. The LSCF/YSZ interfaces were in situ formed in the early stage of polarization at 750 °C, as is evidenced by the decrease in the cell ohmic resistance and the formation of contact marks on the YSZ electrolyte. A Sr-rich layer was formed on the YSZ surfaces of both cells, but the Sr-rich layer was ~ 30 nm after cathodic polarization, much thicker than the 10 nm layer observed after anodic polarization (see Fig. 35a–c) [243]. This indicates that surface segregation of Sr species is substantially depressed under electrolysis, i.e., anodic polarization, compared to that under fuel cell operation, i.e., cathodic polarization. For two identical cells under operation at 0.5 A cm⁻² and 750 °C for 100 h, the operating stability of the cell under cathodic polarization drastically deteriorated, whereas the cell under anodic polarization showed significantly enhanced performance (Fig. 35d) [243]. Similarly, Pan et al.[244, 245] studied LSCF electrodes directly sintered on a barrier-layer-free YSZ electrolyte at 900 °C and observed enhanced electrode operating stability under anodic polarization at 1 A cm⁻² and 800 °C for 158 h, in contrast to the performance decay under open-circuit conditions.

Fig. 35

Reproduced with permission from Ref. [243]. Copyright 2018, Elsevier

STEM-energy-dispersive X-ray spectroscopy (EDS) micrographs of the directly assembled LSCF electrode/YSZ electrolyte interface after polarization at 0.5 A cm⁻² and 750 °C under a an anodic current for 12 h, b an anodic current for 40 h, and c a cathodic current for 40 h. The polarization stability performance of a cell with an LSCF oxygen electrode under fuel cell and electrolysis cell operating conditions is shown in d.

Evidently, the effect of polarization on Sr segregation on LSC-based electrodes is opposite to that observed on LSM electrodes. Cathodic polarization promotes Sr segregation, while anodic polarization inhibits Sr segregation [32, 242, 246]. Such a polarization effect can also be explained based on the nature of LSC-based electrodes such as LSCF. LSCF electrode materials are well-known MIEC materials with high oxygen ion conductivity [247, 248]. This results in significant differences in the electrode behavior of LSCF and LSM. First, as shown in the defect chemistry of LSCF, Sr substitution results in the dominant formation of positively charged oxygen vacancies, in contrast to the positively charged holes in the case of LSM. This indicates the presence of oxygen vacancy defects in the electrode bulk. Second, due to the high redox properties of B-site Co and Fe cations, the elastic interactions due to the size mismatch between substitute Sr and host La cations are much stronger than those in the case of LSM. Third, the effect of cathodic polarization on oxygen vacancy generation occurs on the electrode surface rather than being limited to the electrode/electrolyte interface region, as in the case of the LSM electrode. Kivi et al. [249] investigated the lattice parameters of porous LSC and LSCF electrodes in situ under different atmospheres and polarization conditions using high-temperature XRD. Under open-circuit conditions, the cell volume slightly increases with decreasing oxygen partial pressure. However, the effect of oxygen partial pressure on the cell volume becomes remarkable when applying a cathodic potential. The cell volume increases with increasing cathodic potential, and the degree of volume expansion is more remarkable at a lower oxygen partial pressure. Further studies showed that the effect of a cathodic potential on the changes in lattice parameters is reversible by switching the potential between 0 V and − 0.9 V [206]. The increase in cell volume induced by applying a cathodic potential is probably due to an increase in oxygen vacancies or a decrease in the effective oxidation state of cobalt ions. Cathodic polarization would lead to increased formation of positively charged oxygen vacancies at the electrode surface, enhancing electrostatic interactions. Such electrostatic interactions can either drive the substitute Sr cations to the surface or incorporate the segregated Sr back into the La lattice, as in the case of LSM. This combines with the intrinsic elastic interaction, driving Sr segregation.

Under anodic polarization, the concentration of oxygen vacancies at the electrode surface is reduced, which leads to a decrease in the electrostatic interaction, resulting in a decrease in the driving force for Sr segregation. This in turn indicates the diminished role of the elastic interaction in Sr segregation on LSC-based electrodes under polarization conditions. Thus, the driving force for Sr segregation on LSC-based electrodes under polarization is basically related to the significant change in the electrode surface properties, particularly the positively charged oxygen vacancies at the surface under polarization conditions. The hypothesized Sr segregation/incorporation (or inhibition) on the LSCF electrode surface under cathodic and anodic polarization conditions is given in Fig. 36.

Fig. 36

Reproduced from Ref. [22] under Creative Common CC BY License

Segregation and incorporation (or inhibition) processes of Sr species on the LSCF electrode surface under cathodic and anodic polarization conditions.

Caution should be taken in that if there are traps present in the system that can react with segregated species such as chromium, boron or sulfur, then the segregation processes will be very different. This is because the chemical reaction between segregated species such as Sr and traps will substantially enhance the segregation process.

5.3 Polarization-Induced Phase Migration

More recently, we found that polarization can not only induce interface formation but also cause phase migration. Ai et al. [250, 251] incorporated doped Bi₂O₃ materials such as Er_0.4Bi_1.6O₃ (ESB) into LSM and Sm_0.95Co_0.95Pd_0.05O_3−δ (SmCPd) to form composite electrodes through a direct assembly method and found that ESB-decorated composite electrodes significantly enhance the cathode performance for the ORR in SOFCs. Further studies have shown that ESB decoration substantially increases the power performance and durability of Nb-doped La_0.6Sr_0.4Co_0.2Fe_0.7Nb_0.1O_3−δ (LSCFNb) electrode directly assembled on YSZ electrolyte cells, achieving a maximum power density of 1.32 W cm⁻² and good stability at 750 °C and 250 mA cm⁻² for 100 h [209]. Microstructure analysis indicates the migration of the ESB phase in the ESB/LSCFNb composite toward the electrode/electrolyte interface region under cathodic polarization and the formation of a thin ESB layer at the cathode/electrolyte interface (Fig. 37). Aside from individual and isolated Sr-rich areas/particles in the range of 10–40 nm, La and other elements of LSCFNb are uniformly distributed, indicating significant suppression of Sr segregation and diffusion in LSCFNb electrodes under polarization conditions by ESB decoration. The in situ formed ESB layer can not only prevent direct contact and subsequent reaction between the segregated SrO and YSZ electrolyte but also significantly promote oxygen migration at the interface for the ORR, resulting in remarkable increases in power output and decreases in activation energy. These results clearly demonstrate the benefits of in situ formation of highly functional ESB protective layers on LSC-based cathode/YSZ electrolyte interfaces through the ESB decoration method under SOFC operating conditions. Nevertheless, more work is required to optimize the polarization conditions for these phase migrations and distributions for the electrode/electrolyte interface of SOFCs.

Fig. 37

Reproduced with permission from Ref. [209]. Copyright 2018, American Chemical Society

a STEM-EDS element mapping and b high-resolution TEM (HRTEM) and fast Fourier transform (FFT) micrographs of the directly assembled ESB-LSCFNb electrode/YSZ electrolyte interface of an anode-supported cell after polarization at 250 mA cm⁻² and 750 °C for 100 h. Red arrows indicate lattice distortion.

6 Future Prospects of SSE in SOFCs

Riess discussed general differences between LSE and SSE systems or cells [2]. In addition to the distinct differences in the cell configuration, placement of the RE, the supporting electrolyte, space charge or double layer structure, etc., between the liquid and solid electrolytes, there are two fundamental features that lead to the special positions of the SSE in solid devices such as SOFCs: StS contact and polarization-induced defect chemistry and the interface. Taking water electrolysis as a typical example in liquid electrolyte cells, StS contact only exists between nanoparticles in the electrocatalysts, and polarization primarily affects grain growth and agglomeration of the electrocatalysts. In SOFCs, StS contact is one of the fundamental factors behind the change in and shift of the equipotential line, the constriction effect and the polarization-induced interface. The conductivity and mobility of charge carriers such as oxygen ions, electrons and electron holes affect the electrocatalytic performance in both LSE and SSE but behave in different ways. In LSE, the defect chemistry induced by the mobility of charge carriers only affects the electrochemical or photoelectrochemical activities of the catalysts or electrodes, not that of the liquid electrolyte, e.g., defect-enhanced charge separation in the photoanode for water splitting [252] and oxygen vacancy defect-modulated electrocatalytic activity of Fe–Ni-based double hydroxides for the OER. In SSE, the defect chemistry plays a critical role in both solid electrodes and solid electrolytes and is also strongly dependent on the polarization. The polarization-induced defect chemistry is responsible for the complicated surface segregation and incorporation or inhibition processes of cations on the surface of oxide electrodes of SOFCs. Table 3 lists the main differences between the LSE for water electrolysis and the SSE for SOFCs.

Table 3 Generic comparison of LSE and SSE

The oxygen nonstoichiometry of oxide systems such as perovskite and fluorite structure-based oxides, i.e., oxygen deficiency and oxygen excess, is strongly interrelated with the structural parameters, phase stability, ionic and electronic transport, oxygen storage and catalytic activities [253, 254]. In SOFCs, the oxygen nonstoichiometry of perovskite electrode materials in particular strongly depends not only on the defect chemistry (e.g., doping at the A or B site of the perovskite) but also on the polarization.

Well and purposely designed experiments are essential for the fundamental understanding of the SSE phenomena at porous electrode/dense electrolyte interfaces. The development of in situ/operando characterization techniques, such as SPEM, surface-enhanced Raman spectroscopy (SERS), X-ray absorption spectroscopy (XAS), and time-resolved XRD, is also most important to identify key descriptors/properties for electrode materials or functional heterogeneous interfaces, especially under fuel cell operating conditions [234, 255, 256]. Information from such in situ/operando observations can provide valuable guidance for the design of optimal electrode materials, microstructures and electrode/electrolyte interfaces for SOFCs.

A fundamental and comprehensive understanding of the SSE phenomena and electrode and electrolyte processes is key for the future development and design of next-generation “state-of-the-art” SOFC devices with intermediate- to low-temperature operation with a quality exceeding the limit of conventional IT-SOFCs. With advances in the fundamental understanding of polarization-induced phenomena, the combination of theoretical computational modeling and experimental verification, and further development of special voltage probe techniques and cell configuration, the deep understanding of the SSE will provide new design paradigms for the development of key materials and interfaces in IT-SOFCs (see Fig. 38). Continuous research on and innovative approaches toward a fundamental understanding of the SSE will foreseeably be key for accelerating R&D of the next-generation state-of-the-art IT-SOFCs.

Fig. 38

Schematic diagram of the interrelationship between SSE and SOFCs

Appendix: List of abbreviations

ASR:

Area-specific resistance

BSCF:

Barium strontium cobalt ferrite or (Ba, Sr)(Co, Fe)O₃ (BSCF)

CC:

Current collector

CCCL:

Cathode current-collecting layer

CE:

Counter electrode

CN:

Coordination number

DFT:

Density functional theory

EIS:

Electrochemical impedance spectroscopy

ESB:

Erbium stabilized bismuth or (Er, Bi)₂O₃

GCI:

Galvanostatic current interruption

HOR:

Hydrogen oxidation reaction

IT-SOFC:

Intermediate tempe rature solid oxide fuel cell LSC

LSC:

Lanthanum strontium cobaltite or (La, Sr)CoO_3−δ

LSCF:

Lanthanum strontium cobalt ferrite or (La, Sr)(Co, Fe)O_3−δ

LSCFNb:

Nb-doped La_0.6Sr_0.4Co_0.2Fe_0.7Nb_0.1O_3−δ

LSE:

Liquid state electrochemistry

LSF:

Lanthanum strontium ferrite or (La, Sr)FeO_3−δ

LSM:

Lanthanum strontium manganite or (La, Sr)MnO₃

MIEC:

Mixed ionic and electronic conducting or mixed ionic and electronic conductor

ORR:

Oxygen reduction reaction

PEMFC:

Proton exchange or polymer electrolyte membrane fuel cell

RE:

Reference electrode

SERS:

Surface-enhanced Raman spectroscopy

SOFC:

Solid oxide fuel cell

SPEM:

Scanning X-ray photoelectron microscopy

SSE:

Solid-state electrochemistry

StS:

Solid-to-solid

TPB:

Three- or triple-phase boundary

VP:

Voltage probe

WE:

Working electrode

XAS:

X-ray absorption spectroscopy

YSZ:

Yttria-stabilized zirconia