1 Introduction

Accurate angle measurement is crucial for maintaining product quality in manufacturing [1,2,3,4]. Optical methods are generally preferred because they offer a noncontact approach. Numerous optical techniques have been developed over the years for this purpose [5,6,7,8]. Many angle sensors are also available for wide-range angle measurements [9, 10]. One commonly used angle sensor is the optical encoder, which is mounted on rotary shafts to cover the full 360° angular displacement range of rotation [11,12,13]. Precise measurement for small angle is also necessary for various scenarios, including the measurement of angular error motion in a moving stage, the tilt angle error motion in a rotating spindle, or the roughness measurement on a tilt surface [14,15,16]. Angle sensors based on autocollimation and light interferometry have been proposed for this purpose [17, 18]. These sensors utilize a reflective mirror mounted on a target to measure an angular displacement, with the change in the sensor output corresponding to the magnitude of the angular displacement.

With the continuous development of laser technology, femtosecond mode-locked laser sources are increasingly used in many fields [19,20,21] and investigated in the field of angle measurement. Compared to traditional laser sources, femtosecond mode-locked laser sources contain a series of stable and equally spaced combs in the frequency domain [1]. Therefore, several angle sensors, such as the optical lever, have been proposed, and their high-resolution characteristics have been approved [22]. A Fabry–Pérot etalon was used in this study to modulate the femtosecond laser beam before projecting it onto a grating reflector, where a group of first-order diffracted beams of different modes was generated. The angle measurement range has been expanded to 15,000 arcseconds because the diffraction light of different incident modes on the detector changes with the angular displacement. Meanwhile, the concept of optical frequency domain angle measurement has also been proposed [23, 24]. Unlike the optical lever sensor, the angle measurement sensitivity of the frequency domain angle sensor is independent of the distance between the detector and the grating reflector, enabling a compact design for the setup.

The femtosecond mode-locked laser beam can also produce an extremely high intensity in an ultrashort time scale, which can be utilized to generate various nonlinear optical (NLO) phenomena, including second harmonic generation (SHG) [25]. SHG is a common NLO process that involves the passage of nonlinear material via an incident laser to produce a second-harmonic wave (SHW). The incident laser beam supplies a fundamental wave (FW), which has a frequency of ν1 and a wavelength of λ1. The generated SHW has a frequency ν2, which is double that of the incident laser (ν2 = 2ν1), and a half wavelength λ2 (λ2 = λ1/2). Furthermore, SHG in birefringent materials exhibits a strong angular dependence, which was first discovered in the 1960s [25]. The angular dependence is determined by the phase mismatching magnitude between the incident FW and the SHW in a birefringent crystal. The phase mismatching between the FW and the SHW changes as the laser travels through the crystal at different angles because of the anisotropy of the birefringent crystal. This phase mismatching determines the efficiency of the SHG process and results in an intensity change in the output SHG [26]. Previous research has proposed the use of SHG for angle sensing and designed several measurement prototypes [27, 28]. The first SHG-based angle sensor is intensity-dependent. A lens was employed to focus the femtosecond laser beam into the low-dispersion beta barium borate (β-BBO) crystal. The β-BBO crystal was fixed with the rotary stage, and the photodiode was employed for detection. The detected intensity changes with the stage rotation, and a sub-arcsecond magnitude resolution is realized [27]. However, the measurement sensitivity is restricted by chromatic aberration due to the broad spectrum of the femtosecond laser beam. Therefore, a new wavelength-dependent SHG angle sensor is developed by using a reflectively focused lens to avoid the chromatic effect [28]. In this case, the angle-dependent peak shift of the SHG spectrum is detected by the optical spectrum analyzer in the optical frequency domain. The central wavelength λc of the SHG spectrum quantifies the angle dependence of the peak shift. The measurement range (10,752 arcseconds) and the resolution (3.00 arcseconds) are evaluated by using the central wavelength λc.

The central wavelength λc is a wavelength obtained by a summation weighted by the intensity I2(λ2, θ) in an SHG spectrum. That is to say, the weight of wavelength λ2 is large when the intensity I2(λ2, θ) at wavelength λ2 is high. The central wavelength λc can be applied to a simple case where only one peak is in the spectrum. Multiple peaks emerge in the optical frequency domain when the angle is rotated to the Maker fringe area [29]. However, if the λc is still used for angle measurement in this area, then an inaccuracy in measurement results will occur. Moreover, in actual measurement situations, the relationship between the SHG spectrum and angle positions is remarkably complicated. Their relationship is affected by the assembly precision, the chromatic aberration, or a component of the experiment setup, such as the stability of the femtosecond laser. This effect is usually random and highly nonlinear, increasing the difficulty of obtaining an accurate angle measurement result with the simple central wavelength. The artificial neural network (ANN) was approved in the 1980s due to its capability to fit complex functional relationships arbitrarily [30]. Therefore, ANNs may also be a potential tool for handling the inverse problem of obtaining the angle position from the angle-dependent SHG spectrum. Owing to the rapid development of computation, the deep neural network, also called deep learning [31], has emerged as a powerful tool for tackling problems via data learning. Neural network techniques are gaining widespread attention and increasing interest in many areas of optical metrology [32,33,34,35], including computer vision, medical image processing, computational imaging, and optical scatterometry [36,37,38,39]. In recent years, ANN has also been used for angle measurements, such as error compensation for an optical encoder [40] or calibration for an autocollimator [41], which verified the effectiveness of the ANN.

An application of ANN for angle measurement based on SHG is proposed in this study as a continuation of a previous study. For a brief understanding, the principle of SHG-based angle measurement is first introduced, and the differences between the Maker fringe and phase-matching areas and the limitations of using the central wavelength for the angle measurement are explained. The theoretical details of the proposed method, including the training data collection, data preprocessing, the designed structure of ANN, and training methods, are then described. Finally, the experimental results demonstrate that the proposed method can achieve angle measurement with an angular displacement exceeding 20,000 arcseconds, including the Maker fringe and phase-matching areas. In addition, the angle accuracy based on ANN prediction and the measurement resolution are quantitatively evaluated.

2 Principle and the Proposed Method

2.1 Measurement Principle

The SHG angle measurement system is depicted in Fig. 1. The femtosecond laser source emits the FW along the Z-axis. This wave passes through the nonlinear crystal and generates the SHW. The SHW has a frequency ν2 that is double that of ν1 (ν2 = 2ν1), and the wavelength λ2 is half λ1 (λ2 = λ1/2). The SHW produced is focused on a multiple-mode fiber by an objective lens. An optical spectrum analyzer (OSA) is then employed to detect the intensity spectrum I2 of the SHW. The optic axis of the nonlinear crystal is represented by the dotted green line. The L and d are the length and diameter of the nonlinear crystal, respectively. The θ denotes the angle between the optic axis and the laser beam direction in the crystal (indicated by the red arrow in Fig. 1). The intensity I2(λ2, θ) is related to the angle θ because of the effects of phase-matching and phase-mismatching conditions. Under the simplified plane-wave assumption, I2(λ2, θ) is written as Eq. (1) [42]:

$$I_{2}{ (\lambda_{2} ,\theta )} \propto L^{2} I_{1}^{2} {(\lambda_{1} )}\sin c^{2} {(\Delta k(\lambda_{2} ,{\theta} )}L/2)$$
(1)

where the Δk(λ2, θ) is represented in Eq. (2). In this equation, k1 is the wave number of FW. The n1(λ1) and n2(λ2, θ) denote the refractive indexes of FW and SHW, respectively, and the Δn is the difference in refractive indexes.

$$\Delta k(\lambda_{2} ,\theta ) = \frac{4{\mathrm{\pi}}}{{k_{1} }}\left[ {n_{1} \left( {\lambda_{1} } \right) - n_{2} \left( {\lambda_{2} ,\theta } \right)} \right] \, = \frac{4{\mathrm{\pi}}}{{k_{1} }}\Delta n\left( {\lambda_{2} ,\theta } \right)$$
(2)
Fig. 1
figure 1

Diagram of the second harmonic generation (SHG) angle measurement system (The transmitted FW is not shown)

Full size image

The SHW intensity I2(λ2, θ) is determined by Δn(λ2, θ). If the crystal rotates to a specific phase-matching angle θm(λ2) that makes Δn(λ2, θm(λ2)) = 0 hold, then the peak value of I2(λ2, θ) will be at the specific wavelength λ2 in the SHG spectrum, which is determined by the property of the sinc(.) function. This phenomenon is the identified phase-matching condition reached at wavelength λ2. Suppose total N wavelengths exist in the range from \(\lambda_{2}^{1}\) to \(\lambda_{2}^{N}\). As the θ changes in an angular range \([\theta_{\text{m}} (\lambda_{2}^{1} ), \ldots ,\theta_{\text{m}} (\lambda_{2}^{i} ),\theta_{\text{m}} (\lambda_{2}^{i + 1} ), \ldots ,\theta_{\text{m}} (\lambda_{2}^{N} )]\), the peak wavelengths in the SHG spectrum will continuously change in a range of \([\lambda_{2}^{1} , \ldots ,\lambda_{2}^{i} ,\lambda_{2}^{i + 1} , \ldots ,\lambda_{2}^{N} ]\) because the phase-matching conditions for these wavelengths are reached sequentially. Therefore, the SHG spectrum has a single-peak shift in the phase-matching area as θ continuously changes, as shown in Fig. 2.

Fig. 2
figure 2

Single-peak shift in the phase-matching area. (The green line represents the angle dependence of the central wavelength λc(θ))

Full size image

In the previous research, the central wavelength λc is used to denote the angle dependence of the single-peak shift as Eq. (3) [42]:

$$\lambda_{\text{c}} = \frac{{\sum\nolimits_{i = 1}^{N} {\lambda_{2}^{i} I_{2} (\lambda_{2}^{i} ,\theta )} }}{{\sum\nolimits_{i = 1}^{N} {I_{2} (\lambda_{2}^{i} ,\theta )} }}$$
(3)

The central wavelength λc is suitable when only one peak exists in the phase-matching area. As illustrated in Fig. 2, λc (represented by the green line) decreases as the angle θ increases, and its trend is consistent with the peak-shift direction because the peak wavelength has the largest weight in the spectrum.

However, the concept of λc can only be used when the θ is in the angle range of the phase-matching area. A concept of angle measurement in a Maker fringe area was proposed in previous research, and a theoretical investigation was performed. In this case, multiple peaks are found in the SHG spectra, as shown in Fig. 3 [29], which is different from the case of the angle measurement in the phase-matching area. The λc cannot accurately reflect multiple-peak shifts when the angle θ rotates in the Maker fringe area from \(\theta^1_{\text{mf}}\) to \(\theta^N_{\text{mf}}\). Moreover, the exact model of the measured SHG intensity is not as easy as Eq. (1) due to the involvement of assembly precision and the effect of chromatic aberration. Therefore, analytically resolving the inverse problem of obtaining the angle through the measured SHG spectrum is difficult. Therefore, the use of ANN is proposed to obtain angle information from the measured SHG spectrum and address the inverse problem.

Fig. 3
figure 3

Multiple-peak shifts in the Maker fringe area. (The green line represents the angle dependence of the central wavelength λc(θ))

Full size image

2.2 Theory of the Proposed Method

Three main sequential steps are used to obtain a trained ANN for angle measurement: SHG spectrum collection (Step 1), preprocessing (Step 2), and ANN training (Step 3). As shown in Fig. 4, the stage rotates continuously with the y-axis, and the plane mirror is fixed to the stage. The raw SHG spectra are recorded in the rotation process. Simultaneously, a standard angle measurement instrument is employed to record the referenced angle data θr by its measurement beam. The referenced angle vector θr represents the set of all the recorded angle positions as Eq. (4):

$${{\varvec{\theta}}}_\mathrm{r} = [\theta_\mathrm{r}^{1} , \ldots ,\theta_\mathrm{r}^{m} ,\theta_\mathrm{r}^{m + 1} , \ldots ,\theta_\mathrm{r}^{M} ]\quad m = 1,2, \ldots M$$
(4)

where m denotes the index of the angle position and M is the total number of the angle positions. Notably, the referenced angle θr is the incident angle in the incident plane instead of the angle θ inside the nonlinear crystal [29], and the relation is given as Eq. (9) in a previous study [43]. The bold I2(θr) represents the raw SHG spectrum corresponding to the angle θr as Eq. (5), where N denotes the wavelength sampling number of OSA. One SHG spectrum \({\textbf{\textit{I}}}_{2} (\theta_\mathrm{r})\) and one angle θr form a pair of training data, and M pairs of the training data are available in the training set. The matrix I2 denotes the set of all raw SHG spectrums as Eq. (6), where the matrix I2 is an N × M matrix corresponding to the sampling number of spectrum and angle positions to facilitate the matrix computation of the ANN.

$$\varvec{I}_{2} \left( {\theta_\mathrm{r} } \right) = \left[ {I_{2} \left( {\lambda_{2}^{1} ,\theta_\mathrm{r} } \right), \ldots ,I_{2} \left( {\lambda_{2}^{i} ,\theta_\mathrm{r} } \right),I_{2} \left( {\lambda_{2}^{i + 1} ,\theta_\mathrm{r} } \right), \ldots ,I_{2} \left( {\lambda_{2}^{N} ,\theta_\mathrm{r} } \right)} \right]^\textrm{T}$$
(5)
$$\mathbf{I}_{2} = [\varvec{I}_{2} (\theta_\mathrm{r}^{1} ), \ldots ,\varvec{I}_{2} (\theta_\mathrm{r}^{m} ),\varvec{I}_{2} (\theta_\mathrm{r}^{m + 1} ), \ldots ,\varvec{I}_{2} (\theta_\mathrm{r}^{M} )]\quad m = 1,2, \ldots ,M$$
(6)
Fig. 4
figure 4

Diagram of the angle-dependent second harmonic generation (SHG) spectrum collection

Full size image

Preprocessing the training data before the training process is generally necessary, as shown in Fig. 5 [44]. The raw SHG spectrum I2(θr) is subsequently normalized, filtered, and interpolated. For normalization, the SHG spectrum I2(θr) is first divided by the largest elemental value max(I2(θr)) as shown in Eq. (7), where \({\mathbf{I}}_{2}^{\rm Nor}\) is the result of the normalized SHG matrix containing the normalized SHG spectrum \(\textit{\textbf{I}}_{2}^{{{\text{Nor}}}}\). The filtering is then performed by the denoising algorithm. The built-in MATLAB function is employed to decrease the high-frequency noise in \({\mathbf{I}}_{2}^{{{\text{Nor}}}}\). Finally, the B-spline interpolation operation is also performed on the SHG matrix \({\mathbf{I}}_{2}^{{{\text{Nor}}}}\), increasing the visibility of small features in the spectrum. The dimension of the SHG matrix becomes NI × M after completing the interpolation, where NI denotes the SHG spectrum length after interpolation.

$${\mathbf{I}}_{2}^{\rm Nor} = \left[ {\frac{{\textit{\textbf{I}}_{2} (\theta_\mathrm{r}^{1} )}}{{\max (\textit{\textbf{I}}_{2} (\theta_\mathrm{r}^{1} )}}, \ldots ,\frac{{\textit{\textbf{I}}_{2} (\theta_\mathrm{r}^{m} )}}{{\max (\textit{\textbf{I}}_{2} (\theta_\mathrm{r}^{m} )}},\frac{{\textit{\textbf{I}}_{2} (\theta_\mathrm{r}^{m + 1} )}}{{\max (\textit{\textbf{I}}_{2} (\theta_\mathrm{r}^{m + 1} ))}}, \ldots ,\frac{{\textit{\textbf{I}}_{2} (\theta_\mathrm{r}^{M} )}}{{\max (\textit{\textbf{I}}_{2} (\theta_\mathrm{r}^{M} ))}}} \right]$$
(7)
Fig. 5
figure 5

Diagram of the preprocessing of second harmonic generation (SHG) spectrum

Full size image

Similarly, the referenced angle vector θr is also scaled to the range of [0, 1] by a simple linear transformation as Eq. (8), where the min(θr) and the max(θr) are the minimum and maximum values recorded by the standard instrument, respectively.

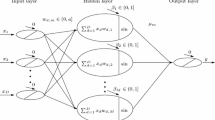
$${\varvec{\theta}}_{\rm r}^{\rm Nor} = \frac{{{\varvec{\theta}}_{\rm r} - \min ({\varvec{\theta}}_{\rm r} )}}{{\max ({\varvec{\theta}}_{\rm r} ) - \min ({\varvec{\theta}}_{\rm r} )}}$$
(8)

The architecture of the ANN and the ANN training process is shown in Fig. 6. Four layers are sequentially found from left to right in the used ANN: one input layer (Layer 1), two hidden layers (Layers 2 and 3), and one output layer (Layer 4). The connection between layers is fully established. The node number of the input layer is NI corresponding to the dimension of the interpolated SHG matrix \({\mathbf{I}}_{2}^{{{\text{Nor}}}}\). The node number of the output layer is 1, corresponding to the predicted angle \({\hat{\varvec{\theta}}}_{{\text{r}}}\). The node number in the hidden layer is Num. In ANN, W(l) (weights) and b(l) (biases) are implemented for the linear transformation between the lth layer and the l + 1th layer. The activation functions σ(.) then map the linear transformation into a nonlinear space. The neural network can learn the nonlinear mapping between \({\mathbf{I}}_{2}^{{{\text{Nor}}}}\) and \({\varvec{\theta}}_{\rm r}^{{{\text{Nor}}}}\) by iteratively training W and b.

Fig. 6
figure 6

a Architecture of artificial neural network (ANN); b cyclical training process

Full size image

The cyclical training process comprises initialization (Step 3.0), forward propagation (Step 3.1), loss computation (Step 3.2), backward propagation (Step 3.3), and parameter optimization (Step 3.4). The initialization indicates that W and b are assigned a small random value before training the network. The forward propagation indicates that the input SHG matrix \({\mathbf{I}}_{2}^{{{\text{Nor}}}}\) is passed forward through the network, layer by layer, to generate the predicted angle \(\hat{\varvec{\theta }}_{\rm r}\) as the output. The forward calculation can be expressed as Eq. (9), where z is the matrix in the layer and a is the matrix operated after the activation function σ(.).

$$\begin{gathered} {\mathbf{z}}^{(2)} = {\mathbf{W}}^{(2)} {\mathbf{I}}_{2}^{{{\text{Nor}}}} + {\mathbf{b}}^{(2)} ,{\mathbf{a}}^{(2)} = \sigma ({\mathbf{z}}^{(2)} ) \hfill \\ {\mathbf{z}}^{(3)} = {\mathbf{W}}^{(3)} {\mathbf{a}}^{(2)} + {\mathbf{b}}^{(3)} ,{\mathbf{a}}^{(3)} = \sigma ({\mathbf{z}}^{(3)} ) \hfill \\ {\mathbf{z}}^{(4)} = {\mathbf{W}}^{(4)} {\mathbf{a}}^{(3)} + {\mathbf{b}}^{(4)} ,\hat{\varvec{\theta }}_{\rm r} = {\mathbf{z}}^{(4)} \hfill \\ \end{gathered}$$
(9)

The numerical difference between the \(\hat{\varvec{\theta }}_{\rm r}\) predicted by ANN and the referenced angle \({\varvec{\theta }}_{\rm r}^{{{\text{Nor}}}}\) can be evaluated by the mean square error (MSE) loss, as shown in Eq. (10), where the ||.|| is the operation of the L2-norm.

$${\text{MSE}} = \frac{1}{2}\left\| {\hat{\varvec{\theta }}_{\rm r} - {\varvec{\theta}}_{\rm r}^{{{\text{Nor}}}} \, } \right\|^{2}$$
(10)

The MSE loss should be minimized to obtain a close predicted angle \(\hat{\varvec{\theta }}_{\rm r}\) to the reference angle \({\varvec{\theta }}_{\rm r}^{{{\text{Nor}}}}\), which is determined by W and b inside the hidden layers. In the training process, W and b are iteratively optimized in accordance with their gradients G. The calculation of the gradients is shown in Eq. (11), where \({{\varvec{\updelta}}}^{(l)}\) is given in Eq. (12). The gradient calculation starts at layer 4 and goes back to layer 2. The parameters W and b are then updated in the gradient direction as Eq. (13), where α is the learning rate. Steps 3.1–3.4 are cyclical until the MSE converges to a stable value and the training process is completed.

$$\begin{array}{*{20}l} {G({\mathbf{W}}^{(l)} ) = \frac{\partial {\text{MSE}}}{{\partial {\mathbf{W}}^{(l)} }} = {{\varvec{\updelta}}}^{(l)} {\mathbf{a}}^{(l - 1)} } \hfill \\ {G({\mathbf{b}}^{(l)} ) = \frac{\partial {\text{MSE}}}{{\partial {\mathbf{b}}^{(l)} }} = {{\varvec{\updelta}}}^{(l)} } \hfill \\ \end{array} {\text{For}}\;l = {4},{ 3},{ 2}$$
(11)
$$\begin{gathered} {\varvec{\updelta}}^{(l)} = (\hat{\varvec\theta }_{\rm r}^{{}} - \varvec\theta_{\rm r}^{\rm Nor} ) \odot \sigma^{\prime } (\mathbf{z}(l))\quad {\text{For}}\;l \, = \, 4 \, \hfill \\ {\varvec{\updelta}}^{(l)} = (\mathbf{W}^{(l + 1)} )^{\rm T} {\varvec{\updelta}}^{(l + 1)} \odot \sigma^{\prime } (\mathbf{z}(l))\quad {\text{For}}\;l \, = \, 2, \, 3 \, \hfill \\ \end{gathered}$$
(12)
$$\begin{array}{*{20}l} {{\mathbf{W}}^{(l)} = {\mathbf{W}}^{(l)} - \alpha G({\mathbf{W}}^{(l)} )} \hfill \\ {{\mathbf{b}}^{(l)} = {\mathbf{b}}^{(l)} - \alpha G({\mathbf{b}}^{(l)} )} \hfill \\ \end{array} \quad {\text{For}}\;l = {4},{3},{2}$$
(13)
$$\hat{\varvec\theta }_{\rm r} = \min (\varvec\theta_{\rm r} ) + \hat{\varvec\theta }_{\rm r} \left( {\max (\varvec\theta_{\rm r} ) - \min (\varvec\theta_{\rm r} )} \right)$$
(14)

The trained ANN can be employed for angle measurement. Notably, the SHG spectrum cannot be directly inputted into the neural network before the preprocessing. In addition, the angle obtained by the trained ANN is normalized and converted into the predicted angle \(\hat{\varvec{\theta }}_{\rm r}\) through a linear transformation, as shown in Eq. (14), where the equal sign “ = ” indicates an assignment.

3 Experimental Results and Discussion

3.1 Measurement Setup

The angle-dependent SHG spectrums are collected by using the collimated SHG sensor, as shown in Fig. 7, to verify the proposed method. The commercial femtosecond laser (C-Fiber High Power, Menlo Systems, Planegg, Germany) supplies the source of the FW. This laser has a maximum average power of 500 mW, a pulse repetition rate of 100 MHz, a pulse duration shorter than 150 fs, and a spectral range from 1480 to 1640 nm. Polarizer 1 (LPIREA050-C, Thorlabs Japan Inc., Tokyo, Japan) is placed after the laser window. The transmission axis of polarizer 1 is parallel to the y-axis to produce an s-polarized laser beam. The plano-convex lens (f1 = 150 mm, f2 = 75 mm) is used to reduce the beam width to half before the laser beam incident on the MgO: LiNbO3 crystal to improve the light intensity (Castech Inc., Fujian, China). The crystal has a length L of 2 mm and a diameter d of 5 mm. This crystal is mounted in the crystal holder, which is motorized by the rotation stage (KRB04017C, Suruga Seiki Co., Ltd., Shizuoka, Japan). The stage has a maximum rotation range of ± 8.5° and a minimum resolution of 0.0067°. This stage is driven by the stepping controller (DS102MS, Suruga Seiki Co., Ltd., Shizuoka, Japan). An initial position maker is found in the rotary stage for the rough alignment. The autocollimator (Elcomat 3000, Moller–Wedel Optical GmbH, Wedel, Germany) is chosen as the standard instrument to record the referenced angle data θr from the measured beam reflected from the plane mirror. The angle-dependent SHW is generated after the FW passes through the crystal, and the generated SHW is p-polarized. The objective lens with an alignment stage (MBT613D/M, Thorlabs Japan Inc., Tokyo, Japan) is employed to focus the SHW into multimode fiber (M42L02, Thorlabs Japan Inc., Tokyo, Japan), and the SHG spectrum I2(θr) is then obtained by the OSA (AQ6370C, Yokogawa Electric, Tokyo, Japan). Polarizer 2 (LPNIRC100, Thorlabs Japan Inc., Tokyo, Japan) is placed behind the nonlinear crystal to avoid the supercontinuum spectrum generated by the nonlinear interaction between the s-polarized FW and the multimode fiber. The transmission axis of polarizer 2 is perpendicular to the y-axis, ensuring that it does not affect the transmission of p-polarized SHW while eliminating FW.

Fig. 7
figure 7

Diagram of the angle-dependent second harmonic generation (SHG) spectrum collection system

Full size image

3.2 Raw SHG Spectrum Collection

The raw SHG spectrum is collected by the data collection system, and the rotary stage is driven by a sampling interval of around 12.1 arcseconds. The total number M of the sampling angular points is 1701. In an angle position θr, the collected SHG spectrum is automatically obtained by the OSA in a wavelength range from 765 to 800 nm. The sampling period of the spectrum is 0.2 nm, which indicates that the SHG spectrum I2(θr) vector has a length of N = 176. The matrix I2 denotes the raw SHG matrix containing the set of all the I2(θr) as shown in Eq. (6). The dimension of the I2 is 176 × 1701.

The raw SHG matrix I2 is plotted in Fig. 8(a), where the horizontal axis denotes the referenced angle θr recorded by the autocollimator, and the vertical axis denotes the wavelength of SHW. The color bar denotes the intensity in the unit of μw. The I2 is roughly divided into one phase-matching and two Maker fringe areas according to the angle range. The phase-matching area has 9719 arcseconds, which range from − 5881 arcseconds to 3838 arcseconds. The two Maker fringe areas range from − 11,317 arcseconds to − 5881 arcseconds and 3838 arcseconds to 9240 arcseconds. The angle-dependent peak shift is denoted by the red arrow in Fig. 8. Figure 8(a) shows that the phase-matching area has a single angle-dependent peak shift, where the peak moves toward the short wavelength as the angle θr increases. The central wavelength λc is calculated in accordance with Eq. (3) and plotted by the green curve, where the angle dependence of λc is consistent with the peak shift direction. Figure 8(b) and (c) provides the details of the zoomed-in Maker fringe areas. The color bar is adjusted to the range of 0 μW to 0.003 μW to demonstrate the multiple angle-dependent peaks shifts. The λc in the Maker fringe areas is also calculated and denoted by the green curve. However, the λc curves are not observed in the direction of multiple-peak shifts in the two Maker fringe areas. The absence of λc curves is due to the λc(θr), which is essentially determined by the intensity distribution of the spectrum I2(θr). Equation (3) shows that the λc is close to the wavelengths λ2(θr) with high light intensity I2(λ2, θr). The phase-matching area has only one main peak in the spectrum; thus, the central wavelength λc is close to the peak position. However, the SHG spectrum has multiple peaks in the Maker fringe areas. In this case, a simple central wavelength λc cannot reflect all the peak positions. Therefore, characterizing the angle-dependent multiple-peak shifts is unsuitable.

Fig. 8
figure 8

a Raw second harmonic generation (SHG) matrix; b zoomed-in picture of Maker fringe area 1; c zoomed-in picture of Maker fringe area 2

Full size image

3.3 Data Preprocessing

The result after normalization is given in Fig. 9(a). This figure reveals that all peak shifts denoted by the red arrow are highly significant due to the normalization, whether in the phase-matching or the Maker fringe areas. Figure 9(b) and (c) also shows the 3D angle-dependent peak shifts. The angle dependence of multiple-peak shifts becomes highly prominent, which is advantageous for the following neural network training. In addition, the nonlinear angle dependence of the peak wavelength becomes increasingly noticeable in the zoomed-in picture of Fig. 9(a) due to the normalization. This finding further confirms the necessity of using ANN to map the correspondence between the SHG spectrum and the angle θr.

Fig. 9
figure 9

a Second harmonic generation (SHG) matrix \({\mathbf{I}}_{2}^{\rm Nor}\) after normalization (The peak wavelength is denoted by the green line.); b Three-plot multiple-peak shifts in the Maker fringe area 1; c 3D plot single-peak shift in the phase-matching area

Full size image

An SHG spectrum in the Maker fringe area is presented in Fig. 10, where the blue line, green dotted line, and red points denote the spectrum after normalization, filtering, and interpolation, respectively. The SHG spectrum length is NI = 800 after the interpolation operation. The figure reveals that the spectral smoothness has been improved after filtering, especially in the part of the spectrum with a relatively low signal-to-noise ratio, such as the last three peaks from 785 to 800 nm. For a better comparison, a zoomed-in picture of the 791–793 nm range is presented in the magnified view of Fig. 10. The peak becomes smooth after filtering, while interpolation increases the visibility of small variations on the peak.

Fig. 10
figure 10

Second harmonic generation (SHG) spectrum of Maker fringe area after filtering and interpolation

Full size image

The SHG matrix \({\mathbf{I}}_{2}^{\rm Nor}\) is further divided into seven areas for ANN training because the signal-to-noise ratio (SNR) of the SHG spectra varies in these angle areas. The division is shown in Fig. 11. Table 1 provides the specific partition information for the area division. For an intuitive presentation, subfigures from (I) to (VII) in Fig. 12 correspond to the typical SHG spectra from seven areas. The horizontal and vertical axes in each subfigure represent wavelength and normalized intensity, respectively. The red curve corresponds to the normalized SHG spectrum \({\varvec{I}}_{2}^{{{\text{Nor}}}}\), and the blue error bars represent the range of fluctuations \(\Delta {\varvec{I}}_{2}^{{{\text{Nor}}}}\) of the normalized SHG spectrum within three times the standard variance, which is calculated by 20 repeat measurements. In subfigures (I) to (VII), the magnified views are provided from 780 to 785 nm to identify the standard variance. As shown in Subfigure VIII, the SNRs of the seven areas are quantitatively evaluated in accordance with Eq. (15). The SNR first increases from 29.03 dB (area I) to 60.16 dB (area IV, phase-matching area) and then decreases to 31.29 dB (area VII). Therefore, the SNR is high when the area is close to the phase-matching area.

$${\text{SNR}} = 20\lg \left( {\frac{{\varvec{I}_{2}^{{{\text{Nor}}}} }}{{\Delta \varvec{I}_{2}^{{{\text{Nor}}}} }}} \right)$$
(15)
Fig. 11
figure 11

Area division for artificial neural network (ANN) training

Full size image
Table 1 SHG matrix division for ANN training
Full size table
Fig. 12
figure 12

(I)–(VII) Typical second harmonic generation (SHG) spectra in the seven divided areas; (VIII) calculated signal–noise ratio (SNR) of the seven divided areas

Full size image

3.4 Training and Measurement Results of ANN

The cyclical training process is realized by using the PyTorch deep learning library on the PyCharm platform. Table 2 provides detailed information on the ANN. The node number of the input layer is set in accordance with the dimension of the interpolated SHG spectrum. The node number of the hidden layer is empirically set at 20. The activation functions of two hidden layers, namely Sigmoid and Relu, are commonly used. The training parameters are also displayed in Table 2. The learning rate α = 0.0001 at the first iteration decreases exponentially as the iteration number increases to facilitate the convergence of ANN. The fold number of cross-validation is 10, which indicates that the training data of each area (areas I–VII) are divided into 10-fold. One of the folds is used for training, while the nine other folds are used for the validation set. The upper iteration limit is 10,000. The shuffle in the PyTorch package is true; thus, the training data are shuffled in every iteration. The shuffle and cross-validation techniques are the most commonly used settings to avoid overfitting in the training process.

Table 2 Parameters for ANN structure and training
Full size table

The ANNs are separately trained in seven areas according to the specified parameters in Table 2. Figure 13 shows the iterative optimization process of MSE during the training process. In this figure, the horizontal and vertical axes represent the iteration number and the logarithmic MSE, respectively. The subfigures (I)–(VII) correspond to the MSE results of areas I–VII. The blue and orange lines in the figure correspond to the MSE of the training and validation sets, respectively. All the MSE results reach a low (less than 10−5 a.u.) and stable level when the iteration number is 10,000. That is, the ANNs have converged to a local optimal level.

Fig. 13
figure 13

(I–VII) Iterative optimization of mean square error (MSE). (The subfigures (I)–(VII) correspond to results of areas I–VII.)

Full size image

The trained ANN is used to predict the output angle \(\hat{\theta }_{\rm r}^{{}}\) by inputting the normalized SHG spectrum \({\varvec{I}}_{2}^{\rm Nor}\). In each area, the 30 test SHG spectrums and their corresponding referenced angles θr are recorded. The MSE between the test spectrums and the training sets of seven areas can be calculated before the test SHG spectrums are sent to the ANN. The test spectrums then belongs to the area that has a spectrum minimizing the MSE value. Therefore, the test spectrums can be sent to the specific ANN for angle prediction. Figure 14 shows the scatter plot of the neural network predicted angle \(\hat{\theta }_{\rm r}^{{}}\) (vertical axis) and the reference angles θr (horizontal axis). The red fitting lines are obtained in each subfigure. The slope values k in all subplots are both close to 1, indicating that the trained neural network has acquired the capability to predict angles in all angle areas.

Fig. 14
figure 14

Scatter plot of the artificial neural network (ANN) predicted angle \(\hat{\theta }_{\rm r}\) and the referenced angle θr. (I)–(VII) Subfigures corresponding to the area number

Full size image

Conventional methods in optical scatterometry include the mentioned maximum likelihood estimation and the library search methods [45]. The developed ANN method and the conventional library search method are compared in this study. For the library search method, we assume that the training spectrum with the minimum MSE computed with the test spectrum is considered the best match, and the corresponding referenced angle is regarded as the measurement value. The absolute deviation \(\left| {\hat{\theta }_{\rm r}^{{}} { - }\theta_{\rm r}^{{}} } \right|\) is used as the evaluation criterion to evaluate the accuracy of the predicted angle. Figure 15 presents the accuracy results of the test set. In this figure, the horizontal axis of subfigures I–VII represents the number of test samples, and the vertical axis represents the deviation between the test results and the referenced angles. The blue circles represent the results of the developed method, while the red circles represent the results of the traditional library search method. Figure VIII shows the average deviation of the two methods in seven areas. For the developed method, the averaged deviation values first decrease from 7.20 arcseconds (area I) to 0.44 arcseconds (area IV) and then increase to 3.70 arcseconds (area VII). This trend is almost opposite to that of SNR in Fig. 12 (VIII). This finding indicates that the accuracy of the proposed method is closely related to the SNR. The accuracy of the library search method ranges from 11.99 arcseconds to 14.81 arcseconds, which does not considerably change in different areas. This phenomenon is due to the limitation of the library search method by the single-step rotation range of the motor during SHG spectrum collection (12.1 arcseconds). By contrast, the neural network method can provide empirical estimation through learning by improving measurement performance.

Fig. 15
figure 15

Absolute deviation \(\left| {\hat{\theta }_{\rm r}^{{}} { - }\theta_{\rm r}^{{}} } \right|\) compared to the autocollimator. (I)–(VII) Subfigures corresponding to the areas I–VII. (VIII) Averaged deviation of seven areas

Full size image

In addition, measurement stability is evaluated by repeat measurements. Figure 16 presents the results of the repeat measurements, which are obtained by using the SHG spectrums in Fig. 13 as the input of the ANN. The horizontal and vertical axes of subfigures I–VII represent the sampling time and the predicted angle \(\hat{\theta }_{\rm r}\), respectively. The repeat measurements are conducted by sampling the SHG spectra 20 times, with a sampling interval of approximately 0.7 s. The vertical axis of all subfigures is limited to a 10-arcsecond range for comparison. The figure shows that area IV (phase-matching area) also has the best measurement stability. The resolution is evaluated in accordance with Eq. (16), where \({{\partial \hat{\theta }_{\rm r} } \mathord{\left/ {\vphantom {{\partial \hat{\theta }_{i} } {\partial \varvec{I}_{2}^{\rm Nor} }}} \right. \kern-0pt} {\partial \varvec{I}_{2}^{\rm Nor} }}\) denotes the reciprocal of angular sensitivity \({{\partial \varvec{I}_{2}^{\rm Nor}} } \mathord{\left/ {\vphantom {{\partial I_{2}^{{{\text{Nor}}}} } {\partial \hat{\theta }_{r} }}} \right. \kern-0pt} {\partial \hat{\theta }_{\rm r} }\), \(\Delta {\varvec{I}}_{2}^{{{\text{Nor}}}}\) denotes the two-time standard deviation of the measured SHG spectra. The results of the measurement resolution are presented in Fig. 16(VIII). This trend is highly similar to measurement accuracy, which increases first and then decreases. The resolution in area IV (phase-matching area) is the best at 0.93 arcseconds. The resolutions of other Maker fringe areas are between 0.97 and 4.28 arcseconds.

$${\text{Res}} = \left\| {\frac{{\partial \hat{\theta }_{\rm r} }}{{\partial \varvec{I}_{2}^{\rm Nor} }}\left( {\Delta \varvec{I}_{2}^{\rm Nor} } \right)} \right\|$$
(16)
Fig. 16
figure 16

Repeat measurement results of artificial neural network (ANN). (I–VII) Subfigures corresponding to areas I–VII. (VIII) Resolution of seven areas

Full size image

The results of previous studies related to angle measurement using the SHG concept are displayed in Table 3. The total measurement range has been expanded to 20,576 arcseconds as shown in Table 3, including the multi-peak Maker fringe and phase-matching areas. The resolution is improved from 6.8 arcseconds to the sub-arcsecond level of 0.93 arcseconds by using a setup similar to the previous study [14]. In addition, the measurement accuracy is evaluated by comparison with the autocollimator, achieving a sub-arcsecond level of 0.44 arcseconds in the phase-matching area. Notably, the measurement rangeæ can be further expanded by improving the output power of the femtosecond laser to observe additional Maker fringes.

Table 3 Benchmarking against the previous studies
Full size table

4 Conclusions

An angle measurement method is proposed in this study using ANN. The angle-dependent SHG spectra are collected in an angular range of 20,576 arcseconds, which contains the phase-matching and Maker fringe areas. The result shows that the central wavelength λc can characterize the angle-dependent peak shift in the phase-matching area. However, this wavelength cannot characterize the angle-dependent multiple-peak shifts in the Maker fringe area. A mapping relationship between the SHG spectrum and the corresponding angle can be established by using a neural network to solve the inverse problem from the SHG spectrum to the angle, regardless of the peak number.

In the preprocessing method, the collected SHG spectra are normalized to determine the angle dependence of the multiple peaks in the Maker fringe area. The spectra are then filtered, interpolated, and divided into seven areas. The SNR is highest in the phase-matching area and low in the Maker fringe area as the distance from the phase-matching area increases.

The designed ANNs are separately trained in seven different areas. The convergence process of the training MSE in these areas is provided. The trained ANNs predict the angle from the unknown SHG spectra, and the predicted results are compared with the autocollimator. The accuracy and the resolution reach sub-arcsecond levels of 0.44 arcseconds and 0.93 arcseconds, respectively, in the phase-matching area, while their performances decrease in the Maker fringe area. In addition, the developed method was compared with the traditional library search method, and the obtained results demonstrated the advantages of the proposed method considering accuracy compared to library search methods.