1 Introduction

Gallium arsenide (GaAs) is one of the hard-brittle materials with desirable characteristics, such as high-temperature resistance [1], large bandgap [2], and high electronic mobility [3] making it superior to silicon as a semiconductor material. Fabrication of nanosize features and shapes on GaAs can be suitably performed by using atomic force microscopy (AFM) tip-based nanoscratching. As a form of contact mode machining, AFM achieves a much higher material removal rate than focused ion beam machining. However, AFM-based nanoscratching has gained pace only since the development of AFM, dating back to the 1990s. Hence, very limited literature exists around AFM-based investigation on a single-crystal material GaAs. An early work explored the possibility of directly patterning the furrows on a single-crystal GaAs surface [4, 5] and demonstrated its feasibility. 5G communication devices are expected to gain extreme popularity soon. Therefore, the mechanism of material removal, the origins of plasticity, and most importantly the kinetic coefficient of friction (COF) GaAs offers to a diamond tool during nanoscratching need to be understood. Obtaining the kinetic COF is an important element in nanotribology, because many analytical equations that are used to obtain insights into wear processes require the value of the COF a priori. However, previously reported values of COF, except those in the work of Komanduri et al. [6], exhibited a wide range, varying from extremely low (~ 0.005) to intermediate values (0.13) to high values (1.2 and 5). Moreover, previous works have investigated nanoscale friction on aluminum, which is a face-centered cubic ductile metal. Hence, some doubt exists as to whether the same conclusions will still apply to a zincblende lattice structure material such as GaAs. A survey of materials in the literature shows a wide range of values for the COF depending on the material’s crystal structure, as listed in Table 1.

Table 1 COF in various materials
Full size table

A similar investigation on a brittle-hard semiconductor material such as GaAs is necessary to ensure whether the nature of atomic-scale friction in this material is similar or different from that of the materials listed in Table 1. An open-ended question is whether GaAs behaves in the same way as aluminum in terms of the nanoscale scratching size effect and whether the force ratio and specific scratching energy in GaAs scale with the scratch depth or remain unchanged. These questions are the primary motivation behind this work. According to the literature review, many molecular dynamics (MD) studies were published during the last decade and further studies on nanomachining of GaAs are emerging. These studies shed light on aspects of crack formation [15] during single-point diamond turning (SPDT), plastic deformation of GaAs [16], and the material removal mechanism during chemo-mechanical polishing [17]. However, these studies did not address aspects of the size effect observed in GaAs much like the other brittle materials, and they also did not clarify whether the kinetic COF is a sufficiently robust indicator to compare simulations and experiments, especially in this era of the digital twin. A well-planned experiment and MD simulation methodology were developed by undertaking a thorough investigation to obtain various insights that are relevant to the cost-effective nanomanufacturing of GaAs; this effort is considered a novel one.

2 Research Methodology

2.1 MD Simulation Methodology

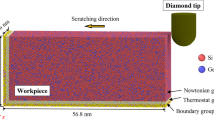
MD simulations were performed via an open-source code, namely, large-scale atomic/molecular massively parallel simulator (LAMMPS) [18]. The three-dimensional (3D) nanoscratching model that is used to emulate the AFM nanoscratching developed in this work is shown in Fig. 1. The atoms of the single-crystal GaAs workpiece are divided into three zones, namely, the Newton atoms, thermostat atoms, and boundary atoms, following the previously published literature on this topic [19,20,21,22]. The boundary atoms were kept fixed to maintain the symmetry of the initial lattice during MD simulation. The thermostat atoms were set to follow the Berendsen thermostatic dynamics [23] to maintain the thermodynamics of the system by using them as a heat dissipate or in place of a coolant, which was not considered in the simulation model. Newton atoms were allowed to follow the Newtonian (NVE) dynamics of LAMMPS. A pyramid-shaped diamond tool was modeled to mimic the AFM tip, which contained nearly 17,132 atoms. The AFM tip was modeled as a rigid non-deformable body because the cutting distance considered in this work was too small, and the intention was not to study the tool wear, which is an aspect that was already reported previously [24]. The diamond tip was prescribed a velocity of 10 m/s into the GaAs workpiece, which was oriented on the (110) plane and cutting in the <001> direction, maintaining the z in the <–110> direction. This plane was chosen for cutting because previous investigations showed that the (110) plane is an easy cutting direction and a favorable orientation for cutting materials such as diamond and zincblende SiC [7]. However, the preferred cutting direction for silicon is the (111) orientation. The prismatic shape of the diamond tip was oriented in such a way that one of its edges was parallel to the z plane of the workpiece in the scratch direction. The model was initially equilibrated for about 20 ps by using the Nose–Hoover method [25]. A 3D stress unit region (containing nearly 44 atoms of GaAs) was chosen to monitor the scalar value of stress acting on the workpiece during the nanoscratching process.

Fig. 1
figure 1

MD simulation model of nanoscratching of GaAs using a rigid AFM-based diamond tip. Detail A refers to a region of atoms used to obtain the scalar value of von Mises stress in the cutting region

Full size image

An important consideration in an MD simulation is to describe the material as realistically possible [26]. For this reason, this investigation used a three-body analytical bond order potential (ABOP) [27, 28] that was fully parameterized to describe the zincblende phase of Ga, As, and C atoms. The cross interactions between C–Ga and C–As atoms were described using the Ziegler–Biersack–Littmark (ZBL) potential function [29]. Further details about the ZBL potential are available on the LAMMPS webpage [30]. To perform image rendering and improve data visualization, another software program called Open Visualization Tool [31] was used. For repeatability, the MD simulation parameters used in this work are described and demonstrated in Table 2. The simulations were performed on the UK’s [32] ARCHER2 High-Performance Computer, which has about 12,800 cores (each node on ARCHER2 has about 128 cores), and each simulation finished within 5 h.

Table 2 Parameters in MD simulations
Full size table

2.2 Experimental Setup

The nanoscratching experiments were performed on the (110)-oriented GaAs surface by using a triangular pyramid diamond tip (Micro Star Technologies Ltd. [US]) on a commercial AFM platform with a Nanoman module (Dimension Icon, Bruker Corporation, Germany). The nanoscratching feed direction was kept perpendicular to the cantilever of the diamond tip to prevent it from bending due to the scratching load [33]. A schematic of the nanoscratching methodology that was followed during the experiments is shown in Fig. 2. The diamond tip was maneuvered into the workpiece at a velocity of 5 µm/s for each scratch under 0.05–0.4 V applied voltage. The preset normal load (FN) from this information can be estimated as FN = Voltage × KN × sensitivity, where KN refers to the spring constant of the cantilever of the diamond tip, which was 200 N/m as specified by the manufacturer. The sensitivity was measured to be 627.5 nm/V by pressing the diamond tip on a sapphire specimen surface. Therefore, the normal load (FN) was estimated to be in the range of 6.28–50.20 µN for the applied voltage of 0.05–0.4 V, respectively. The normal load was set small enough to ensure that the material removal during the nanoscratching occurs in the ductile regime and cracking in the wafer can be avoided. After nanoscratching, a sharp silicon tip was employed to measure the topography of all the nanoscratched surfaces.

Fig. 2
figure 2

Schematic of AFM tip-based nanoscratching on single-crystal GaAs

Full size image

3 Results and Discussion

3.1 Surface Topography of the Nanoscratches

The surface topography of various surfaces obtained at scratch depths of 0.5, 1, 1.5, 2, 2.5, and 3 nm is shown in Fig. 3. The atoms in Fig. 3 are colored by a height map by keeping the bottom of the scratch depth as the 0 nm datum and by measuring the top pile-up height in increasing order. Thus, for instance, for a scratch depth of 0.5 nm, the bottom of the scratch surface has a 0-nm datum, and the theoretical reference surface would be 0.5 nm above the datum, which means that if the height label is 0.8 nm, then the pile-up height is 0.3 nm above the surface. Figure 3 shows that at shallower scratch depths, the pile-up scales linearly as the scratch depth increases. Moreover, the pile-up occurred at only one prismatic side of the tool tip because of the oblique cutting angle presented by the AFM tool tip.

Fig. 3
figure 3

Assessment of the pile-up, flow of cutting chips, and nature of the chip flow during the material removal observed from the MD simulations. Colors represent the height map of the atoms in the vertical Y direction

Full size image

The experimental AFM topography of the measured scratches is shown in Fig. 4. A total of eight scratches were made in the AFM at various loads, and their indicative scratch depths are plotted in the cross section in Fig. 4b. At shallow depths, the pile-up occurred on one side, similar to the condition observed during the MD simulation. The pile-up at shallow depths also scales linearly with increasing depth.

Fig. 4
figure 4

Experimental AFM image a surface morphology of various nanogrooves and b height map of various scratches

Full size image

3.2 Scratch Force, COF, and Specific Scratching Energy

The evolution of the (i) friction force (Fx), which is the force acting in the direction of scratching, and (ii) the normal force (Fy), which is the force acting in the direction perpendicular to the tool movement, is shown in Fig. 5. The resultant force described as the square sum of these forces was estimated using the formula \(\left({Fr} = \sqrt[2]{{F_{x}^{2} + F_{y}^{2} }}\right)\).

Fig. 5
figure 5

Evolution of the Fx and Fy at scratch depths of 0.5, 1, 1.5, 2, 2.5, and 3 nm plotted with respect to the simulation time steps corresponding to a total scratch distance of 20 nm

Full size image

In the early stages of contact, the force increases from 0 to a certain value (in this regime, compression of the workpiece material is dominant); this regime is also referred to as an unsteady cutting state. Thereafter, once the material starts to flow, the shear stress dominates and the force value becomes saturated. This regime is referred to as steady-state cutting. With the increasing scratch depth, the normal force becomes greater than the friction force, thereby indicating the reduced kinetic COF.

Fig. 6
figure 6

Variations in the cutting forces obtained from the MD simulations with Fr as the resultant force

Full size image

Also, the magnitude of the Fy was larger than that of Fx, especially at a greater scratch depth, because of the active negative rake angle presented by the triangular pyramid tip similar to that of a cutting tool used in the machining of brittle materials like silicon during SPDT [34,35,36] or the grinding process [37]. The nature of forces increases linearly as the cutting depth increases. The resultant force multiplied by the scratching distance and divided by the volume of the removed material gives a scalar quantity called specific scratching energy, which is considered independent of the size of the tool and is representative of the material’s resistance to cutting at various depths. The variation in the estimated average cutting force (Fr) and the specific scratch energy at various depth of scratches obtained from the MD simulations are shown in Figs. 6 and 7. The nature of this variation follows an identical trend to that of the force ratio of the kinetic COF (defined by Fx/Fy) shown in Fig. 8. The specific scratching energy was as high as 75 GPa with a kinetic COF approaching a value of 0.87 at a shallow scratch depth of 0.5 nm. This value becomes more saturated at about 17 GPa and 0.62 at higher scratch depths of 3 nm. The steepness of this variation was mild for scratch depths between 1.5 and 3 nm but had a bigger slope of 70 GPa/nm within the scratch depth of 0.5 to 1 nm. The nature and trend of the force ratio and specific scratching energy are reminiscent of the previously reported work on aluminum discussed in the introduction and hence clearly indicated a strong size effect in GaAs much like aluminum.

Fig. 7
figure 7

Variation in the specific scratch energy for different scratch depth cases obtained from the MD simulations

Full size image
Fig. 8
figure 8

Variation in the COF for different scratch depth cases obtained from the MD simulations

Full size image

Figure 9 shows the corresponding AFM experimental results obtained for various scratches performed from 2 to 30 nm scratch depths. Not only did the AFM experiments in common with the MD simulations show an increasing magnitude of the cutting forces with the scratch depth, but the kinetic COF also indicated a strong size effect. The ratio of COF at a shallow scratch depth of 2 nm was approximately close to unity, but it reduced to almost a value of 0.55 at a higher scratch depth of > 15 nm. This finding also indicated the influence of the included angle and the scratch depth. A sharper AFM tip can be expected to achieve lower COF at depths below 15 nm, which was the case in the MD simulation, where the threshold of the size effect occurred at about 2 nm.

Fig. 9
figure 9

Variation in the a scratch forces and b kinetic COF obtained from the AFM experiments

Full size image

3.3 Flow Stress and Plasticity in GaAs

A previous experimental work on doped GaAs material indicated the possibility that the phase transition from a zincblende structure (GaAs-I) to a rocksalt structure (GaAs-II) is responsible for the incipient plasticity during its nanoindentation process [38]. Without offering any direct evidence of the phase transition and at pressures as high as < 12 GPa, the work suggested that the GaAs-I to GaAs-II transition causes the plasticity in the material. During the present investigation, we used stress tensors to obtain the estimated von Mises stress in the cutting zone of the GaAs workpiece by using the same methodology that was previously used [39]. The von Mises stress we obtained in the cutting zone was around 7 GPa, which is closer to the value of the nanoindentation hardness of the GaAs material [40, 41], as illustrated in Fig. 10. The indentation hardness is representative of the plastic property of the material and coincides with the value of flow stress obtained in this work from the MD simulation, which possibly suggests that GaAs can flow plastically at a lower stress value than previously reported [38]. Moreover, the stress that is required to cause a phase transformation from GaAs-I to GaAs-II phase is of the order of 17.3 GPa, which is unlikely to occur during nanoscratching [42,43,44]. Hence, the phase transformation of GaAs during nanoscratching can be ruled out.

Fig. 10
figure 10

Variation in von Mises stress at a scratch depth of 3 nm

Full size image

Furthermore, a Dislocation Extraction Algorithm [45] (DXA) was used to capture an instance of the emission of two dislocations in the subsurface belonging to the Burgers vector family of ½ <110>, as shown in Fig. 11. This idea explains that the nucleation of dislocation can occur much earlier than the phase transformation and hence is energetically more favorable.

Fig. 11
figure 11

Observation of subsurface at a scratch depth of 3 nm

Full size image

Overall, if the potential function used in this investigation (Albe type) is to be trusted, then the dislocation nucleation occurring at a lower stress value of 7 GPa, which coincides with the value of nanoindentation hardness (which is also a plastic property), seems to suggest that the primary reason plasticity occurs in GaAs is dislocation nucleation. This finding challenges existing studies reporting that phase transition is responsible for the ductile plasticity in GaAs.

4 Remarks on Comparing MD Simulations with Experiments

An important detail to recognize is that, while a very good qualitative comparison between the MD simulations and experiments is obtained in this investigation, differences exist in the situations; these differences cannot be neglected, and they require further discussions. Experimental techniques involving scanning probe microscopes such as AFM and STM have large dependencies on the stiffness of the system (cantilever/tip), whereas the MD simulation assumes an infinitely rigid diamond tip. Moreover, the experimental results can be influenced easily by extrinsic factors, such as surface contaminants, surface state, the geometry of the slider, tilting of the substrate or the tip, impurities in the substrate, and contact conditions at the interface. Also, the cutting velocity employed during the AFM scratches was on the order of few microns per second (5 µm/s) as opposed to the velocity of 10 m/s used during the simulations. In view of this situation, the contact conditions during experiments were somewhat close to being quasistatic but were more dynamic during the simulations, thereby pointing us to strong strain rate effects in the MD. However, this condition should not affect the hardness, flow stress, and elastic modulus usually obtained from the MD simulation studies.

A higher cutting and/or sliding velocity needed to be employed to keep the computational requirements of the study within acceptable limits. Therefore, appropriate caution should be exercised in data interpretation. As such, the surface of the GaAs modeled in MD is atomically smooth and completely free of any contaminant, and the entire scratching process took place in a vacuum. With all these differences considered in the background, Fig. 12 shows a comparison of the kinetic COF and the specific scratching energy for the range of depth that is investigated commonly between MD and the AFM experiments.

Fig. 12
figure 12

Comparison of the MD simulation and experimental results a kinetic COF and b specific scratching energy

Full size image

Figure 12 reveals that the comparison of the specific scratching energy showed good proximity between the MD simulation and experiments, whereas the value of the kinetic COF exhibited differences. This finding indicates that the specific scratching energy could be insensitive to the velocity and the geometry of the indenter, but the kinetic COF is perhaps governed by certain other factors that need to be further investigated. In particular, the force ratio was substantially different at a very narrow scratch depth of < 2 nm, which leads us to consider and plan follow-up work to investigate if this situation is due to previous surface amorphization, roughness, or the presence of an oxide layer as opposed to pure GaAs scratched in MD.

5 Conclusions

This work employed MD simulations and AFM scratch experiments to investigate the nanoscale friction and behavior of material removal on single-crystal(110)-oriented GaAs material surface. The following conclusions can be drawn from the aforementioned discussions:

  1. 1.

    A strong size effect was observed during GaAs nanoscratching at depths below 2 nm in the MD simulations and at depths below 15 nm in the AFM experiments. The tip sharpness used in the AFM was much higher than that used in MD. Thus, the size effect observed during nanoscratching can be concluded to be dependent on the geometry of the tip and the scratch depth.

  2. 2.

    During steady-state scratching, when the scratching is performed in a size effect-free regime, the kinetic COF revealed by the experiments and MD simulations was 0.55 and 0.62, respectively. In both cases, the kinetic COF increased to a value of unity when scratching was performed in the size effect regime.

  3. 3.

    Likewise, a size effect was observed in the specific scratch energy because the value obtained while the (110) surface of GaAs was being scratched was about 20 GPa in the size effect-free regime, but it went up to 90 GPa at shallow scratch depths, thereby indicating that the workpiece has strong resistance to plastic deformation at narrower scratch depths.

  4. 4.

    An interesting observation was that the specific scratch energy was insensitive to the scratch speed and geometry of the tip, and good proximity was obtained between the MD simulations and experiments, whereas the kinetic COF showed some variations, albeit reasonably smaller ones. The specific scratch energy is inferred to be a more reliable indicator than the COF to validate the simulation studies where differences in speed and geometry are involved.

  5. 5.

    Contrary to the published experimental results that suggest a phase transformation from GaAs-I to GaAs-II (zincblende to rocksalt phase), which can occur at stress values < 13 GPa only, the simulations performed in this work by using ABOP suggest that the von Mises stress values or the nanoindentation hardness can reach up to 7 GPa only. At this lower stress value, phase transformation cannot take place. Instead, the incipient plasticity in single-crystal GaAs during nanoscratching occurred due to the 1/2<110>-type dislocation nucleated in the subsurface of the GaAs.