FormalPara Key points

Empirical Mode Decomposition applied to the Southern Oscillation Index isolates statistical factors implying physical processes tracking Interannual ENSO-derived variability

Decadal variations for the Nile River basin precipitation correlates strongly, ρ = 0.864 with the isolated processes

The isolated processes are used to predict Blue Nile yield with high significance at 25 aggregated p value of 0.038

1 Introduction

The El Niño Southern Oscillation (ENSO) is a major global contributor to interannual climate variability due to its influence towards disrupting normal large-scale Walker circulation in the South Pacific (Rasmusson and Arkin 1985; Slemr et al. 2016). The source of its disruption stems from the variability in the strength of the easterly trade winds (L’Heureux 2014). ENSO’s impact on a global scale is often reflected in local events such as extreme flooding to extreme drought conditions (Fer et al. 2017). Le et al. (2017) modeled the interaction between large ENSO seasons and drought in North America, confirming the relationships established by Ropelewski et al. (1986), Dai and Wigley (2000), and Holmgren et al. (2006).

In East Africa, the Empirical Orthogonal Teleconnection (EOT) technique is utilized to isolate specific ENSO-driven patterns showing the direct connection with vegetation and agriculture yields (Van Den Dool et al. 2000; Fer et al. 2017). As a driver of interannual climate variability, with great impact on food security, ENSO is known to strongly contribute to Nile River Basin (NRB) precipitation patterns (Abtew et al. 2009). The Nile River in East and Northeast Africa drains an area of 2.9 × 106 km2, and has strongly shaped the economic development of all countries in its drainage basin. Nile river flow plays an important role in all countries within its basin, and is mostly influenced by East and Northeast Africa’s climate. Precipitation in these regions contributes to the overall flow of the River Nile from Tanzania, in the south, to Egypt, in the north. Therefore, an understanding of the driving forces affecting its flow is crucial for the purpose of characterizing its impact on local economies, which in turns, requires the investigation of geographical variability of precipitation within the NRB. The river has two main tributaries, namely, the White Nile, which flows from Lake Victoria along the Kenya/Tanzania Border, and the Blue Nile that flows from Lake Tana in Ethiopia. We will focus our attention on the Blue Nile, since it is known that its flow is affected by the strength in the ENSO cycle (Amarasekera et al. 1997) and it contributes up to 60% of the River Nile yield. Significant negative and positive correlations between Pacific Ocean Sea Surface Temperature (SST) and the Nile River discharge were found (Amarasekera et al. 1997) Specific portions of discharge and precipitation, influenced by Pacific SST variations, were characterized to describe the regional variability for these contributing proportions. Millions of people in the semi-arid to arid regions of Kenya, Ethiopia and other NRB countries are facing water scarcity and frequent drought issues that might be linked to ENSO (Zaroug et al. 2014; Thomas et al. 2019). They found, using a discrete event-based approach that ENSO affects the region around the Blue Nile source in Lake Tana, which contributes around 60–69% of the main Nile discharge. The Pacific Ocean Sea Surface Temperature in the Niño 3.4 region and the meteorological and hydrological drought measurements in the upper catchment of the Blue Nile were used in that analysis. The El Niño and La Niña occurrences and associated intervals matched significantly with the patterns of flooding and drought events. The principal component of precipitation variance is an annual cycle (seasonal variation)—characterized by rainy seasons typically between July to September (Salih et. al 2018.). However, for the purposes of long-term planning, effort has been dedicated into identifying longer-scale variations and the signal driving variation between different years and decades.

In an effort to develop flooding and drought models, Siam and Eltahir (2015) analyzed historical data sets and defined four distinct modes of natural variability in NRB flow. They identified a region in the Southern Indian Ocean that characterizes up to 28% of the interannual variability in Nile River flow. Together with historical ENSO readings, Pacific Ocean SST and SOI variation explain 44% of Nile River flow variability. In addition, they link anomalous events and show that global models incorporating ENSO can be used to characterize the NRB hydrology. To predict river flow at specific locations, Wang and Eltahir (1999) aggregated several historical data sets and other sources of historical information regarding ENSO indices, Ethiopia precipitation, and Nile flow readings, to establish predictive indices for Aswan flow. They applied Bayesian analysis using conditional categorical probabilities to create a discriminant forecasting algorithm. A synoptic index is constructed to characterize the forecast skill. They conclude that ENSO readings are by far the most valuable predictor on large (2–3 months) time scales, but that precipitation and river flow information can be useful in predicting on medium-range (monthly) time scales.

In this study, we further quantify the link between El Niño and decadal-scale variation in NRB precipitation by applying Empirical Mode Decomposition (EMD) and the Hilbert-Huang Transform (HHT) with the purpose of decomposing the signal in terms of a small number of Intrinsic Mode Functions (IMFs) characterizing their non-stationary oscillatory variations. In the process, we find that a specific NRB IMF and a specific Southern Oscillation Index IMF (namely, the IMF characterizing approximately duodecadal variations) are strongly correlated. This seems to imply the existence of a single global physical process driving both NRB precipitation and the interannual variation present in the SOI. In this paper we quantify the nature of this shared causality, and we show that such causality exists at different lagged responses. This link provides us a powerful statistical insight on NRB precipitation on a per-region basis, an important tool for characterizing its long-term variability, and also a viable predictive index for important hydrological measurements such as the Blue Nile yield. It is important to note that the goal is not to establish a causal link between SOI and NRB and Blue Nile Yield, but rather that all three share mutual driving process that influences them, more clearly identifiable using Empirical Mode Decomposition than simple correlation or direct analysis.

The high social importance of these indices in the face of global climate change is a global crisis, as argued at the Davos world economic forum. Transnational water management is a critical issue in the upcoming years as the world moves to address the 2030 Sustainable Development Goals (SDGs), as both a goal contributing to water security in the face of climate change and also as an important indicator (Indicator 6.5.2) of the progress of the global motion towards a sustainable world.

2 Study Area

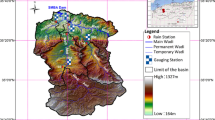
The primary area of study for this paper involves the atmospheric study of the primarily East-Africa Nile River Basin region (depicted in Fig. 1) as it relates to global ENSO effects, and impacts the fields of atmospheric science as well as the mathematical and signal-processing fields of empirical signal decomposition.

Fig. 1
figure 1

taken from Li et. al., 2020, and used with permission)

Nile River Drainage basin, the area of study. (This figure is

Full size image

3 Materials and Methods

3.1 Material

EMD and HHT analysis is performed on precipitation records from the CHIRPS Pentad Dataset (Funk et al. 2014), and also the Southern Oscillation Index, a climatology index associated with ENSO (Chen 1982). SOI data is gathered from the work in Ropelewski and Jones (1987), which contains records starting from January 1866. Historical precipitation (measured as monthly anomalies of the Pentad temporal scale) for the NRB countries of Egypt, Ethiopia, Kenya, South Sudan, Sudan, Tanzania, and Uganda, starting from January 1981 is analyzed. Blue Nile flow data at Grand Ethiopian Renaissance Dam (GERD) measurement station from 1990 to 2014 was available from official GERD communications and resources. Software implementation of EMD is written in Haskell (Le 2018).

3.2 Methods

3.2.1 Empirical Mode Decomposition

EMD has successfully been used to study nonstationary physical systems, in fields ranging from neuroscience (Pachori 2008; Pigorini et al. 2011) to solar surface dynamics (Nakariakov et al. 2010; Bellini et al. 2014). IMFs proved to be powerful tool for predictive analysis, where using statistical models to predict IMFs, one can predict the progression of the time series as a whole (Abadan and Shabri 2014). In this research we applied the EMD and HHT, as a powerful predictive tool, on the NRB precipitation by isolating different physical processes amongst which is the one driven by ENSO as represented by SOI data (Huang et al. 1996, 1998). The power of EMD in isolating physically meaningful signals, driven by El Niño and quasi biennial oscillation, from precipitation and temperature data was proven over South Africa (Zvarevashe et al. 2019) and central and eastern pacific (Kidwell et al. 2014). On the eastern and western US, namely Virginia and California, EMD along with other tools showed the El Niño impact on precipitation variability using rain gauge and climate division data (El-Askary et al. 2004, 2012).

EMD aims to decompose a time series, precipitation in our case, as a sum of a small number of non-stationary components, IMFs, which may be understood and analyzed in isolation. Each IMF traces an independent non-stationary physically meaningful process that contributes to the full series, for example seasonality, annual variability, El Niño cycle, decadal oscillation, etc. The HHT re-frames each series as instantaneous-frequency-over-time (much like sparse wavelet decomposition), tracing the progression of each IMF over instantaneous frequency space as a function of time. Thus, we can trace the process of one single physical process as it moves through instantaneous frequency space over time. For a general real-valued time series (t) of length T, the series is decomposed in terms of a sum of N (typically small) mutually orthogonal IMFs ci(t) and a residual series r(t).

$$x\left(t\right)=\left[{\sum }_{i}^{N}{c}_{i}\left(t\right)\right]+r\left(t\right)$$
(1)

The HHT then allows the visualization of each IMF \({c}_{i}\) as a curve in frequency-time space \({\omega }_{i}(t)\) with a magnitude \({A}_{i}\left(t\right)\) associated at each point.

$${c}_{i}\left(t\right)\Rightarrow \langle {\omega }_{i}\left(t\right),{A}_{i}\left(t\right)\rangle$$
(2)

3.2.2 Physical Interpretation of IMFs for Precipitation and SOI Data

EMD produces IMFs which are mutually orthogonal for practical purposes, and each correspond to the contribution of an independent non-stationary physical process (or the sum of independent physical processes with similar time scales of variability). Junsheng et al. (2006) has shown that when one has a time series when the underlying physical processes are known, EMD yields IMFs that matches on each underlying series. Figure 2 shows EMD applied to the monthly Ethiopia precipitation records (recorded as monthly anomalies in the Pentad temporal scale) since 1980, yielding IMFs with different time scales of variability. The collection of nine IMFs is mutually orthogonal in L^2 (by their construction), and, according to the theory of EMD, each IMF most likely tracks the progression of a separate physical process driving Ethiopia precipitation.

Fig. 2
figure 2

IMFs from EMD applied to historical Ethiopia Precipitation

Full size image

The full decomposition of SOI monthly recordings from January 1866 to January 2019 (Fig. 3) isolates 14 IMFs at varying time scales. Of these, it can be proposed that IMF 6 corresponds to El Niño and La Niña occurrences: its non-stationary periodicity matches the historical record of large El Niño and La Niña events. In particular, the three largest El Niño events in recorded history are observed in 1982–83, 1997–98, and 2014–2016 as negative swings in IMF 6. El Niño events with their varying strength and impact on wetness and dryness were presented using recurrent neural networks by Le et al. (2017). Performing a correlation analysis between annual totals of IMF 6 and other ENSO SST time series (such as NINO 3.4, NINO 1, NINO 4) yields correlation coefficient around 0.5, similar to the results of directly performing correlation analysis between SOI and such SST indices.

Fig. 3
figure 3

IMFs from EMD applied to historical SOI Records

Full size image

4 Results and Discussion

4.1 Hilbert-Huang Transform

Application of the HHT to the SOI shows the progression of each of these IMFs through frequency as a function of time, as depicted in Fig. 4. The transform shows the range of variability in which each IMF dominates. IMFs have been shown to correspond to meaningful physical processes when applied to a wide variety of physical systems. By studying a single IMF, it is possible to analyze a single physical process contributing to the variation of the system at that time scale. It is also possible to match this observed physical subprocess with other known physical processes. For example, IMF 1 accounts for quarterly variations, IMF 3 accounts for annual variations, and IMF 7 accounts for variations on the order of six to twelve years. Longterm 30-year variations are accounted for in IMF 9. By this association, IMF 6 corresponds to variations in the strength of the Easterly Trade Winds and size of Walker Cell disruptions, factoring the influence of climatology as previously discussed (Le et al. 2017). The (nonstationary) oscillation of IMF 6 represents the fundamental periodicity of this cycle, while isolating out variations in El Niño/La Niña intensity as reflected in SOI. It can be used as a binary indicator, if symmetric thresholds are used, to determine if such an event occurs, while not being influenced by the relative intensity of each event. However, on top of the dominant periodicity, there are extra factors that drive the relative strength between El Niño events as reflected by SOI. These factors, by the orthogonality conditions of EMD, are seen to be captured largely in IMFs 7 and 8.

Fig. 4
figure 4

Two displays of data resulting from HHT transformations. a Skeleton lines arising from HHT from historical Ethiopia Precipitation IMFs. b Stacked area plot of SOI IMF relative instantaneous power

Full size image

Therefore, it is clear that the decomposition of the Ethiopia precipitation time series isolates nine independent, mutually orthogonal signals that correspond to non-stationary physical processes at different time scales. Those independent signals form the overall variation of the precipitation record over Ethiopia which can be robustly scaled to the whole NRB region.

In those IMFs, we observe the relative strength of the physical process driving the variation in effects of El Niño events as reflected through negative anomalies in SOI over time, with large swells in times of larger and more intense events. This fact can be seen in the stacked area plot (Fig. 4b) of instantaneous power of each IMF, derived from the HHT. Each layered color represents the relative power of the influence of each IMF at each point in time. While IMF 6 (the primary event signal) has a relatively steady contribution (except during the mid-century lull), IMFs 7 and 8 appear to surge in power during known spikes in event strength.

Therefore, although we found that IMF 6 is tracking the periodic events in SOI itself, there is a separate, orthogonal physical process tracked by IMFs 7 and 8 that drives internnual Niño variability as reflected in SOI. There is therefore an underlying process, which has not yet been identified so far and is currently not yet studied, that contributes to interannual variability. It is an orthogonal physical circulation that strongly determines the relative strength of subsequent events. Hence, the SOI IMF 6 is now considered to be an El Niño indicator index, due to its ability to identify El Niño and La Niña events, isolating out variations in intensity. As a result, the IMF 6 is now useful as a “binary” indicator in establishing whether or not an El Niño or La Niña event is happening (by setting symmetric thresholds about 0). The SOI IMFs 7 and 8 are named the Interannual ENSO Variability Indices (IEVIs), as they are interannual variability indices that are derived from the study of ENSO. We differentiate between them as IEVI α and IEVI β, respectively, as a pair of indices for predicting the intensity of a given El Niño or La Niña event, should one occur in that year. Hence, these IEVIs would shed the light on NRB precipitation linkage as discussed later.

4.2 NRB Precipitation and SOI Data Comparison

Applying the EMD and HHT to NRB precipitation records (as Pentad anomalies) from January 1981 to December 2018, shows that many NRB precipitation IMFs, especially decadal IMF, correlate strongly with the IEVIs, particularly with IEVI β, yet with a varying ranges of lag (Fig. 5). NRB precipitation IMFs correlations with SOI IMFs are represented at different time scales. Each IMF is noted with the timescales it varies in, derived from the HHT, and each correlation coefficient is noted with the NRB IMF delay, computed using direct descent, for that correlation. In this method the lag is increased, up to four years, as long as the correlation also increases, until the point where increasing lag will decrease the correlation coefficient. This provides an effective measure to obtain a meaningful lag without the risk of overfitting which would occur if lags are permitted to slide past a local maximum. It is clear that precipitation for every NRB country yields an IMF that highly correlates with IEVI β, SOI IMF 8, predominantly at zero lag. Yet it is noteworthy that precipitation for the majority of NRB countries still yield an IMF that correlates, in some weaker manner, with IEVI α, SOI IMF 7. Each Precipitation IMF corresponds to an underlying physical process that drives the variation in precipitation for that country. The fact that Ethiopia IMF 7 correlates at ρ = 0.719 with IEVI β at 0 month lag means that the underlying physical process driving the interannual variability (IEVI β) is the same as the one driving variability Ethiopia precipitation between different decades. Therefore, it can confidently be concluded that interannual variability is strongly associated with decadal variability in this case owed to the observed high correlation at 0 lag.

Fig. 5
figure 5

Correlations between NRB nations precipitation IMFs and SOI IMFs. Each IMF is noted with the approximate range of periodic variability the IMF accounts for, and each correlation is noted with the lag of correlation in months

Full size image

4.3 NRB Precipitation and SOI Data Interpretation

The strong correlations between NRB precipitation IMFs and IEVI suggests that the Nile River yield and total accumulation is somehow dependent on ENSO strength and variability.

ENSO strength accounts for ~ 22% of the annual variance in the Blue Nile and Atbara rivers’ flow, which primarily drain Ethiopia, Eritrea, Sudan, and South Sudan (Amarasekera et al. 1997). In agreement with these findings, we suggest that ENSO strength as reflected in the isolated IMF of SOI is strongly linked to precipitation in Ethiopia, the primary drainage basin of these two rivers. Therefore, we can deduce that the Ethiopia, Sudan, and South Sudan precipitation will be strongly linked with the IEVIs and ENSO. Speaking of the NRB countries, the link is established with varying correlative power geographically with IEVI α (SOI 7) and IEVI β (SOI 8) (Fig. 6).

Fig. 6
figure 6

Map of NRB nations colored and overlaid with correlations between national precipitation IMFs and IEVI α (SOI 7) and IEVI β (SOI 8). Insets depict the actual IMF of national precipitation against lagged IEVI component, where are highlighted and discussed in the text

Full size image

For instance, Ethiopia and Sudan show the strongest correlation with IEVI β, at 0.72 and 0.86, respectively, while South Sudan is not much lower, with 0.68. ENSO variation is known to have a much weaker influence on the White Nile flow (Amarasekera et al. 1997). This adds to our confirmed observations that Kenya and Tanzania, out of all NRB countries, have the two lowest correlations with IEVIs. Precipitation IMFs for Ethiopia and northward, downstream of Lake Tana, negatively correlates with IEVI α, opposite to countries extending from Lake Victoria to Sudan. However, precipitation for all NRB countries, except for the Mediterranean bordered Egypt, positively correlates with IEVI β. Because of our usage of IEVI β instead of a direct El Niño index, we can be certain that our claims of dependency and correlation, specifically, result from the interannual variability derived from ENSO, and not simply SST or other environmental internnual factors. In other words, we track ENSO cycle, specifically, and not any other potential overlapping periodicity.

4.4 Blue Nile Yield Prediction

IMFs of physical systems can be predicted using traditional statistical models, such as ARIMA models (Abadan and Shabri 2014). A hybrid discrete Bayesian model proves to be effective in linking ENSO-based factors and NRB precipitation activity (Wang and Eltahir 1999; Siam and Eltahir 2015). If a traditional model can project IEVI α and β, then it is possible to predict on the precipitation levels decadal variability for NRB countries. This is important for NRB nations with lagged correlations between precipitation IMFs and IEVIs. The importance stems from the fact that predictions in IEVIs will manifest as correlations, at a known lag time, in precipitation of NRB countries. Therefore, we can for instance predict any hydrological variable that might be driven by precipitation. To demonstrate this ability the Blue Nile yield will be predicted annually based on IEVIs and autocorrelative terms. The Blue Nile yield data from the GERD measurement site from 1900 to 2014 was made available from official sources through GERD communications. The location of the measurement station with respect to the watershed of the Blue Nile river is depicted in Fig. 7c. Since the IEVIs have a monthly sampling frequency, as opposed to the yearly frequency of our yield data set, next year prediction will be based on two groups of predictors. These are namely, the twelve IEVI α measurements from the year before the observed measurement and the autocorrelative terms represented by the six previous measurements of the Blue Nile yield. For simplicity, this is a simple ARMA model represented as a multivariate linear regression on annual total Blue Nile Yield \({y}_{i}\):

Fig. 7
figure 7

A multivariate linear regression based on IEVI α to predict Blue Nile Yield. a Model output against measured values. b Correlation plot between model and measured values. c Location of measurement station with respect to the Blue Nile watershed (highlighted) and the surrounding regional borders

Full size image
$${y}_{i}={{\varvec{b}}}^{\top }{\boldsymbol{\alpha }}_{i-1}+{d}_{1}{y}_{i-1}+{d}_{2}{y}_{i-2}+\cdots +{d}_{6}{y}_{i-6}$$
(3)

αi is the 6-vector of IEVI α readings for year i for the months of June to November, and yi is the Blue Nile Yield for year i for months June to November. The model is parameterized by a 6-vector \({\varvec{b}} ({b}_{1},\dots ,{b}_{6})\) and the six coefficients d1, …, d7. These parameters are fitted according to ordinary linear least squares estimation (Hayashi 2000). The actual estimation involves a series of matrix multiplications and inversions, involving the Moore–Penrose Pseudoinverse methodology (BenIsrael and Greville 2003).

Our justification for the ARMA model arrives from the fact that it is the simplest possible model requiring the least a priori assumptions: it posits that the Blue Nile Yield has both linear auto-regressive contributions (that is, that it is resistant to sudden year-by-year changes) and a linear moving average contribution from an external contributing factor (IEVI α, in our situation).

Figure 6a, b show the estimated model when fitted to the full time series, compared to actual historical Blue Nile yield. The error in the fully fitted model is RMSE 8.1 × 109m3, with a Pearson correlation coefficient of ρ = 0.52. The fitted model against IEVI α explains 30% of the variability of the Blue Nile Yield.

Other model inputs were considered, such as precipitation, the actual SOI time series, and other IMFs—however, predicting only on IEVI α gives the most significant results against the null hypothesis. Predicting on other parameters using this method tends to overfit. This means that IEVI α is a stronger unbiased predictor than directly using SOI, or even NRB precipitation.

These methods also suggest that, while each SOI IMF is physically meaningful, IEVI α is closely tied with precipitation and related long-term phenomenon, such as drought and periods of heavy rain. This initial model strongly suggests that IEVI α’s inherent physical properties lend itself to be able to predict on significant geophysical and hydrological processes. In the future, more advanced statistical or data-driven models may prove to be even more effective. This is a very important finding where it addresses the Blue Nile Yield as a very a significant measure in addressing a serious societal issue with transboundary implications on Ethiopia, Sudan and Egypt.

5 Conclusions

The 2020 Global Risk Report lists Climate Action failure and Extreme weather as top global risks in terms of both likelihood and impact. The SDGs, established in 2015, set a course of action for addressing upcoming potential global crises; SDG 6 acknowledges the role of Clean Water and Sanitation in sustainable development. The SDG establishes transboundary cooperation as an important indicator in the progress for this goal. Therefore, accurate modeling of transboundary hydrological resources like precipitation runoff and Nile River flow are integral in addressing the future of sustainability and climate action.

We have shown how the introduction of Climate Indices IEVI α and β account for the inter-annual variability of El Niño as reflected by SOI and also drives many physical processes. We have shown that our inter-annual El Niño variability index, expressed by IEVI β has extremely strong correlations (up to ρ = 0.864) for NRB precipitation Decadal variation, as isolated by EMD. We have also shown that a statistically significant association of NRB Precipitation decadal variation is our inter El Niño variability index, expressed by IEVI β, and that these correlations should allow the IEVIs predictive models to characterize decade-to-decade precipitation levels on NRB nations. The geographic distribution of correlation with IEVI β also matches that predicted by the conclusions of the cited works. All countries but Egypt vary in precipitation in the same direction as IEVI β, whereas Egypt varies in the opposite direction. We attribute this change in direction due to Egypt’s influence by the Mediterranean Sea’s dependence on El Nino. A weaker effect (ρ = 0.44) is found in that all southern Nile River Basin countries vary in the same direction as IEVI α, whereas all northern NRB countries downstream of Lake Tana vary in the opposite direction.

Physically, our conclusions match known properties about the NRB. Comparing the relative dependence of Blue Nile and White Nile dependence on ENSO based on established literature, we observe the correct geographical distribution of correlation. We expand on previous results by uncovering a more physically meaningful index on which to build models and make predictions, instead of simply raw SOI and precipitation. By applying EMD, we aimed to isolate a signal corresponding only to inter-event variability. Because of this filtering, our correlation factors are known to correspond only to inter-ENSO variability, and not only significant events themselves. This gives a strong footing on which to base claims about inter-ENSO variability (and not only interannual variability) as it affects Nile River flow. To solidify this claim, we predict on Blue Nile River yield based only on IEVI, with successful results. These results show that EMD has uncovered an underlying process mutually driving both ENSO (as reflected in SOI and precipitation measurements) and also physical processes in the Nile River Basin. It should be noted that this does not attempt to justify a causal link between SOI and NRB processes, but rather a mutual causality. Further study should involve the usage of modeling IEVI β and IEVI α to show the exact accuracy of such models on decadal variability of NRB country precipitation, as well as further studies of the IEVIs against the precipitation and climate of other regions. In addition, further study could link the IEVIs to the variations within swells of the thermocline, Walker Circulation deviations, and Southern Easterly Trade Wind deviations.