Pollution from consumption and urban unemployment in a dual economy

Abstract

By incorporating the environmental problems caused by consumption into a theoretical model of rural–urban migration, this study analyzes the effect of a reduction in pollution generation rate and factor accumulation. The environment of each rural and urban area is assumed to deteriorate due to pollution from consumption of the respective inhabitants. For institutional reasons, the urban wage rate is fixed at a higher level than the rural wage rate, and unemployment exists in the urban area. Rural–urban migration occurs because of differences in utility, which is affected by both the environment and expected earning in each area. This study shows that, although reduction in the pollution generation rate improves the environment in both areas, whether it mitigates urban unemployment depends on certain conditions. Regarding the effect of factor accumulation, this study shows that an increase in capital endowment decreases the level of unemployment if and only if the environmental effect outweighs the Rybczynski effect.

Appendices

Appendix A: Stability

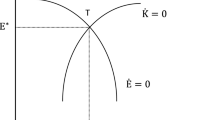
In the short run, for given $E^{M}$ and $E^{A}$, six Eqs. (3), (4), (7), (8), (9), and (16) determine six endogenous variables: $L_{M}$, $L_{U}$, $L_{A}$, $K_{M}$, $K_{A}$, and $w$. Thus, substituting (21) and (25) into (26) and substituting (23) into (28), respectively, the dynamic adjustment process of $E^{M}$ and $E^{A}$ can be expressed as

$$\dot{E}^{M} = g(\bar{E} - E^{M} ) - \lambda (\bar{w}L_{M} + rK) \equiv \phi (E^{M} ,E^{A} ),$$

(34)

$$\dot{E}^{A} = g(\bar{E} - E^{A} ) - \lambda wL_{A} \equiv \varPsi (E^{M} ,E^{A} ).$$

(35)

Necessary and sufficient condition for the linear approximation system of (34) and (35) to be globally stable is that the trace of $S$ (${\text{tr}} S$) is negative and the determinant of matrix $S$ (det $S$) is positive, where $S \equiv \left[ {\begin{array}{*{20}c} {\partial \phi /\partial E^{M} } & {\partial \phi /\partial E^{A} } \\ {\partial \varPsi /\partial E^{M} } & {\partial \varPsi /\partial E^{A} } \\ \end{array} } \right]$.

To investigate the signs of ${\text{tr}} S$ and det $S$, by differentiating (3), (4), (7), (8), (9), and (16), we obtain

$$\left[ {\begin{array}{*{20}c} {pF_{LL}^{M} } & 0 & 0 & {pF_{LK}^{M} } & 0 & 0 \\ 0 & 0 & {F_{LL}^{A} } & 0 & {F_{LK}^{A} } & { - 1} \\ {pF_{KL}^{M} } & 0 & { - F_{KL}^{A} } & {pF_{KK}^{M} } & { - F_{KK}^{A} } & 0 \\ 1 & 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 1 & 0 \\ B & { - C} & 0 & 0 & 0 & { - v_{w}^{A} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\text{d}}L_{M} } \\ {{\text{d}}L_{U} } \\ {{\text{d}}L_{A} } \\ {{\text{d}}K_{M} } \\ {{\text{d}}K_{A} } \\ {{\text{d}}w} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ { - G^{M'} } \\ \end{array} } \right]{\text{d}}E^{M} + \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ {G^{A'} } \\ \end{array} } \right]{\text{d}}E^{A} .$$

(36)

Denoting the determinant of square matrix of (36) as $J$, we have

$$J = p\bar{w}v_{w}^{M} F_{LK}^{M} F_{KL}^{A} L_{A} \left[ {K_{M} /(L_{M} + L_{U} ) - K_{A} /L_{A} } \right]/(L_{M} + L_{U} )K_{A} .$$

Thus, the following relationship holds as regards the sign of $J$:

$$J > ( < )0 \Leftrightarrow K_{M} /(L_{M} + L_{U} ) > ( < )K_{A} /L_{A} .$$

We are now in a position to examine the signs of ${\text{tr}} S$ and det $S$. First, we investigate the sign of ${\text{tr}} S$. From (34) and (35), we have

$$\begin{aligned} {\text{tr}} S & = \partial \phi /\partial E^{M} + \partial \varPsi /\partial E^{A} \\ & = - g - \lambda (\bar{w}\partial L_{M} /\partial E^{M} + K\partial r/\partial E^{M} ) - g - \lambda (L_{A} \partial w/\partial E^{A} + w\partial L_{A} /\partial E^{A} ) \\ & = - g - \lambda \bar{w}\partial L_{M} /\partial E^{M} - g - \lambda w\partial L_{A} /\partial E^{A} \\ & = - 2g - \lambda (\bar{w}\partial L_{M} /\partial E^{M} + w\partial L_{A} /\partial E^{A} ) \\ & = - 2g - \lambda J^{*} /J, \\ \end{aligned}$$

where $J^{*} = p(\bar{w}G^{{M^{\prime}}} F_{LK}^{M} F_{KL}^{A} + wG^{{A^{\prime}}} F_{LL}^{M} F_{KK}^{A} ) > 0$. To derive the last expression, we use $\partial L_{M} /\partial E^{M} = pG^{{M^{\prime}}} F_{LK}^{M} F_{KL}^{A} /J$ and $\partial L_{A} /\partial E^{A} = pG^{{A^{\prime}}} F_{LL}^{M} F_{KK}^{A} /J$ from (36). Thus, the following relationship holds.

$${\text{tr}} S < 0 \Leftarrow J > 0 \Leftrightarrow K_{M} /(L_{M} + L_{U} ) > K_{A} /L_{A} .$$

(37)

Next, det $S$ becomes

$$\begin{aligned} \det S & = (\partial \phi /\partial E^{M} )(\partial \varPsi /\partial E^{A} ) - (\partial \varPsi /\partial E^{M} )(\partial \phi /\partial E^{A} ) \\ & = \left[ { - g - \lambda (\bar{w}\partial L_{M} /\partial E^{M} + K\partial r/\partial E^{M} )} \right]\left[ { - g - \lambda (L_{A} \partial w/\partial E^{A} + w\partial L_{A} /\partial E^{A} )} \right] \\ & \quad - \left[ { - \lambda (L_{A} \partial w/\partial E^{M} + w\partial L_{A} /\partial E^{M} )} \right]\left[ { - \lambda (\bar{w}\partial L_{M} /\partial E^{A} + K\partial r/\partial E^{A} )} \right] \\ & = ( - g - \lambda \bar{w}\partial L_{M} /\partial E^{M} )( - g - \lambda w\partial L_{A} /\partial E^{A} ) - ( - \lambda w\partial L_{A} /\partial E^{M} )( - \lambda \bar{w}\partial L_{M} /\partial E^{A} ) \\ & = g^{2} + \lambda g(\bar{w}\partial L_{M} /\partial E^{M} + w\partial L_{A} /\partial E^{A} ) \\ & = g^{2} + \lambda gJ^{*} /J. \\ \end{aligned}$$

Therefore, the following relationship holds:

$$\det S > 0 \Leftarrow J > 0 \Leftrightarrow K_{M} /(L_{M} + L_{U} ) > K_{A} /L_{A} .$$

(38)

From (37) and (38), if the urban area is more capital abundant than the rural area, that is, $K_{M} /(L_{M} + L_{U} ) > K_{A} /L_{A}$, then the linear approximation system of (34) and (35) is globally stable.

Appendix B: Environmental effect when capital endowment increases

In the following, we show that $L_{M}$, $L_{U}$, and $K_{M}$ decrease due to the environmental effect of an increase in capital endowment. First, we consider the environmental effect on $L_{U}$. Because the part in parentheses of the last expression of (33d) becomes $\begin{aligned} {-}e - G^{{M^{\prime}}} L_{A} d/L_{M} K_{A} & = - G^{{A^{\prime}}} wL_{A} /K_{A} + rG^{{M^{\prime}}} - G^{{M^{\prime}}} L_{A} (\bar{w}L_{M} + rK_{M} )/L_{M} K_{A} \\ & = - G^{{A^{\prime}}} wL_{A} /K_{A} + G^{{M^{\prime}}} \left[ {r(1 - L_{A} K_{M} /L_{M} K_{A} ) - L_{A} \bar{w}/K_{A} } \right] < 0, \\ \end{aligned}$ $L_{U}$ decreases by the environmental effect.

Next, we investigate the environmental effect on $K_{M}$. The sum of the environmental effect of ${\text{d}}K_{M} /{\text{d}}K$ and ${\text{d}}K_{A} /{\text{d}}K$ is zero: by adding $F_{LL}^{M} F_{KK}^{A} ( - J^{*} C + JeK_{A} /L_{A} )$ of (33f) and $F_{LK}^{M} F_{KL}^{A} \left[ {J^{*} (B + C) + JG^{{M^{\prime}}} d/L_{M} } \right]$ of (33g), it becomes

$$\begin{aligned} F_{LL}^{M} F_{KK}^{A} ( - J^{*} C + JeK_{A} /L_{A} ) + F_{LK}^{M} F_{KL}^{A} \left[ {J^{*} (B + C) + JG^{{M^{\prime}}} d/L_{M} } \right] \\ & = F_{LK}^{M} F_{KL}^{A} \left[ {J^{*} ( - CK_{M} L_{A} /L_{M} K_{A} + B + C) + J(eK_{M} /L_{M} + G^{{M^{\prime}}} d/L_{M} )} \right] \\ & = F_{LK}^{M} F_{KL}^{A} \left\{ {J^{*} \frac{{\bar{w}v_{w}^{M} L_{A} \left[ { - K_{M} /(L_{M} + L_{U} ) + K_{A} /L_{A} } \right]}}{{(L_{M} + L_{U} )K_{A} }} + J(G^{{A^{\prime}}} wK_{M} L_{A} /L_{M} K_{A} + G^{{M^{\prime}}} \bar{w})} \right\} \\ & =\, \frac{{(F_{LK}^{M} F_{KL}^{A} )^{2} p\bar{w}v_{w}^{M} L_{A} }}{{(L_{M} + L_{U} )K_{A} }}\left[ {\frac{{K_{M} }}{{(L_{M} + L_{U} )}} - \frac{{K_{A} }}{{L_{A} }}} \right]\left( { - \bar{w}G^{{M^{\prime}}} - \frac{{G^{{A^{\prime}}} wK_{M} L_{A} }}{{L_{M} K_{A} }} + \frac{{G^{{A^{\prime}}} wK_{M} L_{A} }}{{L_{M} K_{A} }} + \bar{w}G^{{M^{\prime}}} } \right) \\ & = 0, \\ \end{aligned}$$

where to obtain the third expression, we use the definitions for $B$, $C$, $e$, and $d$, while to obtain the fourth expression, we use the definitions for $J^{*}$ and $J$. Thus, remembering that the environmental effect of ${\text{d}}K_{A} /{\text{d}}K$ is positive as expressed in (33g), the environmental effect of ${\text{d}}K_{M} /{\text{d}}K$ becomes negative.

Finally, we consider the environmental effect on $L_{M}$. From (3), $L_{M}$ and $K_{M}$ move in the same direction. Therefore, because $K_{M}$ decreases due to the environmental effect, $L_{M}$ also decreases due to the environmental effect.