Introduction

Increasing industrialization since the onset of nineteenth century has created globally a widespread of land, air, and water pollution. Specifically, in Nigeria’s Niger Delta region, the disposal of untreated effluents such as produced water into water bodies has caused harmful impacts on living things and physical aquatic environment [1].

In order to maintain environmental integrity and stability, there is a need to treat the effluents before discharging them into water bodies using one or a combination of these water treatment processes: filtration, neutralization, adsorption, coag-flocculation, sedimentation, ion exchange, etc.

In this study, coag-flocculation is the process of interest and it has the following advantages: simplicity, low operator skill, cost effectiveness, and high low temperature efficiency. Coag-flocculation aims at overcoming the repulsive forces stabilizing the effluent particles in order to initiate flocs growth, and subsequent sedimentation and clarification [2]. Coag-flocculation performance depends on certain factors such as the nature of the coagulant, effluent characteristics, temperature, mixing effect, and pH [3].

The use of traditional inorganic coagulants is linked to health impairment, impact on the pH of the treated water, and generation of high sludge volume with high disposal cost [4, 5], hence the persistent search for alternative bio-coagulants. In this direction, this study X-rays the performance of the Mucuna flagellipes seed as a bio-coagulant.

Mucuna is of an annual twinning tropical plant, which contains thickening seed bean that is composed of soluble proteins (20–30%), lipids, fibers, and minerals [6]. Results obtained from the preliminary application of novel Mucuna seed coagulant (MSC) in the treatment of coal washery effluent indicated its prospects for potential utilization in the treatment of produced water (PW), which constitutes aquatic pollutant in Nigeria’s Niger Delta region [7, 8].

The reduction in the turbidity of the effluent at varying dosages and pH levels was monitored in this study. The data obtained would be used to achieve the following specific objectives:

  1. 1.

    To study the process kinetics and efficiency using statistical tools, such as analysis of variance (ANOVA) and Scheffe’s test. The ANOVA would be used to determine whether there would be any significant differences between the statistical means of two or more independent (unrelated) groups [9].

  2. 2.

    To run a posthoc (Scheffe’s test) test to confirm where the differences occurred between groups [9] if the ANOVA result indicates that there would be significant difference between the statistical means of the groups

  3. 3.

    To study the effectiveness of MSC as a bio-coagulant with respect to the effects of variation of pH levels and dosages and the statistical implication of the variation of such factors on the purification of the PW.

  4. 4.

    To compare relative treatment performances between MSC and conventional alum.

Materials and Methods

Materials Collection and Preparation

Produced Water

The PW used for the study was obtained from an oil facility located in Warri, Delta State, Nigeria. Prior to the characterization of the effluent and the actual experiments, the PW was stored in black plastic gallons in order to avoid photo-induced changes in the properties of the effluent. Characterization of the PW was done using standard methods reported elsewhere [10].

Mucuna Seed

The MS sample was got from the Eke-Awka Market, Awka, Nigeria. Two kilograms of the seed sample was washed and sun-dried for 3 days. The seeds were later ground and sieved using 0.6-mm mesh-sized sieve.

The modified Sutherland method [11] was applied in synthesizing the MSC as a by-product of oil extraction from the Mucuna seed (MS). In this procedure, 40 g of the MS powder was firstly soaked in ethanol contained in a beaker. The mixture was stirred for 1 h using a magnetic stirrer. At the end of 1-h stirring, the mixture was filtered using Whatman filter paper no 3. The residue obtained from the filtration was poured into a beaker containing 1:25 w/v mixture of mixed salts solution (0.75 g/L KCL, 0.7 g/L CaCl2, 30 g/L NaCl, 4 g/L MgCl2) and stirred for 1 h for proper mixing and efficient mass transfer. After this round of mixing, the mixture was sieved using a Whatman filter paper no 3. The filtrate was poured into a clean beaker and was heated to a steady temperature of 70 °C while the mixture was continuously stirred. The heating at 70 °C was kept for 1 min in order to precipitate the desired MSC from the filtrate solution. The same specification of filter paper stated earlier was used to separate the precipitated MSC from the solution. The precipitate which was the desired MSC was allowed to dry under ambient conditions for 24 h.

Material Characterization

Proximate Analyses of Mucuna Seed Sample

Calculation of Bulk Density

53.15 g of Mucuna seed flour (MSF) was used to fill a 100-mL-volume container and the bulk density was determined using Eq. 1

$$ \mathrm{Bulk}\ \mathrm{density}=\frac{W}{V} $$
(1)

where V is the volume of container and W is the weight of MSF.

Calculation of Percentage Yield and Weight Loss

Seventy grams of the seed was processed into MSC of weight B. With this new weight, the percentage yield and weight loss were calculated using Eqs. (2) and (3).

$$ \%\mathrm{yield}=\frac{B}{70}\times 100 $$
(2)
$$ \%\mathrm{weight}\ \mathrm{loss}=\frac{70-B}{70}\times 100 $$
(3)

Calculation of Moisture Content

Two grams of the MSF was added to a pre-weighed crucible. The crucible was put inside an oven and was heated together at 150 °C for 5 h. The crucible was removed from the oven, cooled, and weighed until a constant weight was obtained. The percentage moisture content [12] was calculated using Eq. (4).

$$ \%\mathrm{moisture}\ \mathrm{content}=\frac{W\mathrm{sample}-W\mathrm{dry}}{W\mathrm{sample}}\times 100 $$
(4)

where W sample is the weight of MSF before drying and W dry is the weight of MSF after drying.

Calculation of Percentage Protein

Into a Kjeldahl digestion flask containing 8 g of catalyst (3.5% CuSO4·5H2O, 0.5% selenium dioxide, 96% anhydrous Na2SO4), 2 g of MSF was added. The flask was made to stand at an inclined position while 20 mL of conc. H2SO4 was added to it. The flask was shaken at short intervals for 3 h. The liquid formed thereafter was cooled and washed into a distillation flask using distilled water. Screened methyl red indicator and 50 mL of boric acid solution (2%) were added into the Kjeldahl receiving flask. The distillation apparatus was set up in a way that the delivery tube outlet was immersed into the boric acid solution. The addition of 50% NaOH solution made the diluted digest medium alkaline. About 50 mL of the distillate and sample of blank was collected and titrated with 0.1 M H2SO4 under the same specified condition [12]. Percentage nitrogen and protein content was determined using Eqs. (5) and (6).

$$ \%\mathrm{nitrogen}=\mathrm{volume}\kern0.34em \mathrm{of}\kern0.2em 0.1\kern0.2em \mathrm{M}\kern0.2em {\mathrm{H}}_2{\mathrm{SO}}_4\times 0.28 $$
(5)
$$ \%\mathrm{protein}\ \mathrm{content}=\%\mathrm{nitrogen}\times 6.25 $$
(6)

Calculation of Percentage Ash Content

A Bunsen burner flame was used to burn 2 g of MSF contained in a pre-weighted crucible until smoking ceased. The sample was transferred to a muffle furnace and was heated at temperature of 600 °C until the sample turned gray-white. The ash content was calculated using Eq. (7) after allowing the sample to cool.

$$ \%\mathrm{ash}\ \mathrm{content}=\frac{W\mathrm{ash}}{W\mathrm{sample}}\times 100 $$
(7)

Where W ash is the weight of ash and W sample is the weight of MSF.

Determination of Percentage Oil Yield

Two hundred grams of MSF was put into a porous sack cloth which was wrapped and inserted into a Soxhlet extractor. The Soxhlet extractor was fitted to a round bottom flask containing about 200 mL of hexane solvent. A reflux condenser was also fitted to the Soxhlet extractor thereby completing the extraction setup. The setup was properly clamped and the heat was supplied to the round bottom flask. The extraction process was monitored and at the point when the extracting solvent became clear indicated that the process has completed. In order to obtain the desired solute (oil), the solvent was distilled off. The oil extracted was poured into a conical flask and was kept for 5 days for the remaining trapped solvent to separate [12]. The percentage oil yield was then determined using Eq. (8) after the weight of the extracted oil was measured.

$$ \%\mathrm{oil}\ \mathrm{yield}=\frac{W\mathrm{oil}}{W\mathrm{sample}}\times 100 $$
(8)

W oil is the weight of oil and W sample is the weight of MSF.

Instrumental Characterization of Samples

Characterization of Mucuna seed (MS), Mucuna seed coag-flocculant (MSC), and generated sludge after treatment (GSAT) was examined using the following instruments: (a) Thermo Nicolet Nexus Model 470/670/870 unit for functional groups determination, (b) Model Zeiss Evo®MA 15 EDX/WDS SEM unit for the surface morphology and elemental analyses (c) Model PHILIPS X PERT X-ray diffraction unit with Cu Kr radiation (30 kV and 30 mA) at a scan rate of 1°/min for crystalline analyses, (d) Models TGA–Q50 and DSC–Q200 for thermal analyses.

Coag-Flocculation Test

The coag-flocculation tests were carried out at room temperature.

Influence of MSC Dosage Variation on Coag-Flocculation Performance

  1. i.

    The initial turbidity and pH of the effluent were measured.

  2. ii.

    Different doses of MSC within the range of 100–500 mg/L were added into five different 1000-mL—GG—beakers, each containing 400 mL of PW samples.

  3. iii.

    For 1 min, the mixtures were subjected to a fast mixing at a speed of 250 rpm (G = 550 s−1) after which it was subjected to a 30-min slow mixing at a speed of 30 rpm (G = 22 s−1). The treated samples were then, gently poured into a 500-mL borax measuring cylinder immediately after the slow mixing and allowed to settle for 30 min.

  4. iv.

    Twenty milliliters of the upper layer of the settling effluent (supernatant) was drawn from a depth of 2 cm at 3, 5, 10, 15, 20, 25, 30, 35, and 40 min during the settling period. The collected samples were drained into different 100-mL plastic bottles.

  5. v.

    The samples collected at different times were measured and the residual particles turbidity was recorded. The concentrations of the suspended and dissolved particles (SDP) were obtained as a product of the measured turbidity in nephelometric turbidity unit (NTU) and T f. Where T f is the conversion factor applicable for the conversion of turbidity to milligrams per liter SDP. T f = 2.35 [13].

Influence of PW pH Variation on Coag-Flocculation Performance

  1. i.

    The optimum dose of MSC which had been determined from section 2.3.1 was added into five different beakers, each containing 400 mL of the PW sample. However, just before the samples were dosed with MSC, the pH levels of the PW samples were adjusted to 2, 4, 6, 8, and 10 using 0.1 M NaOH and 0.1 M H2SO4.

  2. ii.

    In order to determine the optimum pH level, steps iii–v of section 2.3.1 were repeated.

Comparative Treatment Performance Between MSC and Alum

  1. i.

    The optimum dosage of MSC was added to a 400 mL of PW sample. Equal quantity of alum was also added to another 400 mL of PW sample.

  2. ii.

    The pH level of the two mixtures was adjusted to the already-determined optimum pH.

  3. iii.

    In order to analyze the comparative performance, the procedures explained in steps iii–v of section 2.3.1 were repeated.

The alum that was used for this analysis was sourced from the staple of Merck, Germany. Also, the alum which was in powdered form has its chemical formula as Al2(SO4)3·18H2O and the following properties: M = 666.42 g/mol, 51–59% Al2(SO4)3, and pH 2.5–4.

Theory

Process Statistics

Analysis of Variance

The ANOVA was used to analyze the differences among and between the group statistical means [14, 15]. In this study, PW pH levels and MSC dosages were the independent variables. These independent variables were compared with those of the coag-flocculation efficiency as a response.

Scheffe’s Test

This is a type of posthoc analysis. Posthoc analysis involves a stepwise multiple comparisons procedure for the identification of sample statistical means that are significantly different from one another. Scheffe’s test applies to a set of estimates of all possible contrasts among the factor level statistical means, not just the pairwise differences considered in Tukey’s method [16].

Assuming μ i, ..., μ k as the means of some variables in k disjoint populations, an arbitrary contrast is thus defined as

$$ C={\sum}_{i=1}^k{c}_i{\mu}_i $$
(9)

where

$$ {\sum}_{i=1}^K{c}_i=0 $$
(10)

When μ i, ..., μ k are all equal to one another, then all contrasts among them are 0. When this is not the case, it implies that some contrasts differ from 0.

Technically, there are countless contrasts. Whether the factor level sample sizes are equal or unequal, the simultaneous confidence coefficient is exactly 1 − α. Usually, only a finite number of comparisons are of interest. In such case, Scheffé’s method is typically quite conservative, and the experimental error rate will generally be much smaller than α. Where α is significance level (which is the probability of rejecting the null hypothesis when it is true). For example, a significance level of 0.05 indicates a 5% risk of concluding that a difference exists when there is no actual difference [17, 18].

C is estimated by

$$ \widehat{C}={\sum}_{i=1}^k{c}_i{\overline{Y}}_i $$
(11)

while the estimated variance is

$$ {S}_{\widehat{C}}^2={\widehat{\sigma}}_e^2{\sum}_{i=1}^k\frac{c_i^2}{n_i}, $$
(12)

where

  • \( {\widehat{\sigma}}_e^2 \) is the estimated variance of the errors.

  • n i is the size of the sample taken from the ith population (whose mean is μ i), and k is the disjoint populations.

It can be shown that the probability is 1 − α, and that all confidence limits of the type

$$ \widehat{C} \pm {\mathcal{S}}_{\widehat{C\ }}\ \sqrt{\left(k-1\right)\ {F}_{\upalpha; k-1;N-k}} $$
(13)

are concurrently correct, where as usual N is the size of the complete population.

Process Kinetics Theory

The extent to which materials contained in aqueous phase decrease the passage of light through the water is a reflection of the turbidity of the water [19], usually measured in nephelometric turbidity units (NTU) and expressed in milligrams per liter with respect to Eq. 14

$$ \mathrm{Turbidity}\ \left(\mathrm{NTU}\right)\times {T}_{\mathrm{f}}=\mathrm{turbidity}\ \left(\mathrm{mg}/\mathrm{L}\right) $$
(14)

where, T f is the conversion factor and T f = 2.35 [13].

For the same aqueous phase, where Brownian motion dominates, the number of collision occurring per unit time per unit volume, K xy , for two particles of volumes V x and V y  is expressed as [20,21,22,23]:

$$ {K}_{xy}={\beta}_{\mathrm{BR}}\left({v}_x{v}_y\right){n}_x{n}_y $$
(15)

where, β BR(v x v y ) is the Brownian aggregation collision frequency which depends on the particle size, temperature, and pressure; n x n y is the particle concentrations for two particles of sizes x and y.

The rate of formation r f of particles of volume, v p as a result of collisions between particles of volumes v x and v y is expressed as [21, 24]:

$$ {r}_f=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\sum}_{x+y=p}{K}_{xy} $$
(16)

Note that x + y = p shows that the summation is governed by collisions for which

$$ {V}_x+{V}_y={V}_{\mathrm{p}} $$
(17)

In a reverse case, the rate of dissociation of particle of volume V p by collision with other particles is given as [21, 24]:

$$ {r}_l={\sum}_{x=1}^{\infty }{K}_{xk} $$
(18)

Hence, the rate of change in the number of density of particles of volume V p is

$$ \frac{\ {dn}_k}{dt}={r}_{\mathrm{f}}-\kern0.5em {r}_{\mathrm{l}}, $$
(19)

Substituting Eqs. (16) and (18) into Eq. (19) yields

$$ \frac{dn_k}{dt}=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\sum}_{x+y}{\beta}_{BR}\left({V}_x{V}_y\right){n}_x{n}_y-{n}_k{\sum}_{x=1}^{\infty }{\beta}_{BR}\left({V}_x{V}_p\right){n}_x $$
(20)

The collision frequency function can be obtained through the steady state particle diffusion as:

$$ {K}_{xy}=4\uppi \left({D}_x+{D}_y\right)\ \left({a}_x+{a}_y\right) $$
(21)

where, D x  + D y  = D p.

Thus, Eq. (21) is simplified to:

$$ {K}_{xy}=4\uppi\ \left({D}_p\right)\left({a}_x+{a}_y\right) $$
(22)

For a mono-disperse system where particles of volume, v x  = v y , Einsten-Stokes relation could be expressed as Eq. (23) [22]:

$$ {D}_x=\frac{KT}{6\uppi \mu {a}_x}\mathrm{and}\kern0.5em {D}_y=\frac{KT}{6\uppi \mu {a}_y} $$
(23)

Hence, the Einsten-Stokes equation is reduced to:

$$ {D}_p=\frac{KT}{6\uppi \mu}\left(\frac{1}{a_x}+\frac{1}{a_y}\right) $$
(24)

Inserting Eq. (24) into Eq. (22) yields:

$$ {K}_{xy}=4\uppi \left(\frac{KT}{6\uppi \mu}\left(\frac{1}{a_x}+\frac{1}{a_y}\right)\left({a}_x+{a}_y\right)\right) $$
(25)
$$ {K}_{xy}=\frac{2}{3}\frac{KT}{\mu }{\frac{\left({a}_x+{a}_y\right)}{a_x{a}_y}}^2 $$
(26)

For the collision frequency function of Eq. (26), for the case of mono-disperse dimmer formation, the following conditions apply:

$$ {\frac{\left({a}_x+{a}_y\right)}{a_x{a}_y}}^2=\left(\genfrac{}{}{0pt}{}{4\ \mathrm{for}\ {a}_x={a}_y}{>4\ \mathrm{for}\ {a}_x\ne {a}_y}\right) $$

and

For the case of a x  = a y , Eq. (26) transforms to Eq. (27):

$$ {K}_{11}=\frac{8 KT}{3\mu } $$
(27)

Where K 11 is the Von Smoluchowski coagulation rate constant

Also, for the case of K xy  → K 11 = β BR(v x v y )n x n y , Eq. (20) solves exactly to yield:

$$ \frac{N_{h(t)}}{N_o}=\frac{{\left({K}_{11}{N}_o\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)}^{h-1}}{{\left(1+{K}_{11}{N}_o\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)}^{h+1}} $$
(28)

It has been established that for aggregating system at h = 1, it could be extended into a flocculation regime, such that

K 11 ≈ K m [8] and Eq. (28) transforms to Eq. (29):

$$ \frac{1}{\sqrt{N_h}}=\left(\frac{K_{\mathrm{m}}{N}_o}{\sqrt[2\kern1.5em ]{N_o}}\right)t+\frac{1}{\sqrt{N_o}} $$
(29)

where, \( {K}_{\mathrm{m}}=\frac{1}{2}{\beta}_{BR}=\frac{2}{3}{\varepsilon}_p\frac{k_BT}{\eta } \)

K m is the Menkonu coagulation-flocculation rate constant accounting for Brownian coagulation-flocculation transport of destabilized particles.

ε p is the collision efficiency

N h is the number of particle concentration at time, t

h (= 1, 2, 3) is the particle cluster distribution

Coagulation-flocculation period is obtained from Eq. (28) as

$$ {\tau}_{1/2}=\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$\left({N}_o{K}_{\mathrm{m}}\right)$}\right. $$
(30)

The physical significance of Eq. (30) is that it represents the time at which the initial total number of particles is reduced by half and it is therefore a coagulation time scale.

Since K 11 ≈ K m [8] and Eq. (30) remains valid, Eq. (28) can be transformed to Eq. (31)

$$ \frac{N_{h(t)}}{N_o}=\frac{{\left[\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{${\tau}_{1/2}$}\right.\right]}^{h-1}}{{\left[1+\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{${\tau}_{1/2}$}\right.\right]}^{h+1}} $$
(31)

Where h = 1 (monomers), 2 (dimmers), and 3 (trimmers)

$$ \mathrm{At}\ h=1:\kern0.5em {N}_{1(t)}=\frac{N_0}{{\left[1+\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{${\tau}_{1/2}$}\right.\right]}^2} $$
(32)
$$ \mathrm{At}\ h=2:\kern0.5em {N}_{2(t)}=\frac{{\left[\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{${\tau}_{1/2}$}\right.\right]}^1}{{\left[1+\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{${\tau}_{1/2}$}\right.\right]}^3}\times {N}_o $$
(33)
$$ \mathrm{At}\ h=3:\kern0.5em {N}_{3(t)}=\frac{{\left[\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{${\tau}_{1/2}$}\right.\right]}^2}{{\left[1+\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{${\tau}_{1/2}$}\right.\right]}^4}\times {N}_O $$
(34)

Eqs. 32–34 were used in generating the data used for the particle distribution plot

The coagulation-flocculation efficiency could be calculated using Eq. (35)

$$ E\ \left(\%\right)=\left[\frac{N_o-{N}_t}{N_o}\right]\mathrm{x}\ 100 $$
(35)

Results and Discussion

Sample Characterization

Characteristics of PW/MS

Presented in Table 1 are the selected major characteristics of PW. The conductivity value shown in Table 1 indicated that PW contained charged ions from different substances that constitute the PW. The conductivity value affects the coag-flocculation performance of MSC. It has been explained that higher conductivity favors coag-flocculation of colloid particles due to reduction in electrostatic repulsion [25]. The high turbidity recorded in Table 1 was due to suspended solids and natural organic matter which accounted for the cloudiness of the effluent [8]. The suitability of the application of coag-flocculation in the treatment of the PW is justified by the relatively high turbidity value obtained in Table 1.

Table 1 Characteristic results of PW
Full size table

Presented in Table 2 are the characteristics of MS. The yield value (89.05%) and protein content (22.70%) shown in Table 2 are significant enough to apply MS as a good precursor for the synthesis of MSC. The protein content of MS provides the active sticking sites for the coagulation to take place.

Table 2 Proximate analysis of MS
Full size table

FTIR Spectra Analyses

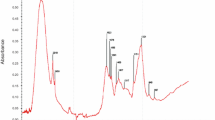
Figure 1 shows the FTIR peaks as related to MS, MSC, and GSAT. The spectral peaks of the investigated samples were assigned to the corresponding functional groups contained in the FTIR library [26]. The bands of 3700–3500 cm−1 are shown in Fig. 1 for: (a) MS, (b) MSC, and (c) GSAT could be linked to O-H groups. The band range of 3288–3335 cm−1 (3288 cm−1 for MS, 3334 cm−1 for MSC, 3335 cm−1 for GSAT) is a characteristic of a secondary N-H stretching. Peaks range 2918–2850 cm−1 (2919 cm−1 (MS), 2918–2850 cm−1(MSC), and 2919–2850 cm−1(GSAT)) was assigned to aliphatic ring. 1720–1528 cm−1 peak range would contain primary amine, secondary amide, and aliphatic nitro compounds. Spectral bands at 1362, 1298, and 1284 cm−1 depicted in Fig. 1a could be associated to the SO2 asymmetric stretching. Furthermore, 1206, 1020, and 944–609 cm−1 bands of Fig. 1a could be assigned to S=O stretching, B–H bending, and C–H bending, respectively. The following peaks at 1456, 1417, and 1488 cm−1 displayed in Fig. 1b, c were attributed to N=N stretching for azo compound. Bands at 897–945 cm−1 and 712–699 cm−1 shown in Fig. 1b, c are linked to C–H and alkyne group, respectively. The disappearance of peaks originally present in MSC and presence of new peaks in GSAT after coagulation indicated uptake of particles from PW.

Fig. 1
figure 1

a FTIR spectrum for MS. b FTIR spectrum for MSC. c FTIR spectrum for GSAT

Full size image

SEM/Elemental Results of MS, MSC, and GSAT

Figure 2a–c shows the surface morphological images of MS, MSC, and GSAT. Two different images (i and ii) were produced at different resolutions for each of Fig. 2a–c. Image of Fig. 2a (i) produced for MS shows a tender looking mass with an aggregated porous network structure. The pores are of different sizes and shapes. Figure 2a (ii) shows an alternate image of MS. The image shows separated but multiple networked voids that are evenly distributed across the biomass. The presence of these pores was an initial indication of active sites for surface activities of MS flour. Figure 2b (i) produced for MSC shows image with greater numerous pores. The predominantly multiple surface pores characterized by rounded protrusions showed increased voids after converting MS into MSC. Figure 2b (ii) shows an alternate image for a single particle of MSC. The image indicates high number of surface pores contain in each of the particles that constitutes the MSC mass. These inter and intra particle pores contained in MSC explain the effective performance of MSC as a coagulant. Figure 2c obtained for GSAT indicates a heavily filled compact structure with no voids. The totally filled voids showed that the coagulating particles readily attached on the pores surfaces to generate the sludge (GSAT). The observed white region could be due to transfer of potassium-based compounds from PW to the MSC in the GSAT. Shown in Table 3 are the elemental compositions of MS, MSC, and GSAT. Apparently, the presence of elements which were originally absent in MSC, but subsequently found in GSAT matrix, was an indication of uptake of elements from the waste water to the coagulant.

Fig. 2
figure 2

a SEM micrographs of MS. b SEM micrographs of MSC. c SEM micrographs of GSAT

Full size image
Table 3 Elemental composition of MS, MSC, and GSAT
Full size table

XRD Result of MS, MSC, and GSAT

The X-ray diffraction for MS, MSC, and GSAT is shown in Fig. 3a–c, respectively. In Fig. 3a, broad peaks were obtained instead of sharp peaks. This indicates that MS is poorly crystalline. However, two clear peaks at 2θ = 21.5° and 25° were observed. For Fig. 3b, five clear peaks at scattering angles of 2θ = 28°, 32°, 41°, 46°, and 51° are observed. Figure 3c depicts 12 clear peaks. The assigned peaks in Fig. 3 were done on the bases of corresponding reflections and planes. The crystal peaks (Fig. 3) on comparison with the standard signature were shifted towards left-right axes, which could be due to the expansion or contraction of crystal planes. Inter-planar spacing of the crystal structure would support that the largest d-spacing occurs for planes with the lowest indices, specifically for 000-hkl system. This implies for this case, Fig. 3 represents samples with a primitive atomic structure in which only MS was poorly crystalline.

Fig. 3
figure 3

a XRD pattern for MS. b XRD pattern for MSC. c XRD pattern for GSAT

Full size image

TGA/DSC of MS, MSC, and GSAT

TGA gives information with respect to the change in weight of a substance due to chemical reaction and physical transition [27,28,29,30]. On the other hand, DSC evaluates the effects of heat with respect to phase transitions and chemical reactions in relation to temperature [29, 30]. TGA and DSC thermograms for MS, MSC, and GSAT are displayed in Figs. 4, 5, and 6, respectively. The TGA profiles for both MS and MSC are shown in Figs. 4a and 5a. Figures 4a and 5a indicated final residual masses of 1.189 and 1.839 mg, respectively, representing 27.5 and 60% of the initial weights. The initial loss in weight noticed in Figs. 4a and 5a could be ascribed to internal moisture and gaseous losses from the sample molecules [30, 31]. Furthermore, the subsequent weight loss recorded could be linked to decomposition of the labile constituent contained in the samples matrix.

Fig. 4
figure 4

a TGA for MS. b DSC for MS

Full size image
Fig. 5
figure 5

a TGA for MSC. b DSC for MSC

Full size image
Fig. 6
figure 6

a TGA for GSAT. b DSC for GSAT

Full size image

Figures 4b and 5b show DSC profiles for the transitional phases over the temperature ranges of 37.5–298 °C and 25–298 °C, with transition enthalpies of 13.779 and 11.8421 kJ/mol, respectively. For the temperature ranges of 68.75–87.5 °C and 125–150 °C shown in Figs. 4b and 5b, transition enthalpies of 13.779 and 11.8421 kJ/mol, respectively, were obtained. Both Figs. 4b and 5b exhibit prevalent coiling of the long-chain protein moiety resulting in spontaneous densification. The mass densification occurred between 125 and 298 °C and 162.5–298.5 °C in which the heat flow discs indicated an exothermic reaction.

Figure 6 shows the TGA/DSC thermograms for GSAT. In Fig. 6a, the TGA shows dehydration and volatilization of the GSAT that progressed (along with temperature) up to a temperature of 262.5 °C, shedding about 10% of its total weight [32]. In addition, the weight loss observed at 262.5 °C was 0.352 mg as shown in Fig. 6a.

The oxidation resulted in a loss of about 15% (0.88 mg) of its weight between 262.5 and 450 °C. At final T max (590 °C), 1.1 mg was lost. Figure 6a shows that the gradual loss in the sample mass was sustained (along with temperature) up to the temperature of 590 °C, hence shedding off 1.1 mg from the original of 3.5200 mg. The implication was that GSAT steadily lost both moisture and volatile matters up to a temperature of 590 °C [32], at which oxidation of the dry samples attained its maximum. Labile component fragmentation or decomposition could contribute to this weight loss.

The interactive effects of MSC with various chemical substances and particles present in PW are depicted as two eutectics downward peaks in Fig. 6b. The existence of the two peaks in Fig. 6b showed that the components of the sample were not a single pure substance. The TGA/DSC profiles generally indicated samples that were thermally stable with significant evidence of surface activity on the MSC.

Process Factors Sensitivity Analyses

The influence of these factors—time, MSC dosage, and PW pH on coag-flocculation performance—was analyzed.

Effect of Time and Dosage Variation on Treatment Efficiency

The variation of treatment performance with time and MSC dosage at initial pH (7.6) of PW is shown in Fig. 7. Generally, the performances of the various dosages increased with increase in time. This was in line with the understanding that the discrete destabilization and floc generation increased correspondingly with increase in time. The results in Fig. 7 showed that maximum efficiency of 76.84% was recorded at 200 mg/L dosage while minimum efficiency of 64.10% was recorded at 500 mg/L dosage. It can be inferred that at pH level of 7.6, MSC recorded relatively low efficiency which could have resulted from diminished protonation of MSC at alkaline conditions (compare Figs. 7 and 8). Generally, coag-flocculation performance could be sensitive to pH, depending on the relative balance on the abundance/scarcity of positive- and negative-charged species supplied by the effluent or coagulant [33]. The optimum dosage (200 mg/L) obtained from Fig. 7 was used as a constant dosage for the evaluation of the effect of pH on coag-flocculation performance.

Fig. 7
figure 7

Temporal performance variation with MSC dosage at pH 7.6

Full size image
Fig. 8
figure 8

Temporal performance variation with pH at 100 mg/L dosage

Full size image

Effect of Time and pH Variation on Treatment Performance

The variation of treatment performance with pH at 200 mg/L is depicted in Fig. 8. It could be observed that the best performances were obtained at acidic condition. These results of good performance in acidic medium are supported by previous reports [6]. Figure 8 specifically revealed that the maximum efficiency of 96.41% was obtained at pH 4. This behavior could be as a result of equilibrated protonation prevalent around pH 4, which brought about optimal aggregation of particles into flocs. Figure 8 shows that relatively low efficiencies were obtained at pH levels10 and 8. These relatively low efficiencies could be due to hyper protonation which was favorable to charge reversal and subsequent flocculation retardation. The retardation was a sequel to electrostatic repulsion among dominant positive charges present in PW effluent.

Evaluation of Comparative Performance Between MSC and Alum

Depicted in Fig. 9 is the comparative performance evaluation between MSC and alum at the established optimum conditions. The result indicates that MSC and alum at early stage recorded relatively high performances above 73%. Specifically, both MSC and alum had 76.95 and 73.87% particles removal efficiencies, respectively, at 3 min. The final performance of MSC at 98.03% was a bit more than that of alum (96.41%). The higher performances of both MSC and alum beyond that obtained for varying pH levels and dosages supported the expected improved performance at optimum conditions.

Fig. 9
figure 9

Temporal comparative performance for alum and MSC at pH 4/200 mg/L MSC

Full size image

Process Statistical Analyses

The results of the temporal statistical mean efficiencies for the various MSC dosages and effluent pH are presented in Table 4. For dosage variations, the highest value of statistical mean efficiency (56.418%) was recorded at 200 mg/L while the lowest statistical mean efficiency (34.17%) was recorded at 500 mg/L. Hence, 56.418 and 34.17% are considered the highest and lowest points in average percentage particle removal from the petroleum effluent.

Table 4 Temporal mean efficiency for the varying dosages and pH levels
Full size table

For pH, the highest and lowest statistical mean performances are recorded at pH 4 (78.027%) and 10 (47.701%), respectively. These represent the points of highest and lowest efficiencies.

One-Way Factorial Analyses for the Effect of Dosage on Treatment Performance

The variations in the efficiencies of MSC at the various dosages were tested using the ANOVA statistical tool. The aim was to establish that the variation in efficiency of MSC following dosage variation was not by chance, but that there was indeed statistical difference in performance for the varying dosages.

According to theory [34, 35] when the probability (p value) is less than a certain threshold (significance level denoted by a), the null hypothesis would be rejected and vice versa. The rejection of the null hypothesis implies that the variation in treatment condition results in change in coag-flocculation performance and vice versa. The threshold level for this ANOVA was 0.05. Table 5 shows that when significant p < 0.05, hence, the null hypothesis would be rejected, indicating statistical difference among the performances at the various dosages.

Table 5 ANOVA on the effect of dosage variation on the process performance
Full size table

The Scheffe’s posthoc analysis was performed as a follow-up test to the ANOVA such that statistical means that are significantly different from one another could be determined. It compared the performance of statistical mean at each dosage to that of others. This posthoc analysis would apply when ANOVA establishes that there is significant difference in performance at the different treatment conditions. Table 6 shows that p < 0.05 for the following compared dosages: 200 and 500, 500 and 200 mg/L while p > 0.05 for the rest of comparisons. This implies that significant difference in performance exists only between 200 and 500 mg/L and 500 and 200 mg/L.

Table 6 Scheffe’s posthoc analysis for the effect of dosage on the process performance
Full size table

One-Way Factorial Analyses for the Effect of Effluent pH on Process Performance.

Table 4 presents the time-based mean performance for the various pH levels at 200 mg/L MSC. As already indicated (Table 4), pH of 4 has the highest mean performance of 78.027% while pH of 10 has the lowest mean performance of 47.701%. This totally agrees with the result presented in Fig. 8.

Results obtained in Table 4 were further subjected to ANOVA (Table 7) to test for significant difference between performances at the various pH conditions. This was to ascertain that the variation in performance was not by chance.

Table 7 ANOVA on the effect of effluent pH variation on the process performance
Full size table

The significance of p < 0.05 as shown in Table 7 indicates that null hypothesis would be rejected on the bases of explanations already given in section 3.1. This would mean that there is statistical difference between the coag-flocculation performances at the various effluent pH levels.

The Scheffe’s posthoc analysis was used to analyze the statistical means of the efficiency at the various pH levels and 200 mg/L MSC. This was conducted to determine the process statistical means that would significantly differ from one another, on comparing the performance statistical mean at each pH to that of others. The results (Table 8) show that significant p < 0.05 is present at the following comparisons: pH 2 and pH 8, pH 2 and pH 10, pH 4 and pH 8, pH 4 and pH 10, pH 6 and pH 10, pH 8 and pH 2, pH 8 and pH 4, pH 8 and pH 10, pH 10 and pH 2, pH 10 and pH 4, pH 10 and pH 6, and finally pH 10 and pH 8. This implied that there existed significant difference in performances at this compared pH levels. For the cases where significant p > 0.05, it showed that there existed no significant difference in performances.

Table 8 Scheffe’s posthoc analysis for the effect of pH variation on the process performance
Full size table

Process Kinetics

Tables 9, 10, and 11 contain a summary of the considered coagulation kinetic parameters. The values of R 2 obtained ranges from 0.869 to 0.997. This range indicates how accurately the experimental data fits with the studied model [11].

Table 9 Coagulation kinetic parameters for various MSC doses at pH 7.6 and 30 °C
Full size table
Table 10 Coagulation kinetic parameters for various PW pH levels at 200 mg/L MSC and 30 °C
Full size table
Table 11 Comparative process kinetic parameters at 200 mg/L (MSC and alum), pH 10, and 30 °C
Full size table

The Menkonu coag-flocculation rate constant, K m, which accounts for the Brownian coag-flocculation transport of destabilized particles was obtained from the slope of the linear plot of \( \frac{1}{\sqrt{N_L}} \) vs. time (t) (plots not shown) for the considered MSC dosages and PW pH. Since K m varies directly with the rate at which coag-flocculation proceeds, it implies that the higher the value of K m, the faster the rate of particle removal from the effluent. The result from the deturbidization kinetics shows that optimum K m (1E−06 L3 g−1 s−1) was recorded at dosage of 200 mg/L for Table 9. For Table 10, the maximum K m was obtained at 9.0E−06 L3 g−1 s−1 . These K m values are in support of the efficiency results obtained for process kinetics. Coagulation period, τ 1/2, represents the settling time at which the initial particle load would be reduced by 50%. The coagulation period is largely rate dependent and has significant implication for process design. This strongly underscores the need to design and fabricate flocculation units with very low periods to ensure economical and efficiently functional water treatment system. The lowest values of τ 1/2 obtained at 200 mg/L dosage (1678.627 s) and effluent pH 4 (186.5141 s) were justified by the corresponding maximum values of K m recorded at those conditions.

The values K11and εp were calculated from Eqs. 27 and 29, respectively. Negligible variation of K11 was obtained as a result of insignificant variations in the values of prevailing temperature and viscosity of PW. For the case of invariant K R, ε p would directly relate to 2K m = β BR [6]. Thus, high ε p translates to high kinetic energy needed to overcome the electrostatic repulsion among the aggregating particles and the MSC active sites. Functional parameters such as τ 1/2, εp, and K R are theoretical effectiveness factors that influence deturbidization before visible floc evolution and settling set in. Generally, the discrepancies observed between the theoretical and physical behaviors of flocculation systems could be due to unattainable assumption that perfect mixing of PW particles and MSC could be achieved within the dispersion medium. Authors [6, 36, 37] have reported similar results previously.

Comparative kinetic parametric results between MSC and alum are shown in Table 11. The rate constants for MSC and alum are 2.0E−05 and 9.0E−06 L3 g−1 s−1, respectively. The respective values of rate constants are in agreement with higher and lower values of coagulation periods recorded for MSC and alum, respectively. Furthermore, Fig. 9 indicates that MSC recorded slightly higher efficiency than that of alum. This was in consonance with higher rate constant and lower period recorded for MSC at the conditions of the experiment.

Particle Size Distribution Plot

Equations 32–34 were used to predict the particle size evolution and distribution of the destabilizing particles. The evolution profiles are graphically presented in Figs. 10 and 11 for the highest and lowest periods, respectively. The two figures indicated graphical trends of similar pattern. For the two cases, as coagulation process progressed, there was a continuous destabilization of the monomer which caused decrease in the concentration of the monomers. This decrease was followed by a simultaneous formation of dimmers and trimmers. The summation of the monomer, dimmer, and trimmer equaled the total number of particles contained in the effluent at any given time.

Fig. 10
figure 10

Particle size distribution plot for a period of 2398.038 s

Full size image
Fig. 11
figure 11

Particle size distribution plot for a period of 186.5141 s

Full size image

The particle size distribution plot associated with higher coagulation period is presented in Fig. 10. The figure shows that the reduction in the concentration of the monomer and the total number of particles was relatively slower due to higher period. The low aggregation was as a result of particle-MSC interaction inertia that restricted successful collisions needed to form a viable floc. This accounted for the lower value of K m (7.0E−07 m3 kg−1 s−1) and higher value of τ 1/2 (2398.038 s) recorded at these conditions.

On the other hand, Fig. 11 presents the particle size distribution plot associated with a lower coagulation period. It would be observed from the plot that there was a rapid evolution of monomers to dimmers and trimmers. This strongly indicates that coag-flocculation occurred at a very fast rate at this condition. The fast aggregation was made possible by a combination of particles bridging and neutralization processes which significantly suppressed or eliminated DLVO repulsive forces. This accounted for the higher value of K m (9E−06 m3 kg−1 s−1) and low value of τ 1/2 (186.5141 s) obtained at this condition.

Conclusion

Produced water, a known pollutant in Nigeria’s Niger Delta region, has been traditionally treated by physical-chemical processes that include the coag-flocculation method. Implementing green coag-flocculation process, which has been experimentally supported in this report, would provide an alternative to conventional use of mineral coagulants. MSC, a novel bio-extract previously subjected to successful preliminary test at specified conditions, but largely not currently utilized for deturbidization of particle-rich effluent such as PW, was studied for coagulation performance. Control coagulant sample (alum) in similar conditions to that of MSC was also used for the treatment of the same batch of PW. MSC slightly recorded better performance than that of alum, though the difference in performance was statistically insignificant.

The process optimal conditions obtained were pH 4, 200 mg/L MSC, and a rate constant of 2.0E−05 m3 kg−1 s−1. Maximum comparative performances at optimal conditions for MSC and alum were 98.03 and 96.41%, respectively.

At the initial produced water pH of 7.6, variation of MSC dosage maintained a significant impact on the MSC efficiency. The highest and lowest coag-flocculation efficiencies were recorded by dosages 200 mg/L (76.84%) and 500 mg/L (64.1%) at the time of 40 min. Furthermore, variation of the produced water pH value maintained significant impact on the effectiveness of MSC with pH 4 having the highest percentage of 96.41% and pH 10 having the lowest (67.68%) at 40 min. It could be inferred that MSC possesses significant potential as an effective bio-extract for the purification of produced water at the conditions of the experiment.