1 Introduction

Forecasting is very important for future planning in many technological areas. Forecasting techniques are attracted by managers and other decision-makers. Forecasting techniques can be based on probability theory, fuzzy set theory or computational techniques. Many of forecasting techniques use fuzzy sets in their algorithms. Fuzzy sets were proposed by Zadeh (1965). Chen (1996a, b) proposed a fuzzy reasoning approach. Chen (1998) proposed a fuzzy system for group decision-making. Bai and Chen (2008a, b) and proposed a method for creating automatically membership functions of fuzzy rules. Bai and Chen (2008a, b) proposed adaptive fuzzy system-based automatically determined concept maps. Fuzzy inference systems and fuzzy time series methods can be used for forecasting. Takagi and Sugeno (1985) system, adaptive network fuzzy inference system proposed by Jang (1993) and a fuzzy function approach proposed by Turksen (2008) are well-known fuzzy inference systems in the forecasting literature. Fuzzy time series methods are also popular methods in the forecasting literature. Song and Chissom (1993) were firstly defined fuzzy time series concept, and they proposed a fuzzy time series forecasting method. Chen and Wang (2010), Chen et al. (2012, 2013), Chen and Chen (2015), Chen and Phuong (2017) and Chen and Jian (2017) proposed forecasting methods based on fuzzy sets.

Recent years, many applications of classical fuzzy systems have been made in the literature. Zarandi et al. (2013) proposed a new fuzzy functions model tuned by hybridizing imperialist competitive algorithm and simulated annealing. Bezdek (2013) used fuzzy objective function algorithms for pattern recognition. Baykasoğlu and Maral (2014) proposed fuzzy functions approach via genetic programming. Baser and Apaydin (2015) proposed a hybrid fuzzy support vector regression analysis. Barak and Sadegh (2016) used ensemble ARIMA-ANFIS hybrid algorithm for forecasting of energy consumption. Goudarzi et al. (2016) proposed an interactively recurrent fuzzy function with multi-objective learning. Aladag et al. (2016) proposed a type 1 fuzzy time series function method based on binary particle swarm optimization. Tan et al. (2017) proposed a new adaptive network-based fuzzy inference system for forecasting. Yang et al. (2017) used linear fuzzy information granules and fuzzy inference system for long-term forecasting of time series. Son et al. (2017) proposed a new neuro-fuzzy inference system for insurance forecasting. Ranganayaki and Deepa (2017) proposed a support vector machine-based neuro-fuzzy model for short-term wing power forecasting. Tak et al. (2018) proposed a recurrent fuzzy function approach for forecasting. Pelka and Dudek (2018) proposed a neuro-fuzzy system for forecasting. Vanhoenshoven et al. (2018) proposed a fuzzy cognitive map employing ARIMA components for time series forecasting. Moreover, there are many fuzzy time series forecasting methods. The fuzzy time series concept was introduced by Song and Chissom (1993). Chen (1996a, b) proposed a fuzzy time series method based on fuzzy relation tables, and it constituted a base for many methods. In recent studies, Chen and Chang (2010), Chen and Chen (2011), Chen et al. (2012), Garg and Garg (2016), Singh (2016), Cagcag Yolcu et al. (2016), Kumar and Gangwar (2016), Kocak (2017), Bose and Mali (2018) and Chang and Yu (2019) proposed fuzzy time series methods. Wang (2018) used a fuzzy time series forecasting method for big data analysis. Bisht and Kumar (2019) used hesitant fuzzy sets based on the computational method for financial time series forecasting. Egrioglu et al. (2019) proposed a forecasting method for single-variable high-order intuitionistic fuzzy time series forecasting model. Gupta and Kumar (2019a) proposed a novel high-order fuzzy time series forecasting method based on probabilistic fuzzy sets. Gupta and Kumar (2019b) proposed a hesitant probabilistic fuzzy set-based time series forecasting method.

Recent years, intuitionistic (hesitant) fuzzy sets have been commonly used in fuzzy techniques. In a fuzzy set, there are membership values for each member of the universal set. Non-membership values can be obtained from membership values by using a simple subtract operation. Atanassov (1983) introduced an intuitionistic fuzzy set. In an intuitionistic fuzzy set, non-membership values have different information than membership values have. Besides, hesitation degrees are obtained from the simple mathematical operation of membership and non-membership values. Atanassov (1986) and Atanassov (1999) gave the details of the theory and some applications for intuitionistic fuzzy sets. Bustince et al. (1995), Cornelis and Deschrijver (2001), Szmidt and Kacprzyk (2001), Marinov and Atanassov (2005), Own (2009) and Davarzani and Khorheh (2013) applied intuitionistic fuzzy sets on different implementations. Moreover, Zheng et al. (2013), Kumar and Gangwar (2016), Wang et al. (2016), Bisht and Kumar (2016) and Fan et al. (2017) proposed intuitionistic fuzzy time series method in their studies. Chen and Chang (2016), Chen et al. (2016a, b) and Liu et al. (2017) applied intuitionistic fuzzy sets in their proposed methods.

Castillo et al. (2007) proposed an intuitionistic fuzzy system for time series analysis. Olej and Hájek (2010a) proposed an intuitionistic fuzzy inference system design for prediction of ozone time series. Olej and Hájek (2010b) showed the possibilities of air quality modeling based on intuitionistic fuzzy set theory. Olej and Hájek (2011) compared of fuzzy operators for intuitionistic fuzzy inference system of Takagi–Sugeno type. Hájek and Olej (2012) used adaptive intuitionistic fuzzy inference system of Takagi–Sugeno type for regression problems. The parameters of the intuitionistic fuzzy inference system are determined by using particle swarm optimization in Angelov (2012), Maciel et al. (2012) and Henzgen et al. (2014). Bas et al. (2019) proposed a type 1 fuzzy function method based on ridge regression for forecasting. Kizilaslan et al. (2019) and Cagcag Yolcu et al. (2019) proposed intuitionistic fuzzy function approaches. Egrioglu et al.(2020) proposed picture fuzzy regression functions method based on picture fuzzy clustering.

The motivation of this paper is explained in the following sentences. Fuzzy inference systems are efficient tools for forecasting purposes. It is possible to create new fuzzy inference systems for obtaining more accurate forecasts. Especially, the intuitionistic fuzzy inference system is needed to improve by using different updated techniques. Because intuitionistic fuzzy inference systems employee non-membership values, they can give more accurate forecast results than classical fuzzy inference systems.

The main contribution of this paper can be expressed as proposing a new intuitionistic fuzzy inference system. In this new system, membership values and non-membership values in intuitionistic fuzzy sets and their nonlinear transformations are used as inputs. Thus, the dimension of the input matrix in type 1 fuzzy function approach is augmented by using non-membership values in intuitionistic fuzzy sets. In the new approach, the membership and non-membership values are obtained from intuitionistic fuzzy c-means as in Chaira (2011). The proposed intuitionistic systems do not need to determine the combination parameter of a dual system which are separately designed according to membership and non-membership. In the second section, the proposed method is summarized. The applications for real data sets are given in the third section. In the last section, conclusions and discussions are given.

2 Intuitionistic fuzzy time series functions approach

In the literature, many of fuzzy inference methods have been proposed. The fuzzy functions approach proposed by Turksen (2008) is fairly different from others because it does not have a rule base and it can use directly linear regression models. Although the fuzzy functions approach uses just fuzzy sets, it does not use intuitionistic fuzzy sets. In the fuzzy functions approach, Turksen (2008) showed that the augmentation of the input matrix’s elements by using nonlinear transformations of membership values can drastically improve prediction performance. In this paper, an intuitionistic fuzzy time series functions approach is proposed. In this approach, the input matrix contains nonlinear transformations of non-membership values as well as membership values. The proposed method is based on the ordinary least square estimation instead of ridge regression like in Kizilaslan et al. (2019). The proposed methods use membership and membership values in the same input matrices apart from Cagcag Yolcu et al. (2019). The proposed approach has the following advantages:

  • The proposed approach employs intuitionistic fuzzy c-means clustering. Creation of intuitionistic fuzzy sets is more realistic than creation fuzzy sets because of using hesitation margin.

  • The input matrix has a higher dimension in the proposed approach so that it uses more information compared with other fuzzy functions approaches.

  • The proposed approach has superior forecasting performance in many real-world time series applications.

  • The proposed intuitionistic systems do not need to determine the combination parameter of a dual system which are separately designed according to membership and non-membership.

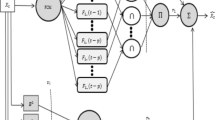
The proposes step-by-step algorithm for intuitionistic fuzzy time series functions algorithm is shown as follows, where its flowchart is given in Fig. 1.

Fig. 1
figure 1

Flowchart for the IFTSF approach

Full size image

Algorithm 1. Intuitionistic Fuzzy Time Series Functions (IFTSF) Algorithm

  • Step 1 Parameters of the method are determined.

  • Parameters are the number of intuitionistic fuzzy clusters (cn), and inputs of the system are the number of lagged variables (p), hesitation margin \((\pi )\), alpha cut (\(\alpha - cut\)) and the length of the test set (ntest).

  • Step 2 Clustering the data.

  • The input and targets are constituted \(IO\) matrix. Intuitionistic fuzzy c-means clustering algorithm proposed by Chaira (2011) is used to obtain memberships and non-memberships.

    $$IO = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & \cdots & {x_{p} } & {x_{p + 1} } \\ {x_{2} } & {x_{3} } & \cdots & {x_{p + 1} } & {x_{p + 2} } \\ . & . & \cdots & . & . \\ . & . & \cdots & . & . \\ . & . & \cdots & . & . \\ {x_{n - p} } & {x_{n - p + 1} } & \cdots & {x_{n - 1} } & {x_{n} } \\ \end{array} } \right]$$
    (1)

  • The last element of cluster centers is excluded, and reduced cluster centers are obtained. Intuitionistic membership values \((\mu_{A} (x))\) and non-membership values \((\vartheta_{A} (x))\) are calculated according to reduced cluster centers. If the \(\mu_{A} \left( x \right) < \alpha - cut\), then \(\mu_{A} \left( x \right) = 0\). Similarly, if the \(\vartheta_{A} \left( x \right) < \alpha - cut\) then \(\vartheta_{A} \left( x \right) = 0\). After applying \(\alpha - cut\) operation, normalization applied to membership and non-membership values is shown \(u_{ij}\) and \(\mu_{ij}\).

  • Step 3 Fuzzy regression functions are obtained by using the least square method. The parameters of linear functions are estimated. Let \(n\) be the length of training time series data.

    $$Input^{\left( i \right)} = \left[ {\begin{array}{*{20}c} 1 & {u_{i1} } & {u_{i1}^{2} } & {\exp (u_{i1} )} & {\mu_{i1} } & {\mu_{i1}^{2} } & {\exp (\mu_{i1}^{2} )} & {x_{1} } & {x_{2} } & \cdots & {x_{p} } \\ 1 & {u_{i2} } & {u_{i2}^{2} } & {\exp (u_{i2} )} & {\mu_{i2} } & {\mu_{i2}^{2} } & {\exp (\mu_{i2}^{2} )} & {x_{2} } & {x_{3} } & \cdots & {x_{p + 1} } \\ . & . & . & . & . & . & . & . & . & \cdots & . \\ . & . & . & . & . & . & . & . & . & \cdots & . \\ . & . & . & . & . & . & . & . & . & \cdots & . \\ 1 & {u_{in} } & {u_{in}^{2} } & {\exp (u_{in} )} & {\mu_{in} } & {\mu_{in}^{2} } & {\exp (\mu_{in}^{2} )} & {x_{n - p} } & {x_{n - p + 1} } & \cdots & {x_{n - 1} } \\ \end{array} } \right]$$
    (2)
    $$Target^{{\left( i \right){\prime }}} = \left[ {\begin{array}{*{20}c} {x_{p + 1} } & {x_{p + 2} } & \cdots & {x_{n} } \\ \end{array} } \right]$$
    (3)
    $$\hat{\theta }^{\left( i \right)} = ( Input^{{\left( i \right){\prime }}} Input^{\left( i \right)} )^{ - 1} Input^{{\left( i \right){\prime }}} Target^{\left( i \right)}$$
    (4)

  • Step 4 Predictions are obtained for training data. Predictions for the training set are obtained by using Eq. (7) by combining outputs of linear functions.

    $$\widehat{Output}_{j}^{\left( 1 \right)} = \frac{{\mathop \sum \nolimits_{i = 1}^{c} u_{ij} Input^{\left( i \right)} \hat{\theta }^{\left( i \right)} }}{{\mathop \sum \nolimits_{i = 1}^{c} u_{ij} }}\quad j = 1,2, \ldots ,n$$
    (5)
    $$\widehat{Output}_{j}^{\left( 2 \right)} = \frac{{\mathop \sum \nolimits_{i = 1}^{c} \mu_{ij} Input^{\left( i \right)} \hat{\theta }^{\left( i \right)} }}{{\mathop \sum \nolimits_{i = 1}^{c} \mu_{ij} }}\quad j = 1,2, \ldots ,n$$
    (6)
    $$\widehat{Output}_{j}^{\text{IFTSF}} = \pi \widehat{Output}_{j}^{\left( 1 \right)} + \left( {1 - \pi } \right)\widehat{Output}_{j}^{\left( 2 \right)}$$
    (7)

  • \(\widehat{Output}_{j}^{\text{IFTSF}}\) is the prediction of intuitionistic fuzzy time series function (IFTSF) method for jth observation.

  • Step 5 Forecasts are obtained for test sets.

  • The design matrix \((Itest^{\left( i \right)} )\) is constituted for each intuitionistic fuzzy cluster and test set. The test set forecasts \((\widehat{Yt}^{\left( i \right)} )\) of each intuitionistic fuzzy regression functions are computed as follows.

    $$Itest^{\left( i \right)} = \left[ {\begin{array}{*{20}c} 1 & {u_{i,n + 1} } & {u_{i,n + 1}^{2} } & {\exp (u_{i,n + 1} )} & {\mu_{i,n + 1} } & {\mu_{i,n + 1}^{2} } & {\exp (\mu_{i,n + 1}^{2} )} & {x_{n - p + 1} } & {x_{n - p + 2} } & \cdots & {x_{n} } \\ 1 & {u_{i,n + 2} } & {u_{i,n + 1}^{2} } & {\exp (u_{i,n + 2} )} & {\mu_{i,n + 2} } & {\mu_{i,n + 2}^{2} } & {\exp (\mu_{i,n + 2}^{2} )} & {x_{n - p + 2} } & {x_{n - p + 3} } & \cdots & {x_{n + 1} } \\ . & . & . & . & . & . & . & . & . & \cdots & . \\ . & . & . & . & . & . & . & . & . & \cdots & . \\ . & . & . & . & . & . & . & . & . & \cdots & . \\ 1 & {u_{i,n + ntest} } & {u_{i,n + ntest}^{2} } & {\exp (u_{i,n + ntest} )} & {\mu_{i,n + ntest} } & {\mu_{i,n + ntest}^{2} } & {\exp (\mu_{i,n + ntest}^{2} )} & {x_{n - p + ntest} } & {x_{n - p + ntest + 1} } & \cdots & {x_{n + ntest - 1} } \\ \end{array} } \right]$$
    (8)
    $$\widehat{Otest}_{j}^{\left( 1 \right)} = \frac{{\mathop \sum \nolimits_{i = 1}^{c} u_{ij} Itest^{\left( i \right)} \hat{\beta }^{\left( i \right)} }}{{\mathop \sum \nolimits_{i = 1}^{c} u_{ij} }}\quad j = n + 1,n + 2, \ldots ,n + ntest$$
    (9)
    $$\widehat{Otest}_{j}^{\left( 2 \right)} = \frac{{\mathop \sum \nolimits_{i = 1}^{c} \mu_{ij} Itest^{\left( i \right)} \hat{\beta }^{\left( i \right)} }}{{\mathop \sum \nolimits_{i = 1}^{c} \mu_{ij} }}\quad j = n + 1,n + 2, \ldots ,n + ntest$$
    (10)
    $$\widehat{Output}_{j}^{\text{IFTSF}} = \pi \widehat{Otest}_{j}^{\left( 1 \right)} + \left( {1 - \pi } \right)\widehat{Otest}_{j}^{\left( 2 \right)} \quad j = n + 1,n + 2, \ldots ,n + ntest$$
    (11)

  • where \(u_{ij}\) and \(\mu_{ij}\) membership and non-membership values are computed by using reduced cluster centers which are obtained in Step 2.

3 Applications

The forecasting performance of the proposed method is investigated by using some real-world time series data sets. The list of time series and their features are given in Table 1. The first data set is daily BIST 100 (Borsa Istanbul 100) index computed for Istanbul Stock Exchange between the years 2009 and 2013 as totally five data sets. The time series were taken from the Turkish Central Bank official Web site. The second data set is the Taiwan Stock Exchange Capitalization Weighted Stock Index (TAIEX) data observed daily between the years 1999 and 2004. The TAIEX data sets were taken from Sarica et al. (2018). The third data set is daily Dow-Jones Industrial Average index between the years 2010 and 2014 as totally five time series. The first three data sets are stock exchange data sets. The last data are Turkey Electricity Consumption (TEC) data observed monthly between the first month of 2002 and last month of 2013. TEC data set was taken from Turkey Energy Ministry.

Table 1 Names and features of time series and parameter values for the proposed method
Full size table

The parameters of the proposed method (p, cn and ntest) are used like in Table 1 for the analysis of all data sets. Firstly, BIST100 data set is analyzed by using ARIMA (Box and Jenkins 1976), ANFIS (Jang 1993) and modified ANFIS (MANFIS) proposed by Egrioglu et al. (2014), fuzzy time series method (SC) proposed by Song and Chissom (1993), AR-ANFIS proposed by Sarica et al. (2018), type 1 fuzzy function (T1FF) proposed by Turksen (2008) and the proposed method in this paper (IFTSF). The root of mean square error (RMSE) and mean absolute percentage error (MAPE) values for test sets of BIST100 are given in Tables 2 and 3, respectively.

Table 2 RMSE values for test sets for BIST100 data set
Full size table
Table 3 MAPE values for test sets for BIST100 data set
Full size table
$${\text{RMSE}} = \sqrt {\frac{1}{ntest}\mathop \sum \nolimits_{t = 1}^{ntest} (y_{t} - \hat{y}_{t} )^{2} }$$
(12)
$${\text{MAPE}} = \frac{1}{ntest}\mathop \sum \limits_{t = 1}^{ntest} \left| {\frac{{y_{t} - \hat{y}_{t} }}{{y_{t} }}} \right|$$
(13)

In Eqs. 12 and 13, \(y_{t}\) and \(\hat{y}_{t}\) are real observations and predicted values, respectively.

The proposed method produces the best forecasts for 50% of all results in BIST100 data set applications according to RMSE value. The similar results are obtained according to the MAPE criterion. Moreover, the proposed method produces the minimum mean of RMSE and MAPE values in Tables 2 and 3 when the proposed method is compared with other methods. When the length of the test set is 7, the success rate of the proposed method is 60%. For the length of the test set 15, the success rate of the proposed method is 40%. As a result of the analysis, IFTSF method can produce better forecasts for a small test set of BIST100 data set. The proposed method produces the competitive results for long test set lengths.

The analyzed results of the TAIEX data set are given in Table 4. In Table 4, it is seen that the proposed method has 83.33% succeeds of all results in TAIEX data set according to RMSE value. Besides this superior succeed performance, the proposed method is the best method for mean statistics of RMSE values among all other analytical methods for TAIEX data set.

Table 4 RMSE values for test sets for TAIEX data
Full size table

Dow Jones data set is analyzed by ANFIS with the grid partition method (ANFISgrid), ANFIS with subtractive clustering (ANFISsub), MANFIS, T1FF and IFTSF. The results of the analysis for Dow Jones data set are given in Tables 5 and 6. The success rate of the IFTSF is 80% according to RMSE criterion, and it is 60% for MAPE criterion. For mean statistics, the proposed method is the best one according to both RMSE and MAPE criteria.

Table 5 RMSE values for test sets of Dow Jones data set
Full size table
Table 6 MAPE values for test sets of Dow Jones data set
Full size table

In the final application, the analyze results of TEC data are given in Table 7. TEC data are analyzed by multilayer perceptron artificial neural network (MLP-ANN), seasonal autoregressive integrated moving average model (SARIMA; Box–Jenkins 1976), single multiplicative neuron model artificial neural network (SMNM-ANN) proposed by Yadav et al. (2007), linear and nonlinear neural network introduced by Yolcu et al. (2013) and TIFF and IFTSF methods.

Table 7 RMSE, MAPE values and forecasts for TEC data
Full size table

It is clearly seen that the proposed method has superior forecasting performance for both RMSE and MAPE criteria. Besides, the graph of real observations and forecasted values is given in Fig. 2.

Fig. 2
figure 2

Graph of real observations and proposed method forecasts for TEC data

Full size image

The best parameter sets in IFTSF method for all analyzed time series are given in Table 8. An important remark in Table 8 is that while the number of clusters is generally obtained as 7, there is no a certain value for the number of lags that means the best results obtained in the different numbers of lags for the BIST 100. Moreover, there are no certain parameter values in other time series.

Table 8 Conditions for the best results of IFTSF
Full size table

4 Conclusion

The main contribution of this paper can be stated that an intuitionistic fuzzy time series functions approach is proposed. The proposed method inspired by T1FF is an improved modification of T1FF with the use of hesitation margins and non-membership values. Non-memberships have different information to determine time series relations from membership values, unlike T1FF approach. The new inference system takes into consideration hesitation values, and it has an additional approach to uncertainty like type 2 fuzzy systems. Because of using second-order uncertainty, the system can define better relations between lagged variables of time series. In IFTSF, input matrix contains non-memberships and their transformations as well as lagged variables, memberships and transformations of memberships. Augmentation of the input matrix provides extra information to the inference mechanism.

The proposed method is compared with some well-known fuzzy inference, fuzzy time series methods, artificial neural networks and classical time series methods. According to analyzing results, it is clearly seen that IFTSF can produce better forecasting results than others for almost all of the time series. Moreover, it can be generally said that the proposed IFTSF has better forecasting performance for short-term or small test sets.

In future studies, the proposed method can be adapted to be working in a dual structure for memberships and non-memberships like other intuitionistic fuzzy inference systems. Input selection can be made by using artificial intelligence optimization techniques. Moreover, the fuzzy functions can be obtained by using artificial neural networks instead of the linear model.