A four-way decision-making approach using interval-valued fuzzy sets, rough set and granular computing: a new approach in data classification and decision-making

Abstract

In this paper, a novel method is presented to solve the problems of classification and decision-making by employing the interval-valued fuzzy set, rough set and granular computing (GrC) concepts. The proposed method can classify the objects available in a system, called an interval-valued fuzzy decision table into the four distinct regions as interval-valued fuzzy-positive region, interval-valued fuzzy-negative region, interval-valued completely fuzzy region and interval-valued gray fuzzy region. These four regions constitute a new space for decision-making, which is termed as a four-way interval-valued decision space (4WIVDS). Based on the classified objects, various decision rules are generated from the distinct regions of the 4WIVDS. The study shows that the interval-valued gray fuzzy region has included most prominent decision rules. For taking precise level of decisions based on this particular region, this study utilizes the GrC to extract granular level of decision rules which are prominent by nature. The proposed 4WIVDS method is verified and validated with various benchmark datasets. Experimental results include statistical and comparison analyses which signify the efficiency of the proposed method in classifying the objects and generating the decision rules.

Appendix

The 4WIVDS exhibits various properties, which are discussed as follows:

• (i) $RS_{B} \in X_N$

• (ii) $X_{N} \ne \emptyset$

• (iii) For $IVFPR^{+}$, it has the following conditions:

  $$\begin{aligned} X_P = {\left\{ \begin{array}{ll} \ne \emptyset; &{} \quad \text{ if } \text{ it } \text{ satisfies } \text{ Eq. } {8}. \\ =\emptyset; &{} \quad \text{ Otherwise. } \end{array}\right. } \end{aligned}$$

• (iv) $X_P \subseteq X_N$

• (v) $X_P \cup X_N \cup X_C \cup X_G = U$

• (vi) $RS_{B} \cap X_G = \emptyset$

• (vii) $X_P \cap X_C = \emptyset$

• (viii) $X_N \cap X_C = \emptyset$

• (ix) $RS_{B} \cap X_C = \emptyset$

• (x) $\overline{(X_P \cup X_N \cup X_G)}=X_C$

• (xi) If $RS_{B} \subseteq X_N$, then each ${d}_{i} \in RS_{B}$ and ${d}_{i} \in X_N$.

Theorem 2

For each of the non-empty sets $X_{P}$ , $X_{N}$ , and $X_{G},$ there exists a set $X_{C}$ if it holds

$$U-(X_{P}\cup X_{N} \cup X_G)=X_{C}.$$

Proof

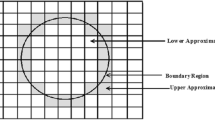
With reference to Fig. 1, it is considered that $X_{P} \ne \emptyset$, $X_{N} \ne \emptyset$, and $X_{G} \ne \emptyset$. Now, we define three different regions in the 4WIVDS as $\gamma_{1}$, $\gamma_{2}$, and $\gamma_{3}$, based on the following set-theoretic operations:

$$U-X_P=\gamma_{1}$$

(27)

$$\gamma_1-X_{N}=\gamma_{2}$$

(28)

$$\gamma _2-X_{G}=\gamma_{3}.$$

(29)

Here, $\gamma_{3}$ represents the $X_{C}$ in the 4WIVDS, where $\gamma _1 \cap \gamma _2 \cap \gamma _3=X_C.$$\square$