Introduction

Shear wave velocity (V S) as a dynamic soil mechanical property can be advantageously measured both in the field and laboratory under real and controlled conditions [16]. The crosshole and downhole testing, suspension logger probing, surface reflection and refraction surveys, and spectral analysis of surface waves, as well as seismic cone penetration test are the direct field measurement methods (e.g. [8, 21, 23, 36]), whereas resonant column tests, bender elements, ultrasonic, torsional shear tests, and modified triaxial tests are the laboratory methods.

The V S is commonly used for dynamic site response, site classification, liquefaction potential analysis, and estimate the in situ strength of granular soils (e.g., [1, 4, 10, 11, 44]).

In the absence of direct measurements, V S can be estimated based on correlations with common in situ tests, such as the cone, piezocone, and standard penetration tests (CPT, CPTu, and SPT). However, direct measurement of Vs is preferred over estimates.

The applicability of CPTu as a standard in situ test method for geotechnical investigation in providing valuable information on soil types and deriving correlations with engineering soil properties for the purposes of hazard analyses, site characterizations, and foundation designs has been approved (e.g. [3, 7, 24, 27, 36, 43]). Furthermore, the seismic CPTu (SCPTu) as an equipped CPTu by sensors can provide V S measurements [9, 24] and has become the most used in situ method for the geotechnical investigations for determining soil properties at small to large strain levels [26].

Therefore, Vs can be correlated with the penetration resistance in these tests, because penetration resistance is also influenced by density (γ), void ratio (e), and vertical effective stress (σ′ vo). Moreover, the established V S-based correlations with in situ and laboratory measurements (e.g., effective confining pressure, e) revealed that it can be utilized to augment designated testing [16]. However, relationships with cone resistance are useful for smaller low-risk projects, where Vs measurements are not always taken, but some variability should be expected due to age and cementation [29, 38].

In the current paper, three known accepted equations for clay and soft clay soils were developed and modified for available soft clays in the southwest of Sweden using a comprehensive provided CPTu database. It is well known that prediction of empirical correlations due to dependency on soil types and involving the various uncertainties, such as soil heterogeneity and genes origin, inherently, are not constant and will vary form case to case, and thus, it can never guarantee appropriate applicability for other different areas. Therefore, the previous proposed correlations maybe not applicable for southwest of Sweden and or high risk during the implementing should be considered. Hence, modification of well-accepted correlations definitely can cove and solve this problem. In the modification process, multivariable regression analysis (MVRA) has been employed. Detailed discussions on results were presented, and modified equations were tested and controlled using various statistical criteria as well as graph analyses. It is found that the best performance in modified models can be observed using the corrected cone tip resistance (q t) and pore pressure ratio (B q) which directly can be obtained from CPTu data.

Brief review of CPT-based V S correlations

V S is a function of γ, e, and σ′ vo which may also be influenced by the age of the deposit, cementation, and stress history [39]. When no direct measurements of V S are available, correlations can be developed between V S and several commonly measured geotechnical properties including CPTu cone tip resistance (q c), sleeve friction resistance (f s), corrected cone resistance (q t), and also SPT N-values.

In the recent years, several empirical relationships have been developed between q c, q t, and Vs (e.g. [5, 6, 12, 14, 15, 17, 23, 28, 30, 35, 38, 42]). However, most of these correlations were developed for either sands or clays and generally relatively young deposits [38].

Sykora and Stokoe [42] developed a relationship between q c and V S based on 256 data points from nine sites. The V S was measured using crosshole logging. Baldi et al. [6] proposed a relation between V S and q t and σ′ vo (MPa) for uncemented, unaged quartzitic sands based on laboratory resonant column tests (Eq. 1).

$$V_{\text{S}} = 227(q_{\text{t}} )^{0.13} \sigma_{\text{vo}}^{\prime \;0.27}$$
(1)

For Mexico City clays, Jamie and Romo [17] proposed Eq. 2.

$$V_{\text{s}} = 0.1q_{\text{c}}$$
(2)

Hegazy and Mayne [15] studied the relationship between V S and four independent parameters (q c, f s, σ′ vo, and e). The dataset included CPT measurements in clays, sands, intermediate soils, and mine tailings collected at 61 sites worldwide (Eqs. 3, 4). Later, Fear and Robertson [12] and Cai et al. [7] demonstrated that for a given uncemented soil of Holocene age (<10,000 years), the q c, q t or V S values in these relationships mostly depend on the e (or density index), σ′ vo, and compressibility.

$$V_{\text{S}} = \left[ {\left( {10.1\;Logq_{\text{t}} } \right) - 11.4} \right]^{1.67} \left[ {100\frac{{f_{\text{s}} }}{{q_{\text{t}} }}} \right]^{0.3}$$
(3)
$$V_{\text{S}} = 118.8\;Log\left( {f_{\text{s}} } \right) + 18.5$$
(4)

However, for a given measurement type, the function that expresses the influence of σ′ vo is relatively constant from one case to another, and the q c, q t or V S values used in the different empirical relationships should first be normalized for the same effective stress (100 kPa) to eliminate the effect of this variable and also the depth. This normalized value essentially represents the e or γ. Based on deep performed investigations which have been reflected in Robertson et al. [35] and Robertson [38], a set of normalized shear wave velocity (V S1) contours (Eqs. 5, 6) was developed on the normalized soil behavior type (SBT) Q tn–Fr chart. Furthermore, Robertson et al. [35], Fear and Robertson [12], Karry et al. [18], and Cai et al. [7] suggested Eqs. 7–10, respectively.

$$V_{\text{s1}} = V_{\text{s}} \times \left( {\frac{{P_{\text{a}} }}{{\sigma_{{{\text{v}}0}}^{\prime } }}} \right)^{0.25}$$
(5)
$$Q_{\text{tn}} = q_{\text{c}} \times \left( {\frac{{P_{\text{a}} }}{{\sigma_{{{\text{v}}0}}^{\prime } }}} \right)^{n}$$
(6)

Where; Q tn : normalized cone tip resistance for the overburden stress (MPa), P a : atmospheric pressure (100 kPa), q c : measured cone tip resistance in the CPT test (MPa), n: stress exponent that varies with the soil type and ranges from 0.5 in sandy soils to 1.0 in clay soils [34], σ′ vo: vertical effective stress (KPa), (P a/σ′ vo)n: correction for overburden stress with a maximum value of 2 and V S1: normalized V S for the vertical effective stress.

$$V_{\text{s1}} = 102\;Q_{\text{tn}}^{0.23}$$
(7)
$$V_{\text{s1}} = 135\;Q_{\text{tn}}^{0.23}$$
(8)
$$V_{\text{s1}} = 149Q_{\text{tn}}^{0.205}$$
(9)
$$V_{\text{s1}} = 38Q_{\text{tn}}^{0.61}$$
(10)

Mayne and Rix [30] using provided dataset by Mayne and Rix [31] from 31 sites worldwide (included both intact and fissured clays with a wide range of plasticity characteristics, sensitivities, and overconsolidation ratios from different clay and clayey sites in Europe and North America) proposed the relationship between V S and clayey soils (Eq. 11). However, due to insensitivity of q c to the factors such as bonding, fabric, degree of cementation, stress and strain level, stress history, stress path, timed dependent effects (aging and creep) and type of loading (monotonic or dynamic), correlations between q c and soil stiffness are unreliable [13, 40].

$$V_{\text{s}} = 1.75\;q_{\text{c}}^{0.627}$$
(11)

Furthermore, Mayne and Rix [30] argued that to reduce scatter, the correlation should be between q c and Vs, as these are both directly measured parameters. Therefore, Eq. 11 can be significantly improved for intact clays if e (can be determined by laboratory testing of intact samples) is known (Eq. 12).

$$V_{\text{s}} = 9.44\;q_{\text{c}}^{0.435} e^{ - 0.532}$$
(12)

Powell and Lunne [33] suggested that Eq. 12 is only slightly better than Eq. 11. Another important issue with both Mayne and Rix [30, 31] is using of the q c which obtained from a non-piezocone, rather than the corrected value (q t), and thus, no correction for pressures acting behind the cone tip was take into account [7]. Moreover, providing the e profile in the in situ test due to, particularly, the cost of high-quality undisturbed sampling is a difficult task. Therefore, Simonini and Cola [41] suggested that in correlations, the e can be replaced with CPTu pore pressure parameter (B q) as defined by Lunne et al. [24]. By taking into account of q t (KPa) and also incorporation of B q, Long and Donohue [23] proposed Eqs. 13–15 for Norwegian soft clays, and then, Cai et al. [7] proposed Eqs. 16–18 for soft clay soils in different sites in China.

$$V_{\text{s}} = 2.944\;q_{\text{t}}^{0.613}$$
(13)
$$V_{\text{s}} = 65\;q_{\text{t}}^{0.150} e^{ - 0.714}$$
(14)
$$V_{\text{s}} = 1.96\;q_{\text{t}}^{0.579} (1 + B_{\text{q}} )^{1.202}$$
(15)
$$V_{\text{s}} = 7.954\;q_{\text{t}}^{0.403}$$
(16)
$$V_{\text{s}} = 90\;q_{\text{t}}^{0.101} e^{ - 0.663}$$
(17)
$$V_{\text{s}} = 4.541\;q_{\text{t}}^{0.487} (1 + B_{\text{q}} )^{0.337}$$
(18)

Site description and data source

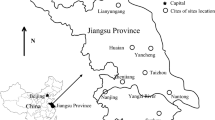
As presented in Fig. 1a and b, the studied region is located in the southwest of Sweden. In the current paper, two tested sites, namely, zone 5 and 7 (Fig. 1c), which are next to the Göta river valley (Fig. 1b) have been considered. All the presented area in Fig. 1b has been subjected to wide geotechnical investigations by Swedish Geotechnical Institute (SGI). This high-risk landslide area/region (e.g. [2, 3, 20, 32]) was likely formed through erosion of a weak zone within the gneissic bedrock. The post-glacial sediments in this area mainly consist of silt and clay deposits which may also be over consolidated [20]. In the selected area, a thick layer of glacial clay dominates the soil profile down to the bedrock. This layer is partly underlain by glaciofluvial deposits, till or different combinations of friction soils [19]. Due to the geological history of the valley, where much of the clay was deposited in a marine environment, there is a significant presence of so-called quick clay in the area. The quick clay exists as layers or planes in clay sediments with normal sensitivity, but in many places, the entire clay stratum is comprised of quick clay (e.g. [22]).

Fig. 1
figure 1

Location of the studied area and the focused subzones in this paper with respect to the distribution of landslide risk areas for Sweden [2]

Full size image

In this paper, a comprehensive database including 70 CPTu test points as well as some laboratory results have been collected and provided from the SGI website. The CPTu data have been used after performing the required processing. A sample of CPTu measurements and executed correction in the selected area accompanying the interpretation and description of soil profile is presented in Fig. 2.

Fig. 2
figure 2

Example of CPTu profile in the studied area to illustrate the soil type description and soil behavior type index

Full size image

New correlations for the southwest of Sweden

As presented in Fig. 3, the provided datasets of the studied sites are normalized in terms of Q tn and Fr (normalized friction ratio) and overlapped with proposed chart by Robertson [38]. The V S can be the outcome of this chart using CPTu data (Eq. 5).

Fig. 3
figure 3

Distribution of available data on provided Q tn–Fr-based developed chart by Robertson [38]

Full size image

Andrus et al. [5] showed that most Holocene-age deposits have V S1 values less than 250 m/s. In general, the Holocene-age data tend to plot in the center-left portion of the SBTn chart, whereas the Pleistocene-age data tend to plot in the center-right portion of the chart [38]. The available CPTu data in terms of V S–q t and V S1–Q tn, were plotted (Fig. 4a, b) in which each data point represents a single high-quality reading and calculating. According to obtained V S1, a purely statistical analysis for the provided database which mainly consists of soft clays was performed and another relationship observed (Fig. 4a, b). It is clear that the form of the established empirical V S–q t relationships varies from case to case. However, the form of obtained relation is similar to Eqs. 7–10 (Fig. 4a) and Eqs. 13 and 16 (Fig. 4b), but it can be valid for soils similar to those encountered in the southwest of Sweden. Those data which show more scatters can be related to relatively higher overconsolidation ratio (OCR) or sensitivity values (Fig. 4a and ellipse 1 in Fig. 5a–c).

Fig. 4
figure 4

Plots of obtained a V S1–Q tn relationships in compare with the previous literature and b V S–q t and V S–q c for the studied area

Full size image
Fig. 5
figure 5

Comparison of predicted Vs using the obtained modified versions with original used correlations in this study

Full size image

Although the problems associated with the determination of e due to requirement for undisturbed samples from the field (e.g., using ground freezing techniques) are well known, interpreting the e profiles from in situ testing provide an alternative approach. The CANLEX sites are unique interpreted e profiles that can be compared directly with the measured e values of frozen samples [7, 45]. For a given uncemented soil of Holocene age (<10,000 years), the q c, q t or V S values mostly depend on the e (or density index), effective stress, and compressibility [7, 12]. However, it is found that the stress–strain and strength behavior of cohesionless soils is too complicated to be represented by only the relative density of the soil [37].

In the provided database for studied area, no measurement for e was available. However, the water content and specific gravity of numerous tested samples were accessible. Therefore, an attempt has been made to determine the e values through the geotechnical formulation from in situ CPTu and laboratory tests data (e.g., [6, 38]).

In this study, the possibility of improvement and modification of previous proposed relations (Eqs. 12, 14 and 15) for studied area was taken into account. The provided comprehensive database for clay and clayey sites andapproximate similarity of investigated soft clays in Norway [23] to those available in the southwest of Sweden are the reason why these relations were selected. Moreover, the observed distance in data scattering regarding to the exact line (1:1 slope line) can be an indication for possible capacity of modification hypothesis (rectangle 2, Fig. 5a–c). The operation process for modifications has been executed through the multivariable regression analysis approach (MVRA), and the results were presented in Fig. 5a–c. In this process, the V S has been calculated for the studied area through Eqs. 12, 14, and 15, and then, the MVRA has been conducted between the measured and predicted V S values. The results of these modifications were presented in Eqs. 19, 20, and 21, respectively.

$$V_{\text{s}} = 5.198\;q_{\text{c}}^{0.475} e^{ - 0.459} \quad R^{2} = 0.83$$
(19)
$$V_{\text{s}} = 6.56\;q_{\text{t}}^{0.435} e^{ - 0.371} \quad R^{2} = 0.79$$
(20)
$$V_{\text{s}} = 3.839\;q_{\text{t}}^{0.5151} (1 + B_{\text{q}} )^{0.174} \quad R^{2} = 0.89$$
(21)

Discussion

The requirement of significant corrections of V S for soft clays is well known and perhaps of the order of 15 % [7, 23]. Equation 12 as the most commonly used correlation relies on q c rather than q t. Moreover, it also relies on the in situ e as an input parameter which is difficult to measure due to high susceptibility to sampling disturbance as well as not always readily available, especially at primary stage in the investigation. Therefore, Eq. 21 which involves B q and q t has been developed for soft clays that do not need laboratory data as input.

The modified relations (Eqs. 19, 20, and 21) showed that the observed distance of data scattering from 1:1 slope line in Fig. 5a–c has been decreased. This can be interpreted that the considered hypothesis for improvement and optimization was a reasonable assumption. Moreover, the predicted V S in modified versions (Eqs. 19, 20, and 21) with lesser scattering indicate better quality in prediction values than Eqs. 12, 14, and 15.

The separated data for investigated subzones (Fig. 1c) based on Eqs. 12, 14, and 15 accompanying their modified versions (Eqs. 19, 20, and 21) were presented in Fig. 6a–c. The observed scattering in subzone 7 (Fig. 6a–c) can be interpreted for high value of OCR and sensitivity in the studied tested points. This has a good adaptability with previous studies in the selected area [3, 25] which indicates the existence of highly sensitive quick clay as well as landslide scar in subzone 7. Moreover, part of the scatter may also be due to uncertainty with respect to age and cementation for these natural deposits.

Fig. 6
figure 6

Comparison of predicted Vs by separation of data scattering based on the studied subzones for both modified and original correlations

Full size image

Although the modified versions (Fig. 6) represented good results as shown in Fig. 5b, the predicted V S using Eq. 20 pointed lower estimate values for studied area with respect to two other modified relations. Moreover, the tested results showed that B q and q t are more reliable than e, q c, and q t.

The coefficient of determination (R 2) is a good indicator to check the performance of the proposed relationship, but not adequate. Hence, the validity and performance assessment of the modified equations (Eqs. 19, 20, and 21) were evaluated using variance account for (VAF), root mean square error (RMSE), residuals, and mean absolute percentage error (MAPE) statistical criteria (Table 1; Fig. 7). Moreover, the obtained correlations were tested for one of the test points and presented in Fig. 7, respectively. The higher values of VAF and R 2 as well as lower RMSE, residuals, and MAPE indicate better model performance in prediction capability. In VAF = 100 % and RMSE = 0, the model performs excellently.

Table 1 Investigation of model performance using statistical analyses for the studied area
Full size table
Fig. 7
figure 7

Comparison of calculated residuals of modified correlations for the studied area and test results for one of the test points

Full size image
$${\text{VAF}} = \left[ {1 - \frac{{{\text{var}} (y - y^{\prime } )}}{{{\text{var}} (y)}}} \right] \times 100$$
(22)
$${\text{RMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} (y - y^{\prime } )^{2} }$$
(23)
$${\text{MAPE}} = \frac{1}{n} \times \left[ {\mathop \sum \limits_{1 = 1}^{n} \left| {\frac{{y - y^{\prime } }}{y}} \right| \times 100} \right]$$
(24)

where y and y′ are the measured and predicted values, while n is number of samples, and var is the variance.

Conclusions

In the current paper, three modified equations to predict V S based on CPTu in situ test data for soft clays in the southwest of Sweden were introduced which can assist engineers in evaluating V S when no direct measurements are available.

The results of modified equations were tested using statistical criteria, and evidences for data scattering were discussed. Equation 21 means that V S can be predicted by only in-situ CPTu test parameters, while in Eqs. 19 and 20, e also should be determined using available formulation or sophisticated direct measurement. Therefore, based on the obtained results from graph analyses and statistical evaluation of model performance, the priority of Eq. 21 due to better reliability than Eqs. 19 and 20 as well as direct dependency to CPTu-related parameters was confirmed.

It can be concluded that application of B q instead of e leads to an improvement in the predictions of V S for the studied area. These modified relationships are applicable for engineering practical purposes in studied area or other regions with similar soil conditions. Using different investigation techniques is then useful, especially if reliable correlations exist between the results of the different types of investigation.