1 Introduction

Learning data embeddings in such a way that similar data points are placed close together while dissimilar data points are separated apart is fundamentally important in the field of machine learning and data mining. Better data embeddings can provide better performance for a wide variety of tasks such as clustering [46], classification [44], retrieval [43], verification [21], visualization [16], and explanatory data analysis [23]. Metric learning explores a way to construct such data embeddings by using label information such as class labels or pair (similar/dissimilar) constraints [4]. It assumes that the training and test data follow the same distributions. However, this assumption is often violated in real-world applications. For example, in face verification, images taken in different conditions follow different distributions [21]. In sentiment analysis, reviews in different product categories follow different distributions [15]. When the training and test distributions are different, standard metric learning cannot work well [29].

This problem can be alleviated by large labeled data, i.e., data with label information, drawn from the test distribution. However, such data are often time-consuming and impractical to collect because labels need to be manually assigned by domain experts. Transfer metric learning aims to find data embeddings that perform well on a testing domain, called a target domain, by using labeled and/or unlabeled data in different domains, called source domains [8, 12, 13, 21, 28, 29, 31, 37, 38]. To adapt to the target domain, this usually requires a small amount of labeled data and/or unlabeled data from the target domain for training. However, training after obtaining data in the target domain is problematic in some real-world applications. For example, with the growth of the Internet of Things (IoT), complex operations need to be performed on devices such as information visualization on mobile devices [7], face verification on mobile devices [22], and character recognition on portable devices [45]. Since these devices do not have sufficient computing resources, training on these devices is difficult even if new target domains appear that contain training data. In cyber-security, a wide variety of devices, such as sensors, cameras, and cars, needs to be protected from cyber attacks [2]. However, it is difficult to protect all these devices quickly with time-consuming training since many new devices (target domains) appear one after another.

Few existing methods can learn domain-invariant data embeddings from labeled data in multiple source domains [5, 11, 34]. When the domain-invariant data embeddings can explain any target domains, they can achieve good performance in the target domains without target specific training. However, this is generally difficult since the characteristics of the domains are different. To adapt to a wide variety of target domains, it is desirable to infer an appropriate domain-specific data embedding for each target domain.

In this paper, we propose a method to infer domain-specific data embeddings for target domains where there are no data in the training phase, called unseen domains, given unlabeled data in the domains in the testing phase and labeled and unlabeled data in the source domains in the training phase. Once training is executed, the proposed method can instantly infer a domain-specific data embedding for the unseen domain given unlabeled data in the domain on the basis of knowledge obtained from the source domains. With the proposed model, each embedding of a sample is represented as a latent variable, called a latent feature vector, and each domain is also represented as a latent variable, called a latent domain vector. The latent domain vectors play an important role in representing the properties of the domains. We assume that each sample is generated depending on its latent feature vector and latent domain vector by modeling the conditional distribution by a neural network. The proposed method models the domain-specific density of observed feature vectors depending the latent domain vector, which improves the flexibility of our model. With label information contained in the source domains, the latent feature vectors are constrained in such a way that similar data points are placed close and dissimilar ones are separated apart in the embedding space of each domain. Although unlabeled data do not have labels, they have geometric information that characterizes domains. The proposed method can incorporate this information in a natural way on the basis of a probabilistic framework. By using both labeled and unlabeled data in the source domains, the proposed method improves its ability to infer appropriate data embeddings for the unseen domains.

To infer both the latent feature vectors and latent domain vectors, the proposed method uses two neural networks. The first models the posterior of the latent feature vector given the observed feature vector and latent domain vector. Since the latent feature vectors depend on the latent domain vector, the proposed method can infer data embeddings considering the properties of the domains. The second models the posterior of the latent domain vector given the set of the observed feature vectors since the domain is usually characterized by the data distribution, which requires the set of observed feature vectors to be estimated. Traditional neural networks take vectors with a fixed size as inputs and cannot handle sets with different sizes. To overcome this problem, we employ the deep sets [49], which are permutation invariant to the order of data points in the sets and thus can take the sets with different sizes as inputs.

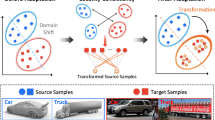
The neural networks for the conditional distributions of the observed feature vectors, the latent feature vectors, and the latent domain vectors are simultaneously optimized by maximizing the variational lower bound using stochastic gradient descent (SGD). Since the proposed method is based on a Bayesian framework, it can infer data embeddings by naturally considering the uncertainty of estimated latent domain vectors, which enables robust prediction. Figure 1 illustrates the proposed method.

In summary, the main contributions of this paper are as follows:

  • We propose a transfer metric learning method to infer domain-specific data embeddings for unseen domains by using both labeled and unlabeled training data in multiple source domains.

  • We develop an efficient training procedure for the proposed model by maximizing the variational lower bound using SGD and the reparameterization trick.

  • Through the experiments using three clustering tasks, we demonstrated that the proposed method can infer better data embeddings than existing metric learning methods.

Fig. 1
figure 1

Illustration of the proposed method. Same colors represent similar data points and different colors represent dissimilar data points, although data points with no color represent unlabeled data. Similar data points are close and dissimilar data points are separated in the latent embedding space. Each domain is represented by a latent domain vector, and data embeddings (latent feature vectors) are inferred by using the latent domain vectors. After training, our method can infer data embeddings for unseen domains given unlabeled data in the domains

Full size image

2 Related Work

Metric learning aims to obtain a proper metric from observed data to reveal the underlying data relationship [4]. Early techniques learn the Mahalanobis metric without explicitly learning data embeddings, where the metric can be factorized as a product of linear transformation of inputs [9, 46]. Many recent metric learning methods explicitly learn data embeddings in the process of learning the metric [4, 36, 44]. Metric learning usually assumes that the training and test distributions are the same. However, our task assumes that both distributions are different.

Transfer metric learning methods can learn appropriate data embeddings for the target domain by using data in the source domains [8, 12, 13, 21, 28, 29, 37, 38]. Existing methods usually assume that labeled and/or unlabeled data in the target domain are available in the training phase. A popular approach is to reduce the discrepancy between the source and target domains. To reduce the discrepancy, some methods use maximum mean discrepancy [19], which is an effective nonparametric criteria that computes two distributions in a reproducing kernel space (RKHS) [13, 21]. As another example, domain adversarial learning, which introduces a domain discriminator to measure the domain discrepancy, is also used [12, 37, 38]. Although these methods are effective when some data in the target domain are available for training, our task cannot use any data in the target domain during training.

Multi-task metric learning methods can improve the quality of data embeddings on several tasks simultaneously by using data from multiple tasks. Although these methods require data in all tasks in the training phase, our task is to adapt to unseen domains, where no data are given in the training phase [47].

Few methods for transfer metric learning or multi-task metric learning can be applied to unseen domains. Fang et al. [11] proposed a method to learn the unbiased distance metric that generalizes better to the unseen domains on the basis of a structural SVM. This method requires additional weak-label information (web images) to select an appropriate metric. Coupled projection multi-task metric learning (CP-mtML) and multi-task large margin nearest neighbor (mt-LMNN) introduced domain-invariant and domain-specific data embeddings (or metrics) [5, 34]. Although they have been proposed for multi-task metric learning, the domain-invariant part can be used for the unseen domains as described by Parameswaran and Weinberger [34]. One method specialized in person re-identification also learns domain-invariant data embeddings [39]. All these methods learn domain-invariant data embeddings that are effective when unseen domains can be explained only by the domain-invariant parts. However, it is generally difficult to explain all the unseen domains since the properties of each domain differ. The proposed method can infer domain-specific data embeddings for the unseen domains by using the sets of feature vectors in the domains given in the testing phase.

In transfer metric learning, it is typically assumed that there are at least some labeled data for every source domains [29]. Since unlabeled data have geometric information that characterizes domains, it is desirable to use information in domains where there are only unlabeled data for training. The proposed method can use these domains in a natural way on the basis of a probabilistic framework. The effectiveness of using these domains will be demonstrated in our experiments.

Domain generalization aims to generalize to unseen domains by using labeled data in multiple source domains [3, 14, 27, 32, 33]. Although the motivations for developing these methods and the proposed method are similar, existing methods for domain generalization do not focus on metric learning.

Meta-learning aims to learn new tasks efficiently and quickly by using knowledge obtained from previous tasks [41]. Some meta-learning methods perform task-specific adaptation without training like the proposed method although they are not methods for metric learning. For example, some methods can infer few-shot classifiers when a small amount of labeled data of new classes is given in the testing phase [35, 40, 42]. Although they use a distance metric to infer classifiers, they are not methods for metric learning. Kumagai and Iwata [26] proposed a method to infer classifiers for new tasks given the sets of the feature vectors in the tasks. These methods cannot use unlabeled data for training. Neural statistician performs few-shot density estimation for new tasks [10]. Neural statistician cannot use any label information for training. Unlike these methods, the proposed method can infer data embeddings for unseen domains (new tasks) on the basis of knowledge obtained from both labeled and unlabeled data in the source domains.

3 Proposed Method

In this section, we first define the task we investigated. Then, we propose our probabilistic model and explain how to learn it. After that, we explain how to infer appropriate data embeddings for unseen domains on the basis of the learned model.

3.1 Notations and Task

We introduce the notations used in this paper and define the task we investigate. Let \(\mathbf{X} _d := \{ \mathbf{x} _{dn} \}_{n=1}^{N_d}\) be a set of data points in the d-th domain, where \(\mathbf{x} _{dn} \in {\mathbb {R}}^{C} \) is the C-dimensional feature vector of the n-th data point, and \(N_d\) is the number of the data points in the d-th domain. The sets of similar and dissimilar data points in the d-th domain are represented as

$$\begin{aligned} \mathbf{S} _d&:= \{ (\mathbf{x} _{dn},\mathbf{x} _{dm}) | \mathbf{x} _{dn} \text { and } \mathbf{x} _{dm} \text { are similar} \}, \\ \mathbf{D} _d&:= \{ (\mathbf{x} _{dn},\mathbf{x} _{dm}) | \mathbf{x} _{dn} \text { and } \mathbf{x} _{dm} \text { are dissimilar} \}, \end{aligned}$$
(1)

respectively. The index set for the similar and dissimilar data points in the d-th domain is represented as

$$\begin{aligned} \mathbf{R} _d := \{ (n,m) | (\mathbf{x} _{dn},\mathbf{x} _{dm}) \in \mathbf{S} _d \text { or } (\mathbf{x} _{dn},\mathbf{x} _{dm}) \in \mathbf{D} _d \}. \end{aligned}$$
(2)

Although we treat the similar and dissimilar information as a running example, the proposed method can also treat class label information by regarding the data points in the same class as similar and the data points in the different classes as dissimilar. Note that the proposed method can be applied to the case in which the range of class labels is not the same in different domains owing to the similar and dissimilar representations. A label \(y_{dnm}=1\) is assigned to \((\mathbf{x} _{dn},\mathbf{x} _{dm}) \in \mathbf{S} _d \), or \(y_{dnm}=0\) is assigned to \((\mathbf{x} _{dn},\mathbf{x} _{dm}) \in \mathbf{D} _d \). The set of labels in the d-th domain is represented as \(\mathbf{Y} _d\). We assume that feature vector size C is the same in all domains.

Suppose we have feature vectors with label (similar and dissimilar) information in D source domains, \({{\mathcal {D}}} := \bigcup _{d=1}^{D} \{ (\mathbf{X} _d, \mathbf{Y} _d) \} \). Our goal is to find data embeddings in such a way that similar data points are placed close together and dissimilar data points are separated in the \(d_{*}\)-th domain where any \(d_{*} \notin \{ 1,2, \dots , D \}\), when the set of feature vectors \(\mathbf{X} _{d_{*}} := \{ \mathbf{x} _{d_{*}n} \}_{n=1}^{N_{d_{*}}}\) is given in the testing phase.

We note that our method can be used when each instance is represented by a vector. Therefore, for example, it can be applied for sequence data by transforming each sequence to a vector by neural network models such as LSTM [20].

3.2 Model

The proposed method assumes that each domain has a \(K_{\mathrm{z}}\)-dimensional latent continuous variable \(\mathbf{z} _{d} \in {\mathbb {R}}^{K_{\mathrm{z}}} \), which is called a latent domain vector in this paper. This latent domain vector \(\mathbf{z} _{d}\) is generated from a standard Gaussian distribution \({{\mathcal {N}}} (\mathbf{z} _{d} | \mathbf{0}, \mathbf{I} )\). In addition, the proposed method assumes that each data point in the d-th domain \(\mathbf{x} _{dn}\) has a \(K_{\mathrm{u}}\)-dimensional latent continuous vector \(\mathbf{u} _{dn} \in {\mathbb {R}}^{K_{\mathrm{u}}} \), called a latent feature vector, and this latent feature vector is also generated from a standard Gaussian distribution \({{\mathcal {N}}} (\mathbf{u} _{dn} | \mathbf{0}, \mathbf{I} )\). Since there are no prior knowledge of the data distribution, we used the standard Gaussian distribution as the prior for the latent feature and domain vectors, which is a standard choice in the probabilistic modeling, such as variational autoencoders [25]

Each feature vector in the d-the domain \(\mathbf{x} _{dn}\) is generated depending on its latent feature vector \(\mathbf{u} _{dn}\) and the latent domain vector \(\mathbf{z} _{d}\). The parameters of the conditional distribution \(p_{{{\theta }}} (\mathbf{x} _{dn}|\mathbf{u} _{dn},\mathbf{z} _{d})\) are modeled by neural networks with parameter \({{\theta }}\). When the feature vector is binary, we can use the following Bernoulli distribution,

$$\begin{aligned}&p_{{{\theta }}} (\mathbf{x} _{dn} |\mathbf{u} _{dn},\mathbf{z} _{d}) = \\&\quad \prod _{c=1}^{C} f_c(\mathbf{u} _{dn},\mathbf{z} _{d};{{\theta }})^{x_{dn,c}} (1-f_c(\mathbf{u} _{dn},\mathbf{z} _{d};{{\theta }}))^{1-x_{dn,c}}, \end{aligned}$$
(3)

where \(x_{dn,c}\) represents the c-th element of the feature vector \(\mathbf{x} _{dn}\), and \(f_c(\mathbf{u} _{dn},\mathbf{z} _{d};{{\theta }})\) denotes the c-th element of the neural network that outputs the probability of \(x_{dn,c}\) being one. Similarly, Gaussian, Gamma, and Poisson distributions with parameters modeled by neural networks can be used in the case of continuous values, non-negative continuous values, and non-negative integers, respectively. When \((n,m) \in \mathbf{R} _d\), the label \(y_{dnm}\) of the pair \(\mathbf{x} _{dn}\) and \(\mathbf{x} _{dm}\) is generated from the following Bernoulli distribution,

$$\begin{aligned} p( y_{dnm} | \mathbf{u} _{dn},\mathbf{u} _{dm})&= (\phi _{dnm})^{y_{dnm}} (1-\phi _{dnm})^{1-y_{dnm}}, \\ \phi _{dnm}&:= \frac{1}{1 + \Vert \mathbf{u} _{dn} - \mathbf{u} _{dm} \Vert ^2} , \end{aligned}$$
(4)

where \(\Vert \cdot \Vert \) denotes Euclidean norm, and \(\Vert \mathbf{u} _{dn} - \mathbf{u} _{dm} \Vert \) represents our metric for the two feature vectors \(\mathbf{x} _{dn}\) and \(\mathbf{x} _{dm}\) in the embedding space. Since \(\phi _{dnm}\) takes one when the distance \(\Vert \mathbf{u} _{dn} - \mathbf{u} _{dm} \Vert \) becomes zero, and \(\phi _{dnm}\) takes zero when \(\Vert \mathbf{u} _{dn} - \mathbf{u} _{dm} \Vert \) becomes infinity, maximizing this probability encourages that the similar data points (\(y_{dnm}=1\)) are placed close together and the dissimilar data points (\(y_{dnm}=0\)) are separated in the embedding space.

Fig. 2
figure 2

Graphical model representation of the generative model and inference model of the proposed method. Here, \(\mathbf{x} _{d\cdot }\), \(y_{d\cdot \cdot }\), \(\mathbf{u} _{d\cdot }\), and \(\mathbf{z} _{d}\) represent a feature vector, label, latent feature vector, and latent domain vector of d-th domain, respectively. Parameters for neural networks are represented by \(\theta \), \(\phi _{\mathrm{z}}\), and \(\phi _{\mathrm{u}}\). The shared and unshared nodes indicate observed and latent variables, respectively. Some pairs of data points in the d-th domain have similar (\(y_{dnm}=1\)) or dissimilar (\(y_{dnm}=0\)) information. The posterior of the domain vector \(\mathbf{z} _{d}\) is estimated from the set of feature vectors \(\mathbf{X} _d = \{ \mathbf{x} _{dn} \} _{n=1}^{N_d}\)

Full size image

For the d-th domain, the joint distribution of the set of feature vectors \(\mathbf{X} _d\), the set of labels \(\mathbf{Y} _d\), the set of latent feature vectors \(\mathbf{U} _d := \{ \mathbf{u} _{dn} \}_{n=1}^{N_d} \), and the latent domain vector \(\mathbf{z} _d\) is represented as

$$\begin{aligned} p_{{{\theta }}} (\mathbf{X} _d,\mathbf{Y} _d, \mathbf{U} _d,\mathbf{z} _d)&= \prod _{(n,m) \in \mathbf{R} _d} p( y_{dnm} | \mathbf{u} _{dn},\mathbf{u} _{dm}) \\&\quad \times \left( \prod _{n=1}^{N_d} p_{{{\theta }}} (\mathbf{x} _{dn}|\mathbf{u} _{dn},\mathbf{z} _{d})p(\mathbf{u} _{dn}) \right) p(\mathbf{z} _d). \end{aligned}$$
(5)

The log marginal likelihood of our model on the training data \({{\mathcal {D}}} \) is given by

$$\begin{aligned} {\ln } \ p({{\mathcal {D}}} ) = {\ln } \prod _{d=1}^{D } \iint p_{{{\theta }}} (\mathbf{X} _d,\mathbf{Y} _d,\mathbf{U} _d,\mathbf{z} _d) d \mathbf{U} _{d} d \mathbf{z} _{d}. \end{aligned}$$
(6)

Note that the proposed method can be applied to the case in which only unlabeled data are given in some source domains (i.e., \(\mathbf{R} _d = \emptyset \) for some d). In this case, the joint distribution for the corresponding domain is represented as follows:

$$\begin{aligned} p_{{{\theta }}} (\mathbf{X} _d,\mathbf{U} _d,\mathbf{z} _d) = \prod _{n=1}^{N_d} p_{{{\theta }}} (\mathbf{x} _{dn}|\mathbf{u} _{dn},\mathbf{z} _{d})p(\mathbf{u} _{dn}) \cdot p(\mathbf{z} _d). \end{aligned}$$
(7)

By using knowledge in these domains, the proposed method can improve the quality of data embeddings for unseen domains, which will be demonstrated in our experiments.

3.3 Learning

We develop the learning procedure for the proposed model. Since our model is represented by using neural networks, analytically obtaining the posterior of the latent domain vector and latent feature vectors is intractable. Therefore, we approximate this posterior distribution with a inference model \(q_{{\phi }}\), which is represented as

$$\begin{aligned} & q_{{\phi }} ( \mathbf{U} _d, \mathbf{z} _d | \mathbf{X} _d )= \prod _{n=1}^{N_d} q_{ \phi _{\mathrm{u}}} ( \mathbf{u} _{dn} | \mathbf{x} _{dn}, \mathbf{z} _d) \cdot q_{\phi _{\mathrm{z}}} ( \mathbf{z} _{d} | \mathbf{X} _{d}), \\ & q_{\phi _{\mathrm{z}}} ( \mathbf{z} _{d} | \mathbf{X} _{d})= {{\mathcal {N}}} (\mathbf{z} _d | \mu _{\phi _{\mathrm{z}}} (\mathbf{X} _d), \mathrm{diag} (\sigma _{\phi _{\mathrm{z}}}^2 (\mathbf{X} _d)) ), \\ & q_{ \phi _{\mathrm{u}}} ( \mathbf{u} _{dn} | \mathbf{x} _{dn}, \mathbf{z} _d) \\ &\quad = {{\mathcal {N}}} (\mathbf{u} _{dn} | \mu _{\phi _{\mathrm{u}}} (\mathbf{x} _{dn}, \mathbf{z} _d), \mathrm{diag} (\sigma _{\phi _{\mathrm{u}}}^2 (\mathbf{x} _{dn}, \mathbf{z} _d))), \end{aligned}$$
(8)

where mean \(\mu _{\phi _{\mathrm{z}}} (\mathbf{X} _d) \in {\mathbb {R}}^{K_{\mathrm{z}}} \) and variance \(\sigma _{\phi _{\mathrm{z}}}^2 (\mathbf{X} _d) \in {\mathbb {R}}^{K_{\mathrm{z}}}_{+} \) are modeled by neural networks with parameters \({\phi _{\mathrm{z}}}\). Similarly, mean \( \mu _{\phi _{\mathrm{u}}} (\mathbf{x} _{dn}, \mathbf{z} _d) \in {\mathbb {R}}^{K_{\mathrm{u}}} \) and variance \( \sigma _{\phi _{\mathrm{u}}}^2 (\mathbf{x} _{dn}, \mathbf{z} _d) \in {\mathbb {R}}^{K_{\mathrm{u}}}_{+} \) are modeled by neural networks with parameters \({\phi _{\mathrm{u}}}\). Here, we denote \(\phi := (\phi _{\mathrm{z}}, \phi _{\mathrm{u}})\). Since the latent feature vector \(\mathbf{u} _{dn}\) depends on the latent domain vector \(\mathbf{z} _d \), it can reflect the property of the domain. Since the latent domain vector \(\mathbf{z} _d \) depends only on the set of feature vectors \(\mathbf{X} _d\), the proposed method can infer the latent domain vectors of unseen domains when the sets of feature vectors in these domains are only given in the testing phase. As a result, the proposed method can instantly infer appropriate domain-specific data embeddings for the unseen domains without training.

Since the \(q_{\phi _{\mathrm{z}}}\) deals with the set of feature vectors \(\mathbf{X} _d\) as an input, the neural networks for the parameters \(\mu _{\phi _{\mathrm{z}}} (\mathbf{X} _d)\) and \({\ln } \ \sigma _{\phi _{\mathrm{z}}}^2 (\mathbf{X} _d)\)Footnote 1 must be permutation invariant to the order of data points in the set. For neural networks satisfying this condition, we use the following neural network architecture proposed by Zaheer et al. [49],

$$\begin{aligned} \tau (\mathbf{X} _d) = \rho \left( \sum _{n=1}^{N_d} \eta ( \mathbf{x} _{dn} ) \right) , \end{aligned}$$
(9)

where \(\tau (\mathbf{X} _d)\) represents one of the \(\mu _{\phi _{\mathrm{z}}} (\mathbf{X} _d)\) and \({\ln } \ \sigma _{\phi _{\mathrm{z}}}^2 (\mathbf{X} _d)\), \(\rho \) and \(\eta \) are any neural networks, respectively. This neural network is obviously permutation invariant due to summation. Although this architecture is simple, it can express any permutation invariant function and preserve all the properties of the sample set with suitable \(\rho \) and \(\eta \) [49]. Thus, we can capture the characteristics of each domain well with this architecture. Figure 2 shows a graphical model representation of the generative model and inference model of the proposed method, where the shared and unshared nodes indicate observed and latent variables, respectively.

We derive a lower bound on the log marginal likelihood \({\ln } \ p({{\mathcal {D}}} )\) using \(q_{\phi } (\mathbf{U} _d, \mathbf{z} _d | \mathbf{X} _d )\) as follows:

$$\begin{aligned}&\mathrm{ln} \ p({{\mathcal {D}}}) = \sum _{d=1}^{D} \mathrm{ln} \iint p_{{{\theta }}} (\mathbf{X} _d,\mathbf{Y} _d,\mathbf{U} _d,\mathbf{z} _d) d \mathbf{U} _{d} d \mathbf{z} _{d} \\&\quad = \sum _{d=1}^{D} \mathrm{ln} \!\iint \! \frac{q_{\phi } (\mathbf{U} _d, \mathbf{z} _d | \mathbf{X} _d ) p_{{{\theta }}} (\mathbf{X} _d,\mathbf{Y} _d,\mathbf{U} _d,\mathbf{z} _d)}{q_{\phi } (\mathbf{U} _d, \mathbf{z} _d | \mathbf{X} _d )} d \mathbf{U} _{d} d \mathbf{z} _{d} \\&\quad \geqq \sum _{d=1}^{D} \!\iint \! q_{\phi } (\mathbf{U} _d, \mathbf{z} _d | \mathbf{X} _d ) \mathrm{ln} \frac{p_{{{\theta }}} (\mathbf{X} _d,\mathbf{Y} _d,\mathbf{U} _d,\mathbf{z} _d)}{q_{\phi } (\mathbf{U} _d, \mathbf{z} _d | \mathbf{X} _d )} d \mathbf{U} _{d} d \mathbf{z} _{d} \\&\quad = \sum _{d=1}^{D} \Biggl [ {\mathbb {E}} _{q_{\phi } (\mathbf{U} _d, \mathbf{z} _{d} | \mathbf{X} _d)} \left[ \sum _{(n,m) \in \mathbf{R} _d} \mathrm{ln} \ p_{{\theta }} (y _{dnm}|\mathbf{u} _{dn}, \mathbf{u} _{dm} ) \right] \\&\qquad + {\mathbb {E}} _{q_{\phi } (\mathbf{U} _d, \mathbf{z} _{d} | \mathbf{X} _d)} \left[ \sum _{n=1}^{N_d} \mathrm{ln} \ p_{{\theta }} (\mathbf{x} _{dn}|\mathbf{u} _{dn}, \mathbf{z} _{d} ) \right] \end{aligned}$$
(10)
$$\begin{aligned}&\qquad - {\mathbb {E}} _{q_{\phi _{\mathrm{z}}} (\mathbf{z} _{d} | \mathbf{X} _d)} \left[ \sum _{n=1}^{N_d} D_{KL} ( q_{\phi _{\mathrm{u}}} (\mathbf{u} _{dn} | \mathbf{x} _{dn}, \mathbf{z} _d) \Vert p(\mathbf{u} _{dn})) \right] \\&\qquad - D_{KL} ( q_{\phi _{\mathrm{z}}} (\mathbf{z} _{d} | \mathbf{X} _d) \Vert p(\mathbf{z} _{d})) \Biggr ] =: {{\mathcal {L}}} ({{\mathcal {D}}} ; {{\theta }}, {{\phi }}), \end{aligned}$$
(11)

where we used Jensen’s inequality [6] to derive the third line and \(D_{KL} ( \cdot \Vert \cdot )\) denotes the Kullback Leibler (KL) divergence. The parameters of the neural networks for the conditional distributions of the feature vectors, the latent feature vectors, and the latent domain vectors, \({\theta }\), \({\phi _{\mathrm{u}}} \), and \({\phi _{\mathrm{z}}}\), are obtained by maximizing this lower bound \( {{\mathcal {L}}} ({{\mathcal {D}}} ; {{\theta }}, {{\phi }})\) using SGD. Although the expectation terms of (10) are still intractable, these terms can be effectively approximated by the reparameterization trick [25]; we draw \(L_{\mathrm{z}}\) samples \(\mathbf{z} _{d}^{(\ell )}\) from \(q_{\phi _{\mathrm{z}}} (\mathbf{z} _{d} | \mathbf{X} _d)\) by

$$\begin{aligned} \mathbf{z} _{d}^{(\ell )} = \mu _{\phi _{\mathrm{z}}} (\mathbf{X} _d) + \epsilon _d^{(\ell )} \odot \sigma _{\phi _{\mathrm{z}}} (\mathbf{X} _d), \end{aligned}$$
(12)

where \(\epsilon _d^{(\ell )} \sim {{\mathcal {N}}} ( \mathbf{0} , \mathbf{I})\) and \(\odot \) is an element-wise product, and we can form Monte Carlo estimates of expectations of some function f with respect to \(q_{\phi _{\mathrm{z}}} (\mathbf{z} _{d} | \mathbf{X} _d)\) as follows:

$$\begin{aligned} {\mathbb {E}} _{q_{\phi _{\mathrm{z}}} (\mathbf{z} _{d} | \mathbf{X} _d)} [ f(\mathbf{z} _d) ] \approx \frac{1}{L_{\mathrm{z}}} \sum _{\ell =1}^{L_{\mathrm{z}}} f(\mathbf{z} _d^{(\ell )}). \end{aligned}$$
(13)

Similarly, we draw \(L_{\mathrm{u}}\) samples \(\mathbf{u} _{dn}^{(\ell ',\ell )}\) from \(q_{\phi _{\mathrm{u}}} (\mathbf{u} _{dn} | \mathbf{x} _{dn}, \mathbf{z} _d^{(\ell )} ) \) by

$$\begin{aligned} \mathbf{u} _{dn}^{(\ell ',\ell )} = \mu _{\phi _{\mathrm{u}}} (\mathbf{x}_{dn}, \mathbf{z} _d^{(\ell )}) + \epsilon _{dn}^{(\ell ')} \odot \sigma _{\phi _{\mathrm{u}}} (\mathbf{x}_{dn}, \mathbf{z} _d^{(\ell )}), \end{aligned}$$
(14)

where \(\epsilon _{dn}^{(\ell ')} \sim {{\mathcal {N}}} ( \mathbf{0} , \mathbf{I})\), and we have

$$\begin{aligned} {\mathbb {E}} _{q_{\phi } (\mathbf{U} _d, \mathbf{z} _{d} | \mathbf{X} _d)} [ f(\mathbf{u} _{dn}, \mathbf{z} _d) ] \approx \frac{1}{L_{\mathrm{z}} L_{\mathrm{u}}} \sum _{\ell ,\ell '=1}^{L_{\mathrm{z}},L_{\mathrm{u}}} f\left( \mathbf{u} _{dn}^{(\ell ',\ell )}, \mathbf{z} _d^{(\ell )}\right) . \end{aligned}$$
(15)

As a result, the objective function to be maximized with respect to the parameters \({{\theta }}\) and \({{\phi }}\) becomes

$$\begin{aligned}&{{\mathcal {L}}} ({{\mathcal {D}}} ; {{\theta }}, {{\phi }} ) \approx \sum _{d=1}^{D} \Biggl [ - D_{KL} ( q_{\phi _{\mathrm{z}}} (\mathbf{z} _{d} | \mathbf{X} _d) \Vert p(\mathbf{z} _{d})) \\&\quad - \frac{1}{L_{\mathrm{z}}} \sum _{\ell =1}^{L_{\mathrm{z}}} \sum _{n=1}^{N_d} D_{KL} \left( q_{\phi _{\mathrm{u}}} \left( \mathbf{u} _{dn} | \mathbf{x} _{dn}, \mathbf{z} _d^{(\ell )}\right) \Vert p(\mathbf{u} _{dn})\right) \\&\quad + \frac{1}{L_{\mathrm{z}} L_{\mathrm{u}}} \sum _{\ell =1}^{L_{\mathrm{z}}} \sum _{\ell '=1}^{L_{\mathrm{u}}} \sum _{n=1}^{N_d} \mathrm{ln} \ p_{{\theta }} \left( \mathbf{x} _{dn}|\mathbf{u} _{dn}^{(\ell ',\ell )}, \mathbf{z} _{d}^{(\ell )} \right) \\&\quad + \left. \frac{1}{L_{\mathrm{z}} L_{\mathrm{u}}^2} \sum _{\ell =1}^{L _{\mathrm{z}}} \sum _{\ell ',\ell ''=1}^{L_{\mathrm{u}}} \sum _{(n,m) \in \mathbf{R} _d} \mathrm{ln} \ p_{{\theta }} \left( y _{dnm}|\mathbf{u} _{dn}^{(\ell ',\ell )}, \mathbf{u} _{dm}^{(\ell '',\ell )} \right) \right] . \end{aligned}$$
(16)

3.4 Inference

Given the set of feature vectors from the unseen domain \(\mathbf{X} _{d_{*}} = \{ \mathbf{x} _{d_{*} n} \} _{n=1}^{N_{d _{*}}}\), the proposed method infers the distribution of the latent feature vector (embedded data point) given the feature vector \(\mathbf{x} _{d _{*} n} \) as follows:

$$\begin{aligned} q(\mathbf{u} _{d_{*}n} | \mathbf{x} _{d_{*}n})&= \int q_{\phi _{\mathrm{u}}} (\mathbf{u} _{d_{*}n}|\mathbf{x} _{d_{*}n}, \mathbf{z} _{d_{*}} ) q_{\phi _{\mathrm{z}}} (\mathbf{z} _{d_{*}} | \mathbf{X} _{d_{*}}) d\mathbf{z} _{d_{*}} \\&\approx \frac{1}{L_{\mathrm{z}}} \sum _{\ell =1}^{L_{\mathrm{z}}} q_{\phi _{\mathrm{u}}} (\mathbf{u} _{d_{*}n}|\mathbf{x} _{d_{*}n}, \mathbf{z} _{d_{*}}^{(\ell )} ), \end{aligned}$$
(17)

where \(\mathbf{z} _{d_{*}}^{(\ell )} \) = \(\mu _{\phi _{\mathrm{z}}} (\mathbf{X} _{d_{*}}) \) + \(\epsilon ^{(\ell )} \odot \sigma _{\phi _{\mathrm{z}}} (\mathbf{X} _{d_{*}}) \) and \(\epsilon ^{(\ell )} \) is a sample drawn from \({{\mathcal {N}}} ( \mathbf{0} , \mathbf{I})\). The proposed method can infer the data embeddings while considering the uncertainty of the latent domain vectors by sampling \(\mathbf{z} _{d _{*}}\) from the posterior distribution \(q_{\phi _{\mathrm{z}}} (\mathbf{z} _{d _{*}} | \mathbf{X} _{d _{*}}) \), which enables robust prediction. In our experiments, we used the mean of (16), i.e., \(\frac{1}{L_{\mathrm{z}}} \sum _{\ell =1}^{L_{\mathrm{z}}} \mu _{\phi _{\mathrm{u}}} (\mathbf{x} _{d_{*}n}, \mathbf{z} _{d_{*}}^{(\ell )})\), as the embedded data of \(\mathbf{x} _{d_{*}n}\).

4 Experiments

We evaluated the quality of data embeddings inferred by the proposed method with the clustering tasks. To cluster the embedded data, we used a K-means [1], which is a commonly used fast clustering algorithm, for all comparison methods and datasets. The number of clusters is fixed to the number of classes of each unseen domain. We created similar and dissimilar pairs from class labels for all datasets. This evaluation procedure is commonly used in metric learning studies [9, 46, 48]. We used the following computers: CPU was Intel Xeon E5-2660v3 2.6 GHz, the memory size was 128 GB, and GPU was NVIDIA Tesla k80.

4.1 Data

We used three real-world datasets: MNIST-r,Footnote 2 Office-Caltech10,Footnote 3 and Amazon-Review.Footnote 4

MNIST-r is commonly used in domain generalization studies [14, 32]. This dataset, which was derived from the handwritten digit dataset MNIST, was introduced by Ghifary et al. [14]. Each domain is created by rotating the images in multiples of 15 degrees: 0, 15, 30, 45, 60, and 75. Thus, this dataset has six different domains. Each domain has 1,000 images, which are represented by 256-dimensional vectors, of 10 classes (digits).

Office-Caltech10 is a widely used real-world dataset for cross-domain object recognition [18]. This dataset consists of object images taken from four domains: Amazon, DSLR, Webcam, and Caltech. Each domain has images represented by SURF features encoded with 800-bin bag-of-words histograms, of 10 object classes. We binarized each feature on the basis of whether the value was more than zero.

Amazon-Review is a widely used real-world dataset for cross-domain sentiment analysis [17]. This dataset consists of product reviews in four domains: kitchen appliances, DVDs, books, and electronics. We used the processed data from Gong et al. [17], in which the dimensionality of the bag-of-words features was reduced to the top 400 words that have the largest mutual information with the labels. Each domain has 1,000 positive and 1,000 negative reviews (two classes). We binarized each feature on the basis of whether the value was more than zero.

4.2 Setting

To evaluate the clustering results, we used the adjusted Rand index (ARI), which is a widely used evaluation measure for clustering tasks. ARI quantifies the similarity between inferred clusters and true clusters, takes the value from \(-1\) to 1, and gives zero for random clustering.

For all datasets, we evaluated ARI on one unseen domain while training on the rest by changing the unseen domain. We considered two types of source domains for all datasets. The first is a source domain where all pairs of data points have label (similar and dissimilar) information, which is a widely used experimental setting in metric learning studies [8, 12, 21, 34]. We call these source domains labeled source domains. The second is a source domain where no data points have label information, i.e., all data points are unlabeled. We call these source domains unlabeled source domains. We included unlabeled source domains to demonstrate that they are useful to learn data embeddings even if they do not have any labels.

For each trial in MNIST-r and Office-Caltech10, we randomly chose five classes in each domain to create a situation in which each domain had different class labels. After that, in each domain used for training, we randomly selected 80% of samples for training and 20% of samples for validation. For each trial in Amazon-Review, we used all classes (two classes) in each domain. In each domain used for training, we chose 1,500 samples for training and 400 samples for validation. We conducted experiments on 10 randomized trials for each unseen domain fixing the ratio of the number of labeled source domains to unlabeled source domains. For each trial, we randomly chose labeled and unlabeled source domains from all the source domains. We reported the mean ARI over unseen domains for all datasets.

4.3 Comparison Methods

We evaluated the following two variants of the proposed method: SS-Proposed and S-Proposed. SS-Proposed uses both labeled and unlabeled source domains for training. S-Proposed uses only the labeled source domains for training. We included S-Proposed in our experiments to evaluate the efficacy of using the unlabeled source domains for training.

We compared the proposed method variants with three transfer metric learning methods and two baseline methods: supervised invariant (S-Invariant), semi-supervised-invariant (SS-Invariant), coupled projection multi-task metric learning (CP-mtML) [5], Direct, and VAE-Direct.

(a) S-Invariant This method infers data embeddings by using all labeled data in the labeled source domains ignoring identification of domains. The probabilistic model for S-Invariant is obtained from the proposed model on the labeled source domains by ignoring the domain index d and latent domain vector \(\mathbf{z}\). Specifically, S-Invariant uses the following probabilistic model, \(\prod _{n<m} p(y_{nm}|\mathbf{u} _{n}, \mathbf{u} _m) \prod _{n=1}^{N} p(\mathbf{x} _n| \mathbf{u} _n) p(\mathbf{u} _n)\), where N is the total number of data points in the labeled source domains. The posterior of the latent feature vector \(\mathbf{u}\) given the feature vector \(\mathbf{x}\) is modeled by a neural network \(q(\mathbf{u}|\mathbf{x})\), and learning is performed by maximizing the variational lower bound like the proposed method. S-Invariant can be regarded as a metric learning variant of the recently proposed domain generalization method (contrastive semantic alignment; CCSA) [32] since CCSA brings data points with the same labels closer and separates data points with different labels in the hidden space.

(b) SS-Invariant This method is a semi-supervised extension of S-Invariant. That is, SS-Invariant infers data embeddings by using all data in both labeled and unlabeled source domains ignoring identification of domains. The probabilistic model for SS-Invariant is obtained from the proposed model on the labeled and unlabeled source domains by ignoring the domain index and latent domain vector. We included S-Invariant and SS-Invariant as comparison methods to demonstrate the effectiveness of considering domain-specific data embeddings since both methods infer domain-invariant data embeddings.

(c) CP-mtML This method is a recently proposed multi-task metric learning method, which defines both task-invariant and task-specific projections. CP-mtML cannot use unlabeled data for training. Following the previous study [34], we used the task-invariant projection for data embeddings of the unseen domains.

(d) Direct This method performs K-means clustering directly against testing data in the unseen domain.

(e) VAE-Direct This method first learns data embeddings of testing data in the unseen domain by using a variational auto-encoder (VAE) [25] and then performs K-means clustering against the embedded data.

Direct and VAE-Direct are baseline methods that do not use any data in the source domains for training.

For S-Invariant, SS-Invariant, and VAE-Direct, we used neural networks with one dense hidden layer and ReLU activations for the encoder \(q(\mathbf{u} _n | \mathbf{x} _n)\) and decoder \(p(\mathbf{x} _n|\mathbf{u} _n)\), respectively. We set the sizes of hidden nodes for both the encoder and decoder as 1,000, 800, and 200 for MNIST-r, Office-Caltech10, and Amazon-Review, respectively. For all datasets, we used Bernoulli distributions for the decoders. For the proposed method variants, same neural networks are used as base models. To infer the mean and variance parameters of latent domain vectors, the shared single-layer neural networks with ReLU activations are used as \(\eta \) in Eq. (9), and different two single-layer neural networks are used for mean and variance outputs as \(\rho \) in Eq. (9). The same two-head architecture is used for the neural network for latent feature vectors. We set the sizes of output nodes of \(\eta \) as 1,000, 800, and 200 for MNIST-r, Office-Caltech10, and Amazon-Review, respectively. In our experiments, we took an average of \(\eta ( \mathbf{x} _{dn} )\) before applying \(\rho \) to reduce the effect of differences in the data size. That is, we used \(\tau (\mathbf{X} _d) = \rho \left( \frac{1}{N_d} \sum _{n=1}^{N_d} \eta ( \mathbf{x} _{dn} ) \right) \) as neural networks for inferring the latent domain vectors, \(\mu _{\phi _{\mathrm{z}}} (\mathbf{X} _d)\) and \({\ln } \ \sigma _{\phi _{\mathrm{z}}}^2 (\mathbf{X} _d)\). Note that this architecture is included in the definition of permutation invariant architectures [49]. The estimated latent domain vector is concatenated with the hidden layers of both the decoder and encoder. For all comparison methods except for CP-mtML and Direct, we used the mean of the encoder \(q(\mathbf{u} |\mathbf{x} )\) as the embedded data of \(\mathbf{x}\). For CP-mtML, we used a neural network with one dense hidden layer and ReLU activations for projections. We set the sizes of hidden nodes as 1,000, 800, and 200 for MNIST-r, Office-Caltech10, and Amazon-Review, respectively. The hidden layer is shared for both task-invariant and task-specific projections. Although linear projections on the original feature space are considered in the original paper, we considered these non-linear projections for fair comparisons, which improved performance.

Table 1 Average and standard deviation of ARI over all unseen domains with \(D_{\mathrm{L}}\) labeled source domains and \(D_{\mathrm{U}}\) unlabeled source domains
Full size table

4.4 Hyper-Parameters

For all methods except for Direct and VAE-Direct, we selected hyper-parameters by using validation mean ARI on the labeled source domains. We selected hyper-parameters for VAE-Direct on the basis of validation loss on the unseen domains since it does not use any label information. We randomly divided testing data into training data (70%) and validation data (30%) to train the VAE. For all methods except for Direct, the dimension of embedded data \(K_{\mathrm{u}}\) (the output size of the encoder) was chosen from \(\{10,20,30\}\). For CP-mtML, the bias term b was selected from \(\{1,2,3\}\). For the proposed method, the dimension of the latent domain vector \(K_{\mathrm{z}}\) was fixed as ten for all datasets, and the sample size of the reparameterization trick \(L_{\mathrm{z}}\) and \(L_{\mathrm{u}}\) was set to one for training and ten for testing. Similarly, for S-Invariant, SS-Invariant, and VAE-Direct, the sample size of the reparameterization trick was set to one for training and ten for testing. For all methods, we used the Adam optimizer [24] with a learning rate of 0.001. The maximum number of epochs was 300 for MNIST-r and Office-Caltech10 and 200 for Amazon-Review, and we used early-stopping based on the validation data to avoid the over-fitting.

4.5 Results

We quantitatively evaluated the clustering results on the unseen domains. Table 1 shows the average and standard deviations of the ARIs over all unseen domains when varying the ratio of \(D_{\mathrm{L}}\) labeled source domains to \(D_{\mathrm{U}}\) unlabeled source domains for all datasets. SS-Proposed showed the best or comparable ARIs in all cases. Both Direct and VAE-Direct tended to perform worse than the others when the number of labeled source domains \(D_{\mathrm{L}}\) were relatively large, which indicates the efficacy of using knowledge (labeled data) in related domains. As for methods that use only labeled source domains for training, S-Proposed performed better than S-Invariant and CP-mtML, which infer domain-invariant data embeddings, in almost all cases (8 out of 9). Similarly, as for methods that use both labeled and unlabeled source domains for training, SS-Proposed performed better than SS-Invariant in almost all cases (7 out of 9). These results indicate that modeling the characteristics of each domain is quite effective to obtain good data embeddings. In addition, SS-Proposed outperformed S-Proposed with MNIST-r and Office-Caltech10, which indicates that unlabeled data are useful to learn domain-specific data embeddings even if they do not have any labels. For Amazon-Review, there was no big difference between SS-Proposed and S-Proposed. This dataset has bag-of-words text features that are less correlated than image features like MNIST-r and Office-Caltech10. This property may possibly make it difficult to extract useful geometrical information from unlabeled source domains. Overall, we found that the proposed method variants (SS-Proposed and S-Proposed) could better obtain data embeddings than other methods.

Fig. 3
figure 3

Visualization of the embedded data for the unseen domain (0-degree domain) on MNIST-r. Each column represents SS-Proposed, S-Proposed, S-Invariant, SS-Invariant, and VAE-Direct, respectively, from left to right

Full size image

We visualized the embedded data for the unseen domain on MNIST-r to qualitatively evaluate the proposed method. Figure 3 shows the embedded data for the unseen domain (0-degree domain) obtained by SS-Proposed, S-Proposed, S-Invariant, SS-Invariant, and VAE-Direct. Note that inferring data embeddings for the 0-degree domain is challenging because the 0-degree is the endmost domain in all domains (0, 15, 30, 45, 60, 75-degree domains) and extrapolation is necessary. Here, we set the dimensions of the embedded data \(K_{\mathrm{u}}\) and the latent domain vectors \(K_{\mathrm{z}} \) to ten. We used t-distributed stochastic neighbor embedding (t-SNE) [30] to reduce the dimensionality of the embedded data to two. When \(D_{\mathrm{L}} : D_{\mathrm{U}} = 2:3\), S-Proposed and S-Invariant could not infer discriminative data embeddings because the number of labeled data was small and the extrapolation was difficult. Similarly, for VAE-Direct, similar data points in green were separated apart since they did not use any training data in the source domains. In contrast, SS-proposed and SS-Invariant were able to infer data embeddings in which similar data points are close to each other since both methods were able to extract useful information for data embeddings from unlabeled data. As the number of labeled source domains increased, SS-Proposed and S-Proposed came to infer good data embeddings in such a way that similar data points are close and dissimilar data points are separated although some dissimilar data points overlapped in both S-Invariant and SS-Invariant. Since the proposed method variants (SS-Proposed and S-Proposed) explicitly model the property of each domain, they can infer appropriate data embeddings for the unseen domains by using labeled data in the related domains.

Fig. 4
figure 4

Average ARI over all unseen domains and the ratio of \(D_L\) to \(D_U\) of each dataset when the value of \(K_{\mathrm{z}}\) was changed

Full size image
Table 2 Average and standard deviation of ARI over all target domains with \(D_{\mathrm{L}}\) labeled source domains and \(D_{\mathrm{U}}\) unlabeled source domains
Full size table

We investigated how the performance of the proposed method changed as the number of the dimensions of the latent domain vectors \(K_{\mathrm{z}}\) changed. Figure 4 shows the average of the ARIs over all unseen domains and the ratio of the number of labeled source domains \(D _L\) to the number of unlabeled source domains \(D_U\) of each dataset when changing the value of \(K_{\mathrm{z}}\) within \(\{ 2, 5, 10, 20 \}\). All methods except for SS-Proposed and S-Proposed had constant average ARIs when the value of \(K_{\mathrm{z}}\) was varied because they do not depend on the value of \(K_{\mathrm{z}}\). We found that SS-Proposed constantly outperformed the others for all datasets when the value of \(K_{\mathrm{z}}\) was changed. As for methods that use only labeled source domains for training, S-Proposed constantly performed better than S-Invariant and CP-mtML for all the values of \(K_{\mathrm{z}}\). These results indicate that the proposed method variants (SS-Proposed and S-Proposed) are robust to the number of dimensions of the latent domain vector \(K_{\mathrm{z}}\).

Although we have focused on inferring data embeddings for unseen domains, from which no data are given in the training phase, unlabeled data in the target domain are sometimes available for training. Therefore, it is also meaningful to investigate the quality of data embeddings when the proposed method uses target unlabeled data for training. Table 2 shows the average and standard deviations of the ARIs over all target domains when varying the ratio of \(D_{\mathrm{L}}\) to \(D_{\mathrm{U}}\) for all datasets. Here, TSS-Proposed and TSS-Invariant are obtained from SS-Proposed and SS-Invariant by also using target testing (unlabeled) data for training, respectively. As expected, TSS-Proposed and TSS-Invariant performed better than SS-Proposed and SS-Invariant on MNIST-r and Office-Caltech10, respectively. For Amazon-Review, TSS-Proposed and TSS-Invariant showed almost the same results as SS-Proposed and SS-Invariant, respectively. This result, i.e., difficulty of using unlabeled data, was consistent with the previous one in Table 1. TSS-Proposed performed better than TSS-Invariant, which indicates the effectiveness of using target unlabeled data for training in our framework.

We investigated the training time of 100 epochs for SS-Proposed, TSS-Proposed, and VAE-Direct on MNIST-r. In this experiment, we set the hyperparameters as follows: \(K_z=10\), \(K_u=10\), and \(L_{\mathrm{z}}\) and \(L_{\mathrm{u}}\) were one for training. Table 3 shows the computation time when \(D_{\mathrm{L}} : D_{\mathrm{U}} = 4:1\). Since TSS-Proposed uses target unlabeled data to learn the target-specific data embeddings, TSS-Proposed took more training time than SS-Proposed. VAE-Direct was able to train the domain-specific data embeddings faster than SS-Proposed and TSS-Proposed although its quality was not good. SS-Proposed can infer the domain-specific data embeddings of any domains given the set of unlabeled data in the domains without re-training. In this experiment, SS-Proposed inferred it with 0.012 seconds when \(L_{\mathrm{z}} = 10\). This was 103 times faster than the training time of VAE-Direct.

Table 3 Computation time (s) on MNIST-r
Full size table

5 Conclusion

In this paper, we proposed a transfer metric learning method to infer appropriate domain-specific data embeddings for unseen domains by using labeled and unlabeled data obtained from multiple source domains. To infer domain-specific data embeddings, the proposed method models each domain as the latent domain vector, which is estimated from the set of feature vectors in the corresponding domain. In experiments using three real-world datasets, the proposed method performed better than existing metric learning methods. In addition, the proposed method showed the effectiveness of using domains, where there are no labeled data.

Several avenues can be pursed as future work. First, we will try to apply the proposed method to other real-world applications such as retrieval and verification. In addition, although we considered class labels and pair (similar and dissimilar) constraints as label information in this paper, we will extend the proposed method to use other label information such as triplet constraints. Finally, we plan to apply our framework to structured data such as graphs and time series.