1 Introduction

Discontinuous deformations are a special type of mining deformations, which roads are very sensitive to [1,2,3,4,5]. Discontinuous deformations deteriorate evenness of the pavement posing a threat to the traffic and lead to loosening the layers of the pavement structure and the subsoil [6, 7].

Loosening of layers and subsoil leads to a reduction in their stiffness expressed by a modulus of elasticity, which results in a decrease in the fatigue life of the pavement, which determines the length of the period between repair works. The available literature often describes changes in the topography of the terrain (road lane) and related damage to the pavement in relation to the location of the operational plots [8,9,10].

However, experiments presenting an assessment of changes in pavement and ground stiffness based on field tests are rarely described [11]. Knowledge of the scale of changes occurring in the pavement and its subsoil due to the formation of discontinuous deformations caused by mining allows for more effective design of reinforcement where the possibility of discontinuous deformations is forecasted.

The article presents the case of a motorway section in which linear discontinuous surface deformations (LDSD) remarkably deteriorating the geometrical and mechanical parameters of the surface were revealed. The geological and mining conditions of the motorway section in question were complicated already at the road construction stage, due to mining operations and the location of two tectonic faults. Discontinuous deformations appeared in a different location from the one indicated at the design stage. The main protection of the pavement structure did not cover the section where the damages eventually appeared. The consequences of the formation of discontinuous deformations have been described broken down into the period of construction and use of the motorway.

Measurements of pavement deflections were carried out using the FWD apparatus in the area of damage. Based on the results of the measurements, the parameters of the pavement and ground layers were calculated. The description of the pavement—subsoil system was made in two ways: a typical in the surface design of the stratified elastic half-space model and a more advanced elastic—perfectly plastic Mohr–Coulomb model in FE analysis. The obtained results are an original contribution to the problem of assessing the impact of discontinuous mining deformations on the road pavement. Identification of pavement—subsoil stiffness by back analysis method also revealed the role of the geosynthetic layer that was built into the pavement structure during the repair.

The results of the analysis allowed for specifying the scale of changes in pavement and subsoil parameters in the area of discontinuous deformations, taking as the reference level the results from the area not affected by discontinuous deformation. Therefore, the presented results broaden the knowledge needed in design and maintenance work to forecast the impact of linear discontinuous surface deformations on the technical condition of the pavement. The formulated goals were achieved thanks to the measurement of deflections with an unusual spacing of geophones and increased test force as well as computational analysis using both the elastic and the elastic—perfectly plastic description [12]. The numerical analysis performed using the FEM program [13] should be treated as a preliminary one, as it will be later developed, among others through the use of more advanced constitutive models.

2 Characteristics of LDSD and the Analysed Section of the Pavement

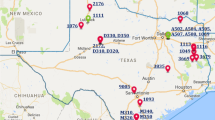
The subject of the research is a motorway A4 lane built in 2002–2005 on the south of Poland. Before the motorway construction works started, the area was subjected to an intensive influence of underground mining. Between 1947 and 2002, coal was mined in fifteen seams, most often with the caving method. The mining operations were conducted at the depths of 200–900 m. They focused in the areas west and east of fault zones III and IV (Figs. 1, 3 and 5). As a consequence of the mining operations there was a large difference in subsidence in the section between the fault zones and outside them. In the section between faults III and IV, the subsidence was approximately 2.0–2.5 m, while east of the fault III the subsidence reached 8 m, and west of the fault IV they reached 10 m (Fig. 1). During the motorway construction works, i.e. in 2002–2005, very intensive mining operations took place. As a result, in the analysed area of the lane, the influence of ten longwalls occurred, of which four had the greatest effect on deformations in the analysed section (Fig. 2). Such intensive mining operations, coinciding with the construction works, caused large subsidence, and, in the area adjacent to the lane, revealed discontinuities in form of terrain thresholds (Fig. 1, Fig. 6c). Geodetic monitoring at points located along the lines separating the lane (Fig. 3) showed that, during the 18-month-long construction works, the subsidence exceeded 2.5 m, west of the fault zone, and 1.7 m, east of the fault zone (Fig. 4). Such large subsidence caused changes in the work schedule and forced a redesign of the road grade line (Fig. 5).

Fig. 1
figure 1

Subsidence of surface in motorway A4 axis before the commencement of construction works in the area of faults III and IV, due to performed mining and estimated horizontal deformation ε [2]

Full size image
Fig. 2
figure 2

Layout of coal mining performed in 2003–2005 in the area of motorway A4

Full size image
Fig. 3
figure 3

Geodetic control network and longwalls mined during the motorway construction works in 2002–2005

Full size image
Fig. 4
figure 4

Measured subsidence of motorway A4 lane, March 2003–November 2004

Full size image
Fig. 5
figure 5

Location of events in the motorway and in the adjacent area (Google Earth) [6]

Full size image

Shortly after the pavement was commissioned in 2005, damage appeared in the form of single linear, roughly transverse, cracks [6] (Fig. 6a, b). The damage observed on the pavement was accompanied by much greater deformations in the area adjacent to the road (Fig. 6c).

Fig. 6
figure 6

Damage observed in 2005: a, b pavement [1], c deformations in the adjacent area

Full size image

In reaction to the cracks, an approximately 20 m long section of the pavement was strengthened. The works were carried out with minimal disturbance to the existing structure, i.e. removing only a package of mineral asphalt layers (MA) and the 22 cm thick base layer of mechanically stabilized aggregate. Finally, the layers of the pavement were as follows:

  • 5 cm, wearing layer SMA 0/12,8,

  • 10 cm, binder BAWMS 0/25,

  • 10 cm, upper base layer BAWMS 0/31,5,

  • 22 cm, lower base layer (aggregate) 0/31,5,

  • heat-welded geogrid (PP),

  • 20 cm, subbase (aggregate) layer 0/63,

  • 25 cm, subbase (slag) 0/63,

  • 25 cm, frost blanket course (burned coal) 0/63,

  • Geotextile,

  • Foil,

  • Approximately 40 cm, improved subgrade (slag + coarse-grained aggregate)

The characteristics of selected properties of the materials used to make the above layers are presented in Tables 1 and 2 and Fig. 7.

Table 1 Selected results of the laboratory tests on mix asphalt layers and unbound aggregate after their built-in in 2003
Full size table
Table 2 Parameters of geogrids
Full size table
Fig. 7
figure 7

Coarse-grained aggregate—improved subgrade

Full size image

It has to be emphasised that under the top layer of the aggregate base, a polypropylene heat-welded geogrid with a tensile strength of 50/50 kN was applied.

Unfortunately, in spite of repairs made in 2005, the discontinuous deformation still reappeared in the pavement in the following years. As a result, between 2005 and 2014, the pavement had to be repaired three more times by profiling the surface of the mineral asphalt package of the pavement (Fig. 8).

Fig. 8
figure 8

a Cracks, 2012, b deformation, 2012, c crack exposed after milling, 2014, d map of subsidence and the required course of the profile grade line, 2014

Full size image

The detailed genesis of discontinuous deformations manifesting on the surface was presented in [1], and [2]. The issues of the technical condition of the surface were addressed in [6], and [7].

3 Ground Conditions

The subsoil of the study area exhibits lithological and geotechnical diversity mainly due to the variability of Quaternary soils. In general, the older subsoil is made of the Carboniferous rocks: shale, less often mudstone, and sandstone, as well as their residuals (saprolite). The deposits are considered the load-bearing ones except for the layer IIId which contains weathered hard coal. Carboniferous deposits make the geological structure complex. In the area of research, the ceiling of the Carboniferous deposits decreases. Younger deposits, which vary genetically, lithologically, and geotechnically, fill the zone above the lowered carboniferous rocks. The younger deposits comprise medium dense sands and cohesive soils of various consistency: from stiff to very soft.

In the area of damaged pavement, the foundation ground was recognized by making boreholes 9 and 10. Figure 5 shows the location of the boreholes 9 and 10. The profile exhibits geotechnical layers which consist of soils with similar physico-mechanical properties. No groundwater appeared in the boreholes. The geotechnical profile in Fig. 9 consists of the following layers:

  • Layer I is a fill made of various soils: both low and high plasticity stiff clays, dense sands, gravel, rock crumbs,

  • Layer IIa is stiff clay locally admixed with gravel and shale crumbs,

  • Layer IIb is soft clay locally admixed with gravel,

  • Layer IIIa is dense weathered sandstone and mudstone in the form of fine or medium sands, containing an admixture of clay or silt, and often also gravel or sandstone crumbs; this layer also includes weathered rubble in the form of sandstone crumbs with sand and sandy silt,

  • Layer IIIb is stiff or firm residual clay with rock crumbs such as: clayey sand, sandy silt, silty loam, clay, sandy loam,

  • Layer IIIc is stiff or firm clay, often containing crumbs of shale,

  • Layer IIId is moist, weathered hard coal.

Fig. 9
figure 9

Geotechnical profile through the boreholes 9 and 10

Full size image

Strong and stiff residual soils (saprolite) with low or medium compressibility of the fourth packages prevail in the ground. The location of the borehole 10 was approximately at km 327 + 712, where the pavement was damaged due to discontinuous surface deformation, and the location of the borehole 9 was at km 327 + 675, where there was no damage to the pavement. The geotechnical profile in Fig. 9 shows also layers of the pavement structure.

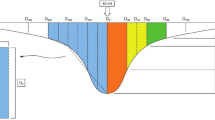
4 Ground Penetration Radar Test

Together with the measurement of pavement deflections (Sect. 5) in June 2015, a GPR test was performed. This study is a continuation of the research [2]. The research results indicate that the largest deformations were developed in the superficial layers of aggregate lying under the mineral-asphalt package in the LDSD zone. In this zone, a settlement amplitude of 10 cm is observed, relative to the reference level determined outside the LDSD zone (Fig. 10). It is to emphasize that the differences in the thickness of asphalt layers result from several repairs carried out between 2005 and 2015, which consisted of profiling the surface of the pavement.

Fig. 10
figure 10

Results of geophysical surveys in the area of LDSD in 2015 [6]

Full size image

5 Measurements with Falling Weight Deflectometer FWD

To assess the influence of LDSD observed in the pavement on the stiffness of the construction layers and subsoil, the deflection was measured with FWD. The measurements were made with very short measuring distances, i.e. between 1 and 10 m, assuming greater spacing between the measuring points farther away from the damage zone. During the measurements, test load of 90 kN was applied, which at the temperature of the mineral asphalt layers of approximately 15 °C has to be considered a high one almost twice as large as 50 kN which is commonly applied in pavement diagnostics). At each point of measurement, three weight drops were carried out, and the response after the last one was taken for further calculations. By applying deflectometer FWD, it is possible to determine the reaction of the pavement to the applied load at several points spaced between 0 and 1.5 m (2.0 m maximum). In the applied measuring set, nine geophones were located at the following distances from the load axis [mm]: 0, 250, 350, 600, 900, 1200, 1500, 1800, 2000 mm. Calculations were made based on the maximum deflections over time (Fig. 11).

Fig. 11
figure 11

a Pavement deflection as a function of time. b Largest deflection as a function of the distance from the load axis [10]

Full size image

6 Back Calculations Methodology

Back calculations using the values of measured deflections on the surface of the structure are classified as so-called non-destructive testing (NDT) of road pavements. The very essence of the process of identifying model parameters is an approximation of the vertical displacements of the surface of the pavement (forming the so-called deflection basin) with displacements calculated in the numerical model [14,15,16].

Back calculations were conducted with application of two models, i.e. the model of layered elastic half-space, which employs the software BISAR 3.0 [12], and the elastic-perfectly plastic Mohr–Coulomb model, introduced into the finite element method software ZSoil [13], to calculate the vertical displacements. Both models assume the static character of the load when the vertical displacements (deflections) from dynamic tests with deflectometer FWD are calculated. This simplification is accepted in the literature [17,18,19,20].

Each layer of the layered elastic half-space model is described with the elastic modulus (E), Poisson’s ratio (ν). The thicknesses of the model layers were determined based on ground-penetrating radar measurements and by drilling boreholes through the pavement. The system of layers where the layers were homogenized, i.e. layers of similar stiffnesses were gathered into one package, was assumed. The final system was as follows (Fig. 12):

  • Layer 1—a package of mineral asphalt layers, thickness h1 = 25 cm, E1, ν1 = 0.30,

  • Layer 2—a package of mechanically stabilised aggregate layers, thickness h2 = 131 cm, E2, ν2 = 0.30,

  • Layer 3—soil, infinite thickness h3 = ∞, E3, ν3 = 0.30.

Fig. 12
figure 12

Homogenisation of the actual layer system for the needs of computational models

Full size image

Considering the relatively small influence of the change of Poisson’s ratio on the calculated displacements in the layered elastic half-space model, its value was assumed to be constant based on the literature data. The calculations focused only on the values of elastic moduli E1, E2, E3, i.e. there were three unknowns to be determined. The calculations were carried out with the following assumptions:

values of moduli are searched until the value Δ < 4% is obtained, which was defined by Szydło [16] as:

$$\Delta = \frac{{\sqrt {\frac{F}{k}} }}{{\sum\nolimits_{{j = 1}}^{k} {w_{j} } }}100\%$$
(1)
$$F = \sum _{{j = 1}}^{k} \left( {w_{j} - u_{j} } \right)^{2}$$
(2)

where wj is the displacement calculated at a distance rj from the load axis, uj is the displacement of pavement’s surface measured at a distance rj from the load axis, k is the number of points forming the deflection basin.

values of moduli ought to fall within the range of values characteristic for a given material, i.e. E1 ≈ 5000–15,000 MPa, E2 ≈ 150–700 MPa, E3 ≈ 25–150 MPa.

The results which do not match the assumptions, ought to be either rejected or require additional analysis to prove their credibility.

In the search for the values of the moduli, the initial value was assumed to be the value of soil modulus determined by (3). First of all, the character of soil reaction was analysed, i.e. if there is a linear reaction, or a non-linear one, determined by (3), describing the distribution of the calculated moduli (Fig. 13) [16]. Such a procedure is recommended by Szydło [16].

$${E}_{g}=\frac{q {a}^{2}\left(1-{\nu }^{2}\right)}{{w}_{r} r}$$
(3)

where Eg is the elastic half-space modulus determined based on deflection wr measured at distance r from the load axis [MPa], wr is the deflection measured at a distance r from the load axis, q is the load [kPa], a is the radius of the loading surface area [m], v—Poisson’s ratio.

Fig. 13
figure 13

Changes in values of soil moduli calculated by (3) as a function of distance from load axis [16]

Full size image

The division of the “pavement—subsoil” system into four layers was assumed for conducting the back analysis with the finite element method (FEM):

  • Layer 1—a package of mineral asphalt layers,

  • Layer 2—a package of mechanically stabilized aggregates forming the upper base part,

  • Layer 3—a package of mechanically stabilized aggregates forming the bottom base part,

  • Layer 4—subsoil (saprolite).

It was assumed that the layer 1 (a package of mineral asphalt layers) is a linearly elastic material, and other layers are elastic—perfectly plastic ones. The values of E and v of the layer 1 and values of four parameters characterizing each of the other three layers of the “pavement—subsoil” system: E, v, c, ϕ, were searched. The thicknesses of the layers were determined for the analysed place based on the results of in situ observations.

Two selected motorway cross-sections were chosen for FEM calculations: in km 327 + 712, where the pavement was damaged due to discontinuous surface deformation, and in km 327 + 675, where there was no damage to the pavement. The layers’ thicknesses in km 327 + 712 were: h1 = 34 cm, h2 = 22 cm, h3 = 109 cm, h4 = 450 cm. The layers’ thicknesses in km 327 + 675 were: h1 = 25 cm, h2 = 22 cm, h3 = 116 cm, h4 = 390 cm. In both cross-sections, the thickness of subsoil h4 was assumed to correspond to the thickness of saprolite, the bottom of which rests on a relatively non-deformable coal layer. The deformability of stiff or firm saprolite is relatively low. Its characteristic in both cross-sections is similar. As mentioned in Sect. 3 the subsoil is lithologically and geotechnically very heterogeneous. For this reason, the computational analysis assumes the subsoil represented by a homogeneous layer with averaged parameters determined using back analysis.

During the calculations, it was found that the values of resilient moduli have the greatest impact on fitting the theoretical and experimental deflections basin. Cohesion c and friction angle ϕ have little influence on the results obtained, which can be seen in Figs. 14 and 15, where deflections are given in micrometers (10–6 m). The coefficient of determination R2 was higher than 0.98 for all theoretical curves. Thus cohesion and friction angle were assumed to be constants typical for residual clay [21,22,23] (Table 3). The assumption enabled substantial simplification of the procedure for selecting values of parameters in back analysis, reducing the number of searched values of parameters to two (E, v).

Fig. 14
figure 14

Changes in values of a subsoil friction angle, b subsoil cohesion, c top base friction angle, d top and bottom base friction angle in km 327 + 712

Full size image
Fig. 15
figure 15

Changes in values of a subsoil friction angle, b subsoil cohesion, c top base friction angle, d top and bottom base friction angle in km 327 + 675

Full size image
Table 3 Values of strength parameters of layers, “pavement – subsoil” system
Full size table

Ψ is the dilation angle characterising volumetric changes during the plastic flow phase with non-associated flow rule.

The FEM models corresponding to the two analysed cross-sections of the motorway are presented in Fig. 16. These are 2D axisymmetric models. Typical kinematic boundary conditions were assumed, which constrain the bottom edges of the models and block horizontal displacement of the vertical edges. The static load was applied over the circular area with a radius of 0.15 m from the axis of symmetry of the models (left edge). The total value of load was 1273 kPa, which corresponded to the force of 90 kN applied during the measurements with deflectometer FWD.

Fig. 16
figure 16

FEM models: a km 327 + 712, b km 327 + 675

Full size image

7 Results of Tests and Calculations

The distribution of measured pavement deflections is presented in Fig. 17. The distribution shows that the pavement was very stiff as the deflection did not exceed 0.20 mm at the temperature of the mineral asphalt package of + 15 °C and the high test force of 90 kN. Certainly, the exception is deflections over the section of about 10 m, where the LDSD influence occurred. In this section, the high softening of the pavement was also observed, which manifested in even threefold higher deflection in comparison with adjacent sections. The adoption of a short measurement step made it possible to capture the increasing deflections approaching the central zone (axis) of LDSD, where the greatest deflection of 0.51 mm occurred.

Fig. 17
figure 17

Measured pavement deflections—northern lane

Full size image

The values of moduli E1, E2, E3 of the layered elastic half-space model, are presented in Fig. 18. The calculated values of moduli for a mineral asphalt package are within the assumed range (5000–15,000 MPa). On average they assume the value of 8000 MPa. In the LDSD zone, there is observed a justified fluctuation of the values (between 3500 and 14,500 MPa), influenced by cracks in the mineral asphalt package and variable thickness of the package, which results from previous repairs (Fig. 18a).

Fig. 18
figure 18

Calculated moduli for a a mineral asphalt package, b a package of aggregate layers, c subsoil

Full size image

For a package of mechanically stabilized mineral layers, the assessment of the obtained moduli indicates three main sections:

  • Section 1, between km 327 + 635 and km 327 + 708, where the moduli fall within the typical range of 150–700 MPa (Fig. 18b);

  • Section 2, between km 327 + 708 and km 327 + 714, where the moduli are lower than 150 MPa, and even drop down to 40 MPa. The values are non-characteristic (atypical). Nevertheless, despite such a low value of the modulus, in the section, there are not any structural ruts, which ought to be a natural consequence of the densification of aggregate layers of such a low modulus. The phenomenon is analyzed in Sect. 9;

  • Section 3, between km 327 + 714 and km 327 + 795, where the moduli are very high (over 1000 MPa) and indicate a bonded structure of at least one of the layers forming the package. It may be expected that the slag used in the frost-protection layer reached the stiffness characteristic for a layer stabilized with cement.

In general, the modulus of subsoil E3 (Fig. 18c) is very high (> 100 MPa). It is to note that the modulus E3 outside the LDSD zone exceeds 300 MPa.

The result of the FEM calculations is the vertical displacements at points corresponding to the distances where geophones recording the pavement deflections during in situ tests were placed. Their locations in the geometric model are presented in Fig. 19.

Fig. 19
figure 19

Location of vertical displacement reading points in the FEM model, cross-section at km 327 + 712

Full size image

The best adjustment of the theoretical deflection basin to the results of measurements was achieved by changing the searched values of parameters by trial and error. Tables 4 and 5 present the vertical displacements (measured and calculated ones), while Figs. 20 and 21 show the matching of theoretical and measured deflection basins.

Table 4 Vertical displacements calculated and measured in the LDSD influence zone, km 327 + 712
Full size table
Table 5 Vertical displacements calculated and measured outside the LDSD influence zone, km 327 + 675
Full size table
Fig. 20
figure 20

Deflection basin, calculated and measured in LDSD influence zone, km 327 + 712

Full size image
Fig. 21
figure 21

Deflection basin, calculated and measured outside LDSD influence zone, km 327 + 675

Full size image

The coefficients of determination R2 = 0.9951 and R2 = 0.9909 were obtained for the presented curves in km 327 + 712 and km 327 + 675, respectively.

The above matching was obtained for the values of parameters of given layers presented in Tables 6 and 7.

Table 6 Final values of parameters obtained for the best match of theoretical and measured deflection basins in the LDSD zone, km 327 + 712
Full size table
Table 7 Final values of parameters obtained for the best match of theoretical and measured deflection basins outside the LDSD zone, km 327 + 675
Full size table

8 Pavement’s Fatigue Life

The fatigue life of the pavement was calculated to compare the impact of the observed discontinuity on the functional properties of the pavement, taking into account three specific sections in terms of stiffness. The calculations were made using the criteria recommended in Poland for dimensioning the pavement [24,25,26,, 27], i.e., the AASHTO 2004 method for assessing fatigue life of asphalt layers and the Asphalt Institute method for determining structural deformations of the ground.

$$N_{{{\text{asf}}}} = 7.3557 \cdot \left( {10^{{ - 6}} } \right) \cdot C \cdot k_{1}^{\prime } \cdot \left( {\varepsilon _{t}^{{ - 3.9492}} } \right) \cdot E^{{ - 1.281}}$$
(4)

where

$$C = 10^{M}$$
(5)
$$M = 4.84 \cdot \left( {\frac{{V_{b} }}{{V_{a} + V_{b} }} - 0.69} \right)$$
(6)

Nasf is the fatigue life (number of equivalent standard axles), εt is the tensile strain (μm/m), E is the stiffness (MPa), Vb is the asphalt content by volume (%v/v), Va is the air voids (% v/v), hac is the total thickness of bituminous layers (cm).

\({k}_{1}^{^{\prime}}\) is a parameter according to the formula:

$$k_{1}^{\prime } = \frac{1}{{0.000398 + \frac{{0.003602}}{{1 + {\text{e}}^{{\left( {11.02 - 1.374 \cdot h_{{ac}} } \right)}} }}}}$$
(7)

The criterion of subgrade strain according to the equation of the Asphalt Institute is:

$${\varepsilon }_{p}=0.0105 \cdot {N}_{gr}^{-0.223}$$
(8)

where Ngr is the life (number of equivalent standard axles), εp-subgrade strain (μm/m).

The lowest value of Nasf and Ngr is considered the durability of the Nmin surface.

Calculations of strains εt and εp were made in the BISAR 3.0 program (elastic model) using the values of moduli calculated based on FWD measurements (Fig. 18). Moduli in the separated specific sections were assumed as the arithmetic mean (Table 8). Calculations were carried out with layers’ thicknesses indicated in Fig. 12. The stiffness modulus of the asphalt layers corresponds to a temperature of + 15 °C (asphalt layers temperature during FWD measurement). The pavement model was loaded with a standard axle with a load of 100 kN (50 kN per wheel) and a contact pressure of q = 850 kPa.

Table 8 Model parameters and calculations results of fatigue life
Full size table

9 Results and Discussion

The results of carried out tests and calculations show the condition of pavement at the time of the test, i.e., in June 2015. The presented technical condition of the pavement is the result of the influence of subsoil deformations, which developed between 2005 and 2015. At that time, deformations grew relatively slowly. However, they caused pavement's unevenness, which required repair works. The works involved milling of existing layers and performing new bonding and wearing courses.

The stiffness of the pavement layers changed as the result of deformations. These changes appear in the distribution of pavement deflections (Fig. 17) and the distribution of moduli calculated from the elastic half-space model (Fig. 18). Surface deflections in the LDSD zone increased three times compared to deflections in the sections outside the LDSD. Substantial reduction of moduli also occurs in the LDSD zone, with a varied scale of changes. The most visible changes in moduli appeared in the aggregate layers package (dolomite, slag, burned shale), separated by a geogrid layer at a depth of about 22 cm below the bottom of the asphalt package. These values in the LDSD zone are in the range between 40 and 150 MPa. Besides the zone, they exceed 400 MPa and 1000 MPa in the extreme. It is to note that approximately 400 MPa is assumed as a typical value for moduli of layers of the base aggregate, and the stiffness less than 100 MPa should be considered as very low. Lower modulus E3 also characterizes the subsoil in the LDSD zone compared to stiffness in sections outside this zone. However, the smallest modulus value is 100 MPa, and it is a higher value than those assumed for the subsoil at the design stage. Subsoil moduli outside the LDSD zone reach 400 MPa.

Observed large values of moduli of the subsoil, especially outside the LDSD zone, are associated with subsoil’s relatively small deformations that occur during the measurements of pavement deflections. It is a result of both, predominant stiff consistency of the soil and the large total thickness of the base layers of mechanically stabilized aggregates built on the subgrade, which exceeds 1.60 m. Usually, the values of resilient moduli of soils are provided for deformations of approximately 0.01 (1%). The results of tests made by measuring the shear wave velocity in soil samples and using local displacement sensors show that the initial stiffness of soil, for very small deformations (approximately 0.001%), is up to 20 times higher [28,29,30]. In the context of the presently discussed results, high stiffness of the subsoil emerging from dynamic measurements with geophones and the deflectometer FWD is not surprising. It is the initial soil stiffness.

Differences in the distribution of moduli in the LDSD zone and beyond mean that the durability of pavement varies greatly. Within the LDSD zone, the pavement is even twenty times less durable than in the sections not affected by discontinuous deformations (Table 8). However, it is to note that in the LDSD section, before the pavement reaches the fatigue failure (4) and (8), it will be necessary to shape the grade line. Such a situation occurred in the analyzed section.

The observed increase in pavement deformation in the LDSD zone, between 2005 and 2015, was gradual thanks to the built-in geogrid. In the geogrid, the membrane tension support mechanism activated as the deformations increased (Fig. 10). Due to the growing tensile forces in the geogrid, loose layers below it might remain uncompacted by the traffic. Over time, creep in the geogrid developed, which caused the geogrid to adapt partially to the deformed subsoil. Despite the creep, it permanently performed “partial” reinforcement, by relieving the layers below it. Low modulus of the entire package of aggregate layers (E2 = 40–190 MPa in Fig. 18b as well as E = 75 MPa of the layer 2 and E = 58 MPa of the layer 3 in Table 6), which was not compacted again under the influence of road traffic proves the effectiveness of reinforcement. The results of the analyses presented in [31] illustrate this phenomenon well. In the absence of a geogrid, the lower layers would be more compacted. Still, the consequence of such a scenario would be faster-growing surface deformations that, for safety reasons, would require immediate intervention to improve the evenness of the pavement.

FE calculations with Mohr–Coulomb model include the influence of the geogrid on improving the stiffness of the package of aggregate layers implicitly. In this analysis, the aggregate package was divided into a layer above and below the geogrid (Fig. 12). The result of the calculation for the section in the zone of LDSD is 29% higher modulus of the aggregate layer above the geogrid (E = 75 MPa for the top base) than below (E = 58 MPa for the bottom base). Moreover, FE back analysis proved nearly the same stiffness of the subsoil within and outside the LDSD zone, which means that the stiffness of the subsoil does not play an essential role in the determination of the pavement condition.

Despite assuming high values of friction angle for base layers (45°) and soil (40°) in the analyzed system, plastic zones occur during simulation of the FWD test (Fig. 22). Thus contrary to the routine practice in the pavement design, elasto-plastic description should be applied in the analysis of the “pavement-subsoil” system subjected to mining operations resulting in LDSD. The differences observed in the range of plastic zones require additional studies, which will be addressed in further research.

Fig. 22
figure 22

Plastic zones a outside LDSD influence zone, km 327 + 712, b within LDSD influence zone, km 327 + 675

Full size image

The stiffer layers of the pavement structure on the section beyond the influence of LDSD limit the range of the impact of the pavement surface load during the FWD test into the subsoil. It can be seen both when comparing the distribution of vertical displacements in Fig. 23 and when comparing the distributions of the major principal stresses σ1 in Fig. 24. In the case of σ1 distributions, its concentrations can be seen primarily in the first pavement layer (M-A package).

Fig. 23
figure 23

Vertical displacement pattern a outside LDSD influence zone, km 327 + 712, b within LDSD influence zone, km 327 + 675

Full size image
Fig. 24
figure 24

Distribution of major principal stress σ1 a outside LDSD influence zone, km 327 + 712, b within LDSD influence zone, km 327 + 675

Full size image

10 Summary

The article presents the causes of LDSD occurrence on the A4 motorway section in southern Poland. In the LDSD zone, there are serious changes in road geometry and a substantial reduction in stiffness of subsoil and pavement layers. The results of the field test and computational analyses allow the formulation of the following conclusions:

  • In the LDSD zone, the stiffness of the subsoil and pavement layers are reduced, which results in the increase in pavement deflections three times larger than outside the LDSD zone,

  • The effect of loosening the pavement layers and the subsoil in the LDSD zone occurs over a length of approximately 11 m,

  • Calculations revealed that resilient modulus of the entire aggregate layers package with one built-in geogrid layer is much less than 300 MPa which must be achieved from acceptance tests during pavement construction; therefore, it can be concluded that the stiffness of aggregate layers in the LDSD zone is at least 75% lower than the required stiffness and at least 85% lower than the stiffness of sections adjacent to the LDSD zone,

  • The subsoil stiffness in the LDSD zone has been reduced by approximately 50% relative to the stiffness of neighbouring sections.

  • In the LDSD zone, the lowest resilient modulus of the subsoil was 102 MPa, and outside the zone it was higher than 250 MPa; even the lowest value of the subsoil modulus in the LDSD zone should be assessed as relatively high. It is to note that FWD tests were carried out when the LDSD zone had already been inactive (there was no movement in the subsoil due to mining operations). It seems that such a high stiffness of the subsoil in the inactive LDSD zone is associated with partial reconstitution of subsoil by the weight of the overlaying aggregate layers with a thickness of about 1 m and lack of the groundwater in the subsoil,

  • The geogrid in the LDSD zone caused the slowdown of the formation of the threshold on the pavement. The strained geogrid worked according to the “strained membrane” mechanism, thus relieving the aggregate layers below. Therefore, the traffic load did not cause re-compaction of aggregate layers below the geogrid.

Considering the issues of engineering security design in areas at risk of LDSD occurrence it is stated that:

  • The use of geosynthetics in the LDSD area is justified due to the slowdown of formation of a full threshold in a pavement,

  • Using one geosynthetic layer in the LDSD zone is insufficient. It is required to use at least a full geo-mattress (geosynthetics at the bottom and the top of a layer). The thickness and the final number of geosynthetic layers should result from computational analysis. In the computational analysis, the values of parameters given in the paper which characterise the state of the layers in the LDSD zone can be used.