Skip to main content
SpringerLink
Log in

Allocation-Based Optimal Reactive Power Dispatch Considering Polynomial Load Model Using Improved Grey Wolf Optimizer

  • Research Paper
  • Published:
Iranian Journal of Science and Technology, Transactions of Electrical Engineering Aims and scope Submit manuscript

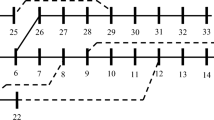
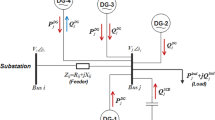
Abstract

Optimal reactive power dispatch (ORPD) problem basically focuses optimally on management of reactive power sources such as distribution generation (DG) units and reactive power compensation (RPC) devices. Its main purpose, especially in distribution grids, is real power loss and reactive power cost minimization subject to satisfying a set of constraints. On the other hand, optimal site of these devices in distribution system and polynomial load model can significantly affect the ORPD problem. In this paper, a new revision of ORPD in distribution grids combined with optimal DG and RPC allocation considering load model-based power flow and a new objective function is introduced. Moreover, improved grey wolf optimizer (IGWO) as a new and powerful optimization technique is proposed to solve this complex problem. The suggested method is implemented on standard IEEE 33-bus distribution system considering various scenarios and load profiles. The obtained results demonstrate the effectiveness of the introduced problem and ability of the proposed algorithm for finding better solutions compared to other presented methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Abbreviations

\(\overrightarrow{a}\left(t\right)\) :

Attacking prey at time \(t\)

\(\overrightarrow{A}\left(t\right)\) :

Random values in interval [\(-2\overrightarrow{a}\left(t\right)\), \(2\overrightarrow{a}\left(t\right)\)]

\({A}_{p}\), \({B}_{p}\), \({C}_{p}\) :

Load coefficients related to active power

\({A}_{q}\), \({B}_{q}\), \({C}_{q}\) :

Load coefficients related to reactive power

\({B}_{k}\) :

Susceptance of the \(k\) th network branch

\({C}_{CAP}\) :

Reactive cost factor of RPC

\({C}_{DG}\) :

Reactive cost factor of DG

\({C}_{loss}\) :

Cost coefficient of the power losses

\(DGCandidateList\) :

DG candidate list

\({f}_{loss}\) :

Total real power losses

\({f}_{RPC}\) :

Cost of RPC devices

\({f}_{R/DG}\) :

Cost of DG’s reactive power generation

\({G}_{k}\) :

Conductance of the \(k\) th network branch

\({h}_{DGi}\) :

Binary variable related to DG installation at bus \(i\)

\({h}_{Ci}\) :

Binary variable related to RPC installation at bus \(i\)

\({\mathrm{Iteration}}_{\mathrm{max}}\) :

Maximum iteration

\(N\) :

Number of wolves

\({N}_{bra}\) :

Number of network branches

\({N}_{C}\) :

Number of installed RPC devices

\({N}_{DG}\) :

Number of DG units

\({N}_{G}\) :

Number of generators

\({N}_{bus}\) :

Number of network nodes

\({N}_{T}\) :

Number of tap setting transformers

\({N}_{DG-Can}\) :

Number of candidate DGs

\({N}_{C-Can}\) :

Number of candidate RPCs

\({P}_{DGi}\) :

Active power output of DG at bus \(i\)

\({P}_{Gi}\) :

Active power generation of the \(i\) th generator

\({P}_{Li}\) :

Active power demand at bus \(i\)

\({P}_{Li0}\) :

Active power demand at bus \(i\) for a specified operating point

\({PEN}_{P}\) :

Maximum penetration of DGs in terms of active power

\({PEN}_{Q}\) :

Maximum penetration of both DGs and RPCs in terms of reactive power

\({Q}_{Ci}\) :

Reactive power output of RPC at bus \(i\)

\({Q}_{DGi}\) :

Reactive power output of DG at bus \(i\)

\({Q}_{Gi}\) :

Reactive power generation of the \(i\) th generator

\({Q}_{Li}\) :

Reactive power demand at bus \(i\)

\({Q}_{Li0}\) :

Reactive power demand at bus \(i\) for a specified operating point

\(\mathrm{Rand}\) :

A random number in interval [0, 1]

\(RPCCandidateList\) :

RPC candidate list

\(S\) :

Line loading

\({V}_{i}\) :

Voltage magnitude of \(i\) th bus

\(\overrightarrow{X}\left(t\right)\) :

Wolf position vector at time \(t\)

\({\overrightarrow{X}}_{\alpha }\left(t\right)\) :

Position of wolf \(\alpha \) at time \(t\)

\({\overrightarrow{X}}_{\beta }\left(t\right)\) :

Position of wolf \(\beta \) at time \(t\)

\({\overrightarrow{X}}_{\delta }\left(t\right)\) :

Position of wolf \(\delta \) at time \(t\)

\({\theta }_{ij}\) :

Phase angle difference between bus i and bus j

2ArchMGWO:

Two-Archive Multi-objective Grey Wolf Optimizer

ABC:

Artificial Bee Colony

BFOA:

Bacterial Foraging Optimization Algorithm

BSO:

Backtracking Search Optimizer

CP:

Constant Power

DAMOPSO:

Dynamically Adaptive Multi-objective Particle Swarm Optimization

DE:

Differential Evolution

DG:

Distributed Generation

DS:

Distribution System

DSA:

Differential Search Algorithm

EMA:

Exchange Market Algorithm

FAHCLPSO:

Fuzzy Adaptive Heterogeneous Comprehensive-Learning Particle Swarm Optimization

FF:

Firefly

GA:

Genetic Algorithm

GBWCA:

Gaussian Bare-bones Water Cycle Algorithm

GWO:

Grey Wolf Optimizer

ICA:

Imperialistic Competitive Algorithm

IGWO:

Improved Grey Wolf Optimizer

IPG-PSO:

Improved Pseudo-gradient search Particle Swarm Optimization

IPSO:

Improved Particle Swarm Optimization

L:

Light

MOALO:

Multi-objective Ant Lion Optimization

MOEA:

Multiple Evolutionary Algorithms

MFO:

Moth-Flame Optimization

N:

Nominal

NM:

Nelder–Mead

NR:

Not Reported

OGWO:

Opposition-based Grey Wolf Optimizer

ORPD:

Optimal Reactive Power Dispatch

P:

Peak

QOTLBO:

Quasi-oppositional Teaching Learning-Based Optimization

RPC:

Reactive Power Compensation

SDP:

Semidefinite Programming

SDR2:

Semidefinite Programming Relaxation

TS:

Transmission System

HTSSA:

Tabu Search-Simulated Annealing Method

ZIP:

It refers to three loads including constant impedance (Z), constant current (I), and constant power (P)

References

  • Abaci K, Yamaçli V (2017) Optimal reactive-power dispatch using differential search algorithm. Electr Eng 99:213–225

    Google Scholar 

  • Ansari J, Gholami A, Kazemi A (2015) Holonic structure: a state-of-the-art control architecture based on multi-agent systems for optimal reactive power dispatch in smart grids. IET Gener Transm Distrib 9:1922–1934

    Google Scholar 

  • Araujo LRD, Penido DRR, Vieira FDA (2013) A multiphase optimal power flow algorithm for unbalanced distribution systems. Int J Electr Power Energy Syst 53:632–642

    Google Scholar 

  • Baran ME, Wu FF (1989) Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans Power Deliv 4:1401–1407

    Google Scholar 

  • Bhattacharya A, Roy PK (2012) Solution of multi-objective optimal power flow using gravitational search algorithm. IET Gener Transm Distrib 6:751–763

    Google Scholar 

  • Bingane C, Anjos MF, Digabel SL (2019) Tight-and-cheap conic relaxation for the optimal reactive power dispatch problem. IEEE Trans Power Syst 34(6):4684–4693

    Google Scholar 

  • Cheng S, Chen M-Y (2014) Multi-objective reactive power optimization strategy for distribution system with penetration of distributed generation. Int J Electr Power Energy Syst 62:221–228

    Google Scholar 

  • Davoodi E, Babaei E, Mohammadi-ivatloo B, Rasouli M (2020) A novel fast semidefinite programming-based approach for optimal reactive power dispatch. IEEE Trans Ind Inform. https://doi.org/10.1109/TII.2019.2918143

    Article  Google Scholar 

  • Eskandari Nasab M, Maleksaeedi I, Mohammadi M, Ghadimi N (2014) A new multiobjective allocator of capacitor banks and distributed generations using a new investigated differential evolution. Complexity 19:40–54

    MathSciNet  Google Scholar 

  • Ettappan M, Vimala V, Ramesh S, Thiruppathy KV (2020) Optimal reactive power dispatch for real power loss minimization and voltage stability enhancement using artificial bee colony algorithm. Microprocess Microsyst 76:1–7

    Google Scholar 

  • Ghasemi M, Ghanbarian MM, Ghavidel S, Rahmani S, Moghaddam EM (2014) Modified teaching learning algorithm and double differential evolution algorithm for optimal reactive power dispatch problem: a comparative study. Inf Sci (Ny) 278:231–249

    MathSciNet  Google Scholar 

  • Ghorbani N, Babaei E (2014) Exchange market algorithm. Appl. Soft Comput 19:177–187

    Google Scholar 

  • Granada M, Rider MJ, Mantovani JRS, Shahidehpour M (2012) A decentralized approach for optimal reactive power dispatch using a Lagrangian decomposition method. Electr Power Syst Res 89:148–156

    Google Scholar 

  • Granville S (1994) Optimal reactive dispatch through interior point methods. IEEE Trans Power Syst 9:136–146

    Google Scholar 

  • Hashemi M, Zarif MH (2019) A novel hierarchical distributed framework for optimal reactive power dispatch based on a system of systems structure. Comput Electr Eng 78:162–183

    Google Scholar 

  • Heidari AA, Abbaspour RA, Rezaee JA (2017) Gaussian bare-bones water cycle algorithm for optimal reactive power dispatch in electrical power systems. Appl Soft Comput 57:657–671

    Google Scholar 

  • Hongxin L, Yinhong L, Jinfu C (2014) Adaptive multiple evolutionary algorithms search for multi-objective optimal reactive power dispatch. Int Trans Electr Energy Syst 24:780–795

    Google Scholar 

  • Jeyadevi S, Baskar S, Babulal CK, Iruthayarajan MW (2011) Solving multiobjective optimal reactive power dispatch using modified NSGA-II. Int J Electr Power Energy Syst 33:219–228

    Google Scholar 

  • Kanwar N, Gupta N, Niazi KR, Swarnkar A, Bansal RC (2017) Simultaneous allocation of distributed energy resource using improved particle swarm optimization. Appl Energy 185:1684–1693

    Google Scholar 

  • Kaur S, Kumbhar G, Sharma J (2014) A MINLP technique for optimal placement of multiple DG units in distribution systems. Int J Electr Power Energy Syst 63:609–617

    Google Scholar 

  • Khodabakhshian A, Andishgar MH (2016) Simultaneous placement and sizing of DGs and shunt capacitors in distribution systems by using IMDE algorithm. Int J Electr Power Energy Syst 82:599–607

    Google Scholar 

  • Kumar Sharma A, Murty VVSN (2014) Analysis of mesh distribution systems considering Load models and load growth impact with loops on system performance. J Inst Eng 95:295–318

    Google Scholar 

  • Lenin K, Reddy BR, Suryakalavathi M (2016) Hybrid Tabu search-simulated annealing method to solve optimal reactive power problem. Int J Electr Power Energy Syst 82:87–91

    Google Scholar 

  • Li Y, Wang Y, Li B (2013) A hybrid artificial bee colony assisted differential evolution algorithm for optimal reactive power flow. Int J Electr Power Energy Syst 52:25–33

    Google Scholar 

  • Mahmoud K, Yorino N, Ahmed A (2016) Optimal distributed generation allocation in distribution systems for loss minimization. IEEE Trans Power Syst 31:960–969

    Google Scholar 

  • Mandal B, Roy PK (2013) Optimal reactive power dispatch using quasi-oppositional teaching learning based optimization. Int J Electr Power Energy Syst 53:123–134

    Google Scholar 

  • Mirjalili S, Mirjalili SM, Lewis A (2014) Grey wolf optimizer. Adv Eng Softw 69:46–61

    Google Scholar 

  • Mohamed Imran A, Kowsalya M (2014) Optimal distributed generation and capacitor placement in power distribution networks for power loss minimization. Int. Conf. Adv. Electr. Eng., Vellore, India: IEEE; p. 1–5

  • Mohamed Imran A, Kowsalya M, Kothari DP (2014) A novel integration technique for optimal network reconfiguration and distributed generation placement in power distribution networks. Int J Electr Power Energy Syst 63:461–472

    Google Scholar 

  • Mohapatra A, Behera S, Nayak S, Panigrahi BK (2012) A study on DG and capacitor placement in radial distribution system. IEEE Int. Conf. Power Electron. Drives Energy Syst., Bengaluru, India: IEEE; p. 1–5.

  • Mouassa S, Bouktir T (2019) Multi-objective ant lion optimization algorithm to solve large-scale multi-objective optimal reactive power dispatch problem. COMPEL Int J Comput Math Electr Electron Eng 38:304–324

    Google Scholar 

  • Naderi E, Narimani H, Fathi M, Narimani MR (2017) A novel fuzzy adaptive configuration of particle swarm optimization to solve large-scale optimal reactive power dispatch. Appl Soft Comput 53:441–456

    Google Scholar 

  • Ng Shin Mei R, Herwan Sulaiman M, Mustaffa Z, Daniyal H (2017) Optimal reactive power dispatch solution by loss minimization using moth-flame optimization technique. Appl Soft Comput Soft Comput 59:210–222

    Google Scholar 

  • Nguyen TT, Vo DN (2019) Improved social spider optimization algorithm for optimal reactive power dispatch problem with different objectives. Neural Comput Appl 1:1–32

    Google Scholar 

  • Nguyen TT, Vo DN, Tran HV, Dai LV (2019) Optimal dispatch of reactive power using modified stochastic fractal search algorithm. Complexity 2019:1–28

    Google Scholar 

  • Niknam T, Narimani MR, Azizipanah-Abarghooee R, Bahmani-Firouzi B (2013) Multiobjective optimal reactive power dispatch and voltage control: a new opposition-based self-adaptive modified gravitational search algorithm. IEEE Syst J 7:742–753

    Google Scholar 

  • Nuaekaew K, Artrit P, Pholdee N, Bureerat S (2017) Optimal reactive power dispatch problem using a two-archive multi-objective grey wolf optimizer. Expert Syst Appl 87:79–89

    Google Scholar 

  • Polprasert J, Ongsakul W, Dieu VN (2016) Optimal reactive power dispatch using improved pseudo-gradient search particle swarm optimization. Electr Power Components Syst 44:518–532

    Google Scholar 

  • Poornazaryan B, Karimyan P, Gharehpetian GB, Abedi M (2016) Optimal allocation and sizing of DG units considering voltage stability, losses and load variations. Int J Electr Power Energy Syst 79:42–52

    Google Scholar 

  • Quintana VH, Santos-Nieto M (1989) Reactive-power dispatch by successive quadratic programming. IEEE Trans Energy Convers 4:425–435

    Google Scholar 

  • Rahmani-andebili M (2012) Effect of load models on optimal capacitor allocation in distribution network. Proc. 17th Conf. Electr. Power Distrib., Tehran, Iran: IEEE; p. 1–4

  • Raj S, Bhattacharyya B (2018) Reactive power planning by opposition-based grey wolf optimization method. Int Trans Electr Energy Syst 28:1–29

    Google Scholar 

  • Rajan A, Malakar T (2015) Optimal reactive power dispatch using hybrid Nelder-Mead simplex based firefly algorithm. Int J Electr Power Energy Syst 66:9–24

    Google Scholar 

  • Rajan A, Malakar T (2016) Exchange market algorithm based optimum reactive power dispatch. Appl Soft Comput 43:320–336

    Google Scholar 

  • Sadighmanesh A, Zare K, Sabahi M (2012a) Distributed generation unit and capacitor placement for loss, voltage profile and ATC optimization. Int J Electr Comput Eng 2:774–780

    Google Scholar 

  • Sadighmanesh A, Zare K, Sabahi M (2012b) Distributed generation unit and capacitor placement for multi-objective optimization. Int J Electr Comput Eng 2:615–620

    Google Scholar 

  • Shaheen AM, El-Sehiemy RA, Farrag SM (2018) Integrated strategies of backtracking search optimizer for solving reactive power dispatch problem. IEEE Syst J 12:424–433

    Google Scholar 

  • Shareef SKM, Rao RS (2018) Optimal reactive power dispatch under unbalanced conditions using hybrid swarm intelligence. Comput Electr Eng 69:183–193

    Google Scholar 

  • Shaw B, Mukherjee V, Ghoshal SP (2014) Solution of reactive power dispatch of power systems by an opposition-based gravitational search algorithm. Int J Electr Power Energy Syst 55:29–40

    Google Scholar 

  • Sheng W, Liu K, Pei H, Li Y, Jia D, Diao Y (2016) A fast reactive power optimization in distribution network based on large random matrix theory and data analysis. Appl Sci 6:1–19

    Google Scholar 

  • Singh H, Laxmi S(2017) Multi-objective optimal reactive power dispatch for distribution system. IEEE Int. Conf. Power, Control. Signals Instrum. Eng., p. 558–63

  • Sulaiman MH, Mustaffa Z, Mohamed MR, Aliman O (2015) Using the gray wolf optimizer for solving optimal reactive power dispatch problem. Appl Soft Comput 32:286–292

    Google Scholar 

  • Zhang X, Chen W, Cai W, Dai C (2010) Dynamic multi-group self-adaptive differential evolution algorithm for reactive power optimization. Int J Electr Power Energy Syst 32:351–357

    Google Scholar 

  • Zhaoa J, Zhang Z, Yao J, Yang S, Wang K (2019) A distributed optimal reactive power flow for global transmission and distribution network. Int J Electr Power Energy Syst 104:524–536

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Electrical Engineering Department, Engineering Faculty, Razi University, Kermanshah, Iran

    Saman Hosseini-Hemati, Gholam Hossein Sheisi & Shahram Karimi

Authors
  1. Saman Hosseini-Hemati
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gholam Hossein Sheisi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shahram Karimi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shahram Karimi.

Appendix

Appendix

As already discussed in the simulation results section, our proposed IGWO is robust and fast. Besides these features, another advantage of the IGWO is that it has few parameters to be set. It is an easy task to choose them for the suggested ORPD problem and they work well for different presented scenarios.

Here, number of grey wolves (\(N\)) and maximum iteration (\({\mathrm{Iteration}}_{\mathrm{max}}\)) are experimented and their influence on the IGWO’s performance is analyzed to determine their optimal settings. Figure 

Fig. 16
figure 16

Effect of the IGWO’s parameters on the objective function

Full size image

16 shows their effects on the final solution in which only the results of scenario 3 based on CP model and load level N are reported. Moreover, several runs with different parameter values were carried out. This figure indicates that:

Number of grey wolves Fig. 16a shows that the best choice for this parameter is \(N=30\) and more wolves can slightly improve the objective function. So, more wolves can’t help search much better solution and result in more computational time.

Number of iterations Fig. 16b clearly indicates that \({\mathrm{Iteration}}_{\mathrm{max}}>200\) can’t remarkably make better results and so just increases the computational time.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hosseini-Hemati, S., Sheisi, G.H. & Karimi, S. Allocation-Based Optimal Reactive Power Dispatch Considering Polynomial Load Model Using Improved Grey Wolf Optimizer. Iran J Sci Technol Trans Electr Eng 45, 921–944 (2021). https://doi.org/10.1007/s40998-021-00419-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40998-021-00419-8

Keywords

Search

Navigation