1 Introduction

Sustainable freshwater supply has become a major challenge in many countries around the world. Population growth and lifestyle changes linked to global warming-related issues that have led to increased droughts, hurricanes, and floods have intensified water scarcity problems worldwide. As a result, seawater desalination has become a primary necessity for ensuring freshwater supply in water-stressed countries. Nevertheless, most seawater desalination technologies are still highly energy-intensive (Khoshgoftar Manesh and Onishi 2021). Indeed, excessive operating costs and relatively high cost of freshwater produced have been the most critical obstacles to the development and expansion of industrial seawater desalination plants in recent years. Hence, integrating desalination systems into existing combined-cycle power plants (CCPP) has emerged as an attractive solution for producing power and freshwater utilities. This is because converting conventional thermal power plants into multi-purpose ones allows for recovering and reusing waste heat to drive the desalination systems, thereby reducing production costs. Yet, the optimal design of integrated thermal power plants and desalination systems is a complex endeavor, which entails the application of advanced energy, exergy, economic, and environmental optimization tools to improve overall system performance and sustainability (Khoshgoftar Manesh et al. 2021).

The energy and exergy analysis of power plants and desalination systems has received increased attention in the literature over the last few years. In this context, Ng et al. (2017) examined the energy efficiency of available large-scale desalination plants according to their energy consumption. They also proposed exergy efficiency as a reasonable indicator for desalination processes. In this case, the authors considered the optimization of the operating conditions of different equipment units by recognizing the destruction of exergy and its relationship with the initial energy inflow. Mohammadi et al. (2018) assessed a water desalination plant in terms of energy consumption and its integration to a power generation unit to determine the optimal operating parameters of the integrated system. For this purpose, the authors developed an approach to optimize the desired power generation, freshwater production, and total energy cost.

Extensive research work has been conducted on the optimal integration of thermal power plants and water desalination units by considering genetic algorithm (GA)-based optimization approaches. Into this framework, Sanaye and Asgari (2013) investigated the integration of a thermal power plant and a multi-stage flash (MSF) desalination system. The authors proposed a GA-based multi-objective method to optimize the objective functions of investment costs and exergy destruction. The authors also performed energy, exergy, economic, and environmental analyses to determine the ideal number of MSF desalination effects and the energy performance parameters of the heat recovery steam generator (HRSG), including its optimal pinch temperature. Mohammed et al. (2021) studied the integration of a multi-effect distillation (MED) desalination unit with an organic Rankine cycle (ORC) for the polygeneration of heating and cooling, electricity and freshwater. They applied energy, exergy, and exergoeconomic (3E) analyses to evaluate the feasibility of the proposed integrated ORC-MED system. The authors also developed a multi-objective GA optimization approach to minimize production costs while maximizing thermal and exergy efficiencies. Shakib et al. (2019) investigated the energy and exergy performance of a hybrid desalination system, composed of reverse osmosis (RO) and multi-effect thermal vapor compression (METVC) units, integrated with a gas turbine power plant through an HRSG unit. The authors proposed six different system configurations and evaluated the results into two scenarios of desalination plant capacity. They also proposed a multi-objective GA-based optimization approach to maximize exergy efficiency and performance ratio of the combined system.

Ahmadi et al. (2017) examined a combined fuel cell and gas turbine system as a heat source for a MED desalination system. The main goal of this study was to reduce operating and maintenance costs of the system and carbon emissions from the fuel cell stack. The authors performed exergy and economic analysis on the integrated system to assess its overall performance. Moreover, their optimization through a GA approach on power plant operating parameters led to an increase in the exergy efficiency of the integrated system. Hafdhi et al. (2018) introduced a mathematical model using EES software to establish a relationship between the energy, exergy, and economic equations of a METVC desalination system coupled to an industrial steam power plant. The authors also proposed an exergoeconomic-based multi-objective optimization model to maximize exergy efficiency while minimizing production costs.

Amiralipour and Kouhikamali (2019) focused on converting a steam power plant into a combined power and desalination system. The authors conducted thermodynamic and economic analyses of an MED desalination unit integrated into the Montazer al-Qaem steam power plant located in Iran, which has a nominal capacity of 166 MW. They also proposed a multi-objective modelling approach based on an evolutionary algorithm to optimize the net power and freshwater selling prices. Ghasemiasl et al. (2020) investigated the energy and exergy performance of a solar-assisted CCPP coupled with a multi-stage vapor desalination unit. The authors also carried out an economic analysis of the integrated power and desalination system using the specific exergy costing (SPECO) methodology. Their results first indicated an increase of 12% in the cost of electricity and a decrease from 52.7 to 52.4% in the exergy efficiency. However, after optimizing the integrated system, the exergy efficiency was slightly improved to 53.6%.

Vazini Modabber and Khoshgoftar Manesh (2020a, 2020b) employed GA for optimizing a power plant coupled with a MED-RO desalination unit located in Qeshm Island, Iran. The authors developed a multi-objective genetic algorithm (MOGA) and a multi-objective water cycle algorithm (MOWCA) to optimize the exergic, economic, and environmental performance parameters of the combined system. Their optimization results indicated a reduction in the environmental impacts and investment costs of the system together with an increase in the plant exergy efficiency. In another study, Khoshgoftar Manesh et al. (2021) developed a mathematical modelling approach for the simulation of an integrated CCPP and RO-MED desalination system. To evaluate the most relevant system operating parameters, the authors also applied conventional and advanced exergy, energy, exergoenvironmental, and exergoeconomic (4E) analyses. Finally, they proposed potential economic, technical, and environmental improvements for different units to increase overall plant efficiency using the previous methodology. Their simulation results revealed overall exergy efficiency of 42.7%, with electricity production cost of ~ 0.04 US$/kWh, whilst the MED and RO freshwater production costs were 2.5 US$/m3 and 1.75 US$/m3, respectively. However, their approach disregards the optimization of energy, exergy, and environmental performance indicators which could lead to enhanced solutions.

The preceding research shows the relevance of integrating other energy conversion subsystems, such as desalination units, into conventional power plants. From this perspective, this paper introduces a new mathematical modelling and optimization approach for a CCPP integrated with a RO-MED desalination system. In addition, the Shahid Salimi Neka CCPP is selected as the base system for a real-world case study. The Shahid Salimi Neka power plant, located in Neka, Mazandaran, Iran, has a strategic role in Iran’s electricity generation. The required water is currently supplied from three deep wells situated 20 km away. However, in recent years, the technical specifications of the water from those wells have decreased significantly. Linked to this issue is the increasing demand for water resources for consumption in various applications, including drinking, agriculture, and other industrial uses. Hence, using the valuable water resource from the Caspian Sea has become inevitable. Because of the importance of water in this region, the integration of RO and MED desalination systems into the Neka CCPP is further investigated in this study. To this end, the integrated CCPP and RO-MED desalination system is thermodynamically modelled using MATLAB and EES software environments. The results are validated via Thermoflex software based on actual data from the Neka CCPP. In addition, comprehensive 4E analyses are performed to assess the main energy, exergy, economic, and environmental performance indicators of the proposed integrated RO-MED and CCPP system, and a MOWCA based on a GA approach is developed to optimize the operating conditions and performance parameters related to the 4E analyses while minimizing the costs and environmental impacts of the integrated system. Therefore, performing the GA-based multi-objective optimization on the new proposed scheme for the Neka CCPP represents the major innovation of this study.

2 System Description

Several gas and steam turbine cycles make up a CCPP, a system for power production. In this type of power plant, the heat in the exhaust gases from the gas turbines is usually used to produce the water vapor required in the steam turbines via a heat recovery boiler. Otherwise, exhaust gases with temperatures up to 600 °C would be discharged directly to the environment, thus wasting their energy content. Hence, CCPPs have increased energy efficiency (around 60%) when compared to conventional power plants with energy efficiencies typically in the range of 25–40% (Khoshgoftar Manesh et al. 2021). Indeed, CCPPs are a highly efficient, flexible, reliable, cost-effective, and environmentally friendly solution for power generation (Cavalcanti 2017). In 2003, one of the most important power plant projects was inaugurated in the north of Iran. The Shahid Salimi Neka plant, also referred to as Neka CCPP or Neka power plant, was built near Neka city in the Mazandaran province, and thus can take advantage of being located alongside the Caspian Sea. The Neka CCPP has two air compressors (ACs), two gas turbines (GTs), one steam turbine (ST), one combustion chamber (CC), two HRSGs, and one plate condenser (Ameri et al. 2008). In the Neka CCPP, the power output of the ST is approximately 160.8 MW whilst the overall capacity is rated at 420 MW.

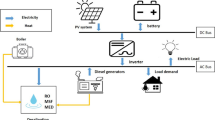
As mentioned above, this study evaluates the feasibility of coupling the Neka CCPP with a RO-MED desalination system using a new MOWCA optimization approach. To this aim, a multi-objective GA-based optimization approach is developed to minimize the costs and environmental impacts of the new integrated polygeneration system. Furthermore, the system optimization can determine the optimal values for the different operating parameters of the integrated power and desalination system, allowing for a more efficient plant operation. Figure 1 portrays a simplified process flow diagram of the proposed Neka CCPP combined with RO and MED desalination units.

Fig. 1
figure 1

Schematic process flow diagram of the proposed Neka combined-cycle power plant (CCPP) integrated with the reverse osmosis and multi-effect distillation (RO-MED) desalination system (adapted from Khoshgoftar Manesh et al. 2021)

Full size image

In Fig. 1, the airflow enters the AC at 20 °C in the GT section, where its pressure increases to 10.8 bar. Next, the compressed air enters the CC and is combusted with the fuel, while the outlet temperature increases to about 970 °C. After that, the gases from the combustion process are sent to the GT, where a portion of the generated energy is used to run the compressor, while the remaining portion is distributed as net output power. The high-temperature exhaustion gases (combustion products) with significant thermal energy pass through the high-pressure superheater (HPSH). This is the initial step in the HRSG unit, where the combustion products are used to produce high-pressure steam at 533 °C, achieving the required conditions for running the ST.

Subsequently, the exhaustion gases are conducted to the high-pressure evaporator (HPEV). In the evaporator, the heat from the previous stream is used for promoting water phase change from liquid to steam as needed by the superheater. After this stage, the exhaustion gases that have experienced a temperature drop are sent to the economizer 2 (HP-EC2). The latter is a heat exchanger that raises the temperature of the inlet water to the saturation point under the same high pressure by using the heat from the airstream. Afterwards, the combustion products go into a preheater, which is used to heat the feed water (FW) stream entering the HP section, and are then released to the environment through the flue-gas stack. Since the HRSG in the Neka CCPP has two different operating pressures, the low-pressure (LP) steam flow is split into two separated streams. Hence, one of the steam streams is conducted to the low-pressure ST section to be mixed with the outlet HPST stream, while the second stream is used to drive the MED desalination plant.

In the MED desalination unit, the saline water is directed to the condenser unit at the inlet seawater temperature of about 20 °C. This feedwater stream serves as cooling water for converting supply steam to a liquid state. Following slight heating, such a stream is split into two separate system units. Thus, one feed saline water stream goes to the MED effects to be desalted, whist the remaining stream is discharged to the sea after being utilized as cooling water. The steam stream from the low-pressure section of the HRSG is used to drive the first MED effect after mixing with a fraction of the steam from the last desalination effect.

In MED effects, the feed water is sprayed onto the tubes conveying hot steam. During this process, the saline water evaporates because of the high-temperature and low-pressure conditions at the desalination effect. The concentrated saline water with gradually higher salt concentrations moves as a brine stream towards the exit of the MED unit, whereas the vapor stream is used to stimulate the next desalination effect. After the first desalination effect, the steam is converted into a liquid stream owing to the loss of heat and exits the MED unit. The resulting outlet stream, called return steam, is merged with the outlet stream from the power plant condenser to generate the feed water flow for the HRSG unit. The brine streams from each effect are combined as high-salinity water, and the freshwater collected in the condenser exits the MED unit as produced freshwater. The schematic diagrams of the RO and MED desalination units are shown in Fig. 2. In this way, Fig. 2a depicts the schematic diagram of the RO desalination unit. The discharged water from the MED unit is used as the feed water stream for the RO unit. First, the feed water stream is pre-treated in the pretreatment unit to remove large and suspended particles which could impair the RO membrane operation. After that, the treated stream is pumped to the RO membrane using an HP pump (RO-pump). The RO membrane uses mechanical pressure to remove salts in the feed water and produce freshwater.

Fig. 2
figure 2

Schematic diagrams of the a reverse osmosis (RO); and b multi-effect distillation (MED) desalination units (adapted from Khoshgoftar Manesh et al. 2021)

Full size image

3 Methodology

The following thermodynamic modelling formulation is implemented in MATLAB and EES software environments to obtain the integrated system's streams pressure, temperature, and enthalpy. The results are validated using Thermoflex software simulations based on actual data from the Neka power plant. The thermodynamic, economic, and environmental assessment-related equations are presented as follows.

3.1 Thermodynamic Analysis

For conducting the thermodynamic analysis of the integrated system, the following assumptions are needed (Mistry et al. 2013; Khoshgoftar Manesh et al. 2021):

  1. i.

    Steady-state plant operation.

  2. ii.

    Negligible pressure drops in piping networks and heat exchanger units.

  3. iii.

    Negligible heat loss in equipment units.

  4. iv.

    The outlet temperatures of freshwater and brine streams from each MED effect should match the temperature of the related desalination effect.

  5. v.

    The properties of seawater can be derived as a function of salinity and temperature.

  6. vi.

    Turbines and pumps follow isentropic efficiency.

  7. vii.

    Kinetic and potential energy changes are disregarded in equipment units.

The following remarks are relevant when considering the previous assumptions.

  1. i.

    Neglecting the pressure drops in piping networks and heat exchanger units can affect the calculated power required by the pumps. However, since the pumps do not consume a considerable amount of power, this assumption does not change the main performance parameters of the system significantly. In addition, pressure drops in equipment units can slightly vary some thermal properties of process streams, such as saturated temperatures in the ST cycle. Nonetheless, because of its minor effect, it can still be considered negligible.

  2. ii.

    Heat loss in equipment units will cause them to operate less efficiently. Therefore, ignoring these losses will increase energy efficiency in those system components. However, this effect will be negligible when compared to the main heat duty of the system units.

  3. iii.

    Since the freshwater and brine streams in each MED effect are produced close to the saturation temperature, which is close to the effect’s temperature, it would be a reasonable to assume that the outlet streams of each effect share the same temperature as their corresponding effect. Moreover, since the seawater stream is in a compressed liquid state, its thermodynamic properties are primarily a function of its temperature and salinity rather than pressure.

  4. iv.

    Considering isentropic efficiency for the turbines and pumps can provide a more realistic model. This is because the isentropic efficiency will capture the non-ideal behavior of those equipment units.

  5. v.

    It is a common and reasonable assumption to neglect the kinetic and potential energy changes of process streams in a power plant system. This is because the thermal energy of the streams (enthalpy) is much more significant than their kinetic and potential energy changes in this type of system.

The system components are subject to the following application of the first law of thermodynamics:

$$\sum {\dot{m}_{{{\text{in}},k}} } = \sum {\dot{m}_{{{\text{out}},k}} }$$
(1)
$$\dot{Q}_{k} - \dot{W}_{k} = \sum {\dot{m}_{{{\text{out}},k}} h_{{{\text{out}},k}} } - \sum {\dot{m}_{{{\text{in}},k}} h_{{{\text{in}},k}} }$$
(2)

where \(\dot{m}\), \(\dot{W}\), \(\dot{Q}\), and \(h\) represent the streams mass flow rate, power, heat transfer rate, and specific enthalpy, respectively.

A list of input parameters for the GT and ST cycles is considered during the Neka CCPP modelling procedure. The data set comes from the actual operation of the power plant and the surrounding environment conditions, as shown in Table 1.

Table 1 Input data for the gas and steam turbine cycles in the combined- cycle power plant (CCPP) (Khoshgoftar Manesh et al. 2021)
Full size table

The MED desalination unit comprises several identical desalination effects. In this approach, each desalination effect is modelled separately in EES software by using the formulation presented in Table 12 of Appendix A. Thereafter, the overall model is thermodynamically analyzed via connecting the different components of the system. Table 2 displays the input data used to model the RO and MED units. The modelling equations of the RO unit are also presented in Table 12 of Appendix A.

Table 2 Input data for the RO and MED desalination units (Mistry et al. 2013; Khoshgoftar Manesh et al. 2021)
Full size table

3.2 Exergy Analysis

The exergy analysis is a valuable tool to assess the streams useful energy and the potential for optimization of different equipment units. In this approach, exergy is stratified into physical and chemical exergy as given by Eqs. (3) and (4).

$$e^{{{\text{PH}}}} = \left( {u - u_{0} } \right) + p_{0} \left( {v - v_{0} } \right) - T_{0} \left( {s - s_{0} } \right)$$
(3)
$$e^{{{\text{CH}}}} = \sum {x_{k} \overline{e}_{k}^{{{\text{CH}}}} + \overline{R}T_{0} } \sum {x_{k} \ln_{k} x}$$
(4)

The specific chemical exergy of the methane stream is expressed by Eq. (5) (Bejan et al. 1996).

$$e_{{{\text{methane}}}}^{{{\text{CH}}}} = 1.037 \times {\text{LHV}}_{{{\text{methane}}}}$$
(5)

The seawater chemical exergy is calculated (in kJ/kmol) as follows (Sharqawy et al. 2011; Dincer and Rosen 2013).

$$e\overline{x}_{{{\text{sw}}}}^{{{\text{CH}}}} = n_{{\text{s}}} \left( {\overline{\mu }_{{\text{s}}} - \overline{\mu }_{{\text{s}}}^{0} } \right) - n_{{\text{w}}} \left( {\overline{\mu }_{{\text{w}}} - \overline{\mu }_{{\text{w}}}^{0} } \right)$$
(6)

where \({n}_{\mathrm{s}}\) and \({n}_{\mathrm{w}}\) denote the salt and water moles in seawater, respectively. In addition, \(\overline{\mu }_{{\text{s}}}\) and \(\overline{\mu }_{{\text{w}}}\) are the molar chemical potential of salt and water, respectively. The superscript zero sets the dead state, given as \({\mathrm{salinity}}_{0}={\mathrm{salinity}}_{\mathrm{feed}}\) and \(\overline{\mu }^{0} = f\left( {P_{0} ,T_{0} ,{\text{salinity}}_{0} } \right)\).

The exergy rate of each stream is obtained by multiplying of the specific exergy rate with mass flow rate as follows.

$${\dot{E}}_{k}={\dot{m}}_{k}\times {e}_{k}$$
(7)

The fuel and product exergy rates are employed to measure the component exergy destruction rate as expressed by Eq. (8).

$${\dot{E}}_{D,k}={\dot{E}}_{F,k}-{\dot{E}}_{P,k}$$
(8)

The exergy efficiency of each equipment unit is defined by Eq. (9).

$${\varepsilon }_{k}=\frac{\dot{E}{x}_{P,k}}{\dot{E}{x}_{F,k}}$$
(9)

It is important to note that the chemical exergy of the fuel contributes to a larger share of the system input exergy:

$$e{x}^{\mathrm{CH}}=\beta \times {\mathrm{LHV}}_{\mathrm{fuel}}$$
(10)

where \(\beta\) is the ratio of the fuel exergy to its low heating value (LHV), which is calculated as follows.

$$\beta =\frac{1.044+0.16\frac{H}{C}-0.34493\frac{O}{C}(1+0.0531\frac{H}{C})}{1-0.4142\frac{O}{C}}$$
(11)

where \(H/C\) and \(O/C\) represent the atomic ratios of the fuel.

The equations regarding the exergy destruction and efficiency of the system components are given in Table 3.

Table 3 Exergy destruction relationships for the distinct integrated system components (Khoshgoftar Manesh et al. 2021)
Full size table

3.3 Exergoeconomic Analysis

In the exergoeconomic assessment, the exergy analysis is combined with economic principles, including investment costs and maintenance and repair expenses. The final exergy destruction cost of the system components is determined through Eq. (12) (Dinçer et al. 2017).

$${\dot{Z}}_{k}=\frac{{\Phi }_{k}\times {\mathrm{PEC}}_{k}\times \mathrm{CRF}}{3600\times N}$$
(12)

where \({\Phi }_{k}\) indicates the maintenance factor (herein 1.06), whereas N is the annual plant operating hours (i.e., 8000 h). Moreover, CRF in previous equation indicates the capital recovery factor as determined by Eq. (13) (Bejan et al. 1996):

$$\mathrm{CRF}=\frac{i\times (1+i{)}^{n}}{(1+i{)}^{n}-1}$$
(13)

where n represents the plant lifetime (i.e., 25 years) and i the rate of interest rate (Bejan et al. 1996; Dinçer et al. 2017). In Eq. (12), \({\mathrm{PEC}}_{k}\) denotes the purchase equipment cost of different system components as charted in Table 4.

Table 4 Purchase equipment cost (PEC) of the different system components
Full size table

After computing each component cost rate, the exergoeconomic balance is applicable by solving the matrix balance equation for each component as given by the following formulation.

$${\dot{C}}_{\mathrm{P},k}={\dot{Z}}_{k}+{\dot{C}}_{\mathrm{F},k}-{\dot{C}}_{L,k}$$
(14)
$$\sum_{i}{{\dot{Z}}_{k}+\dot{C}}_{i,k}+{\dot{C}}_{q,k}=\sum_{e}{{\dot{C}}_{w,k}+\dot{C}}_{e,k}$$
(15)

where \({\dot{C}}_{\mathrm{F}}\) and \({\dot{C}}_{\mathrm{P}}\) are the fuel stream and product stream cost rates of each system component. In addition, the cost of each system stream \({\dot{C}}_{i}\) is determined by multiplying the exergy rate and the specific cost as follows.

$${{\dot{C}}_{i}={\dot{E}}_{i}{\times c}_{i}}$$
(16)

The cost rate of exergy destruction of each system unit is expressed by Eq. (17) (Bejan et al. 1996).

$${\dot{C}}_{D,k}={\dot{E}}_{D,k}{\times c}_{F,k}$$
(17)

The exergoeconomic factor \({f}_{k}\) for the different system units is given as follows.

$${f}_{k}=\frac{{\dot{Z}}_{k}}{{{c}_{f,k}\cdot {\dot{E}}_{D,k}+\dot{Z}}_{k}}$$
(18)

Finally, the relative cost difference for each system unit is expressed as (Bejan et al. 1996):

$${r}_{k}=\frac{{c}_{P,k}-{c}_{F,k}}{{c}_{F,k}}=\frac{1-{\varepsilon }_{k}}{{\varepsilon }_{k}}+\frac{{\dot{Z}}_{k}}{{c}_{f,k}\cdot \dot{E}{x}_{P,k}}$$
(19)

3.4 Exergoenvironmental Analysis

Life cycle assessment (LCA) is an environmental assessment tool used broadly for products, processes, and services. The LCA is usually employed in the follow-up of technical and economic analysis. In this study, LCA is implemented by means of an exergoenvironmental analysis. In this framework, the relationship between each stream exergy and its environmental impacts is expressed by Eq. (20) (Cavalcanti 2017).

$${\dot{B}}_{i}={b}_{i} {\times\dot{E}}_{i}$$
(20)

where \({\dot{B}}_{i}\) is the environmental impact rate expressed in points per second (pts/s), while \({b}_{i}\) indicates the rate of per exergy environmental impact in pts/kJ, and \({\dot{E}}_{i}\) the stream exergy rate in kW.

Similar to the exergoeconomic analysis, the exergoenvironmental analysis can be performed using balance equations as follows (Cavalcanti 2017).

$${\dot{B}}_{P,k}={\dot{B}}_{F,k}-{\dot{B}}_{L,k}+{\dot{Y}}_{k}$$
(21)
$${\sum }_{e}{\stackrel{.}{B}}_{\mathrm{out},k}+{\stackrel{.}{B}}_{w,k}={\stackrel{.}{B}}_{q,k}-{\sum }_{i}{\stackrel{.}{B}}_{\mathrm{in},k}+{\dot{Y}}_{k}$$
(22)

where \({\dot{Y}}_{k}\) is the environmental impact rate of the kth system component, which is defined through ECO Indicator 99 methodology (Goedkoop et al. 2000) as obtained by Eq. (23) (Cavalcanti 2017).

$${Y}_{k}=b{m}_{k}\times {w}_{k}$$
(23)

where \(b{m}_{k}\) and \({w}_{k}\) are the environmental impact per weight expressed in mpts/kg, and the kth component weight function given in tons, respectively. The previous parameters are listed in Tables 5 and 6, correspondently.

Table 5 Environmental impacts per unit weight (\(b{m}_{k}\)) for different system components (Khoshgoftar Manesh et al. 2021)
Full size table
Table 6 Weight functions for different system components (\({w}_{k}\)) (Cavalcanti 2017; Khoshgoftar Manesh et al. 2021)
Full size table

The exergoenvironmental factor is a valuable benchmark expressed as the ratio of the environmental impact of the equipment unit to its total environmental impact accounting for the construction to destruction process. Therefore, a factor close to one in Eq. (24) indicates that the current environmental impact of the equipment is more significant than the environmental impact of its destruction (Cavalcanti 2017).

$${f}_{b,k}=\frac{{\dot{Y}}_{k}}{{\dot{Y}}_{k}+{b}_{f,k}\cdot \dot{E}{x}_{D,k}}$$
(24)

The relative difference in environmental impact is given by Eq. (25) (Cavalcanti 2017).

$$r{b}_{k}=\frac{{b}_{P,k}-{b}_{F,k}}{{b}_{F,k}}=\frac{1-{\varepsilon }_{k}}{{\varepsilon }_{k}}+\frac{{\dot{Y}}_{k}}{{b}_{f,k}\cdot \dot{E}{x}_{P,k}}$$
(25)

The rate of environmental impact related to the RO desalination unit is obtained as follows (mpts/h·m3) (Vazini Modabber and Khoshgoftar Manesh 2020a, b).

$${\dot{Y}}_{\mathrm{RO}}=0.00595+0.0195\left(\frac{\rho \cdot {\dot{W}}_{\mathrm{RO}}}{3600\cdot {\dot{m}}_{\mathrm{RO}-\mathrm{distillate}}}\right)$$
(26)

In this study, the environmental impact rate of the MED unit is considered to be equal to \(1.277\) mpts/(h m3) (Raluy et al. 2006).

3.5 Optimization Procedure

The application of exergic, economic, and environmental analyses paves the way for optimization of energy systems to obtain optimal operating conditions. In this study, the multi-objective genetic algorithm (MOGA) is developed based on the water cycle algorithm (WCA), which is implemented in the MATLAB software environment. The WCA is associated with the movement of rivers and streams in the direction of the sea relating to the water cycle process. Because of this progression, the principal design variable population (specifically, the population of streams) is arbitrarily raised in the event of rain or precipitation. The sea is assumed to be the optimal solution with the highest quality of cost functions. After that, nearby streams exhibiting comparable cost function characteristics are designated as the rivers. Therefore, the remaining solutions are regarded as streams flowing to the sea and the rivers. Finally, a primary population is established for the matrix of the streams during the optimization process. The following algorithm can be developed for N-dimensional optimization (Sadollah et al. 2015):

$${N}_{\mathrm{sr}}=\hbox{number of Rivers}+1$$
(27)
$${N}_{\mathrm{stream}}={N}_{\mathrm{pop}}-{N}_{\mathrm{sr}}$$
(28)

where \(N\) and \({N}_{\mathrm{pop}}\) are the number of design variables and total population, respectively (Sadollah et al. 2015). Moreover,

$${\mathrm{NS}}_{n}=\mathrm{round}\left(\left|\frac{{\mathrm{Cost}}_{n}}{{\sum }_{i=1}^{{N}_{\mathrm{sr}}}{\mathrm{Cost}}_{i}}\right|\times {N}_{\mathrm{stream}}\right)n=1, 2, \dots , {N}_{\mathrm{sr}}$$
(29)

where \({\mathrm{NS}}_{n}\) is the number of streams flowing to specific rivers and the sea.

The location of the streams and the rivers is obtained by Eqs. (30)–(32) (Sadollah et al. 2015):

$${\overrightarrow{X}}_{\mathrm{Stream}}^{i+1}={\overrightarrow{X}}_{\mathrm{Stream}}^{i}+\mathrm{rand}\times C\times ({\overrightarrow{X}}_{\mathrm{River}}^{i}-{\overrightarrow{X}}_{\mathrm{Stream}}^{i})$$
(30)
$${\overrightarrow{X}}_{\mathrm{Stream}}^{i+1}={\overrightarrow{X}}_{\mathrm{Stream}}^{i}+\mathrm{rand}\times C\times ({\overrightarrow{X}}_{\mathrm{Sea}}^{i}-{\overrightarrow{X}}_{\mathrm{Stream}}^{i})$$
(31)
$${\overrightarrow{X}}_{\mathrm{River}}^{i+1}={\overrightarrow{X}}_{\mathrm{River}}^{i}+\mathrm{rand}\times C\times ({\overrightarrow{X}}_{\mathrm{Sea}}^{i}-{\overrightarrow{X}}_{\mathrm{River}}^{i})$$
(32)

where rand denotes a random number, homogeneously distributed between 0 and 1. The new location of the streams is defined as follows (Sadollah et al. 2015).

$${\overrightarrow{X}}_{\mathrm{Stream}}^{\mathrm{New}}=L\overrightarrow{B}+\mathrm{rand}\times (U\overrightarrow{B}-L\overrightarrow{B})$$
(33)

where LB and UB represent the lower and upper bounds, respectively, considered in the problem.

The \({d}_{\mathrm{max}}\) value adaptively reduces as (Sadollah et al. 2015)

$${d}_{\mathrm{max}}^{i+1}={d}_{\mathrm{max}}^{i}-\frac{{d}_{\mathrm{max}}^{i}}{\mathrm{Max Iteration}}$$
(34)

After the generation of the initial population, the WCA is performed to eliminate the weaker solutions (streams). The remaining solutions at the end of this process are considered the dominant solutions. These prevalent solutions are called the Pareto frontier optimal solutions. However, it is appropriate to select one of these solutions as the most suitable one. The decision-making process can be done using the concept of distance, where the nearest point to the ideal point could be identified as the selected optimal solution (SOS). Hence, the ideal point coordinates are taken from the Pareto frontier set of solutions. Each element of this point presents the best conditions in the Pareto frontier. This ideal point is not real and cannot be achieved in practice. However, the nearest solution to this point can be selected as the optimal solution.

4 Results and Discussion

4.1 Thermodynamic Results Validation

In Appendix A, Tables 13 and 14 display the critical process parameters obtained from simulations via Thermoflex and MATLAB software, determined for the system components and process streams. It is noted that the Thermoflex simulation is based on the actual data obtained from the Neka CCPP. Therefore, comparing the results of the developed MATLAB code with Thermoflex simulations will make it possible to validate the modelling results obtained. As shown in Tables 13 and 14, the results of the thermodynamic modelling in MATLAB and the accurate data of Neka CCPP are in reasonable agreement. In addition, since the existing Neka CCPP does not have a RO desalination unit, the developed MATLAB code developed for this unit should be verified by other research sources. Hence, the thermodynamic modelling results of the RO desalination system obtained from MATLAB are compared to previous studies in literature in Table 15. In this case, the modelling results demonstrate good accordance with the studies of Al-Zahrani et al. (2012) and Zhou et al. (2006). Finally, Table 16 presents the MED unit’s validation results using the simulation outputs performed in the Thermoflex software. The MED simulation results also display reasonable agreement with Thermoflex, presenting errors below 4%.

The conventional Neka CCPP's thermodynamic modelling indicates that 8.43 kg/s fuel is fed into the system to co-generate steam power at 80 MW and gas power at 132.15 MW. A stream of 3.6 kg/s is drawn from the low-pressure segment of the CCPP to supply the stimulus vapor of the MED for integration with RO-MED desalination units. Moreover, the outlet mass flow of the MED cooling water section is used as inlet flow of the RO desalination unit. The unit generates freshwater at approximately 20 kg/s stemmed from the seawater with a 12.48 kg/s mass flow rate.

The results also show that the RO unit produces 6.54 kg/s of freshwater. Furthermore, the system integration denotes a 3.79% increase in fuel consumption. In addition, the overall power production is decreased by 19% to produce 26.54 kg/s freshwater. In this case, the Neka CCPP’s energy efficiency is reduced by 2.49% (47.98% to 45.49%) through its integration with desalination units.

4.2 Exergic, Exergoeconomic, and Exergoenvironmental Results

Table 17 exhibits the results from the exergic, exergoeconomic, and exergoenvironmental analyses for different process streams. In addition, the results for system components are presented in Table 18. As observed, the exergy efficiency of MED and RO desalination units and condensers (31.59, 19.51, and 34.56%) is lower than that of the other components. The highest exergy efficiency is attributed to the GT unit at 95.87%. Moreover, the exergoeconomic efficiency of the CC (1.87%) and the condenser (1.46%) is lower in comparison to other system components. The latter result is a consequence of the elevated costs and environmental impacts of exergy destruction in these equipment components, hence presenting greater potential for improving system performance owing to their undesirable effect on costs and the environment, to the detriment of cost increase. Furthermore, the HRSG and condenser with relatively low exergoenvironmental factors (2.19% and 0.003%) show that their exergy destruction has large undesirable impacts on the environment. Therefore, their exergy degradation should be reduced to decrease the environmental impacts of the integrated system.

Table 18 also demonstrates that the difference in the MED relative cost is considerably lower than the RO system. This indicates that the MED desalination system's cost of freshwater production is lower than the RO unit's cost of fuel. Additionally, the MED unit has the highest rate of environmental impact, at 0.025 pts/s, while the GT has the highest cost rate at 0.047 US$/s. When compared to other pieces of equipment, the CC, GT, and ST system units have a greater impact on the environment and incur a higher cost for exergy destruction. Therefore, performance improvement in these equipment units can decrease their exergy destruction and avoid cost waste, in addition to reducing environmental impacts.

The distribution of exergy destruction share in system components is a significant outcome of exergy analysis. In this way, Fig. 3 depicts the exergy destruction distribution share of the different system components in the integrated system. The findings indicate that the CC unit accounts for the largest exergy destruction rate at 57% share. In addition, the HRSG and GT units account for 9% each, while RO and MED desalination systems together represent only a 2% share. The previous results indicate that reducing the GT cycle exergy destruction may have a positive impact on the overall Neka CCPP's performance.

Fig. 3
figure 3

Exergy destruction distribution share of system components

Full size image

4.3 Optimization Results

The optimization results for the integrated RO-MED and CCPP system are presented in this section. Tables 7 and 8 display the Pareto frontier optimal solutions for the decision variables and the objective functions, respectively. As mentioned above, to select the most suitable solution, it is suggested to employ the concept of distance between each solution and the ideal point. The distance for each re-dimensioned solution in the Pareto frontier optimal solutions set is shown in Table 9, which is relevant to the objective functions. Hence, the most suitable solution can be derived by comparison of the results in Table 9 and the calculated distances. This is regarded as the selected optimal solution (SOS), which is the closest to the ideal (equilibrium) point.

Table 7 Pareto frontier optimal solutions for decision variables
Full size table
Table 8 Pareto frontier optimal solutions for objective functions
Full size table
Table 9 Pareto frontier optimal solutions for objective functions in dimensionless form
Full size table

Table 10 shows the selected optimal solution for the objective functions. Additionally, the objective function values in the base case (pre-optimization) and each objective function improvement during the optimization process are presented. Finally, Table 11 displays the selected optimal solutions for the decision variables. The optimum solution is reached by the objective functions using these values.

Table 10 The selected optimal solution for objective functions
Full size table
Table 11 The selected optimal solution for decision variables
Full size table

The results shown in Table 10 indicate that the system optimization improves the exergy efficiency by 8.405% (from 42.731 to 51.136%). At the same time, the power and freshwater costs are reduced from 39.913 to 36.553 \(\mathrm{US\$}/\mathrm{MWh}\) and from 1.342 to 0.948 \(\mathrm{US\$}/{\mathrm{m}}^{3}\) (i.e., by 3.360 \(\mathrm{US\$}/\mathrm{MWh}\) and 0.394 \(\mathrm{US\$}/{\mathrm{m}}^{3}\)), respectively. Furthermore, the power and freshwater environmental impacts are decreased from 22.951 to 19.682 \(\mathrm{pts}/\mathrm{MWh}\) and 1.066 to 0.709 \(pts/{m}^{3}\) (i.e., by 3.268 \(\mathrm{pts}/\mathrm{MWh}\) and 0.357 \(\mathrm{pts}/{\mathrm{m}}^{3}\)), respectively. Accordingly, the optimization approach enhances the objective functions of the integrated system from all exergic, exergoeconomic, and exergoenvironmental perspectives. As these results demonstrate, the system optimization has improved the integrated plant’s performance by boosting the cycle efficiency and reducing product costs and environmental impacts.

Since the optimization process encompasses five objective functions, the results are five-dimensional, which cannot be shown in a graphical form. Therefore, to better demonstrate the optimization results, other two-objective optimizations have been performed in this study, allowing us to obtain additional two-dimensional sets of results. Thus, Fig. 4 shows the Pareto frontier optimal solutions for minimization of power produced cost and exergy efficiency. Also, Fig. 5 displays the Pareto frontier optimal solutions for minimizing of the produced freshwater and power costs.

Fig. 4
figure 4

The Pareto frontier optimal solutions for the objective functions of \({\psi }_{\mathrm{Total}}\) and \({c}_{w,\mathrm{total}}\)

Full size image
Fig. 5
figure 5

The Pareto frontier optimal solutions for the objective functions of \({c}_{w,\mathrm{total}}\) and \({c}_{d,\mathrm{total}}\)

Full size image

It should be noted that the solutions presented in Figs. 4 and 5 remained after the optimization process and are, therefore, the dominant solutions. As explained in the methodology section, the weaker solutions were eliminated via the operators of the optimization algorithm. The selection of the most suitable solution, referred to as the selected optimal solution (SOS), is based on the distance concept. The SOS (represented by a green point in the charts) corresponds to the point closest to the ideal point (blue point).

5 Conclusions

This study investigates the potential integration of a RO-MED desalination system into the existing Neka CCPP via GA-based multi-objective optimization. To this aim, the integrated system is thermodynamically modelled and simulated utilizing the MATLAB and EES software environments. The results for the different integrated system components and process streams are validated via Thermoflex software simulations based on actual data from the Neka power plant. Furthermore, comprehensive energy, exergy, exergoeconomic, and exergoenvironmental (4E) analyses are conducted to assess the performance of the new integrated CCPP and RO-MED system. In addition, a GA-based multi-objective water cycle algorithm (MOWCA) is developed to optimize the operating conditions and energy, exergy, economic, and environmental performance indicators of the integrated system.

The results reveal that the combustion chamber has the largest exergy destruction share of 57%, while the MED and RO desalination units contribute a 2% combined share. The economic and environmental analyses applied to the integrated system indicates that the gas turbine presents the highest investment cost of 0.05 US$/s. Moreover, the highest environmental impact rate is related to the MED desalination unit, at 0.025 pts/s. According to these results, a potential reduction in the system capital investment and operating costs is achievable via the increase in the exergy destruction share of the RO unit owing to its high exergoeconomic factor. Additionally, the economic analysis results indicate that the production cost of electricity from the integrated power and desalination system is 0.04 US$/kWh, while the freshwater production cost via the RO and MED desalination units is 1.8 US$/m3 and 2.5 US$/m3, respectively. Furthermore, the environmental analysis reveals that the gas turbine (96.8%) and the air compressor (84.7%) have the highest exergoenvironmental factor, while the condenser (0.003) and combustion chamber (0.06) have the lowest.

By implementing the multi-objective water cycle algorithm, the power and produced freshwater costs are reduced from 39.9 to 36.5 US$/MWh (8.42%) and 1.3 to 0.9 US$/m3 (29.36%), respectively. The environmental impacts of the produced power and freshwater are also decreased from 22.951 to 19.682 pts/MWh (14.24%) and 1.066 to 0.709 pts/m3 (33.49%), respectively. Accordingly, the objective functions of the integrated system are improved via optimization from exergic, exergoeconomic, and exergoenvironmental perspectives. The findings also indicate that the system optimization has improved the integrated system performance by boosting cycle efficiency and lowering product costs and environmental impacts. Therefore, the results demonstrate that the integration of desalination processes into the Neka CCPP is not only thermodynamically and economically viable, but also a more sustainable solution towards reducing environmental impacts.

Finally, future research will focus on integrating renewable energy resources such as solar energy and biomass. In addition, the feasibility of coupling other technologies for desalination will be investigated, including MSF and MSF-RO, among others. In follow-up studies, the risk and reliability analyses of the use of desalination in the combined power cycle can also be considered.