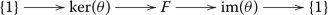Oriented pro-$\ell$ groups with the Bogomolov–Positselski property

Abstract

For a prime number $\ell$ we say that an oriented pro-$\ell$ group $(G,\theta )$ has the Bogomolov–Positselski property if the kernel of the canonical projection on its maximal $\theta$-abelian quotient $\pi ^{\mathrm {ab}}_{G,\theta }:G\rightarrow G(\theta )$ is a free pro-$\ell$ group contained in the Frattini subgroup of G. We show that oriented pro-$\ell$ groups of elementary type have the Bogomolov–Positselski property (cf. Theorem 1.2). This shows that Efrat’s Elementary Type Conjecture implies a positive answer to Positselski’s version of Bogomolov’s Conjecture on maximal pro-$\ell$ Galois groups of a field $\mathbb {K}$ in case that $\mathbb {K}^\times /(\mathbb {K}^\times )^\ell$ is finite. Secondly, it is shown that for an $H^\bullet$-quadratic oriented pro-$\ell$ group $(G,\theta )$ the Bogomolov–Positselski property can be expressed by the injectivity of the transgression map $d_2^{2,1}$ in the Hochschild–Serre spectral sequence (cf. Theorem 1.4).

1 Introduction

By an $\ell$ -oriented profinite group for a prime number $\ell$ we understand a profinite group G together with a continuous homomorphism of profinite groups $\theta :G\rightarrow \mathbb {Z}_\ell ^\times$, where $\mathbb {Z}_\ell ^\times$ denotes the group of units of the ring of $\ell$-adic integers $\mathbb {Z}_\ell$. An $\ell$-oriented pro-$\ell$ group $(G,\theta )$ will be simply called an oriented pro-$\ell$ group. For a field $\mathbb {K}$, we denote by $G_{\mathbb {K}}=\mathrm {Gal}(\bar{\mathbb {K}}^{\mathrm {sep}}/\mathbb {K})$ its absolute Galois group, where $\bar{\mathbb {K}}^{\mathrm {sep}}$ denotes a separable closure of $\mathbb {K}$. For any prime number $\ell$, $G_{\mathbb {K}}$ carries naturally the cyclotomic $\ell$-orientation $\tilde{\theta }_{\mathbb {K},\ell }:G_{\mathbb {K}}\rightarrow \mathbb {Z}_\ell ^\times$ (cf. Example 2.1 and [26, (1.3)]). The following conjecture formulated by L. Positselski in [20, Conjecture 2] was motivated by an earlier conjecture of F. Bogomolov (cf. [2] and [20, Conjecture 1], see also Remark 3.3).

Conjecture 1.1

Let $\mathbb {K}$ be a field containing a primitive $\ell {\mathrm {th}}$-root of unity, and also $\sqrt{-1}$ if $\ell =2,$ and set

$$\begin{aligned} \root \ell ^\infty \of {\mathbb {K}}=\mathbb {K}\left( \root \ell ^n \of {a},a\in \mathbb {K},n\ge 1\right) . \end{aligned}$$

Then the maximal pro-$\ell$ Galois group of $\root \ell ^\infty \of {\mathbb {K}}$ is a free pro-$\ell$ group.

A profinite group G admits a maximal pro-$\ell$ quotient $G(\ell )=G/O^\ell (G)$, where $O^\ell (G)$ is the closed normal subgroup of G being generated by all pro-q Sylow subgroups for all prime numbers $q\not =\ell$. Apart from $\mathrm {ker}(\theta )$, an oriented pro-$\ell$ group $(G,\theta )$ contains the distinguished closed subgroups

$$\begin{aligned} K_\theta (G)&=\mathrm {cl}\left( \left\langle \, h^{-\theta (g)}ghg^{-1}\,\mid \, g\in G,h\in \mathrm {ker}(\theta ) \,\right\rangle \right) \end{aligned}$$

(1.1)

and

$$\begin{aligned} I_\theta (G)&=\mathrm {cl}\left( \left\langle \,h\in \mathrm {ker}(\theta )\,\mid \, \exists k\in \mathbb {N}_0: h^{\ell ^k}\in K_\theta (G) \,\right\rangle \right) \end{aligned}$$

(1.2)

—the former introduced in [10]—i.e., $I_\theta (G)$ is the closure of the isolator (cf. §66 [12]) of $K_\theta (G)$ in $\mathrm {ker}(\theta )$. An oriented pro-$\ell$ group $(G,\theta )$ is said to be $\theta$ -abelian, if the subgroup $K_{\theta }(G)$ is trivial and if $\ker (\theta )$ is a free abelian pro-$\ell$ group (in this case G is a free abelian-by-cyclic pro-$\ell$ group for $\ell \not =2$, cf. Remark 2.2). By definition $K_\theta (G)$ is a closed normal subgroup of G contained in the Frattini subgroup $\Phi (G)=\mathrm {cl}(G^\ell \cdot [G,G])$ of G. Note that

$$\begin{aligned} {[}\mathrm {ker}(\theta ),\mathrm {ker}(\theta )]\subseteq K_\theta (G)\subseteq \mathrm {ker}(\theta ), \end{aligned}$$

(1.3)

so that the quotient $\mathrm {ker}(\theta )/K_\theta (G)$ is an abelian pro-$\ell$ group, and $I_{\theta }(G)/K_\theta (G)$ is its torsion subgroup. In particular, if $\theta :G\rightarrow \mathbb {Z}_\ell ^\times$ is trivial (i.e., $\theta$ is identically equal to 1), then $K_\theta (G)$ coincides with the closure of the commutator subgroup of G.

Every oriented pro-$\ell$ group $(G,\theta )$ admits a maximal $\theta$-abelian quotient $(G(\theta ),\bar{\theta })$, where $G(\theta )=G/I_\theta (G)$ and $\bar{\theta }:G(\theta )\rightarrow \mathbb {Z}_\ell ^\times$ is the homomorphism induced by $\theta$. Namely, $(G(\theta ),\bar{\theta })$ is $\bar{\theta }$-abelian and one has a canonical surjective homomorphism

$$\begin{aligned} \pi ^{\mathrm {ab}}_{G,\theta }:(G,\theta )\longrightarrow (G(\theta ),\bar{\theta }) \end{aligned}$$

of oriented pro-$\ell$ groups satisfying the following: for every morphism $\psi :(G,\theta )\rightarrow (A,\theta ^\circ )$ of oriented pro-$\ell$ groups onto a $\theta ^\circ$-abelian pro-$\ell$ group $(A,\theta ^\circ )$ there exists a unique morphism of oriented pro-$\ell$ groups $\psi ^{\mathrm {ab}}_\theta :(G(\theta ),\bar{\theta })\rightarrow (A,\theta ^\circ )$ such that $\psi =\psi ^{\mathrm {ab}}_\theta \circ \pi ^{\mathrm {ab}}_{G,\theta }$ (cf. Proposition 2.3).

The hypothesis of Conjecture 1.1 on the primitive $\ell {\mathrm {th}}$-roots lying in $\mathbb {K}$ implies that the maximal pro-$\ell$ quotient $G_{\mathbb {K}}(\ell )$ of the absolute Galois group $G_{\mathbb {K}}$ carries naturally an $\ell$-orientation

$$\begin{aligned} \tilde{\theta }_{\mathbb {K},\ell }:G_{\mathbb {K}}(\ell )\longrightarrow \mathbb {Z}_\ell ^\times . \end{aligned}$$

(1.4)

So, Conjecture 1.1 predicts that $I_{\tilde{\theta }_{\mathbb {K},\ell }}(G_\mathbb {K}(\ell ))$ is a free pro-$\ell$ group contained in the Frattini subgroup $\Phi (G_\mathbb {K}(\ell ))$ of $G_\mathbb {K}(\ell )$ (cf. Proposition 2.6 and § 3.1). At this point it should be mentioned that in fact one has to deal with two properties of oriented pro-$\ell$ groups. The oriented pro-$\ell$ group $(G,\theta )$ is said to be Kummerian, if $I_{\theta }(G)=\mathrm {ker}(\pi ^{\mathrm {ab}}_{G,\theta })$ is contained in the Frattini subgroup $\Phi (G)$ of G. This property can be reformulated in several different ways (cf. Proposition 2.6). Bearing this fact in mind we say that the Kummerian (cf. §2.3) oriented pro-$\ell$ group $(G,\theta )$ has the Bogomolov–Positselski property, if $I_\theta (G)=\mathrm {ker}(\pi ^{\mathrm {ab}}_{G,\theta })$ is a free pro-$\ell$ group. For example, the oriented pro-$\ell$ group $(G,\mathbf {1})$, where $\mathbf {1}$ is the trivial $\ell$-orientation on G, is Kummerian if, and only if, the maximal abelian pro-$\ell$ quotient $G^{\mathrm {ab}}=G/G^\prime$ is a free abelian pro-$\ell$ group, and has the Bogomolov–Positselski property if, and only if, it is Kummerian and the closure of the commutator subgroup of G is a free pro-$\ell$ group.

The class of oriented pro-$\ell$ groups $\mathbf {ET}_\ell$ of elementary type is the smallest class of oriented pro-$\ell$ groups containing $\mathbb {Z}_\ell$ with all its $\ell$-orientations, all Demushkin pro-$\ell$ groups with their natural $\ell$-orientation (cf. [26, Proposition 5.2]) and which is closed with respect to free products in the category of oriented pro-$\ell$ groups and fibre products (cf. Sect. 5.3). The Elementary Type Conjecture formulated by Efrat [8] predicts that for every field $\mathbb {K}$ containing an $\ell {\mathrm {th}}$-root of unity (and also $\sqrt{-1}$ if $\ell =2$) satisfying $|\mathbb {K}^\times /(\mathbb {K}^\times )^\ell |<\infty$ the oriented pro-$\ell$ group $(G_\mathbb {K}(\ell ),\tilde{\theta }_{\mathbb {K},\ell })$ must be of elementary type. The first main purpose of this paper is to establish the following theorem relating the Elementary Type Conjecture with Conjecture 1.1.

Theorem 1.2

Every oriented pro-$\ell$ group of elementary type has the Bogomolov–Positselski property.

From Theorem 1.2 one concludes the following (cf. Proposition 5.13):

Corollary 1.3

Let $\mathbb {K}$ be a field containing a primitive $\ell {\mathrm {th}}$-root of 1 (and also $\sqrt{-1}$ if $\ell =2),$ such that the quotient $\mathbb {K}^\times /(\mathbb {K}^\times )^\ell$ is finite. Then Conjecture 1.1 holds true in the following cases:

• (a) $\mathbb {K}$ is finite;

• (b) $\mathbb {K}$ is a pseudo algebraically closed (PAC) field, or an extension of relative transcendence degree 1 of a PAC field;

• (c) $\mathbb {K}$ is an extension of transcendence degree 1 of a local field;

• (d) $\mathbb {K}$ is $\ell$-rigid (for the definition of $\ell$-rigid field see [32, p. 722]);

• (e) $\mathbb {K}$ is an algebraic extension of a global field of characteristic not $\ell$.

By the Norm Residue Theorem (cf. [11, 31, 33, 34]), the mod $\ell$-Milnor K-ring $K_\bullet ^M(\mathbb {K})/\ell$ of a field $\mathbb {K}$ is isomorphic to the cohomology algebra $H^\bullet (G_{\mathbb {K}}(\ell ),\mathbb {F}_\ell )$ provided $\ell \not =\mathrm {char}(\mathbb {K})$ and $\mathbb {K}$ contains a primitive $\ell {\mathrm {th}}$-root of unity. Moreover, L. Positselski showed in [20, Theorem 1.4] that Conjecture 1.1 is a consequence of a strong Koszulity property of the cohomology algebra $H^\bullet (G_{\mathbb {K}}(\ell ),\mathbb {F}_\ell )$.

Our second objective is to establish the following criterion ensuring the Bogomolov-Positselski property of an abstract oriented pro-$\ell$ group $(G,\theta )$. Surprisingly, it only depends on low-dimensional group cohomology, but in a sophisticated way (cf. Theorem 4.5).

Theorem 1.4

Let $(G,\theta )$ be a Kummerian oriented pro-$\ell$ group with a quadratic $\mathbb {F}_\ell$-cohomology algebra $H^\bullet (G,\mathbb {F}_\ell )$, and let

(1.5)

be the canonical extension of pro-$\ell$ groups. Then G has the Bogomolov–Positselski property if, and only if, the transgression map

$$\begin{aligned} d_2^{2,1}:H^2(G(\theta ),H^1(I_\theta (G),\mathbb {F}_\ell ))\longrightarrow H^4(G(\theta ),\mathbb {F}_\ell ) \end{aligned}$$

(1.6)

is injective.

Remark 1.5

As $\mathbf {s}$ is a Frattini pro-$\ell$ cover (i.e., $I_\theta (G)$ is contained in the Frattini subgroup of G, cf. Sect. 3.2), inflation yields an isomorphism $j^1:H^1(G(\theta ),\mathbb {F}_\ell )\rightarrow H^1(G,\mathbb {F}_\ell )$. Since $H^\bullet (G,\mathbb {F}_\ell )$ is quadratic, inflation may also be considered as a surjective homomorphism of graded $\mathbb {F}_\ell$-algebras

$$\begin{aligned} j^\bullet :H^\bullet (G(\theta ),\mathbb {F}_\ell )\longrightarrow H^\bullet (G,\mathbb {F}_\ell ), \end{aligned}$$

(1.7)

where the left-side term of (1.7) is the exterior algebra generated by $H^1(G(\theta ),\mathbb {F}_\ell )$ (cf. Sect. 4.1). By [20, Theorem 1.4], $(G,\theta )$ has the Bogomolov–Positselski property provided $H^\bullet (G,\mathbb {F}_\ell )$ is a Koszul $\mathbb {F}_\ell$-algebra and $\mathrm {ker}(j^\bullet )$ is a Koszul $H^\bullet (G,\mathbb {F}_\ell )$-module (cf. [20, §3.3]). Hence the natural question arising in this context is, whether one can express $\mathrm {ker}(d_2^{2,1})$ in terms of $\mathrm {Ext}^{s,t}_{H^{\bullet }(G,\mathbb {F}_\ell )}(\mathbb {F}_\ell ,\mathrm {ker}(j^\bullet ))$, $s\not =t$.

2 Oriented pro-$\ell$ groups

For a pro-$\ell$ group G and a positive integer n, $G^n$ will denote the closed subgroup of G generated by the n-th powers of all elements of G. Moreover, for two elements $g,h\in G$, we set

$$\begin{aligned} {}^gh=ghg^{-1},\quad \text {and}\quad [g,h]={}^{g}h\cdot h^{-1}, \end{aligned}$$

and for two subgroups $H_1,H_2$ of G, $[H_1,H_2]$ will denote the closed subgroup of G generated by all commutators [g, h] with $g\in H_1$ and $h\in H_2$. In particular, $G'$ will denote the closure of the commutator subgroup of G.

2.1 $\ell$-Orientations of profinite groups

Let $\mathbb {Z}_{\ell }$ denote the ring of $\ell$-adic integers, and let $\mathbb {Z}_{\ell }^\times$ denote its group of units. Note that $\mathbb {Z}_\ell ^\times$ is a virtual pro-$\ell$ group, in more detail:

• (a) if $\ell \ne 2$ then the Sylow pro-$\ell$ subgroup of $\mathbb {Z}_\ell ^\times$ is $1+\ell \mathbb {Z}_\ell =\{1+\ell \lambda \mid \lambda \in \mathbb {Z}_\ell \}$, which is free pro-$\ell$ cyclic;

• (b) if $\ell =2$ then $\mathbb {Z}_2^\times =1+2\mathbb {Z}_2\simeq \mathbb {Z}/2\times (1+4\mathbb {Z}_2)$, and the factor $1+4\mathbb {Z}_2$ is isomorphic to $\mathbb {Z}_2$.

An oriented pro-$\ell$ group $(G,\theta )$ is a pro-$\ell$ group G together with a continuous group homomorphism $\theta :G\rightarrow \mathbb {Z}_\ell ^\times$. Moreover, $(G,\theta )$ is said to be torsion-free if $\ell \ne 2$, or if $\ell =2$ and $\mathrm {im}(\theta )\subseteq 1+4\mathbb {Z}_2$—observe that in a torsion-free oriented pro-$\ell$ group $(G,\theta )$, G need not be a torsion free pro-$\ell$ group, e.g., $(\mathbb {Z}/\ell ,\mathbf {1})$ is a torsion-free oriented pro-$\ell$ as $\mathrm {im}(\mathbf {1})=\{1\}$.

Oriented pro-$\ell$ groups where introduced by Efrat [8] under the name “cyclotomic pro-$\ell$ pairs”. For an oriented pro-$\ell$ group $(G,\theta )$, $\mathbb {Z}_\ell (1)$ will denote the continuous left $\mathbb {Z}_\ell [\![G]\!]$-module which is isomorphic to $\mathbb {Z}_\ell$ as an abelian pro-$\ell$ group, such that $g\cdot v=\theta (g)\cdot v$ for every $g\in G$ and $v\in \mathbb {Z}_\ell (1)$ (cf. [26, § 1]). Conversely, if a pro-$\ell$ group G comes endowed with a continuous left $\mathbb {Z}_\ell [\![G]\!]$-module M which is isomorphic to $\mathbb {Z}_\ell$ as an abelian pro-$\ell$ group, then M induces an orientation $\theta :G\rightarrow \mathbb {Z}_\ell ^\times$ by $\theta (g)\cdot v=g\cdot v$ for every $g\in G$ and $v\in M$, such that $M\simeq \mathbb {Z}_\ell (1)$.

The fundamental examples of oriented pro-$\ell$ groups arise in Galois theory (cf. [10, § 4]).

Example 2.1

For a field $\mathbb {K}$, let $\bar{\mathbb {K}}^{\mathrm {sep}}$ denote a separable closure of $\mathbb {K}$, and let $\mu _{\ell ^\infty }$ denote the group of roots of 1 of $\ell$-power order lying in $\bar{\mathbb {K}}^{\mathrm {sep}}$. If $\mathbb {K}$ contains a primitive $\ell {\mathrm {th}}$-root of unity, then $\mu _{\ell ^\infty }$ is contained in the maximal pro-$\ell$ extension $\mathbb {K}(\ell )$ of $\mathbb {K}$. As $\mu _{\ell ^\infty }\simeq \mathbb {Z}[\frac{1}{\ell }]/\mathbb {Z}$ and $\mathrm {Aut}(\mathbb {Z}[\frac{1}{\ell }]/\mathbb {Z})$ is isomorphic to $\mathbb {Z}_\ell ^\times$, the action of the maximal pro-$\ell$ Galois group $G_{\mathbb {K}}(\ell )=\mathrm {Gal}(\mathbb {K}(\ell )/\mathbb {K})$ of $\mathbb {K}$ on $\mu _{\ell ^\infty }$ fixes the primitive $\ell {\mathrm {th}}$-roots of unity, and induces the $\ell$ -cyclotomic character

$$\begin{aligned} \tilde{\theta }_{\mathbb {K},\ell }:G_{\mathbb {K}}(\ell )\longrightarrow \mathbb {Z}_\ell ^\times . \end{aligned}$$

In particular,

$$\begin{aligned} \sigma (\zeta )=\zeta ^{\tilde{\theta }_{\mathbb {K},\ell }(\sigma )}\quad \text {for all }\sigma \in G_{\mathbb {K}}(\ell ),\zeta \in \mu _{\ell ^\infty }. \end{aligned}$$

Furthermore, one has $\mathrm {im}(\tilde{\theta }_{\mathbb {K},\ell })=1+\ell ^f\mathbb {Z}_\ell$—where f is the positive integer satisfying $|\mu _{\ell ^\infty }\cap \mathbb {K}^\times |=\ell ^f$—in case $\mu _{\ell ^\infty }\cap \mathbb {K}^\times$ is non-empty and finite, and $\mathrm {im}(\tilde{\theta }_{\mathbb {K},\ell })=\{1\}$ if $\mu _{\ell ^\infty }\subseteq \mathbb {K}^\times$. The continuous $G_{\mathbb {K}}(\ell )$-module $\mathbb {Z}_\ell (1)$ induced by the cyclotomic character is called the 1st Tate twist of $\mathbb {Z}_\ell$ (cf. [19, Definition 7.3.6]), and for every $n\ge 1$, $\mathbb {Z}_\ell (1)/\ell ^n$ is isomorphic to the $G_{\mathbb {K}}(\ell )$-module of the $\ell ^n$th roots of 1.

Note that oriented pro-$\ell$ groups form a category $\mathbf {Or}_\ell$, i.e., for $(G,\theta ), (H,\theta ^\prime )\in \mathrm {ob}(\mathbf {Or}_\ell )$ a morphism of oriented pro-$\ell$ groups $\phi :(G,\theta )\rightarrow (H,\theta ^\prime )$ is a continuous group homomorphism $\phi :G\rightarrow H$ of pro-$\ell$ groups satisfying $\theta ^\prime \circ \phi =\theta$.

For an oriented pro-$\ell$ group $(G,\theta )$ one has the following constructions.

• (a) Let N be a normal subgroup of G such that $N\subseteq \mathrm {ker}(\theta )$. Then one has an oriented pro-$\ell$ group

  $$\begin{aligned} (G,\theta )/N:=(G/N,\bar{\theta }), \end{aligned}$$

  where $\bar{\theta }:G/N\rightarrow \mathbb {Z}_\ell ^\times$ is the orientation induced by $\theta$.

• (b) Let A be an abelian pro-$\ell$ group. Then one has an oriented pro-$\ell$ group

  $$\begin{aligned} A\rtimes (G,\theta ):=(A\rtimes G,\tilde{\theta }), \end{aligned}$$

  where $gag^{-1}=a^{\theta (g)}$ for all $g\in G$ and $a\in A$, and $\tilde{\theta }=\theta \circ \pi$, where $\pi :A\rtimes G\rightarrow G$ is the canonical projection.

2.2 The maximal $\theta$-abelian quotient of an oriented pro-$\ell$ group

Let $(G,\theta )$ be a torsion-free oriented pro-$\ell$ group. Then $G/\mathrm {ker}(\theta )\simeq \mathrm {im}(\theta )$ is torsion-free, and thus either trivial or isomorphic to $\mathbb {Z}_\ell$. Therefore, the epimorphism $G\twoheadrightarrow G/\mathrm {ker}(\theta )$ splits, and since $ghg^{-1}\equiv h^{\theta (g)}\bmod K_\theta (G)$ for every $g\in G$ and $h\in \mathrm {ker}(\theta )$, one concludes that

$$\begin{aligned} (G,\theta )/K_\theta (G)\simeq \frac{\mathrm {ker}(\theta )}{K_\theta (G)}\rtimes (\mathrm {im}(\theta ),\mathrm {Id}_{\mathrm {im}(\theta )}). \end{aligned}$$

(2.1)

Remark 2.2

By (2.1), if $(G,\theta )$ is a torsion-free $\theta$-abelian oriented pro-$\ell$ group, then it is isomorphic to the oriented pro-$\ell$ group $\mathrm {ker}(\theta )\rtimes (\mathrm {im}(\theta ),\mathrm {Id}_{\mathrm {im}(\theta )})$. Conversely, if A is a free abelian pro-$\ell$ group, and $(\bar{G},\theta )$ is an oriented pro-$\ell$ group satisfying $\mathrm {ker}(\theta )=\{1\}$, then the oriented pro-$\ell$ group $(G,\tilde{\theta })=A\rtimes (\bar{G},\theta )$ is $\tilde{\theta }$-abelian, since $\mathrm {ker}(\tilde{\theta })=A$ is a free abelian pro-$\ell$ group, and as $ghg^{-1}=h^{\tilde{\theta }(g)}$ for every $g\in \bar{G}$ and $h\in A$ and thus $K_{\tilde{\theta }}(G)=\{1\}$.

Let $(G,\theta )$ be an oriented pro-$\ell$ group. Put $\bar{G}=G/I_\theta (G)$ and let $\bar{\theta }:\bar{G}\rightarrow \mathbb {Z}_\ell ^\times$ denote the induced orientation. Since the quotient $\mathrm {ker}(\theta )/I_\theta (G)$ is torsion-free (cf. Sect. 1), the oriented pro-$\ell$ group $(G(\theta ),\bar{\theta })$ is $\bar{\theta }$-abelian. This group together with the canonical projection

$$\begin{aligned} \pi ^{\mathrm {ab}}_{G,\theta }:G\longrightarrow G(\theta ) \end{aligned}$$

(2.2)

has the following universal property.

Proposition 2.3

Let $(G,\theta )$ be an oriented pro-$\ell$ group, let $(A,\theta ^\circ )$ be an oriented $\theta ^\circ$-abelian pro-$\ell$ group, and let $\psi :(G,\theta )\rightarrow (A,\theta ^\circ )$ be a continuous homomorphism of oriented pro-$\ell$ groups. Then $\psi$ factors through $\pi ^{ab}_{G,\theta },$ i.e., there exists a (unique) continuous group homomorphism

$$\begin{aligned} \psi ^{\mathrm {ab}}_{G,\theta }:(G(\theta ),\bar{\theta })\longrightarrow (A,\theta ^\circ ) \end{aligned}$$

satisfying $\psi =\psi ^{\mathrm {ab}}_{G,\theta }\circ \pi ^{\mathrm {ab}}_{G,\theta }$.

Proof

As $\psi$ is a homomorphism of oriented pro-$\ell$ groups, and as $(A,\theta ^\circ )$ is $\theta ^\circ$-abelian, one has

$$\begin{aligned} \psi (\mathrm {ker}(\theta ))\subseteq \mathrm {ker}(\theta ^\circ ) \quad \text {and}\quad \psi (K_\theta (G))\subseteq K_{\theta ^\circ }(A)=\{1\}. \end{aligned}$$

(2.3)

As $\mathrm {ker}(\theta ^\circ )$ is torsion-free, this implies that $\psi (I_\theta (G))=\{1\}$. Hence the induced homomorphism $\psi ^{\mathrm {ab}}_{G,\theta }:G(\theta )\rightarrow A$ of oriented pro-$\ell$ groups has the desired properties. $\square$

Remark 2.4

Let $(G,\theta )\simeq A\rtimes ((G,\theta )/\mathrm {ker}(\theta ))$ be a torsion-free $\theta$-abelian oriented pro-$\ell$ group. Then for every subgroup H of G one has

$$\begin{aligned} H\simeq (H\cap A)\rtimes (H/\mathrm {ker}(\theta \vert _H)), \end{aligned}$$

and thus the oriented pro-$\ell$ group $(H,\theta \vert _H)$ is split $\theta \vert _H$-abelian (cf. [26, Remark 3.12]).

2.3 Kummerian oriented pro-$\ell$ groups

Let $(G,\theta )$ be an oriented torsion-free pro-$\ell$ group. Since $\mathrm {im}(\theta )\subseteq 1+\ell \mathbb {Z}_\ell$, the action of G on the quotient $\mathbb {Z}_\ell (1)/\ell$ of the continuous G-module $\mathbb {Z}_\ell (1)$ is trivial, i.e., $\mathbb {Z}_\ell (1)/\ell \simeq \mathbb {F}_\ell$ as a trivial left $\mathbb {Z}_\ell [\![G]\!]$-module. In the proof of the subsequent proposition we will make use of the following

Fact 2.5

Let A be an abelian pro-$\ell$ group, and let B be a closed subgroup of A which is a direct summand of A satisfying $B\subseteq A^\ell$. Then $B=\{0\}$.

Proof

Let $A=B\oplus C$. Then $A^\ell =B^\ell \oplus C^\ell$, and as $B^\ell \subseteq B$, and $B\cap C=\{0\}$ one concludes that $B\subseteq B^\ell$, i.e., $B=B^\ell =\Phi (B)$. Hence $B=\{0\}$. $\square$

A torsion-free oriented pro-$\ell$ group $(G,\theta )$ is said to be Kummerian if the following equivalent properties are satisfied.

Proposition 2.6

Let $(G,\theta )$ be a torsion-free oriented pro-$\ell$ group. Then the following are equivalent:

• (i) the map $H^1(G,\mathbb {Z}_\ell (1)/\ell ^n)\longrightarrow H^1(G,\mathbb {F}_\ell )$ induced by the epimorphism of discrete left G-modules $\mathbb {Z}_\ell (1)/\ell ^n\twoheadrightarrow \mathbb {Z}_\ell (1)/\ell \simeq \mathbb {F}_\ell ,$ is surjective for every $n\ge 1$ (cf. [10]).

• (ii) The quotient $\mathrm {ker}(\theta )/K_\theta (G)$ is a free abelian pro-$\ell$ group.

• (iii) The oriented pro-$\ell$ group $(G,\theta )/K_\theta (G)=(G/K_\theta (G),\bar{\theta })$ is $\bar{\theta }$-abelian.

• (iv) $K_\theta (G)$ is isolated in $\mathrm {ker}(\theta ),$ i.e., $I_\theta (G)=K_\theta (G)$.

• (v) The group $H_{\mathrm {cts}}^2(G,\mathbb {Z}_\ell (1))$ is a torsion-free $\mathbb {Z}_\ell$-module.

• (vi) $I_{\theta }(G)\subseteq \Phi (G)$.

(Here $H_{\mathrm {cts}}^*$ denotes continuous cochain cohomology as defined by Tate [30]).

Proof

For G finitely generated the equivalence between (i) and (ii) was shown in [10, Theorem 5.6], and the equivalence between (ii) and (iii) follows from Remark 2.2. For general G the equivalences were shown in [24, Theorem 1.2]. The equivalence between (i) and (v) is shown in [26, Proposition 2.1], and (iii) $\Leftrightarrow$ (iv) is a direct consequence of (2.1) and Remark 2.2. Hence (i)–(v) are equivalent. As $K_\theta (G)\subseteq \Phi (G)$ one has (iv) $\Rightarrow$ (vi). Thus it remains to show that (vi) $\Rightarrow$ (iv). Let $\pi :G\rightarrow G/\Phi (G)$ denote the canonical projection, and let

$$\begin{aligned} \pi _*:\mathrm {ker}(\theta )/K_\theta (G)\cdot \ker (\theta )^\ell \longrightarrow G/\Phi (G) \end{aligned}$$

(2.4)

denote the induced map—note that $K_\theta (G)\ker (\theta )^\ell =\ker (\theta )^\ell [G,\ker (\theta )]$, by (1.1). As $\mathrm {im}(\theta )$—which is isomorphic to either $\mathbb {Z}_\ell$ or $\{1\}$—is projective, the 5-term exact sequence associated to the Hochschild–Serre spectral sequence yields an exact sequence

(2.5)

Thus, by Pontrjagin duality, $\pi _*$ is injective. Note that

$$\begin{aligned} \mathrm {tor}(\mathrm {ker}(\theta )/K_\theta (G))=I_\theta (G)/K_\theta (G) \end{aligned}$$

(2.6)

is a direct summand of the abelian pro-$\ell$ group $\mathrm {ker}(\theta )/K_\theta (G)$ (cf. Sect. 1). Since $\pi (I_\theta (G))=\{1\}$ by (vi), and since $\pi _*$ is injective, one concludes that $I_\theta (G)\subseteq K_\theta (G)\cdot \mathrm {ker}(\theta )^\ell$. Hence $I_\theta (G)/K_\theta (G)=\{1\}$ by Fact 2.5. $\square$

Example 2.7

• (a) If $(G,\theta )$ is a torsion-free $\theta$-abelian pro-$\ell$ group, then, by Proposition 2.6-(ii), $(G,\theta )$ is Kummerian, as $K_\theta (G)=\{1\}$ and $\mathrm {ker}(\theta )$ is free abelian by definition.

• (b) If G is a free pro-$\ell$ group, then by Proposition 2.6-(v) the oriented pro-$\ell$ group $(G,\theta )$ is Kummerian for any orientation $\theta :G\rightarrow \mathbb {Z}_\ell ^\times$, as $\mathrm {cd}(G)=1$ (cf. [19, Proposition 3.5.17]).

• (c) If $(G,\theta )$ is an oriented pro-$\ell$ group with trivial orientation $\theta \equiv \mathbf {1}$, then $(G,\theta )$ is Kummerian if, and only if, the abelianization $G^{\mathrm {ab}}$ is a free abelian pro-$\ell$ group (cf. [10, Example 3.5-(1)]).

The following result is a consequence of Kummer theory (cf. [10, Theorem 4.2]).

Theorem 2.8

Let $\mathbb {K}$ be a field containing a primitive $\ell {\mathrm {th}}$-root of 1 (and also $\sqrt{-1}$ if $\ell =2).$ Then $(G_{\mathbb {K}}(\ell ),\theta _{\mathbb {K},\ell })$ is a torsion-free Kummerian oriented pro-$\ell$ group.

From Proposition 2.3 and Proposition 2.6-(iv), one concludes the following fact.

Corollary 2.9

Let $(G,\theta )$ be a Kummerian torsion-free oriented pro-$\ell$ group. Then $(G/K_\theta (G),\bar{\theta })$ is the maximal $\theta$-abelian quotient of G.

3 The Bogomolov–Positselski property

3.1 Bogomolov’s conjecture

Let $\mathbb {K}$ be a field containing a primitive $\ell {\mathrm {th}}$-root of 1 (and also $\sqrt{-1}$ if $\ell =2$), and let $\mathbb {L}=\root \ell ^\infty \of {\mathbb {K}}$ denote the compositum of all radical extensions $\mathbb {K}(\root \ell ^n \of {a})$, with $a\in \mathbb {K}^\times$ and $n\ge 1$, i.e.,

$$\begin{aligned} \mathbb {L}=\root \ell ^\infty \of {\mathbb {K}}=\mathbb {K}\left( \,\root \ell ^n \of {a}\,\mid \,a\in \mathbb {K}^\times ,n\ge 1\,\right) . \end{aligned}$$

(3.1)

The maximal pro-$\ell$ Galois group $G_{\mathbb {L}}(\ell )$ of the field $\mathbb {L}$ is equal to the pro-$\ell$ group $K_{\tilde{\theta }_{\mathbb {K},\ell }}(G_{\mathbb {K}}(\ell ))$ associated to the oriented pro-$\ell$ group $(G_{\mathbb {K}}(\ell ),\tilde{\theta }_{\mathbb {K},\ell })$ (cf. [10, Theorem 4.2]). Observe that the $\ell$-cyclotomic character associated to the maximal pro-$\ell$ Galois group of $\mathbb {L}$ is the trivial $\ell$-orientation $\mathbf {1}:K_{\tilde{\theta }_{\mathbb {K},\ell }}(G_\mathbb {K}(\ell ))\rightarrow \{1\}\subseteq \mathbb {Z}_\ell ^\times$.

Motivated by a conjecture formulated by Bogomolov [2]—see Remark 3.3, L. Positselski stated the following conjecture on the pro-$\ell$ group $G_{\mathbb {L}}(\ell )=K_{\tilde{\theta }_{\mathbb {K},\ell }}(G_\mathbb {K}(\ell ))$ (cf. [20, Conjecture 1.2]).

Conjecture 3.1

Let $\mathbb {K}$ be a field containing a primitive $\ell {\mathrm {th}}$-root of 1, and also $\sqrt{-1}$ if $\ell =2$. Then the maximal pro-$\ell$ Galois group $G_{\mathbb {L}}(\ell )$ of $\mathbb {L}=\root \ell ^\infty \of {\mathbb {K}}$ is a free pro-$\ell$ group.

Conjecture 3.1 is the motivation for the following definition.

Definition 3.2

A Kummerian oriented pro-$\ell$ group $(G,\theta )$ is said to have the Bogomolov–Positselski property if the subgroup $K_\theta (G)$ is a free pro-$\ell$ group.

Hence, Conjecture 3.1 may be restated as follows: if $\mathbb {K}$ is a field containing a primitive $\ell {\mathrm {th}}$-root of 1 (and also $\sqrt{-1}$ if $\ell =2$), then the oriented pro-$\ell$ group $(G_{\mathbb {K}}(\ell ),\tilde{\theta }_{\mathbb {K},\ell })$ has the Bogomolov-Positselski property.

Remark 3.3

The original formulation of Bogomolov’s conjecture states that if $\mathbb {K}$ is a field containing an algebraically closed field then the (closure of the) commutator subgroup of the Sylow pro-$\ell$ subgroup of the absolute Galois group $G_{\mathbb {K}}$ of $\mathbb {K}$ is a free pro-$\ell$ group. Furthermore, the (closure of the) commutator subgroup of the maximal pro-$\ell$ Galois group $G_{\mathbb {K}}(\ell )$ should be a free pro-$\ell$ group as well (see also [3, Conjecture 6.2] and [18, § 3.1.2], where the conjecture is stated for function fields).

In [20], Positselski observed that the only essential part of the condition about the algebraically closed subfield of $\mathbb {K}$ is that $\mathbb {K}$ should contain all the roots of 1 of $\ell$-power order. Consequently, he formulated the following conjecture (cf. [20, Conjecture 1.1]): the pro-$\ell$ Sylow subgroup of the absolute Galois group $G_{\mathbb {L}}$, with $\mathbb {L}=\root \ell ^\infty \of {\mathbb {K}}$ and $\mathbb {K}$ an arbitrary field, is a free pro-$\ell$ group, i.e., $\mathrm {cd}_\ell (G_{\mathbb {L}})\le 1$ (or, equivalently, $G_{\mathbb {L}}$ is $\ell$-projective, cf. [29, §I.3.4, Proposition 16]). Note that this conjecture is stronger than Conjecture 3.1, and likely hard to approach, while—as stated by Positselski himself, cf. [20, § 1.3]—the latter is closer to Bogomolov’s original conjecture.

Example 3.4

• (a) Let $(G,\theta )$ be a torsion-free $\theta$-abelian oriented pro-$\ell$ group. Then $(G,\theta )$ is Kummerian (cf. Example 2.7-(a)), and by Proposition 2.6-(iv) one has

  $$\begin{aligned} I_\theta (G)=K_\theta (G)=\{1\}. \end{aligned}$$

  So, $(G,\theta )$ has the Bogomolov–Positselski property.

• (b) Let $(G,\theta )$ be an oriented pro-$\ell$ group with G being a free pro-$\ell$ group. Then $(G,\theta )$ is Kummerian by Example 2.7-(b), and it has the Bogomolov–Positselski property as every closed subgroup of G is again a free pro-$\ell$ group.

• (c) Let

  $$\begin{aligned} \begin{aligned} G&= \langle \, x,y,z\,\mid \, [x,y]=z, [x,z]=[y,z]=1\,\rangle \\&= \left\{ \left( \begin{array}{ccc} 1 &{} a &{} c \\ 0 &{} 1 &{} b \\ 0 &{} 0 &{} 1 \end{array} \right) \,\mid \,a,b,c\in \mathbb {Z}_\ell \right\} \end{aligned} \end{aligned}$$

  be the Heisenberg group over $\mathbb {Z}_\ell$, and set $(G,\mathbf {1})$, where $\mathbf {1}:G\rightarrow \mathbb {Z}_\ell ^\times$ is the trivial orientation. Then $K_\theta (G)=G^\prime \simeq \mathbb {Z}_\ell$ is the cyclic pro-$\ell$ subgroup generated by z, and $G^{\mathrm {ab}}\simeq \mathbb {Z}_\ell ^2$. Hence $(G,\theta )$ is Kummerian by Example 2.7-(c), and it has the Bogomolov–Positselski property. Nevertheless, G does not occur as the maximal pro-$\ell$ Galois group of any field containing $\mu _{\ell ^\infty }$ (cf. [23, Example 5.4]).

3.2 Self-isolated pro-$\ell$ groups and Frattini pro-$\ell$ covers

Let G be a pro-$\ell$ group, and let $H\subseteq G$ be a subgroup. The isolator of H is the subgroup

$$\begin{aligned} \mathrm {Iso}(H)=\mathrm {cl}\left( \left\langle \,g\in G\,\mid \,g^n\in H\text { for some }n\ge 1\,\right\rangle \right) \end{aligned}$$

(cf. [12, § 66]). We say that H is self-isolated if $\mathrm {Iso}(H)=H$. In particular, if N is a normal subgroup of G, then G is self-isolated if, and only if, the quotient G/N is a torsion-free pro-$\ell$ group. The following fact is almost straightforward.

Fact 3.5

Let $(G,\theta )$ be a torsion-free $\theta$-abelian oriented pro-$\ell$ group. Let N be a normal subgroup of G contained in both $\mathrm {ker}(\theta )$ and $\Phi (G)$. If N is self-isolated, then $N=\{1\}$.

Proof

By Remark 2.2, $\Phi (G)\cap \mathrm {ker}(\theta )=\mathrm {ker}(\theta )^\ell$. As $N\subseteq \mathrm {ker}(\theta )$ is an isolated subgroup, it is a direct summand of $\mathrm {ker}(\theta )$. Thus by Fact 2.5, N is trivial. $\square$

Fact 3.5 has the following consequence.

Proposition 3.6

Let $(G,\theta )$ be a torsion-free Kummerian oriented pro-$\ell$ group. Let $N\trianglelefteq G$ be a closed normal, self-isolated, subgroup of G contained in $\mathrm {ker}(\theta )$ satisfying

$$\begin{aligned} K_\theta (G)\subseteq N\subseteq \Phi (G). \end{aligned}$$

Then $N=K_\theta (G)$.

A Frattini pro-$\ell$ cover of pro-$\ell$ groups is a short exact sequence of pro-$\ell$ groups

(3.2)

satisfying $N\subseteq \Phi (G)$. One also says that $\tau :G\rightarrow \bar{G}$ is a Frattini pro-$\ell$ cover of $\bar{G}$. One may characterize those pro-$\ell$ groups which may be completed into Kummerian oriented pro-$\ell$ groups with the Bogomolov–Positselski property as follows.

Theorem 3.7

A pro-$\ell$ group G may be completed into a Kummerian oriented pro-$\ell$ group $(G,\theta )$ with the Bogomolov–Positselski property if, and only if, G is a Frattini pro-$\ell$ cover (3.2) of $\bar{G},$ where $(\bar{G},\bar{\theta })$ is a $\bar{\theta }$-abelian oriented pro-$\ell$ group and N is a free pro-$\ell$ group.

Proof

If $(G,\theta )$ is Kummerian with the Bogomolov–Positselski property, then, by Proposition 2.6, $(G/K_\theta (G),\bar{\theta })=(G,\theta )/K_{\theta }(G)$ is $\bar{\theta }$-abelian and $N=K_{\theta }(G)$ is a free pro-$\ell$ group by Definition 3.2. This shows one implication.

Conversely, if $(\bar{G},\bar{\theta })$ is $\bar{\theta }$-abelian, then the epimorphism of oriented pro-$\ell$ groups $(G,\theta )\rightarrow (\bar{G},\bar{\theta })$ factors through $(G,\theta )/I_{\theta }(G)$ by Proposition 2.3. Hence $I_\theta (G)\subseteq N$, while $N\subseteq \Phi (G)$ by hypothesis, thus $(G,\theta )$ is Kummerian by Proposition 2.6:(vi). Thus, $I_\theta (G)=K_\theta (G)$ by Proposition 2.6:(iv), and since

$$\begin{aligned} K_\theta (G)=I_\theta (G)\subseteq N\subseteq \Phi (G), \end{aligned}$$

Proposition 3.6 yields $N=K_\theta (G)$, i.e., $(G,\theta )$ has the Bogomolov–Positselski property. $\square$

4 The Bogomolov–Positselski property and cohomology

4.1 Quadratic cohomology and the Norm Residue Theorem

Let G be a pro-$\ell$ group. The cohomology groups $H^n(G,\mathbb {F}_\ell )$, $n\ge 1$, where $\mathbb {F}_\ell$ is the trivial G-module isomorphic—as abelian group—to $\mathbb {F}_\ell =\mathbb {Z}/\ell \mathbb {Z}$, come endowed with the bilinear cup-product

$$\begin{aligned} H^s(G,\mathbb {F}_\ell )\times H^t(G,\mathbb {F}_\ell )\overset{\cup }{\longrightarrow } H^{s+t}(G,\mathbb {F}_\ell ),\quad s,t\ge 0, \end{aligned}$$

which is associative and graded-commutative, i.e., $\beta \cup \alpha =(-1)^{st}\alpha \cup \beta$ for $\alpha \in H^s(G,\mathbb {F}_\ell )$ and $\beta \in H^t(G,\mathbb {F}_\ell )$ (cf. [19, Chap. I, § 4]). Thus,

$$\begin{aligned} H^\bullet (G,\mathbb {F}_\ell )=\coprod _{n\ge 0}H^n(G,\mathbb {F}_\ell ) \end{aligned}$$

is a connected $\mathbb {N}_0$-graded, graded-commutative, associative $\mathbb {F}_\ell$-algebra.

For an $\mathbb {F}_\ell$-vector space V, let $\mathbf {T}^\bullet V$ denote the $\mathbb {F}_\ell$-tensor algebra, i.e.,

$$\begin{aligned} \mathbf {T}^\bullet V=\coprod _{n\in \mathbb {N}_0} \mathbf {T}^n V\,\quad \text {where}\quad \mathbf {T}^n V=V^{\otimes ^n}. \end{aligned}$$

(4.1)

The $\mathbb {N}_0$-graded associative $\mathbb {F}_\ell$-algebra $\mathbf {A}_\bullet$ is said to be generated in degree 1, if the canonical homomorphism $\phi _\bullet :\mathbf {T}^\bullet \mathbf {A}_1\rightarrow \mathbf {A}_\bullet$ of $\mathbb {N}_0$-graded associative $\mathbb {F}_\ell$-algebras is surjective. Moreover, $\mathbf {A}_\bullet$ is said to be quadratic, if it is 1-generated and $\mathrm {ker}(\phi _\bullet )=\langle \mathrm {ker}(\phi _2)\rangle$, i.e., the ideal $\mathrm {ker}(\phi _\bullet )$ is generated in degree 2.

Definition 4.1

A pro-$\ell$ group G is said to be $H^\bullet$ -quadratic if $H^\bullet (G,\mathbb {F}_\ell )$ is a quadratic algebra.

For an $\mathbb {F}_\ell$-vector space V, let $\varvec{\Lambda }^\bullet V=\mathbf {T}^\bullet V/\langle \, v\otimes v\mid v\in V\,\rangle$ denote the exterior $\mathbb {F}_\ell$-algebra spanned by V, and $\mathbf {S}^\bullet V=\mathbf {T}^\bullet V/\langle \, v\otimes w-w\otimes v\mid v,w\in V\,\rangle$ denote the symmetric $\mathbb {F}_\ell$-algebra spanned by V. Then G is $H^\bullet$-quadratic if the cup-product induces an isomorphism of graded $\mathbb {F}_\ell$-algebras

$$\begin{aligned} \varvec{\Xi }^\bullet H^1(G,\mathbb {F}_\ell )/\langle \, W\,\rangle \overset{\sim }{\longrightarrow }H^\bullet (G,\mathbb {F}_\ell ), \end{aligned}$$

(4.2)

where $\varvec{\Xi }^\bullet =\varvec{\Lambda }^\bullet$ if $\ell$ is odd, and $\varvec{\Xi }^\bullet =\mathbf {S}^\bullet$ if $\ell =2$. Moreover,

$$\begin{aligned} W=\mathrm {ker}\left( \Xi ^2(H^1(G,\mathbb {F}_\ell ))\overset{\cup }{\longrightarrow } H^2(G,\mathbb {F}_\ell )\right) . \end{aligned}$$

(4.3)

By the Norm Residue Theorem, if the field $\mathbb {K}$ contains a primitive $\ell {\mathrm {th}}$-root of unity, then the maximal pro-$\ell$ Galois group $G_{\mathbb {K}}(\ell )$ is $H^\bullet$-quadratic (cf. [21] or [26]).

Remark 4.2

Let $\ell =2$ and let G be a pro-2 group. Then one has $\alpha \cup \alpha =0$ for every $\alpha \in H^1(G,\mathbb {F}_2)$ if, and only if, the map

$$\begin{aligned} H^1(G,\mathbb {Z}/4)\longrightarrow H^1(G,\mathbb {F}_2), \end{aligned}$$

induced by the epimorphism of trivial G-modules $\mathbb {Z}/4\rightarrow \mathbb {F}_2$, is surjective (cf. [26, Fact 7.1]). In particular, if $(G,\theta )$ is a torsion-free Kummerian oriented pro-2 group, one concludes that $\alpha \cup \alpha =0$ for all $\alpha \in H^1(G,\mathbb {F}_2)$. This is the case for $(G_{\mathbb {K}}(2),\tilde{\theta }_{\mathbb {K},2})$, with $\mathbb {K}$ a field containing $\sqrt{-1}$, i.e., $H^\bullet (G_{\mathbb {K}}(2),\mathbb {F}_2)$ is quadratic and also a quotient of the exterior algebra $\varvec{\Lambda }^\bullet H^1(G_{\mathbb {K}}(2),\mathbb {F}_2)$.

Example 4.3

Let $(G,\theta )$ be torsion-free $\theta$-abelian oriented pro-$\ell$ group. Then G is a torsion free powerful pro-$\ell$ group (cf. [5, Chap. 4, § 1]), and

$$\begin{aligned} G\simeq \varprojlim _{i\in I} A_i\rtimes \mathrm {im}(\theta ) \end{aligned}$$

for finitely generated free abelian pro-$\ell$ groups $A_i$. Thus by M. Lazard’s theorem (cf. [14]) one has $\varvec{\Lambda }_\bullet H^1(G,\mathbb {F}_\ell )$ (see, e.g., [26, Theorem 3.13]), and hence G is $H^\bullet$-quadratic.

4.2 Quadratic cohomology and the Bogomolov–Positselski property

Let $(G,\theta )$ be a torsion-free Kummerian oriented pro-$\ell$ group. The short exact sequence of pro-$\ell$ groups

(4.4)

induces the 5-terms exact sequence in cohomology

(cf. [19, Proposition 1.6.7]). As $(G,\theta )$ is Kummerian, one has $I_\theta (G)$ $=K_\theta (G)\subseteq \Phi (G)$ (cf. Proposition 2.6(iv)). Hence $\mathrm {inf}_{ G(\theta ),G}^1$ is an isomorphism and $\mathrm {res}^1_{G,I_\theta (G)}$ is the 0-map. As $(G(\theta ),\bar{\theta })=(G,\theta )/I_\theta (G)$ is $\bar{\theta }$-abelian, one has

$$\begin{aligned} H^\bullet ( G(\theta ),\mathbb {F}_\ell )\simeq \varvec{\Lambda }^\bullet H^1(G,\mathbb {F}_\ell ) \end{aligned}$$

(4.6)

(cf. Example 4.3). If in addition G is $H^\bullet$-quadratic, then $H^\bullet (G,\mathbb {F}_\ell )$ is a quotient of $\varvec{\Lambda }^\bullet H^1(G,\mathbb {F}_\ell )$ (cf. Remark 4.2). In particular, the inflation map $\psi ^\bullet =\mathrm {inf}_{ G(\theta ),G}^\bullet$ induces a surjective homomorphism of $\mathbb {N}_0$-graded $\mathbb {F}_\ell$-algebras

(4.7)

satisfying

$$\begin{aligned} \mathrm {ker}(\psi _n)\simeq \mathrm {ker}(\psi _2)\wedge \left( \Lambda ^{n-2}H^1(G,\mathbb {F}_\ell )\right) \quad \text {for all }n\ge 2. \end{aligned}$$

(4.8)

Since $\mathrm {res}^1_{G,K_\theta (G)}$ is trivial, one concludes from 4.5 that $d_2^{0,1}$ is injective, $\mathrm {im}(d_2^{0,1})=\mathrm {ker}(\psi _2)$, and $H^2(G,\mathbb {F}_\ell )\simeq H^2( G(\theta ),\mathbb {F}_\ell )/\mathrm {im}(d_2^{0,1})$. Thus, as $H^\bullet (G,\mathbb {F}_\ell )$ is quadratic, one has

$$\begin{aligned} H^\bullet (G,\mathbb {F}_\ell )\simeq H^\bullet ( G(\theta ),\mathbb {F}_\ell )/\langle \, \mathrm {im}(d_2^{0,1}) \,\rangle . \end{aligned}$$

(4.9)

4.3 A cohomological criterion

Let $(G,\theta )$ be a Kummerian torsion-free oriented pro-$\ell$ group which is $H^\bullet$-quadratic. Let $(E_r^{s,t},d_r^{s,t})$ denote the Hochschild–Serre spectral sequence with coefficients in $\mathbb {F}_\ell$ associated to the short exact sequence (4.4), i.e.,

$$\begin{aligned} E_2^{s,t}=H^s( G(\theta ),H^t({I}_\theta (G),\mathbb {F}_\ell ))\Longrightarrow E_\infty ^{s,t},\quad s,t\ge 0, \end{aligned}$$

(4.10)

with differentials $d_r^{s,t}:E_r^{s,t}\rightarrow E_r^{s+r,t-r+1}$ satisfying $d_r\circ d_r=0$ (cf. [19, Chap. II, § 4]). In particular, by (4.7) one has $E_2^{\bullet ,0}\simeq \varvec{\Lambda }^\bullet H^1(G,\mathbb {F}_\ell )$. For $\alpha \in E_2^{s,0}=H^s( G(\theta ),\mathbb {F}_\ell )$, $s\ge 0$, and $\beta \in E_2^{0,1}=H^1({I}_\theta (G),\mathbb {F}_\ell )^{ G(\theta )}$, one has

$$\begin{aligned} \begin{aligned}&\alpha \cup \beta \in H^s( G(\theta ),\mathbb {F}_\ell \otimes H^1({I}_\theta (G),\mathbb {F}_\ell ))=E_2^{s,1},\\&d_2^{s,1}(\alpha \cup \beta )=(-1)^{s+1}\alpha \cup d_2^{0,1}(\beta )\in E_2^{s+2,0} \end{aligned} \end{aligned}$$

(4.11)

(cf. [19, Chap. II, Example 4.5]).

Proposition 4.4

Let $(G,\theta )$ be a torsion-free Kummerian oriented pro-$\ell$ group with G being $H^\bullet$-quadratic. Then

• (i) $E_\infty ^{s,t}$ is concentrated on the 0th line, i.e., $E_\infty ^{s,t}=0$ for every $s\ge 0$ and $t\ge 1;$

• (ii) $E_3^{s,0}\simeq E_\infty ^{s,0}\simeq H^s(G,\mathbb {F}_\ell )$ for every $s\ge 0$.

Proof

Since $(G,\theta )$ is Kummerian, by (4.6) one has $E_2^{\bullet ,0}\simeq \varvec{\Lambda }^\bullet H^1(G,\mathbb {F}_\ell )$. For every $t\ge 0$ there exists a descending separating filtration $(F^kH^t(G,\mathbb {F}_\ell ))_{0\le k\le t}$ satisfying $F^0H^t(G,\mathbb {F}_\ell )=H^t(G,\mathbb {F}_\ell )$ and

$$\begin{aligned} F^sH^{s+t}(G,\mathbb {F}_\ell )/F^{s+1}H^{s+t}(G,\mathbb {F}_\ell )\simeq E^{s,t}_\infty \end{aligned}$$

(4.12)

, where $F^{s+t+1}H^{s+t}(G,\mathbb {F}_\ell )=\{0\}$ (cf. [1, p. 99]). By [19, Chap. II, § 4, Example 1], the composite of the maps

is the s -th left edge morphism (cf. [19, p. 99]) and hence coincides with the inflation map $\mathrm {inf}_{G(\theta ),G}^s$, which is surjective by (4.7). Thus $F^0H^t(G,\mathbb {F}_\ell )=H^t(G,\mathbb {F}_\ell )$ for all $t\ge 0$, i.e., $E_\infty ^{\bullet ,0}\simeq H^\bullet (G,\mathbb {F}_p)$, and consequently $E_\infty ^{k,t}=0$ for every $1\le k\le t$. This shows (i).

By (4.11), one has canonical homomorphisms of $\mathbb {N}_0$-graded $\mathbb {F}_\ell$-algebras

$$\begin{aligned} \begin{aligned}&\sigma ^\bullet :H^\bullet ( G(\theta ),\mathbb {F}_\ell )/\langle \, \mathrm {im}(d_2^{0,1}) \,\rangle \longrightarrow E_3^{\bullet ,0},\\&\tau ^\bullet :E_3^{\bullet ,0}\longrightarrow H^\bullet ( G,\mathbb {F}_\ell ). \end{aligned} \end{aligned}$$

(4.13)

Moreover, $\sigma ^\bullet$ and $\tau ^\bullet$ are surjective, $\sigma ^k$ and $\tau ^k$ are isomorphisms for $k\in \{0,1,2\}$, and their composition is an isomorphism of quadratic $\mathbb {F}_\ell$-algebras by (4.9). Thus $\sigma ^\bullet$ and $\tau ^\bullet$ are isomorphisms which shows (ii). $\square$

Let $(G,\theta )$ be a Kummerian torsion-free oriented pro-$\ell$ group, and put $K_\theta (G)^{\mathrm {ab}}=K_\theta (G)/K_\theta (G)'$. Recall that if $\mathbb {K}$ is a field containing a primitive $\ell {\mathrm {th}}$-root of 1 and $(G,\theta )=(G_{\mathbb {K}}(\ell ),\tilde{\theta }_{\mathbb {K},\ell })$, then $K_\theta (G)^{\mathrm {ab}}$ is a free abelian pro-$\ell$ group, as the oriented pro-$\ell$ group $(K_\theta (G),\theta \vert _{K_\theta (G)})$ is again Kummerian, and since $\theta \vert _{K_\theta (G)}$ is trivial. The short exact sequence of pro-$\ell$ groups

(4.14)

where $G(\theta )=G/K_\theta (G)$, defines a cohomology class $u\in H_{\mathrm {cts}}^2( G(\theta ),K_\theta (G)^{\mathrm {ab}})$ (cf. [19, p. 143]), where $K_\theta (G)^{\mathrm {ab}}$ is considered as a topological left $\mathbb {Z}_\ell [\![G(\theta )]\!]$-module and $H_{\mathrm {cts}}^*$ denotes continuous cochain cohomology (cf. [19, Chap. II, § 7]). Since $[G,K_\theta (G)]\subseteq \Phi (G)$, one has

$$\begin{aligned} \mathrm {Hom}(K_\theta (G),\mathbb {F}_\ell )=\mathrm {Hom}(K_\theta (G),\mathbb {F}_\ell )^{ G(\theta )}=E_2^{0,1}. \end{aligned}$$

Thus, the pairing

$$\begin{aligned} \begin{aligned}&K_\theta (G)^{\mathrm {ab}}\times E_2^{0,1}\longrightarrow \mathbb {F}_\ell ,\\&(hK_\theta (G)',\beta )\longmapsto \beta (h),\quad \text {for }h\in K_\theta (G), \end{aligned} \end{aligned}$$

induces a map

$$\begin{aligned} \phi _u:E_2^{2,1}=H^2( G(\theta ),\mathrm {Hom}(K_\theta (G),\mathbb {F}_\ell ))\longrightarrow E_2^{4,0}=H^4( G(\theta ),\mathbb {F}_\ell ) \end{aligned}$$

(4.15)

given by $\phi _u(\alpha )= u\cup \alpha$ (cf. [19, p. 114]).

Theorem 4.5

Let $(G,\theta )$ be a Kummerian torsion-free oriented pro-$\ell$ group with G an $H^\bullet$-quadratic pro-$\ell$ group. Then the following are equivalent.

• (i) $(G,\theta )$ has the Bogomolov–Positselski property;

• (ii) the differential map $d_2^{2,1}:E_2^{2,1}\rightarrow E_2^{4,0}\simeq \Lambda ^4H^1( G(\theta ),\mathbb {F}_\ell )$ is injective;

• (iii) the map $\phi _u$ is injective, i.e., $u\cup \alpha \ne 0$ for every non-trivial $\alpha \in E_2^{2,1}$.

If these conditions hold, then the spectral sequence $E_2^{s,t}\Rightarrow E_\infty ^{s,t}$ collapses at the $E_3$-page, i.e., $E_3=E_\infty$.

Proof

By Proposition 4.4(ii), for every $s\ge 0$ one has $E_3^{s,0}\simeq E_4^{s,0}\simeq \cdots \simeq E_\infty ^{s,0}$. Since, by definition, $E_4^{s,0}=E_3^{s,0}/\mathrm {im}(d_3^{s-3,2})$, one concludes that the maps

$$\begin{aligned} d_3^{s-3,2}:E_3^{s-3,2}\longrightarrow E_3^{s,0}\simeq H^s(G,\mathbb {F}_\ell ) \end{aligned}$$

must be the 0-maps for every $s\ge 3$. In particular, $E_4^{0,2}=\mathrm {ker}(d_3^{0,2})$ is equal to $E_3^{0,2}$, which is $\mathrm {ker}(d_2^{0,2})$ by definition. As $E_r^{s,t}$ is a first-quadrant spectral sequence, one has $E_{r+1}^{0,2}=\ker (d_r^{0,2})$ and the map $d_r^{0,2}:E_r^{0,2}\rightarrow E_r^{r,3-r}=0$ is the 0-map for every $r\ge 4$. This implies that $E_3^{0,2}=E_4^{0,2}=\cdots =E_\infty ^{0,2}$. Thus, applying Proposition 4.4(i), yields

$$\begin{aligned} 0=E_\infty ^{0,2}=E_3^{0,2}=\mathrm {ker}(d_2^{0,2}), \end{aligned}$$

(4.16)

i.e., $d_2^{0,2}:E_2^{0,2}\rightarrow E_2^{2,1}$ is injective.

Moreover, one has $E_3^{2,1}=E_4^{2,1}=E_\infty ^{2,1}$, as $E_{r+1}^{2,1}=\mathrm {ker}(d_r^{2,1})/\mathrm {im}(d_r^{2-r,r})$ and both maps

$$\begin{aligned} d_r^{2,1}:E_r^{2,1}\longrightarrow E_r^{2+r,2-r}=0\quad \text {and}\quad d_r^{2-r,r}:E_r^{2-r,r}=0\longrightarrow E_r^{2,1} \end{aligned}$$

are the 0-maps for every $r\ge 3$. Applying Proposition 4.4(i) again yields

$$\begin{aligned} 0=E_\infty ^{2,1}=E_3^{2,1}=\mathrm {ker}(d_2^{2,1})/\mathrm {im}(d_2^{0,2}), \end{aligned}$$

(4.17)

i.e., $\mathrm {ker}(d_2^{2,1})=\mathrm {im}(d_2^{0,2})$.

Thus, if $(G,\theta )$ has the Bogomolov–Positselski property, then $I_\theta (G)=K_\theta (G)$ is a free pro-$\ell$ group. Then $H^t(K_\theta (G),\mathbb {F}_\ell )=0$ for every $t\ge 2$ (cf. [19, Proposition 3.5.17]), and thus $E_r^{0,t}=0$ for all $r\ge 2$ and $t\ge 2$. In particular, the map $d_2^{0,2}:H^2(I_\theta (G),\mathbb {F}_\ell )^{ G(\theta )}\rightarrow E_2^{2,1}$ is trivial, and hence by (4.17), one has $\mathrm {ker}(d_2^{2,1})=0$. This proves the implication (i)$\Rightarrow$(ii).

Conversely, if $d_2^{2,1}$ is injective, then, by (4.17), one has $\mathrm {im}(d_2^{0,2})=\mathrm {ker}(d_2^{2,1})=0$. Since $d_2^{0,2}$ is injective by (4.16), this implies that $E_2^{0,2}=H^2(I_\theta (G),\mathbb {F}_\ell )^{ G(\theta )}{=0}$. Since G is a pro-$\ell$ group, the equality $H^2(I_\theta (G),\mathbb {F}_\ell )^{ G(\theta )}=0$ implies that $H^2(I_\theta (G),\mathbb {F}_\ell )=0$, and thus $I_\theta (G)$ is free by [19, Proposition 3.5.17]. This proves the implication (ii)$\Rightarrow$(i). The equivalence between (ii) and (iii) follows from [19, Theorem 2.4.4].

Finally, if $I_\theta (G)$ is a free pro-$\ell$ group, one has $E_r^{s,t}=0$ for all $s\ge 0$, $t\ge 2$, and $r\ge 2$. Hence, all maps $d_3^{s,t}$ are trivial, for all $s,t\ge 0$, so that $E_3^{s,t}=E_\infty ^{s,t}$. $\square$

Question 4.6

Let $(G,\theta )$ be a Kummerian torsion-free pro-$\ell$ group with G being an $H^\bullet$-quadratic pro-$\ell$ group, and let $(E_r^{s,t},d_r^{s,t})$ be the Hochschild–Serre spectral sequence associated to (4.4). By Proposition 4.4, for every $s\ge 0$ one has $E_3^{s,0}\simeq E_\infty ^{s,0}$, and $E_\infty ^{s,t}=0$ for $s\ge 0$ and $t\ge 1$. Moreover, by Theorem 4.5, if $(G,\theta )$ has the Bogomolov–Positselski property, then

$$\begin{aligned} E_3^{s,t}\simeq E_\infty ^{s,t}\quad \text {for every }s,t\ge 0, \end{aligned}$$

(4.18)

i.e., $E_r^{s,t}$ collapses at the $E_3$-page. It would be interesting to understand whether (4.18) implies the Bogomolov–Positselski property for $(G,\theta )$. We suspect that the answer should be affirmative. However, we could not find any evidence for this speculation.

Remark 4.7

Let $\mathbb {K}$ be a field containing a primitive $\ell {\mathrm {th}}$-root of unity (and also $\sqrt{-1}$ if $\ell =2$), put $\mathbb {L}=\root \ell ^\infty \of {\mathbb {K}}$ and consider the torsion-free Kummerian oriented pro-$\ell$ group $(G_{\mathbb {K}}(\ell ),\tilde{\theta }_{\mathbb {K},\ell })$. The oriented pro-$\ell$ group $(I_{\tilde{\theta }_{\mathbb {K},\ell }}(G_{\mathbb {K}}(\ell )),\mathbf {1})$ is again Kummerian and torsion free, and thus one has

$$\begin{aligned}&I_{\tilde{\theta }_{\mathbb {K},\ell }}(G_{\mathbb {K}}(\ell ))^\prime =K_{\mathbf {1}}(G_{\mathbb {L}}(\ell ))=G_{\root \ell ^\infty \of {\mathbb {L}}}(\ell ), \end{aligned}$$

(4.19)

$$\begin{aligned}&K_{\tilde{\theta }_{\mathbb {K},\ell }}(G_{\mathbb {K}})^{\mathrm {ab}}=G_{\mathbb {L}}(\ell )^{\mathrm {ab}}=\mathrm {Gal}(\root \ell ^\infty \of {\mathbb {L}}/\mathbb {L}), \end{aligned}$$

(4.20)

where the latter is a free abelian pro-$\ell$ group [cf. Example 2.7-(c)]. Hence, the short exact sequence (4.14) translates into

(4.21)

Recall that by Kummer theory one has an isomorphism of (discrete) $\ell$-elementary abelian groups $H^1(\mathrm {Gal}(\root \ell ^\infty \of {\mathbb {L}}/\mathbb {L}),\mathbb {F}_\ell )\simeq \mathbb {L}^\times /(\mathbb {L}^\times )^\ell$, where $\mathbb {L}^\times =\mathbb {L}\smallsetminus \{0\}$ denotes the multiplicative group of the field $\mathbb {L}$. Then by Theorem 4.5 the cohomology element $u\in H_{\mathrm {cts}}^2(\mathrm {Gal}(\mathbb {L}/\mathbb {K}),\mathrm {Gal}(\root p^\infty \of {\mathbb {L}}/\mathbb {L}))$ associated to the extension of pro-$\ell$ groups (4.21) induces a homomorphism

$$\begin{aligned} \phi _{u,\mathbb {L}}:H^2\left( \mathrm {Gal}(\mathbb {L}/\mathbb {K}),\mathbb {L}^\times /(\mathbb {L}^\times )^\ell \right) \longrightarrow H^4(\mathrm {Gal}(\mathbb {L}/\mathbb {K}),\mathbb {F}_\ell ) \end{aligned}$$

which is injective if, and only if, $\mathbb {L}$ satisfies Conjecture 3.1. In view of Theorem 4.5, the knowledge of the structure of $\mathbb {L}^\times /(\mathbb {L}^\times )^\ell$ as continuous $\mathrm {Gal}(\mathbb {L}/\mathbb {K})$-module, or an arithmetic interpretation of the map $\phi _{u,\mathbb {L}}$, may contribute to the solution of Conjecture 3.1.

5 Oriented pro-$\ell$ groups of elementary type

5.1 Demushkin groups and one-relator pro-$\ell$ groups

A Demushkin group is a Poincaré duality pro-$\ell$ group of dimension 2, namely, a pro-$\ell$ group G whose $\mathbb {F}_\ell$-cohomology satisfies the following conditions:

• (i) $\dim (H^1(G,\mathbb {F}_\ell ))<\infty$;

• (ii) $H^2(G,\mathbb {F}_\ell )\simeq \mathbb {F}_\ell$;

• (iii) cup-product induces a perfect pairing $H^1(G,\mathbb {F}_\ell )\times H^1(G,\mathbb {F}_\ell )\rightarrow H^2(G,\mathbb {F}_\ell );$

(cf. [19, Definition 3.9.9]). Note that by condition (ii) such a pro-$\ell$ group G has a single defining relation, namely, G may be defined as the quotient F/N of a free pro-$\ell$ group F over a normal subgroup $N\subseteq F$ generated as a normal subgroup of F by a single element contained in $\Phi (F)$ (cf., e.g., [19, pp. 231–232]).

A Demushkin group comes equipped with a distinguished orientation $\eth _G:G\rightarrow \mathbb {Z}_\ell ^\times$, induced by the action of G on its dualizing module, described in [13, Theorem 4]. The orientation $\eth _G:G\rightarrow \mathbb {Z}_\ell ^\times$ is the only orientation which completes G into a Kummerian oriented pro-$\ell$ group $(G,\eth _G)$ (cf. [26, Proposition 5.2]). The oriented pro-$\ell$ group $(G,\eth _G)$ enjoys also the Bogomolov–Positselski property.

Theorem 5.1

Let G be a Demushkin group, endowed with the canonical orientation $\eth _G:G\rightarrow \mathbb {Z}_\ell ^\times ,$ and suppose that $\mathrm {im}(\eth _G)\subseteq 1+4\mathbb {Z}_2$ if $\ell =2$. Then the oriented pro-$\ell$ group $(G,\eth _G)$ has the Bogomolov–Positselski property.

Proof

Since $(G,\eth _G)$ is Kummerian, by [26, Proposition 5.2], Proposition 2.6(iii) and Remark 2.2, one has $G/I_{\eth _G}(G)\simeq \mathbb {Z}_\ell ^{d-1}\rtimes \mathbb {Z}_\ell$, with $d=\dim (H^1(G,\mathbb {F}_\ell ))$. Therefore, $I_{\eth _G}(G)=K_{\eth _G}(G)$ is a subgroup of G of infinite index, and thus it is a free pro-$\ell$ group by [29, § I.4.5, Exercise 5(b)]. $\square$

As mentioned above, Demushkin groups have a single defining relation. One may prove the Bogomolov–Positselski property also for 1-relator pro-$\ell$ groups G with quadratic $\mathbb {F}_\ell$-cohomology which can be completed into a Kummerian oriented pro-$\ell$ group $(G,\mathbf {1})$ with a trivial orientation.

Proposition 5.2

Let G be a finitely generated pro-$\ell$ group with a single defining relation such that

• (i) $H^\bullet (G,\mathbb {F}_\ell )$ is a quadratic algebra;

• (ii) $(G,\mathbf {1})$ is Kummerian.

Then $(G,\mathbf {1})$ has the Bogomolov–Positselski property.

Proof

Since $(G,\mathbf {1})$ is Kummerian, the quotient $G^{\mathrm {ab}}$ is a free abelian pro-$\ell$ group (cf. Example 2.7(c)). We need to show that $G^\prime =K_{\mathbf {1}}(G)=I_{\mathbf {1}}(G)$ is a free pro-$\ell$ group.

Since G has a single defining relation, $H^2(G,\mathbb {F}_\ell )\simeq \mathbb {F}_\ell$ (cf. [19, Corollary 3.9.5]). Moreover, since $H^\bullet (G,\mathbb {F}_\ell )$ is quadratic, $H^2(G,\mathbb {F}_\ell )$ is generated by cup products $\chi \cup \psi$ with $\chi ,\psi \in H^1(G,\mathbb {F}_\ell )$, so that the cup product from $H^1(G,\mathbb {F}_\ell )$ to $H^2(G,\mathbb {F}_\ell )$ is not trivial (see also [22, Proposition 4.2]). Consequently, [35, Corollary 2] yields a short exact sequence of pro-$\ell$ groups

which satisfies the following three properties: N is a free pro-$\ell$ group; $\bar{G}$ is a Demushkin group; and for every subgroup S of G containing N, the inflation map

$$\begin{aligned} \mathrm {inf}_{S,N}^2:H^2(S/N,\mathbb {F}_\ell )\longrightarrow H^2(S,\mathbb {F}_\ell ) \end{aligned}$$

(5.1)

is an isomorphism (this last property is shown to hold in the proof of [35, Corollary 2]).

Since G is finitely generated, also $\bar{G}$ is finitely generated. Moreover, by (5.1) the inflation map $H^2(\bar{G},\mathbb {F}_\ell )\rightarrow H^2(G,\mathbb {F}_\ell )$ is an isomorphism, and thus by the five-terms exact sequence (cf. [19, Proposition 1.6.7]) the restriction map

$$\begin{aligned} \mathrm {res}_{G,N}^1:H^1(G,\mathbb {F}_\ell )\longrightarrow H^1(N,\mathbb {F}_\ell )^G \end{aligned}$$

is surjective. Since $(G,\mathbf {1})$ is Kummerian, and since $\mathrm {res}_{G,N}^1$ is surjective, [24, Theorem 1.2] implies that also the oriented pro-$\ell$ group $(\bar{G},\mathbf {1})=(G,\mathbf {1})/N$ is Kummerian. Hence, the canonical orientation $\eth _{\bar{G}}:\bar{G}\rightarrow \mathbb {Z}_\ell ^\times$ must coincide with the trivial orientation $\mathbf {1}$ (cf. [26, Proposition 5.2]). By Theorem 5.1, the oriented pro-$\ell$ group $(\bar{G},\mathbf {1})$ has the Bogomolov–Positselski property, and thus $K_{\mathbf {1}}(\bar{G})$—which coincides with $\bar{G}^\prime$—is a free pro-$\ell$ group.

Let S be the normal subgroup of G containing N such that $S/N\simeq \bar{G}^\prime$. Thus, $G/S\simeq \bar{G}/\bar{G}^\prime$ is abelian, and therefore $S\supseteq G^\prime$. By (5.1), one has $H^2(S/N,\mathbb {F}_\ell )\simeq H^2(S,\mathbb {F}_\ell )$, and the term on the left-hand side is trivial as S/N is a free pro-$\ell$ group. Hence, also $H^2(S,\mathbb {F}_\ell )=0$, and S is a free pro-$\ell$ group (cf. [19, Proposition 3.5.17]). Since $G^\prime \subseteq S$, and $\mathrm {cd}_\ell (G^\prime )\le \mathrm {cd}_\ell (S)=1$, $G^\prime$ must be free (cf. [29, § 3.3, Proposition 14]). $\square$

Remark 5.3

Let F be a finitely generated free pro-$\ell$ group, let r be an element of $\Phi (F)$ and let R denote the normal subgroup of F generated by r. Suppose that $\ell \ne 2$. By [22, Proposition 4.2] and Example 2.7(c), the pro-$\ell$ group $G=F/R$ satisfies the conditions (i)–(ii) in Proposition 5.2 if, and only if, $r\in F'$ and $r\notin F^p\cdot [F',F]$.

5.2 Free constructions

By [8, § 3], the free product of two oriented pro-$\ell$ groups $(G_1,\theta _1)$ and $(G_2,\theta _2)$ is the oriented pro-$\ell$ group $(G,\theta )$ where G is the free pro-$\ell$ product of $G_1,G_2$, and $\theta :G\rightarrow \mathbb {Z}_\ell ^\times$ is the orientation induced by $\theta _1,\theta _2$ via the universal property of G (see also [26, § 3.4]).

One may extend the above definition to free amalgamated pro-$\ell$ products of oriented pro-$\ell$ groups (we refer to [28, § 9.2] for the definition of free amalgamated pro-$\ell$ products).

Definition 5.4

Let $(G_1,\theta _1)$ and $(G_2,\theta _2)$ be two oriented pro-$\ell$ groups such that $G_1$ and $G_2$ have a common subgroup $H\subseteq G_1,G_2$ satisfying $\theta _1\vert _H=\theta _2\vert _H$. The amalgamated pro-$\ell$ product of oriented pro-$\ell$ groups of $(G_1,\theta _1)$ and $(G_2,\theta )$ with amalgamation in H is the oriented pro-$\ell$ group $(G,\theta )=(G_1,\theta _1)\amalg _H^{\hat{\ell }}(G_2,\theta _2)$, where $G=G_1\amalg _H^{\hat{\ell }} G_2$ is the free amalgamated pro-$\ell$ product of $G_1$ and $G_2$ over H, and $\theta :G\rightarrow \mathbb {Z}_\ell ^\times$ is the orientation which makes the diagram

commute.

Note that the morphisms $\varphi _1$ and $\varphi _2$ may not be injective (cf. [28, p. 369]). If they are, the free amalgamated pro-$\ell$ product is said to be proper.

If $H=\{1\}$, then $(G_1,\theta _1)\amalg _H^{\hat{\ell }}(G_2,\theta _2)$ coincides with the free product of oriented pro-$\ell$ groups. In this case we simply write $(G_1,\theta _1)\amalg ^{\hat{\ell }}(G_2,\theta _2)$, instead of $(G_1,\theta _1)\amalg _{\{1\}}^{\hat{\ell }}(G_2,\theta _2)$. Free products of oriented pro-$\ell$ groups preserve Kummerianity (cf. [10, Proposition 7.5]).

Proposition 5.5

Let $(G_1,\theta _1)$ and $(G_2,\theta _2)$ be two Kummerian oriented pro-$\ell$ groups. Then the free product $(G_1,\theta _1)\amalg ^{\hat{\ell }}(G_2,\theta _2)$ is again Kummerian.

We prove that—under certain conditions—if the free amalgamated pro-$\ell$ product of two Kummerian oriented pro-$\ell$ groups with the Bogomolov–Positselski property is again Kummerian, then it has also the Bogomolov–Positselski property.

Theorem 5.6

Let $(G_1,\theta _1)$ and $(G_2,\theta _2)$ be torsion free Kummerian oriented pro-$\ell$ groups with the Bogomolov–Positselski property, with common finitely generated subgroup $U=G_1\cap G_2$ such that $\theta _1\vert _U=\theta _2\vert _U$ and that $(U,\theta _U)$ is $\theta _U$-abelian, where $\theta _U=\theta _i\vert _U$ for $i=1,2$. Suppose that

• (i) the amalgamated pro-$\ell$ product $(G,\theta )=(G_1,\theta _1)\amalg _U^{\hat{\ell }}(G_2,\theta _2)$ is Kummerian;

• (ii) the restriction maps

  $$\begin{aligned} \mathrm {res}_{G,G_i}^1:H^1(G,\mathbb {F}_\ell )\rightarrow H^1(G_i,\mathbb {F}_\ell )\quad \text {and}\quad \mathrm {res}_{G_i,U}^1:H^1(G_i,\mathbb {F}_\ell )\rightarrow H^1(U,\mathbb {F}_\ell ) \end{aligned}$$

  are surjective for both $i=1,2$.

Then $(G,\theta )$ has the Bogomolov–Positselski property.

Remark 5.7

• (a) If U in the statement of Theorem 5.6 is the trivial group, then $(G,\theta )$ is the usual free product of oriented pro-$\ell$ groups, and the two conditions are satisfied by $(G,\theta )$. For condition (i), see Proposition 5.5, and condition (ii) is trivially satisfied. Hence, the Bogomolov–Positselski property is preserved by free products of oriented pro-$\ell$ groups.

• (b) By duality, for $i\in \{1,2\}$ the map $\mathrm {res}_{G,G_i}^1$, respectively the map $\mathrm {res}_{G_i,U}^1$, is surjective if, and only if, the map $\bar{\iota }_{i}:G_i/\Phi (G_i)\rightarrow G/\Phi (G)$ induced by the inclusion $\iota _{i}:U\hookrightarrow G_i$, respectively the map $\bar{\iota }_{U,i}:U/\Phi (U)\rightarrow G_i/\Phi (G_i)$ induced by the inclusion $\iota _{U,i}:U\hookrightarrow G_i$, is injective.

Proof

By [21, Theorem A], U is a uniformly powerful pro-$\ell$ group, and therefore [25, Proposition 5.22] implies that $G=G_1\amalg _U^{\hat{\ell }}G_2$ is a proper amalgam. Moreover, by hypothesis one has the monomorphisms of $\ell$-elementary abelian groups $\bar{\iota }_i$ and $\bar{\iota }_{U,i}$, with $i=1,2$ [cf. Remark 5.7(b)]. Hence, also $\bar{\iota }_U=\bar{\iota }_i\circ \bar{\iota }_{U,i}:U/\Phi (U)\rightarrow G/\Phi (G)$ is injective for both $i=1,2$.

Let $\iota _U:U\hookrightarrow G$ be the inclusion of U in G, and for $i=1,2$, set

$$\begin{aligned} \begin{aligned}&\psi _{U}=\pi _{G,\theta }^{\mathrm {ab}}\circ \iota _{U}:U\longrightarrow G(\theta )=G/K_\theta (G),\\&\psi _i=\pi _{G,\theta }^{\mathrm {ab}}\circ \iota _i:G_i\longrightarrow G(\theta )=G/K_\theta (G). \end{aligned} \end{aligned}$$

Then

$$\begin{aligned} \mathrm {ker}(\psi _{U})=U\cap K_{\theta }(G)\quad \text {and}\quad \mathrm {ker}(\psi _i)=G_i\cap K_\theta (G). \end{aligned}$$

(5.2)

Now consider the commutative diagram

where the dotted arrow from U to $G(\theta )$ is $\psi _U$. By Remark 2.4, the oriented pro-$\ell$ groups $(\mathrm {im}(\psi _U),\theta \vert _{\mathrm {im}(\psi _U)})$ and $(\mathrm {im}(\psi _i),\theta \vert _{\mathrm {im}(\psi _i)})$ are $\theta \vert _{\mathrm {im}(\psi _U)}$- and $\theta \vert _{\mathrm {im}(\psi _i)}$-abelian, respectively. In particular,

$$\begin{aligned} \mathrm {ker}(\psi _i)\supseteq I_{\theta _i}(G_i)=K_{\theta _i}(G_i), \end{aligned}$$

(5.4)

where the left-hand side inclusion follows by Proposition 2.3, and the right-side equality follows by Proposition 2.6(iv), as $(G_i,\theta _i)$ is Kummerian for $i\in \{1,2\}$ by hypothesis. Consequently, the pro-$\ell$ groups $\mathrm {im}(\psi _U)$ and $\mathrm {im}(\psi _i)$ are torsion-free, so that $\mathrm {ker}(\psi _U)$ and $\mathrm {ker}(\psi _i)$ are self-isolated subgroups of U and $G_i$ respectively. On the other hand, by duality one has $\mathrm {ker}(\psi _U)\subseteq \Phi (U)$ and $\mathrm {ker}(\psi _i)\subseteq \Phi (G_i)$, as the maps $\bar{\iota }_U$ and $\bar{\iota }_i$ are injective. Altogether, by (5.2) and (5.4) one has

$$\begin{aligned} K_{\theta \vert _U}(U)=\{1\}\subseteq U\cap K_{\theta }(G)\subseteq \Phi ({U})\quad \text {and}\quad K_{\theta _i}(G_i)\subseteq G_i\cap K_{\theta }(G)\subseteq \Phi (G_i), \end{aligned}$$

and thus $\{1\}= U\cap K_{\theta }(G)$ and $K_{\theta _i}(G_i)= G_i\cap K_{\theta }(G)$ by Proposition 3.6.

Now, let $\mathcal {T}=(\mathscr {V}(\mathcal {T}),\mathscr {E}(\mathcal {T}))$ be the pro-$\ell$ tree whose vertices and edges are given by

$$\begin{aligned} \mathscr {V}(\mathcal {T})=\{\,gG_{1},gG_{2}\,\mid \,g\in G\}\quad \text {and}\quad \mathscr {E}(\mathcal {T})=\{\,gU,\overline{gU}\mid g\in G\,\}, \end{aligned}$$

respectively. In particular, every edge $gU\in \mathscr {E}(\mathcal {T})$ defines an origin, the $G_1$-coset $gG_1$ and a terminus, the $G_2$-coset $gG_2$. For $\overline{gU}\in \mathscr {E}(\mathcal {T})$ the roles of the terminus and origin are interchanged. Then $\mathcal {T}$ is a second countable pro-$\ell$ tree, with a natural G-action (cf. [27, Example 6.2.3]). For $v=gG_i\in \mathscr {V}(\mathcal {T})$ and $\mathbf {e}=hU\in \mathscr {E}(\mathcal {T})$, with $g,h\in G$ and $i\in \{1,2\}$, let $K_v$ and $K_{\mathbf {e}}$ denote the stabilizers of v and $\mathbf {e}$ in $K_\theta (G)$, respectively. Hence

$$\begin{aligned} \begin{aligned}&K_v =\{\,x\in K_\theta (G)\,\mid \,xg\in g G_i\,\}= K_\theta (G)\cap gG_ig^{-1},\\&K_{\mathbf {e}}=\{\,x\in K_\theta (G)\,\mid \,xh\in h U\,\}= K_\theta (G)\cap hUh^{-1}. \end{aligned} \end{aligned}$$

Since $K_\theta (G)$ is a normal subgroup of G, for every $v=gG_i\in \mathscr {V}(\mathcal {T})$ the subgroup $K_v$ is isomorphic to $K_\theta (G)\cap G_i=K_{\theta _i}(G_i)$, which is free by hypothesis; while for every $\mathbf {e}=hU\in \mathscr {E}(\mathcal {T})$ the subgroup $K_{\mathbf {e}}$ is equal to $\{1\}$, and hence no non-trivial element of $K_\theta (G)$ stabilizes an edge. Therefore, by [16, Theorem 5.6], $K_\theta (G)$ has the following decomposition as free pro-$\ell$ product:

$$\begin{aligned} K_\theta (G)=\left( \coprod _{v\in \mathscr {V}'} K_v\right) \amalg F, \end{aligned}$$

(5.5)

for some subset $\mathscr {V}'$ of $\mathscr {V}(\mathcal {T})$, where F is a free pro-$\ell$ group. Hence $K_\theta (G)$ is the free pro-$\ell$ product of free pro-$\ell$ groups, and thus it is a free pro-$\ell$ group as well. $\square$

Example 5.8

Let $(G_1,\theta _1)$ and $(G_2,\theta _2)$ be the oriented pro-$\ell$ groups with

$$\begin{aligned}\begin{aligned} G_1&=\left\langle \, x, y_1,y_3\,\mid \,[y_1,y_3]=1,\,{}^xy_j=y_j^{1+\ell },\;\forall \,j\in \{1,3\}\,\right\rangle \simeq \mathbb {Z}_\ell ^2\rtimes \mathbb {Z}_\ell , \\ G_2&=\left\langle \, x, y_2,y_3\,\mid \,[y_2,y_3]=1,\,{}^xy_j=y_j^{1+\ell },\;\forall \,j\in \{2,3\}\,\right\rangle \simeq \mathbb {Z}_\ell ^2\rtimes \mathbb {Z}_\ell , \end{aligned}\end{aligned}$$

and such that $\theta _i(x)=1+\ell$ and $\theta _i(y_i)=\theta _i(y_3)=1$ for both $i=1,2$. By Remark 2.2, these two oriented pro-$\ell$ groups are respectively $\theta _1$- and $\theta _2$-abelian. Set $U=G_1\cap G_2$—i.e. U is the subgroup generated by $x,y_3$. Clearly, $\theta _1\vert _U=\theta _2\vert _U$, and

$$\begin{aligned} (U,\theta _i\vert _U)=\langle \,y_3\,\rangle \rtimes (\langle \,x\,\rangle ,\theta _i\vert _{\langle \,x\,\rangle }) \quad \text {for both }i=1,2, \end{aligned}$$

which is $\theta _i\vert _U$-abelian by Remark 2.4. Moreover, it is straightforward to see that the maps $\bar{\iota }_{U,i}:U/\Phi (U)\rightarrow G_i/\Phi (G_i)$ are injective for both $i=1,2$. Now let $(G,\theta )$ be the oriented pro-$\ell$ group $(G_1,\theta _1)\amalg _U^{\hat{\ell }}(G_2,\theta _2)$. Then

$$\begin{aligned} G=\left\langle \, x, y_1,y_2,y_3\,\mid \,[y_1,y_3]=[y_2,y_3]=1,\,{}^xy_i=y_i^{1+\ell },\;\forall \,i\in \{1,2,3\}\,\right\rangle \end{aligned}$$

and $\theta (x)=1+\ell$, $\theta (y_j)=1$ for $j=1,2,3$. Moreover, one has an epimorphism of oriented pro-$\ell$ groups $\tau :(G,\theta )\rightarrow (\bar{G},\bar{\theta })$, where

$$\begin{aligned} \bar{G}=\left\langle \, \bar{x}, \bar{y}_1,\bar{y}_2,\bar{y}_3\,\mid \,[\bar{y}_j,\bar{y}_{j'}]=1,\,{}^{\bar{x}}\bar{y}_j=\bar{y}_j^{1+\ell },\;\forall \,j,j'\in \{1,2,3\}\,\right\rangle \simeq \mathbb {Z}_\ell ^3\rtimes \mathbb {Z}_\ell , \end{aligned}$$

and $\bar{x}=\tau (x)$, $\bar{y}_j=\tau (y_j)$ for $j=1,2,3$. By Remark 2.2, $(\bar{G},\bar{\theta })$ is $\bar{\theta }$-abelian, and thus $\mathrm {ker}(\tau )\supseteq I_\theta (G)$ by Proposition 2.3. On the other hand, it is straightforward to see that $\Phi (G)\supseteq \mathrm {ker}(\tau )$, and hence $(G,\theta )$ is Kummerian by Proposition 2.6-(vi). Since $(G_1,\theta _1)$ and $(G_2,\theta _2)$ have the Bogomolov–Positselski property by Example 3.4-(a), Theorem 5.6 implies that also $(G,\theta )$ has the Bogomolov–Positselski property. Observe that G is $H^\bullet$-quadratic (cf. [25, Remark 5.25-(c)]).

5.3 Pro-$\ell$ groups of elementary type

Let $(G,\theta )$ be an oriented pro-$\ell$ group, and let A be a free abelian pro-$\ell$ group. Recall that the semidirect product $A\rtimes (G,\theta )=(A\rtimes G,\theta \circ \pi )$ is the oriented pro-$\ell$ group where $gag^{-1}=a^{\theta (g)}$ for all $a\in A$ and $g\in G$, and $\pi :A\rtimes G\rightarrow G$ is the canonical projection (cf. [8, § 3]).

The following is straightforward (cf., e.g., [10, Proposition 3.6]).

Proposition 5.9

Given an oriented pro-$\ell$ group $(G,\theta )$ and a free abelian pro-$\ell$ group A,  one has $K_{\theta \circ \pi }(A\rtimes G)=K_\theta (G)$. In particular, $A\rtimes (G,\theta )$ is Kummerian if, and only if, $(G,\theta )$ is Kummerian; and $A\rtimes (G,\theta )$ has the Bogomolov–Positselski property if, and only if, $(G,\theta )$ has the Bogomolov–Positselski property.

The family $\mathbf {ET}_\ell$ of oriented pro-$\ell$ groups of elementary type is the smallest class of finitely generated oriented pro-$\ell$ groups satisfying (cf. [8, § 3])

• (a) the oriented pro-$\ell$ group $(G,\eth _G)$, with G a Demushkin group, is of elementary type;

• (b) the oriented pro-$\ell$ group $(\mathbb {Z}_\ell ,\theta )$, with $\theta :\mathbb {Z}_\ell \rightarrow \mathbb {Z}_\ell ^\times$ arbitrary, is of elementary type;

• (c) if the oriented pro-$\ell$ group $(G,\theta )$ is of elementary type and A is a finitely generated free abelian pro-$\ell$ group, then also the semidirect product $A\rtimes (G,\theta )$ is of elementary type;

• (d) if $(G_1,\theta _1)$ and $(G_2,\theta _2)$ are oriented pro-$\ell$ groups of elementary type then also the free pro-$\ell$ product $(G_1,\theta _1)\amalg ^{\hat{\ell }}(G_2,\theta _2)$ is of elementary type.

Remark 5.10

• (a) In the original definition of oriented pro-2 groups of elementary type one has that also the cyclic group $C_2$ of order 2, endowed with the non-trivial orientation $\theta _{C_2}:C_2\twoheadrightarrow \{\pm 1\}\subset \mathbb {Z}_2^\times$, is a pro-2 group of elementary type (cf. [8, p. 242]). Since our results always assume oriented pro-$\ell$ groups to be torsion-free, we may safely exclude $(C_2,\theta _{C_2})$ from the above definition of oriented pro-$\ell$ groups of elementary type.

• (b) From the results in [26, § 3.3–3.4], one may deduce that a finitely generated subgroup H of an oriented pro-$\ell$ groups of elementary type $(G,\theta )$ gives rise to a pro-$\ell$ groups of elementary type $(H,\theta \vert _H)$.

• (c) If $(F,\theta )$ is a torsion-free oriented pro-$\ell$ group with F a finitely generated free pro-$\ell$ group and $\theta :F\rightarrow \mathbb {Z}_\ell ^\times$ any orientation, then $(F,\theta )$ is of elementary type. Indeed, if $\theta =\mathbf {1}$, then $(F,\theta )$ is isomorphic to the free pro-$\ell$ product of d copies of the oriented pro-$\ell$ group $(\mathbb {Z}_\ell ,\mathbf {1})$, where d is the minimal number of generators of F. Otherwise, $\mathrm {im}(\theta )\simeq \mathbb {Z}_\ell$, and the short exact sequence of pro-$\ell$ groups

  

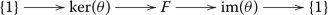
  splits. In this case, let $\{x_1,\ldots ,x_d\}$ be a minimal generating set where $\theta (x_1)\ne 1$ and $\theta (x_i)=1$ for $i\ge 2$, and let H be the subgroup of F generated by $\{x_2,\ldots ,x_d\}$, which is free. Then, $(F,\theta )\simeq (H,\mathbf {1})\amalg ^{\hat{\ell }}(\mathrm {im}(\theta ),\mathrm {id}_{\mathrm {im}(\theta )})$, where both factors are oriented pro-$\ell$ groups of elementary type.

From Example 2.7-(b), Sect. 5.1, and Propositions 5.5 and 5.9, one concludes that oriented pro-$\ell$ groups of elementary type are Kummerian. I. Efrat’s Elementary Type Conjecture states that if $\mathbb {K}$ is a field containing a primitive $\ell {\mathrm {th}}$-root of 1 (and also $\sqrt{-1}$ if $\ell =2$) and if the maximal pro-$\ell$ Galois group $G_{\mathbb {K}}(\ell )$ is finitely generated, then $(G_{\mathbb {K}}(\ell ),\tilde{\theta }_{\mathbb {K},\ell })$ is of elementary type (cf. [6, 7], see also [15, § 10] and [26, § 7.5]).

Example 5.11

The oriented pro-$\ell$ group $(G,\theta )$ as in Example 5.8 is not of elementary type. Indeed, the subgroup of G generated by $\{x,y_1,y_2\}$ contains a finitely generated subgroup which does not complete into a Kummerian oriented pro-$\ell$ group (cf. [24, Example 5.3])—in particular, G does not occur as the maximal pro-$\ell$ Galois group of a field containing a primitive $\ell {\mathrm {th}}$-root of unity (and also $\sqrt{-1}$ if $\ell =2$). Therefore, $(G,\theta )$ is not of elementary type by Remark 5.10-(b).

Theorem 5.12

Let $(G,\theta )$ be an oriented pro-$\ell$ group of elementary type. Then $(G,\theta )$ has the Bogomolov–Positselski property.

Proof

If G is a free pro-$\ell$ group, then $(G,\theta )$ has the Bogomolov–Positselski property by Example 3.4-(a). If G is a Demushkin group and $\theta =\eth _G$, then $(G,\eth _G)$ has the Bogomolov–Positselski property by Theorem 5.1.

By Proposition 5.9, if $(G,\theta )=A\rtimes (G_0,\theta \vert _{G_0})$ where A is a free abelian pro-$\ell$ group and the right side factor is an oriented pro-$\ell$ group of elementary type, then $(G,\theta )$ has the Bogomolov–Positselski property—provided that $(G_0,\theta \vert _{G_0})$ has the Bogomolov–Positselski property.

Finally, by Theorem 5.6, if $(G,\theta )=(G_1,\theta _1)\amalg ^{\hat{\ell }}(G_2,\theta _2)$ and both $(G_1,\theta _1)$ and $(G_2,\theta _2)$ have the Bogomolov–Positselski property, then also $(G,\theta )$ has the Bogomolov–Positselski property. $\square$

Let $\mathbb {K}$ be a field containing a primitive $\ell {\mathrm {th}}$-root of unity, and set $\mathbb {K}^\times =\mathbb {K}\smallsetminus \{0\}$. Since Kummer theory yields an isomorphism of (discrete) $\ell$-elementary abelian pro-$\ell$ groups $H^1(G_{\mathbb {K}}(\ell ),\mathbb {F}_\ell )^\vee \simeq \mathbb {K}^\times /(\mathbb {K}^\times )^\ell$, the pro-$\ell$ group $G_{\mathbb {K}}(\ell )$ is finitely generated if, and only if, the quotient $\mathbb {K}^\times /(\mathbb {K}^\times )^\ell$ is finite. One has the following (see [17, Theorem D], and [9] for item (f)).

Proposition 5.13

Let $\mathbb {K}$ be a field containing a primitive $\ell {\mathrm {th}}$-root of 1 (and also $\sqrt{-1}$ if $\ell =2$), such that the quotient $\mathbb {K}^\times /(\mathbb {K}^\times )^\ell$ is finite. Then the oriented pro-$\ell$ group $(G_{\mathbb {K}}(\ell ),\theta _{\mathbb {K},\ell })$ is of elementary type in the following cases:

• (a) $\mathbb {K}$ is finite;

• (b) $\mathbb {K}$ is a pseudo algebraically closed (PAC) field, or an extension of relative transcendence degree 1 of a PAC field;

• (c) $\mathbb {K}$ is an extension of transcendence degree 1 of a local field;

• (d) $\mathbb {K}$ is $\ell$-rigid (cf. [32, p. 722], see also [4, § 3]);

• (e) $\mathbb {K}$ is algebraic extension of a global field of characteristic not $\ell ;$

• (f) $\mathbb {K}=\Bbbk (\!(T)\!),$ where $(G_{\Bbbk }(\ell ),\theta _{\Bbbk ,\ell })$ is of elementary type.

Corollary 1.3 follows from Theorem 5.12 and Proposition 5.13.