A large arboreal Galois representation for a cubic postcritically finite polynomial

Abstract

We give a complete description of the arboreal Galois representation of a certain postcritically finite cubic polynomial over a large class of number fields and for a large class of basepoints. This is the first such example that is not conjugate to a power map, Chebyshev polynomial, or Lattès map. The associated Galois action on an infinite ternary rooted tree has Hausdorff dimension bounded strictly between that of the infinite wreath product of cyclic groups and that of the infinite wreath product of symmetric groups. We deduce a zero-density result for prime divisors in an orbit under this polynomial. We also obtain a zero-density result for the set of places of convergence of Newton’s method for a certain cubic polynomial, thus resolving the first nontrivial case of a conjecture of Faber and Voloch.

1 Introduction

Let K be a field and $f \in K[z]$ a polynomial of degree $d \ge 2$. Consider the Galois groups of polynomials of the form

$$\begin{aligned} f^n(z) - x, \end{aligned}$$

where $x \in K$, and $f^n = f \circ \cdots \circ f$ is the n-th iterate of f (with the convention that $f^0(z) = z$). Such groups are called arboreal Galois groups because (under certain hypotheses) they can be made to act on trees.

Let $T_n$ be the graph whose vertex set is

$$\begin{aligned} \bigsqcup _{0 \le i \le n} f^{-i}(x), \end{aligned}$$

and where we draw an edge from $\alpha$ to $\beta$ if $f(\alpha ) =\beta$. Let $G_n = {\text {Gal}}\left( f^n(z) - x / K\right)$. Clearly, $G_n$ acts faithfully on $T_n$, so that $G_n \hookrightarrow {\text {Aut}}(T_n)$. Provided there is no critical point of f among the points of the above vertex set, the graph $T_n$ is a regular d-ary rooted tree with root x. For such f, ${\text {Aut}}(T_n)$ is isomorphic to the n-fold iterated wreath product $[\mathfrak {S}_d]^n$ of the symmetric group $\mathfrak {S}_d$ on d letters. Odoni and Juul [9, 12] showed that if $\mathrm {char}(K)$ and the degree are not both 2, and if f is chosen generically (in the Zariski sense), then $G_n \cong {\text {Aut}}(T_n) \cong [\mathfrak {S}_d]^n$.

By contrast, for specific choices of f and x, the corresponding Galois groups may be much smaller (see [6, §3] for a high-level explanation and [2, 4, 8, 14] for detailed examples). Consider a polynomial f that is postcritically finite, or PCF for short, meaning that all of its critical points have finite orbit under the iteration of f. The simplest examples of PCF polynomials are the power maps $f(z) = z^d$ and the Chebyshev polynomials defined by $f\left( z + 1/z\right) = z^d + 1/z^d$. These two examples arise from the d-power endomorphism of the algebraic group $\mathbb {G}_m$, which gives a foothold on the associated arboreal Galois representation. (A third type of example, Lattès maps, arises from an endomorphism of an elliptic curve; however, Lattès maps are never conjugate to polynomials. See [15, §6.4].)

Jones and Pink [6, Thm. 3.1] have shown that for PCF maps, the Galois groups $G_n$ have unbounded index inside ${\text {Aut}}(T_n)$ as $n\rightarrow \infty$. However, their proof does not explicitly describe $G_n$. One can give an upper bound for $G_n$ inside ${\text {Aut}}(T_n)$ by realizing it as a specialization of ${\text {Gal}}\left( f^n(z) - t / K(t)\right)$, with t transcendental over K. The latter group may be embedded in the profinite monodromy group $\pi _1^{\acute{\mathrm{e}}\mathrm{t}}(\mathbb {P}^1_{K} \smallsetminus P)$, where P is the strict postcritical orbit; this is precisely the tack taken by Pink [14] in the case of quadratic PCF polynomials.

In this paper, we give the first complete calculation of the arboreal Galois group attached to a PCF polynomial over a number field that is not associated with an endomorphism of an algebraic group. More specifically, we describe the Galois groups $G_n = {\text {Gal}}\left( f^n(z) - x / K\right)$ for the polynomial

$$\begin{aligned} f(z) = -2z^3 + 3z^2 \end{aligned}$$

over a number field K, where x is chosen to satisfy a certain local hypothesis at the primes 2 and 3. In Sect.  2 we will define groups $E_n$ that fit between ${\text {Aut}}(T_n)\cong [\mathfrak {S}_3]^n$ and its Sylow 3-subgroup $[C_3]^n$—the iterated wreath product of cyclic groups of order 3. The groups $E_n$ are somewhat tricky to handle because their action on the tree lacks a certain rigidity property: for $m < n$, the kernel of the restriction homomorphism $E_n \rightarrow E_m$ is not the direct product of copies of $E_{n-m}$. That is, in contrast to $[\mathfrak {S}_3]^n$ and $[C_3]^n$, the action of $E_n$ on one branch of the tree above $T_m$ is not independent of its action on another branch. Our main result is the following.

Theorem 1.1

Let K be a number field, let $f(z) = -2z^3 + 3z^2\in K[z]$, and let $x \in K$. Suppose there exist primes $\mathfrak {p}$ and $\mathfrak {q}$ lying over 2 and 3, respectively, such that $v_\mathfrak {q}(x) = 1$, and either $v_\mathfrak {p}(x) = \pm 1$ or $v_\mathfrak {p}(1-x) = 1$. Then for each $n \ge 1$,

• (1) The polynomial $f^n(z) - x$ is irreducible over K.

• (2) We have an isomorphism ${\text {Gal}}\left( f^n(z) - x / K\right) \cong E_n \subset {\text {Aut}}(T_n)$.

Let $E_{\infty }=\varprojlim E_n$ and ${\text {Aut}}(T_\infty ) = \varprojlim {\text {Aut}}(T_n)$ be the corresponding inverse limits. Then the Hausdorff dimension of $E_\infty$ in ${\text {Aut}}(T_\infty )$ is

$$\begin{aligned} \lim _{n \rightarrow \infty } \frac{\log |E_n|}{\log |{\text {Aut}}(T_n)|} = 1 - \frac{1}{3} \ \frac{\log 2}{\log 6} \approx 0.871. \end{aligned}$$

(1)

Remark 1.2

In this article, we implicitly work in the category of groups with an action on the regular rooted tree $T_n$. This applies, for example, to the isomorphism between $E_n$ and the Galois group in the theorem.

The Galois group ${\text {Gal}}\left( f^n(z) - x / K\right)$ depends a priori on the number field K and the basepoint x, but Theorem 1.1 shows that many choices of K and x give the same isomorphism type. One key reason is that the discriminant of the second iterate is a square:

$$\begin{aligned} \text {For any}~x, \quad \mathrm {Disc}\left( f^2(z) - x\right) = \left[ 2^{16} \cdot 3^9 \cdot x^2(x-1)^2\right] ^2. \end{aligned}$$

(2)

This observation will be vital for forcing the Galois group of $f^n(z) - x$ to lie inside $E_n$. To fill out the entire group $E_n$, we utilize ramification above the primes 2 and 3. (See the proof of Proposition 3.6.) These two features are the only arithmetic-dynamical inputs to the theorem; the rest is general theory of groups acting on regular rooted trees.

We are also able to deduce that the geometric Galois group has the same structure:

Corollary 1.3

Let $f(z) = -2z^3 + 3z^2$. Let t be transcendental over $\mathbb {Q}$. For every $n \ge 1$, we have

$$\begin{aligned} {\text {Gal}}\left( f^n(z) - t / {\bar{\mathbb {Q}}}(t)\right) \cong E_n. \end{aligned}$$

For a polynomial $g \in \mathbb {Q}[x]$, there are two profinite monodromy groups:

$$\begin{aligned} G_g^{\mathrm {geom}}&= \lim _{\begin{array}{c} \leftarrow \\ n \end{array}} {\text {Gal}}\left( g^n(z) - t / {\bar{\mathbb {Q}}}(t)\right) \qquad \text {(geometric monodromy)} \\ G_g^{\mathrm {arith}}&= \lim _{\begin{array}{c} \leftarrow \\ n \end{array}} {\text {Gal}}\left( g^n(z) - t / \mathbb {Q}(t)\right) \qquad \text {(arithmetic monodromy)}. \end{aligned}$$

In general, one knows that $G_g^{\mathrm {geom}} \subset G_g^{\mathrm {arith}}$. Theorem 1.1 and its corollary imply that $G_f^{\mathrm {geom}} = G_f^{\mathrm {arith}}$ for our special cubic PCF polynomial $f(z) = -2z^3 + 3z^2$. By contrast, Pink has shown that $G_g^{\mathrm {geom}} \subsetneq G_g^{\mathrm {arith}}$ for all quadratic PCF polynomials g over the rationals [14, Thm. 2.8.4, Cor. 3.10.6]. Similar statements hold upon replacing $\mathbb {Q}$ by essentially any other number field.

While $E_n$ is not an iterated wreath product, it does satisfy the following self-similarity property: the action of $E_n$ on the subtree of height $n-1$ stemming from any fixed vertex at level 1 is isomorphic to $E_{n-1}$. This self-similarity is a property of geometric iterated monodromy groups [11, Prop. 6.4.2], and $E_n$ is such a group by Corollary 1.3.

Odoni [13] has shown that descriptions of iterated Galois groups of this sort give rise to applications on the density of prime divisors in certain dynamically defined sequences. (See also [5, 9, 10].) More precisely, after counting elements of $E_n$ that fix a leaf of the tree $T_n$, we have the following arithmetic application.

Theorem 1.4

Let K be a number field for which there exists an unramified prime above 2 and above 3. Let $y_0 \in K \smallsetminus \{0,1,3/2,-1/2\}$, and define the sequence $y_i = f^i(y_0)$. Then the set of prime ideals $\mathfrak {P}$ such that

$$\begin{aligned} y_i \equiv 0 \text { or } 1 \!\!\!\!\pmod \mathfrak {P}\quad \text { for some } i \ge 0 \end{aligned}$$

has natural density zero. In particular, the set of prime divisors of the sequence $(y_i)$ has natural density zero.

Our choice of the polynomial $f(z) = -2z^3 + 3z^2$ was originally motivated by the following conjecture of Faber and Voloch [3].

Conjecture 1.5

(Newton Approximation fails for 100% of primes) Let g be a polynomial of degree $d \ge 2$ with coefficients in a number field K and let $y_0 \in K$. Define the Newton map $N(z) = z - g(z) / g'(z)$ and, for each $n \ge 0$, set $y_{n+1} = N(y_n)$. Assume the Newton approximation sequence $(y_n)$ is not eventually periodic. Let $C(K, g, y_0)$ be the set of primes $\mathfrak {P}$ of K for which $(y_n)$ converges in the completion $K_{\mathfrak {P}}$ to a root of f. Then the natural density of the set $C(K, g, y_0)$ is zero.

Faber and Voloch showed that Conjecture 1.5 holds for any polynomial g with at most 2 distinct roots. Thus, the first nontrivial case of the conjecture is a separable cubic polynomial. For reasons explained in [3, Cor. 1.2], the simplest such cubic polynomial is $g(z) = z^3 - z$, whose associated Newton map turns out to be conjugate to our polynomial $f(z) = -2z^3 + 3z^2$. Our results therefore yield a proof of the first nontrivial case of the Faber–Voloch conjecture:

Theorem 1.6

Let K be a number field for which there exists an unramified prime over 2 and over 3. Let $g(z) = z^3 - z$. Choose $y_0 \in K$ such that the Newton iteration sequence $y_i = N^i(y_0)$ does not encounter a root of g. Then the set of primes $\mathfrak {P}$ of K for which the Newton sequence $(y_i)$ converges in $K_\mathfrak {P}$ to a root of g has natural density zero.

The first and third authors, in collaboration with several others, obtained a weak form of Theorem 1.6 for a wide class of polynomials [1, Thm. 4.6]. More precisely, they showed that the density of primes as in the theorem has natural density strictly less than one.

The outline of the paper is as follows. In Sect. 2, we will define and discuss the group $E_n$ and compute the Hausdorff dimension of Eq. (1). We will then prove the rest of Theorem 1.1 in Sect. 3. Next, we consider the case that K is the field of rational functions ${\bar{\mathbb {Q}}}(t)$, proving Corollary 1.3 in Sect. 4. In Sect. 5, we compute the proportion of elements of $E_n$ that fix at least one leaf of the tree $T_n$, and in Sect. 6, we prove Theorems 1.4 and 1.6.

2 Tree automorphisms

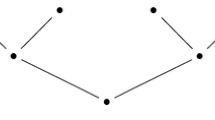
Let $T_n$ denote the regular ternary rooted tree with n levels, as in Fig. 1. Note that $T_n$ has $3^n$ leaves and $1 + 3 + \cdots + 3^n$ vertices. Our results and many arguments will depend on an implicit labeling of the vertices of $T_n$. We will make this labeling explicit now for purposes of rigor, but we will not comment on it again afterward.

Fig. 1

The ternary rooted tree $T_n$ with n levels

• The level of a vertex is its distance from the root.

• A vertex at level i is given a label $(\ell _1, \ldots , \ell _i)$, where $\ell _j \in \{1,2,3\}$. The root is given the empty label ().

• No two vertices at the same level have the same label.

• The unique path from the root to the vertex with label $(\ell _1, \ldots , \ell _i)$ consists of the vertices with labels $(), (\ell _1), (\ell _1,\ell _2), \ldots , (\ell _1, \ell _2, \ldots , \ell _i)$.

This labeling enables us to identify certain canonical subtrees of $T_n$. For example, for each $i \in \{1,2,3\}$, we consider the subtree T that is induced by the set of vertices with labels of the form $(i,*,\ldots , *)$; then T is isomorphic to $T_{n-1}$.

The automorphism group ${\text {Aut}}(T_n)$ of the regular rooted ternary tree is isomorphic to the n-fold iterated wreath product $[\mathfrak {S}_3]^n$. Indeed, we may decompose $T_n$ as a copy of $T_1$ (vertices of level at most 1) with 3 copies of $T_{n-1}$ attached along the leaves of $T_1$, so that

$$\begin{aligned} {\text {Aut}}(T_n) \cong {\text {Aut}}(T_{n-1}) \wr {\text {Aut}}(T_1) \cong [\mathfrak {S}_3]^{n-1} \wr \mathfrak {S}_3 = [\mathfrak {S}_3]^n. \end{aligned}$$

(3)

Our labeling has the effect of fixing an isomorphism ${\text {Aut}}(T_1) \cong \mathfrak {S}_3$. For any elements $a_1,a_2,a_3 \in {\text {Aut}}(T_{n-1})$ and any $b \in {\text {Aut}}(T_1)$, the element

$$\begin{aligned} \big ( (a_1,a_2,a_3),b\big ) \in {\text {Aut}}(T_{n-1}) \wr {\text {Aut}}(T_1) \cong {\text {Aut}}(T_n) \end{aligned}$$

acts on the tree by first acting on the 3 copies of $T_{n-1}$ via $a_1, a_2$, and $a_3$, respectively, and then by permuting these $T_{n-1}$’s via b. More precisely, if we label a vertex y of $T_n$ by (x, i), where x is a vertex of $T_{n-1}$ and $i \in \{1,2,3\}$ is the vertex at level 1 that lies below y, then

$$\begin{aligned} \big ((a_1,a_2,a_3),b\big ).(x,i) = (a_i.x, b.i). \end{aligned}$$

A labeling of the leaves of $T_n$ induces an injection ${\text {Aut}}(T_n) \hookrightarrow \mathfrak {S}_{3^n}$. Changing the labeling corresponds to conjugating by an element of $\mathfrak {S}_{3^n}$, and so each automorphism of $T_n$ has a well-defined sign attached to it, corresponding to the parity of the number of transpositions needed to represent it. Thus, for each $n\ge 1$, we have a homomorphism

$$\begin{aligned} \mathrm {sgn}:{\text {Aut}}(T_n) \rightarrow \{\pm 1\}. \end{aligned}$$

Lemma 2.1

Let $g = \big ( (a_1,a_2,a_3),b\big )$ be an element of ${\text {Aut}}(T_n)$ for some $n \ge 2$, where $b \in {\text {Aut}}(T_1)$, and $a_i \in {\text {Aut}}(T_{n-1})$ for $i=1,2,3$. Then

$$\begin{aligned} \mathrm {sgn}(g) = \mathrm {sgn}(b) \ \prod _{i=1}^3 \mathrm {sgn}(a_i). \end{aligned}$$

Proof

Partition the leaves of $T_n$ into three disjoint sets $L_1, L_2, L_3$ so that the elements of $L_i$ lie over leaf i of $T_1$, for $i=1,2,3$. Note that $|L_i| = 3^{n-1}$. With this notation, $\mathrm {sgn}(a_i)$ is the sign of $a_i$ acting as a permutation on the set $L_i$.

Consider first the case that $b = 1$. Then g permutes the elements of each $L_i$ separately; hence, $\mathrm {sgn}(g) = \prod \mathrm {sgn}(a_i)$.

Next, consider the case that $g = \big ( (1,1,1), b\big )$ for arbitrary $b \in {\text {Aut}}(T_1)$. We have already proven the desired result if $b = 1$. If b is a 2-cycle—say $b = (ij)$—then the induced permutation on the leaves of $T_n$ decomposes as a product of $3^{n-1}$ disjoint 2-cycles $(a_i a_j)$, where $a_i \in L_i$ and $a_j \in L_j$. Therefore,

$$\begin{aligned} \mathrm {sgn}(g) = (-1)^{3^{n-1}} = - 1 = \mathrm {sgn}(b). \end{aligned}$$

Similarly, if b is a 3-cycle, then the induced permutation on the leaves of $T_n$ decomposes as a product of $3^{n-1}$ disjoint 3-cycles. Hence,

$$\begin{aligned} \mathrm {sgn}(g) = 1 = \mathrm {sgn}(b). \end{aligned}$$

Finally, we consider the general case $g = \big ((a_1,a_2,a_3), b\big )$. Define $h = \big ((1,1,1), b^{-1}\big )$. Then $hg = \big ((a_1,a_2,a_3),1\big )$. The previous two paragraphs show that

$$\begin{aligned} \prod _{i=1}^3\mathrm {sgn}(a_i) = \mathrm {sgn}(hg) = \mathrm {sgn}(h) \ \mathrm {sgn}(g) = \mathrm {sgn}(b^{-1}) \ \mathrm {sgn}(g). \end{aligned}$$

$\square$

For any $m \le n$, we have a restriction homomorphism $\pi _m :{\text {Aut}}(T_n) \rightarrow {\text {Aut}}(T_m)$, where $T_m$ is the subtree with m levels with the same root vertex as $T_n$. We write $\mathrm {sgn}_m = \mathrm {sgn}\circ \pi _m$ for the composition of restriction followed by the sign map. Define a sequence of subgroups $E_n \subset {\text {Aut}}(T_n)$ by the following formula:

$$\begin{aligned} E_n = {\left\{ \begin{array}{ll} {\text {Aut}}(T_1) &{} \quad \text {if}~n = 1, \\ \left( E_{n-1} \wr {\text {Aut}}(T_1) \right) \cap \ker (\mathrm {sgn}_2) &{} \quad \text {if}~n \ge 2. \end{array}\right. } \end{aligned}$$

Here we use the embedding

$$\begin{aligned} E_{n-1} \wr {\text {Aut}}(T_1) \hookrightarrow {\text {Aut}}(T_{n-1}) \wr {\text {Aut}}(T_1) \cong {\text {Aut}}(T_n) \end{aligned}$$

from Eq. (3). Thus, for $n\ge 2$, writing a given automorphism $\sigma \in {\text {Aut}}(T_n)$ as $\sigma = \big ((a_1,a_2,a_3), b \big )$, we have

$$\begin{aligned} \sigma = \big ((a_1,a_2,a_3), b \big ) \in E_n \qquad \text {if and only if}\qquad a_1,a_2,a_3\in E_{n-1} \text { and } \mathrm {sgn}_2(\sigma ) = 1 . \end{aligned}$$

(4)

Proposition 2.2

For $n \ge 1$, we have $\displaystyle |E_n| = 2^{3^{n-1}} \cdot 3^\frac{3^n-1}{2}$.

Proof

Since ${\text {Aut}}(T_1) \cong \mathfrak {S}_3$, the result is clear for $n = 1$. Suppose it holds for some $n\ge 1$. Let $\phi$ be the composition

$$\begin{aligned} E_{n} \wr {\text {Aut}}(T_1) \hookrightarrow {\text {Aut}}(T_{n+1}) \mathop {\rightarrow }\limits ^{\mathrm {sgn}_2} \{\pm 1\}. \end{aligned}$$

By definition, $E_{n+1} = \ker (\phi )$, and $\phi$ is onto because $((1,1,1),\epsilon ) \mapsto -1$ for any transposition $\epsilon$ of the leaves of $T_1$. Thus,

$$\begin{aligned} |E_{n+1}|= & {} \frac{1}{2} \left| E_n \wr {\text {Aut}}(T_1) \right| = \frac{1}{2} |{\text {Aut}}(T_1)| \cdot |E_n|^3 = \frac{1}{2} \cdot 6 \cdot \left( 2^{3^{n-1}} \cdot 3^{\frac{3^n-1}{2}} \right) ^3 \\ {}= & {} 2^{3^n} \cdot 3^{\frac{3^{n+1}-1}{2}}. \end{aligned}$$

$\square$

Our construction of $E_n$ depends on an identification of $T_{n-1}$ with the subtree of $T_n$ lying above a vertex at level 1, which in turn depends on the labeling we have assigned to $T_n$. In other words, $E_n$ is not normal in ${\text {Aut}}(T_n)$ (for $n \ge 3$): a different labeling yields a conjugate subgroup in ${\text {Aut}}(T_n)$.

Proposition 2.3

$E_n$ is normal in ${\text {Aut}}(T_n)$ if and only if $n = 1$ or 2.

Proof

We have $E_1 = {\text {Aut}}(T_1)$, and $E_2$ has index 2 in ${\text {Aut}}(T_2)$. It remains to show that $E_n$ is not normal in ${\text {Aut}}(T_n)$ for $n \ge 3$. To that end, we first construct some special elements of ${\text {Aut}}(T_n)$.

Define $\nu _n \in {\text {Aut}}(T_n)$ inductively for $n\ge 1$ as follows:

$$\begin{aligned} \nu _n = {\left\{ \begin{array}{ll} (12) &{} \quad n = 1, \\ \big ((\nu _{n-1},1,1), 1 \big ) &{} \quad n \ge 2. \end{array}\right. } \end{aligned}$$

Thus, $\nu _n$ transposes two leaves at the n-th level and acts trivially on the rest of $T_n$. In particular, $\mathrm {sgn}(\nu _n) = -1$. This yields $\nu _2 \not \in E_2$, and by induction, it follows that $\nu _n \not \in E_n$ for $n \ge 2$. Note further that $\nu _n^{-1} = \nu _n$.

Next, for fixed $n\ge 3$, define $a=\big ( (1,1,1), (123) \big )\in {\text {Aut}}(T_n)$. Then $a\in E_n$ by (4). However,

$$\begin{aligned} \nu _n \, a \, \nu _n^{-1} = \big ( (\nu _{n-1},1,1),1 \big ) \big ( (1,1,1),(123) \big ) \big ( (\nu _{n-1},1,1),1 \big ) = \big ( (\nu _{n-1},1,\nu _{n-1}),(123) \big ), \end{aligned}$$

which does not belong to $E_n$ since $\nu _{n-1} \not \in E_{n-1}$ for $n \ge 3$. It follows that $E_n$ is not normal in ${\text {Aut}}(T_n)$, as desired. $\square$

Write $T_\infty = \bigcup _{n \ge 1} T_n$ for the infinite ternary rooted tree, which has automorphism group

$$\begin{aligned} {\text {Aut}}(T_\infty ) = \varprojlim {\text {Aut}}(T_n), \end{aligned}$$

where the inverse limit is taken with respect to the restriction homomorphisms

$$\begin{aligned} \pi _m:{\text {Aut}}(T_n) \rightarrow {\text {Aut}}(T_m) \quad \text {for}\quad m \le n. \end{aligned}$$

The recursive definition of $E_n$ implies that we also have restriction homomorphisms $E_n \rightarrow E_m$ for $m \le n$. Passing to the inverse limit gives a subgroup

$$\begin{aligned} E_\infty = \varprojlim E_n \end{aligned}$$

of ${\text {Aut}}(T_\infty )$.

Corollary 2.4

The Hausdorff dimension of $E_\infty$ in ${\text {Aut}}(T_\infty )$ is given by Eq. (1).

Proof

Using the facts that ${\text {Aut}}(T_n) \cong {\text {Aut}}(T_{n-1}) \wr {\text {Aut}}(T_1)$ and that ${\text {Aut}}(T_1)\cong \mathfrak {S}_3$, a simple induction shows that

$$\begin{aligned} |{\text {Aut}}(T_n)| = 6^{\frac{3^n - 1}{2}}. \end{aligned}$$

(5)

Combining this fact with Proposition 2.2 gives the desired result. $\square$

Corollary 2.5

$E_\infty$ has infinite index in ${\text {Aut}}(T_\infty )$.

Comparing the cardinalities of $E_n$ and ${\text {Aut}}(T_n)$, we see that they share a Sylow 3-subgroup. We can describe one such subgroup explicitly as follows. Let $C_3$ be the cyclic 3-subgroup of ${\text {Aut}}(T_1) \cong \mathfrak {S}_3$. Define a sequence of groups $H_n$ by the following formula:

$$\begin{aligned} H_n = {\left\{ \begin{array}{ll} C_3 &{} \text {if}~n = 1, \\ H_{n-1} \wr C_3 &{} \text {if}~n \ge 2. \end{array}\right. } \end{aligned}$$

We identify $H_n$ with a subgroup of ${\text {Aut}}(T_n)$ using the embedding

$$\begin{aligned} H_n = H_{n-1} \wr C_3 \hookrightarrow {\text {Aut}}(T_{n-1}) \wr {\text {Aut}}(T_1) \cong {\text {Aut}}(T_n). \end{aligned}$$

Evidently, $H_n \cong [C_3]^n$, the iterated wreath product. By induction, we see that

$$\begin{aligned} |H_n| = 3^{\frac{3^n - 1}{2}}, \end{aligned}$$

(6)

so that $H_n$ is a Sylow 3-subgroup of ${\text {Aut}}(T_n)$.

Proposition 2.6

For $n \ge 1$, $H_n$ is a Sylow 3-subgroup of $E_n$. It is normal in $E_n$ if and only if $n=1$.

Proof

For $n = 1$, $H_n$ is an index-2 subgroup of $E_1 = {\text {Aut}}(T_1)$ and, hence, it is normal. Next, for some $n\ge 1$, suppose we know that $H_n$ is a subgroup of $E_n$. By their recursive definitions, to see that $H_{n+1} \subset E_{n+1}$ it suffices to show that any $h \in H_{n+1}$ restricts to an even permutation on $T_2$. The restriction of h to $T_2$ has the form $\big ((a_1,a_2,a_3), b\big )$, where each of $a_1, a_2, a_3$, and b is either trivial or a 3-cycle. By Lemma 2.1, we conclude that $\mathrm {sgn}_2(h) = 1$. Hence, $h \in E_{n+1}$, as desired.

Since $|H_n|$ is the 3-power part of $|E_n|$, we have proven the first statement of the proposition. It remains to show that $H_n$ is not normal in $E_n$ for $n \ge 2$.

For each $n\ge 1$, define $\tau _n \in {\text {Aut}}(T_n)$ inductively as follows:

$$\begin{aligned} \tau _n = {\left\{ \begin{array}{ll} (12) &{}\quad n = 1, \\ \big ((\tau _{n-1},1,1), (12) \big ) &{}\quad n \ge 2. \end{array}\right. } \end{aligned}$$

(7)

We claim that $\tau _n \in E_n$ for all $n\ge 1$. This is clear for $n=1$. Suppose that it holds for some $n\ge 1$. Then $\big ((\tau _n, 1, 1), (12)\big ) \in E_{n+1}$ if and only if its restriction to $T_2$ acts by an even permutation. The restriction to $E_2$ is given by $\big ( ( (12),1,1), (12) \big )$, which has positive sign by Lemma 2.1.

Note that for $n \ge 2$, we have $\tau _n^{-1} = \big ((1, \tau _{n-1}^{-1}, 1), (12)\big )$. Note also that for $n\ge 1$, we have $\tau _n\not \in H_n$, since the restriction of $\tau _n$ to $T_1$ is $(12)\not \in C_3$.

Next, for fixed $n\ge 2$, define $a= \big ( (1,1,1), (123) \big )\in H_n$. Then

$$\begin{aligned} \tau _n \, a \, \tau _n^{-1}= & {} \big ( (\tau _{n-1},1,1),(12) \big ) \big ( (1,1,1),(123) \big ) \big ((1,\tau _{n-1}^{-1},1),(12) \big ) \\= & {} \big ((1,\tau _{n-1}^{-1},\tau _{n-1}),(132) \big ), \end{aligned}$$

which does not belong to $H_n$, since $\tau _{n-1}\not \in H_{n-1}$. $\square$

Proposition 2.7

The Hausdorff dimension of $H_\infty$ in ${\text {Aut}}(T_\infty )$ is

$$\begin{aligned} \lim _{n \rightarrow \infty } \frac{\log |H_n|}{\log |{\text {Aut}}(T_n)|} = \frac{\log 3}{\log 6} \approx 0.613. \end{aligned}$$

Proof

Immediate from Eqs. (5) and (6). $\square$

Since $H_n \subseteq E_n \subseteq {\text {Aut}}(T_n)$, the preceding proposition and Corollary 2.4 show that for large n, $E_n$ is substantially larger than $H_n$, but much smaller than ${\text {Aut}}(T_n)$.

Finally, we will need a lemma that constructs certain special elements of $E_n$:

Lemma 2.8

Let $n \ge 2$ and let $g \in {\text {Aut}}(T_n)$ be any element that acts as follows:

• On the copy of $T_{n-1}$ with the same root as $T_n$, g acts by the identity.

• On each copy of $T_2$ rooted at a vertex of $T_n$ of level $n-2$, g acts by an even permutation of the 9 leaves.

Then $g \in E_n$.

Proof

We proceed by induction on n. For $n=2$, the second condition on g implies that $\mathrm {sgn}(g) = 1$, so $g \in E_2$. Suppose that the lemma holds for $n-1$, and let $g \in {\text {Aut}}(T_n)$ satisfy the given conditions. Let $u_1,u_2,u_3$ be the vertices of $T_n$ at level 1. Write $T_{n-1}(u_i)$ for the copy of $T_{n-1}$ inside $T_n$ that is rooted at $u_i$. Then g restricts to an element of ${\text {Aut}}(T_{n-1}(u_i))$ that satisfies the two conditions of the lemma. By the induction hypothesis, $g|_{T_{n-1}(u_i)} \in E_{n-1}$ for $i = 1,2,3$. In addition, g is the identity and, hence, is even, on $T_2$. Thus, $g\in E_n$ by the criterion of Eq.  (4). $\square$

3 Main theorem

Let K be a field of characteristic zero, and consider the polynomial

$$\begin{aligned} f(z) = -2z^3 + 3z^2 \in K[z]. \end{aligned}$$

The critical points of f in $\mathbb {P}^1$ are 0, 1, and $\infty$, all of which are fixed by f. Hence, f is PCF and, in fact, the union of the forward orbits of its critical points is $\{0,1,\infty \}$. Choose a point $x\in K\smallsetminus \{0,1\}$ to be the root of our preimage tree. Note that there is no critical point in the backward orbit of x—i.e., the set $f^{-1}(x) \cup f^{-2}(x) \cup \cdots$.

For each $n \ge 1$, define

$$\begin{aligned} K_n=K\big (f^{-n}(x)\big ) \qquad \text {and}\qquad G_n = {\text {Gal}}(K_n / K). \end{aligned}$$

(8)

Lemma 3.1

For any field K of characteristic zero and any $x\in K\smallsetminus \{0,1\}$, the Galois group $G_n$ of Eq.  (8) is isomorphic to a subgroup of $E_n$.

Proof

Because there is no critical point in the backward orbit of x, the set $f^{-i}(x)$ consists of exactly $3^i$ distinct elements for each $i\ge 0$. Identify the vertices of the ternary rooted tree $T_n$ with the set $\bigsqcup _{0 \le i \le n} f^{-i}(x)$, with vertex y lying immediately above $y'$ if and only if $f(y)=y'$. This identification induces a faithful action of $G_n$ on $T_n$ and, hence, $G_n$ may be identified with a subgroup of ${\text {Aut}}(T_n)$.

To see that this subgroup $G_n$ lies inside $E_n$, we proceed by induction on n. For $n=1$, this is clear because $E_1={\text {Aut}}(T_1)$.

Fix $n\ge 2$, and assume we know the lemma holds for $n-1$. Write $f^{-1}(x)=\{y_1,y_2,y_3\}$. For each $i=1,2,3$, applying the lemma to the field $K(y_i)$ with root point $y_i$ shows that

$$\begin{aligned} {\text {Gal}}\Big (K\big (f^{-(n-1)}(y_i)\big )/K(y_i)\Big ) \end{aligned}$$

is a subgroup of $E_{n-1}$ (The labeling of $T_n$ allows us to identify the portion of $T_n$ above $y_i$ with $T_{n-1}$). Since ${\text {Gal}}(K_1/K)$ is a subgroup of ${\text {Aut}}(T_1)$, it follows that $G_n$ is isomorphic to a subgroup $B_n$ of $E_{n-1} \wr {\text {Aut}}(T_1)$.

It remains to show that $B_n\subseteq \ker (\mathrm {sgn}_2)$. Direct computation shows that the discriminant of the degree-nine polynomial $f^2(z) - x$ is given by Eq. (2). Since this discriminant is a square in K, all elements of $B_n$ act as even permutations of the nine points of $f^{-2}(x)$. Thus, $B_n\subseteq \ker (\mathrm {sgn}_2)$, as desired. $\square$

Our goal is to compute the arboreal Galois groups $G_n$ in the case that K is a number field and that the basepoint $x \in K\smallsetminus \{0,1\}$ satisfies the following local hypothesis:

$$\begin{aligned}&\text {There exist primes}~\mathfrak {p}~\mathrm{and}~\mathfrak {q}~\mathrm{of}~K~\text {lying above}~2~\mathrm{and}~3, \mathrm{respectively,} \quad \quad \quad \quad (\dagger ) \\&\text {such that}~v_{\mathfrak {q}}(x) = 1,~\text {and either}~v_{\mathfrak {p}}(x) = \pm 1~\mathrm{or}~v_{\mathfrak {p}}(1-x) = 1. \end{aligned}$$

If this hypothesis holds, we will say that the pair (K, x) satisfies property $(\dagger )$ (relative to $\mathfrak {p}$ and $\mathfrak {q}$).

Example 3.2

If $K = \mathbb {Q}$, then the pairs $(\mathbb {Q},3)$ and $(\mathbb {Q},3/2)$ both satisfy property $(\dagger )$. The latter pair will be important for our arithmetic applications.

Lemma 3.3

Suppose that (K, x) satisfies $(\dagger )$ relative to $\mathfrak {p}$ and $\mathfrak {q}$. Then $f^n(z) - x$ is Eisenstein at $\mathfrak {q}$ for all $n \ge 1$. In particular, $f^n(z) - x$ is irreducible for all $n \ge 1$.

Proof

A simple induction shows that $f^n(z) \equiv z^{3^n} \pmod \mathfrak {q}$ and $f^n(0) = 0$. Since $v_{\mathfrak {q}}(x) = 1$, it follows immediately that $f^n(z) - x$ is Eisenstein at $\mathfrak {q}$. $\square$

Proposition 3.4

Let K be a number field, and let $x \in K$. Suppose that (K, x) satisfies property $(\dagger )$ relative to primes $\mathfrak {p}$ and $\mathfrak {q}$. Let $n\ge 0$, and let $y\in f^{-n}(x)$. Then:

• (1) There are primes $\mathfrak {p}'$ and $\mathfrak {q}'$ of K(y) lying above $\mathfrak {p}$ and $\mathfrak {q}$, respectively, such that

  $$\begin{aligned} e(\mathfrak {p}'/\mathfrak {p}) = 2^n \quad \text {and}\quad e(\mathfrak {q}' / \mathfrak {q}) = 3^n. \end{aligned}$$

• (2) The pair (K(y), y) satisfies property $(\dagger )$ relative to $\mathfrak {p}'$ and $\mathfrak {q}'$.

Proof

We proceed by induction on n. The statement is trivial for $n=0$. We therefore assume for the rest of the proof that $n\ge 1$ and that the statement holds for $n-1$.

Given $y\in f^{-n}(x)$, let $y''=f(y)\in f^{-(n-1)}(x)$. By our inductive hypothesis, there are primes $\mathfrak {p}''$ and $\mathfrak {q}''$ of $K(y'')$ lying over $\mathfrak {p}$ and $\mathfrak {q}$ satisfying the desired properties for $n-1$. The polynomial

$$\begin{aligned} f(z)-y'' = -2z^3 + 3z^2 - y'' \in K(y'')[z] \end{aligned}$$

is Eisenstein at $\mathfrak {q}''$. Thus, there is only one prime $\mathfrak {q}'$ of K(y) lying above $\mathfrak {q}''$, with ramification index $e(\mathfrak {q}' / \mathfrak {q}'') = 3$, and with $v_{\mathfrak {q}'}(y) = 1$. Moreover,

$$\begin{aligned} e(\mathfrak {q}' / \mathfrak {q}) = e(\mathfrak {q}' / \mathfrak {q}'') \cdot e(\mathfrak {q}'' / \mathfrak {q}) = 3 \cdot 3^{n-1} = 3^n . \end{aligned}$$

Meanwhile, by statement (2) for $n-1$, we have either $v_{\mathfrak {p}''}(y'')=1$, $v_{\mathfrak {p}''}(1-y'')=1$, or $v_{\mathfrak {p}''}(y'')=-1$. We consider these three cases separately.

If $v_{\mathfrak {p}''}(y'')=1$, then the Newton polygon of $f(z)-y''$ at $\mathfrak {p}''$ has a segment of length 2 and height 1. Thus, there is a prime $\mathfrak {p}'$ of K(y) lying above $\mathfrak {p}''$, with ramification index $e(\mathfrak {p}' / \mathfrak {p}'') = 2$, and with $v_{\mathfrak {p}'}(y) = 1$. Moreover,

$$\begin{aligned} e(\mathfrak {p}' / \mathfrak {p}) = e(\mathfrak {p}' / \mathfrak {p}'') \cdot e(\mathfrak {p}'' / \mathfrak {p}) = 2 \cdot 2^{n-1} = 2^n . \end{aligned}$$

If $v_{\mathfrak {p}''}(1-y'')=1$, note that f is self-conjugate via $z\mapsto 1-z$; that is, $1-f(1-z) = f(z)$. Thus, $1-y\in f^{-1}(1-y'')$, and the previous paragraph applied to $1-y$ gives the desired conclusion.

Finally, if $v_{\mathfrak {p}''}(y'')=-1$, then because $v_{\mathfrak {p}''}(-2)\ge 1$, the Newton polygon of $f(z)-y''$ at $\mathfrak {p}''$ has a segment of length 2 and height $-1$. Thus, there is a prime $\mathfrak {p}'$ of K(y) lying above $\mathfrak {p}''$, with ramification index $e(\mathfrak {p}' / \mathfrak {p}'') = 2$, and with $v_{\mathfrak {p}'}(y) = -1$. Once again, then, we have $e(\mathfrak {p}'/\mathfrak {p})=2^n$. $\square$

Corollary 3.5

Let K and x be as in Proposition 3.4. Let $n\ge 1$ and let $K_n$ be the splitting field of $f^n(z)-x$ over K. Then

$$\begin{aligned} 6^n \big | [K_n : K] . \end{aligned}$$

Proof

Pick $y\in f^{-n}(x)$, and let $\mathfrak {p}'$ and $\mathfrak {q}'$ be the primes of K(y) given by Proposition 3.4. Since $K_n/K$ has intermediate extension K(y) / K, the ramification index of some prime of $K_n$ over $\mathfrak {p}$ must be divisible by $e(\mathfrak {p}'/\mathfrak {p})=2^n$. Similarly, the ramification index of some prime of $K_n$ over $\mathfrak {q}$ must be divisible by $e(\mathfrak {q}'/\mathfrak {q})=3^n$. Thus, $6^n \mid [K_n:K]$. $\square$

Proposition 3.6

Let K and x be as in Proposition 3.4. Then

$$\begin{aligned} {\text {Gal}}\Big (K\big (f^{-1}(x)\big ) / K\Big ) \cong E_1 \cong \mathfrak {S}_3 \quad \text {and} \quad {\text {Gal}}\Big ( K\big (f^{-2}(x) \big ) / K \Big ) \cong E_2. \end{aligned}$$

Proof

Let $K_1=K(f^{-1}(x))$ and $K_2= K(f^{-2}(x))$. Then, as a splitting field of a cubic polynomial, $K_1$ is Galois over K with ${\text {Gal}}(K_1/K)$ isomorphic to a subgroup of $\mathfrak {S}_3$. By Corollary 3.5 with $n=1$, we have $6\mid [K_1:K]$. Hence, ${\text {Gal}}(K_1/K)\cong \mathfrak {S}_3$.

By Lemma 3.1, ${\text {Gal}}(K_2/K)$ acts on $f^{-2}(x)$ as a subgroup of $E_2$. It suffices to show that every element of $E_2$ is realized in ${\text {Gal}}(K_2/K)$.

Write $f^{-1}(x) = \{ u_1, u_2, u_3 \}$, and for each $i=1,2,3$, write

$$\begin{aligned} f^{-1}(u_i) = \{v_{i1}, v_{i2}, v_{i3} \} . \end{aligned}$$

Claim 1 There exists $\tau \in {\text {Gal}}(K_2/K_1) \subseteq {\text {Gal}}(K_2/K)$ that

• fixes $v_{1j}$ for each $j=1,2,3$,

• acts as a 2-cycle on the set $f^{-1}(u_2) = \{v_{21}, v_{22},v_{23} \}$, and

• acts as a 2-cycle on the set $f^{-1}(u_3) = \{v_{31}, v_{32},v_{33} \}$.

To prove Claim 1, note that $36 \mid [K_2:K]$ by Corollary 3.5 and, hence, $6 \mid [K_2 : K_1]$, since $[K_1:K]=6$. By Cauchy’s Theorem, there is some $\tau _1\in {\text {Gal}}(K_2/K_1)$ of order 2. Since $\tau _1$ fixes each $u_i$, it must act on each set $f^{-1}(u_i)$ as an element of $\mathfrak {S}_3$ of order dividing 2. Thus, for each $i=1,2,3$, $\tau _1$ acts as either a 2-cycle or the identity on $f^{-1}(u_i)$. In addition, $\tau _1$ is even as a permutation on $f^{-2}(x)$ but (being of order 2) is not the identity. Thus, $\tau _1$ acts as a 2-cycle on the preimages of exactly two of $u_1,u_2,u_3$, and as the identity on the preimage of the third, $u_m$.

Choose $\gamma ' \in {\text {Gal}}(K_1/K)$ with $\gamma '(u_1)=u_m$, and lift $\gamma '$ to $\gamma \in {\text {Gal}}(K_2/K)$. Let $\tau = \gamma ^{-1}\tau _1\gamma$. Then $\tau (u_i)=u_i$ for each i, and $\tau$ satisfies each of the three bulleted properties, proving Claim 1.

Claim 2 There exists $\rho \in {\text {Gal}}(K_2/K_1) \subseteq {\text {Gal}}(K_2/K)$ that acts as

• a 3-cycle on $f^{-1}(u_1) = \{v_{11}, v_{12},v_{13} \}$,

• either a 3-cycle or the identity on $f^{-1}(u_2) = \{v_{21}, v_{22},v_{23} \}$, and

• either a 3-cycle or the identity on $f^{-1}(u_3) = \{v_{31}, v_{32},v_{33} \}$.

To prove Claim 2, we again note that $6 \mid [K_2 : K_1]$. Hence, by Cauchy’s Theorem, there is some $\rho _1\in {\text {Gal}}(K_2/K_1)$ of order 3. We have $\rho _1(u_i)=u_i$ for each i, with $\rho _1$ acting as a 3-cycle on either one, two, or all three of $f^{-1}(u_i)$, and as the identity on the others. Lifting some appropriate $\gamma '\in {\text {Gal}}(K_1/K)$ to $\gamma \in {\text {Gal}}(K_2/K)$, we can ensure that $\rho = \gamma ^{-1}\rho _1\gamma$ satisfies the desired properties, proving Claim 2.

By the conclusions of Claims 1 and 2, the permutation $\tau \rho$ acts as

• a 3-cycle on $f^{-1}(u_1) = \{v_{11}, v_{12},v_{13} \}$,

• a 2-cycle on $f^{-1}(u_2) = \{v_{21}, v_{22},v_{23} \}$, and

• a 2-cycle on $f^{-1}(u_3) = \{v_{31}, v_{32},v_{33} \}$.

Let $\sigma =(\tau \rho )^2$. Then $\sigma$ acts as a 3-cycle on $f^{-1}(u_1)$ and as the identity on $f^{-1}(u_2) \cup f^{-1}(u_3)$.

Conjugating $\sigma$ by permutations $\gamma$ as in the proof of Claim 1 and then composing the resulting conjugates with one another, we see that ${\text {Gal}}(K_2/K_1)$ contains each element of $E_2$ that is the identity on $f^{-1}(x)$ and is either the identity or a 3-cycle on each $f^{-1}(u_i)$. There are $3^3=27$ such permutations.

Conjugating $\tau$ by permutations from the previous paragraph, as well as by permutations $\gamma$ as in the proof of Claim 1, we also see that ${\text {Gal}}(K_2/K_1)$ contains each element of $E_2$ that is the identity on $f^{-1}(x)$, is a 2-cycle on exactly two of $f^{-1}(u_1)$, $f^{-1}(u_2)$, and $f^{-1}(u_3)$, and is the identity on the third. There are $3^3=27$ such permutations.

Composing the maps of the previous two paragraphs, we see that ${\text {Gal}}(K_2/K_1)$ contains each element of $E_2$ that is the identity on $f^{-1}(x)$, is a 2-cycle on exactly two of $f^{-1}(u_1)$, $f^{-1}(u_2)$, and $f^{-1}(u_3)$, and is a 3-cycle on the third. There are $3^3 \cdot 2 = 54$ such permutations.

Thus, $[K_2 : K_1] \ge 27 + 27 + 54 = 108$, and, hence,

$$\begin{aligned} \,[K_2:K] \ge 6\cdot 108= 648 = |E_2|. \end{aligned}$$

Since ${\text {Gal}}(K_2/K)$ is isomorphic to a subgroup of $E_2$, we must have ${\text {Gal}}(K_2/K)\cong E_2$. $\square$

We are now prepared to prove part (b) of Theorem 1.1, which we restate here.

Theorem 3.7

Let K and x be as in Proposition 3.4. Then for any $n\ge 1$,

$$\begin{aligned} {\text {Gal}}\Big ( K\big (f^{-n}(x) \big ) / K \Big ) \cong E_n. \end{aligned}$$

Fig. 2

The locations of x, $u_1$, $u_2$, $u_3$ and y in $T_{n+1}$

Proof

By Lemma 3.1, we know that the Galois group is isomorphic to a subgroup of $E_n$. We must show that this subgroup is $E_n$ itself. We proceed by induction on n. For $n=1,2$, we are done by Proposition 3.6. Assuming we know the statement (for any such K and x) for a particular $n\ge 2$, we will now show it for $n+1$.

Let

$$\begin{aligned} K_n= K\big (f^{-n}(x)\big ) \quad \text {and}\quad K_{n+1}= K\big (f^{-(n+1)}(x)\big ). \end{aligned}$$

Write $f^{-1}(x) = \{u_1,u_2,u_3\}$. By Proposition 3.4, each of the pairs $(K(u_i),u_i)$ satisfies property $(\dagger )$ for $i=1,2,3$. Thus, our induction hypothesis says that ${\text {Gal}}(K_n/K)$ and all three of the Galois groups

$$\begin{aligned} {\text {Gal}}\Big (K\big (f^{-n}(u_i)\big ) / K(u_i) \Big ), \qquad \text {for}\; i=1,2,3 \end{aligned}$$

are isomorphic to $E_n$. Pick

$$\begin{aligned} y\in f^{-(n-2)}(u_3) \subseteq f^{-(n-1)}(x) . \end{aligned}$$

See Fig. 2.

Our main goal, which we will achieve at the end of Step 3 below, is to construct an element $\lambda \in {\text {Gal}}(K_{n+1} / K)$ that is the identity on

$$\begin{aligned} f^{-(n+1)}(x) \smallsetminus f^{-2}(y) \quad \text {and on}\quad f^{-1}(y), \end{aligned}$$

but which acts as two disjoint 2-cycles on $f^{-2}(y)$.

Step 1. Define

$$\begin{aligned} H= {\text {Gal}}\Big (K\big (f^{-n}(u_3)\big ) / K(u_3) \Big ). \end{aligned}$$

By the induction hypothesis, $H \cong E_n$. By Lemma 2.8 there is some $\sigma _1 \in H$ that is the identity on

$$\begin{aligned} f^{-n}(u_3) \smallsetminus f^{-2}(y) \quad \text {and on}\quad f^{-1}(y) \end{aligned}$$

and acts as two 2-cycles on $f^{-2}(y)$. Lift $\sigma _1$ to

$$\begin{aligned} \sigma \in {\text {Gal}}\big (K_{n+1} / K(u_3) \big )\subseteq {\text {Gal}}(K_{n+1} / K). \end{aligned}$$

Thus, $\sigma$ acts as we would like $\lambda$ to act on $f^{-n}(u_3)$, but we have no idea how it acts on $f^{-n}(u_1)$ and $f^{-n}(u_2)$.

Step 2. By Lemma 2.8, we may pick $\tau _1\in {\text {Gal}}(K_n/K)\cong E_n$ that is the identity on

$$\begin{aligned} f^{-n}(x) \smallsetminus f^{-1}(y) \end{aligned}$$

and acts as a 3-cycle on $f^{-1}(y)$. Lift $\tau _1$ to $\tau \in {\text {Gal}}(K_{n+1} / K)$.

Then $\tau \sigma \tau ^{-1}\in {\text {Gal}}(K_{n+1}/K)$ acts as

• the identity on $f^{-n}(u_3) \smallsetminus f^{-2}(y)$ and $f^{-1}(y)$,

• two 2-cycles on $f^{-2}(y)$, and

• the same as $\sigma$ on $f^{-(n-1)}(\{ u_1, u_2\})$,

where the two 2-cycles on $f^{-2}(y)$ for $\tau \sigma \tau ^{-1}$ do not occur above the same two elements of $f^{-1}(y)$ as the two 2-cycles for $\sigma$.

Thus, $\tau \sigma \tau ^{-1}\sigma ^{-1}\in {\text {Gal}}(K_{n+1}/K)$ acts as

• the identity on $f^{-n}(u_3) \smallsetminus f^{-2}(y)$ and $f^{-1}(y)$,

• two 2-cycles and (perhaps) a separate 3-cycle on $f^{-2}(y)$, and

• the identity on $f^{-(n-1)}(\{ u_1, u_2\})$.

Cubing to kill the possible 3-cycle in $f^{-2}(y)$, we see that

$$\begin{aligned} \rho = (\tau \sigma \tau ^{-1}\sigma ^{-1})^3 \in {\text {Gal}}(K_{n+1}/K) \end{aligned}$$

acts as

• the identity on $f^{-n}(x)$,

• the identity on $f^{-n}(u_3) \smallsetminus f^{-2}(y)$, and

• two 2-cycles on $f^{-2}(y)$.

Step 3. Consider the permutations $\tau ,\rho \in {\text {Gal}}(K_{n+1}/K)$ of Step 2. Then $\tau \rho \tau ^{-1}\rho ^{-1}$ acts as

• the identity on $f^{-n}(x)$,

• the identity on $f^{-n}(u_3) \smallsetminus f^{-2}(y)$,

• two 2-cycles and (perhaps) a separate 3-cycle on $f^{-2}(y)$, and

• for each $v\in f^{-(n-1)}(\{u_1,u_2\})$, an even permutation of $f^{-1}(v)$.

The even permutations of the last bullet point above are even permutations in $\mathfrak {S}_3$, and, hence, each is either the identity or a 3-cycle. Cubing, we see that

$$\begin{aligned} \lambda = (\tau \rho \tau ^{-1}\rho ^{-1})^3 \in {\text {Gal}}(K_{n+1}/K) \end{aligned}$$

acts as the identity on

$$\begin{aligned} f^{-(n+1)}(x) \smallsetminus f^{-2}(y) \quad \text {and on}\quad f^{-1}(y), \end{aligned}$$

and it acts as two 2-cycles on $f^{-2}(y)$, achieving the main goal from the start of the proof.

Step 4. Recall $H={\text {Gal}}(K(f^{-n}(u_3)) / K(u_3))\cong E_n$. Pick $w\in f^{-1}(y)$. By Lemma 2.8, we can pick $\gamma _1\in H$ that is the identity on

$$\begin{aligned} f^{-n}(u_3) \smallsetminus f^{-1}(w) \end{aligned}$$

and acts as a 3-cycle on $f^{-1}(w)$. Lift $\gamma _1$ to $\gamma \in {\text {Gal}}(K_{n+1}/K)$.

Conjugating the permutation $\lambda$ (of Step 3) by various products of $\gamma$ and the permutation $\tau$ (of Step 2), we see that ${\text {Gal}}(K_{n+1}/K)$ contains each of the 27 permutations that is the identity on

$$\begin{aligned} Y= \big ( f^{-(n+1)}(x) \smallsetminus f^{-2}(y) \big ) \cup f^{-1}(y) \end{aligned}$$

and acts as two disjoint 2-cycles on $f^{-2}(y)$. In addition, taking products of pairs of such permutations, ${\text {Gal}}(K_{n+1}/K)$ contains all 27 permutations that are the identity on Y and products of disjoint 3-cycles on $f^{-2}(y)$. Still taking products of pairs, ${\text {Gal}}(K_{n+1}/K)$ also contains all 54 permutations that are the identity on Y and the product of a disjoint 3-cycle and two 2-cycles on $f^{-2}(y)$. Together, then, ${\text {Gal}}(K_{n+1}/K)$ contains a subgroup $H_y$ that acts trivially on Y, with $|H_y|=108 = 2^2 \cdot 3^3$.

Since $f^{n-1}(z) - x$ is irreducible over K, for each root $y' \in f^{-(n-1)}(x)$ there is some

$$\begin{aligned} \delta _1\in {\text {Gal}}(K_{n-1}/K)\cong E_{n-1} \end{aligned}$$

with $\delta _1(y')=y$. Lift $\delta _1$ to $\delta \in {\text {Gal}}(K_{n+1}/K)$. Then,

$$\begin{aligned} H_{y'} = \delta ^{-1} H_y \delta \end{aligned}$$

is a 108-element subgroup of ${\text {Gal}}(K_{n+1}/K)$ that acts trivially on

$$\begin{aligned} Y' = \big ( f^{-(n+1)}(x) \smallsetminus f^{-2}(y') \big ) \cup f^{-1}(y'). \end{aligned}$$

There are $3^{n-1}$ choices for $y'$, and any two of the resulting subgroups $H_{y'}$ act nontrivially on disjoint portions of the preimage tree. In addition, they all act trivially on $f^{-n}(x)$ and, hence, trivially on $K_n$. Thus, the product of all of them forms a subgroup $B\subseteq {\text {Gal}}(K_{n+1}/K_n)$ of order

$$\begin{aligned} \big ( 2^2 \cdot 3^3 \big )^{3^{(n-1)}} = \frac{|E_{n+1}|}{|E_n|}, \end{aligned}$$

by Proposition 2.2. Hence,

$$\begin{aligned} \big |{\text {Gal}}(K_{n+1}/K)\big | = \big |{\text {Gal}}(K_{n+1}/K_n)\big | \cdot \big |{\text {Gal}}(K_n/K)\big | \ge |B| \cdot |E_n| = |E_{n+1}| . \end{aligned}$$

Since ${\text {Gal}}(K_{n+1}/K)$ is isomorphic to a subgroup of the finite group $E_{n+1}$, we must therefore have ${\text {Gal}}(K_{n+1}/K)\cong E_{n+1}$. $\square$

4 The geometric representation

Let L be a number field, and consider the rational function field $K=L(t)$. Since $t\in L(t) \smallsetminus \{0,1\}$, Lemma 3.1 states that the Galois group of $L(f^{-n}(t))$ over L(t) is a subgroup of $E_n$. In fact, we have the following much stronger statement.

Proposition 4.1

Let L be a number field and t a transcendental element over L. Then

$$\begin{aligned} {\text {Gal}}\Big (L\big (f^{-n}(t)\big )/L(t)\Big )\cong E_n. \end{aligned}$$

Proof

Let $G_n={\text {Gal}}(L(f^{-n}(t))/L(t))$. We can choose $x\in L$ such that the pair (L, x) satisfies property $(\dagger )$ of Sect. 3. By Theorem 3.7, we have

$$\begin{aligned} {\text {Gal}}\Big (L\big (f^{-n}(x)\big )/L(x)\Big ) = {\text {Gal}}\Big (L\big (f^{-n}(x)\big )/L\Big ) \cong E_n. \end{aligned}$$

Therefore, the specialization lemma of [12, Lem. 2.4] implies that $G_n$ has a subgroup isomorphic to $E_n$. On the other hand, applying Lemma 3.1 to $G_n$ shows that $G_n$ is isomorphic to a subgroup of $E_n$. Since $E_n$ is finite, $G_n$ must be isomorphic to $E_n$. $\square$

Corollary 4.2

${\text {Gal}}\Big ({\bar{\mathbb {Q}}}\big (f^{-n}(t)\big )/{\bar{\mathbb {Q}}}(t)\Big )\cong E_n$.

Proof

Since the previous proposition holds for any number field, $\mathbb {Q}$ must be algebraically closed in $\mathbb {Q}(f^{-n}(t))$. Hence,

$$\begin{aligned} {\text {Gal}}\Big ({\bar{\mathbb {Q}}}\big (f^{-n}(t)\big )/{\bar{\mathbb {Q}}}(t)\Big ) \cong {\text {Gal}}\Big (\mathbb {Q}\big (f^{-n}(t)\big )/\mathbb {Q}(t)\Big )\cong E_n. \end{aligned}$$

$\square$

5 Counting elements that fix leaves of $T_n$

Write $E_{n,fix }$ for the set of elements of $E_n$ that fix at least one leaf of $T_n$. We have already seen that $E_\infty = \varprojlim E_n$ is the geometric monodromy group of the PCF polynomial $f(z) = -2z^3 + 3z^2$. Using this fact, one could apply [7, Thm. 1.1] to show that the ratio $|E_{n,fix }|/|E_n|$ tends to zero with n. And while this would be sufficient for the arithmetic applications in the next section, we are able to obtain a more refined statement by working directly with the group structure of $E_n$:

Theorem 5.1

The proportion of elements of $E_n$ that fix a leaf of $T_n$ is

$$\begin{aligned} \frac{|E_{n,fix }|}{|E_n|} = \frac{2}{n}\left( 1 + O\left( \frac{\log n}{n}\right) \right) \quad \text {as}~n \rightarrow \infty . \end{aligned}$$

Remark 5.2

The proportion of elements of ${\text {Aut}}(T_n)$ that fix a leaf of $T_n$ obeys the same asymptotic as for $E_n$ [12, §4]. By way of contrast, consider $H_n \cong [C_3]^n$, the Sylow 3-subgroup of $E_n$ from Proposition 2.6. The proportion of elements of $H_n$ that fix a leaf of $T_n$ is half that of $E_n$: $\frac{1}{n}\left( 1 + O\left( \frac{\log n}{n}\right) \right)$.

We begin by finding a recursive formula for $|E_{n,fix }|$ in terms of certain auxiliary quantities. For $n \ge 1$ and $i \in \{1,2,3\}$, we define the following:

$$\begin{aligned} A_{n,i}&= \Big | \big \{ s \in E_n \, \big | \, s \text { acts as an element of order}~i~\mathrm{on}~T_1 \big \} \Big |, \\ A_{n,i}'&= \Big | \big \{ s \in E_n \, | \, s \text { acts as an element of order}~i~\mathrm{on}~T_1~\text {and fixes a leaf of}~T_n \big \} \Big |. \end{aligned}$$

For example, if $n = 1$, we have

$$\begin{aligned} A_{1,1} = 1 \quad&\quad A_{1,1}' = 1 \\ A_{1,2} = 3 \quad&\quad A_{1,2}' = 3 \\ A_{1,3} = 2 \quad&\quad A_{1,3}' = 0. \end{aligned}$$

For any $n\ge 1$, note that $A_{n,3}'=0$, because an element s that permutes the leaves of $T_1$ by a 3-cycle cannot fix a leaf of $T_n$. It follows that

$$\begin{aligned} |E_{n,fix }| = A_{n,1}' + A_{n,2}' \quad \text {and} \quad |E_n| = A_{n,1} + A_{n,2} + A_{n,3}. \end{aligned}$$

Lemma 5.3

For $n \ge 1$, we have

$$\begin{aligned} A_{n,2} = 3A_{n,1}, \qquad A_{n,3} = 2 A_{n,1}, \qquad |E_n| = 6 A_{n,1}, \qquad \text {and} \qquad |E_{n+1}| = 3 |E_n|^3. \end{aligned}$$

Proof

The restriction homomorphism $\pi :E_n \rightarrow E_1 \cong \mathfrak {S}_3$ is onto since $\pi \big ( (1,1,1), (123) \big ) = (123)$ and $\pi (\tau _n) = (12)$, where $\tau _n$ was defined in Eq. (7). The first three equalities follow from the fact that $A_{n,1} = |\ker (\pi )|$. For the final equality, apply Proposition 2.2. $\square$

Lemma 5.4

For $n \ge 1$, we have

$$\begin{aligned} A_{n+1,1}' = 54A_{n,1}^2\left( A_{n,1}' + A_{n,2}'\right) - 9 A_{n,1}\left( A_{n,1}' + A_{n,2}'\right) ^2 + 3A_{n,1}'\left( A_{n,2}'\right) ^2 + \left( A_{n,1}'\right) ^3. \end{aligned}$$

Proof

Let $s \in E_{n+1}$ be an element that acts as the identity on $T_1$. Then the restriction of s to $T_2$ is of the form $\big ((a_1,a_2,a_3),1\big )$ for some $a_1,a_2,a_3\in {\text {Aut}}(T_1)$. By Lemma 2.1, the fact that this element lies in $E_2$ means $1 = \prod \mathrm {sgn}(a_i)$. So among the $a_i$’s, there are either zero 2-cycles or exactly two 2-cycles. We treat these cases separately.

Case 1: Zero 2-cycles. As an element of $E_{n+1}$, we have $s = \big ((\tilde{a}_1, \tilde{a}_2, \tilde{a}_3), 1 \big )$, where each $\tilde{a}_i \in E_n$ restricts to either the identity or a 3-cycle on $T_1$. The total number of elements $\tilde{a}_i$ of this shape is $A_{n,1} + A_{n,3}$, while the number that do not fix a leaf of $T_n$ is $\big (A_{n,1} + A_{n,3} - A_{n,1}'\big )$. Thus, the number of elements of $E_{n+1,fix }$ that act as the identity on $T_1$ but with no 2-cycle on $T_2$ is

$$\begin{aligned} \left( A_{n,1} + A_{n,3}\right) ^3 - \left( A_{n,1} + A_{n,3} - A_{n,1}'\right) ^3 = 27 A_{n,1}^2 A_{n,1}' - 9 A_{n,1} \left( A_{n,1}'\right) ^2 + \left( A_{n,1}'\right) ^3, \end{aligned}$$

(9)

where we applied Lemma 5.3 when we expanded the two expressions.

Case 2: Two 2-cycles. As an element of $E_{n+1}$, we have $s = \big ((\tilde{a}_1, \tilde{a}_2, \tilde{a}_3), 1 \big )$, where two of the $\tilde{a}_i \in E_n$ restrict to 2-cycles on $T_1$, and the remaining $\tilde{a}_i$ restricts to the identity or a 3-cycle. There are three choices for the index $i_0$ such that $\tilde{a}_{i_0}$ is the identity or a 3-cycle. For a given choice of $i_0$, there are

$$\begin{aligned} (A_{n,1}' + A_{n,3}')A_{n,2}^2 = A_{n,1}'A_{n,2}^2 = 9 A_{n,1}^2 A_{n,1}' \end{aligned}$$

choices of triples $(\tilde{a}_1,\tilde{a}_2,\tilde{a}_3)$ such that s fixes a leaf of the copy of $T_n$ above the $i_0$-leaf of $T_1$.

For s not to fix a leaf of the $T_n$ above the $i_0$-leaf, at least one of the other two $\tilde{a}_i$’s (each of which acts as a 2-cycle on $T_1$) must fix a leaf of $T_n$. By inclusion-exclusion, the number of choices for this pair of $\tilde{a}_i$’s is

$$\begin{aligned} 2A_{n,2}A_{n,2}' - \left( A_{n,2}'\right) ^2 = \left( 6 A_{n,1} - A_{n,2}' \right) A_{n,2}' . \end{aligned}$$

For $i=i_0$, the element $\tilde{a}_i\in E_n$ acts as the identity or as a 3-cycle on $T_1$ but fixes no leaf of $T_n$. The number of such elements of $E_n$ is

$$\begin{aligned} A_{n,1} + A_{n,3} - A_{n,1}' = 3 A_{n,1} - A_{n,1}'. \end{aligned}$$

(Again, we have applied Lemma 5.3 in all three displayed equations above.)

Thus, the number of elements $s\in E_{n+1,fix }$ that act as the identity on $T_1$ and as two 2-cycles on the leaves of $T_2$ is

$$\begin{aligned} 3\Big [ 9A_{n,1}^2A_{n,1}' + \left( 3A_{n,1} - A_{n,1}'\right) \left( 6A_{n,1} - A_{n,2}'\right) A_{n,2}' \Big ]. \end{aligned}$$

(10)

Adding Eqs. (9) and (10) and expanding yields the desired result. $\square$

Using the same counting technique as in the preceding proof, one obtains:

Lemma 5.5

For $n \ge 1$, we have

$$\begin{aligned} A_{n+1,2}' = 54 A_{n,1}^2 \left( A_{n,1}' + A_{n,2}'\right) . \end{aligned}$$

Lemma 5.6

Let $\phi (t) = t - \frac{1}{2}t^2 + \frac{1}{3}t^3$. Then $\phi$ is increasing on (0, 1), and

$$\begin{aligned} \phi ^n(1) = \frac{2}{n}\left( 1 + O\left( \frac{\log n}{n}\right) \right) \text { as } n \rightarrow \infty . \end{aligned}$$

Proof

The first statement is evident from looking at the derivative. For the second, we set

$$\begin{aligned} \psi (z) = \frac{1}{\phi (z^{-1})} = z + \frac{1}{2} - \frac{z+2}{2(6z^2 - 3z + 2)}. \end{aligned}$$

Let $R(z) = \frac{z+2}{2(6z^2 - 3z + 2)}$ be the final term. Then, by induction, we have

$$\begin{aligned} \psi ^n(z) = \frac{1}{\phi ^n(z^{-1})} = z + \frac{n}{2} - \sum _{i=0}^{n-1} R\left( \psi ^i(z)\right) . \end{aligned}$$

Since $\phi ^n(1) = 1 / \psi ^n(1)$, to complete the proof it suffices to show that $\sum _{i=0}^{n-1} R\left( \psi ^i(1)\right) = O(\log n)$.

By elementary algebra, one verifies that $R(z) \le \frac{1}{3z}$ for all $z>0$. Now we show, by induction, that $\psi ^n(1) \ge (n+5)/5$ for $n\ge 1$. Both sides equal 6 / 5 for $n=1$. Given $n\ge 1$ for which the inequality holds, we find $R(\psi ^n(1)) \le \frac{1}{3\psi ^n(1)} \le \frac{5}{3n+15}$, and hence

$$\begin{aligned} \psi ^{n+1}(1)&= \psi ^n(1) + \frac{1}{2} - R(\psi ^n(1)) \ge \frac{n+5}{5} + \frac{1}{2} - \frac{5}{3n+15} \\&= \frac{n+6}{5} + \frac{9n-5}{30(n+5)} > \frac{n+6}{5}, \end{aligned}$$

completing the induction.

Using our inequalities for R(z) and $\psi ^n(1)$, we conclude that

$$\begin{aligned} 0 \le \sum _{i=0}^{n-1} R\left( \psi ^i(1)\right)< \sum _{i=0}^{n-1} \frac{1}{\psi ^i(1)} < 5 \sum _{i=0}^{n-1} \frac{1}{i+5} = O(\log n). \end{aligned}$$

$\square$

One can apply the technique in the previous proof to obtain the following similar result:

Lemma 5.7

Let $\rho (t) = t - \frac{1}{2}t^2$. Then $\rho$ is increasing on (0, 1), and

$$\begin{aligned} \rho ^n(2/3) = \frac{2}{n}\left( 1 + O\left( \frac{\log n}{n}\right) \right) \text { as } n \rightarrow \infty . \end{aligned}$$

Proof of Theorem 5.1

By adding the terms $\left( A_{n,2}'\right) ^3$ and $3A_{n,2}'\left( A_{n,1}'\right) ^2$ to the formula in Lemma 5.4, we obtain the estimate

$$\begin{aligned} A_{n+1,1}' \le 54A_{n,1}^2\left( A_{n,1}' + A_{n,2}'\right) - 9 A_{n,1}\left( A_{n,1}' + A_{n,2}'\right) ^2 + \left( A_{n,1}' + A_{n,2}'\right) ^3. \end{aligned}$$

Adding this to the formula in Lemma 5.5, we find that

$$\begin{aligned} |E_{n+1,fix }|&= A_{n+1,1}' + A_{n+1,2}'\\&\le 108A_{n,1}^2\left( A_{n,1}' + A_{n,2}'\right) - 9 A_{n,1}\left( A_{n,1}' + A_{n,2}'\right) ^2 + \left( A_{n,1}' + A_{n,2}'\right) ^3 \\&= 3\left( 6A_{n,1}\right) ^2 |E_{n,fix }| - \frac{3}{2} \left( 6A_{n,1}\right) |E_{n,fix }|^2 + |E_{n,fix }|^3 \\&= 3 |E_n|^2 \cdot |E_{n,fix }| - \frac{3}{2} |E_n| \cdot |E_{n,fix }|^2 + |E_{n,fix }|^3, \end{aligned}$$

where we have used Lemma 5.3 to write $6A_{n,1} = |E_n|$. Dividing by $|E_{n+1}| = 3|E_n|^3$, we find that

$$\begin{aligned} \frac{|E_{n+1,fix }|}{|E_{n+1}|} \le \frac{|E_{n,fix }|}{|E_n|} - \frac{1}{2}\left( \frac{|E_{n,fix }|}{|E_n|}\right) ^2 + \frac{1}{3}\left( \frac{|E_{n,fix }|}{|E_n|}\right) ^3 = \phi \left( \frac{|E_{n,fix }|}{|E_n|}\right) , \end{aligned}$$

(11)

where $\phi$ is the polynomial from Lemma 5.6.

Similarly, by discarding the final two terms of the formula in Lemma 5.4 and adding the formula from Lemma 5.5, we obtain the estimate

$$\begin{aligned} |E_{n+1,fix }| = A_{n+1,1}' + A_{n+1,2}'&\ge 108A_{n,1}^2\left( A_{n,1}' + A_{n,2}'\right) - 9 A_{n,1}\left( A_{n,1}' + A_{n,2}'\right) ^2 \\&= 3 |E_n|^2 \cdot |E_{n,fix }| - \frac{3}{2} |E_n| \cdot |E_{n,fix }|^2. \end{aligned}$$

As above, this yields

$$\begin{aligned} \frac{|E_{n+1,fix }|}{|E_{n+1}|} \ge \frac{|E_{n,fix }|}{|E_n|} - \frac{1}{2}\left( \frac{|E_{n,fix }|}{|E_n|}\right) ^2 = \rho \left( \frac{|E_{n,fix }|}{|E_n|}\right) , \end{aligned}$$

(12)

where $\rho$ is the polynomial from Lemma 5.7.

Set $x_n = \frac{|E_{n,fix }|}{|E_n|} \in [0,1]$. Equations (11) and (12) show that $\rho (x_n) \le x_{n+1} \le \phi (x_n)$. As $\rho$ and $\phi$ are increasing on (0, 1), we find that

$$\begin{aligned} \rho ^n(2/3) = \rho ^n(x_1) \le \rho ^{n-1}(x_2) \le \cdots \le \rho (x_n) \le x_{n+1} \end{aligned}$$

and

$$\begin{aligned} x_{n+1} \le \phi (x_n) \le \phi ^2(x_{n-1}) \le \cdots \le \phi ^n(x_1) \le \phi ^n(1). \end{aligned}$$

By Lemmas 5.6 and 5.7, the first and last quantities have the same asymptotic value, namely $\frac{2}{n}\left( 1 + O\left( \frac{\log n}{n}\right) \right)$, and hence, so does $x_{n+1}$. The proof is complete since this asymptotic is unchanged upon replacing n with $n-1$. $\square$

6 Arithmetic applications

We now prove our applications on density of prime divisors in orbits and Newton’s method. If K is a number field and $\mathfrak {P}$ is a prime ideal of the ring of integers of K with residue field $k(\mathfrak {P})$, there is a surjective reduction map $K \rightarrow k(\mathfrak {P}) \cup \{\infty \}$. We write $x \equiv y \pmod \mathfrak {P}$ whenever $x,y \in K$ have the same reduction.

Proposition 6.1

Let K be a number field and $x \in K$ an element such that (K, x) satisfies property $(\dagger )$ of Sect. 3. Choose $y_0 \in K \smallsetminus (x)$ and define a sequence $(y_i)_{i\ge 0} \subseteq K$ by $y_i = f^i(y_0)$. Then the set of prime ideals $\mathfrak {P}$ of K such that

$$\begin{aligned} y_i \equiv x \! \! \! \! \pmod \mathfrak {P}\quad \text { for some } i \ge 0 \end{aligned}$$

has natural density zero.

Proof

Note that for all $i\ge 0$, we have $y_i \ne x$. This inequality holds for $i = 0$ by hypothesis. Furthermore, if it failed for some $i > 0$, $y_0$ would be a K-rational root of $f^i(z) - x$, which is absurd since this polynomial is irreducible over K by Lemma 3.3.

For each $n\ge 1$, define $S_n$ to be the set of prime ideals $\mathfrak {P}$ of K such that

• x is not integral at $\mathfrak {P}$, or

• $y_i \equiv x \! \pmod \mathfrak {P}$ for some $0\le i \le n-1$.

Then $S_n$ is finite.

Let $n\ge 1$. Let $\mathfrak {P}\not \in S_n$ be a prime ideal of the ring of integers of K such that $y_i \equiv x \pmod \mathfrak {P}$ for some $i \ge n$. Then $f^n(y_{i-n}) \equiv x \pmod \mathfrak {P}$, and therefore the polynomial $f^n(z) - x$ has a $k(\mathfrak {P})$-rational root. Write $\delta (S)$ for the natural density of a set of prime ideals S (if it exists). For each $n\ge 1$, the Chebotarev Density Theorem and the finiteness of $S_n$ yield

$$\begin{aligned} \delta \big ( \big \{ \mathfrak {P}\, \big | \,&y_i \equiv x \! \! \! \! \pmod \mathfrak {P}\text { for some } i \ge 0 \big \}\big ) \\&\le \delta \big ( \big \{ \mathfrak {P}\, \big | \, \mathfrak {P}\not \in S_n, \,f^n(z) - x \text { has a}\,\, k(\mathfrak {P})\text {-rational root} \big \}\big ) \\&= \frac{\Big |\Big \{s \in {\text {Gal}}\big (K(f^{-n}(x))/K\big ) \, \Big | \, s \text { fixes some root of } f^n(z) - x\Big \}\Big |}{\big |{\text {Gal}}\big (K(f^{-n}(x))/K\big )\big |} = \frac{| E_{n,fix }|}{|E_n|}. \end{aligned}$$

The final equality uses Theorem 3.7 to identify the Galois group of $f^n(z)-x$ over K with $E_n$. By Theorem 5.1, this last quantity tends to zero as $n\rightarrow \infty$. $\square$

Recall that the critical points for f are $0,1,\infty$, and that they are all fixed by f.

Corollary 6.2

Let K be a number field for which there exist unramified primes above 2 and above 3. Let $y_0 \in K{\smallsetminus }(0,1,3/2, {-}1/2)$, and define a sequence $(y_i)_{i\ge 0} {\subseteq } K$ by $y_i {=} f^i(y_0)$. Then the set of prime ideals $\mathfrak {P}$ of K such that

$$\begin{aligned} y_i \equiv 0 \text { or } 1 \! \! \! \! \pmod \mathfrak {P}\quad \text { for some}~i \ge 0 \end{aligned}$$

has natural density zero. In particular, the set of prime divisors of the sequence $(y_i)_{i\ge 0}$ has natural density zero.

Proof

We begin by showing that the set of primes $\mathfrak {P}$ such that $y_i \equiv 0 \pmod \mathfrak {P}$ for some $i \ge 0$ has natural density zero. Let S be the set of primes $\mathfrak {P}$ of K for which

• $\mathfrak {P}$ lies above 2, or

• $y_0 \equiv 0 \pmod \mathfrak {P}$.

Notice that since $y_0 \ne 0$, S is a finite set, and we may safely ignore primes in S for the remainder of the proof.

Suppose now that $\mathfrak {P}\not \in S$ is such that $y_i \equiv 0 \pmod \mathfrak {P}$ for some $i \ge 1$. We may assume without loss that i is minimal with this property. Then

$$\begin{aligned} y_i = f(y_{i-1}) = -2y_{i-1}^3 + 3y_{i-1}^2 = - 2 y_{i-1}^2\left( y_{i-1} - \frac{3}{2}\right) , \end{aligned}$$

which implies that $y_{i-1} \equiv \frac{3}{2} \pmod \mathfrak {P}$. We claim that $y_{i-1} \ne \frac{3}{2}$. This is true by hypothesis if $i = 1$. If it were to fail for some $i > 1$, then the polynomial $f^{i-1}(z) - 3/2$ would have $y_0$ as a K-rational root. But our hypothesis on K implies that (K, 3 / 2) satisfies property $(\dagger )$, and so we have a contradiction to Lemma 3.3. It follows that

$$\begin{aligned} \delta \Big ( \big \{ \mathfrak {P}\, \big | \, y_i\equiv & {} 0 \!\!\!\! \pmod \mathfrak {P}\text { for some } i \ge 0 \big \} \Big ) \\= & {} \delta \bigg ( \Big \{ \mathfrak {P}\, \Big | \, y_i \equiv \frac{3}{2} \!\!\!\!\pmod \mathfrak {P}\text { for some } i \ge 1 \Big \} \bigg ). \end{aligned}$$

Since (K, 3 / 2) satisfies property $(\dagger )$, the density on the right is zero by Proposition 6.1.

Now we show that the density of primes $\mathfrak {P}$ such that $y_i \equiv 1 \pmod \mathfrak {P}$ for some $i \ge 0$ also has natural density zero. Define $w_i = 1 - y_i$ for $i \ge 0$. As $y_0 \not \in \{1,-1/2\}$, we see that $w_0 \not \in \{0,3/2\}$. Moreover, because $1 - f(z) = f(1-z)$, we find that

$$\begin{aligned} f(w_i) = f(1-y_i) = 1 - f(y_i) = 1 - y_{i+1} = w_{i+1}. \end{aligned}$$

Thus, we may apply the first part of the proof to the sequence $(w_i)_{i\ge 0}$ to deduce that

$$\begin{aligned} \delta \big (\{ \mathfrak {P}\,\big | \, w_i \equiv 0 \!\!\!\! \pmod \mathfrak {P}\text { for some}~i \ge 0\} \big )= 0. \end{aligned}$$

Since $w_i \equiv 0 \! \pmod \mathfrak {P}\ \Leftrightarrow \ y_i \equiv 1 \! \pmod \mathfrak {P}$, we are done. $\square$

We now prove a special case of the Faber–Voloch conjecture. Recall that the Newton map associated to a polynomial $g(z) \in K[z]$ is the rational function

$$\begin{aligned} N_g(z) = z - \frac{g(z)}{g'(z)}. \end{aligned}$$

The simple roots of g are critical fixed points of $N_g$. Hence, for any completion $K_v$ of K, the roots of g are super-attracting fixed points of the map $N_g$, viewed as a dynamical system acting on $\mathbb {P}^1(K_v)$.

Corollary 6.3

Let K be a number field for which there exist unramified primes above 2 and above 3. Let $g(z) = z^3 - z$. Choose $y_0 \in K$ such that the Newton iteration sequence $y_i = N_g^i(y_0)$ does not encounter a root of g. Then the set of primes $\mathfrak {P}$ of K for which the Newton sequence $(y_i)_{i\ge 0}$ converges in $K_\mathfrak {P}$ to a root of g has natural density zero.

Proof

The Newton map for g is

$$\begin{aligned} N_g(z) = \frac{2z^2}{3z^2 - 1}. \end{aligned}$$

Let $\eta (z)=1/(1-2z)$. Then

$$\begin{aligned} \eta ^{-1} \circ N_g \circ \eta (z) = -2z^3 + 3z^2 = f(z). \end{aligned}$$

(13)

For each $i\ge 0$, define $w_i = \eta ^{-1}(y_i)$. Then it is immediate from Eq.  (13) that $w_{i+1} = f(w_i)$. Moreover, if we had $w_0 \in (0,1,3/2,-1/2, \infty )$, then the sequence $(w_i)_{i\ge 0}$ would encounter a fixed point of f, in which case $(y_i)_{i\ge 0}$ would encounter a fixed point of $N_g$ and, hence, a root of g, contradicting our hypotheses. Thus, $w_0 \not \in (0,1,3/2,-1/2, \infty )$. Corollary 6.2 therefore shows that the set of prime ideals $\mathfrak {P}$ for which $w_i \equiv 0 \text { or } 1 \!\pmod \mathfrak {P}$ has density zero.

On the other hand, the proof of the main theorem of Faber–Voloch [3] shows that for all but finitely many prime ideals $\mathfrak {P}$ of K, the sequence $(y_i)_{i \ge 0}$ converges in $K_\mathfrak {P}$ to a root of g if and only if $g(y_i) \equiv 0 \! \pmod \mathfrak {P}$ for some $i \ge 0$. Factoring g, this condition is equivalent to saying that $y_i \equiv 0, \pm 1 \!\pmod \mathfrak {P}$ for some $i \ge 0$, which in turn is equivalent to saying that $w_i \equiv 0,1, \text { or } \infty \!\pmod \mathfrak {P}$. (Here, $w\equiv \infty \!\pmod \mathfrak {P}$ means w is not integral at $\mathfrak {P}$). Clearly, the set of primes $\mathfrak {P}$ for which $w_i \equiv \infty \!\pmod \mathfrak {P}$ is zero, since f is a polynomial, and so the proof is complete. $\square$