Modeling and optimization of extrusion process parameters for the development of Nylon6–Al–Al₂O₃ alternative FDM filament

Abstract

The present work focused the detailed investigation on the development of Nylon6–Al–Al₂O₃-based alternative fused deposition modeling process (FDM) feedstock filament (in lieu of commercial acrylonitrile butadiene styrene filament) by optimizing the process parameters of single-screw extruder (such as composition, mean barrel temperature, and die temperature) in terms of responses (tensile strength and diameter deviation) using response surface methodology. Initially, the suitability of alternative material as an alternative FDM filament has been verified by rheological investigations and the tensile testing (according to ASTM-638 standard). The tensile strength of feedstock filament was significantly affected by the variation of major input parameters during the processing of alternative material on single-screw extruder. A second-order regression equation for each process response (obtained by ANOVA) validates the modeling goodness of fit and selects proper forms of influentially significant process variables (main, two-way interaction, and pure quadratic terms) within 95 % of confidence interval (p value ≤0.05). A multi-objective and multi-response optimization techniques based on the use of desirability function concept have been applied for the response regression equations to simultaneously find a set of optimal input parameters, yielding the maximum tensile strength along with the minimum deviation in feedstock filament diameter. The predicted optimal results were also validated experimentally with an error <4 %. In addition to above, the dynamic mechanical analysis was performed, which indicate that the filament fabricated with optimum combination of parameters have adequate stiffness and is suitable for FDM system.

1 Introduction

Additive manufacturing (AM) is the combination of the techniques and processes used to fabricate parts of complicated geometry in less time, without the assistance of tooling as compared to the traditional practices adopted so far [1–3]. The parts produced by AM can be used for assembly match up, product trial [4], design verification, testing, and industrial and medical applications [5]. AM technologies are generally recognized for flexible production which is necessary due to short product life cycle and short cycle time in new product development. Various types of AM techniques, such as stereo-lithography (SLA), selective laser sintering (SLS), laminated object manufacturing (LOM), fused deposition modeling (FDM), 3D printing, and sanders prototyping [6–8] are available in market, which works on AM principle. Among all, FDM process is second most prominent AM technique after stereo-lithography [9], gains popularity due to its short cycle time, high dimensional accuracy, desktop facility, and safe to use. Moreover, it can be easily integrated with various CAD softwares [4]. The technique gains popularity day-by-day due to advancements in system configuration and filament materials.

FDM have a distinct ability to fabricate complex-shaped 3D physical prototype and functional parts. The major research issues have been focused on maintaining balance to produce aesthetically appealing looking products with functionality. The accuracy and efficiency of FDM parts can be further improved by optimizing the process parameters [10]. Although FDM is world widely used efficient process, still it has limited applications because of its compatibility with recommended materials only [11]. This limitation can be overcome with the development of new material, having compatibility with technology and have superior characteristics than commercial grades of acrylonitrile butadiene styrene (ABS) material which is most widely used in FDM [1]. The applicability of FDM system can be increased through the development of materials having targeted properties [12]. Rocha et al. [11] developed multiple blends of ABS, styrene ethylene butadiene styrene (SEBS), and ultrahigh molecular weight polyethylene (UHMWPE) which possessed different physical properties and compatible with 3D printing system. Some researchers used wax, nylon, resins, paper, metal and ceramics as an alternative material in FDM system [6]. Turner et al. [13] outlined typical FDM processes, including the material feed mechanism, liquefier and print nozzle, the build surface and environment. Mireles et al. [14] modified FDM 3000 system to achieve controlled deposition of eutectic Bi58Sn42 and non-eutectic Sn60Bi40 materials and fabricate metal parts directly for jigs and fixtures, electroforming mandrels, encapsulation molds, dies, electronic joining applications and printing three-dimensional circuitry. Durgun and Ertan [15] investigated the effect of raster angles and orientation on mechanical properties and surface roughness of FDM parts and found that orientation have more significance than raster angles. Espalin et al. [16] studied the build process variation for FDM with different layer thicknesses and road widths on surface roughness, production times, and mechanical properties, and additionally developed new FDM process that enabled the deposition of discrete multiple materials at different layers and regions within layers. The fabricated parts of modified system have improved the surface roughness and reduction in fabrication time while retaining mechanical properties as compared to the standard FDM process. Lee and Huang [17] conducted mechanical testing of FDM dog bones based on UNI EN ISO 527-1 (1997) fabricated using different grades of ABS materials to identify the fatigue characteristics of materials. Torrado Perez et al. [18] studied the mechanical testing (as per ASTM-638) of ABS-based composite materials specimens, and found that ABS reinforced with 5 % by weight TiO₂ exhibited the highest ultimate tensile strength as compared to pure ABS material. Many researchers [15, 17] conducted mechanical testing of FDM parts fabricated by varying various build parameters (raster angle, orientation, slice thickness, and density of part), but very less has been reported on the investigations of the mechanical testing of FDM filament, which is necessary before the loading of alternate material filament in the FDM system. The present study has been focused on the optimization of single-screw extruder parameters for the development of FDM feedstock material using relatively low-cost composite material other than commercial available ABS material. The various steps for the development process of FDM feed stock filament are shown in Fig. 1.

Fig. 1

Flow chart of feedstock filament development

2 Experimental work

2.1 Material selection

Nylon6 (E-35 grade) was selected as a binder material due to its outstanding properties as compared to other grades of nylon and very much suitable for extrusion applications. Nylon6 has medium melt viscosity and most widely used for producing monofilaments, strapping, zippers, cords, and profiles. It is semi-crystalline engineering thermoplastic having good sliding properties, abrasion resistant, chemical resistance too many oils, greases, diesel, petrol, cleaning fluids, very tough, rigid, and electrically insulated, and can be easily machined, welded, and bonded. The important properties of Nylon6 are listed in Table 1. The material was supplied by Gujarat State Fertilizer Limited, India, in granular form having average particle size 4–5 mm and was crushed to powder size (500–800 µm) with the cryogenic grinding process.

Table 1 Properties of Nylon6 (supplier’s data).

In this work, pure aluminum metal (Al) and aluminum oxide (Al₂O₃) were selected as filler materials. The reinforcement of filler material in polymeric matrix increases the internal shear stress, which hinders molecular mobility. Therefore, plasticizers are added to provide lubricity and reduce internal friction, but the use of plasticizers adversely affects the performance of polymeric materials. The pure Al metal powder has self-lubricating property, avoids the use plasticizes. Moreover, it has outstanding properties, such as light weight, corrosion resistance, ductility, and high specific thermal conductivity (two times more than copper metal), which suggests its usability in number of rapid tooling applications (metal matrix composition, functional parts). On the other hand, aluminum oxide (Al₂O₃) was added in the matrix to produce parts having good tribological properties. The reinforcement of Al₂O₃ also improves thermal stability and flame retardancy of FDM printed parts. The particles of filler particles act as thermodynamic sink in the matrix. The pure Al metal powder (325 mesh) and Al₂O₃ (100–125 mesh) were supplied by Thomas Bakers, India. The various important properties of Al and Al₂O₃ are summarized below in Table 2.

Table 2 Properties of filler materials (supplier’s data)

2.2 Processing of material

The binder material (Nylon6), which is hygroscopic in nature, and filler materials (Al, Al₂O₃) were heated individually in vacuum oven by maintaining temperature 50 °C for 10 h at absolute zero pressure. This is necessary to remove moisture and oil traces from the materials, so that no oxidation can take place during the processing of material in screw extruder. The proportions of various ingredients were mixed in tumbler mixer by rotating at the speed of 200 rpm for 2 h. As already mentioned, due to self-lubricating property of Al and good binding properties of Nylon6 material, no surfactants or plasticizers were required in the mixture.

2.3 Rheological behavior

The successful processing of new filament material in the FDM system depends upon the fabrication of strong and spoolable feed stock filament, having required consistent diameter and stiffness. This can be achieved by careful selection of different proportions of binder materials and filler materials [5]. Thus, it is required to investigate the rheological behavior of composite material with respect to the processing conditions (temperature, velocity, and pressure drop) in liquefier head of FDM [19]. The reinforcement of fillers in Nylon6 modified its structure and properties, and it is necessary to investigate their affect, particularly for the analysis and design of processing operations [20]. Shenoy et al. [21] generated curves by conduct melt flow test of polymer composites which show the relationship between viscosity, temperature, and shear rate. Many researchers [19, 22–24] studied the thermal and flow behavior of biopolymers by modeling with the finite-element analysis. Melt flow index (MFI) is an alternative measure of viscosity for comparative purpose. In this work, the MFI tester (SE-MFI-I) was supplied by Shanta Engineering, Mumbai (India). The test was conducted by maintaining cylinder temperature of melt flow tester at 230 °C and weight 3.8 kg. The average value of ten observations was recorded for each composition. Figure 2 shows weighted percentage loading of Al and Al₂O₃ in Nylon6 matrix. This is generally a comparative study of flow rate under similar processing conditions and limits the practical level, up to which filler materials can be incorporated into the thermoplastic polymers.

Fig. 2

MFI of different weight proportions of Al and Al₂O₃ in Nylon6 matrix

Depending upon the application, the various properties can be tailor made by varying the loading of the filler material and binder material. From the MFI test, the index value of pure ABS is 2.215 and Nylon6 is 10.61. Under similar processing conditions, Nylon6 can be loaded up to limit that its MFI should commensurate with pure ABS material. The MFI value of 40 % loading of Al powder is 3.975 and 50 % loading is 2.175. Therefore, approximately 45 % loading of Al is possible in Nylon6 to obtain the same flow rate and flexibility as the ABS material have during the processing of the FDM process. Similarly for Al₂O₃, less than 40 % loading is possible (see Fig. 2). It is very much convenient to specify relative filler amount in volume fraction rather than mass fraction, but this experimentation commences with the comparative study of MFI value. The MFI value of alternative material should be commensurate with the MFI value of ABS (standard material). As the unit of MFI is grams per 10 min; Therefore, in this work, mass/weight proportions were considered.

In the present study, up to 40 % loading of filler materials in Nylon6 matrix was selected. Table 3 summarized the weight proportions of different compositions and their respective MFI values. With the increase of Al₂O₃ content and decrease of Al in composition, MFI value decreases and density of the composition increases. This is due to increase in the proportion of large particle size (Al₂O₃) in the polymeric matrix. The composite density was calculated using the following formula:

$$ \rho_{\text{c}} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\left\{ {\left( {\frac{{W_{\text{s}} }}{{\rho_{\text{s}} }}} \right) + \left( {\frac{{W_{\text{m}} }}{{\rho_{\text{m}} }}} \right) + \left( {\frac{{W_{\text{p}} }}{{\rho_{\text{p}} }}} \right)} \right\}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\left\{ {\left( {\frac{{W_{\text{s}} }}{{\rho_{\text{s}} }}} \right) + \left( {\frac{{W_{\text{m}} }}{{\rho_{\text{m}} }}} \right) + \left( {\frac{{W_{\text{p}} }}{{\rho_{\text{p}} }}} \right)} \right\}}$}} $$

where ρ _c = density of composition; ρ _s = density of Al; ρ _p = density of Nylon6; ρ _m = density of Al₂O_3; W _s = weight proportions of Al; W _m = weight proportions of Al₂O₃; W _p = weight proportions of Nylon6.

Table 3 Weight proportion of compositions

2.4 Fabrication of filament on single-screw extruder

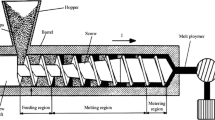
Single-screw extruder was selected for the fabrication of filament and its various specifications are shown in Table 4. The variable parameters of extrusion process are mean barrel temperature, screw speed, die temperature, take up unit speed, water tank temperature, and die nozzle diameter. The die nozzle diameter is 4 mm, and the diameter of extruded filament was controlled by adjusting take up unit speed and water tank temperature. To reduce the friction and wear during the processing of composite materials, the barrel was made hard tempered. The screw and die nozzle were chrome plated, so that material flows continuously without sticking with screw and nozzle surface. In this work, four parameters, such as material composition, mean barrel temperature, die temperature, and screw speed were selected. The single-screw extruder barrel, consists of three heaters (Heater 1, Heater 2, and Heater 3), each having a capacity of 1 KW and equipped with zone temperature control (see Fig. 3). The single-screw extruder (SS-11-E) was supplied by M/s Binflex Plastic Industry, Ludhiana (India).

Table 4 Specifications of single-screw extruder

Fig. 3

3D view of heating arrangement of barrel for single-screw extruder

In addition, water cooling temperature control system is also available. The barrel length is 750 mm and each heater is placed with a gap of 80 mm. The ‘heater 1’ adjoining feeding section (hopper) was maintained at a lowest temperature and ‘heater 3’ near die section at a highest temperature. The selection of temperature range of heaters depends upon the material to be processed. The ‘thermocouple 1’ measures the average temperature of ‘heater 1 and 2,’ where as ‘thermocouple 2’ measures the temperature of ‘heater 3’. The average value of heat input available at ‘thermocouple 1’ and ‘thermocouple 2’ was considered as mean barrel temperature. Based upon pilot study conducted, the mean barrel temperature was kept judicially in the range of 160–180 °C. In this work, the water tank temperature was kept at room temperature (35 °C). As the dimensional variation of filament diameter is a critical parameter; therefore, large variations on diameter adversely affect the FDM process, but throughout the experimentation, it was easily controlled within the specified limits (1.75 ± 0.03 mm) by adjusting the speed of take up unit.

2.5 Design of experiments (DOE)

During pilot experimentation, a number of trials were conducted by some hit and trail method and output of all these trials, give a working range with in which critical parameters, such as mean barrel temperature, die temperature and composition can be varied for the processing of alternative material on single-screw extruder. Table 5 shows the levels of selected single-screw extruder parameters. It was worked out that variation within these limits produces a strong spoolable filament suitable for the FDM system, and outside from these limits causes interrupted flow of material through screw extruder which causes geometric defects, such as inconsistent diameter, ovality, and poor strength of feedstock filament. However, in actual working conditions, the behavior of particular parameter is affected by the level of other parameters due to their mutual interaction. Therefore, to visualize the effect of variation of all critical factors, it is necessary to use the DOE techniques. The DOE techniques provide the simultaneous variation of all the influencing factors and systematically evaluate the significance of each factor.

Table 5 Process parameters

2.6 Response surface methodology (RSM)

In this work, RSM approach was applied for the design and analysis of experiments. It is a sequential procedure generally applied to determine the optimum operating conditions for the process and is a combination of statistical and mathematical techniques for the modeling and analysis of problems, having an aim to understand the influence of process variables on responses and optimizing these responses [25]. From various experimentation designs, as available in RSM, the central composite design is generally selected for accurately predict the optimize value of input analytical variables in the regard of desired responses [26]. The quantitative form of relationship between independent input variables and desired response could be represented as:

$$ \begin{aligned} Y & = f\left( {x_{ 1} ,x_{ 2} ,x_{ 3} ,x_{ 4} , \ldots ,x_{n} } \right) \pm \varepsilon \\ \eta & = f\left( {x_{ 1} ,x_{ 2} ,x_{ 3} ,x_{ 4} , \ldots ,x_{n} } \right) \\ Y & = \eta \pm \varepsilon \\ \end{aligned} $$

(1)

where ‘Y’ is the desired response, ‘f’ is the function of input variables, ‘η’ is the response surface, x ₁, x ₂, x ₃, x ₄,…, x _n are the independent input variables, and ‘ε’ is the fitting error.

The appearance of response surface represents the expected response. The functional relationship between the ‘Y’ and the entire space of the input variables can be determined by selecting the polynomial of higher order [25]. Moreover, it determines the curvature in a system. In addition, estimation of response model can be done more efficiently by the selection of proper experiment design for data collection. In this study, the approximation of ‘Y’ has been proposed, using fitted second-order polynomial regression model (called quadratic model) and can be written as the following:

$$ Y = a_{0} + \sum\limits_{i = 1}^{n} {a_{i} x_{i} + \sum\limits_{i = 1}^{n} {a_{ii} x_{i}^{2} + \sum\limits_{i < j}^{n} {a_{ij} x_{i} x_{j} + \varepsilon } } } $$

(2)

where a _i represents the linear effect of x _i , a _ii represents the full quadratic effect of x _i and a _ij , and reveals the linear-by-linear interaction between x _i and x _j . Then, response surface ‘Y’ contains the linear terms, squared terms, and cross product terms. In this study, this quadratic model of ‘Y’ not only investigates the entire factor space, but also to locate region of desired target, where the response approaches its optimum or near optimal value.

The cause and effect diagram (Fig. 4) illustrates various factors influencing mechanical properties and geometrical features of FDM feedstock filament.

Fig. 4

Cause and effect diagram of single-screw extrusion process

As mentioned earlier, three factors each have three levels were used in this investigation and other factors were kept constant. The experiments were conducted based upon central composite full unblocked design with all combination of factors at two levels (high, +1 and low, −1) and central point (0) which is the midpoint of high and low level. The design consists of eight cubic points, six axial points, and zero center point in axial. The six center points of cube were selected to estimate the experimental error. As already mentioned above that the MFI value cannot be varied beyond the selected range; therefore, face-centered central cubic design (FCCCD), in which α = 1 was considered. The experiments were performed as per the experiment run order (Table 6) suggested by the software. Each row represents the test condition, which was formed by the combination of different levels of the selected parameters, together with the response value of tensile strength (TS) and diameter deviation (DD) of alternative material feedstock filament.

Table 6 Experimental layout using response surface methodology

The responses, such as ‘tensile strength’ and ‘diameter deviation,’ were obtained by conducting three sets of trials. The tensile strength of composite material feedstock filaments was tested according to ASTM-638 standard. Specimen sample used for tensile testing is shown in Fig. 5a, and was tested on universal testing machine. The specimen, before and after the testing, is shown in Fig. 5b and c, respectively. The filament diameter and deviations in diameter are measured by micrometer (least count 0.001 mm).

Fig. 5

Tensile testing of filament a specimen sample; b and c testing on universal tensile testing machine (UTM-SL-10A; Shanta Engineering, Mumbai)

Although as shown in Table 6, the tensile strength of the alternative material filament varies in a narrow range (20.90–21.60 MPa) which is within range of typical experimental error, but it was considered for the optimization of single-screw extrusion process parameters. The reason is that the tensile strength of FDM filament is one of the critical parameter. The effort has been made to maintain tensile strength of alternative material filament wire near to the tensile strength of commercial ABS wire. However, for better understanding of the process, other response parameters like percentage elongation, Young’s modulus, yield strength, etc., of alternative filament wire may be considered.

As a matter of fact, the tensile strength of binder material decreases with the reinforcement of filler material into its matrix, and it should be limited up to a level, so that the alternative material filament should have adequate strength to force the material through the FDM nozzle without buckling at the entrance of liquefier head. The tensile strength of alternative material should be approximately equal to the tensile strength of standard ABS material, for which the FDM is designed. Moreover, loading of filler material in Nylon6 can be done up to a limit, so that its MFI value should commensurate with the MFI value of standard ABS material under similar processing conditions. If the loading is more than this limit it causes chocking in extruder die and in FDM nozzle die. If it is less than this limit, it increases the flow rate of material through liquefier head (adversely affects the surface finish), as there is no change of hardware and software of the FDM system. The excessive material flow through FDM nozzle deteriorates the part building process and adversely affects the dimensional accuracy of FDM parts. Therefore, the filler loading (Al and Al₂O₃) in Nylon6 matrix was varied in a narrow range for its successful run on the FDM system.

2.7 Dynamic mechanical analysis

To counter verify the results obtained from optimization plot, the dynamic mechanical analysis (DMA) test had been performed. The DMA test was carried out using Netzesh DMA (model 242e, Germany) under air atmosphere with a temperature range of 25–150 °C. The specimens had dimensions 20 mm × 9.5 mm × 1.75 mm, and were prepared on FDM with normal solid mode having raster angle 45°, as shown in Fig. 6. The samples of Nylon6 material are cut from the sheet. The tests were performed in a three-point bending mode at a fixed frequency of 1 Hz. The heating rate was 2 °C/min with a maximum dynamic force of 10 N. The specimens were initially dried before the test in a vacuum over at a temperature of 50 °C for 8 h.

Fig. 6

FDM printed samples for DMA

3 Results and discussion

ANOVA generally considered for the statistical validation of results [27]. It accounts the variation of all sources as well as error sources. The experimental errors are due to the replication of experiments. The ANOVA analysis was carried out on the MINITAB 17 software. The signal to noise measures the sensitivity of quality characteristics from desired value. The test for significance of the regression model, the test for significance on individual model coefficients, and test for lack-of-fit are required to be performed, in regard to ensure the goodness of fit of the full quadratic model.

3.1 Analysis of variance (ANOVA) and regression analysis

As the single-screw extrusion process for the fabrication of alternative feedstock filament for the FDM system was non-linear in nature. The linear polynomial was not suitable for providing more accurate results; therefore, the second-order model (full quadratic model) is used in this work. On the basis experimental data obtained, ANOVA and statistical regression have been done to explain the correlation of data of process variables and their corresponding responses, such as TS and DD. The ANOVA table for the TS response (Table 7) shows that the second-order model is statistically significant, since its respective p value is very low being almost zero, while the lack-of-fit has also been found to be insignificant (with a p value 0.052 being larger than 0.05) which is desirable. The variable P2, square of P3, and two-way interaction of P1 × P3 and P2 × P3 found to be insignificant (as their respective p value is more than 0.05). The effects of insignificant parameters are insensible on the respective response.

Table 7 Analysis of variance for responses

Similarly, from Table 7, in the case of DD response, the second-order model is statistically significant, since its respective p value is very low being almost zero, while the lack-of-fit has also been found to be insignificant (with a p value 0.923 being larger than 0.05) which is desirable. For this response, variable P1, square of P3, and two-way interaction of P1 × P2, found to be insignificant, as their respective p value is more than 0.05. As the ANOVA table determined the individual significant term at 95 % of confidence level, the final response surface equations for TS and DD given in regression equation in terms of un-coded units are as follows:

$$ \begin{aligned} {\text{TS}} & = - 2 5 8.0 + 2 3 1. 3 {\text{P1}} - 0. 1 5 9 {\text{P2}} + 0. 2 9 8 {\text{P3}} - 4 3. 4 3 {\text{P1}} \times {\text{P1}} + 0.00 1 5 8 6 {\text{P2}} \times {\text{P2}} \\ & \quad - 0.000 3 6 4 {\text{P3}} \times {\text{P3}} - 0. 1 4 5 8 {\text{P1}} \times {\text{P2}} - 0.0 4 5 8 {\text{P1}} \times {\text{P3}} - 0.000 2 50 {\text{P2}} \times {\text{P3}} \\ \end{aligned} $$

(3)

$$ \begin{aligned} {\text{DD}} & = - 1. 7 4+ 2. 4 4 1 {\text{P1}} - 0.00 6 30 {\text{P2}} - 0.00 4 4 6 {\text{P3}} - 0. 6 8 2 {\text{P1}} \times {\text{P1}} + 0.0000 2 5 {\text{P2}} \times {\text{P2}} \\ & \quad + 0.00000 5 {\text{P3}} \times {\text{P3}} + 0.000 8 3 3 {\text{P1}} \times {\text{P2}} + 0.00 2 500{\text{P1}} \times {\text{P3}} - 0.0000 20{\text{P2}} \times {\text{P3}} \\ \end{aligned} $$

(4)

In the case of TS, the estimated standard deviation value (about the regression line) of 0.05913 is obtained for the coefficient of determination (R ²) which signifies that the model explains 92.96 % of the variability of TS, whereas the adjusted R ² (adj) is 86.62 % (Table 8). Similarly, the variability of DD in the model is 92.21 %, whereas the value of adjusted R ² (adj) is 85.21 %. In both the cases, the values of R ² and R ² (adj) are close to each other which shows the fitness of model [28]. Moreover, the higher value of R ² is more suitable for determining the coefficient of regression equation [29]. The response model fits the actual data accurately, as the value of R ² approaches unity [30]. The standard deviation value is a measurement of error [29], and it should be remain smaller as possible. In the case of DD, it is very small (0.00129), which shows goodness of fit. In addition, both the responses have, R ² and R ² (adj) values near to unity [28]. This shows the fitness of model. It should be noted that the regression model of DD is less deviated from the regression line as compare to the TS model.

Table 8 Regression analysis summary

The above model can be used to predict rapidly the tensile strength and diameter deviation of alternative material feedstock filament within the limits of the factors being established. The residuals are the difference between observed value and predicted value. The residuals are generally examined to investigate the violations of the basic assumptions and model adequacy [25]. Normal probability plot and histogram are plotted to verify the normality assumption. Figures 7 and 8 display the normal probability plot of the residuals for both TS and DD, respectively. Residual plots are generally examined to check the validation of the formulated model. In both the cases, the plots show a random pattern, indicating a decent fit of models. Moreover, it is realize that the residuals generally fall on a straight line implying that the errors are normally distributed. Furthermore, it validates adequacy of the least-square fit.

Fig. 7

Residual plot for TS

Fig. 8

Residual plot for DD

The response surface generally depicts the variability of process parameters and their influence on the desired response. The shape of response surface can be clearly visualized by the contour plots. The contour plots illustrate the lines of constant response in a plane of two input process variables, and it is easy to locate the optimum region with reasonable precision [25]. The fitted second-order model formulated above outline the contour plots of TS and DD, as shown in Figs. 9 and 10, respectively. The contour plots for both the responses are drawn with the hold value of parameters at center point, i.e., composition (P1) ‘B’ having MFI 2.25 with barrel temperature (P2) 170 °C and die temperature (P3) 195 °C. The color coding mapped the respective response range. As shown in Figs. 9 and 10, the response contour plots are drawn with respect to two input parameters, and third parameter is kept constant at hold value.

Fig. 9

Contour plot for TS

Fig. 10

Contour plot for DD

3.2 Response optimization

Ultimately, our aim was to maximize the value of TS and minimize the value of DD. From the experimental data, it was observed that maximum value of tensile strength is 21.6 MPa and minimum DD is 0.045 mm. Here, Table 9 shows the multi-response optimization of responses (TS and DD). For optimization, equal weight age and importance were given to both the responses. As illustrated in the optimization plot (Fig. 11), every column of plots represents a process analytical parameter and each row the response. Furthermore, each cell shows the response variation as a function of one of the process analytical parameters while keeping the other parameters unchanging. In addition, the vertical lines (red) inside the cells show current optimal parametric setting, whereas the dotted horizontal lines (blue) depict the current response values. The figure shows that the desirability of 0.86478 was obtained for TS with maximum value of 21.5 MPa, and in the case of DD, the desirability is 0.89 with minimum value of 0.45 mm. The composite desirability (D) was noted to be 0.8814, assuring the existence of optimum points to satisfy the objective functions. As a whole, the optimal input parameter setting, 2.31(MFI, Composition C) with mean barrel temperature of 160 °C and die temperature of 193.485 °C, is recorded from Fig. 10. Furthermore, the composite desirability in close to 1, it can be concluded that all the analytical parameters are within their working range [29].

Table 9 Multi-response optimization of TS and DD

Fig. 11

Optimization plot

The confirmation experiments were also conducted at the predicted optimum setting, and the results have been compared with predicted ones. Table 10 indicates the results of verification experiment and the amounts of relative errors. With the optimum combination of process parameters, it is predicted that this combination fabricate filament having highest tensile strength and minimum diameter deviation, and is suitable for the FDM system without any modification in its hardware and software.

Table 10 Confirmation results

Corollary I For instant, the predicted values of TS and DD can be calculated by substituting the optimum values of analytical parameters in Eqs. 3 and 4, respectively as shown below:

$$ \begin{aligned} {\text{DD}} & = - 1.74 + 2.441 \times 2.31 - 0.00630 \times 160 - 0.00446 \times 193.485 - 0.682 \times 2.31 \\ & \quad \times \;2.31 + 0.000025 \times 160 \times 160 + 0.000005 \times 193.485 \times 193.485 \times 0.000833 \times \, 2.31 \\ & \quad \times 160 + 0.002500 \times 2.31 \times 193.485 - 0.000020 \times 160 \times 193.485 = 0.04632 \\ \end{aligned} $$

$$ \begin{aligned} {\text{TS}} & = - 258.0 \, + 231.3 \times 2.31 - 0.159 \times 160 + 0.298 \times 193.485 - 43.43 \times 2.31 \\ & \quad \times 2.31 + 0.001586 \times 160 \times 160 - 0.000364 \times 193.485 \times 193.485 - 0.1458 \times 2.31 \\ & \quad \times 160 - 0.0458 \times \, 2.31 \times 193.485 - 0.000250 \times 160 \times 193.485 = 21.5053 \\ \end{aligned} $$

3.3 Dynamic mechanical analysis

DMA realized the phase structure, inter phase mixing of blends, and provides information about glass transition temperature [32]. Arivazhagan and Massod [31] concluded that, the specimens prepared on FDM system with normal build style have more strength than the sparse and double dense build style. The tan δ which is a ratio of loss modulus and storage modulus is plotted as a function of temperature for the specimens prepared with an alternative material filament fabricated using the optimum combination of parameters are given in Fig. 6. The average of five observations of glass transition temperature (obtained from storage modulus curve) and maximum peak of tan δ curve is recorded in Table 11. The maximum peak points of damping factor (tan δ) highlight the glass transition temperature (T _g) which was found to be 63.5, 93.5, and 107.5 °C of Nylon6, alternative material, and ABS (standard material), respectively. As already mentioned above, the alternative material contains 60 % by weight proportion of Nylon6 material which has T _g less than ABS material. Therefore, the T _g of alternative material is less than ABS material. Furthermore, Table 11 also indicates maximum peak of tan δ curve of ABS, alternative material, and Nylon6 material which are 0.055, 0.0808, and 0.115, respectively.

Table 11 DMA results

Although, the tan δ results highlight that the ABS material is stiffer than Nylon6 and alternative material, but the alternative material have adequate stiffness to force the material through liquefier head. It was confirmed during the fabrication of samples for DMA analysis that alternative material filament runs successfully without buckling and chocking in liquefier head of the FDM system. There reinforcement of filler material reduces the tan δ curve peak by restricting the movement of polymer molecules [33]. With the filler loading in Nylon6 matrix, the tan δ value decreases and the T _g show a shifting toward higher value. The shifting of T _g toward higher temperatures indicates the decreased mobility of the chains with the reinforcement of fillers. The lowering of tan δ value indicates the improvement in interfacial bonding within the alternative material matrix [34]. In addition, T _g, is considered as a measure of interfacial interaction among the molecules. The composites with poor interface bonding tend to dissipate more energy than those with good interfacial bonding [35]. Thus, poor interface bonding results in high tan δ value. The SEM image as shown in Fig. 12 illustrates the dispersion of filler material in Nylon6 matrix. Although the distribution of particles are uniform, but some agglomeration of particles are also observed. The distribution of particles can further be improved using twin-screw extruder.

Fig. 12

SEM image (50×) of composite material

4 Conclusions

The above discussion systematically summarized the evaluation of optimum single-screw extrusion parameters (composition, mean barrel temperature, and die temperature) using RSM approach. Among these analytical parameters, the composition is found to be most significant parameter for tensile strength, and mean barrel temperature is most significant for diameter deviation. The experimentation results are summarized are hereunder:

• The potential to develop an alternative material filament, is to fabricate parts on the FDM system having customized properties, such as wear resistance and thermal properties. Moreover, fabricated parts with alternative material filament used directly as end-use product (RM) or used for rapid tooling (RT) applications.

• The rheological study of MFI value (as per ASTM D1238-73 standard) indicates the limits of reinforcement of filler content (Al + Al₂O₃) in Nylon6 matrix. Moreover, the study establish the limits of different weight proportions of filler contents in binder material within which the analysis can be carried out.

• The attempts have been made to optimize the single-screw extruder process parameters using the RSM technique with the help of the MINITAB 17 software. The analysis realized the influence of analytical process parameters, such as composition, mean barrel temperature, and die temperature, and their levels on the desired responses (tensile strength and diameter deviation) with the confidence level of 95 %.

• The combination of optimum parameters is 2.31(MFI, Composition C) with mean barrel temperature of 160 °C and die temperature of 193.485 °C. Based upon the above criteria of experimental design, a full quadratic regression equation was developed by the software and found to be valid for predicting the tensile strength and diameter deviation of alternative feed stock FDM filament. The experimental results in regard to both the responses at the optimum combination of analytical screw extruder parameter are verified by predicted values and error of <5 % recorded when compared with experimental values.

• The DMA test indicates that the filament fabricated with the combination of optimum parameters shows adequate stiffness, which is most desirable for the successful run of filament on the FDM system.