Heat Transfer Coefficient Determination in a Gravity Die Casting Process with Local Air Gap Formation and Contact Pressure Using Experimental Evaluation and Numerical Simulation

Abstract

Anticipating the processes and parameters involved for accomplishing a sound metal casting requires an in-depth understanding of the underlying behaviors characterizing a liquid melt solidifying inside its mold. Heat balance represents a major factor in describing the thermal conditions in a casting process and one of its main influences is the heat transfer between the casting and its surroundings. Local heat transfer coefficients describe how well heat can be transferred from one body or material to another. This paper will discuss the estimation of these coefficients in a gravity die casting process with local air gap formation and heat shrinkage induced contact pressure. Both an experimental evaluation and a numerical modeling for a solidification simulation will be performed as two means of investigating the local heat transfer coefficients and their local differences for regions with air gap formation or contact pressure when casting A356 (AlSi7Mg0.3).

Introduction

Casting is performed by pouring a superheated molten metal into a molded cavity of the desired geometry. Solidification, representing the next process step, involves a liquid/solid phase change, followed by thermal contraction during further cooling, which both result in volume shrinkage. During this process, heat balance is a key factor that determines the development of these two underlying effects. The heat flow through the mold walls is the main cause of heat extraction and has a direct influence on the solidification rate and the corresponding microstructure as well as on the mechanical properties of the casting. The formation of shrinkage defects, distortion and residual stresses are also consequences of the direction and rate of heat exchange with the mold. In addition, mold expansion or shrinkage due to heating and cooling cycles influence the dimensional accuracy of the cast parts. For these reasons, a precise description of heat transfer in casting processes is of high importance with the heat transfer coefficient (“HTC”) being the physical quantity that describes the magnitude of potential heat exchange at the interface between two bodies. There are numerous parameters that influence the HTC such as mold temperature, contact pressure, gap formation, thermal conductivities of the materials involved, surface roughness at the interface as well as applied coatings as they are usually used on permanent molds in a foundry process.1,2

In this paper, the determination of HTCs present in regions with contact pressure and gap formation is performed based on both an experimental evaluation and a numerical solidification simulation of a setup identical to the experiment. The determination of appropriate HTCs during the entirety of a casting process represents a focus in research and industry in order to lead to a higher understanding of the underlying processes as well as to more accurate predictions of the solidification time, casting structure, defects and mechanical properties. The description of an entire casting process in a simulation is difficult in several respects. Especially for the solidifying alloy, not only has the material behavior in the solid and liquid state to be known, but the processes and property behaviors in the mushy range during phase transition also have to be described. This includes the solidification process, the mechanical behavior in the semi-liquid state3 up to the actual thermophysical data, which often can hardly be measured experimentally.

Heat transfer has already been considered in numerous analytical and numerical investigations, whereby for the most part only single contact mechanisms have been considered.4,5 In a casting process, however, various contact conditions coexist. A general distinction between a liquid–solid contact during the phase with liquid melt being in direct contact with the mold and a solid–solid contact during the phase with solidified casting alloy at the casting–mold interface can be made. Once a solid–solid contact has been established, its heat transfer can either increase due to induced contact pressure on the surface or decrease due to air gap formation. Coherence of the solidifying alloy can be seen as the turning point between the liquid–solid and solid–solid contact condition.

If the temperature of the casting interface is above the coherence temperature (temperature at which a solid skeleton has formed which can absorb forces for the first time), liquid casting metal is in contact with the mold. At this temperature, parameters such as wettability of the mold surface, amount of melt, amount of superheat, surface roughness, mold temperature, kinetic energy, turbulence of the melt, thermal conductivity of the mold and the hydrostatic pressure influence the heat transfer coefficient.6 As a result, a high heat exchange is to be expected for such a contact.

Below coherence temperature, a solidified thin load-bearing chill forms at the casting–mold interface which changes the contact condition. After initial quasi pressureless contact, volume shrinkage due to phase change of the solidifying cast metal and negative thermal expansion during further cooling lead to either air gap formation as the metal shrinks away from the interface or to heat shrinkage as the cast metal shrinks on to, e.g., an inner core resulting in increased contact pressure. The heat transfer through the air gap is characterized both by radiation exchange between the casting and the mold as well as by heat conduction of the air-filled gap. The latter mechanism is regarded as dominant in low-melting alloys.1,7 In steel casting, however, the radiation contributes about 50 % to the heat transfer at the interface.8 Unless strong pressures (like in high pressure die casting) are present, the respective HTCs are determined to be significantly smaller than those for liquid–solid contacts. Especially the heat transfer through an air gap represents a rather high thermal resistance, as the heat conductivity of air is significantly smaller than those of metal-to-metal contacts. A suggestion for a comprehensive HTC model considering these phenomena was proposed by Laschet et al.9

The experimental evaluation is based on previous research activities10,11 and utilizes temperature, gap size and pressure measurements to reconstruct the heat fluxes between casting and die to deduce the HTC development. The numerical simulations apply an inverse and manually parametrized model for the local HTC using thermal simulation in Magmasoft and thermomechanical simulation via the software Abaqus. The simulation results are then compared to experimental measurements and evaluated continuing previous research.12,13

Experimental Setup and Modeling

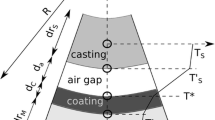
The investigations performed are based on the experimental setup shown in Figure 1.14 Here a “bowl”, i.e. a cylindrical and thus rotationally symmetric part, is casted on an inner core. The aluminum casting alloy A356 used in the experiments is supplied in form of premade ingots already featuring a (Ti–) grain refinement and (Sr–) modification (cf. Table 1). After degassing with Ar-gas the alloy is gravity casted into the central feeder inside the sand cover at 720 °C. The filling time of the casting process amounts to approx. 5 s. While the outer die as well as the inner core are made of tool steel, the actual outer wall of the casting cavity itself consists of copper inserts which are put into the outer steel die and are temperature controlled via cooling channels filled with circulating oil. The feeder, also acting as sprue, is built in form of a sand cover that is put on top of the permanent mold. This way the heat extraction from the casting can be considered as a quasi-one-dimensional process due to the rotational symmetry and the flow of heat is either directed to the inner steel core or to the outer copper inserts.

Figure 1

Experimental setup for the casting of a “bowl” geometry with measuring instrumentation for temperature, gap width and contact pressure.14

Table 1 Chemical Composition of the A356 Ingots [mass-%]

Three quantities are measured by the applied instrumentation (cf. Figure 2 left): Type K thermocouples (“TCs”) measure the temperature development inside of the die walls as well as inside the melt. The exact positions are shown in Figure 2 right. Via quartz rods inserted into both the die and the melt the second quantity of local material movement is measured. Linear variable differential transformers (“LVDTs”) outside of the mold record the respective movement which is transmitted to them via the rods. This also enables the determination of the air gap that forms between the copper inserts and the casting as a gap forms along the entire outer cavity wall due to the volume shrinkage of the casting. Analogously the contact pressure on the surface of the inner core is being measured via an inserted rod transferring the respective forces to a load cell, thus representing the third measured quantity.

Figure 2

Overview of the measurement instrumentation (left) and exact positions of the thermocouples (right).

Concerning the experimental procedure, in addition to mounting the respective thermocouples and glass rods the mold walls were finished with a ceramic, mica-based foundry coating via spraying. The cooling channels inside the copper inserts were used for oil tempering with each insert being supplied by a separate hot cooling aggregate. The oil tempering serves both as heating to increase the die temperature to the desired level during preheating and cooling once the molten metal has been poured. As actual oil tempering temperatures 30, 100 and 200 °C were chosen. This covers the experimentally possible range with room temperature as lower limit and 200 °C as the upper limit to the possible temperature range due to the necessity of avoiding the oil’s evaporation temperature of 370 °C in order to prevent damage caused by sudden gas expansion. The chosen oil temperature remains constant for the respective experiment during both the preheating phase prior to casting the aluminum alloy and the cooling phase after mold filling. Since the experimental setup and the measuring instrumentation do not allow casting in series, each casting experiment was preceded by a 60-min preheating phase in order to heat the die to stable temperatures corresponding to the selected tempering level. Regarding the thermocouples all 12 measuring positions depicted in Figure 2 were always fitted with type K thermocouples in all experiments. Pairs of LVDTs measuring the casting and die movements are placed at three positions with 120 ° spacing circularly around the experimental setup at identical height. The pressure measurement was only performed at one position. Due to the elaborate preparations needed and the loss of the quartz rods with every performed casting experiment, only one component was casted for each oil temperature setting.

The experimental evaluation of the heat transfer coefficient h for the case of air gap with width ∆x is determined by the thermal conductivity of the air ${\lambda }_{\text{Fourier}}$ according to Fourier’s Eqn. 1, where ${\lambda }_{air}$ is the temperature-dependent thermal conductivity of air.11 It is assumed that the heat flow through the air gap is constant per time step, since the specific heat of the air and that of the ceramic coating is small. Prior to solidification, there is a solid–liquid contact. Its hydrostatic pressure of up to 0.0043 MPa can be neglected. The utilization of Eqn. 1 leads to a false estimate of h with an infinite value when the gap width approaches zero. The introduction of a high initial heat transfer coefficient ${h}_{init}$ solves this problem. In order to determine a suitable value for ${h}_{\mathrm{init}}$, the mean heat flow ${q}_{\mathrm{casting}\to \mathrm{die}}=\frac{{q}_{\mathrm{casting}}+{q}_{\mathrm{die}}}{2}$ is calculated according to Eqn. 2, where ${q}_{\mathrm{casting}}$ represents the heat flow from the casting into the gap and ${q}_{\mathrm{die}}$ represents the heat flow from the gap into the die. Both are calculated from the respective temperature gradients determined within the casting and mold at the interface.15

Inside the experimental setup, the casting shrinks onto the core. At the core surface, the formed thin load-bearing solid chill exerts a contact pressure p on the core surface. For the calculation of the heat transfer coefficient under contact pressure, the model suggested by Mikić,16 applied as per Eqn. 3, is used ${\lambda }_{s}$, ${E}^{^{\prime}}$ and ${\sigma }_{s}$ are the equivalent thermal conductivity, the equivalent Young’s modulus and the surface roughness of the contacting solid surfaces, respectively.

$${h_{{\text{Fourier}}}} = \frac{{{\lambda _{{\text{air}}}}}}{{\Delta x}}$$

(1)

$$ h_{1 \to 2} = \frac{{q_{1 \to 2} }}{{\left( {T_{1} - T_{2} } \right)}} $$

(2)

$$ h_{{{\text{Mikic}}}} = 1.9 \cdot \frac{{\lambda_{s} }}{{\sigma_{s} }} \cdot \left( {\frac{p}{{E^{\prime}}}} \right)^{0.94} $$

(3)

The geometries of the experimental setup were transferred to Abaqus to perform a solidification simulation. Due to the symmetrical conditions, only one third of the geometry had to be modeled (cf. Figure 3 right). The simulation model is then setup and meshed to support a thermomechanical simulation. This enables the thermomechanical stresses and deformations of solidification to be incorporated in order to extract local information about parameters such as gap widths and contact pressures from the simulation and to use them in the heat transfer model.

Figure 3

Fraction solid development for an A356 alloy as function of temperature determined via coupled phase field simulations using Micress18 (left) ; Abaqus thermomechanical simulation model overview (right).

For the phase change of the liquid melt into the solid state, an algorithm for the release of the latent heat as a result of the phase transformation is integrated into the Abaqus HETVAL routine. The basis for this is a temperature-dependent development of the solid phase fraction, which was extracted from a 3D, thermodynamically coupled phase field simulation of the microstructure development under thermal boundary conditions similar to the current experiment.17 Here, the solidification processes of A356 alloy are addressed starting with a heterogeneous nucleation, followed by the primary and eutectic solidification, so that these processes are taken into account when applying the temperature-dependent fraction solid data set.18 Figure 3 left shows the applied temperature-dependent evolution in fraction solid.

In addition to the description of the heat source of the liquid–solid phase transformation, the heat balance also is defined by the heat dissipation from the cast component. Here, the heat transfer between the casting and the surrounding mold is of central importance. Two models are used to describe the local HTCs: One model is based on the inverse HTC determination approach using the experimentally measured data, and the other model is based on phenomenological considerations which aim at describing the HTC by manually adjusting model parameters. Both models are implemented via the Abaqus GAPCON routine.

The contact conditions occurring during the casting process cannot be uniformly assigned to all contact surfaces (both locally as well as with respect to time). Prior to solidification, a liquid–solid contact condition is present in the entire casting cavity. As solidification progresses, one of two effects occurs as a result of volume shrinkage and stress build-up: Either an air gap is formed or the contact pressure of the solid–solid contact increases. Based on the considerations of Laschet et al.,9 the manually parametrized HTC model distinguishes between four states (cf. Eqns. 4–7), whereby reaching the coherence temperature is used as transition condition between a liquid–solid and a solid–solid contact:18

• (A) liquid–solid contact:

  $$ h_{{{\text{liq}}}} = 2000\frac{W}{{{\text{m}}^{2} \cdot K}} $$

  (4)

• (B) pressureless solid contact:

  $$ h_{0} = 1000\frac{W}{{m^{2} \cdot K}} $$

  (5)

• (C) contact pressure:

  $$ h_{{{\text{pressure}}}} = h_{0} + \left( {1 - e^{{ - {\text{pressure}}}} } \right) \cdot 3000\frac{W}{{m^{2} \cdot K}} $$

  (6)

• (D) air gap:

  $$ h_{{{\text{gap}}}} = \frac{{\lambda_{{{\text{air}}}} }}{{\frac{{\lambda_{{{\text{air}}}} }}{{h_{0} }} + {\text{gap width}}}} $$

  (7)

For the inverse HTC model, on the other hand, no model assumptions are used, but the experimentally measured data are used to describe the HTC. For this purpose, a simulation model was setup in the Magmasoft software suite to simulate the casting and solidification processes (cf. Figure 4). A parametrized function for the HTC was used for both the outer surfaces of the bowl geometry, where a gap is formed, and for the inner surfaces, where a contact pressure builds up. An optimization by variation of the function parameters was carried out and the quality of the adaptation was determined by comparison of the experimental temperature measurement with the simulated data for the cooling curves. Thus, the optimal parameters of the HTC function could be determined. Figure 5 shows the resulting curves for the inversely determined HTCs.

Figure 4

Magmasoft simulation model setup (left) ; mesh (middle) ; fraction solid result during ongoing solidification (right).

Figure 5

HTC determination via inverse simulation for the contact conditions at the outer die (left) and at the inner core (right) displayed for different oil temperature settings.

Results

Regarding the experimental evaluation of the HTC development and the influence of the different die temperature control temperatures (i.e. the oil tempering of the die), the experimental results will be discussed first. Figures 6 and 7 show the temperatures measured at all thermocouples in the setup for a die temperature of 100 °C at the upper close to outer die thermocouple positions TC1 to TC6 and lower close to die thermocouple positions TC7 to TC12 (cf. Figure 2). Derived temperatures like the extrapolated cooling curves at the casting/die interface and the assumed air temperature inside the air gap developing on the outer surface of the casting are shown as well. The two measurement positions considered differ in terms of their cooling conditions. A quasi one-dimensional, radial heat flow from the melt either outwards into the die or inwards into the core always is present due to the rotationally symmetrical geometry of the experimental setup. The lower measuring position is in a thinner-walled area where heat is dissipated on both sides via the outer copper insert and the inner steel core. This leads to comparatively high cooling rates in this region. The upper measuring position is characterized by a direct heat dissipation via the outer copper insert only and is located next to a mass accumulation of the casting, due to which this region has a larger melt volume and does not dissipate heat to an inner core. As a result, this region has comparatively lower cooling rates.

Figure 6

Cooling curves at the upper measuring positions for 100 °C oil tempering temperature.

Figure 7

Cooling curves at the lower measuring positions for 100 °C oil tempering temperature.

Development of the Experimentally Measured Temperature

The influence of the oil tempering via the cooling channels on the outer die and inner core leads to a lesser increase in temperature for the die than it is the case for the core. After about 1 min of process time, the die temperatures reach their peak and cool down again from this point onwards. The lack of actively cooling the core leads to temperatures that conform to the casting part temperatures, coherently decreasing as time proceeds. As the air inside the gap that forms between casting and outer die, is in contact with both interfaces, the mean temperature of the two interfaces is assumed to be the air temperature.

The influence of the different temperature settings for the oil tempering is shown in Figures 8 and 9 for the upper and lower measuring positions at the thermocouples closest to the outer die (TC4 and TC7). The data presented use the maximum temperature which each thermocouple measured as the respective starting point of the measurement. This approach incorporates a thermocouple inertia, which prevents the recording of reliable data during the first moments of a sudden and strong temperature rise. Only after having reached a temperature close to the level of the surrounding melt (represented by reaching peak temperature) do they settle sufficiently and no longer result in highly fluctuating values.

Figure 8

Cooling curves for upper, close to outer die (TC4) measuring position.

Figure 9

Cooling curves for lower, close to outer die (TC7) measuring position.

The difference in cooling rates is clearly visible when comparing the graphs of Figures 8 and 9, as low temperatures are reached faster at the lower measuring position. The same applies to the solidification times, which at the lower position take between approx. 15 and 35 s depending on the die temperature control while ranging between 40 and 70 s for the upper position. It is also evident that the characteristics of eutectic solidification, consisting of primary and eutectic solidification, are recognizable.

Development of the Experimentally Measured Air Gap and Contact Pressure

As the casting starts to shrink, either an air gap forms, or a contact pressure builds up, respectively. These contact conditions lead to different HTC developments which will be evaluated in detail. Coherence represents the deciding criterion for initial shrinkage as only after coherence is reached, the not yet completely solidified dendrite skeleton is able to take up and transmit forces. For an AlSi7 alloy, coherence is reached at a temperature of 565 °C. This criterion can be verified when evaluating the experimental measurements. Figure 10 left shows the development of air gap width plotted over casting temperature close to the interface. At around 565 °C the slopes of the gap width curves increase significantly showing a stronger increase for casting temperatures below 565 °C. This can be attributed to the formation of a sufficiently coherent solid shell at the outer die interface that can shrink off the interface. The small gap width that has formed prior to cooling down to 565 °C is a result of heat expansion of the outer die which due to its cylindrical form expands away from the interface. As the displacement of both the melt and the die was measured via the LVDTs, Figure 10 right shows the quantity of the movement of the casting metal and of the die. While the contribution of the casting displacement keeps on increasing, the movement of the die reaches a maximum after around 1 min into the process and decreases again past this point in time. This behavior can be explained by the active cooling of the outer die which cools it down to its initial temperature and compensates the effect of the thermal expansion, leaving only the effect of the progressive casting contraction as source for the final gap width.

Figure 10

Gap width at the lower measuring position for different die tempering temperatures (left) ; Die and casting surface movement contribution to the total gap width for different die tempering temperatures (right).

A similar behavior can be identified when evaluating the pressure measurement as displayed in Figure 11 left. The plotted pressure developments show a change in behavior at around 565 °C which is an evidence for established coherence at this temperature.

Figure 11

Pressure development for different die tempering temperatures (left); Measured pressure development for 30 °C tempering level and reconstructed pressure curve gained via numerical simulation results (right).

A problem with the 30 °C pressure measurement can be seen in Figure 11 right. After a process time of approx. 60 s, the measured pressure level begins to drop and stay at a certain level until rising again after around 120 s. This behavior happens due to a movement of the measuring setup, which is prone to settling of the die parts under mechanical stresses. A blockage of the rod transmitting the forces of the pressure measurement (cf. Figure 1) can be the result. In case of the 30 °C measurement, there is only a temporary disturbance as later on in the process rising pressure values are recorded again. While not being negatively affected by this phenomenon, the settling effect of the setup can also be identified in the gap measurement as the 30 °C curve shows a small instability at the exact same process time. In order to perform further evaluation for the 30 °C temperature control setting, the pressure measurement up to the point of settling is used. The following pressure levels then are reconstructed by using the pressure curve gained from the numerical simulations (cf. section F). The reconstructed pressure curve is shown in Figure 11 right.

Figure 12 shows the development of the contact pressure at the inner core as a function of time and cast metal temperature. As the casting shrinks onto the inner core, increasing pressures occur during solidification or further cooling. When comparing the pressure development for the different die temperature control levels, a clear influence can be determined even though the inner core itself is not actively tempered via cooling channels. During the first approx. 60 s process time, all curves are almost identical. This changes in the further course of the process. The reconstructed pressure curve at 30 °C and the experimentally measured curve at 100 °C temperature control show a very similar pressure development with slightly higher final values for the 30 °C case. Here, the highest determined pressure of approx. 25 MPa is reached. In comparison, the measured maximum pressure for the 200 °C level only reaches approx. 14 MPa with lower pressure rise rates compared to the processes with lower tempering levels and a shorter time span until the maximum pressure is reached. When comparing the contact pressure with the respective casting metal temperature at the interface (cf. Figure 12 right), it can be seen that there is no uniform pressure increase in terms of a function of temperature (as the initial data for high casting metal temperatures all develop differently). Instead, a reduced tempering level ensures that the same pressure levels are shifted to lower cast metal temperatures until the pressure curves run almost parallel to each other. Oil tempering hence can influence the maximum applied pressure as well as the temperatures in the casting corresponding to a certain contact pressure. The reason for this can be traced back to the starting temperature of the inner core. Even if there is no direct initial heating, the inner core is indirectly heated during casting preparation by the oil circuits in the outer die. Higher temperature levels result in a higher starting temperature of the inner core. When getting in contact with the melt, there is a correspondingly lower temperature difference, i.e., the core will experience less absolute heating, and therefore expands to a lesser degree.

Figure 12

Experimental pressure measurement for different tempering temperatures with the reconstructed 30 °C pressure development as function of time (left) and as function of casting metal temperature (right).

Experimental Evaluation of the Heat Transfer Coefficient

The initial value of the heat transfer coefficient on the core side, ${h}_{\mathrm{init}\text{\_}\mathrm{core}}$ = 3500 W/m²K, is calculated on the basis of the heat flow into the core (cf. Eqn. 2). The development of the pressure-dependent HTCs as defined in the Mikić model (cf. Eqn. 3) over the entire solidification time is shown on the left half of Figure 13. The quasi linear behavior of the HTC development, as predetermined by the model equation, can be seen. When comparing the HTC for the three different temperature control levels, a slight increase in heat transfer with increasing temperature is present.

Figure 13

Experimentally determined heat transfer coefficient as a function of the contact pressure (left half) and as a function of the gap width (right half) for different oil tempering temperatures and the initial HTC values interpolated between ${h}_{init\_core}$ and ${h}_{init\_gap}$ for core and outer die side.

The right half of Figure 13 shows the development of HTC over gap width at the outer die for different oil temperature levels. If a small gap is formed, it is assumed that the heat transfer coefficient is limited to an initial value calculated for the point of reaching the coherence temperature. This is necessary because the temperature field on the gap side can only be reliably extrapolated after the coherence temperature has been reached, so that the value for no or very small gaps cannot be experimentally determined (with the asymptotic behavior of the HTC function running toward infinity for small gap width values). Equations 8–10 show the definition for a family of curves describing the air gap HTC for different oil temperature levels ${T}_{\mathrm{oil}}$ . The results show that a higher oil and thus also die temperature lead to higher HTCs. This can be explained via the increased thermal conductivity of the air in the gap between casting and die. The HTC approaches a value of approx. 100 W/m²K for large air gaps and with the described coherence limit ${h}_{\mathrm{init}\_\mathrm{gap}}$ maximum values as given in Table 2 are determined for small air gaps.

$$ h_{{{\text{gap\_family}}}} = A \cdot \left( {\Delta x} \right)^{ - B} $$

(8)

$$ A = 2.235E{ - 0}5 \cdot T_{{{\text{oil}}}}^{2} + 0.01949 \cdot T_{{{\text{oil}}}} + 33.61 $$

(9)

$$ B = 1.218E{ - }06 \cdot T_{{{\text{oil}}}}^{2} - 1.155E{ - }04 \cdot T_{{{\text{oil}}}} + 1.121 $$

(10)

$$ h_{{{\text{init\_gap}}}} = 0.00642 \cdot T_{{{\text{oil}}}}^{2} - 5.07 \cdot T_{{{\text{oil}}}} + 2229.4 $$

(11)

Table 2 Air Gap Formation HTC Limit at Coherence Temperature for Different Oil Temperature Levels

As the HTCs for both the contact pressure and the gap formation-driven regions have been defined, the final aspect that must be addressed is the pressureless and gapless intersection of the two contact conditions. For this purpose, a linear connection between the core side with ${h}_{\mathrm{init}\text{\_}\mathrm{core}}$ derived from Eqn. (2) and the respective ${h}_{\mathrm{init}\text{\_}\mathrm{gap}}$ on the outer die side, as calculated via Eqn. 11, is created. This way Figure 13 displays the HTC development for the two contact conditions after coherence is reached.

Evaluation of the Simulated Cooling Curves

The results of the simulations using the two HTC models are qualitatively evaluated on the basis of the resulting cooling curves as shown in Figure 14 for the experiment and the extracted cooling curves of the parametrized and inverse HTC model simulations for thermocouple 7 (cf. Figure 2). A discussion of the 30 °C temperature controlled case only will serve as introduction to the specifics of the simulation before going into detail regarding the other temperature levels. Focusing on the position of TC7 will also serve as the basis for the following discussions as the other evaluated positions in the lower part of the casting show an identical temperature behavior as displayed in Figure 7. In addition to this, the HTC at the interface with contact pressure is expected to deliver values a magnitude higher than for the gap formation case. For this reason, evaluating a position closer to the outer die with air gap formation at the casting–die interface will deliver the strongest influence of the air gap HTC on the cooling behavior when considering the three experimental measuring positions in this area.

Figure 14

Cooling curves resulting from the experimental measurement and thermomechanical simulation using the inverse and parametrized HTC model for 30 °C tempering level.

Since the thermocouples are limited by their thermal inertia, the experimental measurement delivers reliable data only after a few seconds into the process, i.e., during the stage of primary solidification. Therefore, there is no information for the beginning of the process, i.e., especially at the time of the purely liquid state of the melt. The simulated cooling curves provide temperature values over the entire period and thus clearly show the liquid range, the start of primary solidification at 612 °C and the stage of eutectic solidification at approximately 565 °C. As both HTC models use the same data and algorithms to describe the development of the solid phase fraction and the release of the latent heat, the curves during solidification are almost identical and show good agreement with the experimentally measured values. This changes after a time of 30 or 60 s for the inverse and parametrized model, respectively, where a deviation between the measured and the simulated curves emerges. Toward the end of the evaluated time frame, an almost parallel course of the curves can be stated. In order to find an explanation for this behavior, a more elaborate examination of the significant HTC model parameters and their development over time is required.

Evaluation of the Simulated Gap Formation

The left side of Figure 15 shows the gap width development from experiment and simulation evaluated for local gap formation at the level of experimental LVDT measurement near the upper end of the casting (cf. Figure 2 left). While all data show the same increasing trend, a systematic discrepancy between experiment and simulation can be observed. On the one hand, there is a difference in the time of initial gap formation. Experimental data show that the gap starts to form immediately as solidification begins, while for the simulation a gap at the evaluated position only develops after solidification ends. On the other hand, the final values of the gap width are 0.05 mm (approx. +15 %) higher than those of the experiment, with the curves crossing and running quasi parallel from a point in time of 150 s onwards, which then leads to an overestimation of the simulated gap size of approx. 20%.

Figure 15

Gap size development for the 30 °C experiment and simulation (left); Gap size development with artificial shift of the experimental curve to match time of initial gap formation (right).

Nevertheless, the general trend of the calculated gap development has a good qualitative agreement with experiment. This agreement can be more easily evaluated when shifting the experimental curve to match the onset of the gap formation as per Figure 15 right.

Further consideration of the time discrepancy between experimental and simulated gap formation shows that in the simulations no homogeneous gap formation takes place along the outer wall of the casting. A gap is initially formed at the lower end of the casting and as time passes, areas higher along the outer surface of the casting begin to also form a gap. This effect is shown in Figure 16 together with the final warpage on the entire component giving a visual impression of the final gap sizes.

Figure 16

Gap formation on the outer wall after 20 s (left) and 30 s (middle); Final total warpage of the casting with exaggerated visual 3D geometry warpage (right).

Another comparison between gap developments is shown in Figure 17. Here, the experimentally determined data is compared to simulated data extracted at the height level of the lower thermocouples. This comparison exhibits a good trend and timing agreement between the experiment and simulation. The high accordance of this alternative simulation curve with the experimental data measured at a higher height level (cf. Figure 2) underlines the impact of the time delay in simulated initial gap formation.

Figure 17

Gap size development as experimentally measured in comparison with simulated results at the height of the lower thermocouple measurement at 30 °C tempering level.

Further statements regarding the time-dependent formation of the outer gap can unfortunately hardly be made as the gap width was measured only at one height level in the experiment. Considering the experimentally measured immediate gap formation in the upper part of the casting, it can be assumed though that the gap forms simultaneously on the entire outer wall of the component during the experiment. This could be due to the fact that during the contact between melt and mold a load-bearing chill is formed, which is not present in the simulation because of the mesh density of the discretization not being sufficiently high to map the formation of such a thin solid shell. Meshing in a sufficiently high density would lead to unfeasibly high computing times and memory requirements and was not applied for these reasons.

Evaluation of the Simulated Contact Pressure

There is no gap formation on the inside of the casting as there is an increasing contact pressure resulting from the thermal volume shrinkage which represents the dominant influence of the HTC in this region. Figure 18 shows the experimentally recorded and simulated course of pressure development on the inner core. The given curves are in good agreement up to a time of approx. 60 s. Then a pressure decrease happens for the experimental measurement, while the simulations show a continuous pressure increase. This phenomenon already has been identified in section B as a settling of the setup. The effects on the pressure measurement are more pronounced than for the gap development, which is due to the higher sensitivity of the pressure measurement, which is particularly prone to jamming. In the given case, there is no complete jamming, but the settling of the setup temporarily disturbs the measurement considerably. As soon as rising pressures are measured again in the experimental measurement, the course of pressure development for experiment and simulation coincide again, so that the curves run quasi parallel to each other.

Figure 18

Pressure development on the inner core for experimental measurement and simulated results for the 30 °C case.

Comparison of the Inverse and Parametrized HTC Model for the 30 °C Case

Based on these findings, the evaluation of the HTC development provided by the two models can now be discussed. Figure 19 shows the evolution of the HTC for the two models over time. While both models provide very similar results for the exterior side with gap formation, there are significant differences in the description of heat transfer on the contact pressure dominated interior side. With a starting value of 2000 W/m²K on the outer wall, both the parametrized and inverse models start with an identical value. In the further, decreasing course of the HTC describing the air gap formation there are only minor differences and both models end asymptotically with a heat transfer coefficient of approx. 100 W/m²K. Thus, the inverse HTC determination confirms the assumptions made for the parametrized model. Therefore, there is a very good agreement between the HTC of the gap width dependent manually parametrized model and the inverse, purely temperature-dependent determination for gap size-driven regions.

Figure 19

Development of heat transfer coefficient with 30 °C tempering level for the outer region with gap formation (left) and inner region with contact pressure (right).

For the contact pressure-dependent inner side of the casting, the inverse and parametrized models begin with similar values of 2500 and 2000 W/m²K, respectively. While the inverse model shows a continuous increase to 3000 W/m²K in the ongoing process, the pressure-dependent parametrized model initially shows a drop to 1000 W/m²K. This drop corresponds to the transition of the liquid–solid contact to an almost pressure-free solid–solid contact just after solidification is complete. As the contact pressure increases, this value multiplies starting at a point in time of 20 s, which, as can be seen in Figure 10, is the point in time at which the pressure increase begins due to shrinkage onto the inner core. A final heat transfer coefficient of approx. 4300 W/m²K is achieved following the parametrized HTC model. The direct relationship between pressure and HTC is shown in Figure 20. Here, the lack of an adequate representation of the phenomenology for the inverse model becomes obvious as there is no distinct pressure dependence for this modeling approach.

Figure 20

Pressure dependence of the HTC for the inverse and parametrized model for the 30 °C case.

Evaluation of the HTC Model Predictions at Different Die Temperature Control Levels and Comparison with the Experimentally Determined HTC Development for Gap Formation

Figure 21 shows the HTC development over casting temperature at the interface for the gap formation as evaluated experimentally and as modeled for the 30, 100 and 200 °C temperature control of the copper inserts. While the experimental curves show the HTC development as defined via Eqn. 1, the curves for the inverse and parametrized model also show the predicted liquid–solid HTC of 2000 W/m²K which represents the upper limit of the HTC modeling. The general trend is identical for all three evaluation approaches: After reaching coherence and thus allowing for an actual air gap formation, the HTC drops significantly with reduced casting metal temperature. Due to an asymptotic behavior present for all evaluated tempering levels, a final minimum for the HTC can be assumed below 400 °C.

Figure 21

Development of the HTC for gap formation as described by the experimental evaluation (left), inverse model (middle), parametrized model (right) for different tempering levels.

The experimental evaluation shows the characteristic of an exponential function closing in on its asymptote which corresponds to coherence temperature. After reaching a certain HTC in the low 100s W/m²K, the slope suddenly is strongly reduced leading to a quasi linear behavior from this point on. Both the inverse and parametrized model follow the same exponential nature of HTC development although their transition from a quasi linear to the strong increase over temperature is less abrupt and more fluent.

As for the influence of the oil temperature control a trend showing increased HTCs with increased oil temperature can be seen. With higher mold temperatures leading to higher temperatures inside the air gap, this behavior was to be expected as a higher air temperature increases the air’s heat conductivity. The corresponding influence only has a small impact as the absolute difference in heat conductivity change for the considered temperature range is small. An increase in HTC with higher tempering levels is especially visible for the experimental evaluation and the inverse models. Here, a nearly identical behavior for the 30 and 100 °C case can be seen while the 200 °C case leads to clearly higher HTCs once the initial strong drop, after having cooled down enough for reaching coherence, has finished. The differences between the respective tempering levels in the parametrized model, which applies Eqn. 7 for the HTC determination, are existent but negligibly low. Table 3 shows a comparison of the displayed HTCs at a casting interface temperature of 400 °C.

Table 3 HTC Values for Gap Formation at 400 °C Given in [W/(m²K)]

Figure 22 shows the air gap formation HTC curves for the 30 and 200 °C temperature control setting which displays the differences between the modeling approaches more clearly. In addition to the previous discussion, it can be seen that although the parametrized model does not show a noticeable influence of the variation in oil temperature, it manages to reach a closer accordance with the experimental evaluation than the inverse model. Especially for the 30 °C and 100 °C cases, the final HTC values at low casting temperatures are nearly identical and the strong initial exponential drop of the HTC values, once coherence is reached, is represented closer for the parametrized than for the inverse model.

Figure 22

Superposition of the experimental and simulated HTC development at the outer interface plotted over casting temperature for 30 and 200 °C oil temperature control.

Overall, the evaluations show a consistent modeling of the HTC for air gap formation with slight differences in curve progression and extent of the oil temperature influence.

Evaluation of the HTC Model Predictions at Different Die Temperature Control Levels and Comparison With the Experimentally Determined HTC Development for Contact Pressure Build-up

A comparison of the contact pressure-driven HTC development for different tempering levels as described via experimental evaluation, inverse and parametrized model is shown in Figure 23. As every evaluation uses a different approach to describe the HTC at the casting–core interface, each approach leads to a unique behavior. The experimental evaluation is based on the Mikić model. As a result, the HTC development is a quasi linear, monotonically increasing function as predetermined by the functional relation in the model itself where an increased temperature level leads to slightly higher HTCs. The inverse model with its limited ability to accommodate the influence of pressure on the HTC has no direct link to the pressure, and thus, a nearly constant HTC is the result. Only a weak relation between temperature and pressure in the first stages of pressure build-up once coherence is reached can be found. This is represented by an initial value for the pressureless contact which is slightly lower than the final, quasi constant HTC present at higher pressures. The transition between initial and final value takes place fluently in the domain between 0 and 10 MPa. Increasing die temperature leads to lower initial HTC values and thus to a more distinct transition with a final HTC value of 3000 W/m²K for all investigated temperature control settings. The parametrized model follows Eqn. (6), beginning with an HTC of 1000 W/m²K for the pressureless contact. It shows a strong increase with initial pressure build-up until having reached a maximum of 4000 W/m²K at 4 MPa pressure. As pressure increases further, a slight quasi linear increase in HTC occurs. Due to the pressure being the only variable in the parametrized model, there is no influence of the temperature level on the HTC development.

Figure 23

Development of the HTC for contact pressure as described by the experimental evaluation (left), inverse model (middle), parametrized model (right) for different tempering levels.

Figure 24 shows a direct comparison for pressure dependent HTC evaluations. As each approach has only little variation regarding the influence of the oil temperature, the graphs are nearly identical. When putting the results in perspective, the results for the contact pressure-driven HTC development seem to be contradicting as they can lead to strongly different results. Yet a comparison to the results of the simulated cooling curves as displayed in Figure 14 shows a high accordance to the measured curve—especially during phase change. In addition to that the heat transfer coefficients at the casting–core interface are about a magnitude higher than those at the outer interface with gap formation making it the major source for heat extraction.

Figure 24

HTC development as function of the contact pressure at the core interface as described by experimental evaluation and simulation for 30 and 200 °C temperature control.

With the Mikić model predicting even higher HTCs than the parametrized model does, this gives a hint to an explanation for this behavior as even higher HTCs seem to be fitting. The manually parametrized model was created in order to create a relation between the conditions in gap width and contact pressure that leads to HTCs, which when applied result in a high accordance between experimentally measured and simulated cooling curve. Here, the experimental setup must be kept in mind though. Only the outer copper inserts are actively heated / cooled via the oil circuits. The inner core is indirectly heated to a temperature close to that of the outer inserts during the preheating phase. This heat exchange happens slowly though giving it little importance for the casting process and its cooling curves. What is of importance is the increase of the core temperature due to heat exchange with the casting. As Figure 7 shows, it even reaches surface temperatures nearly identical to those of the casting a few minutes into the process. This results in a decreasing temperature gradient at the casting–core interface which leads to a decrease in heat exchange between core and casting. For this reason, different HTC values for the inverse and parametrized model can still lead to good accordance with respect to the cooling curves. This also puts the even higher HTC values as derived via the Mikić model into perspective. The slight quasi linear increase in HTC as displayed by the parametrized model is not the result of the physical description of the HTC development under pressure, but is the direct result of the decrease in temperature gradient. The observed decreasing heat transfer leads to a model description that will display a limit in maximal HTC value when being used as basis for fitting the parameters of the HTC model. This derived limit of the HTC for increasing pressure will not be physically present and is just the result of the adaption of measured temperature data to the HTC model. The actual HTC will keep on increasing as described by the Mikić model. In terms of the heat balance an increase in HTC will not result in significant increases in heat transfer as it is hindered by the low temperature gradient between the interfaces. The potential of an improved contact simply cannot be utilized which leads to similar results when assuming an HTC that is lower than the physically present one.

Development of the HTC Upon Initial Contact Pressure Build-up

When comparing the Mikić and the parametrized model with focus on the initial HTC in terms of a pressureless contact (cf. Figure 24), a different behavior as a result of the predetermined model assumptions can be seen. The parametrized model starts with an initial HTC value of 1000 W/m²K for pressureless contact followed by a strong increase to 4000 W/m²K at around 4 MPa. The predetermined initial HTC ${h}_{init\text{\_}core}$ used in the Mikić model is assumed to be at 3500 W/m²K. Still when evaluating the Mikić HTC curves in Figure 24, it can be seen that the pressure dependent development is not always quasi linear, but for the 100 and 200 °C evaluation a short gradual increase of the curves can be seen when pressure starts to build up initially. The 30 °C evaluation lacks a description of the HTC development in the first moments of pressurized contact due to the initially recorded pressure showing a decrease due to a not yet stabilized measurement. So, a gradual increase also is the case for the Mikić model even when being less pronounced and at other values than for the parametrized model. It must be kept in mind though that the Mikić model represents an empiric expression meant to describe the heat transfer coefficient for pressurized contacts. An evaluation of a pressureless condition lies beyond the scope of its intended utilization. Therefore, a stronger drop to a lower HTC than the assumed 3500 W/m²K, as it is the case for the parametrized model, could be possible. Furthermore Figure 25 displays the respective HTCs for the contact pressure conditions for an oil temperature set at 30 °C as a function of the casting temperature. Here, it can be seen that the predicted HTC of the Mikić and parametrized model coincide once the parametrized model has finished its initial build-up. Further deviations below 400 °C are the cause of the already discussed apparent limit in HTC due to reduced temperature gradients between the casting and the inner core the parametrized model tries to reproduce. This way when evaluating the HTC as function of the casting temperature, it becomes clear that the Mikić and parametrized model lead to HTC developments that are more conforming than implied by the plot over pressure as displayed in Figure 24.

Figure 25

HTC plotted over casting temperature at the core interface for experimental and simulated models at 30 °C oil tempering.

Conclusion

The current experimental setup was able to effectively vary the die temperature and record the cooling curves at different positions in casting, outer die and inner core which made the extrapolation of the interface temperatures possible. Furthermore, the development of the air gap width at the outer die/casting interface and the contact pressure developed at the inner core/casting interface was successfully measured. Based on the thermal conductivity of the air gap and the measured temperature gradients, an HTC model was fitted to the experimental data. The Mikić model was applied to describe the contact pressure dependence of the HTC. For the heat transfer through the air-filled gap between casting and outer die, Fourier’s law was used to determine the HTC at this interface. A limit for the calculated air gap HTC had to be established though as the asymptotic behavior of the Fourier’s law for very small gaps leads to unrealistically high HTCs. For this reason, the HTC calculated for coherence temperature was used as the maximum limit for air gap HTC. In addition to the experimental evaluation being able to successfully describe the respective HTC development, it also could be shown that an increased oil tempering level leads to an increase in heat transfer coefficient. In relation to the absolute values present this increase is marginally low though in the range of 30 to 200 °C oil temperature control and this most probably is valid even beyond that range.

The cooling curves predicted by the inverse and parametrized HTC models have a good qualitative agreement with the experimental measurements. In combination with the solidification model driven by the phase field simulation-based, temperature-dependent fraction solid data, the results for the critical phase change regime of the process yields a high accordance between simulated and measured temperatures. Thus, the transfer from microstructural data delivered by phase field simulation into the macroscopic process simulation proves to be a valid approach for providing a basis for the modeling of the solidification phenomena of a eutectic alloy. When comparing the HTC development for both simulation models, the heat transfer due to air gap formation is described in a very similar way and the inverse model even validates assumptions for fitting parameters in the parametrized model. For a contact condition where heat is being transferred via air over a gap between two interfaces, a purely temperature-dependent description of the process was found to be sufficient. A good qualitative agreement between the experiment and the two suggested simulation models for the gap formation dependent HTC was achieved, and in addition a quantitative agreement was also revealed at low casting temperatures.

While the precise representation of the temperature development in the first stages of the process is given for both HTC models, a deviation between measured and simulated cooling curves occurs later on in the process. It is the parametrized model that manages to maintain a cooling behavior very close to the measured temperatures for a longer period of time. The reason for this lies within its capability of describing the phenomena of the pressurized contact. Not only does pressure represent a parameter very sensible to location and time, but if applied at a contact of two surfaces its amount also strongly influences the heat transfer. This behavior is attributed to real surfaces being microscopically rough and thus establishing contact with each other across certain asperities only. As these asperities form the contact spots with just a fraction of the nominal contact area, an applied contact pressure is distributed over a comparatively small area. Elastic or plastic deformations of the surface asperities are the consequence leading to an increased contact area, and thus less thermal resistance, i.e., an increase in HTC. This leads to the conclusion that a purely temperature-dependentdescription, as applied for the inverse model, is insufficient for describing a pressurized contact condition due to the lack of a direct correlation between pressure and local temperature.

Outlook

Being able to use the pressure data resulting from the thermomechanical stress calculations turns out to be a benefit for increasing the precision of an HTC model. It must be kept in mind though that the benefit of having the additional data a coupled thermomechanical simulation provides in comparison with a purely thermal or non-coupled simulation also leads to an increase in modeling complexity and computing times. There also still are unresolved issues to this kind of simulation like deviation in outer gap formation due to the simulations not being able to reproduce the effects of a thin load-bearing chill due to limitations in meshing resolution. Both HTC models also suffer from certain limitations. The inverse model always needs an extensive experimental data basis in order to be applied which might not be present. The parametrized model, while being quite independent from extensive experimental data, relies on certain parameters that might have to be adapted when using the model for a different process. Therefore, the next step in HTC model development could be the creation of a purely physical HTC model relying solely on physical equations and material parameters.

Further investigations and model improvements for the experimental evaluation are planned for future work. In addition, the effective heat transfer coefficients are to be determined inversely with the help of numerical optimization algorithms. This method improves the data basis and also allows the coupling and assignment to the individual mechanisms described above. The development of a model for the further determination of the influence of the mold temperature is also planned for future work.