1 Introduction

1.1 Scientific background

In the last few decades, human activities concerning geo-reservoirs, including natural gas production, water waste disposal (Hincks et al. 2018), hydraulic fracturing (Davies et al. 2013), CO2 storage, and geothermal energy production (Grünthal 2014), have caused induced seismicity. The mechanism is somewhat similar to natural earthquakes. Many earthquake events and earthquake sequences are attributed to injection or extraction operations (Ellsworth 2013). For example, in the Groningen gas field in the Netherlands, induced seismic events have been reported to have increased in frequency and magnitude over time due to gas extraction (Lele et al. 2016). The largest event, M = 3.6 at the center of the gas field, was recorded in 2012. An earthquake of magnitude 5.5 in Pohang, South Korea, which occurred during the site development of the geothermal project, was provoked by the injection process (Grigoli et al. 2018).

Multiple studies have been conducted to better understand the causes of induced seismicity (Keranen and Weingarten 2018; Raleigh et al. 1976; Zoback and Gorelick 2012). Increasing the fluid pressure reduces the effective normal stress resolved on the fault plane. As a result, the shear resistance is reduced, allowing slip under tectonic shear stresses in the field (Kisslinger 1976; Segall 1989). Also, increasing the pore pressure during injection for hydraulic fracturing purposes can create fractures causing seismicity (Grigoli et al. 2018). Moreover, there is convincing evidence that a decline in the pore pressure (production) can induce seismicity in gas fields (Segall and Fitzgerald 1998). A decrease in fluid pressures causes poroelastic changes and differential compaction, perturbing the stress path around the reservoir that, under appropriate circumstances, can lead to earthquakes.

While most of the mechanisms that cause induced seismic events are well understood, few studies have focused on mitigating and reducing fluid-induced seismicity. For example, the aim can be to reduce the magnitude of the largest events triggered by fluid injection. Thus, each field must be assessed individually to determine the maximum allowable magnitude (Hofmann et al. 2018; Westaway and Younger 2014). Another possibility can be replacing or compensating the largest magnitude event with a group of smaller events (Yoon et al. 2014). Regarding this goal, injection rate, protocol, volume, and temperature can play an important role (Hofmann et al. 2018; Zang et al. 2019). Proposed solutions to mitigate and avoid larger induced earthquakes in numerical and experimental studies have been formulated that the seismic response of cyclic fluid injection differs from the response to monotonic injection, thereby reducing induced seismicity (Patel et al. 2017; Yoon et al. 2014; Zang et al. 2013). Zang et al. (2019) concluded that by using cyclic injection (hydraulic fatigue), the magnitude of the largest induced seismic event can be reduced. Also, a seismic traffic light system is sometimes adopted in which injection rates and pressures are modified based on predefined thresholds of recorded seismic magnitudes or other factors (Baisch et al. 2019; Bommer et al. 2015; Hofmann et al. 2018).

The few existing studies into the mitigation of induced seismicity have focused on low-porosity or non-porous rocks and not on high-porosity rocks (Ji et al. 2021a; b; Niemz et al. 2020; Zang et al. 2019). Furthermore, most studies focus on mechanical evolution rather than seismicity patterns. In this study, the differences in seismicity patterns in high-porosity Red Felser sandstone samples are studied by subjecting them to three different stress patterns and rates. In particular, we focus on the energy, maximum amplitude, amplitude-frequency distribution of seismicity events, and failure pattern under different stress patterns and rates.

1.2 Stress pattern and rate effect

Cyclic loading may cause different forms of mechanical behaviour in the rock material (Fuenkajorn and Phueakphum 2010; Peng et al. 2020; Stavrogin and Tarasov 2001). Rocks experience accumulation of damage, cycle after cycle, which, depending on the stress regime (deformation regime), can be in the form of compaction, dilation, and microcracking (Eberhardt et al. 1999; Hernandez et al. 2022; Pijnenburg et al. 2019). Damage accumulation can alter elastic parameters and the failure pattern of the rocks. Few studies confirmed that, in contrast with a monotonic injection or loading pattern that produces a large extensive planar fracture, cyclic patterns induce a more complex fracture pattern (Cerfontaine and Collin 2018; Erarslan 2016; Niemz et al. 2020; Yin et al. 2023; Zang et al. 2019). Also, the amplitude and waveform of cycles influences the mechanical behaviour (Fuenkajorn and Phueakphum 2010; Liu and Dai 2021; Ma et al. 2013).

In addition to stress patterns, stress rate can significantly influence the deformation behavior of the rock. The stress-rate dependence of failure mechanisms in rock can be attributed to the rate-dependent behaviour of microcrack and fractures in the rock medium (Fuenkajorn et al. 2012; Li and Xia 2000). Fracture toughness is another parameter that can be changed by changing the stress rate (Zhang and Zhao 2013). Dynamic fracture toughness and crack propagation velocities increase with loading rates, while static fracture toughness remains constant (Swanson 1984; Zhang et al. 1999). According to Imani et al. (2017), the number of tensile and shear fractures increases simultaneously as the strain rate increases; while the number of shear fractures increases more than the number of tensile fractures. However, most of the studies mentioned above on the effect of stress patterns and rates are concentrated on the mechanical evolution compared to the acoustic and seismicity response.

2 Experimental methodology

2.1 Starting sample and apparatus

The Rotliegend formation was formed during the early Permian, and consists of fluvial, sandstones, and shales. The Red Felser sandstone used in our experiments was obtained from the Palatine forest near Kaiserslautern, Germany, as part of the Rotliegend formation (van Uijen 2013). The Red Felser is a homogeneous and isotropic sandstone at the scale of a large block (several decimetres in size). Cylindrical Red Felser sandstones used in this study were obtained from the same large block by diamond drilling. They were cut into cylinders of 30 mm and 75mm in diameter and length, respectively. Multiple cylindrical samples of the Red Felser were subjected to preliminary tests to extract the basic mechanical and physical properties of the samples. The connected porosity of the samples was determined using a gas expansion (Helium) pycnometer to be 23% ± 0.5%. We selected samples with porosity falling within the range of the average porosity ± 1% standard deviation for the tests. This selection was made to ensure optimal reproducibility among the samples. In addition, we performed three repeat experiments with each stress pattern to ensure that results are not affected by some other factors. Table 1 summarizes the key parameters of the Red Felser sandstone, including physical and mechanical properties.

Table 1 Key mechanical and physical parameters of the Red Felser sandstone
Full size table

2.2 Loading system and AE data acquisition system

Uniaxial compression tests were performed using a servo-control loading machine manufactured by the TU Delft. The loading system can provide static and dynamic loading conditions with a maximum capacity of 500 kN (Fig. 1). A Richter acoustic emission system was used to record and detect microseismic activities during various stress patterns and rates (Fig. 1). The Richter is a multi-purpose, multi-channel, 16-bit ADC resolution data acquisition. The system provides simultaneous and synchronous sampling of all input channels. Using the ExStream software, continuous waveforms were meticulously recorded at a sampling rate of 2 MHz, with an input impedance of 50 Ω. While the ExStream software of the Richter system records the acoustic emission data, the raw continuous waveform data is processed and managed by the Insite Seismic Processor software.

Fig. 1
figure 1

Schematic illustration of the loading and acoustic emission system. (1) AE sensor (11 sensors were used); (2) radial strain gauge; (3) rock sample embedded in the loading machine; and (4) Linear Variable Differential Transformer (LVDT) for measuring axial deformation

Full size image

The continuous waveform data is converted to single waveforms for further analysis using a predefined trigger logic. An event is recorded if five or more transducers exceed a voltage threshold of about 1mV within a time window of 480 μs and a sampling rate of 2 MHz. The amplitude threshold was carefully established at 1mV, employing the widely accepted 'pencil lead break test (PLB)’ method, as used in previous investigations (de Almeida et al. 2014; Grosse and Ohtsu 2008). This threshold was selected, taking into account the diverse sources of background noise prevalent in the laboratory environment. Also, a thin layer of acoustic coupling agent was used between the sensors and the rock surface to enhance the quality of signal recording (Bi et al. 2023). Each test was conducted using an array of 11 AE transducers, and an identical sensor configuration was consistently employed for all tests (Fig. 1). To maintain data integrity, any initial recorded events, attributed to the settling of loading plates and friction between the loading piston and the rock sample at the onset of the loading process, were excluded from the dataset.

2.3 Experimental procedure

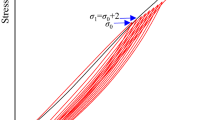
Three different stress schemes (six schemes considering different rates) were used in this study, which are shown in Fig. 2: (1) A monotonic stress scheme, equivalent to a conventional uniaxial test, (2) a cyclic recursive (CR) stress scheme in which, after each cycle, stress is reduced to 5MPa as a reference stress level, and stress increases 5MPa per cycle up to achieving the final strength of the sample, (3) a cyclic progressive (CP) stress scheme in which, unlike the CR scheme, stress is not reduced to a reference stress level and instead is reduced with an amount of 5 MPa, and similar to CR, is increased with 5 MPa in each for following cycle. In addition, three different stress rates (displacement control) were applied for the monotonic and cyclic recursive stress patterns: low, medium, and high rates that are \({10}^{-4} \mathrm{mm}/\mathrm{s}\), \({5\times 10}^{-4} \mathrm{mm}/\mathrm{s}\), and \({5\times 10}^{-3} \mathrm{mm}/\mathrm{s}\), respectively. Following ISRM and ASTM recommendations, we selected the medium strain rate aiming for sample failure within 2–15 min (Fairhurst and Hudson 1999; Standard 2014). We used a standard strain rate of \({5\times 10}^{-4} \mathrm{mm}/\mathrm{s}\), causing Red Felser sandstone to fail within 10 min. Additionally, we tested rates ten times faster and five times slower to explore the effect of stress rates on seismicity evolution. The cyclic stress was applied approximately within the elastic (linear) zone of the stress–strain plot, which means between 10–85% of the final strength of the sample. Concerning the final strength, elastic zone, and cyclic pattern (stress step of 5 MPa), seven cycles were applied before the failure of the sample. Therefore, the upper limit of the last stress cycle for both cyclic recursive and cyclic progressive was approximately 85% of the final strength (yield zone) of the Red Felser sandstone under UCS test conditions. The naming of the experiments is based on the stress pattern and rate applied (cyclic recursive high rate is thus named CRH).

Fig. 2
figure 2

Schematic illustration of three stress schemes: from left to right monotonic, cyclic recursive, and cyclic progressive

Full size image

2.4 Acoustic emission monitoring

2.4.1 AE energy

The true AE energy is proportional to the area beneath the acoustic emission waveform. Electrical signals are assumed to have an energy proportional to the square of their voltage (Eq. 1), (Grosse and Ohtsu 2008; Khazaei et al. 2015; Naderloo et al. 2019).

$${E}_{i}= \frac{1}{R}{\int }_{{t}_{0}}^{{t}_{1}}{V}_{i}{(t)}^{2}dt,$$
(1)

where \({V}_{i}\) is the voltage of each trace point that exceeds the threshold amplitude; \({t}_{0}\) and \({t}_{i}\) are the starting and ending times of the transient voltage record; and R is equal to 50 Ω representing the input impedance of the AE system. By using Eq. (1), the AE energy was calculated for the entire recorded signals of each stress pattern.

2.4.2 b-value analysis (frequency-magnitude distribution)

According to earthquake seismology, the occurrence frequency of events with large magnitudes is lower than events with smaller magnitudes. This concept can be described or quantified in terms of a magnitude-frequency relationship proposed by Gutenberg and Richter (Eq. 2) (Gutenberg and Richter 1944; Lombardi 2003):

$${log}_{10}N=a-b{M}_{l,}$$
(2)

where N is the number of events with a magnitude larger than or equal to \({M}_{l}\), and a and b are empirical constants. The b value is the negative slope of the log frequency-magnitude graph. A high b value implies a high number of small events relative to large ones, which is desirable for seismicity mitigation (Lei et al. 2018). The maximum-likelihood technique is one of the most appropriate methods to estimate the b-value (Woessner and Wiemer 2005):

$$b= \frac{{log}_{10}(e)}{\left[\left(M\right)-({M}_{c}- \frac{{\Delta M}_{bin}}{2})\right]},$$
(3)

where \(M\) is the mean magnitude of the sample, \({\Delta M}_{bin}\) is the binning width of the catalog, and \({M}_{c}\) is defined as the minimum magnitude in which 100% of the events in a space–time volume are detected. (Aki 1965; Kurz et al. 2006; Liu et al. 2020; Lockner 1993; Woessner and Wiemer 2005).

Based on the discussion above, the b-value was estimated for each stress pattern and rate. The b-value was calculated for the entire AE events of each experiments after filtering the events below the threshold and early events from the adjustment of loading pistons. The number of events (cluster) required to calculate the b-value meets the condition of having more than 200 events (Amorese et al. 2010; Roberts et al. 2015).

2.4.3 AE parameters analysis (RA and AF value)

Crack growth has been observed to have a different acoustic emission signature depending on the crack growth mode (shear, tensile, and mixed; see Fig. 3). The AE signals with short rise times (the time needed to achieve maximum amplitude after the first arrival) and high frequencies are characteristics of tensile crack mode, which involves opposing movement of crack surfaces (Fig. 3b). In contrast, longer rise time (RT) and low-frequency waveforms are attributed to shear-type of cracks (Fig. 3c) (Aggelis 2011; Niu et al. 2020). The shear waveforms are slower, and the maximum peak of the waveform takes longer to achieve after the initial longitudinal arrivals (Fig. 3c) (Ohno and Ohtsu 2010).

Fig. 3
figure 3

Crack classification the AF and RA value: a Relationship between the Rise Angle (RA) and Average Frequency (AF) value; b The tensile event with short rise time and duration; c shear event with long rise time and duration (Zhu et al. 2022)

Full size image

The cracking mode influences two critical parameters: the average frequency (AF), which is the ratio of the number of threshold crossings and the signal length, and the rise angle (RA), which is the rise time divided by the maximum amplitude. As illustrated in Fig. 3a, the RA value and AF ratio can distinguish the crack modes as shear, mixed, and tensile by considering an empirical transition line (Aggelis 2011). This method can be considered a relative classification method due to the assumptions for determining the transition line, the amplitude threshold selection, and the limitation of AE recording devices for triggering. The transition line is mainly derived from an empirical relationship that can be different for materials. According to Zhang and Deng (2020), the optimal ratio of the RA and the AF values for brittle rock is approximately between 1:100 and 1:500 under compressional loading conditions. Various studies have employed diverse approaches, including clustering, Gaussian mixture modeling, and kernel density estimation (KDE) function, to determine optimal transition lines and crack classification (Lian et al. 2023). Nonetheless, the most dependable approach involves applying these methods to test the same material under varying loading conditions, such as shearing, tensile, and compression (J. Li et al. 2022; Lian et al. 2023; Ma and Wu 2023). Since the dominant cracking mode can play an essential role in fracturing, we aim to investigate the possible effects of stress pattern and rate on the distribution of AE events in AF-RA space.

3 Experimental results and analysis

3.1 AE events pattern

Figure 4 shows the typical stress-time, the amplitude of AE events, and cumulative AE for the three different stress schemes at the same rate. During loading with the monotonic medium rate (MM) stress pattern, AE events (clusters) were detected as of approximately 80% of the final strength, typically known as the yield zone (Fig. 4a). However, for cyclic stress schemes, either cyclic recursive medium rate (CRM) or cyclic regressive medium rate (CPM), AE events were observed from approximately 33% of the final strength, i.e., within the fully elastic region. Additionally, the Kaiser effect can be observed after the second cycle during both CRM and CPM experiments (Fig. 4b, c). The Kaiser effect is defined as the absence of detectable acoustic emissions until the previously applied stress level is exceeded (Lavrov 2003). During the reloading phase of each cycle, AE events appear when the previous maximum stress level is exceeded, as shown in Fig. 4b, c.

Fig. 4
figure 4

Typical stress-time, AE amplitude and cumulative AE events for the three different stress schemes at the same rate (medium rate). a monotonic stress (MM); b cyclic recursive (CRM); c cyclic progressive (CPM). Cumulative AE is denoted by the solid black line, and the memory effect is denoted by black dots

Full size image

After the fifth cycle in both the CRM and CPM stress patterns, the AE events start to appear before achieving the maximum previous stress (see Fig. 4b, c, points A1-A3 and points B1-B3, which shows the turning point of the cumulative curve of AE). This phenomenon implies a hysteric behaviour or memory effect in the Red Felser sandstone (Zhang et al. 2017). Considering the CRM stress pattern, the axial inelastic deformation accumulates cycle after cycle (Fig. 5b). At the end of the last cycle, on average, 33% of the total deformation is inelastic. Total inelastic deformation was calculated from the stress–strain curves shown in Fig. 5b. The accumulation of inelastic deformation within the elastic zone occurs through compaction and grain (micro-cracks) sliding (Pijnenburg et al. 2019). Therefore, the cyclic stress pattern induces inelastic deformation, which we interpret as the reason for observation of the Kaiser effect and the appearance of the memory effect.

Fig. 5
figure 5

a Average total number of events from three different stress patterns with the same rate (medium rate); b Calculation of the inelastic strain from the stress–strain data of the CRM test

Full size image

Figure 5a shows the average total number of AE events for each stress scheme at the same rate (medium rate), in which cyclic stress patterns, especially CPM, are characterized by a high number of total generated events. The high number of total events can be due to the induced damage (inelastic deformation) and hysteresis from cyclic stress. However, the question is, can we replace the large events with small events using cyclic stress patterns? To answer this question, we will analyse microseismicity in terms of maximum amplitude, maximum energy, and magnitude-frequency distribution (b-value).

3.2 Amplitude and radiated AE energy

Reducing the maximum magnitude and seismic energy radiation is desirable from a seismicity mitigation perspective. Figure 6 shows the recorded maximum AE amplitude for each stress pattern and rate versus final strength (breakdown stress). Although there is no strong correlation between maximum AE amplitude and final strength, one trend can be observed by increasing final strength; the maximum AE amplitude increases as well. In Fig. 6, red and grey dashed lines indicate the average values of the maximum AE amplitudes obtained from the monotonic and cyclic tests. The average amplitude for cyclic stress patterns is 20% lower than monotonic loadings (grey dashed line in Fig. 6). In general, a high recorded maximum AE amplitude characterizes samples subjected to a monotonic stress pattern. The CRL pattern results in a 74% and 30% decrease in maximum amplitude and final strength, respectively, compared to the high monotonic rate (MH).

Fig. 6
figure 6

The maximum observed amplitude of AE events and final strength for each stress pattern and rate. Red and grey dashed lines indicate average values of amplitude for monotonic and cyclic tests, respectively

Full size image

Figure 7 indicates the effect of stress rate on the maximum radiated AE energy and final strength (breakdown stress). The horizontal and vertical dotted lines show the average maximum radiated AE energy and the average final strength for each stress rate. The stress rate has a significant effect on final strength. By increasing the stress rate from low to medium to high, the final strength increases on average by 33% and 10%, respectively (Fig. 7). The stress rate also significantly affects the maximum radiated AE energy. As is shown in Fig. 7, the maximum radiated AE energy for experiments with a low-stress rate (violet markers) is very small compared to samples subjected to a high-stress rate (red markers).

Fig. 7
figure 7

The maximum radiated AE energy versus final strength for different stress rates. The horizontal and vertical dotted lines indicate the average maximum radiated AE energy, and the average final strength, for each stress rate

Full size image

3.3 b-value analysis (frequency-amplitude distribution)

Figure 8 shows the frequency-amplitude distributions of the events for different stress patterns. Considering three different stress patterns with the same rate (medium rate), the CPM pattern has an increased number of small events relative to the large ones as indicated by a high b-value (see Fig. 8). The MM and CRM patterns lead to the generation of more large events and have a lower b-value. A detailed analysis of the amplitude distribution is provided in Fig. 9. The CPM pattern is characterized by the highest frequency of low amplitude events (Fig. 9e), while the MM pattern shows a low frequency in the zone with small amplitude events (Fig. 9a). Focusing on the tail of the frequency-amplitude distributions shows that the frequencies of events with medium and large amplitudes for the CRM and MM are higher than to frequency for the CPM pattern (Fig. 9b, d, and f). Additionally, the tail of the distribution for the MM pattern ends at a high amplitude (80 mv) as shown by the arrow in Fig. 9b. While the frequency-amplitude distribution for the CRM pattern shows a high frequency of small events compared to the MM, the estimated b-value for both patterns is approximately equal. In other words, the CRM pattern shows an increased number of both small and large events.

Fig. 8
figure 8

The frequency-amplitude distributions of the events for three types of stress patterns. The bottom left plus sign indicates an increase in the number of small events, and the minus sign indicates an increase in the number of large-amplitude events. Thus, A high b-value corresponds to observations of more events toward the small amplitudes relative to the higher amplitudes resulting in a steeper gradient

Full size image
Fig. 9
figure 9

A comparison of AE amplitude distributions for three different stress patterns at the medium rate. Figures a, c, and e show the frequency-amplitude distribution for MM, CRM, and CPM, respectively. Figures b, d, and f show the tails of the frequency-amplitude distributions from 10 to 82 mv (red dotted box) for MM, CRM, and CPM, respectively

Full size image

3.4 Mechanical evolution

Cyclic loading patterns can influence the fracturing process by changing the fracture process zone, accumulating inelastic deformation, and adding hysteresis behaviour (Eberhardt et al. 1999; Erarslan 2016; Milad Naderloo et al. 2023; Pijnenburg et al. 2019). As shown in Fig. 10, samples subjected to cyclic stress display more complex fracture patterns and disintegration, whereas samples with monotonic experiments display one large fracture and less disintegration (decohesion). This difference in failure pattern can be due to the accumulation of the damage cycle after cycle and creating more possible routes for fracture to propagate. In addition to the stress pattern, the stress rate also clearly affects the fracture pattern of the samples. Experiments at low-stress rates are characterized by intense disintegration and crushing (Fig. 11), especially for low-rate cyclic cases (CRL). Thus, combining cyclic stress patterns and low-stress rates leads to more intense disintegration and powdering of the sample. Besides, The stress rate significantly affects final strength, and applying the high-stress rate increases the average final strength by 33% and 10% in comparison to low and medium rates, respectively (see the final strength (\({\sigma }_{c}\)) for each test in Table 2).

Fig. 10
figure 10

Illustration of fracture patterns in the samples after subjecting them to cyclic and monotonic stress patterns

Full size image
Fig. 11
figure 11

Disintegration and fragmentation in samples subjected to low stress rate after final failure: a Cyclic recursive low rate (CRL); b Monotonic low rate (ML)

Full size image
Table 2 Summary of the experiments and important parameters based on different stress patterns and rates
Full size table

3.5 AE signal analysis (stress pattern and rate effect)

As mentioned before, we can obtain information about the failure and cracking mode by using the RA and AF parameters. Note that the transition line depends on the material and type of test. We used two transition lines (AF = 100 × RA and AF = 500 × RA) from the study conducted by Zhang and Deng. (2020) to investigate event distribution from different stress patterns and rates in the AF-RA space. In Fig. 12, AF versus RA is depicted with two transition lines for the experiments from three different stress rates. Stress rate significantly affects the crack classification or event distribution in the AF-RA space. Based on Fig. 12, events from samples subjected to low-stress rates are concentrated on the side with higher AF and lower RA, and by increasing the stress rate, events are more spread to the zone with low AF and high RA values (shear zone and below transition lines). This agrees with the study by Imani et al. (2017). They observed that tensile and shear fractures increase with increasing strain rate; however, the number of shear fractures increases more than the number of tensile fractures. Also, Liang et al. (2023) showed that the contribution of shear failure increases with increasing the strain rate.

Fig. 12
figure 12

Plotting AF versus RA with two transition lines for cyclic recursive experiments at three different rates. The grey and black lines represent the transition lines corresponding to AF values of 100 × RA and 500 × RA, respectively

Full size image

Figure 13b, d, and f illustrate the AF-RA density map for three different stress rates. To create the density maps (Figs. 13 and 14), we utilized a 2D histogram-based density estimation with a predetermined number of bins (Eilers and Goeman 2004). Following the density estimation, we employed a Kernel smoothing function to assign weights to data points based on their proximity to each point of interest. These weights are determined by the distance between data points and the point of interest, with closer points receiving higher weights. As shown in Fig. 13b, d, and f the maximum density zone moves towards lower AF values with increasing stress rates. Additionally, an extension of events toward a high RA zone can be observed for medium and high-stress rate cases. Alongside density maps, 3D plots were generated by combining the energy of events with the AF-RA diagram. The low-stress rate case shows the occurrence of low energy events concentrated in the high AF and low RA regions (Fig. 13e, f). Samples subjected to medium and high-stress rates show scattered high-energy events in AF-RA space (Fig. 13a–d). Therefore, increasing the stress rate generates high rise angle and high energy events.

Fig. 13
figure 13

AF-RA density and 3D plots for three different stress rates including events energy; a and b High rate; c and d Medium rate; and e and f Low rate

Full size image
Fig. 14
figure 14

Density map distribution of events in AF-RA space for three different stress schemes with medium rate; Cyclic progressive (CPM); Cyclic recursive (CRM); and Monotonic (MM))

Full size image

Moreover, AF-RA space density maps were generated for the samples subjected to different stress patterns but at the same stress rate (Fig. 14). Events from samples subjected to the CPM stress pattern are more concentrated in the high AF zone than those from the other stress patterns. The AF-RA patterns for the MM and CRM stress schemes are approximately similar (Fig. 14). Therefore, stress patterns, and especially stress rate, appear to influence fracturing mode and consequently signal properties of AE events.

3.6 Interpretation and discussion

In recent years, the interest into controlled adjustment of injection operations for different purposes, such as geothermal projects, hydraulic fracturing, and temporal energy storage projects, is increasing. The main goals are mitigating induced seismicity and increasing injection efficiency (Patel et al. 2017; Zang et al. 2013). Different behaviour in seismicity and fracturing patterns due to different stress rates and cyclic schemes in our experiments may provide more information to adjust injection operations to large‐scale hydraulic stimulation and traffic light systems for subsurface-related projects (Hofmann et al. 2018).

3.7 Effect of stress pattern

Patel et al. (2017) and Zhuang et al. (2020) reported an increase in the total number of AE events using cyclic injection. We also observed an increase in the total number of AE events for samples subjected to medium rate cyclic recursive (CRM) and the cyclic progressive (CPM) stress patterns compared to the medium rate monotonic (MM) stress pattern (Fig. 5a). The details of seismic responses under different stress patterns merit further discussion.

First, from a mitigation perspective, reducing the amplitude (magnitude) of the biggest event is important. Zhuang et al. (2020) observed a reduction in the largest event (maximum amplitude) using a cyclic progressive injection pattern. In general, in the present study, samples subjected to cyclic stress patterns are characterized by a lower maximum amplitude (Fig. 6). The lowest maximum AE amplitude and final strength are attributed to the low-rate cyclic recursive stress pattern (CRL). These differences in maximum recorded amplitude can be related to mechanical and failure responses under different stress patterns. Recent experiments using the hydraulic fatigue concept showed that fractures resulting from the continuous injection are elongated fracture planes with stable orientations, while cyclic progressive injection induces a more complex fracture pattern with branching (Niemz et al. 2020; Yin et al. 2023; Zang et al. 2000, 2013). Also, many studies confirmed the differences between the Fracture Process Zone (FPZ) formed during monotonic and cyclic mechanical loading (Cerfontaine and Collin 2018; Erarslan 2016; Liu et al. 2017). In the present study (Fig. 10), samples subjected to cyclic stress displayed more complex fracture patterns and disintegration, whereas samples with monotonic experiments displayed large fractures and less disintegration (decohesion). This observation is similar to those from earlier studies. Although we applied a cyclic pattern within the so-called “fully elastic zone”, approximately 33% of inelastic strain was captured at the end of the last cycle for the CR experiments (Fig. 5b). Pijnenburg et al. (2019) observed inelastic deformation within the fully elastic zone by performing a cyclic triaxial experiment on the Slochteren sandstone. They showed that inelastic deformation within the elastic zone is due to the intergranular normal and/or shear displacements, squeezing clay films at grain contacts, and damage closure from the early loading stage. Hence, it can be inferred that the seismic energy is released through many small events and reduces the maximum induced magnitude. In other words, for cyclic stress cases, the fracture plane propagates through a rock volume that previously has experienced inelastic damage and micro-fracturing. Thus, less fracture energy is required, and less AE energy is radiated (Zang et al. 2019).

Also, in our experience, seismicity mitigation cannot be achieved by just decreasing either maximum magnitude or energy. The amplitude (magnitude) distribution obtained from the entire experiment is important. Niemz et al. (2020) performed a mine-scale experiment both continuous and cyclic injection. They concluded that the cyclic progressive pattern is characterized by a lower maximum magnitude and significantly larger b-values. A comparison of the frequency–amplitude distributions of the AE events from our experiments showed that there are three ranges of b-value (Table 2); (1) lower range (b-value ≤ 2.1), medium range (2.1 < b-value < 2.5), and (2) higher range (2.5 ≤ b-value). The seismicity induced by the cyclic progressive medium rate (CPM) has an increased number of small events relative to the large ones, indicating a high b-value (Figs. 8 and 9e). All estimated b-values from the CPM pattern are categorized as a high-range b-value group (2.5 ≤ b-value), which on average, shows higher values than the samples subjected to the MM and CRM patterns at the medium rate (see Table 2).

Although both CRM and CPM stress patterns result in a high total number of events and lower maximum amplitudes, however; estimated b-values to the CRM pattern are lower than those to the CPM pattern. Compared to the CPM pattern, cycles in the CRM pattern have a higher amplitude and also are reduced down to reference stress (5 MPa), which causes compaction and closure of microcracks. Compaction and closure require more energy (strain) to be removed, and consequently, more large amplitude events are generated during the CRM experiments (Fig. 9c, d).

We speculate that the accumulation of inelastic deformation and micro-cracks per cycle induced by cyclic stress could reduce large events through increasing the occurrence of small events. All observations show that with the same stress rate, the CPM stress pattern results in better seismicity mitigation in terms of maximum amplitude and b-value compared to the CRM and MM patterns.

3.8 Effect of stress rate

We observed a significant effect of stress rate on seismicity and mechanical properties of samples. Decreasing the stress rate decreases the maximum radiated AE energy and final strength (Fig. 7). Besides, the stress rate significantly affected event distribution in the AF-RA space (Figs. 12 and 13). Most of the events from low-stress rate cases occur in the high AF or tensile mode zones, while events from high-stress rate cases extend into the shear zone (high RA zones). Differences in the AF-RA distribution can be also seen in the failure pattern of the samples. As shown in Fig. 11, samples subjected to a low-stress rate are characterized by intense disintegration and crushing instead of extended shear failure planes. Several studies show that by decreasing the strain/stress rate, Young’s modulus decreases, which shows that time-dependent behaviour is involved in the elastic zone (Wasantha et al. 2015; Zhang and Zhao 2013; Zhou et al. 2015). The time-dependent process can accelerate deformation and disintegration. Also, Zhao et al. (2021) showed that at low strain rates, numerous tiny fragments adhere to fractures, filling intergranular cracks with debris. Higher strain rates reduce the number of fragments, focusing fractures on grain cementation surfaces. With high loading rates, trans-granular and inter-granular cracks intersect, further reducing tiny fragments. Therefore, due to the decrease in final strength and the disintegration of grains using a low-stress rate, the possibility of an extensive shear fracture plane is low during failure. Consequently, smaller and low-energy events are generated by splitting and disintegration. The low-stress rate and cyclic recursive composition resulted in the highest b-value, which is 75% higher than the lowest b-value (Table 2). Inelastic deformation and grain disintegration induced by a combination of cyclic patterns and low-stress rates result in lower seismicity.

4 Implications for induced seismicity

Our experimental results demonstrate that applying cyclic stresses even within a fully elastic zone can help seismicity mitigation. Besides, a low-stress rate can complement a cyclic stress pattern. From a seismicity mitigation perspective, low rate and cyclic stress composition lead to a better seismicity pattern.

Increasing permeability and reaching a safe (avoiding seismicity) or target fluid pressure is crucial for hydraulic fracturing, geothermal energy production, and water waste disposal. (Hofmann et al. 2018; Ji et al. 2021a, b; Zang et al. 2019). Seismicity mitigation can be considered a balance between different parameters, including maximum magnitude, radiated energy, the total number of events, and b-value (magnitude distribution). It will be desirable to reduce maximum magnitude and energy and increase the b-value by generating more small or low-magnitude events compared to large-magnitude events. The maximum allowable magnitude depends on the local surface infrastructure and the vicinity to populated areas. One policy is replace single large-magnitude event by many low magnitudes ones (Yoon et al. 2014). Our experiments indicate that more total events were generated by applying cyclic stress patterns. As illustrated by an increase in b-value in the cyclic progressive stress pattern, this results in replacing the largest magnitudes by many low magnitudes events.

Another policy for managing seismicity management is using a traffic light system (TLS) (Bommer et al. 2015; Hofmann et al. 2018). For designing the TLS systems, the injection scheme and flow rate are important. In our current study, besides stress patterns, we investigated the effect of stress rates on seismicity patterns. According to our results, the composition of a cyclic stress scheme with a low stress rate can result in a significantly higher b-value and low maximum magnitude and energy. Therefore, results from our study may be of help to design injection protocols.

5 Conclusion

We conducted uniaxial compression tests on high porous Red Felser sandstone under different stress schemes by changing the stress pattern and rates to investigate their role on seismicity and failure. Our findings are summarized as follows:

  1. 1.

    Cyclic stress patterns and especially cyclic progressive patterns are characterized by a high number of AE events.

  2. 2.

    Generally, cyclic stress patterns lower the maximum AE amplitude, where a low-rate cyclic recursive stress pattern displays by the lowest maximum AE amplitude and final strength.

  3. 3.

    The stress rate strongly affects the maximum AE energy and final strength; by reducing the stress rate, they both decrease.

  4. 4.

    Considering the same stress rate, a medium-rate cyclic progressive stress pattern displays the highest b-value, implying an increased number of small events relative to large ones.

  5. 5.

    Stress rate remarkably affects the distribution of events in the average frequency vs. rise angle (AF-RA) space. While events from low stress rates are concentrated in the zone with high AF (above the transition line), events are more spread towards the zone with low AF and high RA values by increasing the stress rate.

  6. 6.

    An intense disintegration and powdering characterize experiments at low stress rates.