1 Introduction

The Lannigou gold deposit in Guizhou is the largest Carlin-type gold deposit in the “Golden Triangle” of Guangxi, Guizhou, and Yunnan, with a resource reserve of 126.25t, as a result of the influence of various tectonic movements, it clearly exhibits structural ore-controlling characteristics (Chen et al. 2011). According to the assessment of resource potential, just 34.16% of the area's gold resources have been identified, and there is a vast amount of gold resource exploration potential. The tectonic stress field has a strong influence on the occurrence of metallogenic processes, which is a significant controlling factor of gold mineralization (Deng et al. 2008, 2011). On the scale of the basin, the development and evolution of the basin are controlled by the tectonic stress field, and also controls the development and combination of secondary structures in the basin; The regularity of tectonic fractures and development strength, as well as the degree of rock compaction, are all controlled by the tectonic stress field, and the sealing of faults in terms of deposit scale, the ore-forming fluid migration pathways are the fractures generated by tectonic stress, and are also ore-holding spaces for ore-bearing hydrothermal fluids, which often directly control the migration and accumulation of ore-forming fluids. As a result, predicting the distribution of fractures in deposits by tectonic stress field analysis is of great significance for ore prospecting in practice (Wan et al. 1995; Zeng et al. 2013a; Jiu et al. 2013; Ju et al. 2016; Wu et al. 2017).

Although various factors, such as lithology and occurrence, affect fracture formation, the paleotectonic stress field environment has the greatest influence on the development law, morphology, and spatial distribution characteristics of fractures (Mckinnon et al. 1998; Zeng et al. 2010; Ding et al. 2012). The paleotectonic stress field inversion method is therefore widely used by researchers to predict fractures. Due to the rapid development of computer hardware and software, tectonic stress field numerical simulation to predict fractures has substantially improved, fracture prediction is now successfully accomplished utilising the numerical inversion of the tectonic stress field (Jiu et al. 2013; Zerrouki et al. 2014; Ding et al. 2016; Wu et al. 2017; Guo et al. 2019). Zeng et al. (2013a, b) estimated the fracture distribution in the region by simulating the 2D tectonic stress field of the Longmaxi Formation shale reservoir in south-east Chongqing using rock failure criteria and ANSYS software. Using the finite element method, Wang et al. (2017) numerically simulated the tectonic stress field of the Dabei gas field in the Tarim Basin, investigated the tectonic stress field's distribution law, and discussed the connection between the tectonic stress field, tectonic fractures, and natural gas productivity. Su et al. (2014) used a numerical modelling technique to invert the tectonic stress field in the studied area, and used the rock failure criterion to determine the degree of fracture development; Scholars have recently used finite element methods to redraw such large-scale simulations, to predict fracture development and distribution, as well as the Mohr–Coulomb criterion and the Griffith failure criterion (Zeng et al. 2013a, b; Jiu et al. 2013; Guo et al. 2016; Ju et al. 2016). Xue et al. (2023a, b) showed that there were significant differences in fracture and permeability in various directions under tectonic stress. However, multi-period changes are typical of the evolution of the tectonic stress field, the formation of fractures is influenced by the variations and superposition of stress fields during different tectonic evolution periods, and from a mechanical perspective, their intricacy severely limits the characteriszation and prediction of fractures. However, the superposition impact of multiple-stage tectonic stress fields was not considered in the earlier studies, which only modelled one stage of the tectonic stress field. Furthermore, the accuracy of tectonic stress field prediction is heavily dependent on the establishment of geological models, and the establishment of fine geological models must rely on the guidance and constraints of geological laws and understanding. However, due to the intricacy of 3D geological modelling, the majority of stress field simulations in earlier studies used 2D or oversimplified 3D geological models, the model cannot show the real structural shape, let alone the real contact relationship between different strata and the spatial coupling relationship between the structure and different strata, which greatly reduces the reliability of numerical simulation results and fracture prediction accuracy (Hashimoto et al. 2006; Zeng et al. 2013a; Ding et al. 2016; Ju et al. 2016; Wu et al. 2017; Liu et al. 2017; Liu et al. 2018). The numerical simulation of the tectonic stress field and the prediction of ore deposit fractures, however, are processes that result from the intersection and organic combination of geology, mechanics, and mathematics (Zeng et al. 2013b; Yang et al. 2014; Wu et al. 2017), the topic of how to construct a more realistic 3D geological model and a prediction method that takes into account the superposition effect of multi-period tectonic stress fields has sparked increased interest and created new challenges (Ding et al. 2016; Guo et al. 2016, 2019).

The Lannigou gold deposit, the object of this research, is recreated by a 3D geological model based on the GOCAD platform, after collecting significant geological and geophysical data and understanding the deposit's geological background. By combining an investigation of regional tectonic evolution history, geological interpretation, acoustic emission testing, and rock mechanics experiment, a 3D geomechanical model of the study area was created using the finite element method (FEM). The paleotectonic stress field after the Indosinian and Yanshanian movements were superimposed was simulated, and the comprehensive fracture rate parameter (Iz) is introduced in combination with the rock failure criterion to quantitatively predict the fractures distribution. This study can provide an important method for fracture prediction in the study area, and the research results have important reference value for determining new exploration targets.

2 Geological setting

2.1 Introduction to the study area

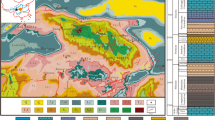
The Lannigou gold deposit is located in the first-level tectonic belt of the Qiangtang-Yangtze-South China plate, the second-level southwestern margin of the Yangtze block, the third-level Jiangnan orogenic belt, and the fourth-level Youjiang rift-foreland basin area. The deposit is located on the Laizishan anticline, and the ore-controlling fault is closely related to the anticline. The secondary folds and faults are extremely developed in the fault zone of the mining area, and there are many types of secondary folds, which are obviously related to the ore-controlling faults (Fig. 1a). Platforms and basins are two structural types that make up the Lannigou gold mining region (Fig. 1c). The platform is in the west and is made of limestone from the Carboniferous and Permian with a stable and gentle occurrence. To the east is the basin, which consists of a series of strongly folded and thrust Triassic terrigenous clastic rocks. Near the edge of the platform, especially near the syngenetic fault, the folds are very strong, often forming a large inverted complex anticline and syncline, and thrust faults are developed. Away from the edge of the platform, the intensity of folds decreases (broad and gentle folds are often formed), and the development of faults is weakened. The entire clastic rock basin area shows a very complete tectonic assemblage of folds and thrusts (Fig. 1b).

Fig. 1
figure 1

Regional geology of Lannigou gold deposit

Full size image

The region has experienced multiple periods of tectonic movements such as the Hercynian, Indosinian and Yanshanian periods, which served as the impetus for activation and migration, resulting in the formation of the Carlin-type gold deposits in the study area, the complex fault system generated by the multi-stage tectonic movement provides favorable metallogenic space for the ore body to be located, so that the ore is enriched in favorable structural parts (Chen et al. 2011). In the mining area, the Middle Triassic Xuman Formation (T2xm), Bianyang Formation (T2by), and Niluo Formation (T2nl) are the most prominent exposed strata, and the predominant lithology is terrigenous clastic turbidite from deep-water basins (Fig. 2a).

Fig. 2
figure 2

Stratigraphic histogram and tectonic evolution of the study area (Chen et al. 2011)

Full size image

The mining area mainly develops three groups of structural lines, namely NS-trending, NW-trending and NE-trending, among which NW-trending folds and thrust faults formed during orogeny control the overall structural framework of the study area (Chen et al. 2011). The near-NS-trending faults are large in scale and stable in strike extension. Together with the NW-trending folds, they control the overall tectonic framework of the study area. The overall performance is the nature of thrust faults, but many evidences show that there is a significant right-lateral-normal fault movement after the thrust, mainly the F7 fault (Luo 1993).

The tectonic deformation of the Lannigou gold deposit has mainly experienced four stages: contemporaneous rifting, orogenic compression, lithospheric extension and lateral compression of post-collisional orogenic ridge (Fig. 2b). The initial structurally weak surface for subsequent tectonic processes is provided by the contemporaneous faults created during the basin rifting (D2-T2), and became the main hydrothermal channel. The structural framework of the mining area was developed by the NW-trending structural line (fold-fault structural combination) produced during the orogenic extrusion (T3). Lateral compression during the post-collisional orogeny (J1) refolds the folds formed during the orogenic period, forming superimposed folds and reactivating the faults, resulting in the right-lateral-positive slip motion of F3, the mineral liquid settles into place along the stretched space.

2.2 Natural fractures

In this study, outcrop and downhole observation, core observation and electron microscope scanning experiment were used to study the fracture development characteristics. Shear fractures and filling fractures are commonly developed in outcrops and downholes (Fig. 3a, b); Fractures are mostly NW–SE, NE–SW, and S–N trending fractures that are substantially developed throughout the entire research area as a result of the influence of multi-stage tectonic movements (Fig. 4a). The tectonic evolution of this region and this area are well-congruent (Chen et al. 2011). Due to the composite superposition of tectonic movements, the deposit has generated a significant number of high-angle fractures, and only a few low-angle structural fractures have developed (Fig. 4b); Vertical fractures, interlayer fractures and high-angle shear fractures are the most common types of core fractures. These fractures have been partially or completely filled with minerals as calcite and quartz (Fig. 3c–e).

Fig. 3
figure 3

Fracture development characteristics in the study area

Full size image
Fig. 4
figure 4

Statistical distribution of fractures in the study area; a fracture trending, mainly NW–SE, NE–SW and S-Ntrending; b fracture dip, the main dip of the fracture is inclination

Full size image

3 The significance of the superposition principle in geological structures analysis

During the formation process of the ore deposit, the formation and evolution of its structure are often complex. Due to the influence of multiple tectonic movements, the formation of its final structure is usually the product of the superposition of multiple tectonic movements. Tectonic superposition is a general term for various phenomena in which various tectonic components of various tectonic systems interpenetrate, interfere, combine, combine and merge with each other in the same area in various ways. It is the result of two or more tectonic forces acting independently successively in the same area. This phenomenon is ubiquitous in the lithosphere, and it is a record of the multi-stage development of tectonic movements. An essential component of the study of geomechanics is the analysis and study of the tectonic superposition phenomenon. More and more studies have shown that the formation and distribution of various minerals are closely related to the phenomenon of structural superposition, which has practical significance for regional ore prospecting and geological disaster study (Qiu 1998; Wu et al. 2017; Guo et al. 2019).

The two stages of structures in the superimposed tectonic process are commonly referred to as early and late structures. A region is often affected by tectonic forces in different ways or in different directions. The stress field and strain field controlled by the tectonic force acting on the geological body will affect the formation of each stage of the structure (Hu et al. 2005). Distinct tectonic deformations correspond to different stages of mechanical activity, and the development of tectonic deformation over time is actually a mechanical process. The early structure typically experiences only one mechanical action, and it is a rather simple structure. Its tectonic deformation, strain field, and stress field are all quite simple under the influence of tectonic stress. During late tectonic deformation, rock occurrence, structure, and rock continuity and homogeneity are quite different from those in early deformation. The lithological conditions and boundary conditions will be more complex, and the tectonic force may also have changed, thus, compared to the early stage, the tectonic stress field and strain field will be more complex. The elastic mechanics superposition principle states that the deformation caused by the stress acting on the object simultaneously or successively can produce the superposition of geometric effects (Yue et al. 1987; Wu et al. 2017). Huang et al. (1996) have shown that the multi-phase deformation superposition in tectonic geology mainly includes the superposition of folds and the superposition of failure mechanical properties. The following assumptions are usually made when performing a superposition analysis: (1) The research object (such as formation, etc.) is a uniform continuous medium; (2) The deformation caused by the geological structure is mainly determined by the stress; (3) The stress field is not affected by deformation.

Because multiple-stage structures are superimposed, the spatial distribution of fractures and the nature of fracture structures have changed, multi-stage tectonic movements make fractures more developed and change their properties, which is more conducive to the migration and enrichment of ore-bearing hydrothermal fluids. At the same time, structural superposition also controls the development degree of local structural fractures and the distribution of regional fractures. Usually, a large number of fractures are generated in the superimposed parts of the structure, which greatly enhances its seepage capacity and improves the metallogenic conditions.

4 Samples and testing

To establish accurate mechanical models, 60 samples were collected from various depths in the study area for rock mechanics experiments and rock acoustic emission tests. According to “Engineering Rock Mass Test Method Standard” (GB/T50266-2013) and “Rock Physical and Mechanical Properties Test Regulations” (DZ/T 0276-2015), a standard cylinder specimen is made with a diameter of 25 mm and a height of 50 mm. The diameter error is less than 0.3 mm, and the non-parallelism of the two ends is not more than 0.05 mm. The end face should be perpendicular to the axis of the specimen, and the maximum deviation should not exceed 0.25°. The Key Laboratory of Geotechnical Engineering at Sichuan University conducted the experiment on rock mechanics, measuring the rock’s strength and elastic modulus through uniaxial compression, triaxial compression experiments are used to determine the internal friction angle and cohesive force of the rock, and the applied confining pressures are 0, 5 and 10 MPa respectively, and the accuracy is 1.0%. At the same time, the rock is made into a standard disc specimen with a diameter of 50 mm and a thickness of 25 mm, and the allowable variation of the specimen size did not exceed 5%, and the Brazilian splitting test is used to determine the rock's tensile strength. Table 1 shows the test results for the rock's mechanical parameters.

Table 1 Rock mechanical properties in the study area
Full size table

Acoustic emission experiment as an effective method for determining paleotectonic stress values (Qin et al. 2004; Zeng et al. 2013a; Wu et al. 2017), in essence macroscopic failure of rocks is the result of the accumulation of damage associated with mesoscopic cracks, the evolution of which is the most intuitive manifestation of rock failure, acoustic emission experiment is an effective tool for studying rock mesoscale failure process and damage evolution, Xue et al. (2023a, b) showed that the evolution of the meso-structure of coal bodies can be inferred from the analysis of acoustic emission signals. Thence, this method was used to determine the values of the paleotectonic stress in the research area. The test was conducted in the Key Laboratory of Geotechnical Engineering at Sichuan University, and the test cores were obtained from various strata in the research area. In the laboratory, the samples were drilled into standard cylindrical specimens with a height of 50 mm and a diameter of 25 mm. The heterogeneity of the rock will lead to the discreteness of the test results, so three samples were drilled along Y direction, the X direction and the the XY45°direction, respectively (Fig. 5), for the acoustic emission test. American Physical Acoustics Company’s PAC PCI-2 12-channel acoustic emission tester and MTS815 Flex Test GT program-controlled servo rock mechanics test system are the two pieces of test equipment used in this experiment. Table 2 shows the maximum principal stress values of various strata samples at each tectonic movement stage, and the maximum principal stress corresponding to the Kaiser effect point is shown in Fig. 6. It is obvious from the analysis of the history of regional tectonic evolution that the tectonic stress field in the studied area has gone through three stages: that is, the Indosinian, Yanshanian and Himalayan periods, of which the Indosinian movement is the most intense tectonic movement experienced in the study area (Chen 2007). It is also the main period for the formation of fault structures, which provided ore-conducting channels and ore-accommodating space for the large-scale mineralization of the Yanshan period, basically laid the framework for the current structure (Chen et al. 2007, 2011). Therefore, the numerical simulation of the paleotectonic stress field can be approximated by using the present geological model, based on the measurement results of rock acoustic emission tectonic stress in Table 2, we have reason to believe that the maximum tectonic stress in the study area in the Indosinian period is between 138.78 and 140.41 MPa, with an average value of 139.59 MPa; the maximum tectonic stress in Yanshan period is between 84.08 and 92.04 MPa, with an average value of 88.18 MPa; and the maximum tectonic stress in the Himalayan period is between 64.29 and 66.94 MPa, with an average value of 66.53 MPa.

Fig. 5
figure 5

Sampling direction of Kaiser effect specimen

Full size image
Table 2 The result of tectonic stress measurement from the acoustic emissions
Full size table
Fig. 6
figure 6

Acoustic emission paleotectonic stress measurement curve of rock sample

Full size image

5 Method simulation and fracture distribution prediction for 3D palaeotectonic stress fields

5.1 3-D multi-period paleotectonic stress field simulation

The in-situ stress field that results in tectonic movement is referred to as a “tectonic stress field” (Bayly 1992), according to the different time series, there are two types of tectonic stress fields: the present tectonic stress field and the paleotectonic stress field. The state of tectonic stress during geological history is referred as the paleotectonic stress field, the paleotectonic stress field is actually a continuous time-dependent function because of the continuity of tectonic stress. It controls how fractures are formed and distributed, and its study will help reveal the relationship between the tectonic stress field and the migration of ore-forming fluids, so as to identify possible fluid flow paths, which is of great guiding significance for deep and peripheral ore prospecting. Since the Indosinian and Yanshanian periods are the main metallogenic periods in the study area, the midas GTS software is used in this study to superimpose and analyze the Indosinian and Yanshanian tectonic stress fields.

The following five steps are primarily involved in the simulation of the paleotectonic stress field: (1) The accurate geological model establishment; (2) The acquisition of rock mechanical parameters and the establishment of mechanical models; (3) The mathematical model establishment; (4) Determine the inversion criteria and boundary conditions; (5) Paleotectonic stress field simulation and result analysis.

5.1.1 3-D geological model establishment

The premise for accurately simulating the tectonic stress field is the creation of a 3D geological entity model. The 3D geological model is a virtual deposit based on geographic coordinates and digitally displayed in 3D. The core idea is to use the 3D visualization platform to solve practical geological problems related to spatial location or attributes as a whole.

In this study, 67 measured geological profiles with an interval of 100 m are collected, a depth of 600 m on average, and 322 boreholes with a 450 m average depth, a accurate 3D geological model of the research region is created using GOCAD software after data processing, with a plane area of 3.2 km2 and a depth of 750 m, and the modelling techniques and specifics won’t be repeated (Jin et al. 2019; Mao et al. 2019), the established stratigraphic model and structural model are shown in Fig. 7.

Fig. 7
figure 7

3D geological model of stratigraphy and structure in the study area; a fault model; b stratigraphic model

Full size image

5.1.2 Determination of mechanical model

A complete conversion of the GOCAD 3D geological model into the midas GTS mechanical model is critical for accurately simulating the tectonic stress field. In this paper, the GOCAD 3D geological entity model is converted into the midas GTS geometric model through the reverse engineering of the 3D point cloud, the realization process of point cloud reverse engineering is as follows: (a) In midas GTS software, modeling is not carried out in the form of points, lines, and surfaces, but the point cloud data output from GOCAD software is used for positioning, the point cloud data is imported into midas GTS, and the RCP format is formed through data indexing; (b) Re-insert the point cloud data in RCP format into midas GTS software; (c) Image display of point cloud data in a computer, showing blurred graphics; (d) Identification of the 3D positioning coordinates of the different geological bodies (faults, strata) in the study area in midas GTS, and creation of brushes to outline the different geological bodies; (e) Remove the point cloud data, form a BIM model, and complete the reverse modeling. The geological information was fully converted into a midas GTS computational model by the above processing, which greatly improves the accuracy of the geometric model, the constitutive equations are used to describe the material characteristics of each part of the geological model, and a mechanical model based on the geological model is generated (Camac et al. 2009). On the premise of defining material properties, different types of material units are divided, including fault zones and normal deposition zones, and the rock mechanical properties and attributes are assigned to different material units. The main rock mechanical parameters considered are shown in Table 1, and the specific process of building a 3D geomechanical model is shown in Fig. 8.

Fig. 8
figure 8

Flow chart of construction of 3D geomechanical model in the study area

Full size image

The following three aspects are primarily involved in the creation of the geomechanical model: (1) Boundary conditions, which ascertain the loading approach, magnitude, and constraint situations of the geological body's boundary tectonic stress; (2) Determine the mechanical characteristics of the rocks in various strata and geological units; (3) Establish a treatment plan for the study area's fault zone, as the consequences of the simulation of the tectonic stress field will directly depend on how accurate this plan is.

5.1.2.1 Boundary conditions determination

The geological body is divided into several uniform rock bodies macroscopically. If the simulation object is defined as plastic material, it will result in unmanageable nonlinear issues in the results of the numerical simulation, and even make the simulation results seriously deviate from reality. There are typically brittle fractures in the rocks in the research area. Therefore, the geological body is defined as an elastic body for numerical simulation calculation (Wang et al. 2004). From a mechanical point of view, the model has two boundary conditions that can be used. One is the displacement boundary condition; the other is the force boundary condition. Assuming that the force on the boundary has a certain value, the force acting on the boundary of the study area can be regarded as uniformly distributed under the condition that the strength of the force on each point of the boundary cannot be determined (Guo et al. 2016). This model’s boundary forces are primarily horizontal tectonic force and vertical gravity, the density of the rock layers and the acceleration of gravity are used to compute the vertical gravity. The tectonic force is loaded in two stages, namely Indosinian and Yanshanian. To get rid of boundary effects and make applying constraints easier, the 3D geological model of the study area is embedded in a rectangular frame to ensure that horizontal tectonic forces can be applied vertically to the rectangular boundary.

Due to the strong tectonic movement in the Mesozoic Indosinian period, a large number of ore-conducting channels and ore-accommodating spaces were formed in the study area, resulting in large-scale ore-forming fluids forming in the Yanshan period (Chen et al. 2011). Therefore, we have reasons to suppose that the maximum principal stress in the Indosinian movement is 139.59 MPa based on the test results shown in Table 2, in the Yanshan movement is 88.18 MPa, and in the Himalayan movement is 66.53 MPa. Since there was no mineralization in the Himalayan period, we only reverse the Indosinian and Yanshanian periods' tectonic stress fields. The research area experiences a compressive stress field from the NE to the SW during the Indosinian movement (Chen et al. 2011). Following are the geological model’s displacement constraints: The depth is shown by the Z axis, the Y and X axes point to the NE and SE, respectively, and the vertical upward is positive. Movement in the Z direction is restricted to the model's bottom, whereas movement in the horizontal direction is possible. At the upper right and lower left boundaries, the maximum principal stress is 139.59 MPa, and in the shallow crust (depth < 4 km), we consider the ratio maximum principal stress/minimum principal stress to be 2.1 (Zeng et al. 2013a, b; Ju et al. 2016; Guo et al. 2016; Wu et al. 2017). Therefore, on the upper left and bottom right boundaries, the computed minimum principal stress (66.47 MPa) is implemented. Moreover, gravity is applied to the whole model because its top is a free surface (Fig. 9a).

Fig. 9
figure 9

Mechanical loading model of the study area; a Indosinian mechanical model; b Yanshanian mechanical model

Full size image

The research area experienced Yanshanian movement, which resulted in a more complicated geological structure and evolution of the region. The Yanshanian tectonic deformation is closely related to the Indosinian tectonic form, and has a significant inheritance and superposition relationship, the Yanshanian movement made the Indosinian structure (fault) have the inheritance of deformation enhancement. The studied area experiences a compressive stress field from the NW to the SE during the Yanshanian movement (Chen et al. 2011), the boundary conditions of it’s geological model are as follows: The depth is shown by the Z axis, the Y and X axes point to the NE and SE, respectively, and the vertical upward is positive. Movement in the Z direction is restricted to the model's bottom, whereas movement in the horizontal direction is possible. At the upper left and lower right boundaries, the maximum principal stress is 88.18 MPa, on the lower left and upper right boundaries, the computed minimum principal stress (41.99 MPa) is implemented. Moreover, gravity is applied to the whole model because its top is a free surface (Fig. 9b).

5.1.2.2 Determination of the mechanical parameters for various rock units

To convert the geological model into a mechanical model that can be used for finite element numerical simulation, it is necessary to determine the rock mechanical properties, including the elastic modulus, rock density, and Poisson's ratio, of various geological units. The main geological models in the study area include T2by, T2xm4-3, T2xm4-4, T2nl strata and faults (Fig. 7). The average mechanical parameters of rocks in different formations in the study area are determined by rock mechanics experiments (Table 1), in the numerical simulation of the tectonic stress field, the elastic modulus, compressive strength, and Poisson's ratio are utilised as the main simulation parameters.

5.1.2.3 Determine the mechanical parameters of the fault zone

It is difficult to directly obtain the mechanical characteristics of the fault unit, treating the fault and the nearby rock units as a fault zone is currently the more developed and useful treatment approach. The fault zone is defined as a soft zone, and the mechanical parameters of the rock within an appropriate range on both sides of the fault are reduced by a certain proportion, and its elastic modulus is usually 60% of the corresponding normal sedimentary layer, and the normal sedimentary layers often have smaller Poisson's ratio than fault zones, with the difference between the two values typically falling between 0.02 and 0.1 (Liu et al. 2008; Jiu et al. 2013, 2016). It should be noted that, relative to the Poisson's ratio and elastic modulus, the rock density of the fault unit is generally not much different from that of the stratigraphic unit, so the rock density of the fault unit is treated as slightly smaller than that of the stratigraphic unit (Table 3). A total of 8 faults in the NS, NW, and NE directions were chosen as the simulation objects based on the 3D geological model of the study area (Fig. 7).

Table 3 Physical and mechanical parameters of faults
Full size table

5.1.3 Mathematical model establishment

The mathematical model is built on the finite element principle, and its fundamental idea is to divide the continuous field function domain that needs to be solved into a number of units, with the units only being connected by nodes, and the function value of the unknown point inside the unit is obtained by interpolating the selected functional relationship. For this method, determining the unit division scheme and unit type in accordance with the mechanical model and the 3D geological model is of utmost importance. The accuracy of the calculation and simulation findings is typically higher the more finely the geological body unit is divided. For mesh division, a method combining automatic control and manual control is utilised to highlight the stress characteristics of important components and decrease manual errors. Taking into account the computer’s capability and the model's complexity, the established 3D geological model is divided into tetrahedral unit types, and the mathematical model contains 153,584 nodes and 888,873 grid units (Fig. 10). For the calculation results to be as accurate as possible, the fault zone is usually divided into finer meshes, while other parts are divided into coarser meshes.

Fig. 10
figure 10

3D finite element analysis model of Lannigou gold mine

Full size image

The interior points of the geological unit body will move along the three coordinate axes of space (x, y, and z) when it is subjected to tectonic action. In this process, a series of interrelationships and corresponding equations of stress, strain and displacement are involved. Here, u, v, and w which are all functions of the point's coordinates, are used to indicate each point's displacement along the three directions, and can be defined as in Eq. 1, where the displacements along the x, y, and z axes are represented by u, v, and w.

$$\left\{ {\begin{array}{*{20}l} {u = u(x,y,z)} \hfill \\ {\upsilon = \upsilon (x,y,z)} \hfill \\ {\omega = \omega (x,y,z)} \hfill \\ \end{array} } \right.$$
(1)

λxy, λyz, λzx, εx, εy, εz, are the definitions of the three shear strain components and three linear strain components of the geological unit during deformation. At the same time, the definitions of τxy, τyz, τzx, σx, σy, σz, respectively, for the three shear stress components and normal stress components at any point are presented. There is a specific relationship between the mentioned strain and displacement in accordance with the principles of elastic mechanics, and the geometric equation is shown in Eq. 2. Hence, according to Eq. 2, the relationship between nodal displacement matrix and strain can be simplified as in Eq. 3, where A is the geometric matrix, and σ is the stress matrix of the node.

$$\left\{ {\begin{array}{*{20}l} {\varepsilon_{x} = \frac{\partial u}{{\partial x}},\,\,\lambda_{xy} = \lambda_{yx} = \frac{\partial u}{{\partial y}} + \frac{\partial \upsilon }{{\partial x}}} \hfill \\ {\varepsilon_{y} = \frac{\partial \upsilon }{{\partial y}},\,\,\lambda_{yz} = \lambda_{zy} = \frac{\partial \upsilon }{{\partial z}} + \frac{\partial \omega }{{\partial y}}} \hfill \\ {\varepsilon_{z} = \frac{\partial \omega }{{\partial z}},\,\,\lambda_{zx} = \lambda_{xz} = \frac{\partial \omega }{{\partial x}} + \frac{\partial u}{{\partial z}}} \hfill \\ \end{array} } \right.$$
(2)
$$\varepsilon = A\sigma$$
(3)

According to the theory of elasticity, strain and stress can be expressed by physical equations as in Eq. 4, where E is the elastic modulus and μ is Poisson's ratio, Eq. 5 shows the relationship between the constants E, G and μ. Therefore, Eq. 4 can be transformed to obtain its matrix formula as in Eq. 6, where [B] is the elastic matrix.

$$\left\{ {\begin{array}{*{20}l} {\varepsilon_{x} = \frac{1}{E}\left[ {\sigma_{x} - \mu (\sigma_{y} + \sigma_{z} )} \right],\,\,\,\,\lambda_{xy} = \frac{{\tau_{xy} }}{G}} \hfill \\ {\varepsilon_{y} = \frac{1}{E}\left[ {\sigma_{y} - \mu (\sigma_{x} + \sigma_{z} )} \right],\,\,\,\,\lambda_{yz} = \frac{{\tau_{yz} }}{G}} \hfill \\ {\varepsilon_{z} = \frac{1}{E}\left[ {\sigma_{z} - \mu (\sigma_{x} + \sigma_{y} )} \right],\,\,\,\,\lambda_{zx} = \frac{{\tau_{zx} }}{G}} \hfill \\ \end{array} } \right.$$
(4)
$$G = \frac{E}{2(1 + \mu )}$$
(5)
$$\left[ \sigma \right] = \left[ B \right]\left[ \varepsilon \right]$$
(6)

5.1.4 Simulation results of palaeotectonic stress field

The study area’s paleotectonic stress field from the Indosinian and Yanshanian periods was simulated using the midas GTS software based on the established mathematical model. The spatial distribution of the stress field and the tectonic stress characteristics were systematically analysed based on the results of the numerical simulation of the tectonic stress field in the study area. The relationship between faults and mineralisation in the study area is analysed in accordance with the characteristics of the maximum principal stress and maximum shear stress distribution, and the fractures development under the affect of multi-stage tectonic stress fields is also discussed. The relationship between ore-forming fluids and structures is two important factors affecting the ore-forming process, the main driving force for ore-forming fluid migration and sedimentary ore forming is tectonic stress, by analysing the superposition of multiple tectonic stress fields, the migration and accumulation laws of ore-forming fluids can be inverted, and the metallogenic laws can be analyzed.

The minimum principal stress σ3, maximum shear stress τmax, and maximum principal stress σ1 distributions are primarily included in the simulation results of the tectonic stress field. The maximum shear stress controls the shear failure of rock to a large extent, and the fracture formation caused by rock failure mainly depends on the maximum principal stress. Therefore, according to the results of the stress field inversion, this section will concentrate on analysing the effects of the distribution characteristics of the maximum principal stress and the maximum shear stress on the diagenesis and mineralisation of the study area. We are able to identify the characteristics of the spatial distribution of ore deposits and calibrate advantageous metallogenic regions by inverting the accumulation law of ore-forming fluids.

5.1.5 Reliability validation of the inversion results

The analysis of the tectonic stress field is typically getting more difficult because it takes into account multiple tectonic movement stages, and reasonable results can only be obtained after multiple forward and inversion calculations (Wu et al. 2017). The inversion standard used in this study is the paleostress value obtained from acoustic emission test results, and the paleostress value of the core specimen is compared with the maximum principal stress at the core position in the finite element model. After many trial calculations, reasonable simulation results were obtained.

The simulation results of the Indosinian tectonic stress field in the study area (Fig. 11) show that the maximum principal stress values calculated at the sampling points of samples BY-1, BY-2 and BY-3 are between 143 and 149 MPa, which is close to the acoustic emission test's measured maximum principal stress value (139.59 MPa). The distribution of the maximum principal stress values calculated at the sampling points of samples P3M-1, P3M-2, and P3M-3 during the Yanshanian period is shown in Fig. 12 and ranges from 90 to 94 MPa, the consequence is fairly consistent with the acoustic emission test's maximum principal stress value (88.18 MPa). Meng et al. (2009) demonstrates that the numerical simulation findings are regarded as reliable when the relative error between the finite element calculation value and the experimental test value is within 20%. Therefore, the numerical simulation results of this study are reliable.

Fig. 11
figure 11

Distribution of maximum principal stress during Indosinian period in Lannigou gold deposit

Full size image
Fig. 12
figure 12

Distribution of maximum principal stress during Yanshanian period in Lannigou gold deposit

Full size image

5.2 Fracture distribution prediction method

The amount of brittleness a rock exhibits is primarily controlled by its mineral makeup. Mudstone, limestone, siltstone, and fine sandstone compose the majority of the lithology of the strata in the study area, these rocks contain more brittle minerals, such as calcite, quartz, feldspar, etc. (Fig. 13). Hence, the rock mass is readily fractured when subjected to tectonic stress. Tensile fracture and shear fracture are the two primary types of rock fracture that often occur when force is applied to the rock. Among them, the shear failure is mainly judged according to the Mohr–Coulomb shear failure criterion, and the tension failure is mainly judged by the Griffith rupture criterion. Therefore, the Griffith and Mohr–Coulomb criterion can be used to describe fractures, respectively.

Fig. 13
figure 13

Mineral composition and content distribution of rocks

Full size image

5.2.1 Mohr–Coulomb shear failure criterion

In accordance with the Mohr–Coulomb criterion, shear failure of rock along a specific section is related to both shear stress on the section and normal stress on the surface, that is, the interaction of normal stress and shear stress on a plane is what causes shear failure. Equation 7 can be used to express the Mohr–Coulomb shear failure criterion, where \(\tau\) is the rock shear strength (MPa); C is the cohesion (MPa); σ is the normal stress (MPa) and \(\phi\) is the internal friction angle (°).

$$\left| \tau \right| = C + \sigma \tan \phi$$
(7)

5.2.2 3D Griffith failure criterion

In 1921, Griffith put forward a strength theory for brittle material failure (Griffith 1921). According to theory, brittle material with numerous small, elliptical-shaped cracks will produce tangential tensile stress concentration around the cracks when subjected to the action of the stress field, when the tangential tensile stress reaches the material's molecular cohesive strength value and becomes highly concentrated somewhere near the end of the fracture periphery, at that point, brittle failure of the material will start to occur in a specific direction. When the 3D failure criterion expression of Griffith's strength theory is σ1 + 3σ3 ≥ 0, the failure criterion can be expressed as in Eq. 8. When σ1 + 3σ3 < 0, the failure criterion can be expressed as in Eq. 9, where σT represents the rock's tensile stress and σ1, σ2, σ3 represent the maximum, intermediate, and minimum principal stresses, respectively.

$$\begin{aligned} & \left( {\sigma_{1} - \sigma_{2} } \right)^{2} + \left( {\sigma_{2} - \sigma_{3} } \right)^{2} + \left( {\sigma_{1} - \sigma_{3} } \right)^{2} \\ & \quad + 24\left( {\sigma_{1} + \sigma_{2} + \sigma_{3} } \right)\sigma_{T} = 0 \\ \end{aligned}$$
(8)
$$\sigma_{3} + \sigma_{T} = 0$$
(9)

5.2.3 Determine the degree of fracture development

To determine the stress distribution of each geological unit, the tensile stress and shear stress of rock during tectonic movement can be calculated through the numerical simulation of a 3D tectonic stress field. By comparing it with the rock's shear and tensile strengths, it can be judged whether the rock is failure. The degree of rock fracture formation varies because of different physical characteristics and stress states of different geological bodies. Therefore, to facilitate computer processing and quantitative prediction analysis and calculation of fractures, the shear rupture rate In and tensile rupture rate It of fractures are introduced here, expressed as in Eqs. 10 and 11, where σT is the effective tensile stress (MPa); σt is the tensile strength of the rock (MPa); τn is the effective shear stress (MPa); and \(\tau\) is the shear strength of the rock (MPa). When \(I_{t} \ge 1\) or \(I_{n} \ge 1\), the rock is in failure.

$$I_{t} = \sigma_{T} /\sigma_{t}$$
(10)
$$I_{n} = \tau_{n} /\left| \tau \right|$$
(11)

However, in the study area, tensile fractures and shear fractures frequently occur simultaneously, and the two are in a symbiotic or associated relationship, and both tensile stress and shear stress are fully reflected in the failure mode of rock. Consequently, in order to more accurately quantify the degree of fracture development in the study area, a comprehensive rupture rate parameter was introduced, as expressed in Eq. 12, where, according to core observation, a and b represent the proportions of tension fractures and shear fractures, respectively.

$$I_{z} = aI_{t} + bI_{n}$$
(12)

According to the statistical results of core fractures, the ratio of the number of tension fractures to shear fractures in the study area is finally determined to be 6:4. When the Iz is larger, the comprehensive fracture rate value of the rock is higher, and the fracture degree is larger (Jiu et al. 2013). The development degree of formation fractures can be quantitatively assessed by examining the distribution characteristics of Iz on the plane.

6 Results and discussion

6.1 Numerical simulation results of multi-period tectonic stress field

The stress field of the Yanshanian period was superimposed on the Indosinian deformation to analyse the 3D tectonic stress field. The simulation results of the superimposition of the paleotectonic stress field in the study area (Fig. 14) show that the maximum principal stress (compression) ranges between 153.85 and 189.53 MPa, with a distribution closely related to the distribution of NE–SW and NW–SE faults. During the Indosinian and Yanshanian periods, the study area was impacted by tectonic stresses with NE–SW and NW–SE trends, respectively, and the maximum principal stress direction transitioned from NE to NW compression. Under the action of this composite tectonic stress, there are well-developed NW–SE trending and NE–SW trending fault structures in the study area. The NW–SE trending structures of the Yanshanian period transformed the ore bodies formed in the early stage, and the widely distributed fault structures provided a good ore-holding space for the migration of ore-bearing fluids and the enrichment and integration of ore in the study area. Because the direction of the maximum principal stress varied between the Indosinian and Yanshanian periods, the tectonic stress in the fault zone and the intersection of the faults has undergone a transition stage from compression to extension, forming a good decompression and expansion deformation zone. The rock masses in these areas are usually subjected to multiple periods of tectonic movements to make them more fragmented. Thus, joints are developed, which leads to obvious stress concentration, and the maximum principal stress is mainly distributed between 183.69 and 189.53 MPa. A metamorphic interaction with the surrounding rock happens to generate ore bodies when ore-bearing hydrothermal fluid migrates in fissures and joints. Particularly, the areas along the fissures are more mineralized in the surrounding rock, such as pyrite mineralization, quartz mineralization, etc. Simultaneously, the vein-like orebodies developed along the fault fracture zone, indicating that the output form of the orebodies is controlled by the fault structure. The mineralization occurred in the tectonic transition period from Indosinian compressional orogeny to Yanshanian extensional transition, which is consistent with previous research conclusions (Chen et al. 2007).

Fig. 14
figure 14

The maximum principal stress distribution in the study area after superposition

Full size image

The study area’s maximum shear stress distribution, as shown in Fig. 15, ranges between 83.53 and 98.42 MPa after superimposition. Near the fault zone and where the faults intersect, there is a clear concentration of shear stress, because of the Yanshanian tectonic movement's superimposed modification of the Indosinian tectonic stress field, when the shear strength of the rock is less than the stress strength in the area where the shear stress is concentrated, it will cause the rock to failure, resulting in the expansion space with large porosity and permeability. The movement of hydrothermal fluids bearing ore is greatly facilitated by a favourable expansion space, after the ore-bearing fluid migrates to the expansion space, the volume expands. Due to the influence of multi-stage tectonic movements, the surrounding rock will be squeezed twice, which will further increase the expansion space. Then, the state of ore-bearing hydrothermal fluids in the expansion space will change from migration to enrichment, which will lead to the formation of large-scale ore bodies. Multiple tectonic movements promote the superimposed metallization of gold. It is worth mentioning that in the northeastern part of the study area, due to the complex lithological conditions, an obvious shear stress change gradient zone has occurred in this area, which makes the rock strata deform strongly, resulting in an increase in rock porosity, thus forming a good expansion space. The interbedded zones formed between different lithologies are favorable ore-hosting sites, which is consistent with the metallogenic facts in the study area, that is to say, the ore bodies in the study area are mainly distributed in the favorable lithological combination of sandstone and claystone in the lower part of the Bianyang Formation, and the interbedded zone is usually rich in grade and good in mineral content (Luo 1993). There are gold displays in different strata in the study area, and the gold-bearing horizons are relatively wide, the NW, NE, SN and NWW directions all have ore body production or gold mineralization, indicating that the mineralization has the characteristics of multi-phase; 8 major faults in the N–S, NE–SW, and NW–SE trends control the ore bodies in the study area, and the ore-bearing hydrothermal fluids take these 8 faults as the main ore-conducting channels. The secondary structures formed along the high shear stress concentration area after the up-invasion migrate, and the ore is enriched in the areas with ore-accommodating and ore-storing conditions, such as the interlayer fissure zone and the fault-fracture zone. To sum up, the author believes that the interbedded zone (intersection of strata) of two different types of lithology, the shear stress concentration area near 8 major faults in the area and the intersection of faults, and the shear stress variation gradient zone formed by the difference of fault distribution and lithology may have high metallogenic potential, which can be used as a favorable position for demarcating the target area.

Fig. 15
figure 15

Maximum shear stress distribution in the study area after superposition

Full size image

6.2 Quantitative prediction of fractures distribution

Combining the aforementioned criteria for rock failure with the results of the numerical simulation of the superimposed tectonic deformation of the Indosinian and Yanshanian periods, a comprehensive rock fracture rate parameter Iz was constructed to quantitatively predict the development of fractures in the study area. Through the data extraction and processing of the numerical simulation results of the tectonic stress field, combined with Eqs. 10–12, the distribution characteristics of the comprehensive fracture value Iz in the study area can be calculated. Due to the study area's complicated stratigraphic distribution and highly developed structures, which are criss-crossed, the distribution of fractures in 3D space lacks intuitiveness and appears very scattered. To show the distribution of fractures more clearly, and to better classify the development of fractures, the section of the study area was cut in the form of a vertical overall structural framework (X, Y, Z), and a total of 14 sections were cut in the study area, as shown in Figs 16, 17, 18.

Fig. 16
figure 16

Fracture distribution in the study area after the superposition of Indosinian and Yanshanian periods (from west to east)

Full size image
Fig. 17
figure 17

Fracture distribution in the study area after the superposition of Indosinian and Yanshanian periods (from south to north)

Full size image
Fig. 18
figure 18

Fracture distribution in the study area after the superposition of Indosinian and Yanshanian periods (from top to bottom)

Full size image

It can be seen from Figs 16, 17, 18 that the comprehensive fracture value Iz is distributed between 0.35 and 1.74. The area where fractures may occur can be predicted by the value of Iz, so as to find possible fluid flow paths, it provides reference for the delineation of favorable metallogenic areas. Previous studies have shown that the development degree of fractures can be quantified according to the value of the fracture development index I, which can usually be divided into the following four grades: that is, the undeveloped fracture area (0 < I < 0.4), the slightly developed fracture area (0.4 < I < 0.8), the more developed fracture area (0.8 < I < 1.2), and the developed fracture area (I > 1.2) (Ding et al. 2013; Li 2014). Referring to this standard classification of fracture development degree, this study divides the fracture development degree in the study area into 4 grades. The integrated rupture value Iz of the interior of the fault zone, the intersection of different fault zones and the turning point of the fault zone is relatively large, and its values are all above 1.2, indicating that the fractures are developed. In the fault zone and the edge area of the intersection of the fault zone, the comprehensive rupture value Iz at the end of the fault zone is between 0.8 and 1.2, which is the area with relatively developed fractures. In the deep central and western parts of the study area and the shallow areas in the northeastern part of the study area, due to the relatively single lithology (most of which are Xuman Formation strata), the comprehensive fracture value Iz is between 0.4 and 0.8, indicating that the fractures are slightly developed. Since the transition area of adjacent fault zones is divided by faults, the elastic energy stored in the rock layers is partially released, the rock formation is less affected by tectonic stress, and its rock mass has a low degree of fracture, resulting in a small comprehensive fracture value Iz, which is mostly below 0.4, which belongs to the underdeveloped fracture area.

It is obvious that 8 major faults in the NE–SW, N–S, and NW–SE trends control the fracture development degree and the fractures distribution in the study area, the secondary structures formed along the high shear stress concentration area after the up-invasion migrate, and the ore is enriched in the areas with ore-accommodating and ore-storing conditions, such as the interlayer fissure zone and the fault-fracture zone. This understanding is consistent with previous research conclusions, that is, the Lannigou gold deposit has typical structural ore-controlling characteristics (Chen et al. 2011). Through the comparative analysis of the distribution of known ore bodies and the distribution of fracture development index Iz in the study area, it is believed that the distribution of ore bodies and fault structures are closely related, the prospecting potential in the relatively developed and fracture development areas is considered to be very large. It is recommended to select the fracture development area and the relatively developed area for the next key prospecting area.

7 Conclusions

  1. (1)

    By systematically analysing and processing the geological data of the study area, a comprehensive database of multiple information was constructed; a 3D geological model of the study area was established based on the GOCAD 3D geological software platform, and the GOCAD 3D geological entity model was converted into midas GTS geometric model through 3D point cloud reverse engineering, which realizes the accurate description of the geometric model of the study area.

  2. (2)

    Based on the analysis of regional tectonic evolution history, geological interpretation, rock mechanics experiment and acoustic emission test results, the paleostress field is inverted using the finite element method (FEM) while taking into account multi-stage tectonic superposition; The results show that the maximum principal stress value in the study area after superposition is mainly distributed between 153.85 and 189.53 MPa, and the maximum shear stress ranges from 83.53 to 98.42 MPa, and its distribution characteristics are mainly affected by the faults spatial distribution. At the end of the fault, the intersection of the fault, and the area around the fault zone, different levels of stress concentration occurred, and the stress level was significant, while the stress value between the faults was relatively low.

  3. (3)

    On the basis of tectonic stress field simulation, combined with rock failure criterion, the fracture development zone (Iz > 1.2) in the study area is primarily distributed in the interior of the fault zone, in accordance with the results of fracture distribution prediction, the intersection of different fault zones and the turning point of the fault zone. The area with more developed fractures (0.8 < Iz < 1.2) is mainly distributed in the fault zone and the edge area of the intersection of the fault zone. The slightly developed fracture areas (0.4 < Iz < 0.8) are mainly distributed in the deep central and western parts of the study area and the shallow areas in the northeastern part. Additionally, the transition zone between adjacent fault zones is where the underdeveloped fracture zone (Iz < 0.4) is generally found. The fractures development degree and the fractures distribution are controlled by major faults. It is recommended to select fracture development areas and relatively developed areas for key prospecting areas in the future.

  4. (4)

    The translation of the 3D geological model of the study area to the geomechanical model is made achievable by the combined modelling technique of the GOCAD software and midas GTS software; and a set of comprehensive fracture distribution prediction techniques for the superposition of multi-stage tectonic stress fields in deposits of complex tectonic zones has been developed.