Modelling of fatigue damage in granitic rock by piezoelectric effect in quartz phase due to alternating current excitation

Abstract

This paper considers numerical modelling of hypothetical fatigue damage in granitic rock by alternating current (AC) excitation of piezoelectric properties of Quartz. For this end, a numerical method consisting of a rock mineral mesostructure model, an implicit time stepping scheme to solve the piezoelectro-mechanical problem, and a fatigue damage model was developed. The rock material was assumed to be heterogenous linear elastic and isotropic, save the Quartz piezoelectric properties, which are anisotropic. An evolution equation-based continuum scalar damage model based on an evolving back stress tensor and a moving Drucker–Prager type of endurance surface was applied to compute the damage inflicted by the AC excitation. The damage was computed in a post-processed mode, i.e., un-coupled to the material model, at this stage of investigations. Some preliminary axisymmetric simulations are presented with a rock mesotructure based on electron backscatter diffraction data. These simulations corroborate the hypothesis that fatigue damage can be induced on granitic rock by converse piezoelectric effect in the Quartz phase by sinusoidal alternating current. More specifically, fatigue damage was induced on a disc-shaped numerical rock sample at a voltage of 15 kV with 2.5 kHz of frequency.

Article highlights

• An EBSD data-based rock mesostructure description using polygonal finite elements to model the grain behaviour was developed.

• An evolution equation-based fatigue damage model accurately predicting typical S–N curve for rock was developed.

• A hypothesis of inducing fatigue damage on Quartz bearing rock by converse piezoelectric effect was numerically confirmed.

1 Introduction

Low energy efficiency and excessive tool wear are the major cost-incurring problems in comminution and excavation of rocks and ores (Klein et al. 2018; Sefiu et al. 2020). For this reason, new energy efficient methods are presently being intensively searched. One such, albeit still hypothetical, method uses high-voltage and high-frequency alternating current (HV-HF-AC) excitation of piezoelectric properties of Quartz in granite to induce damage by the converse piezoelectric effect. The rationale behind this idea is that while only Quartz is a piezoelectric mineral in, e.g., granite rock, the permittivity of the granite forming minerals (Quartz, Feldspars and Micas) are of similar magnitude. Therefore, it might be possible to actuate the Quartz phase in granite by converse piezoelectric effect and thus induce cracks to Quartz itself and the surrounding Feldspar and Mica phases by electric current. It should, however, be reminded that in the natural Quartz bearing rocks, as aggregates of different minerals and grains, the piezoelectric effect is at least two orders of magnitude weaker than that of a single Quartz crystal (Parkhomenko 1971; Bishop 1981).

Notwithstanding, Saksala (2021) demonstrated by numerical simulations that cracks can be induced on cylindrical rock samples made of granite by sinusoidal AC excitation at the frequency of ~ 100 kHz and the amplitude of ~ 10 kV. The fracture mechanism is probably related to the resonance phenomenon appearing in forced vibration of the sample, i.e. the frequency of the excitation needs to match one of the natural frequencies of the sample.

Unfortunately, such frequencies may be difficult to reach in practice. However, it is postulated here that damage can still be inflicted on Quartz bearing rocks by the converse piezoelectric effect using lower frequencies, which do not trigger the resonance of the sample but, when coupled with a high voltage, cause damage by fatigue mechanisms. In fact, there exist, as already mentioned by Saksala (2021), some unpublished experimental work carried out at Sintef, Norway (Novel concept… 2021), where granite samples were exposed to sinusoidal AC excitation at a voltage of ~ 10 kV with frequencies varying from 50 to 2.5 kHz. The treated samples were subjected to the Sievers minidrill test (an abrasive rotary drilling test (Dahl et al. 2007)), and it was found that the drillability of the treated samples improved by 20–50% compared to untreated samples. As there were millions of loading cycles in these tests, fatigue seems a plausible mechanism for the improvement of the drillability. Moreover, rocks do show fatigue phenomena akin to metals with the endurance limit being 60–90% of the tensile strength (Cerfontaine and Collin 2018; Liu and Dai 2021).

In this paper, we will test this hypothesis numerically. For this end, a FEM-based numerical method consisting of a rock mesostucture model, an implicit time stepping scheme to solve the piezoelectro-mechanical problem, and a continuum fatigue damage model was developed. At this scale of modelling, homogenization techniques are inappropriate, as granite forming minerals have different mechanical properties. Thereby, the numerical rock is assumed to be linear elastic, heterogenous but isotropic material consisting of Quartz, Feldspars and Biotite, while the mineral texture with the mechanical properties is generated with the open source Matlab code MTEX (Mainprice et al. 2014; Bachmann et al. 2011). However, the Quartz piezoelectric properties are taken, as they truly are, anisotropic. As to the damage model, an evolution equation-based continuum damage approach based on the evolving back stress tensor and moving Drucker-Prager type of endurance surface, by Ottosen et al. (2008), is applied to compute the damage inflicted by the AC excitation. The damage is computed as post-processed, i.e. uncoupled to the material model, at this stage of investigations.

It should finally be emphasized that this paper is of theoretical-speculative nature, i.e. we do not present any experiments to validate the simulations. Instead, by way of numerical modelling, we provide a possible mechanism behind the observed improvement in the drillability of the treated samples discussed above. Thereby, we hope this work spurs further experimental work either to falsify or to corroborate the present hypothesis of piezoelectrically induced fatigue damage in granite by AC excitation. Finally, we note that we cannot replicate the Sievers minidrill results with the present choice of axisymmetric modelling.

2 Numerical methods

2.1 Strong form of the governing piezolectro-mechanical problem

The problem of a rock sample exposed to alternating current excitation is governed by the linear elastic piezoelectro-mechanical problem. For a body ${\Omega } \in {\mathbb{R}}^{3}$, the relevant equations can be written (in tensor index form) as

$$\rho \ddot{u}_{i} - \sigma_{ij,j} - f_{i}^{B} = 0$$

(1)

$$D_{i,i} - \varrho = 0$$

(2)

where $\sigma_{ij}$, $f_{i}^{B}$, $\rho$ and $\ddot{u}_{i}$ denote, respectively, the stress tensor, the body force, the density of the material and the acceleration, while $D_{i}$ is the electric flux density and $\varrho$ is the electric charge. Equations (1) and (2) are the balance of linear momentum electrostatic equilibrium, respectively. The corresponding constitutive equations for a piezoelectric material are

$$\sigma_{ij} = { }C_{ijkl} \varepsilon_{kl} - e_{kij} E_{k}$$

(3)

$$D_{i} = e_{ikl} \varepsilon_{kl} - \in_{ij} E_{k}$$

(4)

where $C_{ijkl}$ is the elasticity tensor, $\varepsilon_{kl}$ is the mechanical strain tensor, $e_{kij}$ is the piezoelectric coupling tensor, $E_{k}$ is the electric field, and $\in_{ij}$ is the dielectric constants tensor. The electric field is given by the gradient of the scalar electric potential $\phi$: $E_{i} = - \nabla \phi_{,i}$. Equations (3) and (4) describe the behavior of a piezoelectric material under the combined effect of the mechanical strain ($\varepsilon_{kl}$) and the electric field ($E_{k}$). For a more detailed treatment of piezoelectric phenomena in rocks, the reader is referred to Parkhomenko (1971).

Exposing a material to electric current may also generate heat due to the Joule effect (Ohmic heating). As rocks are poor electric conductors, this effect is expected to be negligible. This appears indeed to be the case for granite, as shown in Appendix, where the temperature rise due to Ohmic heating in a numerical granite sample exposed to 500 cycles of sinusoidal AC current with 30 kV of voltage and 2.5 kHz of frequency is only 0.05 °C.

2.2 Finite element discretized piezoelectro-mechanical problem and its solution

The weak, finite element discretized form of the governing Eqs. (1) and (2) can be presented as (Allik and Hughes 1970)

$${\mathbf{M}}\ddot{{\mathbf{u}}}_{{t + {\Delta }t}} +{\mathbf{C}}\dot{{\mathbf{u}}}_{{t + {\Delta }t}} +{\mathbf{K}}_{u} {\mathbf{u}}_{{t + {\Delta }}} +{\mathbf{K}}_{u{{\phi}} } {\varvec{\phi}}_{{t + {\Delta }t}} = 0$$

(5)

$${\mathbf{K}}_{\phi u} {\mathbf{u}}_{{t + {\Delta }t}} + {\mathbf{K}}_{\phi } {\varvec{\phi}}_{{t + {\Delta }t}} = 0\quad {\text{with}}$$

(6)

$${\mathbf{M}} = {\mathbf{A}}_{e = 1}^{{N_{e} }} \mathop \int \limits_{{{\Omega }_{e} }} {\mathbf{N}}_{u}^{e,T} {\mathbf{N}}_{u}^{e} d{\Omega },\quad {\mathbf{C}} = \alpha {\mathbf{M}},\quad {\mathbf{K}}_{u} = {\mathbf{A}}_{e = 1}^{{N_{e} }} \mathop \int \limits_{{{\Omega }_{e} }} {\mathbf{B}}_{u}^{e,T} {\mathbf{C}}_{e} {\mathbf{B}}_{u}^{e} d{\Omega }$$

(7)

$${\mathbf{K}}_{\phi } = {\mathbf{A}}_{e = 1}^{{N_{e} }} \mathop \int \limits_{{{\Omega }_{e} }} {\mathbf{B}}_{\phi }^{e,T} {\varvec{\upvarepsilon}}{\mathbf{B}}_{\phi }^{e} d{\Omega },\quad {\mathbf{K}}_{u\phi } = {\mathbf{A}}_{e = 1}^{{N_{e} }} \mathop \int \limits_{{{\Omega }_{e} }} {\mathbf{B}}_{u}^{e,T} {\mathbf{eB}}_{\phi }^{e} d{\Omega },\quad {\mathbf{K}}_{\phi u} = {\mathbf{K}}_{u\phi }^{T}$$

(8)

where the symbol meanings are as follows: M is the consistent mass matrix; K_u is the stiffness matrix; C is the material damping matrix and α is a coefficient; $\ddot{{\mathbf{u}}},\dot{{\mathbf{u}}},\mathbf{u}$ are the acceleration, velocity and displacement vectors, respectively; ${\varvec{\phi}}$ is the electric potential vector; ${\varvec{\upvarepsilon}}=\varepsilon \mathbf{I}$ is the (diagonal) dielectric constants matrix; $\mathbf{e}=\mathbf{d}{\mathbf{C}}_{\mathrm{e}}$ is the piezoelectric coupling matrix with d being the piezoelectric constants matrix and C_e the elasticity matrix; A is the standard finite element assembly operator; ${\mathbf{N}}_{\mathrm{u}}^{\mathrm{e}}$ and ${\mathbf{B}}_{\mathrm{u}}^{\mathrm{e}}$ are the displacement interpolation matrix and the kinematic matrix (mapping the nodal displacement into element strains); ${\mathbf{N}}_{\upphi }^{\mathrm{e}}$ and ${\mathbf{B}}_{\upphi }^{\mathrm{e}}$ are the electric potential interpolation matrix and its gradient.

It should be noted that there are no forcing or loading terms in the balance Eqs. (5) and (6) as the loading comes from the essential boundary conditions, which are specified at a part of the model boundary. This problem is solved with a staggered implicit time marching based on the Newmark scheme applied here in the case of the unconditionally stable midpoint rule, i.e. β = 1/4, γ = 1/2. Thereby, the solution of the problem defined by Eqs. (5) and (6) is as follows:

$$\begin{aligned} & {\text{Predict: }}\;\;{\mathbf{u}}_{t +\Delta t}^{{*}} = {\mathbf{u}}_{t} + {\Delta }t{\dot{{\mathbf{u}}}}_{t} + \frac{1}{2}{\Delta }t^{2} \left( \left({1 - 2\beta } \right){{\ddot{{\mathbf{u}}}}_{t} } \right) \\ &{\text{Solve:}}\;\;{\mathbf{K}}_{\phi u} {\mathbf{u}}_{t + \Delta t}^{{*}} + {\mathbf{K}}_{\phi } \phi_{t + \Delta t} = 0 \to \phi_{{t + {\Delta }t}} \\ & {\text{Set:}}\;\;{\tilde{\mathbf{M}}} = {\mathbf{M}} + {\Delta }t\gamma {\mathbf{C}} + {\Delta }t^{2} \beta {\mathbf{K}}_{u} \\ & \quad \quad {\mathbf{F}}_{{{\text{tot}}}} = -{\mathbf{K}}_{{{\text{u}}\phi }} \phi_{{t + {\Delta }t}} -{\mathbf{C}}\left( {{\dot{{\mathbf{u}}}}_{t} + \left( {1 - \gamma }\right){\Delta }t{{\ddot{{\mathbf{u}}}}}_{t} } \right) -{\mathbf{K}}_{{\text{u}}} \left( {{\mathbf{u}}_{t} + {\Delta }t{\dot{{\mathbf{u}}}}_{t} + \left( {\frac{1}{2} - 2\beta }\right){\Delta }t^{2} {{\ddot{{\mathbf{u}}}}}_{t} } \right) \\ &{\text{Solve: }}\;\;{{\tilde{{\mathbf{M}}}\ddot{{\mathbf{u}}}}}_{{t + {\Delta }t}} = {\mathbf{F}}_{{{\text{tot}}}} \to {{\ddot{{\mathbf{u}}}}}_{{t + {\Delta }t}} \\ &{\text{Predict}}\;{\text{and}}\;{\text{correct:}}\;\;{\dot{{\mathbf{u}}}}_{{t + {\Delta }t}} = {\dot{{\mathbf{u}}}}_{t} + {\Delta }t\left( {\left({1 - \gamma } \right){{\ddot{{\mathbf{u}}}}}_{t} + \gamma {{\ddot{{\mathbf{u}}}}}_{{t + {\Delta }t}} } \right) \\ & \quad \quad \quad \quad \quad \quad \quad \quad \;\;{\mathbf{u}}_{{t +{\Delta }t}} = {\mathbf{u}}_{t + \Delta t}^{{*}} + {\Delta }t^{2} \beta {{\ddot{{\mathbf{u}}}}}_{{t + {\Delta }t}} \\\end{aligned}$$

When solving for $\mathbf{\phi}_{{t + {\Delta }t}}$, the system needs to be partitioned into inactive and active degrees of freedom, which are solved, while the inactive ones are defined as the positive and negative (ground) electrodes on the model boundaries. Finally, the constitutive Eq. (3) is written here in form ${\varvec{\upsigma}}={\mathbf{C}}_{\mathrm{e}}:({\varvec{\upvarepsilon}}-\mathbf{d}\mathbf{E})$, where ε is the strain and E is the electric field given as a gradient of the potential, i.e $\mathbf{E}=-\nabla \phi$.

2.3 Rock mesostructure description with polygonal elements

At this preliminary stage of the present research project, proper EBSD data on the granite of interest. i.e. Kuru grey, was not available. Therefore, we use the example data on Mylonite (from Western Gneiss Province, Norway) coming with the MTEX Matlab code (Mainprice et al. 2014; Bachmann et al. 2011). This rock consists of Andesine, Orthoclase, Quartz, and Biotite minerals. As Andesine and Orthoclase belong to the group of Feldspars, this rock can be used for present purposes of demonstration instead of granite. Figure 1a shows the piece of MTEX data used to generate the numerical rock in Fig. 1b, where Andesine and Orthoclase are combined to represent Feldspar. The size of the specimen is roughly the same as that in the experiments mentioned in Introduction.

Fig. 1

Numerical rock mesostructure 1: a EBSD example data 1 for Mylonite from MTEX; b axisymmetric polygonal finite element mesh (1960 polygons, 3 = Quartz, 2 = Feldspar, 1 = Biotite); c Weibull distributed tensile strength distribution; d map of Quartz grain orientations

The numerical rock in Fig. 1b was generated from the EBSD data by taking grain centroids as a seed data for the PolyMesher code by Talischi et al. (2012a), which generates Voronoi tessellations. The numerical rock in Fig. 1b thus consists of centroidal convex polygons that represent the rock grains in the finite element method sense. Two iterations with the Lloyd’s algorithm (Talischi et al. 2012a) were also carried out on the EBSD data piece in order to achieve a more regular mesh. It should be noted that these polygons are themselves finite elements so that there is no need to mesh the mesotexture therein. Moreover, the EBSD plot in Fig. 1a has been magnified substantially to get the laboratory sample scale mesotexture in Fig. 1b.

The Matlab implementation of the polygonal finite elements by Talischi et al. (2012b) was employed here. The formulation therein uses the standard isoparametric mapping from a reference element to the physical element, as illustrated in Fig. 2.

Fig. 2

Polygonal finite element: a illustration of the triangular areas used in the definition of Wachspress shape function, and the triangulation of the reference regular polygon with three integration points in each triangle; b iso-parametric mapping to a physical element

The specific interpolation functions used here are the barycentric Wachspress shape functions, which at node i of a reference n-gon reads

$$N_{i} \left( {\varvec{\xi}} \right) = \frac{{\alpha_{i} \left( {\varvec{\xi}} \right)}}{{\sum_{j = 1}^{n} \alpha_{j} \left( {\varvec{\xi}} \right)}},\quad \alpha_{i} \left( {\varvec{\xi}} \right) = \frac{{A\left( {{\varvec{p}}_{i - 1} ,{\varvec{p}}_{i} ,{\varvec{p}}_{i + 1} } \right)}}{{A\left( {{\varvec{p}}_{i - 1} ,{\varvec{p}}_{i} ,{\varvec{\xi}}} \right)A\left( {{\varvec{p}}_{i} ,{\varvec{p}}_{i + 1} ,{\varvec{\xi}}} \right)}}$$

(9)

where A(a, b, c) is the signed area of triangle a, b, c (Fig. 2a). A sub-divison of the reference polygon into triangles and applying a three-point quadrature for each triangle (resulting 3n integration points for each n-gon) was applied as the numerical integration (Fig. 2b).

The rock material is described as isotropic but heterogeneous. However, the anisotropy of the piezoelectric properties for Quartz is retained. The piezoelectric properties of the Quartz grains are rotated to the global coordinate system by the Euler angles data provided with the EBSD data. The heterogeneity is described by assigning each mineral phases with the mineral specific material properties. Moreover, the Weibull distribution is applied on the tensile strength of the minerals to obtain more variation on the rock strength. The rationale behind this is as follows: the reported tensile strength for a rock is an average value measured for a laboratory specimen, while, at the material point level, the tensile strength varies, in addition to being different for each mineral phase, from virtually zero for a microdefect to couple of tens of megapascals for a sound grain/crystal. As the present method does not account for material defects explicitly, it seems that the Weibull distribution is an appropriate way to account for these local weaknesses.

The approach by Tang (1997) was followed here. Accordingly, the 3-parameter Weibull distribution

$$\Pr ({\text{x}}) = 1 - \exp \left( { - \left( {\frac{{x - x_{u} }}{{x_{0} }}} \right)^{{m_{w} }} } \right)$$

(10)

where m_w is the shape parameter that can be interpreted as a homogeneity index in the present context. Moreover, the scale parameter x₀ can be taken as the measured average value of a material property, and the location parameter x_u specifies the lower bound of a material property. Equation (10) was used to generate spatially heterogeneous strength distribution for each numerical mineral as follows. First, a random number, Pr(x) in (10), uniformly distributed between 0 and 1 was generated for each element in the mesh representing the mineral phase. Then, the value for the strength, x, was solved from Eq. (10), see an example in Fig. 1c representing the tensile strength distribution with the parameters x₀ = 10, 8, 7 MPa for Quartz, Feldspar, Biotite, respectively, and m_w = 3, x_u = 0 for each mineral. In this realization, the maximum and minimum values of the tensile strength are 20.3 and 0.49 MPa.

2.4 Continuum fatigue damage model

The isotropic continuum fatigue damage model by Ottosen et al. (2008), originally developed for metals in high cycle fatigue regime, is applied to predict possible fatigue damage in the numerical rock in Fig. 1 under piezoelectric excitation. The model is based on a moving endurance surface, shown in Fig. 3, which, along with evolution laws for a damage variable and a back stress tensor, traces the damage accumulated during cyclic loading. The model components are:

$$\beta = \frac{1}{{\sigma_{{{\text{so}}}} }}\left( {\sigma_{{{\text{eff}}}} + AI_{1} - \sigma_{{{\text{so}}}} } \right),\quad \beta \ge 0,\quad \dot{\beta } \ge 0$$

(11)

$$\sigma_{{{\text{eff}}}} = \sqrt {\frac{3}{2}\left( {{\mathbf{s}} - {{\varvec{\upalpha}}}} \right):\left( {{\mathbf{s}} - {{\varvec{\upalpha}}}} \right)} ,\quad {\mathbf{s}} = {{\varvec{\upsigma}}} - \frac{1}{3}I_{1} {\mathbf{I}},\quad I_{1} = {\text{tr}}\left( {{\varvec{\upsigma}}} \right)$$

(12)

$${\dot{\mathbf{\alpha }}} = C\left( {{\mathbf{s}} - {{\varvec{\upalpha}}}} \right)\dot{\beta },\quad \dot{D} = K\exp (L\hat{\beta })\dot{\beta },\quad \hat{\beta } = \beta /\left( {1 - \tanh (\xi I_{1} /\sigma_{t} } \right))$$

(13)

Fig. 3

a The concept of moving endurance surface in the deviatoric plane with the evolution conditions for D and α; b endurance limit in the Haigh-diagram

The symbols in (11)–(13) are as follows: β is the endurance surface; ${\sigma }_{\text{so}},{\sigma }_{\text{eff}},{\sigma }_{\mathrm{t}}$ are the endurance limit of the material, the effective (von Mises) stress, and the tensile strength, respectively; $\mathbf{s},{\varvec{\upalpha}},{\varvec{\upsigma}}$ are the deviatoric stress, the back stress, and the stress tensor, respectively; ${I}_{1}\text{ and }\mathbf{I}$ are the first invariant of the stress tensor and the identity tensor, respectively; D is the damage variable; A, C, K, L, and ξ are parameters to be determined based on experimental data. The Eqs. (11)–(13) can be readily solved with a suitable time integrator. Equation (13) shows the evolution equations for the damage variable and the back stress. The original evolution law for the damage variable was modified by adding the term containing the hyperbolic tangent function ($\widehat{\beta }\equiv \beta$ in the original) to better match the fatigue data for rocks in the low cycle regime.

Figure 3a illustrates the conditions for damage and back stress evolution, i.e. the loading–unloading conditions, while Fig. 3b illustrates the endurance surface in the Haigh-diagram. Obviously, the parameter A controls the effect of the mean stress on the fatigue limit.

It should be noted that rocks are highly sensitive to the loading rate, i.e. frequency, under cyclic loading (Cerfontaine and Collin 2018; Liu and Dai 2021). However, this feature is not taken into account by the present model. Moreover, before moving on to the calibration of the model parameters, a justification for the choice of the Ottosen et al. fatigue damage model is briefly addressed. First, the Ottosen et al. model is phenomenological, i.e. it is not derived from the fatigue micromechanisms. The present approach is also phenomenological from the fatigue mechanism point of view, i.e., we will calibrate the model by identifying the model parameters so that the material point level model matches the fatigue data for rocks measured at the laboratory sample size level. Second, Ottosen et al. (2008) develop their model for materials for which endurance limits exist. As demonstrated by Cerfontaine and Collin (2018) and Liu and Dai (2021), different rocks have endurance limits. Therefore, the usage of the Ottosen et al. approach is justified at this preliminary level of study.

2.5 Calibration of the damage model parameters

The fatigue damage model has four parameters to be determined based on experimental data. Parameter A can be obtained from the Haigh diagram, as illustrated in Fig. 3b. The rest of the parameters, C, K, L, and ξ, can be obtained by an optimization process described in Ottosen et al. (2008). The indentified parameter values are:

$$A = 0.1,\quad C = 0.2,\quad K = 1 \times 10^{ - 7} ,\quad L = 38,\quad \xi = 1.75$$

(14)

The performance of these values is illustrated in Fig. 4 against experimental data collected by Cerfontaine and Collin (2018). In this data, the endurance limit is set to 70% of the tensile strength, i.e., σ_0e = 0.7σ_t. It should be admitted that some guess work had to be done to reach the values of the parameters matching the rock data. Namely, since no good data on the effect of mean stress were found in the literature, the parameter A was adjusted in the estimation starting from the value 0.225 obtained for a steel by Ottosen et al. (2008).

Fig. 4

S–N curve for rock: prediction with the present model vs experiments (regenerated from (Cerfontaine and Collin 2018) by visual inspection and digitalization)

It is finally noted that the parameter values in Eq. (14) are strictly speaking valid at the laboratory sample level behavior. Here they are, however, used at the material point (Gauss point) level with the damage fatigue model presented above. This means that the rock constituent minerals are assumed to behave identically with respect to fatigue damage. However, the elasticity properties are mineral specific (see Sect. 3.1), and the local endurance limit is, as noted, set to 70% of the local (grain level) tensile strength, which in turn is Weibull distributed, as shown in Fig. 1c. It should finally be admitted that the fatigue behavior is probably not identical for each mineral, as assumed here. Nevertheless, it is an appropriate first assumption at this preliminary level of research, being in line with the assumption of isotropic linear elastic behavior of each mineral. In a more advanced, mineral specific fatigue model, the mineral anisotropy should also be included.

2.6 Material properties and model parameters

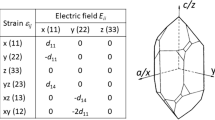
The material properties for the numerical granite are listed in Table 1. The elasticity moduli are generated with the MTEX software (Mainprice et al. 2014), and the rest of the parameters are from Mahabadi (2012). In the present axisymmetric conditions, the matrix of piezoelectric constants in Eq. (8) becomes

$${\mathbf{d}}^{q} = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {d_{11} } & 0 & {\begin{array}{*{20}c} 0 & { - d_{11} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} 0 & 0 & { - 2d_{11} } & 0 \\ \end{array} } \\ \end{array} } \right)$$

(15)

where d₁₁ is given in Table 1. Matrix d gives the piezoelectric constants in the local crystal coordinate system, which in the present finite element context is the local element coordinate system. Therefore, matrix (15) needs to be rotated to the global coordinates with the Euler angles data given by the Mylonite example data, as mentioned above.

Table 1 Material properties for simulations (ε₀ = 8.854E−12 F/m)

The dielectric constants in Table 1 are given relative to the permittivity of vacuum ε₀.

3 Numerical results and discussion

3.1 Piezoelectric actuation of rock: direct current voltage

First, a direct current (DC) loading is applied on the numerical rock in Fig. 1. The left vertical edge of the rock sample is the axis of rotational symmetry while the electrode configuration is shown in Fig. 5a. A voltage (ϕ₀) of 100 kV was applied at the positive electrode. The radius of the positive electrode is 75% of the rock sample radius (R_ϕ/R = 0.75), while the dimensions of the numerical rock can be read in Fig. 1. This setup is chosen to prevent the plasma channel formation in the air instead of rock during possible future experimental verification of these simulations. However, the air surrounding the model setup was ignored.

Fig. 5

Simulation results with the DC voltage: a model setup and boundary conditions; b normalized potential field (voltage); c magnitude of electric field; d first principal stress field

The simulation results in Fig. 5b–d show that the 100 kV voltage induces tensile tresses exceeding 5 MPa at many locations in the rock. The maximum was 9.4 MPa at a location close to the edge of the positive electrode, where the electric field magnitude has the maximum value due to the boundary effect. While this stress clearly exceeds the tensile strength of Feldspar and Biotite, the voltage required to produce it being so large, may not be practical. Moreover, the electric breakdown strength of granite is 100–150 kV/cm, which means that, as the thickness of the sample is only 8 mm, a plasma channel could be formed in the sample. Therefore, we changed the loading to AC excitation with a substantially lower voltage.

3.2 Piezoelectric actuation of rock: alternating current excitation

3.2.1 Effect of excitation voltage

Sinusoidal excitation is applied at the positive electrode. As mentioned, the fatigue damage model is implemented as uncoupled to the constitutive equation. However, the damage update, i.e., the solution of the model (11)–(13), is performed at each time step. The frequency of the sinusoidal excitation is first set to 2500 Hz while the amplitude voltage is varied. The time step is chosen so that 50 sampling points are taken for a single cycle of the sinusoidal excitation. The simulation results for damage fields and effective stresses (Eq. (12)) are shown in Fig. 6.

Fig. 6

Simulation results for damage (after 300 cycles) and effective stress (at the crest of the first cycle) with the AC voltage (f = 2500 Hz): a ϕ₀ = 15 kV; b ϕ₀ = 30 kV; c ϕ₀ = 60 kV

The results demonstrate that the fatigue damage initiate at the very localized zone (Fig. 6a) for this specific numerical rock when the excitation voltage amplitude is 15 kV. The maximum effective stress induced by this amplitude of excitation is ~ 1 MPa, which means that the sample response is well within the elastic regime. However, due to the Weibull distributed tensile strength and thus the fatigue limit, it was enough to initiate fatigue damage, which reaches its maximum value of 0.1667 after couple of tens of cycles. It should be mentioned that this stabilization of the damage evolution to a constant value under a constant amplitude loading is a characteristic property of the present evolution equation-based fatigue damage model (Ottosen et al. 2008). This follows from the relationship between the back stress tensor and the moving endurance surface evolutions in Eq. (13) (see also Fig. 3a).

When the amplitude of the excitation increases, the damage induced naturally increases as well. At the level of ϕ₀ = 60 kV, the damage, plotted here at mesh nodes as averaged from the surrounding Gauss points, reaches 1 at the edge of the potential (voltage) boundary condition, where the electric field magnitude has a high value.

3.2.2 Effect of excitation frequency

Possible effects of the frequency of the excitation are also tested. The amplitude of the excitation is set to 30 kV. The simulation results with frequencies 250 Hz and 25 kHz are shown in Fig. 7.

Fig. 7

Simulation results for damage (after 300 cycles) with the AC voltage (ϕ₀ = 30 kV): a f = 250 Hz; b f = 25 kHz

Comparison to Fig. 6b confirms that decreasing or increasing the excitation frequency by one order of magnitude has no notable effect on the simulation results. It should be noted that the maximum frequency used here, 25 kHz, is four times smaller than that leading to cracking by resonance effects in the 3D numerical study by Saksala (2021). Moreover, the present axisymmetric setting cannot reproduce the eigen mode obtained therein since it was not axisymmetric. This means that inertia played a negligible role in these simulations.

3.2.3 Effects of Weibull distributed tensile strength

As the Weibull distribution of the numerical rock in Fig. 1 is random, it surely has an effect. Thereby, two additional Weibull distributed tensile strength fields, in Fig. 8, were generated and tested.

Fig. 8

Simulation results for damage (after 300 cycles) with the AC voltage (ϕ₀ = 30 kV, f = 2500 Hz): a damage field with Weibull distributed tensile strength 2; b damage field with Weibull distributed tensile strength 3

The simulation results for the damage fields are shown in Fig. 8. The values of damage are similar to those in Fig. 6b obtained with the Weibull distributed tensile strength in Fig. 1. However, the location of damage spots differs as the Weibull distributed tensile strength is spatially heterogeneous.

3.2.4 Effects of EBSD data

The final simulation involves testing another sample from the Mylonite EBSD data in MTEX software. The numerical rock and the sample are shown in Fig. 9. As the sample data therein is not very extensive, some overlapping occurs between numerical rocks in Figs. 1 and 9. However, here we use the centroids of the grains generated by MTEX software and feed them to PolyMesher software to obtain the mesostructure in Fig. 9b without applying the Lloyd’s algorithm. The mesh is thus more random and closer to the grain plot in Fig. 9a than the corresponding mesh in Fig. 1.

Fig. 9

Numerical rock mesostructure 2: a EBSD example data 2 for Mylonite from MTEX; b axisymmetric polygonal finite element mesh (1863 polygons, 3 = Quartz, 2 = Feldspar, 1 = Biotite); c Weibull distributed tensile strength field; d map of Quartz grain orientations

One simulation with ϕ₀ = 30 kV and f = 2500 Hz is carried out on this numerical rock.

The damage pattern with the numerical rock sample in Fig. 10 exhibits similar values than that with the numerical rock in Fig. 1 albeit with different details, i.e. the locations of damage differ with the maximum value, 0.5, occurring at the lower edge this time. Interestingly, there is no damage at position on the upper edge where the voltage BC has the jump. In any case, it can be concluded that, at this level of excitation voltage, fatigue damage can be induced on granitic rocks by converse piezoelectric AC excitation.

Fig. 10

Simulation results with numerical rock 2 for damage (after 500 cycles) and effective stress (at the crest of the first cycle) with the AC voltage (ϕ₀ = 30 kV, f = 2500 Hz): a damage field; b effective stress field

4 Conclusions

A novel numerical method to predict fatigue damage in a granitic rock due to piezoelectric excitation of the quartz mineral phase by alternating current was presented and applied in this paper. Following conclusions can be drawn:

• The developed EBSD data-based rock mesostructure description does not need a conventional finite element mesher, since the mineral grain phase map from MTEX software was converted to a polygonal finite element mesh using Voronoi tessellations. However, as the original grain texture gets distorted in this process to some extent, the virtual element method, enabling virtually arbitrary element shape, should be employed in future.

• In the rock heterogeneity description, the mineral phases were explicitly modelled based on the EBSD data but the grain boundaries within a single phase were ignored. Rock microdefects were considered as a Weibull distributed tensile strength field. This method gives the model some reality, but it requires a proper method to determine the Weibull distribution parameters.

• The modified evolution equation-based fatigue damage model for rock accurately predicts typical S–N curve for rock both in low and high cycle regimes, while the original model was developed for metals in the high cycle regime only. However, a systematic parameter calibration model should be developed in the future considerations.

• The hypothesis that fatigue damage can be induced on granitic rock by converse piezoelectric effect in the quartz phase by sinusoidal alternating current excitation can be cautiously confirmed based on the simulations presented. Namely, fatigue damage was induced on a disc-shaped numerical rock sample at a voltage of 15 kV. This voltage is far below the electric breakdown strength of granite, which is ~ 100 kV in the present case of sample size.

• At a higher excitation voltage of 30 kV, considerable damage was induced on two different numerical samples. Similar values of damage with locally differing patterns were observed irrespective of the numerical sample, i.e. the mesostructure and the Weibull distributed tensile and fatigue strength. Moreover, the damage patterns were independent of the excitation frequency in the present axisymmetric conditions.

Finally, three further research topics are mentioned. First, the fatigue damage model was applied in the post-processing mode, i.e. uncoupled to the rock constitutive model. As this is not appropriate under excessive damaging, a coupled approach should be considered. Second, rock fatigue phenomenon is highly rate sensitive, which should be taken into account in the next version of the model. Third, the present study considered only the axisymmetric idealization while the real rocks do not exhibit axisymmetry due to heterogeneities. Therefore, a 3D version of the present study should be carried out. Moreover, the 3D version would enable to numerically replicate the Sievers drillability tests.

Appendix

The Joule (Ohmic) heating effect is numerically studied here in case of numerical rock sample in Fig. 1. The coupled equations system governing the initial/boundary value problem of Joule heating consists of the piezoelectric balance Eq. (6), with u ≡ 0, i.e., ignoring mechanical effects, and the heat equation (Fukushima et al. 2022; Kovaleva et al. 2021)

$$\rho c\dot{\theta } = - \nabla \cdot {\mathbf{q}} + Q_{{\text{J}}} , \; Q_{{\text{J}}} = \frac{1}{2}\omega \varepsilon_{0} \varepsilon {\text{tan}}\delta \left\| {\mathbf{E}} \right\|^{2} ,\;\; {\text{tan}}\delta = \frac{{\omega \varepsilon^{\prime \prime } + \sigma }}{\omega \varepsilon }$$

(16)

where the symbol meanings are as follows; $\rho$ and c are the density and the specific heat capacity of the material; $\dot{\theta }$ is the rate of change of temperature; q is the heat flux vector related to temperature gradient $\nabla \theta$ and the conductivity k by the Fourier’s law $\mathbf{q}=-k\nabla \theta$; ${Q}_{\mathrm{J}}$ is the heat source term consisting of the electro-magnetic dissipation; $\omega =2\uppi f$ is the circular frequency with f being the frequency of the excitation; $\mathrm{tan}\delta$ is the dielectric loss tangent with electric conductivity $\sigma$ and loss factor ${\varepsilon}^{{\prime}{\prime}}$. The loss factors for the minerals are 0.014, 0.118 and 0.456 for Quartz, Feldspar and Biotite, respectively (Pressacco et al. 2023). Moreover, the electric conductivities are 1 × 10^–11 S/m, 1 × 10^–14 S/m and 1 × 10^–6 S/m for Quartz, Feldspar and Biotite, respectively (Fukushima et al. 2022). The specific heat capacities for Quartz, Feldspar and Biotite are 730 J/kgK, 730 J/kgK, and 770 J/kgK, respectively, while the thermal conductivities for the same minerals are 4.94 W/mK, 2.34 W/mK, and 3.14 W/mK, respectively. The rest of the material parameters can be found in Table 1.

The simulation results for the electric field strength and temperature rise after 500 cycles of sinusoidal AC current with 30 kV of voltage and 2.5 kHz of frequency are shown in Fig. 

Fig. 11

Temperature rise due to Joule heating after 500 cycles (ϕ₀ = 30 kV, f = 2500 Hz): a electric field strength; b temperature rise

11.

The maximum temperature is only 0.05 °C, which means that temperature effects are insignificant in the present application.